An Improved Set-Membership Proportionate Adaptive Algorithm for a Block-Sparse System
Abstract
:1. Introduction
2. Review of Corresponding Algorithms
2.1. The PNLMS Algorithm
2.2. Review of the SM Principle and Corresponding Algorithm
3. The New BS-SMPNLMS and BS-SMIPNLMS Algorithms
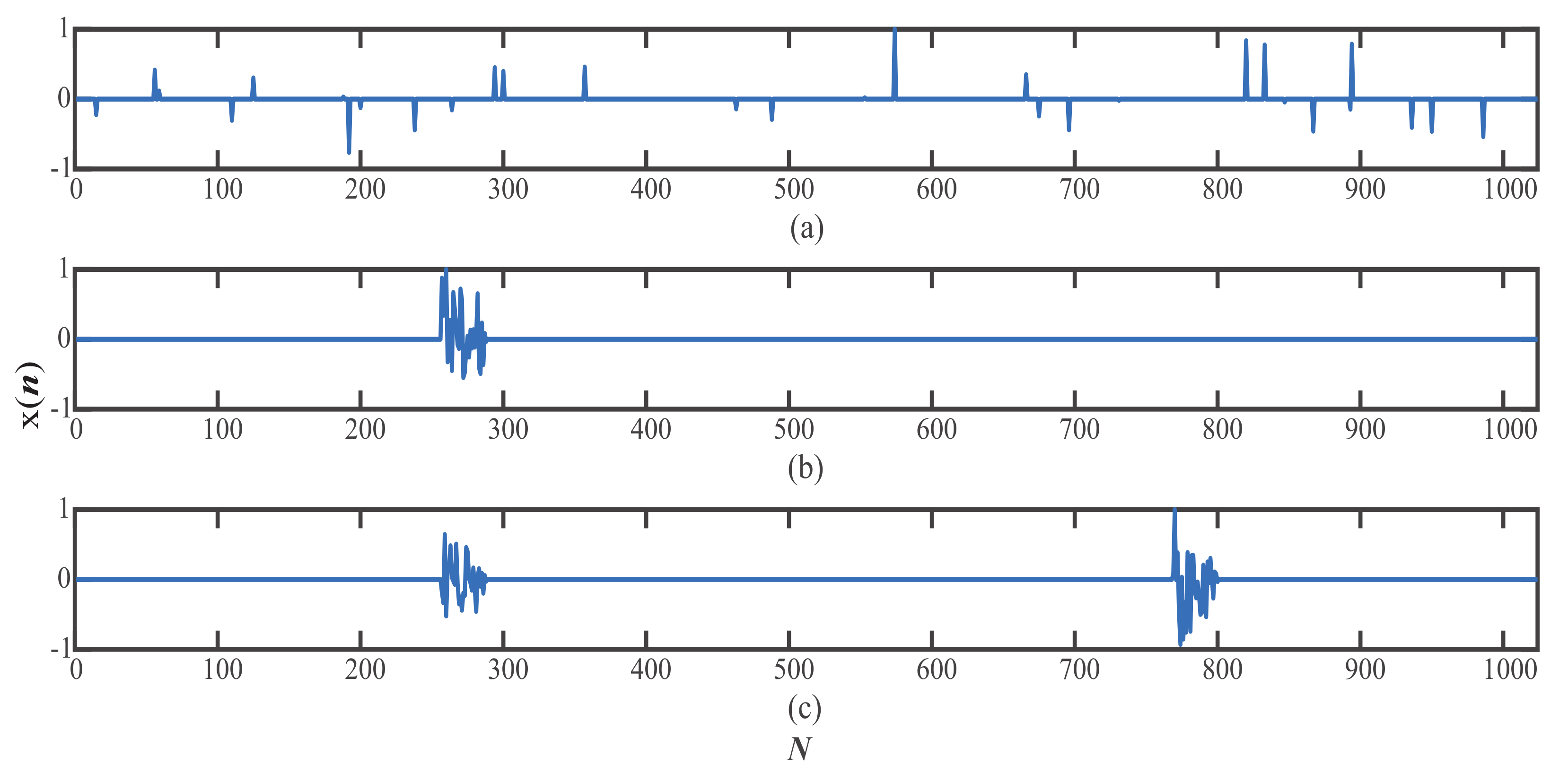
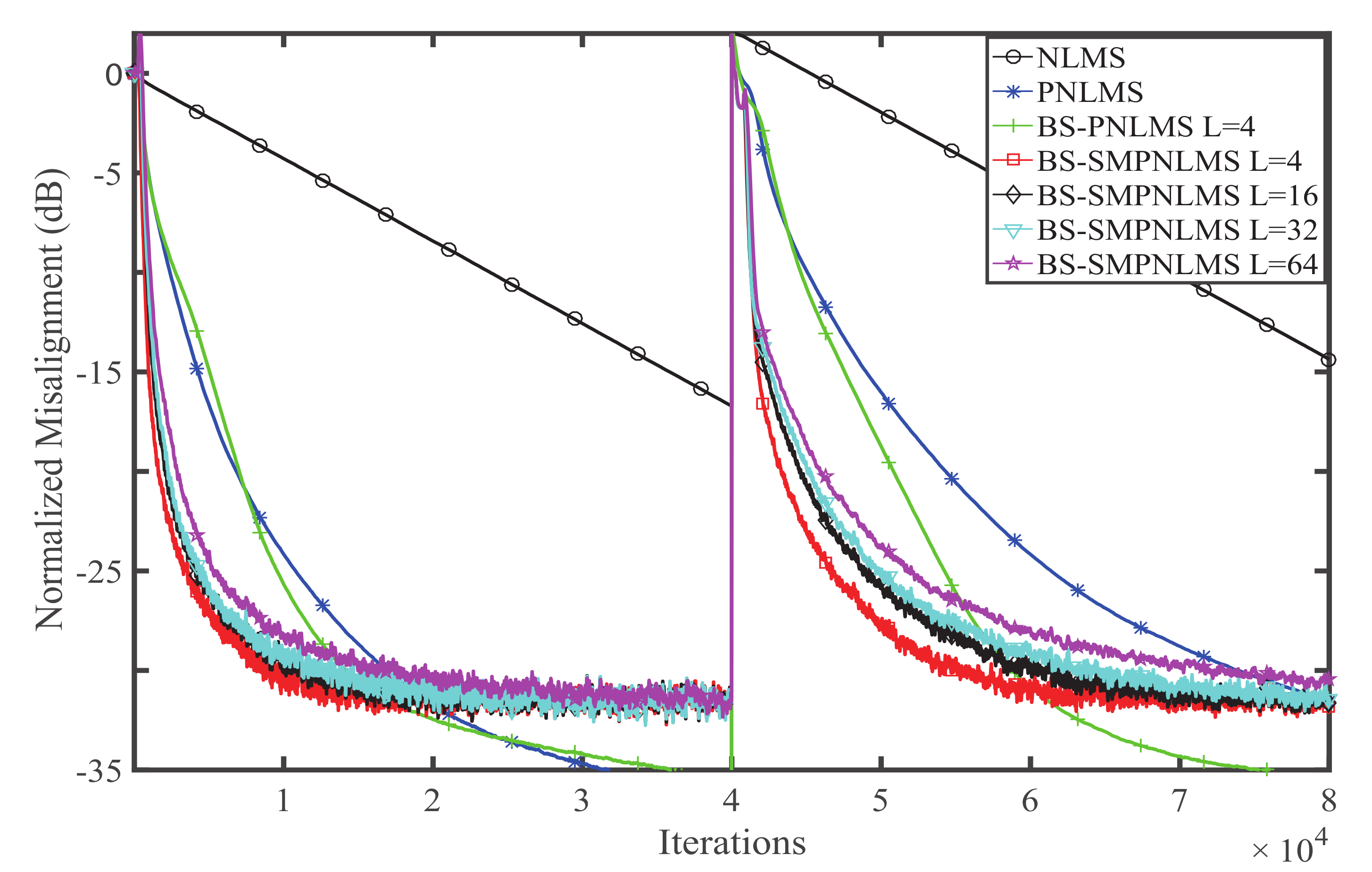
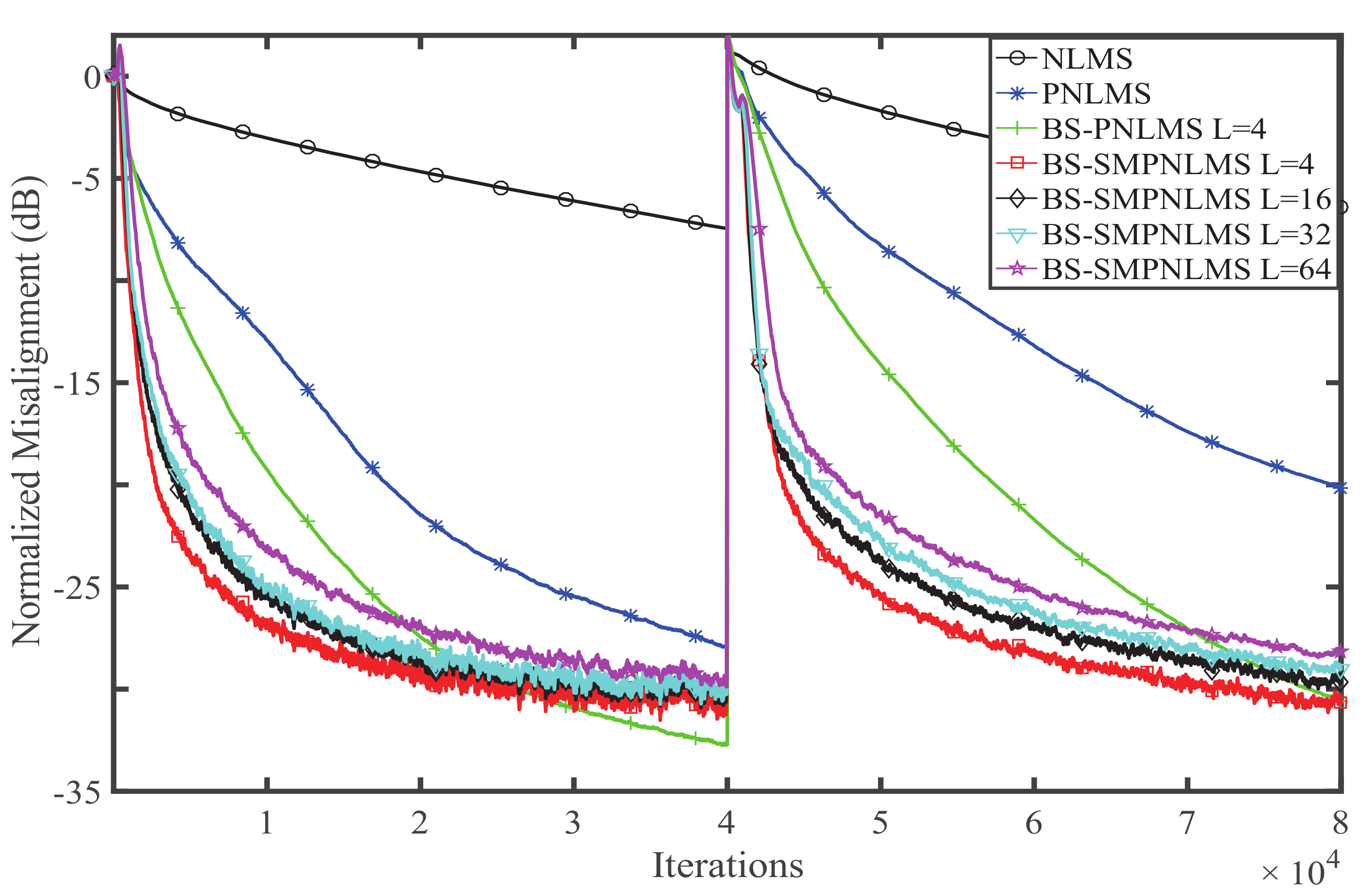
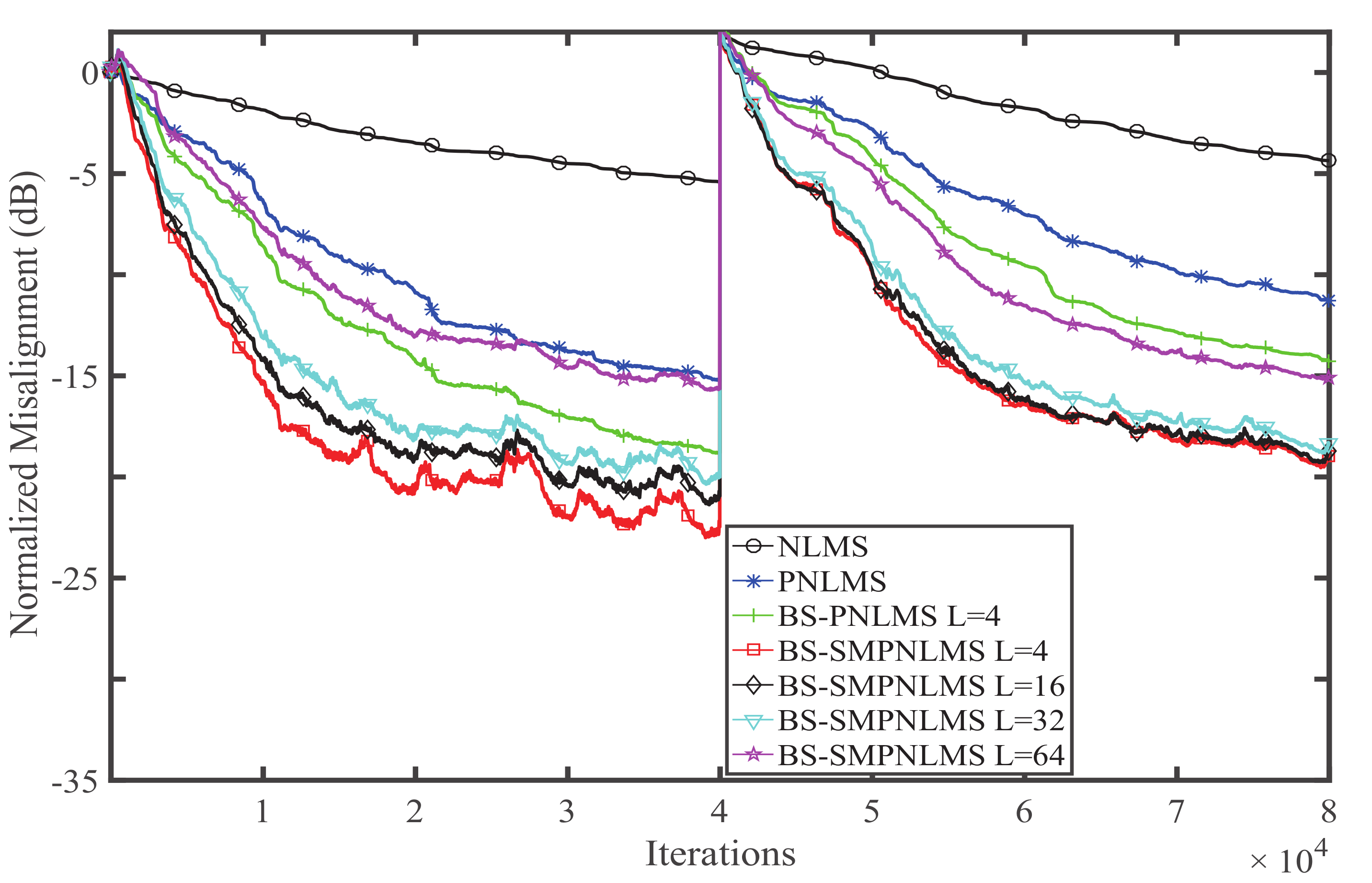
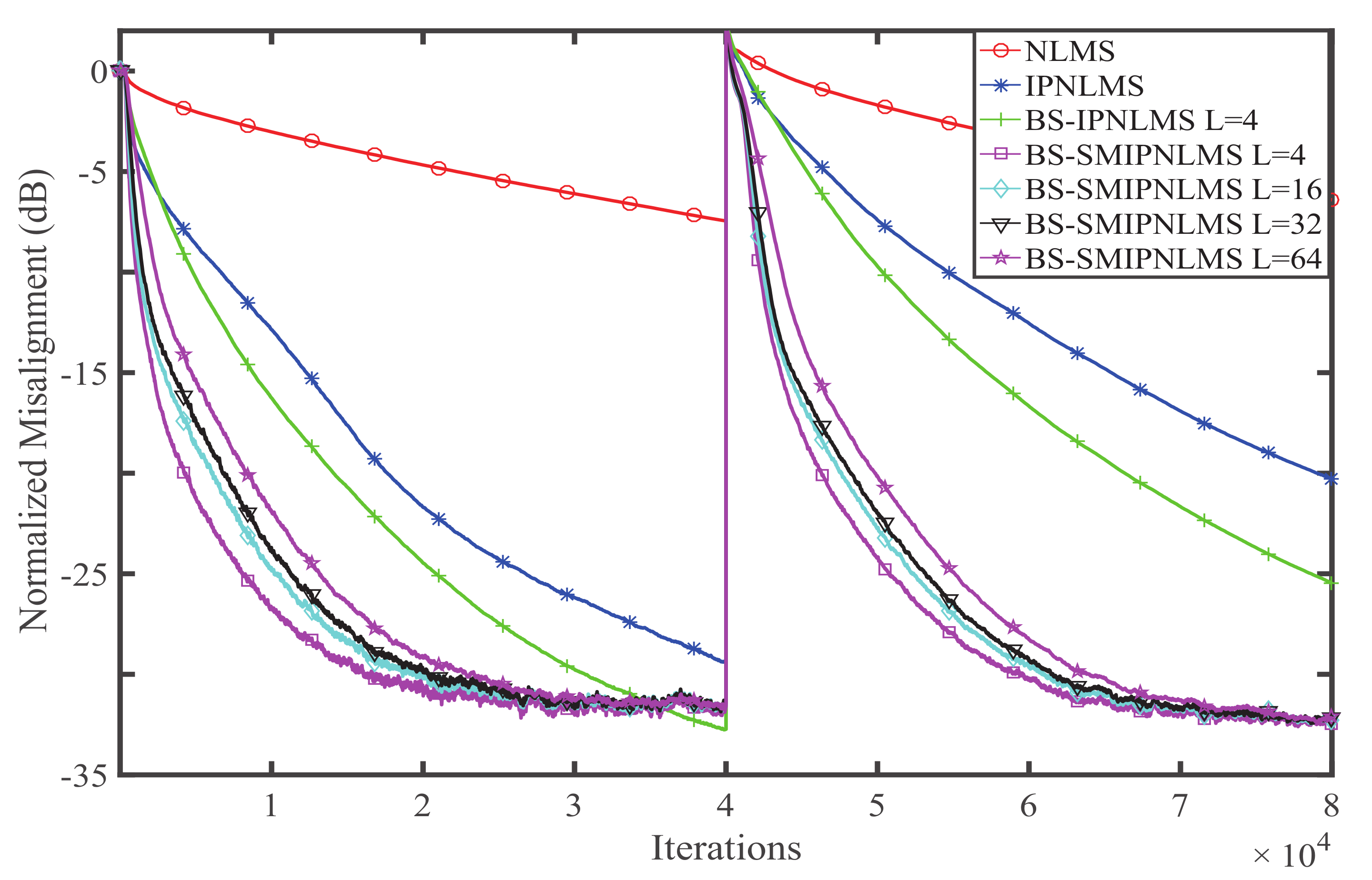
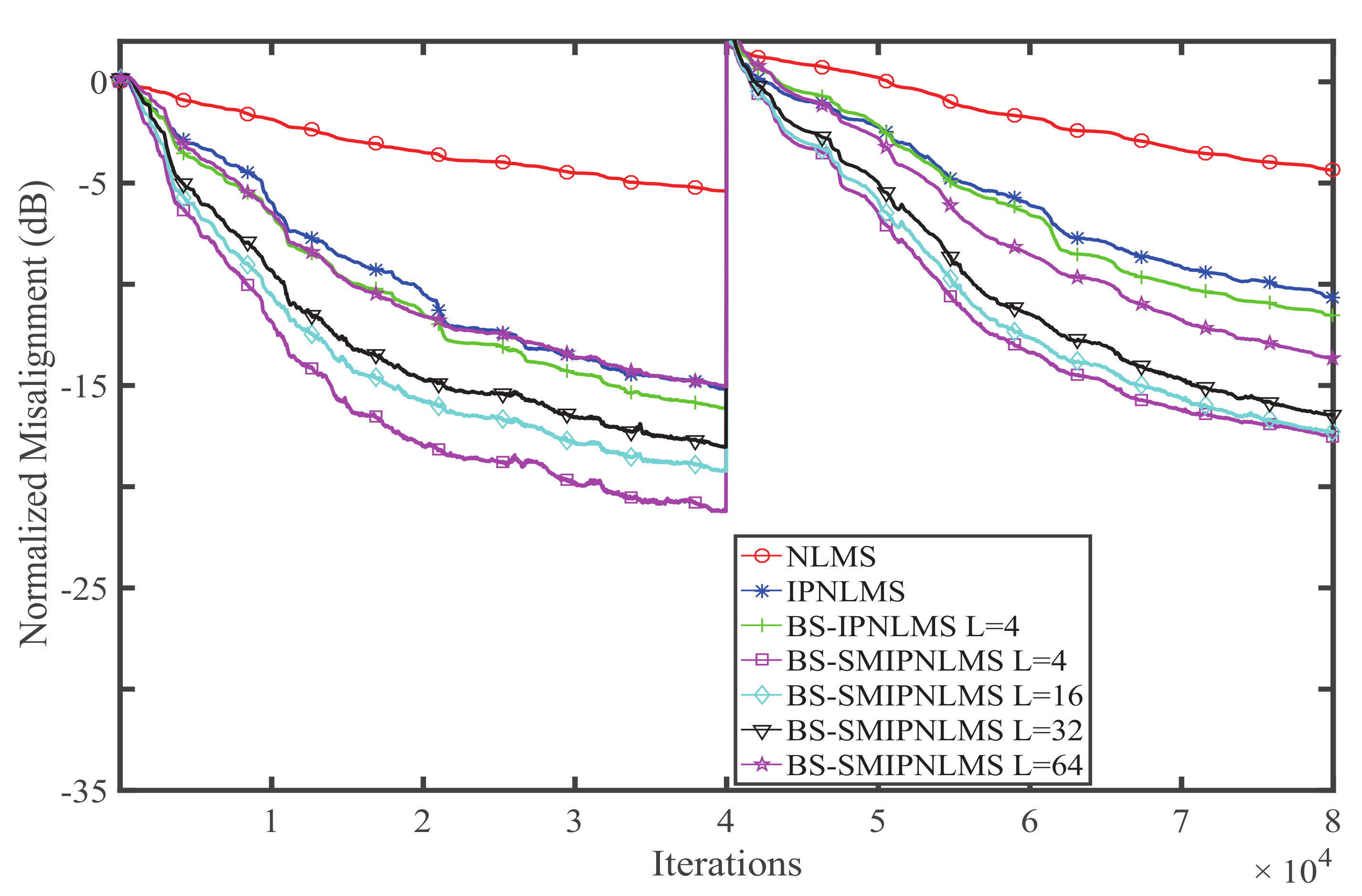
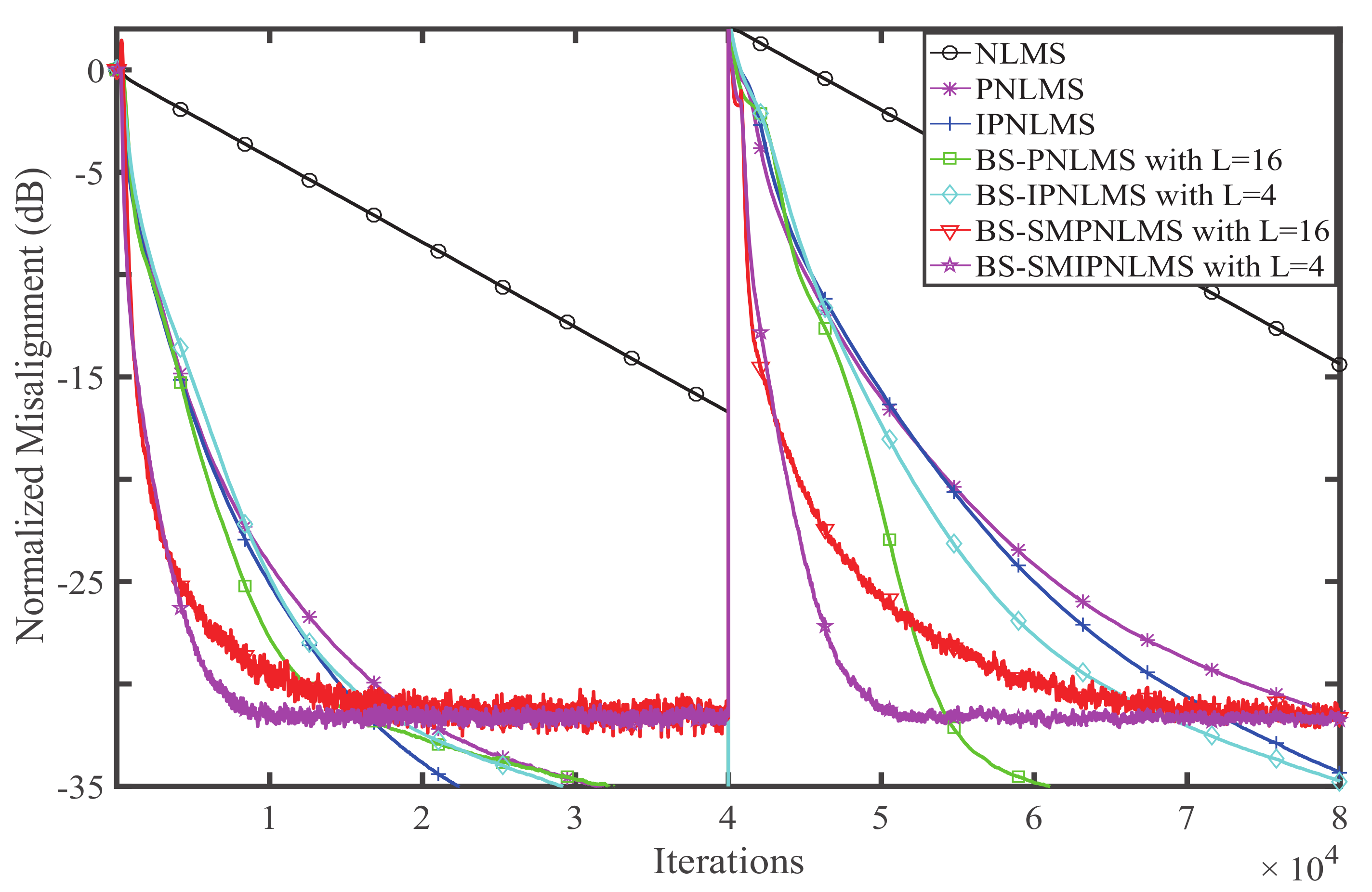
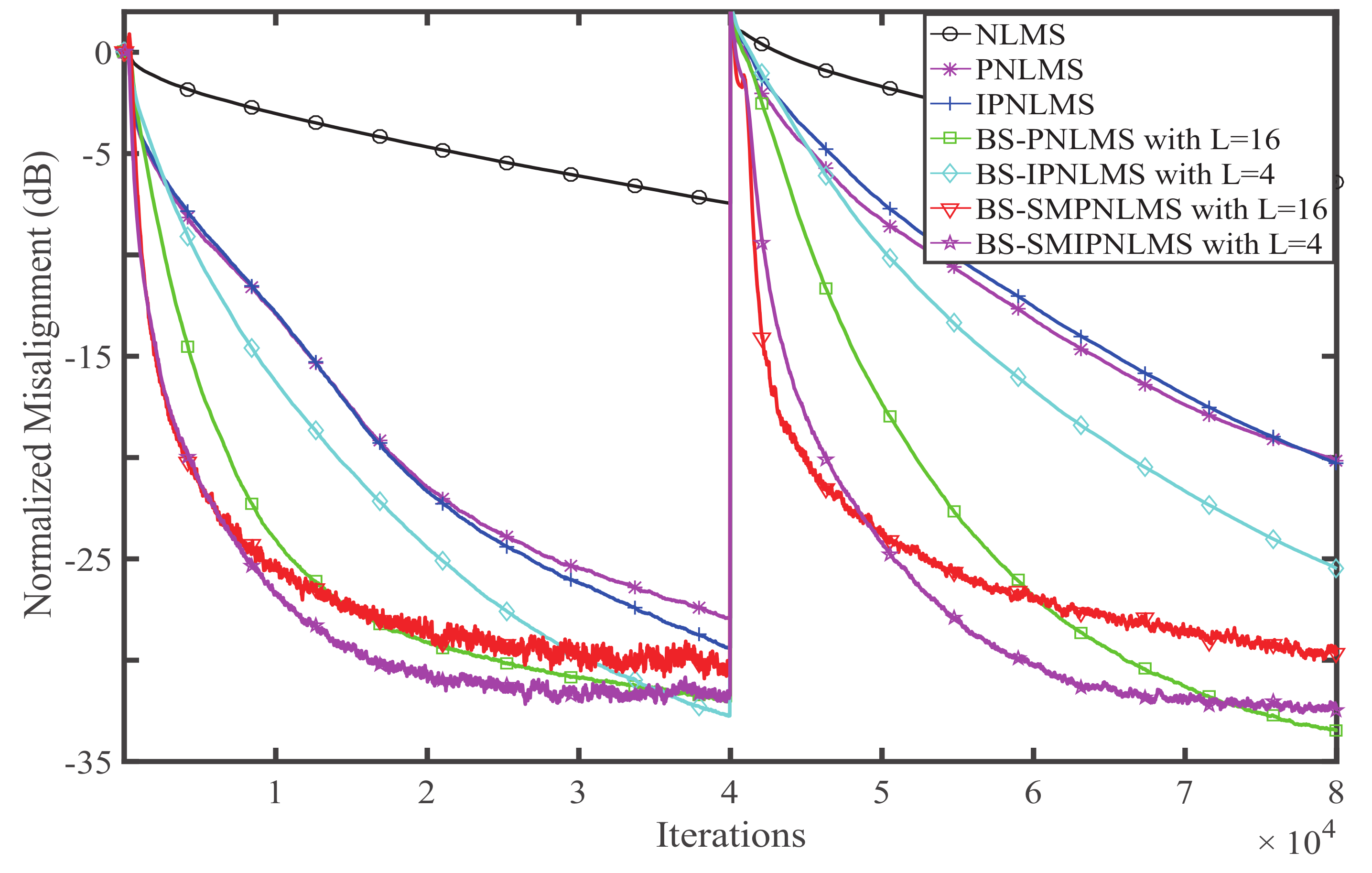
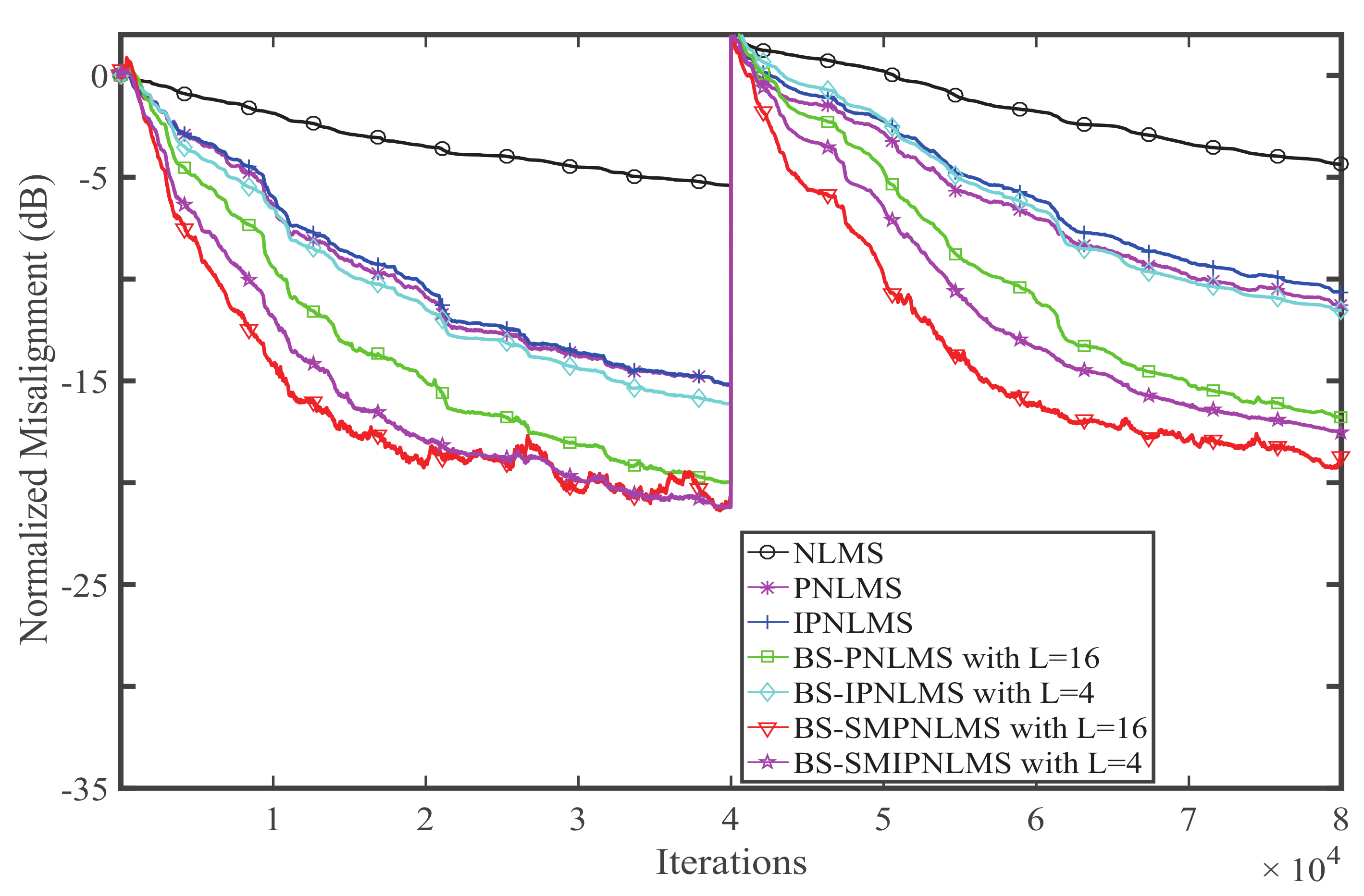
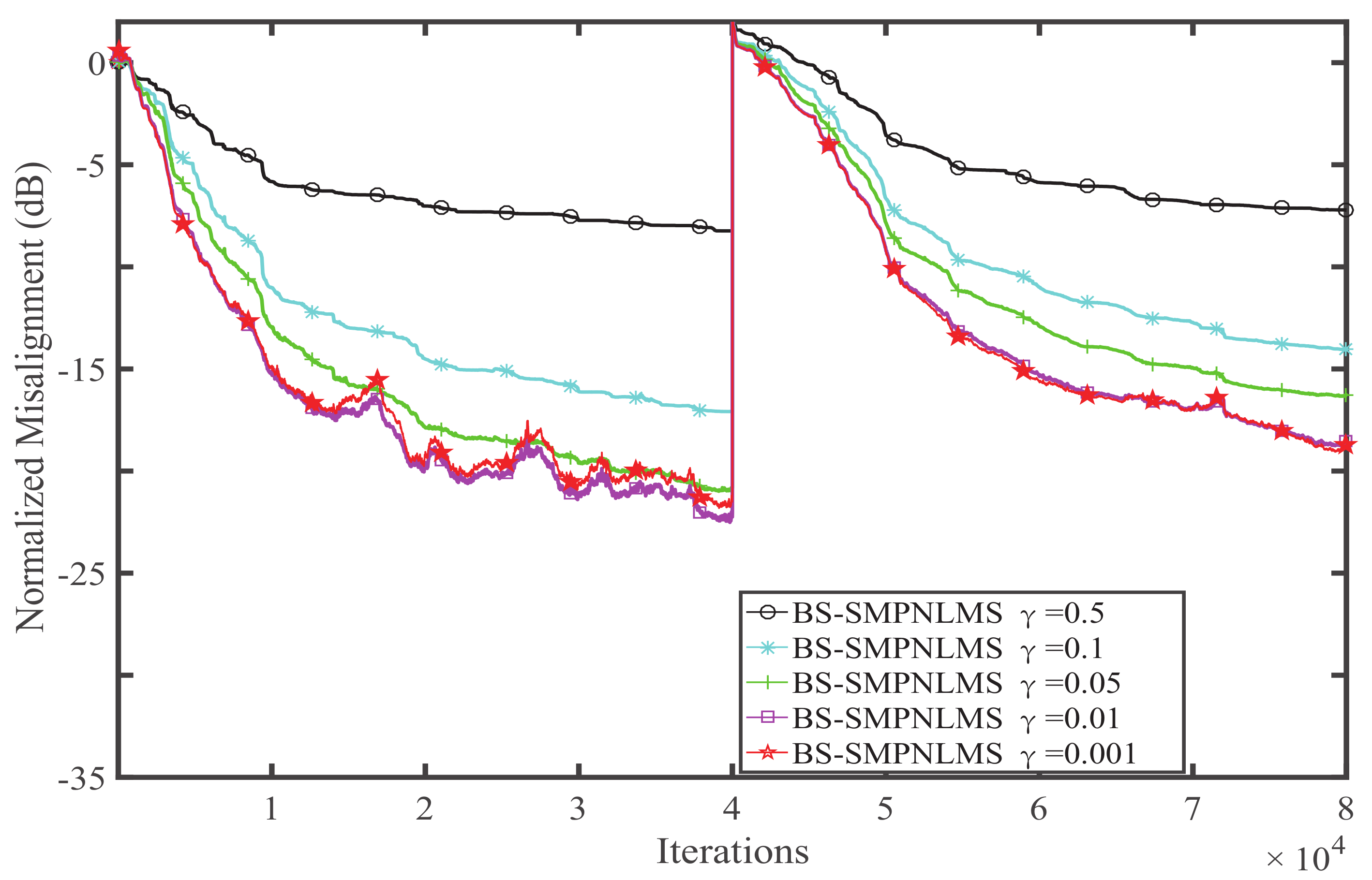
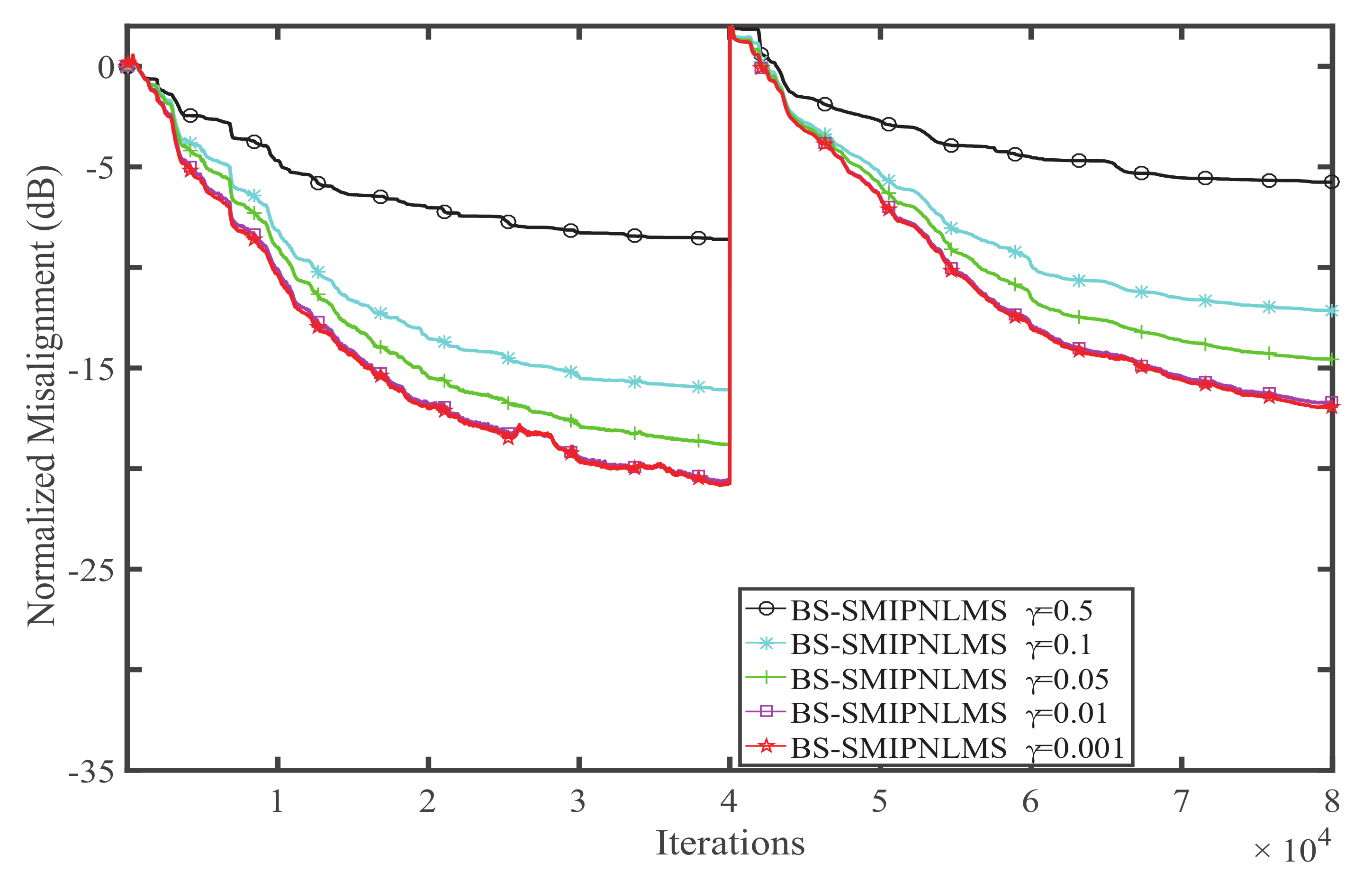
4. Simulation and Result Analysis
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Benesty, J.; Gaensler, T.; Morgan, D.R.; Sondhi, M.M.; Gay, S.L. Advances in Network and Acoustic Echo Cancellation; Springer: Berlin, Germany, 2001. [Google Scholar]
- Haykin, S. Adaptive Filter Theory, 4th ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 2002. [Google Scholar]
- Diniz, P.S.R. Adaptive Filtering: Algorithms and Practical Implementation, 4th ed.; Springer: New York, NY, USA, 2013. [Google Scholar]
- Sayed, A.H. Fundamentals of Adaptive Filtering; Wiley-IEEE: New York, NY, USA, 2003. [Google Scholar]
- Digital Network Echo Cancellers; ITU-T Recommendation G.168; International Telecommunication Union: Geneva, Switzerland, 2009.
- Duttweiler, D.L. Proportionate normalized least-mean-squares adaptition in echo cancelers. IEEE Trans. Speech Audio Process. 2000, 8, 508–518. [Google Scholar] [CrossRef]
- Gu, Y.; Jin, J.; Mei, S. l0 norm constraint LMS algorithms for sparse system identification. IEEE Signal Process. Lett. 2009, 16, 774–777. [Google Scholar]
- Deng, H.; Doroslova, M. Improved convergence of the PNLMS algorithm for sparse impluse response identification. IEEE Signal Process. Lett. 2005, 12, 181–184. [Google Scholar] [CrossRef]
- Li, Y.; Jin, Z.; Wang, Y. Adaptive channel estimation based on an improved norm constrained set-membership normalized least mean square algorithm. Wirel. Commun. Mobile Comput. 2017, 2017, 8056126. [Google Scholar] [CrossRef]
- Gui, G.; Mehbodniya, A.; Adachi, F. Least mean square/fourth algorithm for adaptive sparse channel estimation. In Proceedings of the 24th IEEE International Symposium on Personal Indoor and Mobile Radio Communications (PIMRC), London, UK, 8–11 September 2013; pp. 296–300. [Google Scholar]
- Gui, G.; Peng, W.; Adachi, F. Sparse least mean fourth algorithm for adaptive channel estimation in low signal-to-noise ratio region. Int. J. Commun. Syst. 2014, 27, 3147–3157. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Jiang, T. Sparse channel estimation based on a p-norm-like constrained least mean fourth algorithm. In Proceedings of the 7th International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 15–17 October 2015; pp. 1–4. [Google Scholar]
- Li, Y.; Hamamura, M. Zero-attracting variable-step-size least mean square algorithms for adaptive sparse channel estimation. Int. J. Adapt. Control Signal Process. 2015, 29, 1189–1206. [Google Scholar] [CrossRef]
- Li, Y.; Hamamura, M. An improved proportionate normalized least-mean-square algorithm for broadband multipath channel estimation. Sci. World J. 2014, 2014, 572969. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wang, Y.; Jiang, T. Norm-adaption penalized least mean square/fourth algorithm for sparse channel estimation. Signal Process. 2016, 128, 243–251. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Yang, R. Sparse adaptive channel estimation based on mixed controlled l2 and lp-norm error criterion. J. Frankl. Inst. 2017, 354, 1–25. [Google Scholar] [CrossRef]
- Gay, S.L. An efficient, fast converging adaptive filter for network echo cancellation. In Proceedings of the Conference Record of the Thirty-Second Asilomar Conference on Signals, Systems Computers, Pacific Grove, CA, USA, 1–4 November 1998. [Google Scholar]
- Benesty, J.; Gay, S.L. An improved PNLMS algorithm. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Orlando, FL, USA, 13–17 May 2002. [Google Scholar]
- Paleologu, C.; Benesty, J.; Ciochina, S. An improved proportionate NLMS algorithm based on the l0 norm. In Proceedings of the 2010 IEEE International Conference on Acoustics Speech and Signal Processing (ICASSP), Dallas, TX, USA, 14–19 March 2010. [Google Scholar]
- Dong, Y.; Zhao, H. A new proportionate normalized least mean square algorithm for high measurement noise. In Proceedings of the 2015 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Ningbo, China, 19–22 September 2015. [Google Scholar]
- Liu, J.; Grant, S.L. A generalized proportionate adaptive algorithm based on convex optimization. In Proceedings of the 2014 IEEE China Summit & International Conference on Signal and Information Processing (ChinaSIP), Xi’an, China, 9–13 July 2014. [Google Scholar]
- Jiang, S.; Gu, Y. Block-Sparsity-Induced Adaptive Filter for Multi-Clustering System Identification. IEEE Trans. Signal Process. 2014, 63, 5318–5330. [Google Scholar] [CrossRef]
- Loganathan, P.; Habets, E.A.P.; Naylor, P.A. A partitioned block proportionate adaptive algorithm for acoustic echo cancellation. In Proceedings of the Asia-Pacific Signal and Information Processing Association, Singapore, 14–17 December 2010. [Google Scholar]
- De Souza, F.D.C.; Tobias, O.J.; Seara, R. A PNLMS algorithm with individual activation factors. IEEE Trans. Signal Process. 2010, 58, 2036–2047. [Google Scholar] [CrossRef]
- Cui, J.; Naylor, P.; Brown, D. An improved IPNLMS algorithm for echo cancellation in packet-switched networks. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Montreal, QC, Canada, 17–21 May 2004. [Google Scholar]
- Liu, J.; Grant, S.L. Proportionate Adaptive Filtering for Block-Sparse System Identification. IEEE/ACM Trans. Audio Speech Lang. Process. 2015, 24, 623–630. [Google Scholar] [CrossRef]
- Liu, J.; Grant, S.L. Proportionate affine projection algorithms for block-sparse system identification. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016. [Google Scholar]
- Liu, J.; Grant, S.L. Block sparse memory improved proportionate affine projection sign algorithm. Electron. Lett. 2015, 51, 2001–2003. [Google Scholar] [CrossRef]
- Combettes, P.L. The foundations of set theoretic estimation. Proc. IEEE 1993, 81, 182–208. [Google Scholar] [CrossRef]
- Nagaraj, S.; Gollamudi, S.; Kapoor, S.; Huang, Y.F. An adaptive set-membership filtering technique with sparse updates. IEEE Trans. Signal Process. 1999, 47, 2928–2941. [Google Scholar] [CrossRef]
- Werner, S.; Diniz, P.S.R. Set-membership affine projection algorithm. IEEE Signal Process. Lett. 2001, 8, 231–235. [Google Scholar] [CrossRef]
- Gollamudi, S.; Nagaraj, S.; Huang, Y.F. Set-membership filtering and a set-membership normalized LMS algorithm with an adaptive step size. IEEE Signal Process. Lett. 1998, 5, 111–114. [Google Scholar] [CrossRef]
- Lin, T.M.; Nayeri, M.; Deller, J.R., Jr. Consistently convergent OBE algorithm with automatic selection of error bounds. Int. J. Adapt. Control Signal Process. 1998, 12, 302–324. [Google Scholar] [CrossRef]
- Gollamudi, S.; Nagaraj, S.; Huang, Y.F. Blind equalization with a deterministic constant modulus cost-a set-membership filtering approach. In Proceedings of the 2000 IEEE International Conference on Acoustics, Speech, and Signal Processing, Istanbul, Turkey, 5–9 June 2000. [Google Scholar]
- Diniz, P.S.R. Adaptive Filtering: Algorithms and Practical Implementations, 2nd ed.; Kluwer: Boston, MA, USA, 2002. [Google Scholar]
- De Lamare, R.C.; Sampaio-Neto, R. Adaptive reduced-rank MMSE filtering with interpolated FIR filters and adaptive interpolators. IEEE Signal Process. Lett. 2005, 12, 177–180. [Google Scholar] [CrossRef]
- De Lamare, R.C.; Diniz, P.S.R. Set-membership adaptive algorithms based on time-vary error bounds for CDMA interference suppression. IEEE Trans. Veh. Technol. 2009, 58, 644–654. [Google Scholar] [CrossRef]
- Bhotto, M.Z.A.; Antoniou, A. Robust set-membership affine projection adaptive-filtering algorithm. IEEE Trans. Signal Process. 2012, 60, 73–81. [Google Scholar] [CrossRef]
- Clarke, P.; de Lamare, R.C. Low-complexity reduced-rank linear interference suppression based on set-membership joint iterative optimization for DS-CDMA systems. IEEE Trans. Veh. Technol. 2011, 60, 4324–4337. [Google Scholar] [CrossRef]
- Cai, Y.; de Lamare, R.C. Set-membership adaptive constant modulus beamforming based on generalized sidelobe cancellation with dynamic bounds. In Proceedings of the 10th International Symposium on Wireless Communication Systems, Berlin, German, 9–13 December 2013. [Google Scholar]
- Li, Y.; Wang, Y.; Jiang, T. Sparse-aware set-membership NLMS algorithms and their application for sparse channel estimation and echo cancelation. AEU Int. J. Electron. Commun. 2016, 70, 895–902. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y. Sparse SM-NLMS algorithm based on correntropy criterion. IET Electron. Lett. 2016, 52, 1461–1463. [Google Scholar] [CrossRef]
- Eldar, Y.C.; Mishali, M. Robust Recovery of Signals From a Structured Union of Subspaces. IEEE Trans. Inf. Theory 2009, 55, 5302–5316. [Google Scholar] [CrossRef]
- Stojnic, M.; Parvaresh, F.; Hassibi, B. On the Reconstruction of Block-Sparse Signals With an Optimal Number of Measurements. IEEE Trans. Signal Process. 2009, 57, 3075–3085. [Google Scholar] [CrossRef]
- Stojnic, M. l2/l1-Optimization in Block-Sparse Compressed Sensing and Its Strong Thresholds. IEEE J. Sel. Top. Signal Process. 2010, 4, 3025–3028. [Google Scholar]
- Liu, J.; Jin, J.; Gu, Y. Efficient Recovery of Block Sparse Signals via Zero-point Attracting Projection. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012. [Google Scholar]
- Elhamifar, E.; Vidal, R. Block-Sparse Recovery via Convex Optimization. IEEE Trans. Signal Process. 2012, 60, 4094–4107. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, Z.; Li, Y.; Liu, J. An Improved Set-Membership Proportionate Adaptive Algorithm for a Block-Sparse System. Symmetry 2018, 10, 75. https://doi.org/10.3390/sym10030075
Jin Z, Li Y, Liu J. An Improved Set-Membership Proportionate Adaptive Algorithm for a Block-Sparse System. Symmetry. 2018; 10(3):75. https://doi.org/10.3390/sym10030075
Chicago/Turabian StyleJin, Zhan, Yingsong Li, and Jianming Liu. 2018. "An Improved Set-Membership Proportionate Adaptive Algorithm for a Block-Sparse System" Symmetry 10, no. 3: 75. https://doi.org/10.3390/sym10030075




