New Similarity Solutions of a Generalized Variable-Coefficient Gardner Equation with Forcing Term
Abstract
:1. Introduction
2. Symmetry
3. Symmetry Reduction
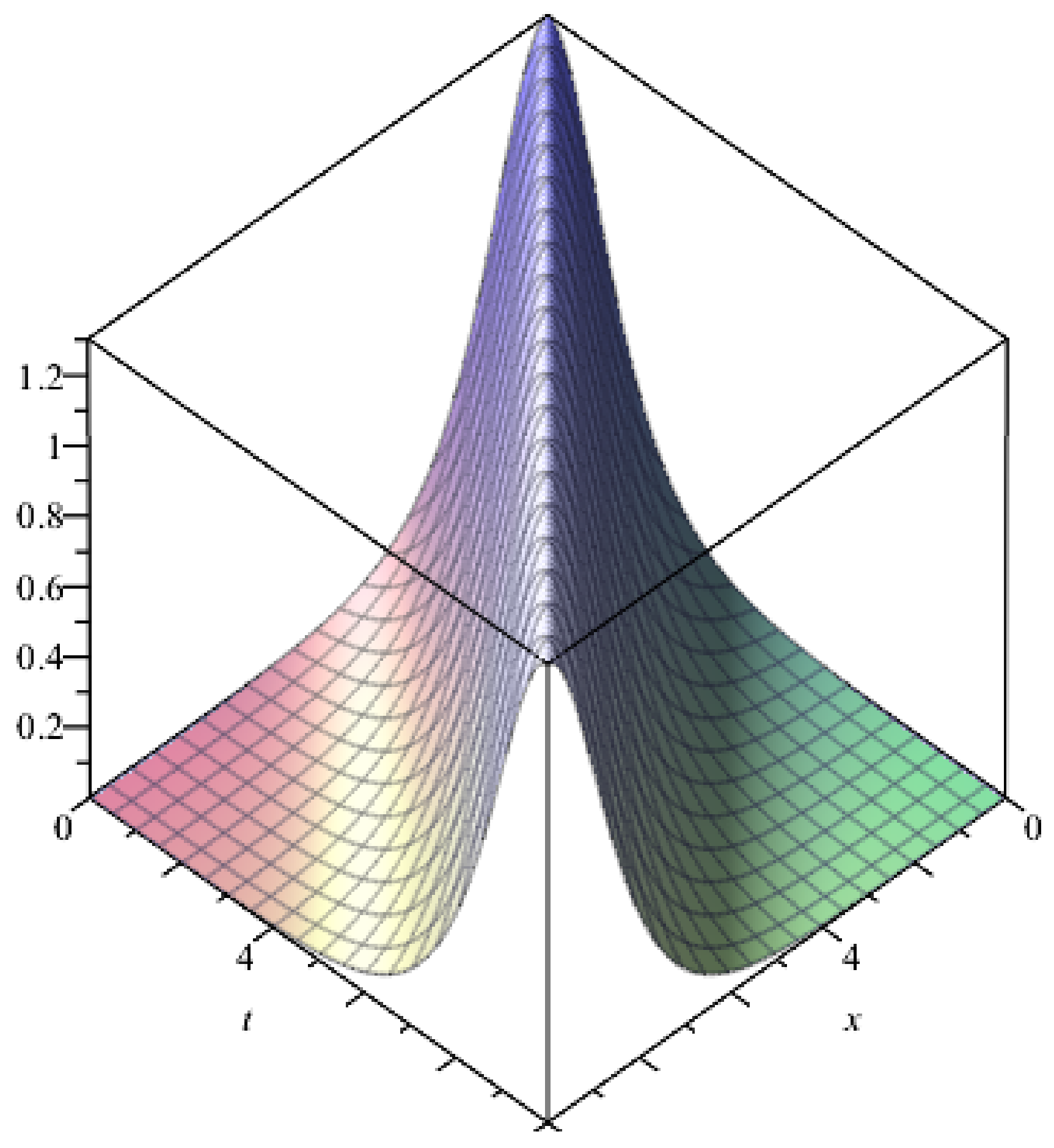
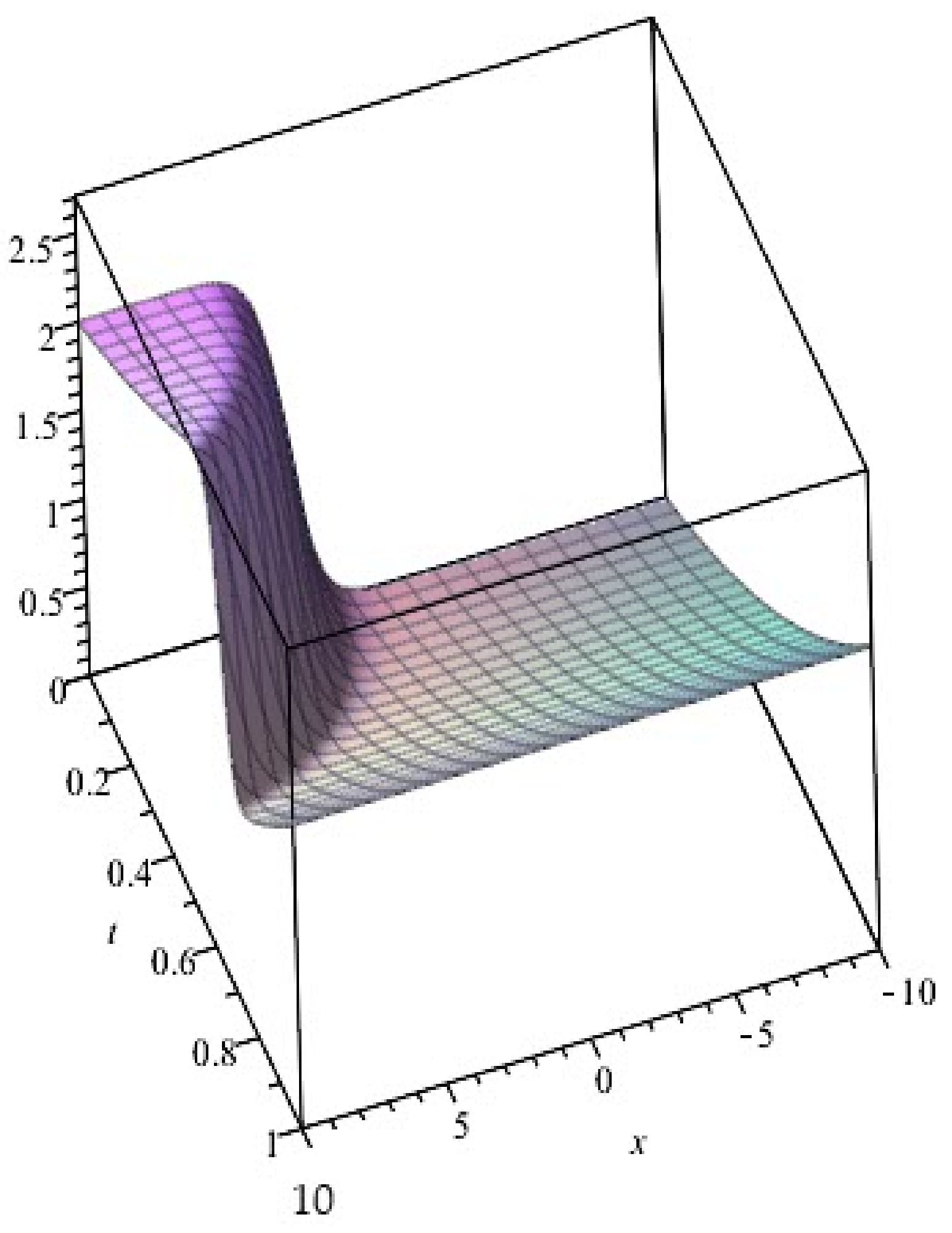
4. Similarity Solutions
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lou, S.; Huang, G.; Ruan, H. Exact solitary waves in a convecting fluid. J. Phys. A Gen. Phys. 1991, 24, 587–590. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Y.; Dong, H. Interaction solutions of a (2+1)-dimensional dispersive long wave system. Comput. Math. Appl. 2018. [Google Scholar] [CrossRef]
- Gardner, C.S.; Greene, J.M.; Kruskal, M.D.; Miura, R.M. Method for solving the Korteweg-deVries equation. Phys. Rev. Lett. 1967, 19, 1095. [Google Scholar] [CrossRef]
- Wang, M.; Zhou, Y.; Li, Z. Applications of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics. Phys. Lett. A 1996, 216, 67–75. [Google Scholar] [CrossRef]
- Naher, H.; Abdullah, F.A. New approach of (G′/G)-expansion method and new approach of generalized (G′/G)-expansion method for nonlinear evolution equation. AIP Adv. 2013, 3, 032116. [Google Scholar] [CrossRef]
- Dong, H.; Zhao, K.; Yang, H.; Li, Y. Generalised (2+1)-dimensional super MKdV hierarchy for integrable systems in soliton theory. East Asian J. Appl. Math. 2015, 5, 256–272. [Google Scholar] [CrossRef]
- Wazwaz, A.M. A sine-cosine method for handling nonlinear wave equations. Math. Comput. Model. 2004, 40, 499–508. [Google Scholar] [CrossRef]
- Fang, Y.; Dong, H.; Hou, Y.; Kong, Y. Frobenius integrable decompositions of nonlinear evolution equations with modified term. Appl. Math. Comput. 2014, 226, 435–440. [Google Scholar] [CrossRef]
- Zhang, S.; Li, J.; Zhou, Y. Exact solutions of non-linear lattice equations by an improved exp-function method. Entropy 2015, 17, 3182–3193. [Google Scholar] [CrossRef]
- Demiray, S.T.; Bulut, H. New exact solutions of the new Hamiltonian amplitude-equation and Fokas Lenells equation. Entropy 2015, 17, 6025–6043. [Google Scholar] [CrossRef]
- Yang, X.; Gao, F.; Srivastava, H.M. Exact travelling wave solutions for the local fractional two-dimensional Burgers-type equations. Comput. Math. Appl. 2017, 73, 203–210. [Google Scholar] [CrossRef]
- Hirota, R. Exact solution of the Korteweg-de Vries equation for multiple collisions of solitons. Phys. Rev. Lett. 1971, 27, 1192–1194. [Google Scholar] [CrossRef]
- Zhao, H.; Ma, W. Mixed lump-kink solutions to the KP equation. Comput. Math. Appl. 2017, 74, 1399–1405. [Google Scholar] [CrossRef]
- Ma, W.; Zhou, Y. Lump solutions to nonlinear partial differential equations via Hirota bilinear forms. J. Differ. Equ. 2018, 264, 2653–2659. [Google Scholar] [CrossRef]
- Zhao, Q.; Li, X.; Liu, F. Two integrable lattice hierarchies and their respective Darboux transformations. Appl. Math. Comput. 2013, 219, 2693–5705. [Google Scholar] [CrossRef]
- Xu, X.; Sun, Y. An integrable coupling hierarchy of Dirac integrable hierarchy, its Liouville integrability and Darboux transformation. J. Nonlinear Sci. Appl. 2017, 10, 3328–3343. [Google Scholar] [CrossRef]
- Bluman, G.W.; Cole, J.D. The general similarity of the heat equation. J. Math. Mech. 1969, 18, 1025–1042. [Google Scholar]
- Clarkson, P.A.; Kruskal, M.D. New similarity solutions of the Boussinesq equation. J. Math. Phys. 1989, 30, 2201–2213. [Google Scholar] [CrossRef]
- Cherniha, R.; King, J.R. Lie symmetries of nonlinear multidimensional reaction-diffusion systems: I. J. Phys. A Math. Gen. 2000, 33, 267. [Google Scholar] [CrossRef]
- Cherniha, R.; King, J.R. Lie symmetries of nonlinear multidimensional reaction-diffusion systems: II. J. Phys. A Math. Gen. 2003, 36, 405–425. [Google Scholar] [CrossRef]
- Moleleki, L.D.; Johnpillai, A.G.; Khalique, C.M. Symmetry reductions and exact solutions of a variable coefficient (2+1)-Zakharov-Kuznetsov equation. Math. Comput. Appl. 2012, 17, 132–139. [Google Scholar] [CrossRef]
- Nucci, M.C.; Sanchini, G. Symmetries, Lagrangians and conservation laws of an Easter Island population model. Symmetry 2015, 7, 1613–1632. [Google Scholar] [CrossRef]
- Dong, H.; Chen, T.; Chen, L.; Zhang, Y. A new integrable symplectic map and the lie point symmetry associated with nonlinear lattice equations. J. Nonlinear Sci. Appl. 2016, 9, 5107–5118. [Google Scholar] [CrossRef]
- Cherniha, R.; Davydovych, V.; Liliia, M. Lie symmetries of the shigesada-Kawasaki-Teramoto system. Commun. Nonlinear Sci. Numer. Simul. 2017, 45, 81–92. [Google Scholar] [CrossRef]
- Huang, D.; Li, X.; Yu, S. Lie symmetry classification of the generalized nonlinear Beam equation. Symmetry 2017, 9, 115. [Google Scholar] [CrossRef]
- Hydon, P.E. Symmetry Methods for Differential Equations: A Beginner’s Guide; Cambridge University Press: New York, NY, USA, 2000. [Google Scholar]
- Yan, Z.; Liu, X. Symmetry and similarity solutions of variable coefficient generalized Zakharov-Kuznetsov equation. Appl. Math. Comput. 2006, 180, 288–294. [Google Scholar] [CrossRef]
- Yan, Z.; Zhou, J.; Liu, X. Symmetry reductions and similarity solutions of the (3+1)-dimensional breaking soliton equation. Appl. Math. Comput. 2008, 201, 333–339. [Google Scholar] [CrossRef]
- Yan, Z.; Zhou, J. New explicit solutions of (1+1)-dimensional variable-coefficient Broer-Kaup system. Commun. Theor. Phys. 2010, 54, 965. [Google Scholar]
- Zhang, S. Exact solutions of Wick-type stochastic Korteweg-de Vries equation. Can. J. Phys. 2012, 90, 181–186. [Google Scholar] [CrossRef]
- Gupta, R.; Singh, M. Nonclassical symmetries and similarity solutions of variable coefficient coupled KdV system using compatibility method. Nonlinear Dyn. 2017, 87, 1543–1552. [Google Scholar] [CrossRef]
- Hong, B.; Lu, D. New exact solutions for the generalized variable-coefficient Gardner equation with forcing term. Appl. Math. Comput. 2012, 219, 2732–2738. [Google Scholar] [CrossRef]
- Li, J.; Xu, T.; Meng, X.; Zhang, Y.; Zhang, H.; Tian, B. Lax pair: Bäcklund transformation and N-soliton-like solution for a variable-coefficient Gardner equation from nonlinear lattice, plasma physics and ocean dynamics with symbolic computation. J. Math. Anal. Appl. 2007, 336, 1443–1455. [Google Scholar] [CrossRef]
- Xu, X.; Meng, X.; Gao, Y.; Wen, X. Analytic N-solitary-wave solution of a variable-coefficient Gardner equation from fluid dynamics and plasma physics. Appl. Math. Comput. 2009, 210, 313–320. [Google Scholar] [CrossRef]
- Bulut, H.; Sulaiman, T.; Baskonus, H.M.; Sandulyak, A.A. New solitary and optical wave structures to the (1+1)-dimensional combined KdV-mKdV equation. Optik 2017, 135, 327–336. [Google Scholar] [CrossRef]
- Latif, M.A. Some exact solutions of KdV equation with variable coefficient. Commun. Nonlinear Sci. Numer. Simul. 2009, 16, 1783–1786. [Google Scholar] [CrossRef]
- Johnpillai, A.G.; Khalique, C.M. Group analysis of KdV equation with time dependent coefficients. Appl. Math. Comput. 2010, 216, 3761–3771. [Google Scholar] [CrossRef]
- Johnpillai, A.G.; Khalique, C.M. Lie group classification and invariant solutions of mKdV equation with time-dependent coefficients. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1207–1215. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Wang, Y.; Wang, Y.; Yan, Z.; Wang, Z. New Similarity Solutions of a Generalized Variable-Coefficient Gardner Equation with Forcing Term. Symmetry 2018, 10, 112. https://doi.org/10.3390/sym10040112
Zhou J, Wang Y, Wang Y, Yan Z, Wang Z. New Similarity Solutions of a Generalized Variable-Coefficient Gardner Equation with Forcing Term. Symmetry. 2018; 10(4):112. https://doi.org/10.3390/sym10040112
Chicago/Turabian StyleZhou, Jianping, Yuan Wang, Yang Wang, Zhilian Yan, and Zhen Wang. 2018. "New Similarity Solutions of a Generalized Variable-Coefficient Gardner Equation with Forcing Term" Symmetry 10, no. 4: 112. https://doi.org/10.3390/sym10040112




