Multiple Solutions to Implicit Symmetric Boundary Value Problems for Second Order Ordinary Differential Equations (ODEs): Equivariant Degree Approach
Abstract
:1. Introduction
1.1. Subject and Goal
1.2. Method
1.3. Overview
2. G-Actions and Equivariant Degree without Parameters for Multivalued Fields
2.1. G-Actions
2.2. Equivariant Degree for Multivalued Vector Fields
- (i)
- there exists , such that and for all ;
- (ii)
- for all , , i.e., (by the same token, F has no fixed-points in ).
- (a)
- , , for all ;
- (b)
- for all .
- (M1)
- (M2)
- (Additivity) Let and be two disjoint open G-invariant subsets of Ω, such that, for any , one has . Then:
- (M3)
- (Homotopy) If is an Ω-admissible G-homotopy of multivalued G-equivariant compact fields, then:
- (M4)
- (Normalization) Let Ω be a G-invariant open bounded neighborhood of zero in . Then:
- (M5)
- (Multiplicativity) For any
3. Symmetric Differential Inclusions
3.1. Basic Definitions and Facts
- (i)
- for every , the multivalued map is measurable;
- (ii)
- for every , the multivalued map is upper semicontinuous.
- (A)
- For any bounded set, , there exists , such that:
3.2. Hypotheses
- (H0)
- F is a Carathéodory map satisfying condition (A), and there exists a constant , such that:
- (H1)
- for any satisfying , there is , such thatwhere ;
- (H2)
- there exist α, , such that, for all :for a.e. and all ;
- (H3)
- there is a function, , such that the function, , , belongs to , , and for all with ,
- (H4)
- ;
- (H5)
- the linear system:has only the trivial solution, , i.e., , where stands for the spectrum of C.
- (H6)
- the multivalued map, , is G-equivariant, i.e.:(as usual, G is supposed to act trivially on ), and the linear map, , is G-equivariant, as well.
- (H7)
- for every non-zero, , there is , such that:where
3.3. Operator Reformulation in Functional Spaces and the Existence of Multiple Symmetric Solutions: Abstract Result
- (a) for every , there exists a non-zero solution, , to (11), such that .
- (b) If, in addition, is a maximal orbit type in , then .
4. Symmetric Implicit Boundary Value Problems
4.1. General Result
- (A0)
- is a Carathéodory function and there exist a Carathéodory function,, and a constant, , such that:and:and for all , , , where
- (A1)
- for any satisfying , there exists , such that if , then:where is given in (A0);
- (A2)
- There exist constants, κ, , such that:and for all u, v, with and (where is given in the condition (A0));
- (A3)
- There is a function, , such that , , belongs to , , and:and u, v, , with and (where is given in the condition (A0)).
- (A4)
- For any , the function, , is differentiable at ; also, , and , , with and ;
- (A5)
- the characteristic equation, , , where , associated with the system linearized at , has no characteristic roots of the form ().
- (A6)
- the function, , is G-equivariant, i.e.:
- (A7)
- the function satisfies the condition: for any , there is , such that:where is given in (A0).
- (a) satisfies conditions (H0)–(H7);
- (b) any solution, , to (11) is also a solution to (3).
4.2. General Formula for
5. Examples of Implicit -Symmetric BVPs with Multiple Solutions
5.1. A Class of Maps Satisfying (A0)–(A7)
- (g1)
- g is -equivariant (in particular, continuous);
- (g2)
- there exist real constants, and , such that for all ;
- (g3)
- for all ;
- (g4)
- ;
- (g5)
- .
5.2. Example

- (a1)
- (a2) (for simplicity).
Acknowledgements
Conflicts of Interest
Appendix 1: Equivariant Degree without Parameters: Single-Valued Maps
A1.1. G-Equivariant Degree: Domain and Range of Values
A1.2. G-Equivariant Degree: Basic Properties and Recurrence Formula
- (G1)
- (Existence) If G-, i.e., there is in (60) a non-zero coefficient, , then , such that and .
- (G2)
- (Additivity) Let and be two disjoint open G-invariant subsets of Ω, such that Then:
- (G3)
- (Homotopy) If is an Ω-admissible G homotopy, then:
- (G4)
- (Normalization) Let Ω be a G-invariant open bounded neighborhood of zero in V. Then:
- (G5)
- (Multiplicativity) For any :where the multiplication “·” is taken in the Burnside ring, .
- (G6)
- (Suspension) If is an orthogonal G-representation and is an open bounded invariant neighborhood of , then:
- (G7)
- (Recurrence Formula) For an admissible G-pair , the G-degree (10) can be computed using the following recurrence formula:where stands for the number of elements in the set, X, and is the Brouwer degree of the map on the set, .
A1.3. G-Equivariant Degree of Linear G-Isomorphisms
- (i)
- for each , put:and call the number, , the -multiplicity of the eigenvalue, λ, of T;
- (ii)
- for any irreducible representation, , put:and call the basic G-degree corresponding to the representation, .
Appendix 2: Dihedral Group and Its Representations
A2.1. Dihedral Group
A2.2. Irreducible -Representations and Basic Degrees
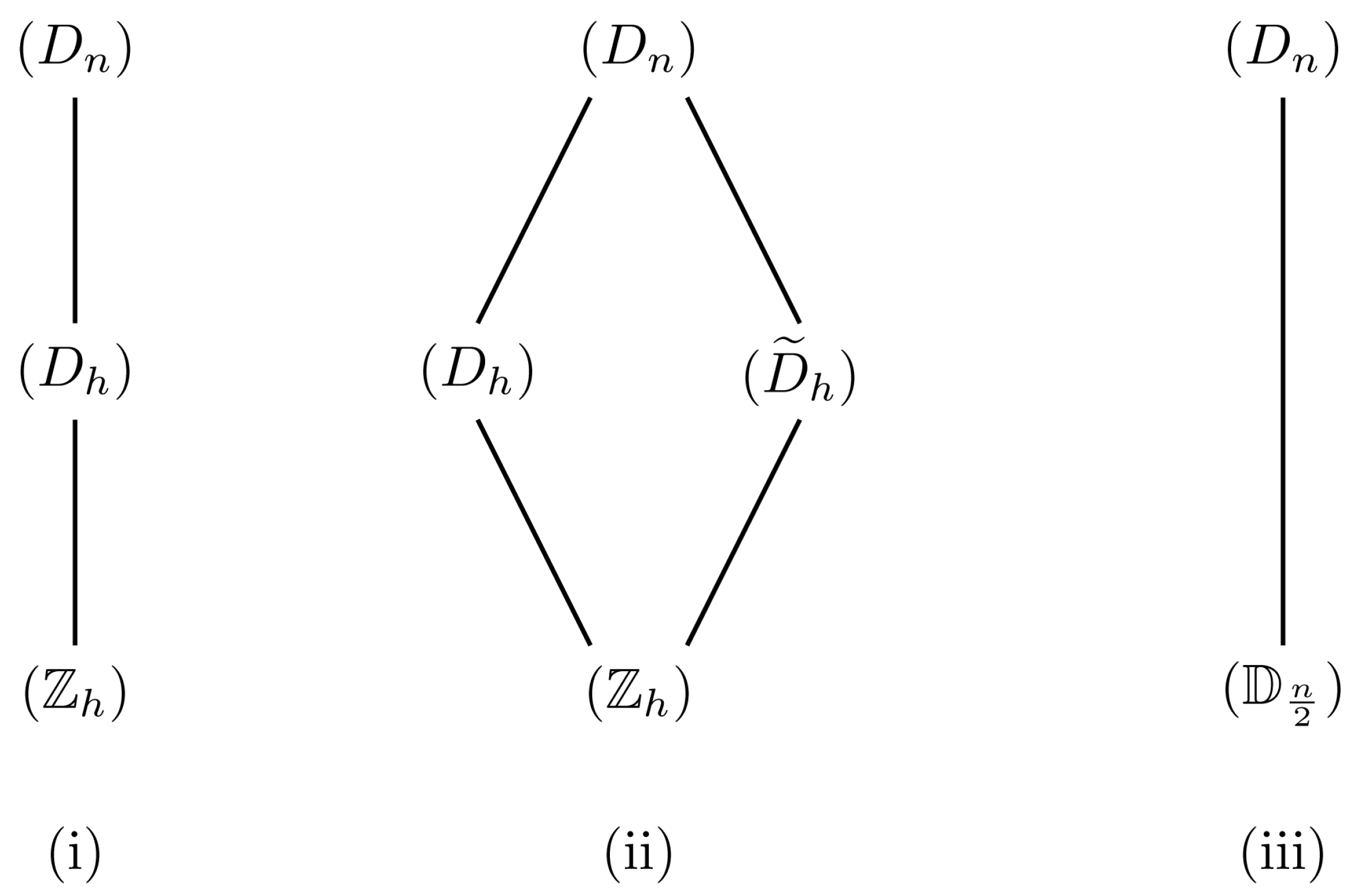
A2.3. -Representations Induced by Coordinate Permutations
References
- Coddington, E.; Levenson, N. Theory of Ordinary Differential Equations; McGraw-Hill: New York, NY, USA, 1955. [Google Scholar]
- Hartman, P. Ordinary Differential Equations; John Wiley & Sons: New York, NY, USA, 1964. [Google Scholar]
- Mawhin, J. Seventy-Five Years of Global Analysis around the Forced Pendulum Equation. In Proceedings of the Equadiff 9 Proceedings, Conference on Differential Equations and Their Applications, Brno, Czech Republic, 25–29 August 1997; Agarwal, R.P., Neuman, F., Vosmanský, J., Eds.; Masaryk University: Brno, Czech Republic, 1998; pp. 115–145. [Google Scholar]
- Hartman, P. On boundary value problems for systems of ordinary nonlinear second order differential equations. Trans. Am. Math. Soc. 1960, 96, 493–509. [Google Scholar] [CrossRef]
- Knobloch, H.W. On the existence of periodic solutions for second order vector differential equations. J. Differ. Eq. 1971, 9, 67–85. [Google Scholar] [CrossRef]
- Bebernes, J.W.; Schmidt, K. Periodic boundary value problems for systems of second order differential equations. J. Differ. Eq. 1973, 13, 33–47. [Google Scholar] [CrossRef]
- Mawhin, J. Some boundary value problems for Hartman-type perturbations of the ordinary vector p-Laplacian. Nonlinear Anal. TMA 2000, 40, 497–503. [Google Scholar] [CrossRef]
- Mawhin, J. Periodic Solutions of Systems with p-Laplacian-Like Operator. In Nonlinear Analysis and its Applications to Differential Equations; Progress in Nonlinear Differential Equations and Their Applications; Birkhäuser Boston: Boston, MA, USA, 2001; Volume 43, pp. 37–63. [Google Scholar]
- Mawhin, J.; Urena, A. A Hartman-Nagumo inequality for the vector ordinary p-Laplacian and applications to nonlinear boundary value problems. J. Inequal. Appl. 2002, 7, 701–725. [Google Scholar] [CrossRef]
- Balanov, Z.; Krawcewicz, W.; Nguyen, M. Multiple Solutions to Implicit Symmetric Boundary Value Problems for Second Order ODEs: Equivariant Degree Approach. Nonlinear Anal. Theory Methods Appl. 2013, 94, 45–64. [Google Scholar] [CrossRef]
- Balanov, Z.; Krawcewicz, W.; Rybicki, S.; Steinlein, H. A short treatise on the equivariant degree theory and its applications. J. Fixed Point Theory Appl. 2010, 8, 1–74. [Google Scholar] [CrossRef]
- Dzedzej, Z. Equivariant degree of convex-valued maps applied to set-valued BVP. Cent. Eur. J. Math. 2012, 10, 2173–2186. [Google Scholar] [CrossRef]
- Petryshyn, W.V. Solvability of various boundary value problems for the equation x′′ = f(t, x, x′, x′′) - y. Pac. J. Math. 1986, 122, 169–195. [Google Scholar] [CrossRef]
- Erbe, L.; Krawcewicz, W. Nonlinear boundary value problems for differential inclusions y′′ ∈ F(t, y, y′). Ann. Pol. Math. 1991, 3, 195–226. [Google Scholar]
- Erbe, L.; Krawcewicz, W.; Kaczynski, T. Solvability of two-point boundary value problems for system of nonlinear differential equations of the form y′′ = g(t, y, y′, y′′). Rocky Mount. J. Math. 1990, 20, 899–907. [Google Scholar] [CrossRef]
- Golubitsky, M.; Stewart, I.N.; Schaeffer, D.G. Singularities and Groups in Bifurcation Theory; Applied Mathematical Sciences 69; Springer: New York, NY, USA, 1988; Volume II. [Google Scholar]
- Balanov, Z.; Schwartzman, E. Morse complex, even functionals and asymptotically linear differential equations with resonance at infinity. Topol. Methods Nonlinear Anal. 1998, 12, 323–366. [Google Scholar]
- Bartsch, T. Topological Methods for Variational Problems with Symmetries. In Lecture Notes in Mathematics 1560; Springer: Berlin, Germany, 1993. [Google Scholar]
- Mawhin, J.; Willem, M. Critical Point Theory and Hamiltonian Systems; Applied Mathematical Sciences 74; Springer: New York, NY, USA, 1989. [Google Scholar]
- Rabinowitz, P.H. Minimax Methods in Critical Point Theory with Applications to Differential Equations; American Mathematical Society: Providence, RI, USA, 1986. [Google Scholar]
- Dihedral Calculator Home Page. Available online: http://dihedral.muchlearning.org/ (accessed on 31 October 2013).
- Ize, J.; Vignoli, A. Equivariant Degree Theory. In De Gruyter Series in Nonlinear Analysis and Applications; Walter de Gruyter: Berlin, Germany, 2003; Volume 8. [Google Scholar]
- Krawcewicz, W.; Wu, J. Theory of Degrees with Applications to Bifurcations and Differential Equations. In Canadian Mathematical Society Series of Monographs and Advanced Texts; John Wiley & Sons: New York, NY, USA, 1997. [Google Scholar]
- Kushkuley, A.; Balanov, Z. Geometric Methods in Degree Theory for Equivariant Maps. In Lecture Notes in Mathematics 1632; Springer-Verlag: Berlin, Germany, 1996. [Google Scholar]
- Balanov, Z.; Krawcewicz, W.; Steinlein, H. Applied Equivariant Degree. In AIMS Series on Differential Equations & Dynamical Systems; AIMS: Springfield, IL, USA, 2006; Volume 1. [Google Scholar]
- Dieck, T. Transformation Groups; Walter de Gruyter: Berlin, Germany, 1987. [Google Scholar]
- Borisovich, G.; Gelman, B.D.; Myshkis, A.D.; Obukhovskii, V.V. Introduction to the Theory of Multivalued Mappings and Differential Inclusions; URSS: Moscow, Russian, 2005. [Google Scholar]
- Bredon, G.E. Introduction to Compact Transformation Groups; Academic Press: New York, NY, USA, 1972. [Google Scholar]
- Kawakubo, K. The Theory of Transformation Groups; The Clarendon Press: Oxford, UK, 1991. [Google Scholar]
- Bröcker, T.; Dieck, T. Representations of Compact Lie Groups; Springer-Verlag: Berlin, Germany, 1985. [Google Scholar]
- Gorniewicz, L. Topological Fixed Point Theory of Multivalued Mappings; Springer: Berlin, Germany, 1999; Volume 495. [Google Scholar]
- Pruszko, T. Some applications of the topological degree theory to multivalued boundary value problems. Diss. Math. 1984, 229, 1–48. [Google Scholar]
- Pruszko, T. Topological degree methods in multivalued boundary value problems. Nonlinear Anal. 1978, 2, 263–309. [Google Scholar]
- Davis, P.J. Circulant Matrices; John Wiley and Sons: New York, NY, USA, 1979. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Balanov, Z.; Krawcewicz, W.; Li, Z.; Nguyen, M. Multiple Solutions to Implicit Symmetric Boundary Value Problems for Second Order Ordinary Differential Equations (ODEs): Equivariant Degree Approach. Symmetry 2013, 5, 287-312. https://doi.org/10.3390/sym5040287
Balanov Z, Krawcewicz W, Li Z, Nguyen M. Multiple Solutions to Implicit Symmetric Boundary Value Problems for Second Order Ordinary Differential Equations (ODEs): Equivariant Degree Approach. Symmetry. 2013; 5(4):287-312. https://doi.org/10.3390/sym5040287
Chicago/Turabian StyleBalanov, Zalman, Wieslaw Krawcewicz, Zhichao Li, and Mylinh Nguyen. 2013. "Multiple Solutions to Implicit Symmetric Boundary Value Problems for Second Order Ordinary Differential Equations (ODEs): Equivariant Degree Approach" Symmetry 5, no. 4: 287-312. https://doi.org/10.3390/sym5040287



