Effect of Symmetry Breaking on Electronic Band Structure: Gap Opening at the High Symmetry Points
Abstract
:1. Introduction
2. Experimental Details and Method of Calculations
2.1. Experimental Details
2.2. Calculation Method
3. Results and Discussion
3.1. Symmetry Analysis
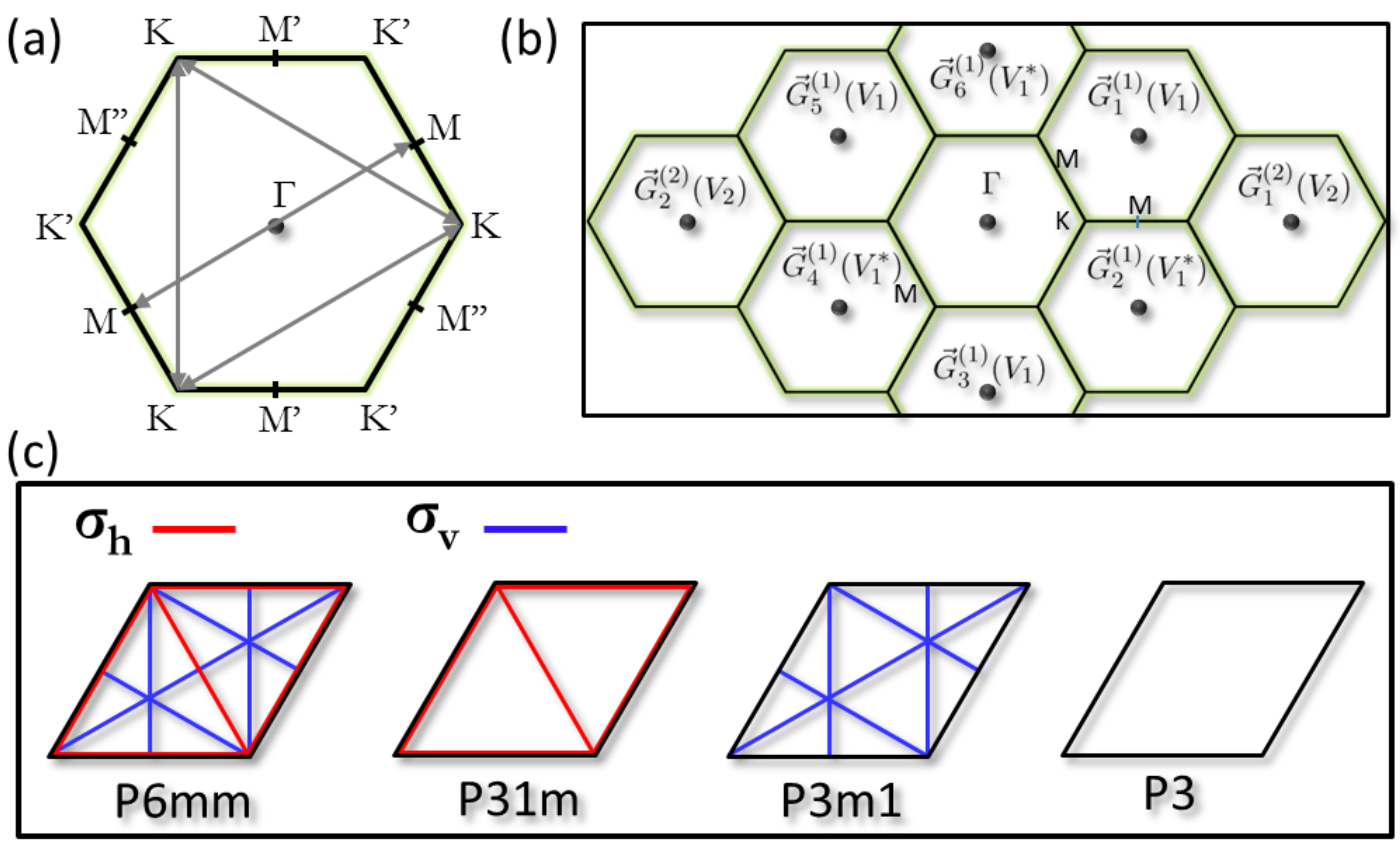
3.2. The Ag/Cu(111) Reconstruction
3.3. Symmetry and Potential Properties
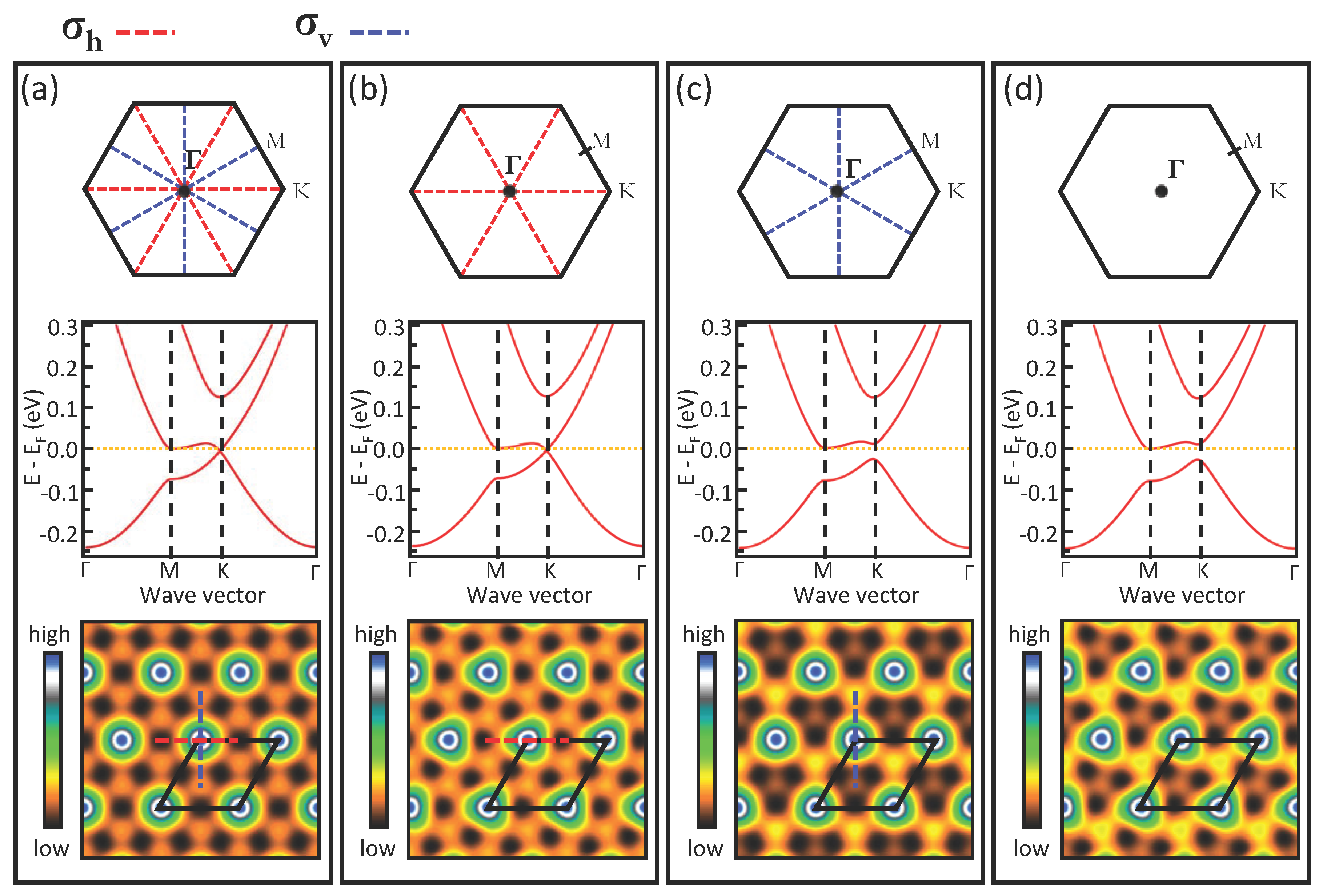
3.4. Electronic Properties of Ag/Cu(111)
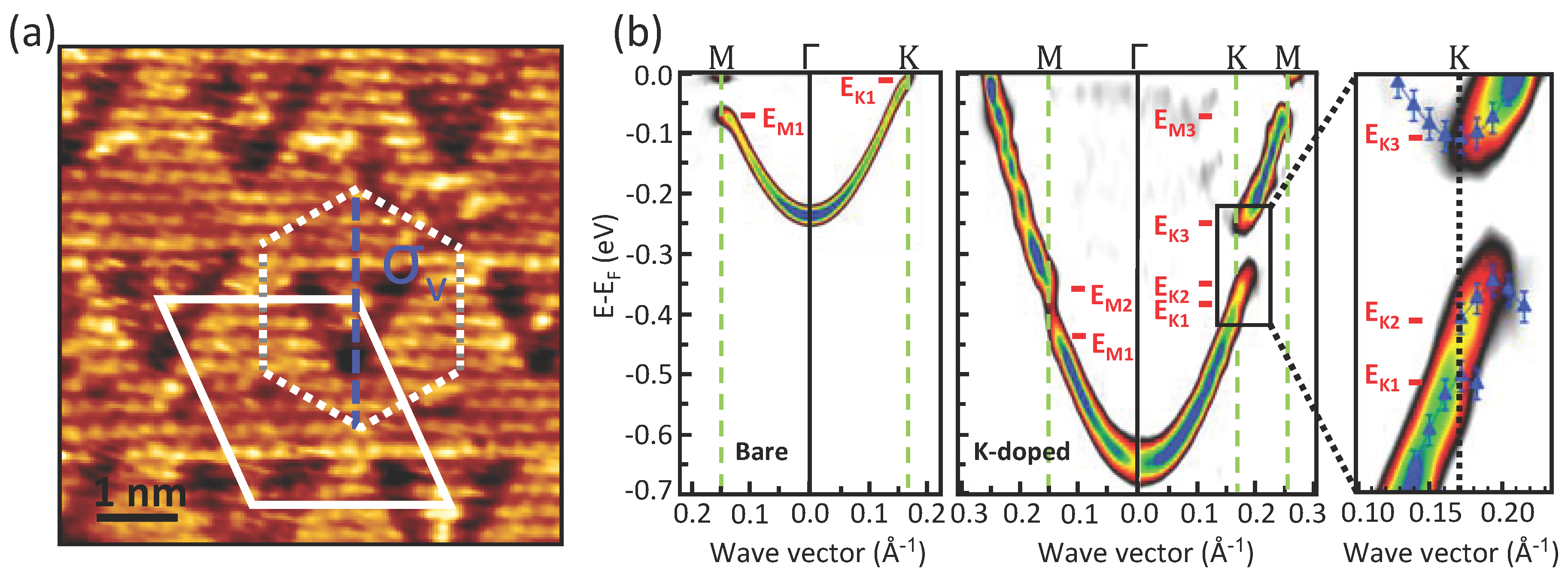
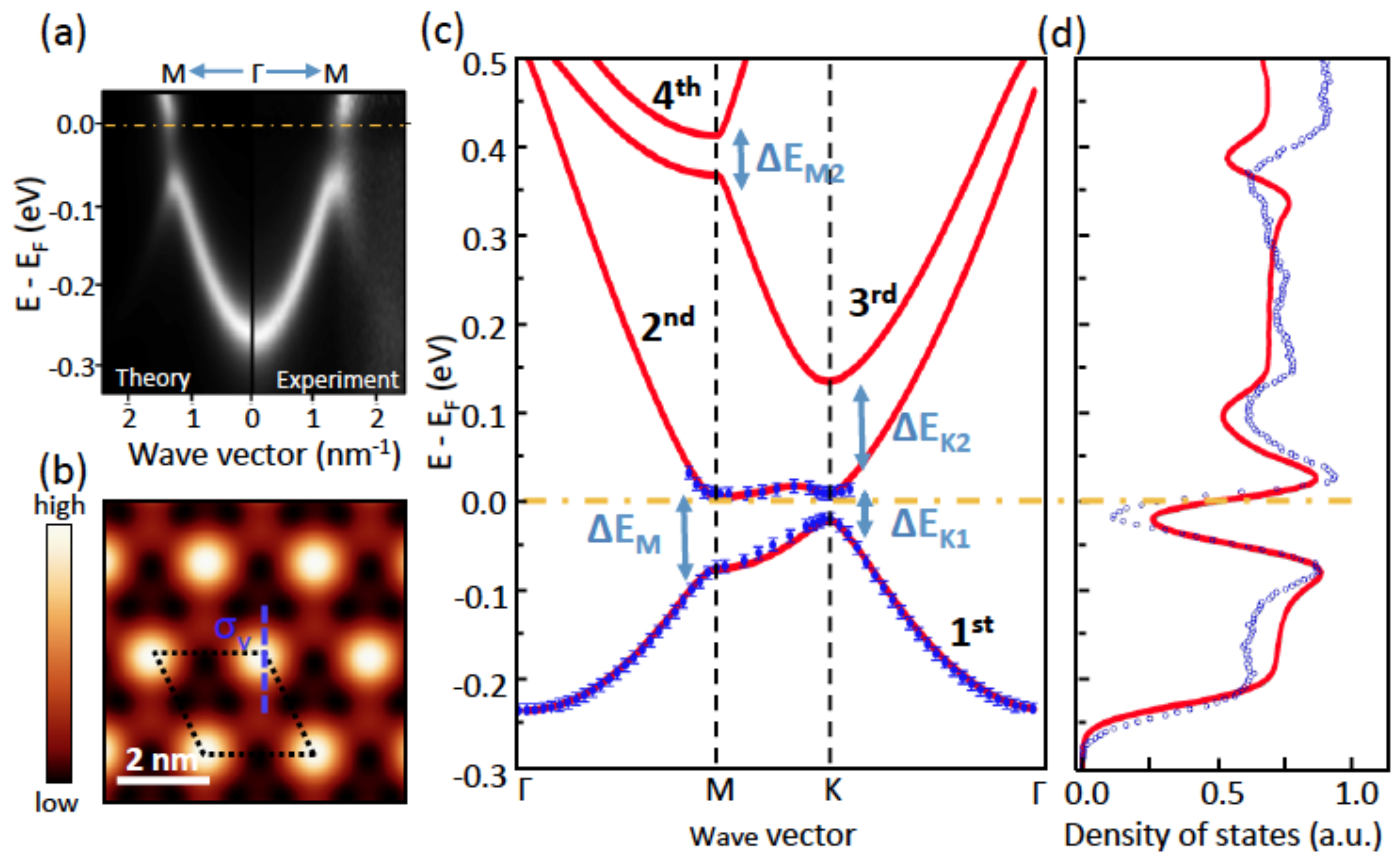
4. Conclusions
Conflicts of Interest
References
- Anderson, P.W. More is different. Science 1972, 177, 393–397. [Google Scholar] [CrossRef] [PubMed]
- Higgs, P.W. Broken symmetries and the masses of gauge bosons. Phys. Rev. Lett. 1964, 13, 508–509. [Google Scholar] [CrossRef]
- Anderson, P.W. Basic Notions of Condensed Matter Physics; The Benjamin/Cummings Publishing Company, Inc.: Menio Park, CA, USA, 1984. [Google Scholar]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef]
- Kogan, E.; Nazarov, V.U. Symmetry classification of energy bands in graphene. Phys. Rev. B 2012, 85, 115418:1–115418:5. [Google Scholar] [CrossRef]
- Starodub, E.; Bostwick, A.; Moreschini, L.; Nie, S.; El Gabaly, F.; McCarty, K.F.; Rotenberg, E. In-plane orientation effects on the electronic structure, stability, and Raman scattering of monolayer graphene on Ir(111). Phys. Rev. B 2011, 83, 125428:1–125428:9. [Google Scholar] [CrossRef]
- Meunier, I.; Tréglia, G.; Gay, J.-M.; Aufray, B.; Legrand, B. Ag/Cu(111) structure revisited through an extended mechanism for stress relaxation. Phys. Rev. B 1999, 59, 10910–10917. [Google Scholar] [CrossRef]
- N’Diaye, A.T.; Bleikamp, S.; Feibelman, P.J.; Michely, T. Two-dimensional Ir cluster lattice on a graphene moiré on Ir(111). Phys. Rev. Lett. 2006, 97, 215501:1–215501:4. [Google Scholar] [CrossRef]
- Reinert, F.; Nicolay, G.; Schmidt, S.; Ehm, D.; Hüfner, S. Direct measurements of the L-gap surface states on the (111) face of noble metals by photoelectron spectroscopy. Phys. Rev. B 2001, 63, 115415:1–115415:7. [Google Scholar] [CrossRef]
- Bendounan, A.; Cercellier, H.; Fagot-Revurat, Y.; Kierren, B.; Yurov, V.Y.; Malterre, D. Modification of Shockley states induced by surface reconstruction in epitaxial Ag films on Cu(111). Phys. Rev. B 2003, 67, 165412:1–165412:10. [Google Scholar] [CrossRef]
- Schiller, F.; Cordón, J.; Vyalikh, D.; Rubio, A.; Ortega, J.E. Fermi gap stabilization of an incommensurate two-dimensional superstructure. Phys. Rev. Lett. 2005, 94, 016103:1–016103:4. [Google Scholar] [CrossRef]
- Bendounan, A.; Forster, F.; Ziroff, J.; Schmitt, F.; Reinert, F. Influence of the reconstruction in Ag/Cu(111) on the surface electronic structure: Quantitative analysis of the induced band gap. Phys. Rev. B 2005, 72, 075407:1–075407:6. [Google Scholar] [CrossRef]
- Bendounan, A.; Forster, F.; Reinert, F.; Kierren, B.; Fagot-Revurat, Y.; Malterre, D. Comment on fermi gap stabilization of an incommensurate two-dimensional superstructure. Phys. Rev. Lett. 2006, 96. [Google Scholar] [CrossRef]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Cengage Learning: Stamford, CT, USA, 1976. [Google Scholar]
- Abd El-Fattah, Z.M.; Matena, M.; Corso, M.; García de Abajo, F.J.; Schiller, F.; Ortega, J.E. Lifshitz transition across the Ag/Cu(111) superlattice band gap tuned by interface doping. Phys. Rev. Lett. 2011, 107, 066803:1–066803:5. [Google Scholar] [CrossRef]
- García de Abajo, F.J.; Cordón, J.; Corso, M.; Schiller, F.; Ortega, J.E. Fermi gap engineering by Au doping of the Ag/Cu(111) dislocation network. Nanoscale 2010, 2, 717–721. [Google Scholar] [CrossRef] [PubMed]
- Vasseur, G.; Fagot-Revurat, Y.; Kierren, B.; Sicot, M.; Malterre, D. Electronic surface potential from angle resolved photoemission. Phys. Rev. B. 2013, in press. [Google Scholar] [CrossRef]
- Malterre, D.; Kierren, B.; Fagot-Revurat, Y.; Pons, S.; Tejeda, A.; Didiot, C.; Cercellier, H.; Bendounan, A. ARPES and STS investigation of Shockley states in thin metallic films and periodic nanostructures. New J. Phys. 2007, 9, 391:1–391:29. [Google Scholar] [CrossRef]
© 2013 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vasseur, G.; Fagot-Revurat, Y.; Kierren, B.; Sicot, M.; Malterre, D. Effect of Symmetry Breaking on Electronic Band Structure: Gap Opening at the High Symmetry Points. Symmetry 2013, 5, 344-354. https://doi.org/10.3390/sym5040344
Vasseur G, Fagot-Revurat Y, Kierren B, Sicot M, Malterre D. Effect of Symmetry Breaking on Electronic Band Structure: Gap Opening at the High Symmetry Points. Symmetry. 2013; 5(4):344-354. https://doi.org/10.3390/sym5040344
Chicago/Turabian StyleVasseur, Guillaume, Yannick Fagot-Revurat, Bertrand Kierren, Muriel Sicot, and Daniel Malterre. 2013. "Effect of Symmetry Breaking on Electronic Band Structure: Gap Opening at the High Symmetry Points" Symmetry 5, no. 4: 344-354. https://doi.org/10.3390/sym5040344




