Dynamical Symmetries and Causality in Non-Equilibrium Phase Transitions
Abstract
:1. Introduction
1.1. Conformal Algebra
1.2. Schrödinger Algebra
- Why should it be obvious that the time difference , to make the power-law prefactor real-valued ?
- Given the convention that , the condition is also required in order to have a decay of the two-point function with increasing distance .
- In applications to non-equilibrium statistical physics, one studies indeed two-point functions of the above type, which are then interpreted as the linear response function of the scaling operator ϕ with respect to an external conjugate fieldwhich in the context of the non-equilibrium Janssen–de Dominicis theory [2] can be re-expressed as a two-point function involving the scaling operator ϕ and its associate response operator . In this physical context, one has a natural interpretation of the “complex conjugate” in terms of the relationship of ϕ and .Then, the formal condition simply becomes the causality condition, namely that a response will only arise at a later time after the stimulation at time .
1.3. Conformal Galilean Algebra
- Why should one have for the time difference, as required to make the power-law prefactor real-valued ?
- Even for a fixed vector of rapidities, and even if could be taken for granted, how does one guarantee that the scalar product , such that the two-point function decreases as ?
1.4. Ageing Algebra
1.5. Langevin Equation and Reduction formulæ
2. Representations
| Generator | Continuum | Lattice |
|---|---|---|
3. Dual Representations
3.1. Schrödinger Algebra
3.2. Conformal Galilean Algebra I
3.3. Conformal Galilean Algebra II
3.4. Parabolic Sub-Algebras
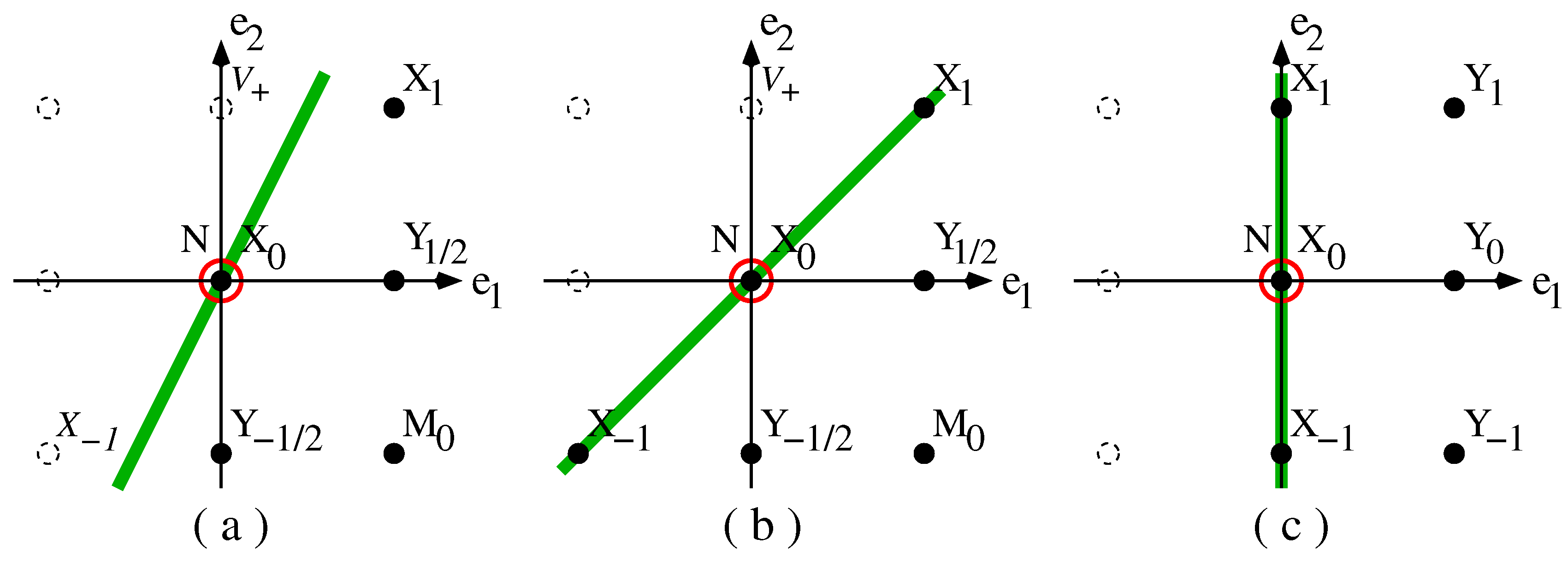
4. Causality
5. Conclusions
Acknowledgments
Conflicts of Interest
References and Notes
- Henkel, M.; Pleimling, M. Non-Equilibrium Phase Transitions Volume 2: Ageing and Dynamical Scaling Far from Equilibrium; Springer: Heidelberg, Germany, 2010. [Google Scholar]
- Täuber, U.C. Critical Dynamics: A Field Theory Apporach to Equilibrium and Non-Equilibrium Scaling Behaviour; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Cartan, É. Les groupes de transformation continus, infinis, simples. Ann. Sci. Ecole Norm. S. 1909, 26, 93–161. [Google Scholar]
- Belavin, A.A.; Polyakov, A.M.; Zamolodchikov, A.B. Infinite conformal symmetry in two-dimensional quantum field-theory. Nucl. Phys. B 1984, 241, 333–380. [Google Scholar] [CrossRef]
- Di Francesco, P.; Mathieu, P.; Sénéchal, D. Conformal Field-Theory; Springer: Heidelberg, Germany, 1997. [Google Scholar]
- Unterberger, J.; Roger, C. The Schrödinger–Virasoro Algebra; Springer: Heidelberg, Germany, 2011. [Google Scholar]
- Henkel, M. Schrödinger-invariance and strongly anisotropic critical systems. J. Stat. Phys. 1994, 75, 1023–1061. [Google Scholar] [CrossRef]
- Henkel, M. Phenomenology of local scale invariance: From conformal invariance to dynamical scaling. Nucl. Phys. B 2002, 641, 405–486. [Google Scholar] [CrossRef]
- Roger, C.; Unterberger, J. The Schrödinger–Virasoro Lie group and algebra: From geometry to representation theory. Ann. Henri Poincare 2006, 7, 1477–1529. [Google Scholar] [CrossRef]
- To see this explicitly, one should exponentiate these generators to create their corresponding finite transformations, see [11].
- Henkel, M.; Unterberger, J. Schrödinger invariance and space-time symmetries. Nucl. Phys. B 2003, 660, 407–435. [Google Scholar] [CrossRef]
- Lie, S. Über die Integration durch bestimmte Integrale von einer Klasse linearer partieller Differentialgleichungen. Arch. Math. Nat. 1881, 6, 328–368. [Google Scholar]
- Jacobi, C.G. Vorlesungen über Dynamik (1842/43), 4. Vorlesung. In Gesammelte Werke; Clebsch, A., Lottner, E., Eds.; Akademie der Wissenschaften: Berlin, Germany, 1866. [Google Scholar]
- Niederer, U. The maximal kinematical invariance group of the free Schrödinger equation. Helv. Phys. Acta 1972, 45, 802–810. [Google Scholar]
- Unitarity of the representation implies the bound [16].
- Lee, K.M.; Lee, Sa.; Lee, Su. Nonrelativistic Superconformal M2-Brane Theory. J. High Energy Phys. 2009. [Google Scholar] [CrossRef]
- Bargman, V. On unitary ray representations of continuous groups. Ann. Math. 1954, 56, 1–46. [Google Scholar] [CrossRef]
- Henkel, M. Extended scale-invariance in strongly anisotropic equilibrium critical systems. Phys. Rev. Lett. 1997, 78, 1940–1943. [Google Scholar] [CrossRef]
- Ovsienko, V.; Roger, C. Generalisations of Virasoro group and Virasoro algebras through extensions by modules of tensor-densities on S1. Indag. Math. 1998, 9, 277–288. [Google Scholar] [CrossRef]
- The name was originally given since at that time, relationships with physical ageing (altern in German) were still expected.
- Cherniha, R.; Henkel, M. The exotic conformal Galilei algebra and non-linear partial differential equations. J. Math. Anal. Appl. 2010, 369, 120–132. [Google Scholar] [CrossRef]
- Bagchi, A.; Mandal, I. On representations and correlation functions of Galilean conformal algebra. Phys. Lett. B 2009, 675, 393–397. [Google Scholar] [CrossRef]
- Havas, P.; Plebanski, J. Conformal extensions of the Galilei group and their relation to the Schrödinger group. J. Math. Phys. 1978, 19, 482–488. [Google Scholar] [CrossRef]
- Martelli, D.; Tachikawa, Y. Comments on Galiean conformal field-theories and their geometric realisation. J. High Energy Phys. 2010, 1005:091. [Google Scholar] [CrossRef]
- Negro, J.; del Olmo, M.A.; Rodríguez-Marco, A. Nonrelativistic conformal groups. J. Math. Phys. 1997, 38, 3786–3809. [Google Scholar] [CrossRef]
- Negro, J.; del Olmo, M.A.; Rodríguez-Marco, A. Nonrelativistic conformal groups II. J. Math. Phys. 1997, 38, 3810–3831. [Google Scholar] [CrossRef]
- In the context of asymptotically flat 3D gravity, an isomorphic Lie algebra is known as BMS algebra, [28,29,30,31,32].
- Bagchi, A.; Detournay, S.; Grumiller, D. Flat-space chiral gravity. Phys. Rev. Lett. 2012, 109. [Google Scholar] [CrossRef] [PubMed]
- Bagchi, A.; Detournay, S.; Fareghbal, R.; Simón, J. Holographies of 3D flat cosmological horizons. Phys. Rev. Lett. 2013, 110, 141302:1–141302:5. [Google Scholar] [CrossRef] [PubMed]
- Barnich, G.; Compère, G. Classical central extension for asymptotic symmetries at null infinity in three spacetime dimensions. Class. Quantum Grav. 2007, 24. [Google Scholar] [CrossRef]
- Barnich, G.; Compère, G. Classical central extension for asymptotic symmetries at null infinity in three spacetime dimensions (corrigendum). Class. Quant. Grav. 2007, 24, 3139. [Google Scholar] [CrossRef]
- Barnich, G.; Gomberoff, A.; González, H.A. Three-dimensional Bondi-Metzner-Sachs invariant two-dimensional field-theories as the flat limit of Liouville theory. Phys. Rev. D 2007, 87. [Google Scholar] [CrossRef]
- Henkel, M.; Schott, R.; Stoimenov, S.; Unterberger, J. The Poincaré algebra in the context of ageing systems: Lie structure, representations, Appell systems and coherent states. Conflu. Math. 2012, 4, 1250006:1–1250006:19. [Google Scholar] [CrossRef]
- Lukierski, J.; Stichel, P.C.; Zakrewski, W.J. Exotic galilean conformal symmetry and its dynamical realisations. Phys. Lett. A 2006, 357, 1–5. [Google Scholar] [CrossRef]
- Lukierski, J.; Stichel, P.C.; Zakrewski, W.J. Acceleration-extended galilean symmetries with central charges and their dynamical realizations. Phys. Lett. B 2007, 650, 203–207. [Google Scholar] [CrossRef]
- Henkel, M.; Hosseiny, A.; Rouhani, S. Logarithmic exotic conformal galilean algebras. Nucl. Phys. B 2014, 879, 292–317. [Google Scholar] [CrossRef]
- An infinite-dimensional extension of ecga does not appear to be possible.
- Henkel, M.; Enss, T.; Pleimling, M. On the identification of quasiprimary operators in local scale-invariance. J. Phys. A Math. Gen. 2006, 39, L589–L598. [Google Scholar] [CrossRef]
- Stoimenov, S.; Henkel, M. Non-local representations of the ageing algebra in higher dimensions. J. Phys. A Math. Theor. 2013, 46. [Google Scholar] [CrossRef]
- Minic, D.; Vaman, D.; Wu, C. Three-point function of aging dynamics and the AdS-CFT correspondence. Phys. Rev. Lett. 2012, 109. [Google Scholar] [CrossRef] [PubMed]
- Knapp, A.W. Representation Theory of Semisimple Groups: An Overview Based on Examples; Princeton University Press: Princeton, NJ, USA, 1986. [Google Scholar]
- Duval, C.; Horváthy, P.A. Non-relativistic conformal symmetries and Newton–Cartan structures. J. Phys. A Math. Theor. 2009, 42. [Google Scholar] [CrossRef]
- Although it might appear that z = 2, the renormalisation of the interactions, required in interacting field-theories, can change this and produce non-trivial values of z, see e.g., [2].
- Picone, A.; Henkel, M. Local scale-invariance and ageing in noisy systems. Nucl. Phys. B 2004, 688, 217–265. [Google Scholar] [CrossRef]
- Polyakov, A.M. Conformal symmetry of critical fluctuations. Sov. Phys. JETP Lett. 1970, 12, 381–383. [Google Scholar]
- Barabási, A.-L.; Stanley, H.E. Fractal Concepts in Surface Growth; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Henkel, M.; Durang, X. Spherical model of interface growth. J. Stat. Mech. 2015. [Google Scholar] [CrossRef]
- For d = 1, the dynamics of the Arcetri model is identical [47] to the one of the spherical Sherrington–Kirkpatrick model. The model is defined by the classical hamiltonian , where the are independent centred gaussian variables, of variance ∼O(1/), and the si satisfy the spherical constraint . As usual, the dynamics if given by a Langevin equation [49]. This problem is also equivalent to the statistics of the gap to the largest eigenvalue of a × gaussian unitary matrix [50,51], for → ∞. Work is in progress on identifying interface growth models with .
- Cugliandolo, L.F.; Dean, D. Full dynamical solution for a spherical spin-glass model. J. Phys. A Math. Gen. 1995, 28. [Google Scholar] [CrossRef]
- Fyodorov, Y.V.; Perret, A.; Schehr, G. Large-time zero-temperature dynamics of the spherical p = 2 spin model of finite size. Available online: http://arxiv.org/pdf/1507.08520.pdf (accessed on 4 November 2015).
- Perret, A. Statistique D’extrêmes de Variables Aléatoires Fortement Corréées. Ph.D. Thesis, Université Paris Sud, Orsay, France, 2015. [Google Scholar]
- Glauber, R.J. Time-dependent statistics of the Ising model. J. Math. Phys. 1963, 4, 294. [Google Scholar] [CrossRef]
- Godrèche, C.; Luck, J.-M. Response of non-equilibrium systems at criticality: Exact results for the Glauber-Ising chain. J. Phys. A Math. Gen. 2000, 33. [Google Scholar] [CrossRef]
- Henkel, M.; Schütz, G.M. On the universality of the fluctuation-dissipation ratio in non-equilibrium critical dynamics. J. Phys. A Math. Gen. 2004, 37, 591–604. [Google Scholar] [CrossRef]
- Lippiello, E.; Zannetti, M. Fluctuation-dissipation ratio in the one-dimensional kinetic Ising model. Phys. Rev. E 2000, 61, 3369–3374. [Google Scholar] [CrossRef]
- A historical comment: We have been aware of this since the very beginning of our investigations, in the early 1990s. The exact result Equation (33) looked strange, since the time-space response of the Glauber–Ising model does have the nice form , as expected from Galilei-invariance. Only several years later, we saw how the representations of the Schrödinger algebra had to be generalised, which was only possible by giving up explicitly time-translation-invariance [38,44].
- Henkel, M. On logarithmic extensions of local scale-invariance. Nucl. Phys. B 2013, 869, 282–302. [Google Scholar] [CrossRef]
- Henkel, M.; Noh, J.D.; Pleimling, M. Phenomenology of ageing in the Kardar–Parisi–Zhang equation. Phys. Rev. E 2012, 85. [Google Scholar] [CrossRef] [PubMed]
- Henkel, M.; Rouhani, S. Logarithmic correlators or responses in non-relativistic analogues of conformal invariance. J. Phys. A Math. Theor. 2013, 46. [Google Scholar] [CrossRef]
- The specific structure of the dynamical functional , see Equation (22), of the Arcetri model (and, more generally, of the kinetic spherical model [44]) leads to , such that time-translation-invariance appears to be formally satisfied, in contrast to the 1D Glauber–Ising model, where .
- Henkel, M.; Schütz, G. Schrödinger invariance in discrete stochastic systems. Int. J. Mod. Phys. B 1994, 8, 3487–3499. [Google Scholar] [CrossRef]
- The scaling from Equation (39) is indeed recovered in several simple lattice models, see [61] for more details.
- Stoimenov, S.; Henkel, M. On non-local representations of the ageing algebra. Nucl. Phys. B 2011, 847, 612–627. [Google Scholar]
- See [39] for an application to the kinetics of the phase-separating (model-B dynamics) spherical model.
- Gurarie, V. Logarithmic operators in conformal field theory. Nucl. Phys. B 1993, 410, 535–549. [Google Scholar] [CrossRef]
- Mathieu, P.; Ridout, D. From Percolation to Logarithmic Conformal Field Theory. Phys. Lett. B 2007, 657, 120–129. [Google Scholar] [CrossRef]
- Mathieu, P.; Ridout, D. Logarithmic (2, p) minimal models, their logarithmic coupling and duality. Nucl. Phys. B 2008, 801, 268–295. [Google Scholar] [CrossRef]
- Rahimi Tabar, M.R.; Aghamohammadi, A.; Khorrami, M. The logarithmic conformal field theories. Nucl. Phys. B 1997, 497, 555–566. [Google Scholar] [CrossRef] [Green Version]
- Saleur, H. Polymers and percolation in two dimensions and twisted N = 2 supersymmetry. Nucl. Phys. B 1992, 382, 486–531. [Google Scholar] [CrossRef]
- Hosseiny, A.; Rouhani, S. Logarithmic correlators in non-relativistic conformal field-theory. J. Math. Phys. 2010, 51. [Google Scholar] [CrossRef]
- Hosseiny, A.; Rouhani, S. Affine extension of galilean conformal algebra in 2 + 1 dimensions. J. Math. Phys. 2010, 51. [Google Scholar] [CrossRef]
- Hosseiny, A.; Naseh, A. On holographic realization of logarithmic Galilean conformal algebra. J. Math. Phys. 2011, 52. [Google Scholar] [CrossRef]
- Moghimi-Araghi, S.; Rouhani, S.; Saadat, M. Correlation functions and AdS/LCFT correspondence. Nucl. Phys. B 2000, 599, 531–546. [Google Scholar] [CrossRef]
- Gray, N.; Minic, D.; Pleimling, M. On non-equilibrium physics and string theory. Int. J. Mod. Phys. A 2013, 28. [Google Scholar] [CrossRef]
- Hyun, S.; Jeong, J.; Kim, B.S. Aging logarithmic conformal field theory: A holographic view. Nucl. Phys. B 2013, 874. [Google Scholar] [CrossRef]
- Giulini, D. On Galilei-invariance in quantum mechanics and the Bargmann superselection rule. Ann. Phys. 1996, 249, 222–235. [Google Scholar] [CrossRef]
- Henkel, M.; Stoimenov, S. Physical ageing and Lie algebras of local scale-invariance. In Lie Theory and Its Applications in Physics; Dobrev, V., Ed.; Springer: Heidelberg, Germany, 2015; Volume 111, pp. 33–50. [Google Scholar]
- Dobrev, V.K. Non-relativistic holography: A group-theoretical perspective. Int. J. Mod. Phys. A 2013, 29. [Google Scholar] [CrossRef]
- Son, D.T. Towards an AdS/cold atom correspondence: A geometric realisation of the Schrödinger symmetry. Phys. Rev. D 2008, 78. [Google Scholar] [CrossRef]
- Aizawa, N.; Dobrev, V.K. Intertwining Operator Realization of Non-Relativistic Holography. Nucl. Phys. B 2010, 828, 581–593. [Google Scholar] [CrossRef]
- Perrroud, M. Projective representations of the Schrödinger group. Helv. Phys. Acta 1977, 50, 233–252. [Google Scholar]
- Akhiezer, N.I. Lectures on Integral Transforms (Translations of Mathematical Monographs); American Mathematical Society: Providence, RI, USA, 1988. [Google Scholar]
- Hille, E. Ordinary Differential Equations in the Complex Domain; Wiley: New York, NY, USA, 1976. [Google Scholar]
- In the numerous numerical tests of Schrödinger-invariance, the causality of the response function is simply taken for granted in the physics literature; for a review see e.g., [1]. For more recent applications and extensions, see [59].
- Ivashkevich, E.V. Symmetries of the stochastic Burgers equation. J. Phys. A Math. Gen. 1997, 30, L525–L533. [Google Scholar] [CrossRef]
- Hartong, J.; Kiritsis, E.; Obers, N. Schrödinger-invariance from Lifshitz isometries in holography and field-theory. Phys. Rev. D 2015, 92. [Google Scholar] [CrossRef]
- Setare, M.R.; Kamali, V. Anti-de Sitter/boundary conformal field theory correspondence in the non-relativistic limit. Eur. Phys. J. C 2012, 72. [Google Scholar] [CrossRef]
- Stoimenov, S.; Henkel, M. From conformal invariance towards dynamical symmetries of the collisionless Boltzmann equation. Symmetry 2015, 7, 1595–1612. [Google Scholar] [CrossRef]
- How should one dualise in the ecga? With respect to θ or to the rapidity vector γ?
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Henkel, M. Dynamical Symmetries and Causality in Non-Equilibrium Phase Transitions. Symmetry 2015, 7, 2108-2133. https://doi.org/10.3390/sym7042108
Henkel M. Dynamical Symmetries and Causality in Non-Equilibrium Phase Transitions. Symmetry. 2015; 7(4):2108-2133. https://doi.org/10.3390/sym7042108
Chicago/Turabian StyleHenkel, Malte. 2015. "Dynamical Symmetries and Causality in Non-Equilibrium Phase Transitions" Symmetry 7, no. 4: 2108-2133. https://doi.org/10.3390/sym7042108





