Some Invariants of Jahangir Graphs

Abstract

In this report, we compute closed forms of M-polynomial, first and second Zagreb polynomials and forgotten polynomial for Jahangir graphs J_n,_m for all values of m and n. From the M-polynomial, we recover many degree-based topological indices such as first and second Zagreb indices, modified Zagreb index, Symmetric division index, etc. We also compute harmonic index, first and second multiple Zagreb indices and forgotten index of Jahangir graphs. Our results are extensions of many existing results.

1. Introduction

In mathematical chemistry, mathematical tools like polynomials and topological-based numbers predict properties of compounds without using quantum mechanics. These tools, in combination, capture information hidden in the symmetry of molecular graphs. A topological index is a function that characterizes the topology of the graph. Most commonly known invariants of such kinds are degree-based topological indices. These are actually the numerical values that correlate the structure with various physical properties, chemical reactivity, and biological activities [1,2,3,4,5]. It is an established fact that many properties such as heat of formation, boiling point, strain energy, rigidity and fracture toughness of a molecule are strongly connected to its graphical structure and this fact plays a synergic role in chemical graph theory.

Algebraic polynomials play a significant part in chemistry. Hosoya polynomial [6] is one such well-known example which determines distance-based topological indices. M-polynomial [7], introduced in 2015, plays the same role in determining closed forms of many degree-based topological indices [8,9,10,11]. The main advantage of M-polynomial is the wealth of information that it contains about degree-based graph invariants.

The Jahangir graph J_n,_m is a graph on $nm+1$ vertices and $m(n+1)$ edges $\forall n\ge 2$ and $m\ge 3$. J_n,_m consists of a cycle $c_{nm}$ with one additional vertex which is adjacent to m vertices of $c_{nm}$ at distance to each other. Figure 1 shows some particular cases of J_n,_m.

The Figure $J_{2,8}$ is carved on Jahangir’s tomb. It is situated 5 km northwest of Lahore, Pakistan. In [12], Laurdusamy et al. computed the pebbling number of Jahangir graph $J_{2,m}$ for $m\ge 8$. Mojdeh et al. in [13] computed domination number in $J_{2,m}$ and Ramsey number for $J_{3,m}$ in [14] by Ali et al. Weiner index and Hosoya Polynomial of $J_{2,m}$ $J_{3,m}$ and $J_{4,m}$ are computed in [15,16,17]. All these results are partial and need to be generalized for all values of m and n.

In this article, we compute M-polynomial, first and second Zagreb polynomials and forgotten polynomial of J_n,_m. We also compute many degree-based topological indices for this family of the graph. We analyze these indices against parametric values m and n graphically and draw some nice conclusions as well.

Throughout this report, G is a connected graph, V(G) and E(G) are the vertex set and the edge set, respectively, and $d_v$ denotes the degree of a vertex v.

Definition 1.

The M-polynomial of G is defined as [7]:

$$M\left(G,x,y\right)={\displaystyle \sum _{\delta \le i\le j\le \Delta }{m}_{ij}\left(G\right)x^i{y}^j}$$

where $\delta =Min\left\{d_v\right|v\in V(G)\},$ $\Delta =Max\left\{d_v\right|v\in V(G)\},$ and $m_{ij}(G)$ is the edge $vu\in E(G)$ such that $\left\{d_v,d_u\right\}=\left\{i,j\right\}.$

The first topological index was introduced by Wiener [18] and it was named path number, which is now known as Wiener index. In chemical graph theory, this is the most studied molecular topological index due to its wide applications, see for details [19,20]. Randic index [21], denoted by $R_{-\frac{1}{2}}(G)$ and introduced by Milan Randic in 1975 is also one of the oldest topological indexes. The Randic index is defined as:

$$R_{-\frac{1}{2}}(G)={\displaystyle \sum _{uv\in E(G)}\frac{1}{\sqrt{d_u{d}_v}}}$$

In 1998, Ballobas and Erdos [22] and Amic et al. [23] gave an idea of generalized Randic index. This index is equally popular among chemists and mathematicians [24]. Many mathematical properties of this index have been discussed in [25]. For a detailed survey, we refer to the book [26].

The general Randic index is defined as:

$$R_{\alpha }(G)={\displaystyle \sum _{uv\in E(G)}\frac{1}{{(d_u{d}_v)}^{\alpha }}}$$

and the inverse Randic index is defined as $R{R}_{\alpha }(G)={\displaystyle \sum _{uv\in E(G)}{(d_u{d}_v)}^{\alpha }.}$

Obviously, $R_{-\frac{1}{2}}(G)$ is the particular case of $R_{\alpha }(G)$ when $\alpha =-\frac{1}{2}$.

The Randic index is the most popular, most often applied and most studied among all other topological indices. Many papers and books [27,28] are written on this topological index. Randic himself wrote two reviews on his Randic index [29,30]. The suitability of the Randic index for drug design was immediately recognized, and eventually, the index was used for this purpose on countless occasions. The physical reason for the success of such a simple graph invariant is still an enigma, although several more-or-less plausible explanations were offered.

Gutman and Trinajstic’ introduced first Zagreb index and second Zagreb index, which are defined as: $M_1(G)={\displaystyle \sum _{uv\in E(G)}(d_u+d_v)}$ and $M_2(G)={\displaystyle \sum _{uv\in E(G)}(d_u\times d_v)}$ respectively. The second modified Zagreb index is defined as:

$${}^m{M}_2\left(G\right)={\displaystyle \sum _{uv\in E(G)}\frac{1}{d(u)d(v)}}$$

For details on these indices, we refer [31,32,33,34] to the readers.

The Symmetric division index is defined as:

$$SDD(G)={\displaystyle \sum _{uv\in E(G)}\left\{\frac{\min (d_u,d_v)}{\max (d_u,d_v)}+\frac{\max (d_u,d_v)}{\min (d_u,d_v)}\right\}}$$

Another variant of Randic index is the harmonic index defined as:

$$H(G)={\displaystyle \sum _{vu\in E(G)}\frac{2}{d_u+d_v}}$$

The Inverse sum-index is defined as:

$$I(G)={\displaystyle \sum _{vu\in E(G)}\frac{d_u{d}_v}{d_u+d_v}}$$

The augmented Zagreb index is defined as:

$$A(G)={\displaystyle \sum _{vu\in E(G)}{\left\{\frac{d_u{d}_v}{d_u+d_v-2}\right\}}^3}$$

and it is useful for computing heat of formation of alkanes [35,36].

Recently, in 2015, Furtula and Gutman introduced another topological index called forgotten index or F-index.

$$F\left(G\right)={\displaystyle \sum _{uv\in E\left(G\right)}\left[{\left(d_u\right)}^2+{\left(d_v\right)}^2\right]}$$

We give derivations of some well-known degree-based topological indices from M-polynomial [7] in

Table 1. Derivation of some degree-based topological indices from M-polynomial.

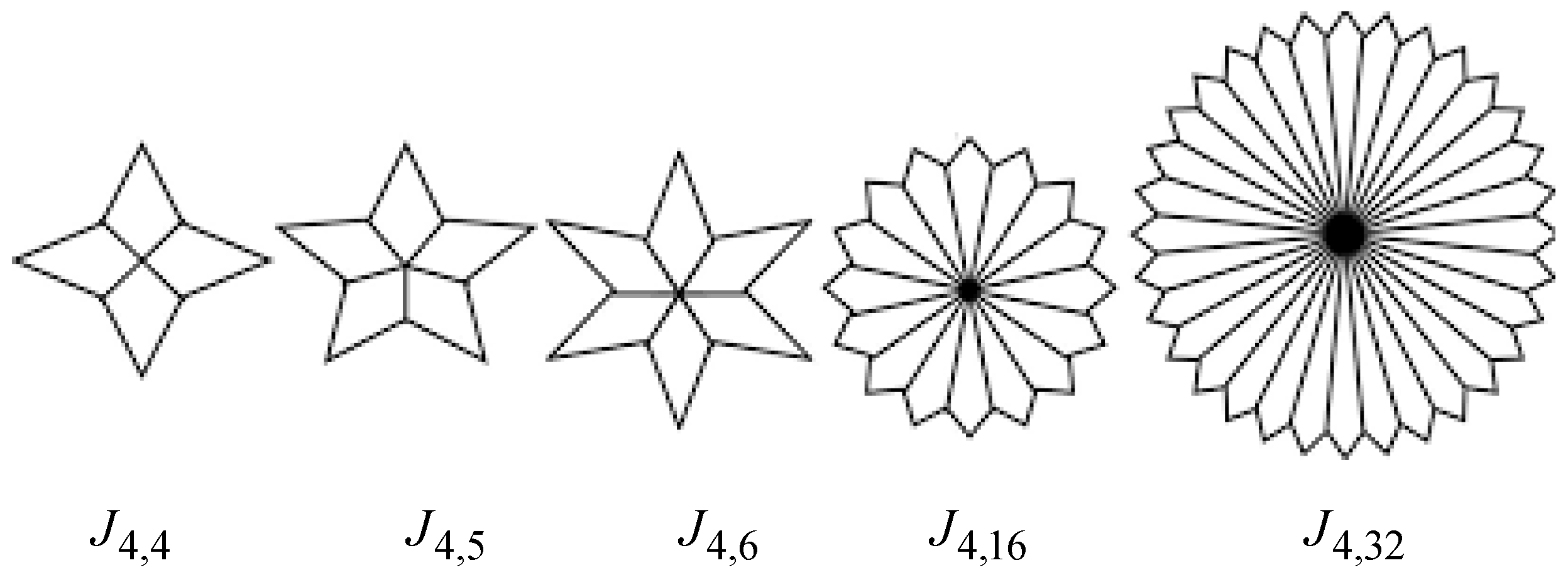
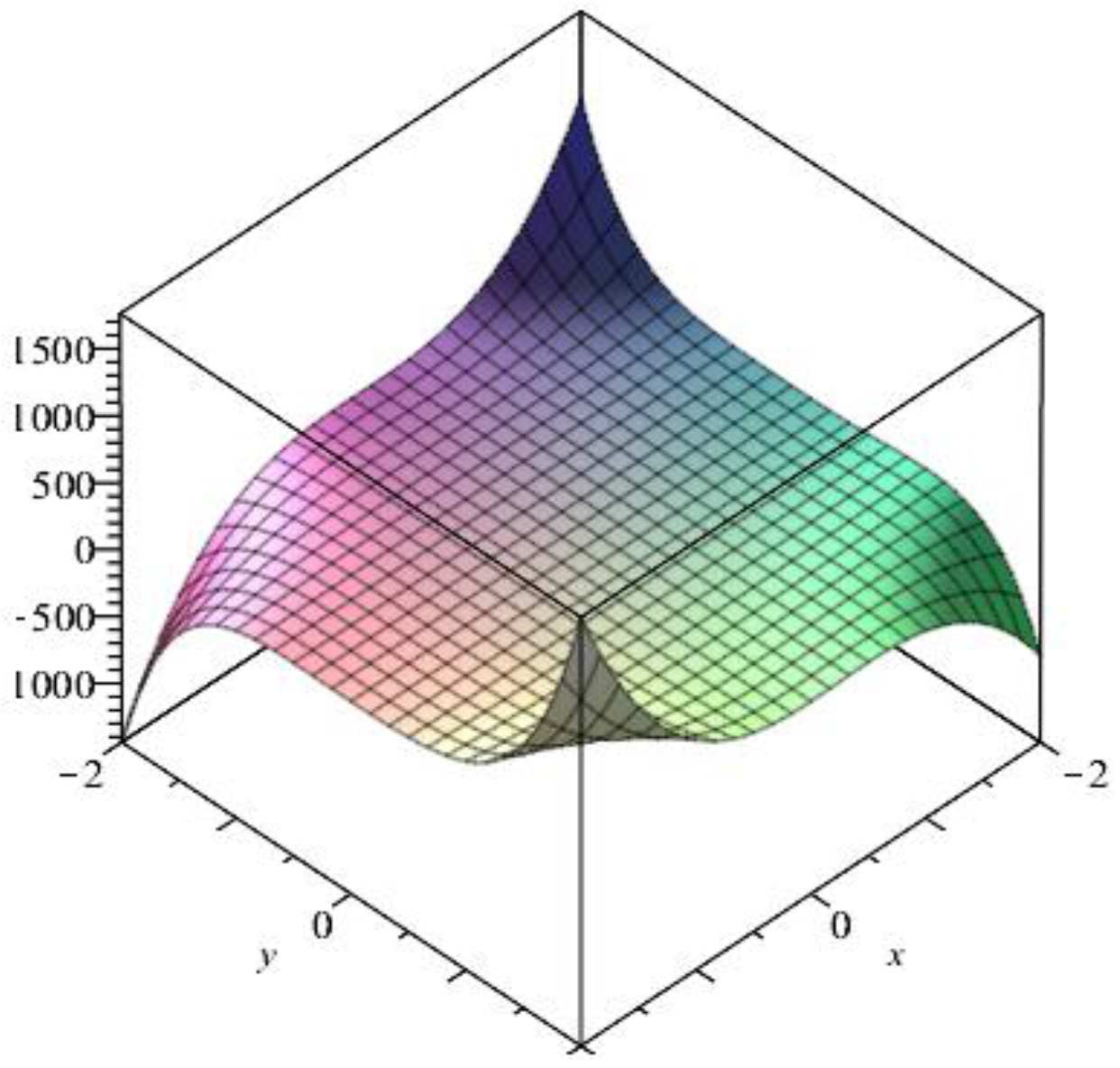
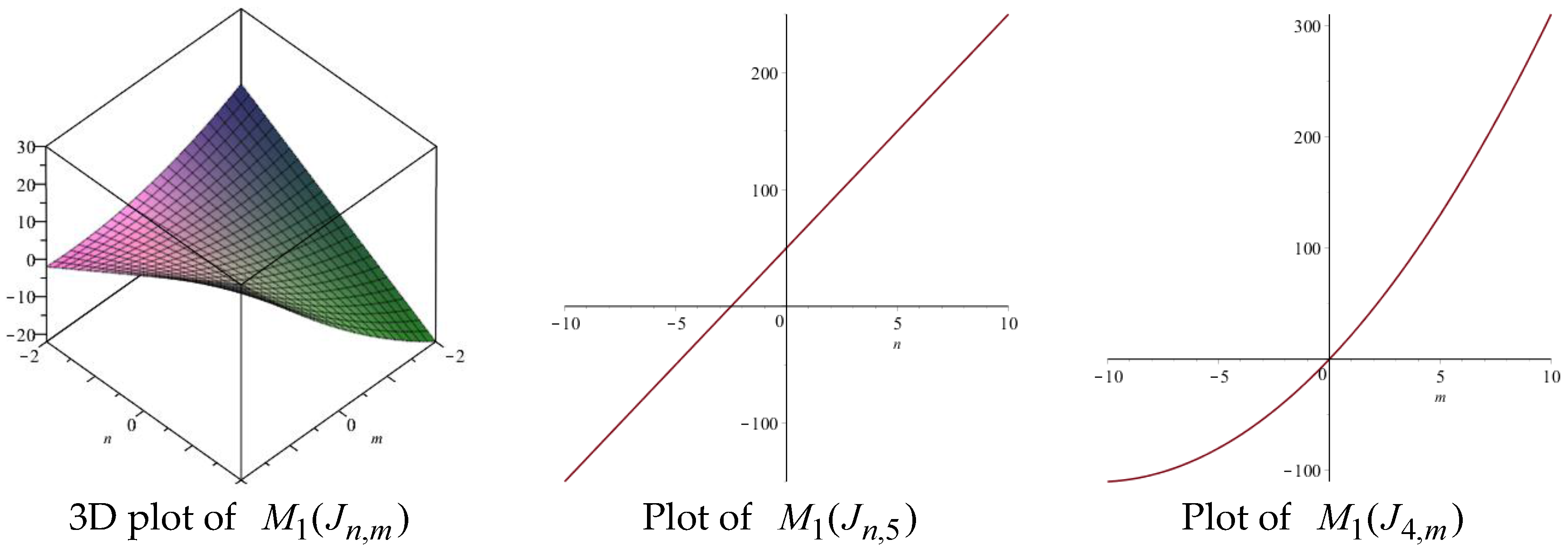
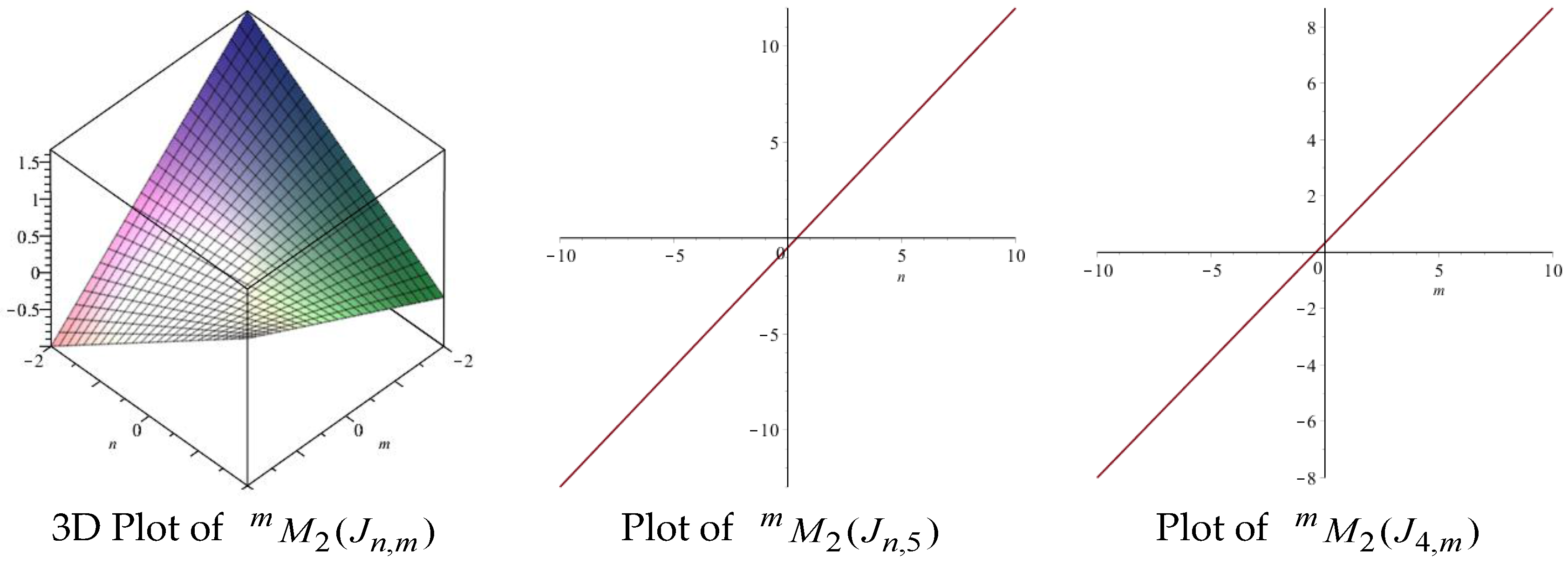
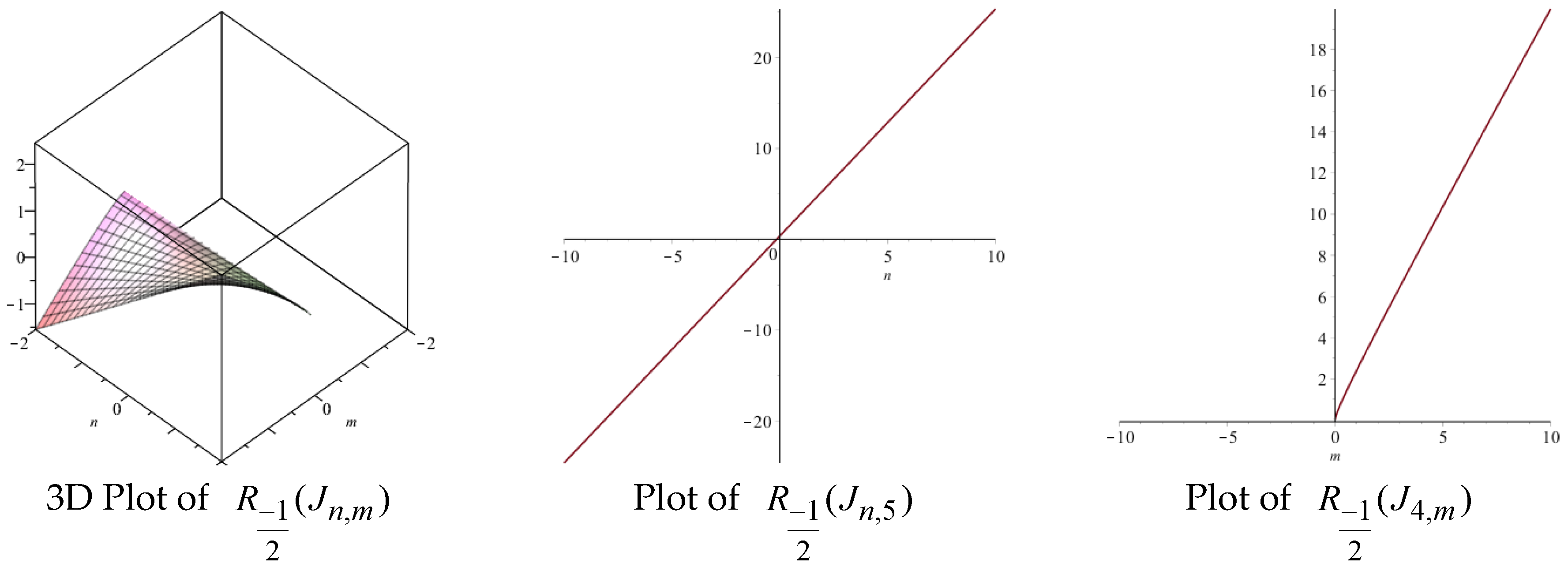
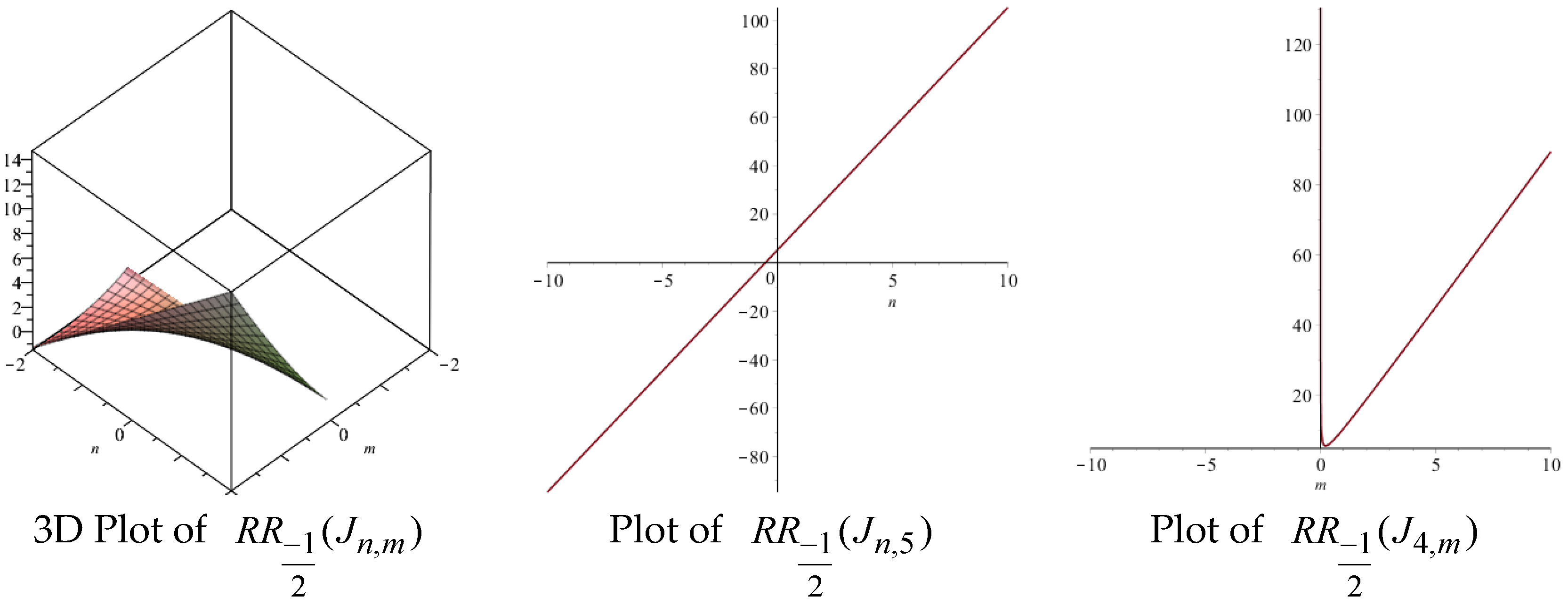
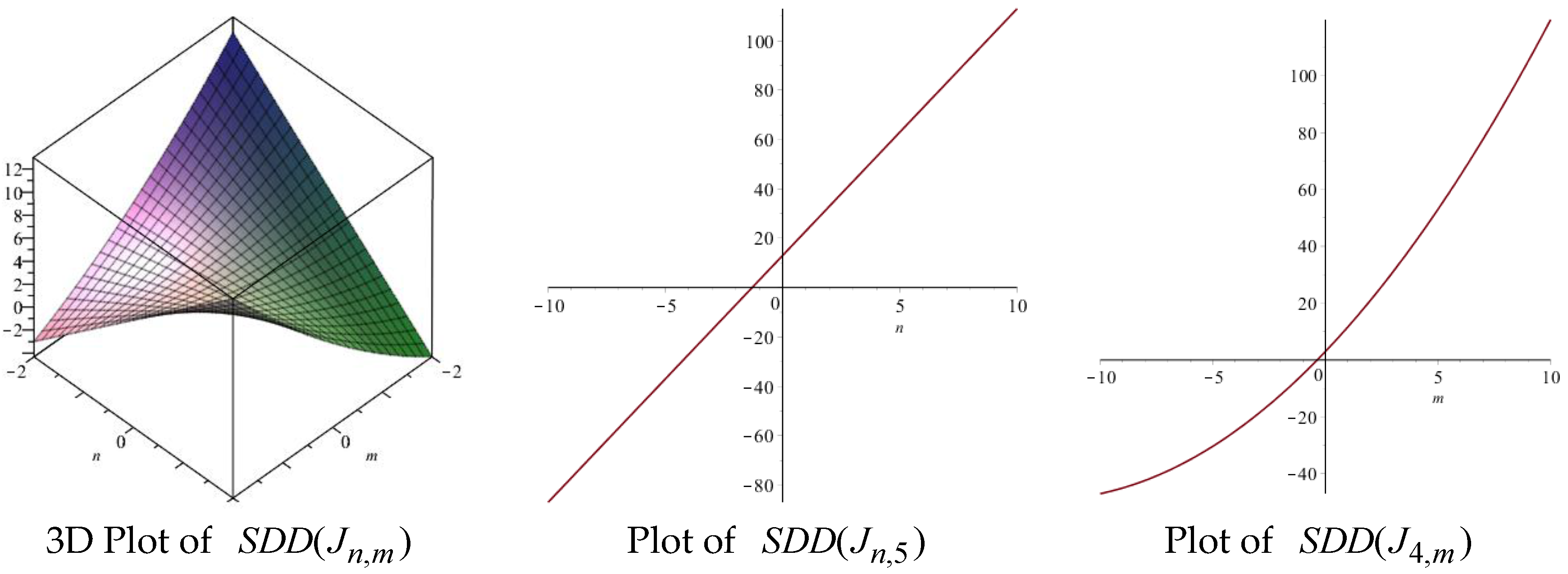
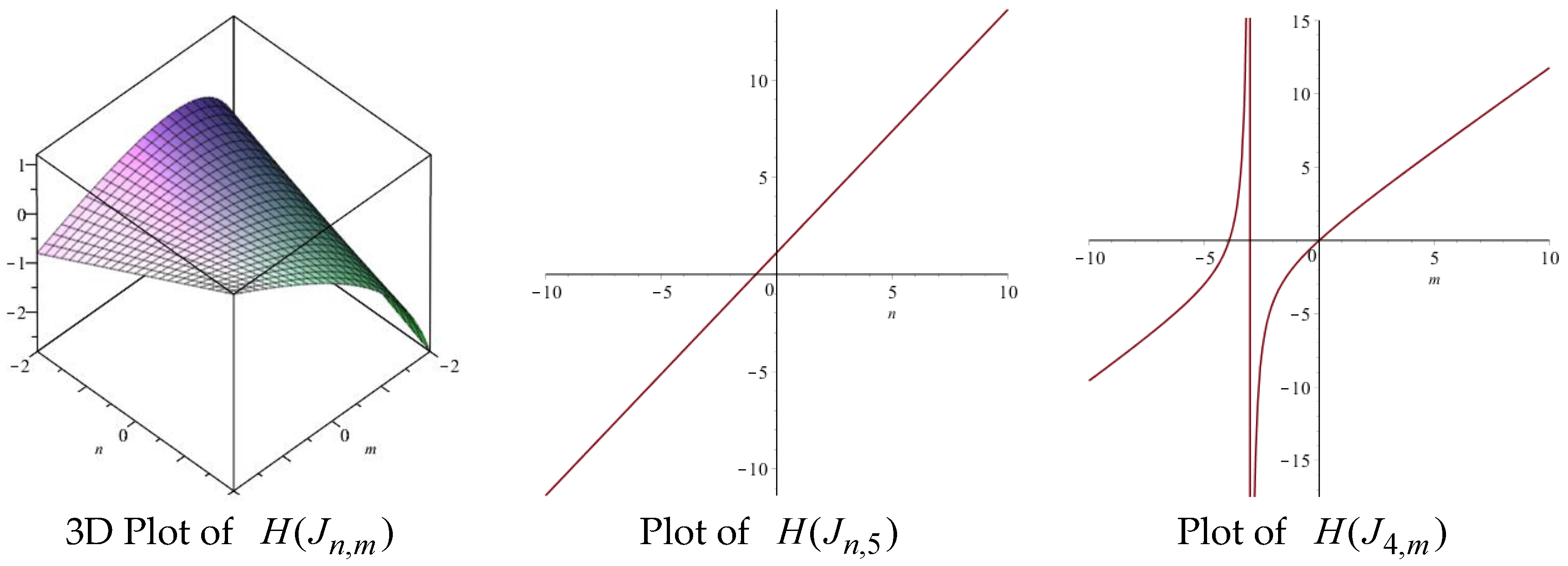
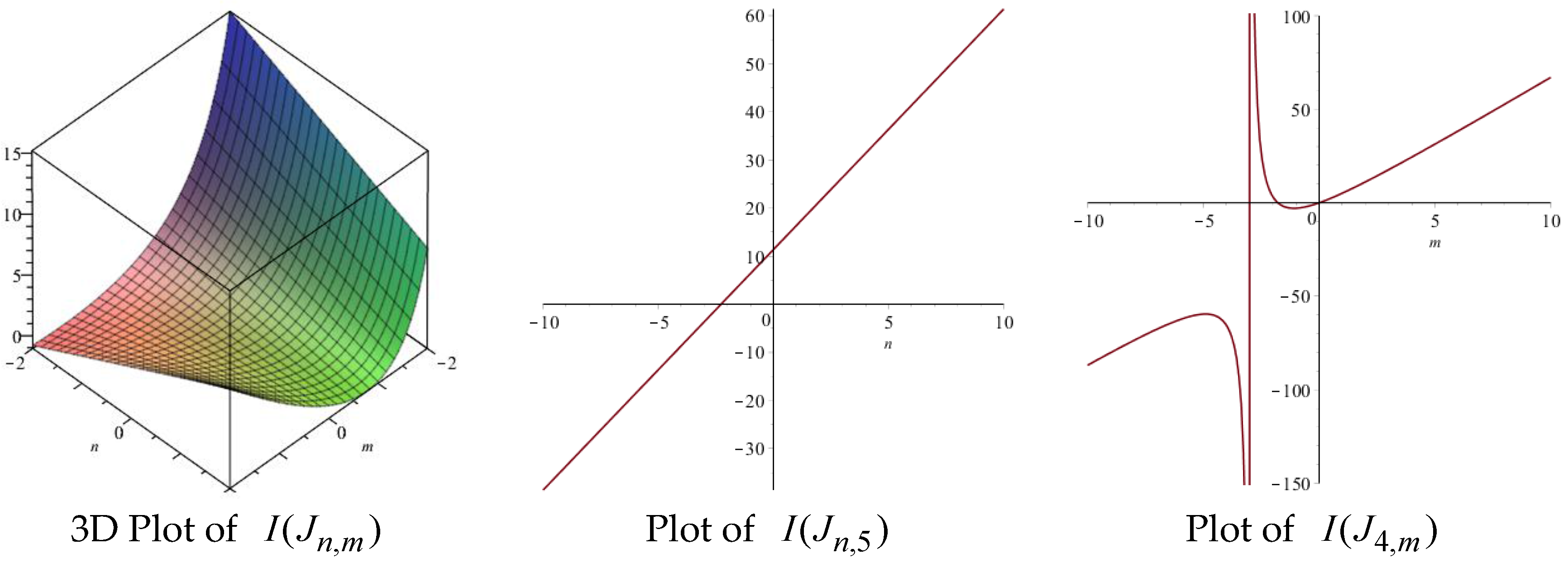
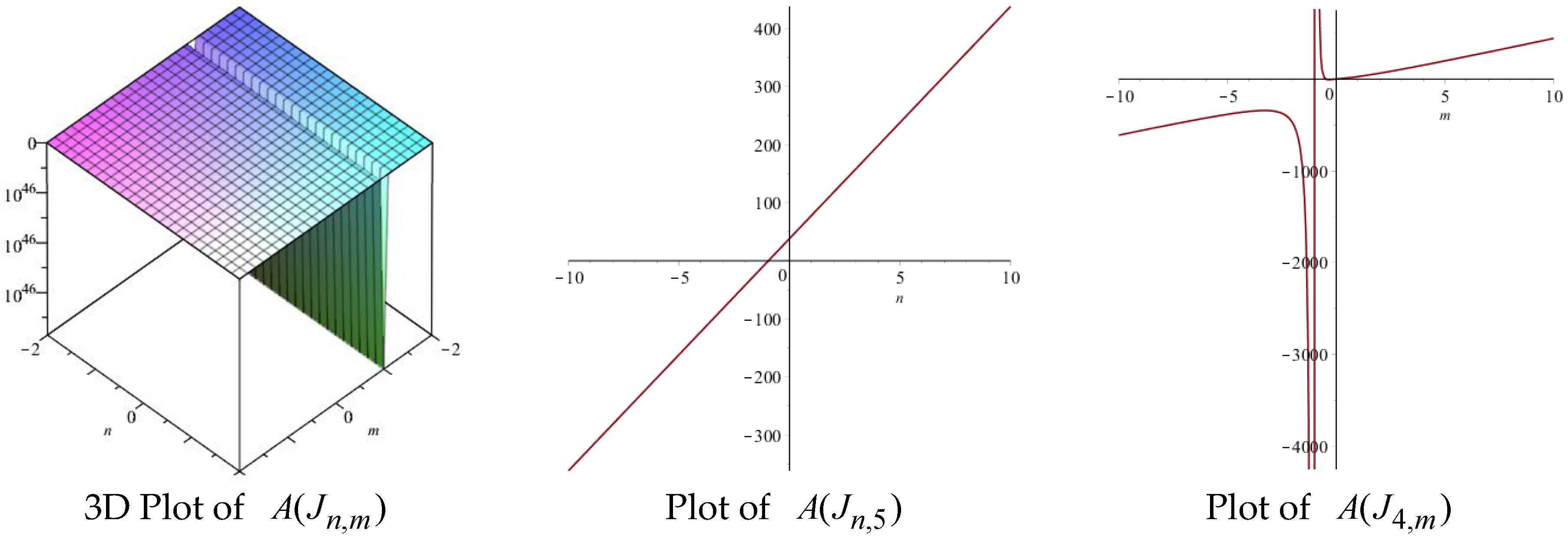
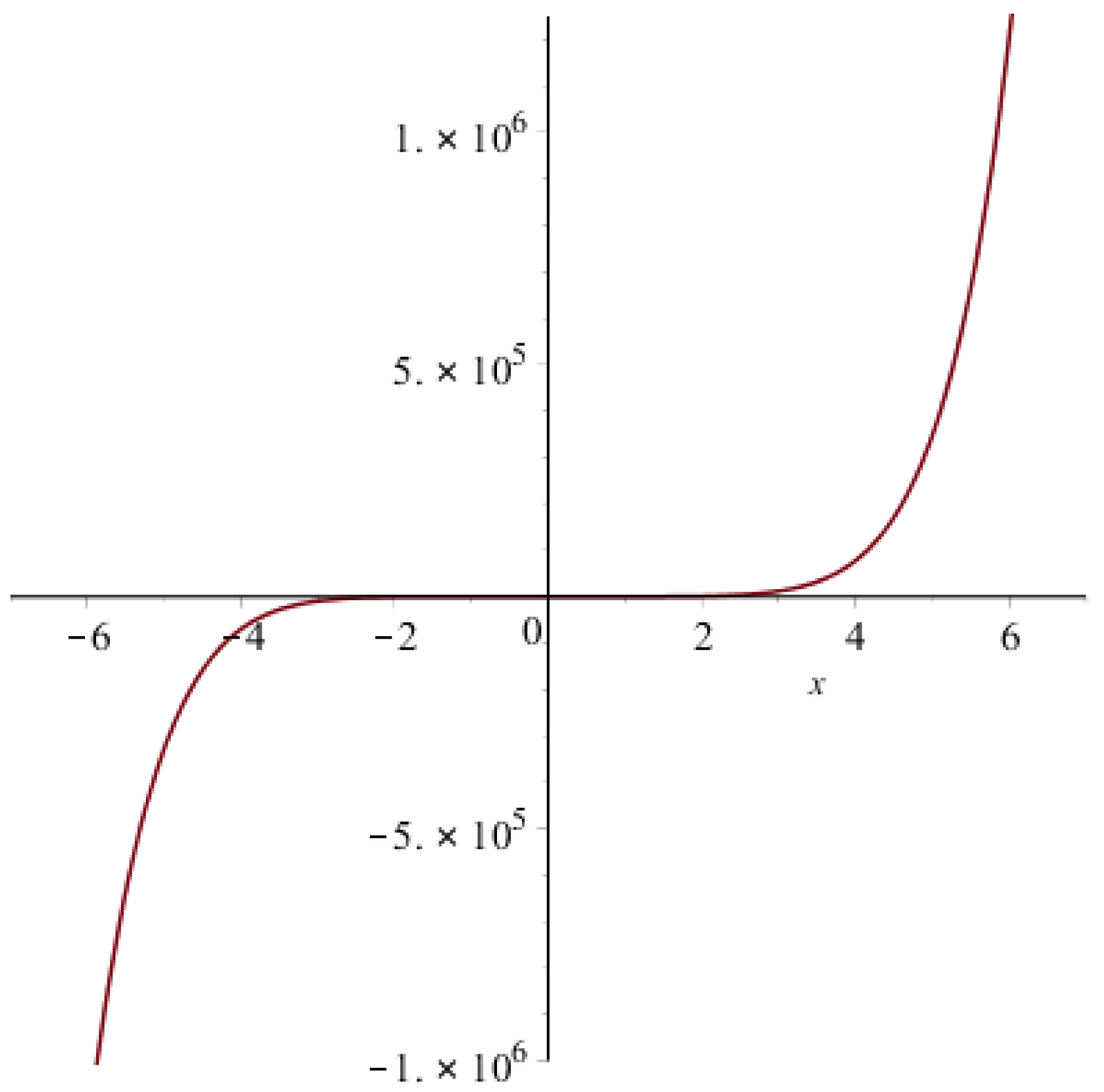
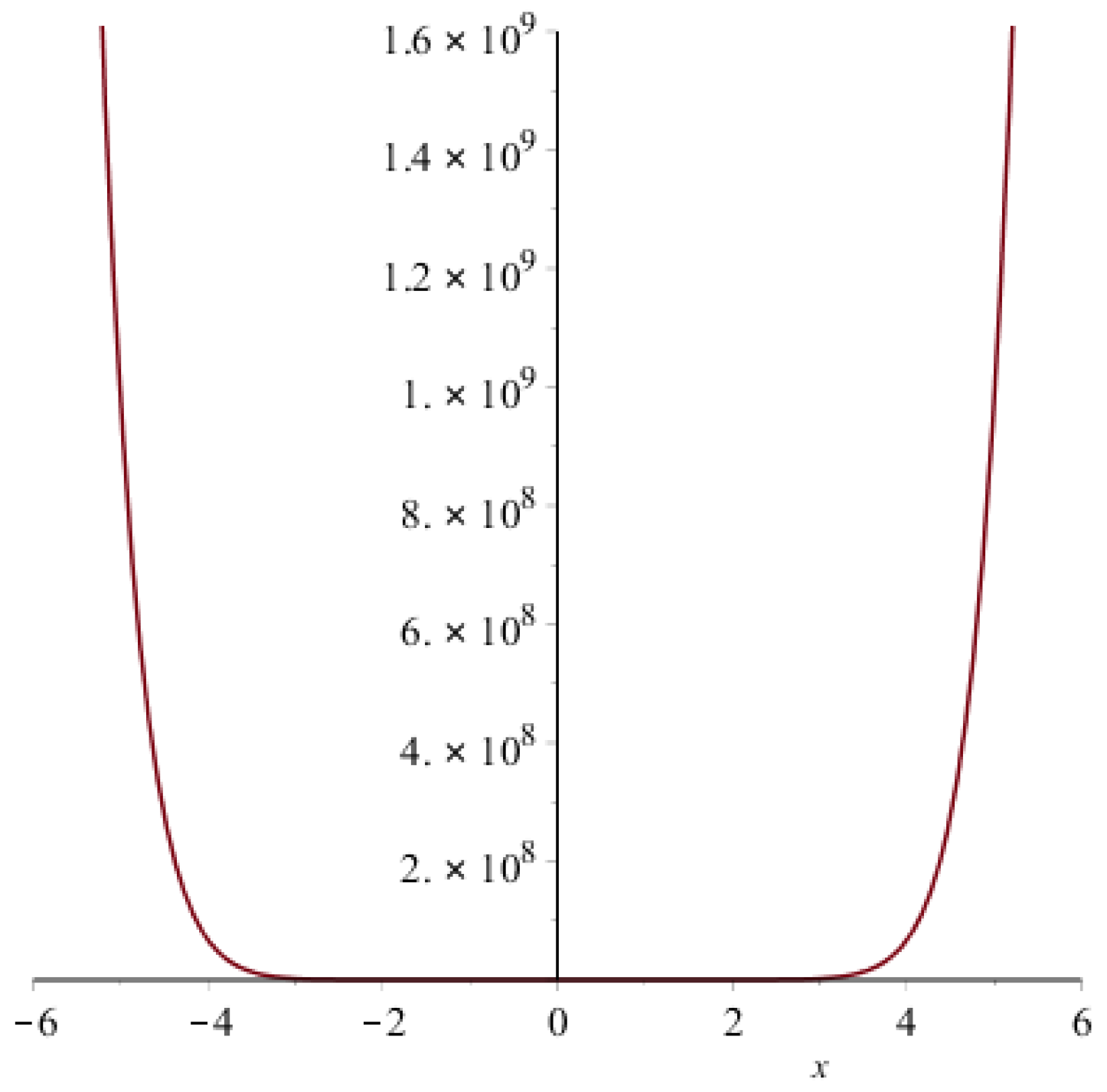
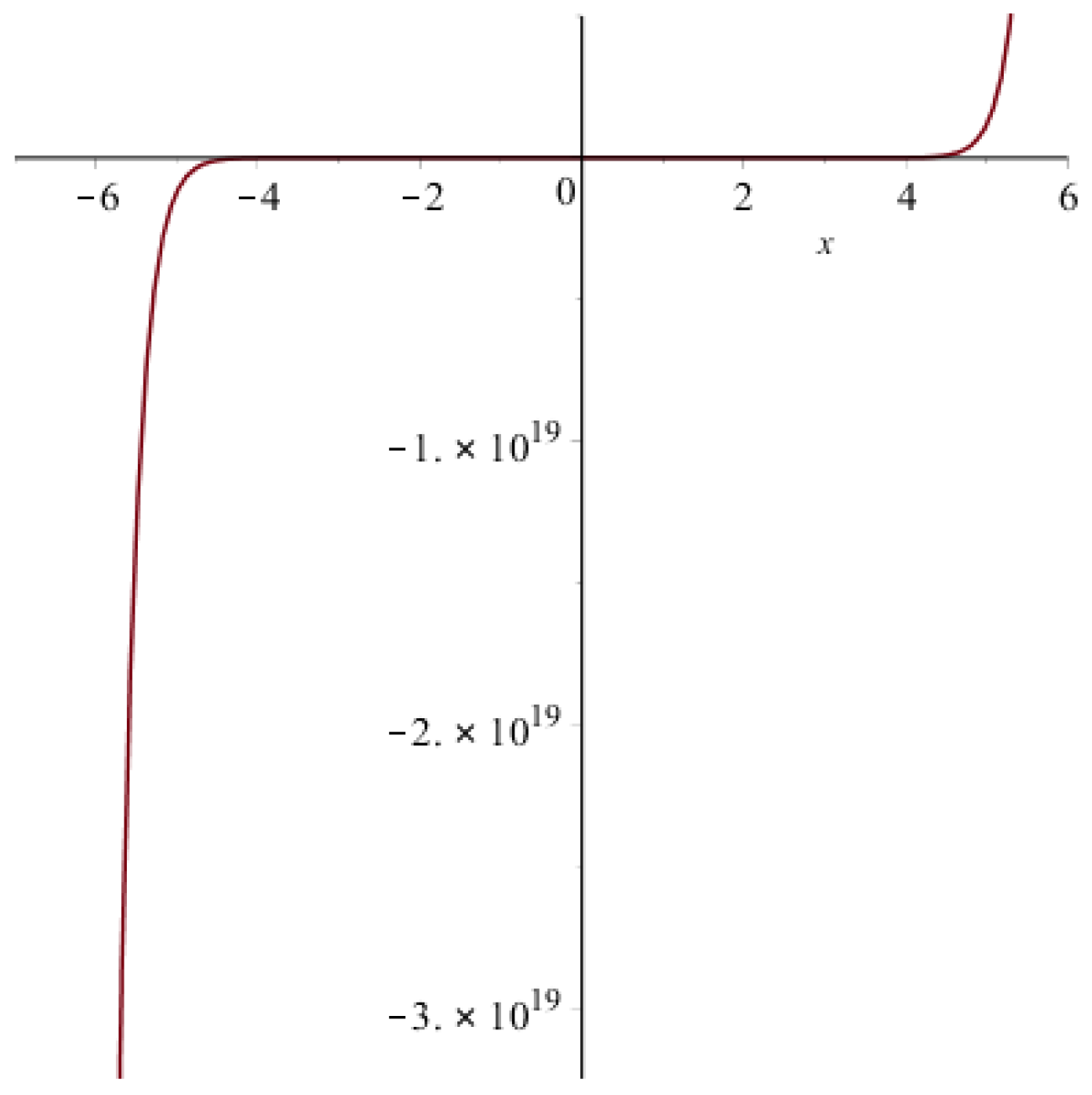
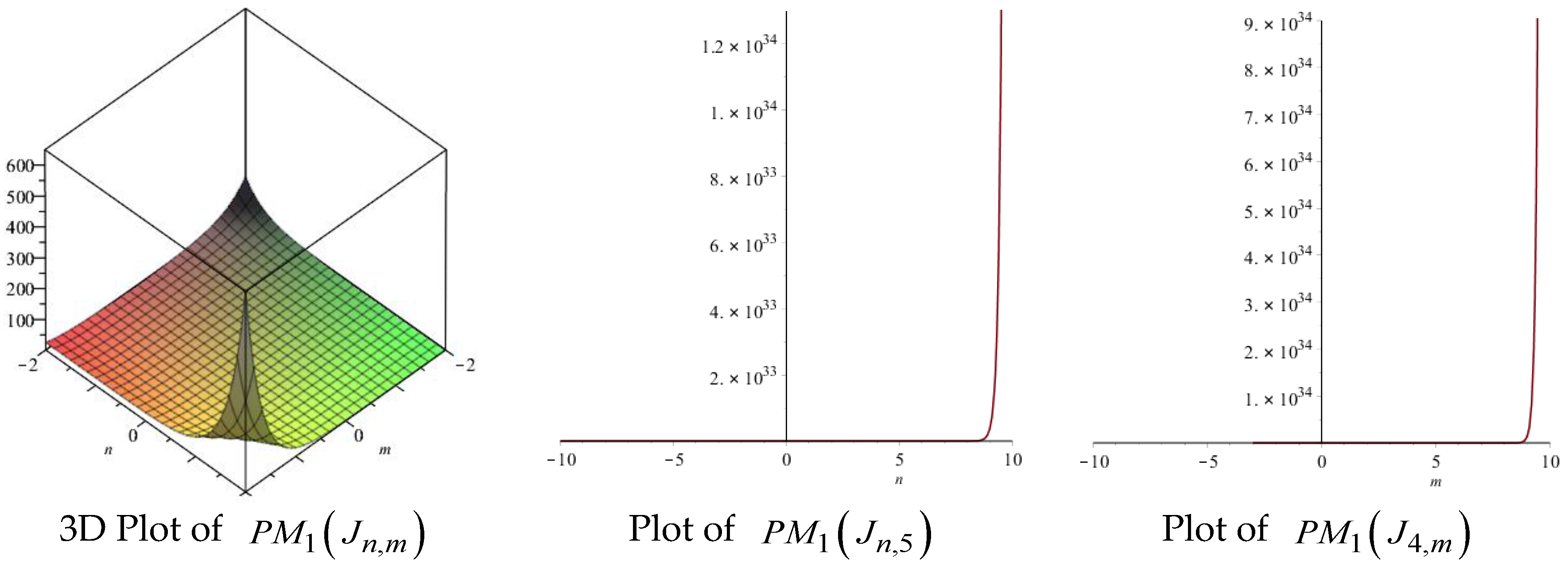
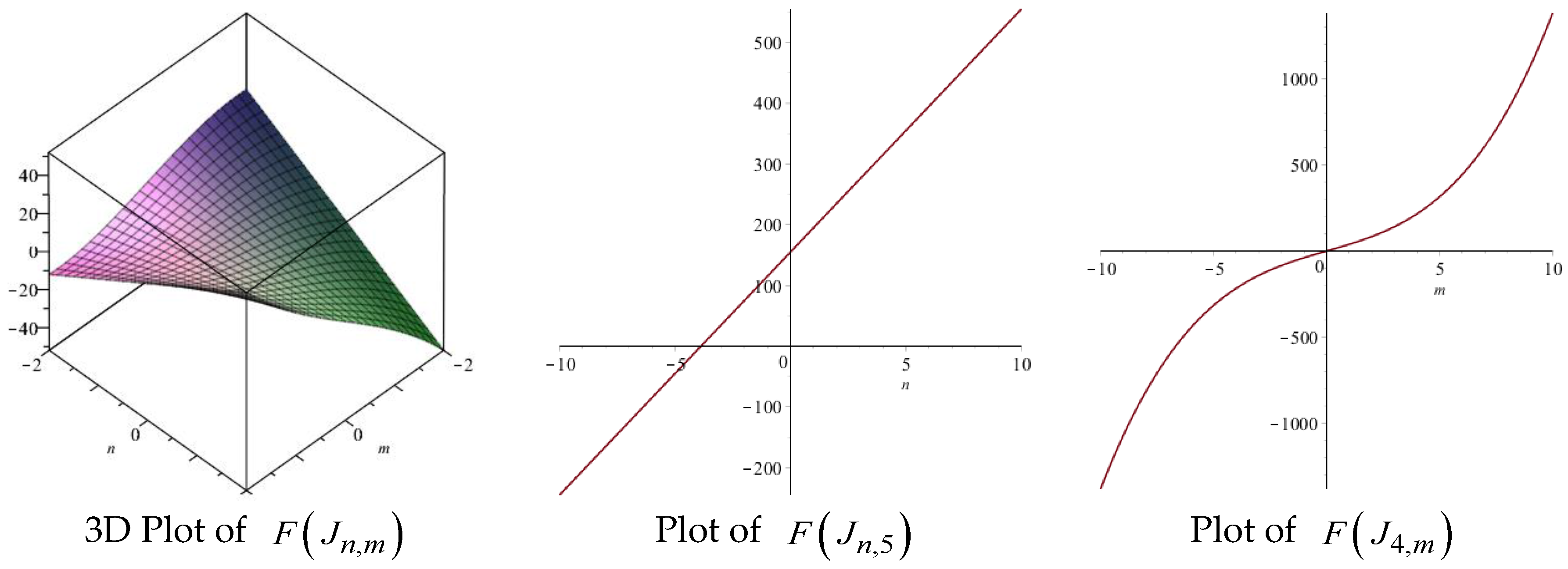
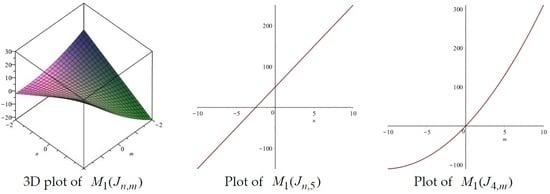
Topological Index	Derivation from $\mathit{M}(\mathit{G};\mathit{x},\mathit{y})$
First Zagreb	$\left(D_x+D_y\right){(M(G;x,y))}_{x=y=1}$
Second Zagreb	$\left(D_x{D}_y\right){(M(G;x,y))}_{x=y=1}$
Second Modified Zagreb	$\left(S_x{S}_y\right){(M(G;x,y))}_{x=y=1}$
Inverse Randic	$\left(D_x^{\alpha }{D}_y^{\alpha }\right){(M(G;x,y))}_{x=y=1}$
General Randic	$\left(S_x^{\alpha }{S}_y^{\alpha }\right){(M(G;x,y))}_{x=y=1}$
Symmetric Division Index	$\left(D_x{S}_y+S_x{D}_y\right){(M(G;x,y))}_{x=y=1}$
Harmonic Index	$2S_{x}J{(M(G;x,y))}_{x=1}$
Inverse sum Index	$S_{x}J{D}_x{D}_y{(M(G;x,y))}_{x=1}$
Augmented Zagreb Index	${S_x}^3{Q}_{-2}J{D_x}^3{D_y}^3{(M(G;x,y))}_{x=1}$

where $D_x=x\frac{\partial (f\left(x,y\right)}{\partial x},D_y=y\frac{\partial (f\left(x,y\right)}{\partial y},S_x=\underset{0}{\overset{x}{{\displaystyle \int }}}\frac{f\left(t,y\right)}{t}dt,S_y=\underset{0}{\overset{y}{{\displaystyle \int }}}\frac{f\left(x,t\right)}{t}dt,J\left(f\left(x,y\right)\right)=f\left(x,x\right),Q_{\alpha }\left(f\left(x,y\right)\right)=x^{\alpha }f\left(x,y\right)$.

.

In 2013, Shirdel et al. in [37] proposed “hyper-Zagreb index” which is also degree based index.

Definition 2.

Let G be a simple connected graph. Then the hyper-Zagreb index of G is defined as:

$$HM\left(G\right)={\displaystyle \sum }_{uv\in E\left(G\right)}{\left[d_u+d_v\right]}^2$$

In 2012, Ghorbani and Azimi [38] proposed two new variants of Zagreb indices.

Definition 3.

Let G be a simple connected graph. Then the first multiple Zagreb index of G is defined as:

$$P{M}_1\left(G\right)={\displaystyle \prod }_{uv\in E\left(G\right)}\left[d_u+d_v\right]$$

Definition 4.

Let G be a simple connected graph. Then the second multiple Zagreb index of G is defined as:

$$P{M}_2\left(G\right)={\displaystyle \prod }_{uv\in E\left(G\right)}\left[d_u\cdot d_v\right]$$

Definition 5.

Let G be a simple connected graph. Then the first Zagreb polynomial of G is defined as:

$$M_1\left(G,x\right)={\displaystyle \sum }_{uv\in E\left(G\right)}{x}^{\left[d_u+d_v\right]}$$

Definition 6.

Let G be a simple connected graph. Then second Zagreb polynomial of G is defined as:

$$M_2\left(G,x\right)={\displaystyle \sum }_{uv\in E\left(G\right)}{x}^{\left[d_u\cdot d_v\right]}$$

Definition 7.

Let G be a simple connected graph. The Forgotten polynomial of G is defined as:

$$F\left(G,x\right)={\displaystyle \sum }_{uv\in E\left(G\right)}{x}^{\left[{\left(d_u\right)}^2+{\left(d_v\right)}^2\right]}$$

2. Main Results

In this part, we give our main computational results.

Theorem 1.

Let $J_{n,m}$ be the Jahangir graph. Then, the M-polynomial of $J_{n,m}$ is:

$$M\left(J_{n,m};x,y\right)=m\left(n-2\right)x^2{y}^2+2m{x}^2{y}^3+m{x}^3{y}^m$$

Proof. 

Clearly, we have $\left|V(J_{n,m})\right|=8n+2$ and $\left|E(J_{n,m})\right|=10n+1$. From the decision on above, we can divide the edge set into following three partitions:

$$E_1(J_{n,m})=\left\{e=uv\in E(J_{n,m}):d_u=d_v=2\right\}$$

$$E_2(J_{n,m})=\left\{e=uv\in E(J_{n,m}):d_u=2,d_v=3\right\}$$

$$E_3(J_{n,m})=\left\{e=uv\in E(J_{n,m}):d_u=3,d_v=m\right\}$$

In addition:

$$\left|E_1(J_{n,m})\right|=m\left(n-2\right)$$

$$\left|E_2(J_{n,m})\right|=2m$$

$$\left|E_3(J_{n,m})\right|=m$$

Now, by definition of M-polynomial, we have:

$$\begin{array}{ll}M\left(J_{n,m};x,y\right)& ={\displaystyle {\displaystyle \sum }_{i\le j}}{m}_{ij}{x}^i{y}^j\\ & ={\displaystyle {\displaystyle \sum }_{2\le 2}}{m}_{22}{x}^2{y}^2+{\displaystyle {\displaystyle \sum }_{2\le 3}}{m}_{23}{x}^2{y}^3+{\displaystyle {\displaystyle \sum }_{3\le m}}{m}_{3m}{x}^3{y}^m\\ & ={\displaystyle {\displaystyle \sum }_{uv\in E_1(J_{n,m})}}{m}_{22}{x}^2{y}^2+{\displaystyle {\displaystyle \sum }_{uv\in E_2(J_{n,m})}}{m}_{23}{x}^2{y}^3+{\displaystyle {\displaystyle \sum }_{uv\in E_3(J_{n,m})}}{m}_{3m}{x}^3{y}^m\\ & =\left|E_1(J_{n,m})\right|x^2{y}^2+\left|E_2(J_{n,m})\right|x^2{y}^3+\left|E_3(J_{n,m})\right|x^3{y}^m\\ & =m\left(n-2\right)x^2{y}^2+2m{x}^2{y}^3+m{x}^3{y}^m.\end{array}.$$

The Figure 2 below is the 3D plot of M-polynomial of Jahangir graph $J_{4,5}$.

Now, we compute some degree-based topological indices of Jahangir graph from this M-polynomial.

Proposition 2.

Let $J_{n,m}$ be the Jahangir graph. Then:

1

$M_1(J_{n,m})=m^2+4mn+5m,$

2

$M_2(J_{n,m})=3m^2+4mn+4m,$

3

${}^m{M}_2(J_{n,m})=(1/4)mn-(1/6)m+1/3,$

4

$R_{\alpha }\left(J_{n,m}\right)=4^{a}m(n-2)+2m{6}^a+m^{(a+1)}{3}^a,$

5

$R{R}_{\alpha }\left(J_{n,m}\right)=m(n-2)4^{(-a)}+2m{6}^{(-a)}+m^{(1-a)}{3}^{(-a)},$

6

$SSD(J_{n,m})=2mn+(1/3)m+3+(1/3)m^2,$

7

$H\left(J_{n,m}\right)=(1/4)mn-(1/10)m+m/(m+3),$

8

$I(J_{n,m})=mn+(2/5)m+3m^2/(m+3),$

9

$A(J_{n,m})=8mn-8m+27m^4/{(1+m)}^3.$

Proof. 

Let $M(J_{n,m};x,y)=f(x,y)=m\left(n-2\right)x^2{y}^2+2m{x}^2{y}^3+m{x}^3{y}^m.$

Then:

$$D_{x}f(x,y)=2m\left(n-2\right)x^2{y}^2+4m{x}^2{y}^3+3m{x}^3{y}^m,$$

$$D_{y}f(x,y)=2m\left(n-2\right)x^2{y}^2+6m{x}^2{y}^3+m^2{x}^3{y}^m,$$

$$D_y{D}_{x}f(x,y)=4m\left(n-2\right)x^2{y}^2+12m{x}^2{y}^3+3m^2{x}^3{y}^m,$$

$$S_y(f(x,y))=\frac{m}{2}\left(n-2\right)x^2{y}^2+\frac{2}{3}m{x}^2{y}^3+x^3{y}^m,$$

$$S_x{S}_y(f(x,y))=\frac{m}{4}\left(n-2\right)x^2{y}^2+\frac{1}{3}m{x}^2{y}^3+\frac{1}{3}{x}^3{y}^m,$$

$${D_y}^{\alpha }(f(x,y))=2^{\alpha }m\left(n-2\right)x^2{y}^2+2\times 3^{\alpha }m{x}^2{y}^3+m^{\alpha +1}{x}^3{y}^m,$$

$${D_x}^{\alpha }{D_y}^{\alpha }(f(x,y))=2^{2\alpha }m\left(n-2\right)x^2{y}^2+2^{\alpha +1}\times 3^{\alpha }m{x}^2{y}^3+3^{\alpha }{m}^{\alpha +1}{x}^3{y}^m$$

$${S_y}^{\alpha }(f(x,y))=\frac{m}{2^{\alpha }}\left(n-2\right)x^2{y}^2+\frac{2}{3^{\alpha }}m{x}^2{y}^3+\frac{m}{m^{\alpha }}{x}^3{y}^m,$$

$${S_x}^{\alpha }{S_y}^{\alpha }(f(x,y))=\frac{m}{2^{2\alpha }}\left(n-2\right)x^2{y}^2+\frac{2}{2^{\alpha }{3}^{\alpha }}m{x}^2{y}^3+\frac{m}{3^{\alpha }{m}^{\alpha }}{x}^3{y}^m,$$

$$S_y{D}_x\left(f(x,y)\right)=m\left(n-2\right)x^2{y}^2+\frac{4}{3}m{x}^2{y}^3+3x^3{y}^m,$$

$$S_x{D}_y\left(f(x,y)\right)=m\left(n-2\right)x^2{y}^2+3m{x}^2{y}^3+\frac{m^2}{3}{x}^3{y}^m,$$

$$Jf(x,y)=m\left(n-2\right)x^4+2m{x}^5+m{x}^{3+m},$$

$$S_{x}Jf(x,y)=\frac{m}{4}\left(n-2\right)x^4+\frac{2}{5}m{x}^5+\frac{m}{3+m}{x}^{3+m},$$

$$J{D}_x{D}_{y}f(x,y)=4m\left(n-2\right)x^4+12m{x}^5+3m^2{x}^{3+m},$$

$$S_{x}J{D}_x{D}_{y}f(x,y)=m\left(n-2\right)x^4+\frac{12}{5}m{x}^5+\frac{3}{3+m}{m}^2{x}^{3+m},$$

$${D_y}^{3}f(x,y)=2^{3}m\left(n-2\right)x^2{y}^2+2\times 3^{3}m{x}^2{y}^3+m^4{x}^3{y}^m,$$

$${D_x}^3{D_y}^{3}f(x,y)=2^{6}m\left(n-2\right)x^2{y}^2+2^4\times 3^{3}m{x}^2{y}^3+3^3{m}^4{x}^3{y}^m,$$

$$J{D_x}^3{D_y}^{3}f(x,y)=2^{6}m\left(n-2\right)x^4+2^4\times 3^{3}m{x}^5+3^3{m}^4{x}^{3+m},$$

$$Q_{-2}J{D_x}^3{D_y}^{3}f(x,y)=2^{6}m\left(n-2\right)x^2+2^4\times 3^{3}m{x}^3+3^3{m}^4{x}^{1+m},$$

$${S_x}^3{Q}_{-2}J{D_x}^3{D_y}^{3}f(x,y)=2^{3}m\left(n-2\right)x^2+2^{4}m{x}^3+3^3{(1+m)}^{-3}{m}^4{x}^{1+m}.$$

Now, from Table 1:

1. First Zagreb Index

$$M_1(J_{n,m})={\left(D_x+D_y\right)f(x,y)|}_{x=y=1}=m^2+4mn+5m$$

Figure 3 is the graphs of the first Zagreb index, 3D (left), for m = 5 (middle) and for n = 4 (right).

2. Second Zagreb Index

$$M_2(J_{n,m})={D_y{D}_x(f(x,y))|}_{x=y=1}=3m^2+4mn+4m.$$

Figure 4 is the graphs of the second Zagreb index, 3D (left), for m = 5 (middle) and for n = 4 (right).

3. Modified second Zagreb Index

$${}^{m}M_2(J_{n,m})={S_x{S}_y(f(x,y))|}_{x=y=1}=(1/4)mn-(1/6)m+1/3$$

Figure 5 is the graphs of the modified second Zagreb index, 3D (left), for m = 5 (middle) and for n = 4 (right).

4. Generalized Randic Index

$$R_{\alpha }\left(J_{n,m}\right)={D_x^{\alpha }{D}_y^{\alpha }(f(x,y))|}_{x=y=1}=4^{a}m(n-2)+2m{6}^a+m^{(a+1)}{3}^a$$

Figure 6 is the graphs of the generalized Randic index, 3D (left), for m = 5 (middle) and for n = 4 (right).

5. Inverse Randic Index

$$R{R}_{\alpha }\left(J_{n,m}\right)={S_x^{\alpha }{S}_y^{\alpha }(f(x,y))|}_{x=y=1}=m(n-2)4^{(-a)}+2m{6}^{(-a)}+m^{(1-a)}{3}^{(-a)}$$

Figure 7 is the graphs of the inverse Randic index, 3D (left), for m = 5 (middle) and for n = 4 (right).

6. Symmetric Division Index

$$SSD(J_{n,m})={\left(S_y{D}_x+S_x{D}_y\right)\left(f(x,y)\right)|}_{x=y=1}=2mn+(1/3)m+3+(1/3)m^2$$

Figure 8 is the graphs of the symmetric division index, 3D (left), for m = 5 (middle) and for n = 4 (right).

7. Harmonic Index

$$H\left(J_{n,m}\right)=2S_{x}J\left(f(x,y)\right){|}_{x=1}=(1/4)mn-(1/10)m+m/(m+3)$$

Figure 9 is the graphs of the harmonic index, 3D (left), for m = 5 (middle) and for n = 4 (right).

8. Inverse Sum Index

$$I(J_{n,m})=S_{x}J{D}_x{D}_y{\left(f(x,y)\right)}_{x=1}=mn+(2/5)m+3m^2/(m+3)$$

Figure 10 is the graphs of the inverse sum index, 3D (left), for m = 5 (middle) and for n = 4 (right).

9. Augmented Zagreb Index

$$A(J_{n,m})={S_x}^3{Q}_{-2}J{D_x}^3{D_y}^3\left(f(x,y)\right)|x=1=8mn-8m+27m^4/{(1+m)}^3$$

Figure 11 is the graphs of the augmented Zagreb index, 3D (left), for m = 5 (middle) and for n = 4 (right).

Theorem 3.

Let $J_{n,m}$ be the Jahangir graph. Then first Zagreb polynomial, second Zagreb polynomial and forgotten polynomial of $J_{n,m}$ are:

$$M_1\left(J_{n,m},x\right)=m\left(n-2\right)x^4+2m{x}^5+m{x}^{3+m}$$

$$M_2\left(J_{n,m},x\right)=m\left(n-2\right)x^4+2m{x}^6+m{x}^{3m}$$

$$F(J_{n,m},x)=m(m-2)x^8+2m{x}^{13}+m{x}^{9+m^2}$$

Proof. 

By the definition the first Zagreb polynomial:

$$\begin{array}{ll}{M}_1\left(J_{n,m},x\right)& ={\displaystyle {\displaystyle \sum }_{uv\in E\left(J_{n,m}\right)}}{x}^{\left[d_u+d_v\right]}\\ & ={\displaystyle {\displaystyle \sum }_{uv\in E_1\left(J_{n,m}\right)}}{x}^{\left[d_u+d_v\right]}+{\displaystyle {\displaystyle \sum }_{uv\in E_2\left(J_{n,m}\right)}}{x}^{\left[d_u+d_v\right]}+{\displaystyle {\displaystyle \sum }_{uv\in E_3\left(J_{n,m}\right)}}{x}^{\left[d_u+d_v\right]}\\ & =\left|E_1\left(J_{n,m}\right)\right|x^4+\left|E_2\left(J_{n,m}\right)\right|x^5+\left|E_3\left(J_{n,m}\right)\right|x^{3+m}\\ & =m\left(n-2\right)x^4+2m{x}^5+m{x}^{3+m}\end{array}$$

In Figure 12, we give graphical representation of the first Zagreb polynomial of $J_{5,4}.$

Now by definition the second Zagreb polynomial:

$$\begin{array}{ll}{M}_2\left(J_{n,m},x\right)& ={\displaystyle {\displaystyle \sum }_{uv\in E\left(J_{n,m}\right)}}{x}^{\left[d_u\times d_v\right]}\\ & ={\displaystyle {\displaystyle \sum }_{uv\in E_1\left(J_{n,m}\right)}}{x}^{\left[d_u\times d_v\right]}+{\displaystyle {\displaystyle \sum }_{uv\in E_2\left(J_{n,m}\right)}}{x}^{\left[d_u\times d_v\right]}+{\displaystyle {\displaystyle \sum }_{uv\in E_3\left(J_{n,m}\right)}}{x}^{\left[d_u\times d_v\right]}\\ & =\left|E_1\left(J_{n,m}\right)\right|x^4+\left|E_2\left(J_{n,m}\right)\right|x^6+\left|E_3\left(J_{n,m}\right)\right|x^{3m}\\ & =m\left(n-2\right)x^4+2m{x}^6+m{x}^{3m}\end{array}$$

In Figure 13, we give graphical representation of the second Zagreb polynomial of $J_{5,4}.$

$$\begin{array}{ll}F\left(J_{n,m},x\right)& ={\displaystyle {\displaystyle \sum }_{uv\in E\left(J_{n,m}\right)}}{x}^{\left[{d_u}^2+{d_v}^2\right]}\\ & ={\displaystyle {\displaystyle \sum }_{uv\in E_1\left(J_{n,m}\right)}}{x}^{\left[{d_u}^2+{d_v}^2\right]}+{\displaystyle {\displaystyle \sum }_{uv\in E_2\left(J_{n,m}\right)}}{x}^{\left[{d_u}^2+{d_v}^2\right]}+{\displaystyle {\displaystyle \sum }_{uv\in E_3\left(J_{n,m}\right)}}{x}^{\left[{d_u}^2+{d_v}^2\right]}\\ & =\left|E_1\left(J_{n,m}\right)\right|x^8+\left|E_2\left(J_{n,m}\right)\right|x^{13}+\left|E_3\left(J_{n,m}\right)\right|x^{9+m^2}\\ & =m\left(n-2\right)x^8+2m{x}^{13}+m{x}^{9+m^2}\end{array}$$

In Figure 14, we give graphical representation of the forgotten polynomial of $J_{5,4}.$

Proposition 4.

Let $J_{n,m}$ be the Jahangir graph. Then:

$$HM(J_{n,m})=m(m^3+9m^2+27m+16n+45)$$

$$P{M}_1\left(J_{n,m}\right)=4^{m(n-2)}{\left(25\right)}^m{(m+3)}^m$$

$$P{M}_2\left(J_{n,m}\right)=4^{m(n-2)}{\left(36\right)}^m{3}^m{m}^m$$

$$F(J_{n,m})=m^3+8mn+6m$$

Proof. 

By definition of hyper-Zagreb index:

$$\begin{array}{ll}HM\left(J_{n,m}\right)& ={\displaystyle {\displaystyle \sum }_{uv\in E\left(J_{n,m}\right)}}{\left[d_u+d_v\right]}^2\\ & ={\displaystyle {\displaystyle \sum }_{uv\in E_1\left(J_{n,m}\right)}}{\left[d_u+d_v\right]}^2+{\displaystyle {\displaystyle \sum }_{uv\in E_2\left(J_{n,m}\right)}}{\left[d_u+d_v\right]}^2+{\displaystyle {\displaystyle \sum }_{uv\in E_3\left(J_{n,m}\right)}}{\left[d_u+d_v\right]}^2\\ & =16\left|E_1\left(J_{n,m}\right)\right|+25\left|E_2\left(J_{n,m}\right)\right|+{\left(3+m\right)}^2\left|E_3\left(J_{n,m}\right)\right|\\ & =m(m^3+9m^2+27m+16n+45)\end{array}$$

Figure 15 is the graphs of the hyper Zagreb index, 3D (left), for m = 5 (middle) and for n = 4 (right).

By the definition of first multiple Zagreb index:

$$\begin{array}{ll}P{M}_1\left(J_{n,m}\right)& ={\displaystyle {\displaystyle \prod }_{uv\in E\left(J_{n,m}\right)}}\left[d_u+d_v\right]\\ & ={\displaystyle {\displaystyle \prod }_{uv\in E_1\left(J_{n,m}\right)}}\left[d_u+d_v\right]\times {\displaystyle {\displaystyle \prod }_{uv\in E_2\left(J_{n,m}\right)}}\left[d_u+d_v\right]\times {\displaystyle {\displaystyle \prod }_{uv\in E_2\left(J_{n,m}\right)}}\left[d_u+d_v\right]\\ & =4^{\left|E_1\left(J_{n,m}\right)\right|}\times 5^{\left|E_2\left(J_{n,m}\right)\right|}\times {(3+m)}^{\left|E_3\left(J_{n,m}\right)\right|}\\ & =4^{(m(n-2))}{25}^m{(m+3)}^m\end{array}$$

Figure 16 is the graphs of the first multiple Zagreb index, 3D (left), for m = 5 (middle) and for n = 4 (right).

By the definition of second multiple Zagreb index:

$$\begin{array}{ll}P{M}_2\left(J_{n,m}\right)& ={\displaystyle {\displaystyle \prod }_{uv\in E\left(J_{n,m}\right)}}\left[d_u\times d_v\right]\\ & ={\displaystyle {\displaystyle \prod }_{uv\in E_1\left(J_{n,m}\right)}}\left[d_u\times d_v\right]\times {\displaystyle {\displaystyle \prod }_{uv\in E_2\left(J_{n,m}\right)}}\left[d_u\times d_v\right]\times {\displaystyle {\displaystyle \prod }_{uv\in E_2\left(J_{n,m}\right)}}\left[d_u\times d_v\right]\\ & =4^{\left|E_1\left(J_{n,m}\right)\right|}\times 6^{\left|E_2\left(J_{n,m}\right)\right|}\times {(3m)}^{\left|E_3\left(J_{n,m}\right)\right|}\\ & =4^{m(n-2)}{\left(36\right)}^m{3}^m{m}^m\end{array}$$

Figure 17 is the graphs of the second multiple Zagreb index, 3D (left), for m = 5 (middle) and for n = 4 (right).

By the definition of forgotten index:

$$\begin{array}{ll}F\left(J_{n,m}\right)& ={\displaystyle {\displaystyle \sum }_{uv\in E\left(J_{n,m}\right)}}\left[{d_u}^2+{d_v}^2\right]\\ & ={\displaystyle {\displaystyle \sum }_{uv\in E_1\left(J_{n,m}\right)}}\left[{d_u}^2+{d_v}^2\right]+{\displaystyle {\displaystyle \sum }_{uv\in E_2\left(J_{n,m}\right)}}\left[{d_u}^2+{d_v}^2\right]+{\displaystyle {\displaystyle \sum }_{uv\in E_3\left(J_{n,m}\right)}}\left[{d_u}^2+{d_v}^2\right]\\ & =\left|E_1\left(J_{n,m}\right)\right|8+\left|E_2\left(J_{n,m}\right)\right|13+\left|E_3\left(J_{n,m}\right)\right|(9+m^2)\\ & =m^3+8mn+6m\end{array}$$

Figure 18 is the graphs of the forgotten index, 3D (left), for m = 5 (middle) and for n = 4 (right).

It is worth mentioning that above-plotted surfaces and graphs show the dependence of each topological index on m and n. From these figures, one can imagine that each topological index behaves differently from other against parameters m and n. These figures also give us some extreme values of the certain topological index. Moreover, these graphs give an insight view to control the values of topological indices with m and n.

3. Conclusions and Discussion

In this article, we computed closed forms of many topological indices and polynomials of $J_{n,m}$ for all values of m and n. These facts are invariants of graphs and remain preserved under isomorphism. These results can also play a vital role in industry and pharmacy in the realm of that molecular graph which contains $J_{n,m}$ as its subgraphs.