1. Introduction
Various types of uncertainties exist in real life situations, which calls for useful mathematic tools to meet various information process demands. Usually complicated problems take place with uncertainties, and most of these complex situations can not be handled by adopting classical mathematic methods, considering the fact that with classical mathematic tools all notions are requested to be strict. Up to now, abundant mathematic tools such as fuzzy set theory [
1] and rough set theory [
2,
3] have already been developed and proved to be useful in handling several kinds of the problems that contain uncertainties, and all of these theories share a common inherent difficulty, which is mainly the inadequacy of the parametrization tool [
4,
5]. However, it is noticed that, without proper parametrization tools, sometimes a practical problem can not be described in a way as much as information collected from different aspects could be taken into account. To handle this issue and to enrich mathematical methodologies for coping with uncertainties, soft set theory was initially proposed by Molodtsov [
4] in 1999, which considers every specific object from different attributes’ aspects, in this way, this new model goes beyond all other existing mathematical tools to avoid the above-mentioned difficulties. After soft set theory comes out, in the past few years, there appears a continuous growth of interest in studying theoretical aspects of soft set theory, as well as the practical applications of soft sets.
Abundant mathematical models have already been designed in order to model and process vague concepts, among which it is noteworthy that fuzzy set theory and rough set theory have already drawn worldwide attention from researchers. The development of these two theories makes contributions to handle lots of complicated problems in engineering, economics, social science, et al. The main character of fuzzy set theory is that it describes a vague concept by using a membership function, and the allowance of partial memberships contributes to providing an appropriate framework to represent and process vague concepts. The character of rough set theory relies on handling vagueness and granularity in information systems by indirectly describing a vague concept through two exact concepts called its lower and upper approximations. In Pawlak’s rough set model, the equivalence relation is a vital concept, by replacing the equivalence relation with a fuzzy similarity relation, fuzzy rough sets and rough fuzzy sets have been proposed [
6].
The combinations of soft sets, rough sets and fuzzy sets have been extensively studied to benefit each other and to take the best advantage of them. Research on generalization models of soft sets is promising since usually the generalized models are not short of parameter tools, that is, all of the generalized soft set models usually keep the most important feature of soft set theory in considering issues from various aspects. The history of research on extending soft sets applying fuzzy set theory goes beyond fifteen years already since Maji et al. introduced fuzzy soft sets in [
7]. Therefore far, the soft sets have been extended to intuitionistic fuzzy soft sets [
8], interval-valued intuitionistic fuzzy soft sets [
5,
9], vague soft sets [
10], soft interval sets [
11] and many other hybrid soft sets models. The history of research on the generalization of soft sets by using rough set theory is relatively short. To introduce parametrization tools to rough set theory, Feng et al. [
12,
13] initially put forward the concept of soft rough sets and soft rough fuzzy sets, in which a soft set looks for the lower and upper approximations of a subset of the universe. Afterwards, Meng et al. [
14] proposed soft fuzzy rough set, in which model the fuzzy soft set has been adopted into granulate the universe. Benefitting from similarity measures induced by soft sets and soft fuzzy sets, Qin et al. [
15] provided several soft fuzzy rough set models through introducing confidence threshold values. Recently, Shabir et al. [
16] noticed that Feng et al.’s soft rough sets [
12] suffer from some unexpected properties such as the upper approximation of a non-empty set might be empty and a subset set
X might not be contained in its upper approximation. To resolve this problem, Shabir et al. [
16] modified their soft rough sets and introduced the modified soft rough set (MSR set), which has already been extended to fuzzy soft sets [
17], and
Z-soft rough fuzzy sets was proposed, and its application in decision-making problems was analyzed.
The exploitation of soft sets and hybrid soft sets models in decision-making shows a great development in the recent years [
18,
19,
20,
21,
22]. The utilization of soft rough sets models in decision-making shows a promising prospect. Different decision-making approaches have been put forth based on MSR set [
20], Z-soft rough fuzzy sets [
17], Z-soft fuzzy rough set [
21], and other soft rough sets models [
23,
24]. If the researchers could have a thorough knowledge of the connections among various soft rough sets, we believe that decision-making approaches under framework of soft rough sets could be applied in a more flexible and reliable way. However, the relationships among these hybrid sets have not been systematically studied so far. Furthermore, we notice that a soft set
S can be looked upon an information system
. Based on this information system, we can establish Pawlak rough approximations and rough fuzzy approximations. What is the relationship between soft rough approximations (soft rough fuzzy approximations) in
S and Pawlak rough approximations (rough fuzzy approximations) in
? Additionally, soft set and formal context are mathematically equivalent. The relationships among soft rough approximation operators and derivation operators used in formal concept analysis (FCA) are also interesting issues to be addressed. In this paper, we will concentrate on the discussion of these problems. The paper is structured as follows:
Section 2 revises several basic concepts of soft sets, fuzzy sets and rough set.
Section 3 studies relationships among several soft rough sets. The properties of MSR approximation operators and different connections between MSR approximation operators and
F-soft rough approximation operators are analyzed. It is shown that MSR approximation operators and a kind of Pawlak approximation operators are equivalent, while
Z-soft rough fuzzy approximation operators and a kind of rough fuzzy approximation operators are equivalent. The relationships among
F-soft rough fuzzy sets,
M-soft rough fuzzy sets and
Z-soft rough fuzzy sets have also been investigated.
Section 4 discusses the relationship between
F-soft rough sets and modal-style operators in formal concept analysis.
Section 5 proposes a new generalization of F-soft rough set, which is called a soft rough soft set, and a simple application of soft rough soft sets in group decision-making has been studied. Eventually,
Section 6 concludes the paper by presenting some remarks and future works.
2. Preliminaries
Here, several concepts of fuzzy sets, soft sets and rough sets are briefly reviewed. Please refer to [
1,
2,
4,
7] for details.
An advantageous framework has been offered by fuzzy set theory [
1] to handle vague concepts through the allowance for partial memberships. Let
U be the universe set. Define a fuzzy set
on
U by its membership function
.
indicates the degree to which
x belongs to the fuzzy set
for all
. In what follows, we denote the family of all subsets of
U by
and the family of all fuzzy sets on
U by
. The operations of fuzzy sets can be found in [
1].
Molodtsov [
4] introduced the concept of soft set. Let
U be the universe set and
E the set consisted of all parameters that is related to
U. Hence, a soft set is defined as below:
Definition 1. A pair is called a soft set over U, where and F is a mapping given by [4]. The soft set is characterized by a parameter set and a function defined on the parameter set. For every parameter , is said to be the e-approximate elements and, correspondingly, the soft set can be viewed as a parameterized family of subsets of U.
A soft set
is called a full soft set if
[
12];
is called a relative null soft set (with respect to the parameter set
A), if
for all
;
is called a relative whole soft set (with respect to the parameter set
B) if
for all
[
25]. Maji et al. in [
7] introduced the concept of fuzzy soft set.
Definition 2. Let be a soft space. A pair is called a fuzzy soft set over U, where and F is a mapping defined as [7]. The fuzzy soft set is also characterized by a parameter set and a function on the parameter set, whereas a fuzzy set on U takes place of a crisp subset of U corresponds to each parameter. It follows that, to a certain degree, a soft set can also be viewed as a special kind of fuzzy soft set.
Pawlak introduced rough set theory in [
2], the application of which is based on a structure called information system.
Definition 3. An information system is a pair of non-empty finite sets U and A, where U is a set of objects and A is a set of attributes; each attribute is a function , where is the set of all values (called domain) of attribute a [3]. Soft sets and information systems are closely related [
13,
26,
27].
is assumed to be a soft set over
U and
an information system induced by
S. For any attribute
, a function
is defined by
if
; or else
. In this way, every soft set could be viewed as an information system. In what follows,
is called the information system induced by soft set
S.
By contrast, suppose the information system,
. It uses a parameter set as
and it follows that through setting
for each
and
, a soft set
can be defined, which is the soft set induced by
I.
Let
U be the universe of discourse and
R be an equivalence relation on
U.
is called Pawlak approximation space. For each
, the upper approximation
and lower approximation
of
X with respect to
are defined as [
2]:
X is so-called definable in if , or else X is a rough set. Thus, in rough set theory, a rough concept is characterized by a couple of exact concepts, namely, its lower approximation and upper approximation. and are the R-positive region and R-negative region of X, respectively. Furthermore, is called the R-boundary region.
Up to now, various types of extension models of the Pawlak rough set have been proposed to enrich the theory and to meet different application demands [
28,
29]. In [
12], by the combination of soft set, rough set and fuzzy set theory, soft rough sets and soft rough fuzzy sets were introduced. To make them easy to be distinguished from other models mentioned in the current work and also to facilitate the discussion, these two notions are called
F-soft rough sets and
F-soft rough fuzzy sets.
Definition 4. Let be a soft set over U. is called a soft approximation space. Two operations can be defined based on P as follows [12]:For all , and are respectively called the F-lower and F-upper soft rough approximations of X in S. X is F-soft definable in P if , or else X is a F-soft rough set. It is noted that we can present
and
in a more concise manner [
13]:
In this definition, the soft set
S is regarded as the elementary knowledge on the universe.
F-lower and
F-upper soft rough approximation operators are not dual to each other, that is,
usually does not hold, where the complement of set
X is computed by
. If the condition
holds in a soft set
over
U, this soft set is a full soft set [
12]. In this case,
comes into being a cover of the universe
U. It is pointed out that
,
and covering rough approximations [
30] are closely related but fundamentally different [
13]. Additionally, if
forms a partition of
U, we will call
a partition soft set [
13,
31].
It is pointed out by Shabir et al. [
16] that ∃
s.t.
for all
, if
is not a full soft set. In other words,
for all
. Thus,
and some basic properties of rough set do not hold in general. Based on these observations, modified soft rough sets (MSR sets) was defined as follows.
Definition 5. Let be a soft set over U and be a map defined as . Then, is called MSR-approximation space and for any , its lower MSR approximation and upper MSR approximation are defined as [16]:X is MSR definable if the condition holds, or else X is a MSR set. Mathematically speaking,
can be looked upon a soft set over
A. In [
32],
was considered as a pseudo soft set that is induced by
, afterwards a decision-making method related to pseudo soft set was provided.
5. A New Generalization of F-Soft Rough Set: Soft Rough Soft Sets
In this section, by extending the notion of F-soft rough set, a new generalization model called soft rough soft set will be proposed. In this new model, we use a soft set is as the elementary knowledge to compute the approximations of soft set. In this way, parameterized tools can be used to the greatest extent. Some basic properties of the new proposed model are discussed. A multi-group decision-making approach based on soft rough soft sets has been provided.
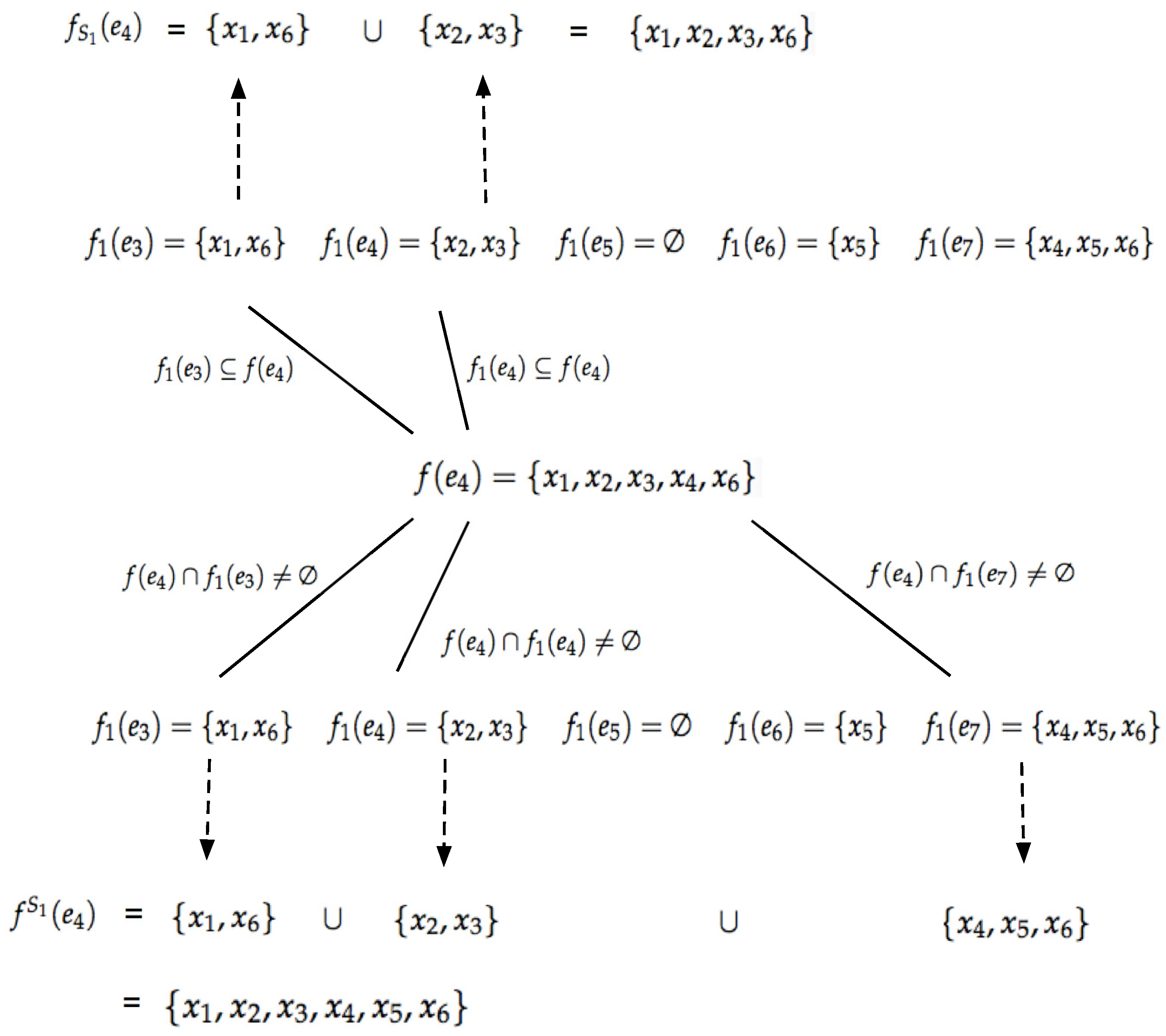
Definition 11. Let U be the universe set and A, be parameter sets. Let be a full soft set over U and be a soft approximation space. Let be a soft set over U. The lower and upper soft rough approximations of in are denoted by and , which are soft sets over U defined by:for all . , are the lower and the upper soft rough approximation operators on soft set , respectively. If , the soft set is soft definable, or else is so-called a soft rough soft set. Example 2. Suppose that the universe set and the parameters set . Let and . Let be a full soft set and be a soft set over U as shown by Table 1 and Table 2, respectively. In the soft approximation space , by Definition 11, we get the lower soft rough approximation and the upper soft rough approximation of soft set , as shown by Table 3 and Table 4, respectively. In order to facilitate the readers to understand, Figure 1 is given to show the process of computing and from . Proposition 1. Let be a full soft set over U and be a soft approximation space. Let be a soft set over U. The following properties hold:
- (1)
,
- (2)
,
- (3)
.
Proof. The lower and upper soft rough approximations of in are denoted by and ; the lower and upper soft rough approximations of in are denoted by and .
(1a) For all , if , then we obtain , so ;
(1b) For all , if , since is a full soft set, we obtain that , s.t. , then , then , that is, and for all .
Hence, we know that for all , that is, .
(2a) By the definition of relative null soft set, we know for all . For all , we have , that is, ;
(2b) By the definition of relative null soft set, we know for all . For all , we have , that is, .
(3a) By the definition of relative whole soft set, we know for all . For all , we have , that is, .
(3b) By the definition of relative whole soft set, we know for all . Since is a full soft set over U, for all , we have , that is, . ☐
Proposition 2. Suppose that is a full soft set over U and is a soft approximation space. Let , be two soft sets over U. The following properties hold:
- (1)
,
- (2)
,
- (3)
,
- (4)
,
- (5)
,
- (6)
.
Proof. The lower and upper soft rough approximations of in are denoted by and ; the lower and upper soft rough approximations of in are denoted by and .
(1) If , then for all , we have . Assume that . From , we obtain . Therefore, we get for all , i.e., ;
(2) If , then for all , we have . Assume that , from , we obtain , s.t. , so , it follows that for all , i.e., ;
(3) It is obvious that and . From property (1), we obtain and . Thus, .
(4) It is obvious that and . From property (1), we obtain and . Thus, .
(5) It is obvious that and . From property (2), we obtain and . Thus, .
(6) It is obvious that and . From property (2), we obtain and . Thus, . ☐
Proposition 3. Let be a full soft set over U and be a soft approximation space. Let be a soft set over U. The following properties hold:
- (1)
,
- (2)
.
Proof. From property (1) in Proposition 1, it is obvious that . From property (1) and (2) in Proposition 2, we get and , respectively. ☐
In [
12], a group decision-making approach based on F-soft rough sets was proposed; however, if we carefully check their decision scheme, it is not hard to find that they actually use the tool of a soft rough soft set since the best alternatives provided by each specialist gather together to form a soft set and they compute the upper and lower soft rough approximations (soft sets) on the preliminary evaluation soft set during the decision process. That is, although the concept has not been formally proposed, the application of soft rough soft sets has already appeared in literature. From another perspective, the decision-making problem that can be solved by F-soft rough sets in [
12] can also be solved by using soft rough soft sets. It is necessary to propose the concept for soft rough soft sets as well as its application to introduce parameter tools to the universe description, that is, make it feasible to describe objects in the universe from different aspects at the same time, information obtained from different aspects be able to be handled as a whole before the approximations of a soft set are computed, and allow the flexibility to make operations such as the restricted intersection “∩” [
25] on soft sets whose soft rough approximations need to be computed; in this way, soft rough soft sets have the potential to be applied in more complex decision-making situations to meet demands of applications in real life cases. As follows, we provide a simple application of soft rough soft sets in decision-making.
Let and be two groups of specialists to evaluate all the candidates . In group G, each specialist is asked to point out if the candidates satisfy benefit properties in or not. In this way, a serious of evaluations provided by specialists are obtained as , , , ⋯, . Afterwards, the evaluation made by group G could be obtained by . Meanwhile, in another group , the specialists are under time pressure, and a lack of patience, or, because of some other issues, each specialist only points out the best alternatives; however, we have no clear idea about which properties are under their consideration. The best alternatives chosen by specialists in group form another soft set . We say the assessments provided by group G are more reliable since the assessments provided by them are more specific than group . However, in order to make full use of information provided by the two independent groups, we can compute the lower soft rough approximation on in soft approximation space . If , from the axiomatic definition of soft rough soft sets, we know that the best alternatives of one or more specialists in are totally contained in , that is, the best alternatives chosen by some specialists in certainly occupy property , which indicates that this benefit property considered by group G may also be very important to group . The final decision is to select the alternative that occupies the most number of beneficial properties that may be important for both groups.
The steps of this soft rough soft sets based multi-group decision-making approach can be listed as:
Step 1. Input the evaluations on alternatives provided by specialists group as , , , ⋯, .
Step 2. Input the best alternatives selected by specialists group as .
Step 3. Compute the group evaluation made by the specialists in G as .
Step 4. Compute the lower soft rough approximation of in , i.e. .
Step 5. Compute the score of alternatives of each () as , and the decision result is if it satisfies .
Example 3. Suppose that a factory needs to purchase the best machine from according to evaluations provided by two specialists groups G and , which form a multi-group decision-making problem. consists of four specialists and each of them provides assessments on machines in U with respect to beneficial properties , . Each specialist in G points out if the machines satisfy properties in A or not. In this way, a serious of evaluation soft sets provided by specialists are obtained as , , , (see Table 5, Table 6, Table 7 and Table 8 as their tabular representations) and the group evaluation of G can be computed by (see also Table 2 as the tabular representation for ). Meanwhile, each specialist in another specialist group only points out the best machines according to his/her own cognition, which form soft set (replace by and see also Table 1 for its tabular representation). The lower soft rough approximation of in can be easily computed as (see also Table 3 for its tabular representation). It is easy to obtain that , and , hence should be the machine purchased by the factory since it satisfies largest number of beneficial properties that are important to two groups. As is mentioned at the beginning of this section, soft rough soft set is an extension model of F-soft rough set. Sometimes, in a practical situation, the universe set that needs to be granulated is presented from different attributes’ aspects simultaneously. In other words, the parameter tools are necessary not only for the knowledge presentation, but also for the universe description. The new model provides a framework for dealing with these kinds of problems and the exploration of its potential use in decision-making is promising. Compared to F-soft rough sets, soft rough soft sets introduce parameter tools to the universe description and a soft set (instead of a subset of the universe) is approximated. Compared to rough soft set [
12], a soft set instead of an equivalence relation has been adopted in soft rough soft sets to compute the approximations of soft sets [
36,
37]. In this section, only a small application attempt of soft rough soft sets in decision-making has been provided, which is far from enough to meet various demands in real life situations. More flexible and effective approaches need to be developed in the future.