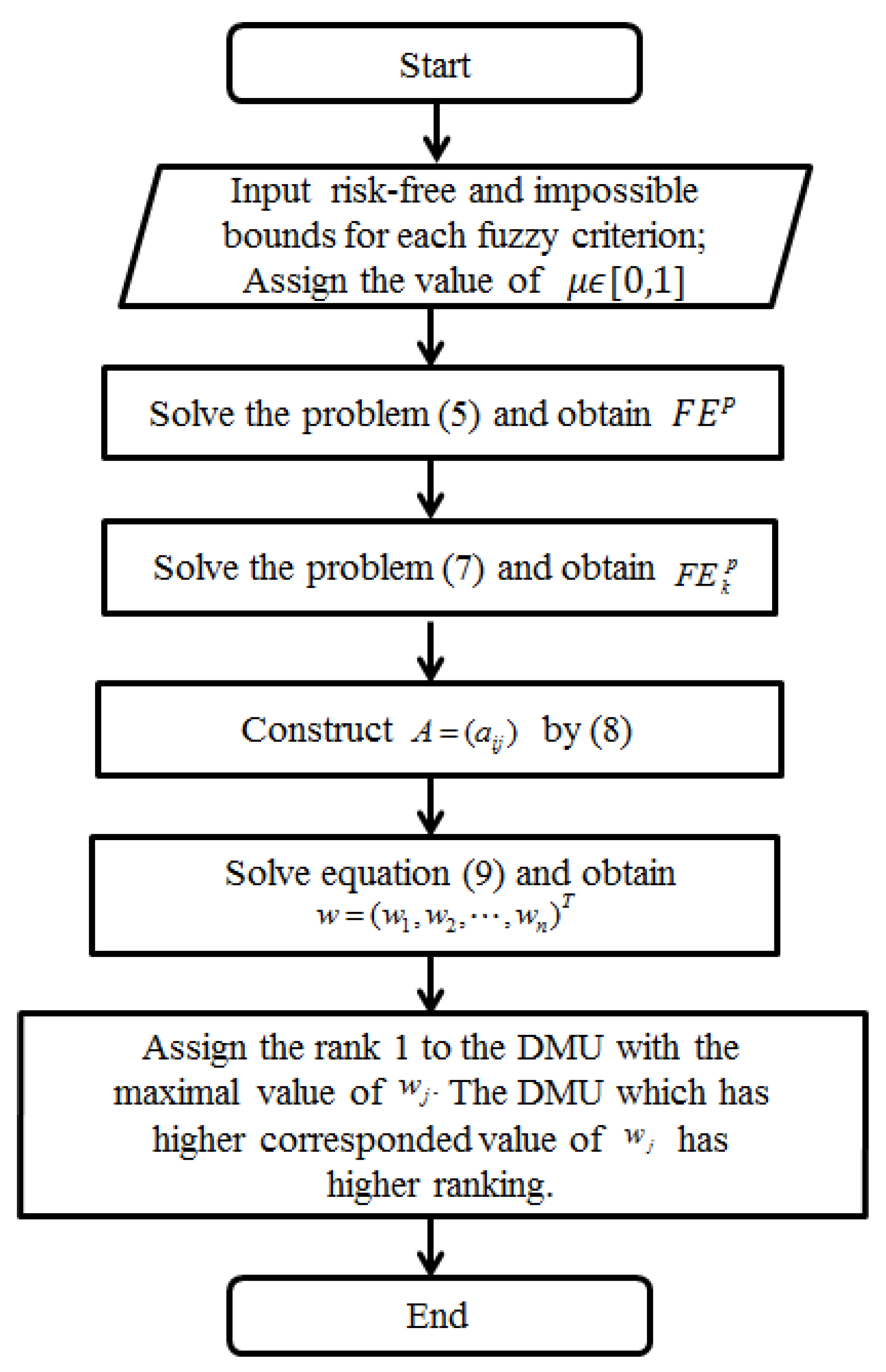
The hybrid fuzzy DEA/AHP approach consists of two stages for ranking DMUs with multiple fuzzy criteria. In the first stage of the ranking method, fuzzy DEA is employed to construct the pairwise comparisons of AHP based on results of the average of efficiencies. In the second stage of the ranking method, a single level AHP is utilized to fully rank units according to the pairwise evaluation matrix generated in the first stage.
Section 2.1 presents the construction of pairwise comparisons of AHP by fuzzy DEA and
Section 2.2 presents the ranking by AHP.
2.1. Construction of Pairwise Comparisons of AHP
In the proposed approach, the AHP pairwise comparisons are derived from the results of average of efficiencies, which is the average of any DMUs before and after removing other DMUs [
14]. To obtain the efficiency of DMUs, the input-orientated fuzzy CCR model named after Charnes, Cooper, and Rhodes [
10] is employed. Suppose there are
m inputs,
s outputs and
n DMUs being evaluated. Denote
as the
i-th fuzzy input and
as the
r-th fuzzy output of the
j-th DMU. The input-oriented CCR model with multiple fuzzy criteria for measuring the efficiency of
can be formulated as:
where
is a column vector of a linear combination of
n DMUs and
is the efficiency score of
. The interpretation of the input-oriented fuzzy CCR model can be found in many references [
22]. In the input-oriented fuzzy CCR model, an efficiency score is generated for a DMU by minimizing inputs with fixed outputs and for each observed
an imaginary composite unit is constructed that outperforms
In addition,
represents the proportion to which
is used to construct the composite unit for
In problem (
1), the composite unit produces inputs that are at most equal to a proportion
of the inputs of
with
and consumes at least the same levels of outputs as
[
23]. If
is not efficient and the parameter
indicates the extent by which
has to decrease its inputs to become efficient. Moreover, it could be easily checked that problem (
1) has a feasible solution when
for
and
Since the input and output variables in problem (
1) are not known precisely, problem (
1) cannot be solved by a standard linear programming solver. The decision maker may define the risk-free and impossible bounds for each fuzzy input and output variables for transforming the fuzzy optimization problem (
1) to a traditional linear program. Risk-free bounds are interpreted as the conservative values that are most realistically found, whereas the impossible bounds are associated with the values that are the least realistic. For each fuzzy input and output variable, the change from its risk-free to impossible bounds is represented by its membership function. It is assumed that membership functions of each fuzzy input and output variable are monotonically linear, and are equal to zero, if the input or output bounds are impossible, and are equal to one if they are risk free. Suppose that
and
represent the impossible and risk-free bounds of the
i-th fuzzy input of the
j-th DMU, respectively. A possible linear membership function associated with the
i-th fuzzy input for the
j-th DMU is given by:
Suppose also that
and
represent the risk-free and impossible bounds of the
r-th fuzzy output of the
j-th DMU, respectively. A possible linear membership function associated with the
r-th fuzzy output for the
j-th DMU is given by:
According to (
2) and (
3),
and
can be replaced by the new variables
and
which locate the levels of inputs and outputs within the impossible and risk-free bounds, as follows:
With these transformations, we have:
According to [
24], the fuzzy decision of (
4) can be reached with the membership degree:
For a specific
problem (
4) is rewritten as the linear programming problem:
The efficiency of
can then be obtained by solving the linear programming problem (
5).
Moreover, define
the efficiency of
after removing the
k-th DMU from the observation set of DMUs, which can be described by the fuzzy DEA model:
As similar to the discussion on solving problem (
1), for
the efficiency of
after removing the
k-th DMU defined in (
6) can be obtained by solving the linear programming problem:
where
and
represent the impossible and risk-free bounds of the
i-th fuzzy input of the
j-th DMU, respectively, and
and
represent the risk-free and impossible bounds of the
r-th fuzzy output of the
j-th DMU, respectively. For each
we solve problem (
7) and obtain the efficiency of unit after removing the
k-th DMU,
.
Table 2 lists the results.
Using the results in
Table 2, for each pair of DMU
i and
the priority of DMU
i to DMU
j is defined as [
14]:
where
and
are the efficiencies of the
i-th and
j-th DMU after removing the
s-th DMU, respectively;
and
are efficiencies of the
i-th and
j-th DMU obtained by solving problem (
5), respectively. It should be noticed that the priority of the
i-th DMU to the
j-th DMU,
defined in (
8) is the ratio of two averages. The first one is the average of efficiencies of the
i-th DMU after removing the
s-th DMU
and the efficiency of the
i-th DMU. The second average is a similar average of efficiencies of the
j-th DMU after removing the
s-th DMU
and the efficiency of the
j-th DMU.
The pairwise comparison matrix
generated by (
8) is utilized to fully rank DMUs in the second stage of the proposed method via a single level AHP.
2.2. Ranking with AHP
The AHP is a method developed for subjective evaluation of a set of alternatives based on multiple criteria. It provides a structured framework for setting priorities on each level of the hierarchy using pairwise comparisons that are subjective created by decision makers. Let
A be a pairwise comparison matrix of AHP:
where
denotes pairwise comparison between criteria/units,
and
for every
If
for
in a pairwise comparison matrix of
then
is completely compatible; otherwise, it is said to be incompatible [
5].
Theorem 1. [25] Suppose that is a pairwise comparison matrix, if is compatible, then its maximal eigenvalue Otherwise . According to Theorem 1, a pairwise comparison matrix, for which its maximum eigenvalue is closer to the matrix dimension, has less incompatibility [
5].
With the pairwise comparison matrix
A constructed in the first stage of the proposed, a single hierarchical level AHP is run to determine the weight vector
by the following characteristic equation:
where
is the maximal eigenvalue of
Such a method for determining the weight vector of a pairwise comparison matrix is referred to as the principal right eigenvector method [
1]. The
j-th component of
reflects the relative importance given to the
j-th DMU. The DMU that has higher corresponding value of
has higher ranking. We assign the rank 1 to the DMU with the maximal value of