Aesthetic Patterns with Symmetries of the Regular Polyhedron
Abstract
:1. Introduction
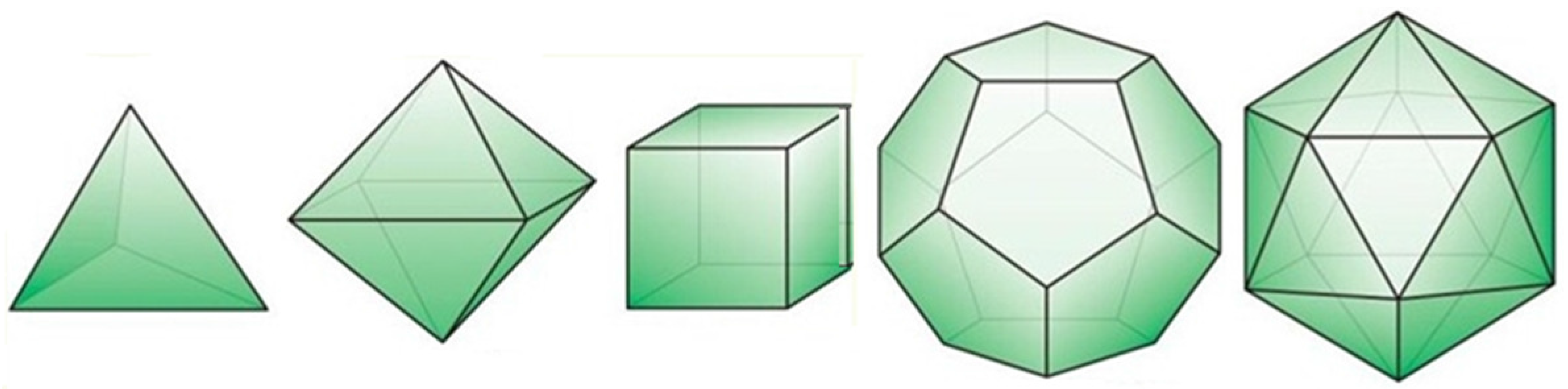
2. Symmetry Groups of Regular Polyhedra
- ■
- Tetrahedral group :
- ■
- Octhedral group :
- ■
- Icosahedral group :
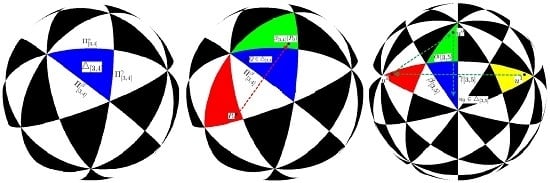
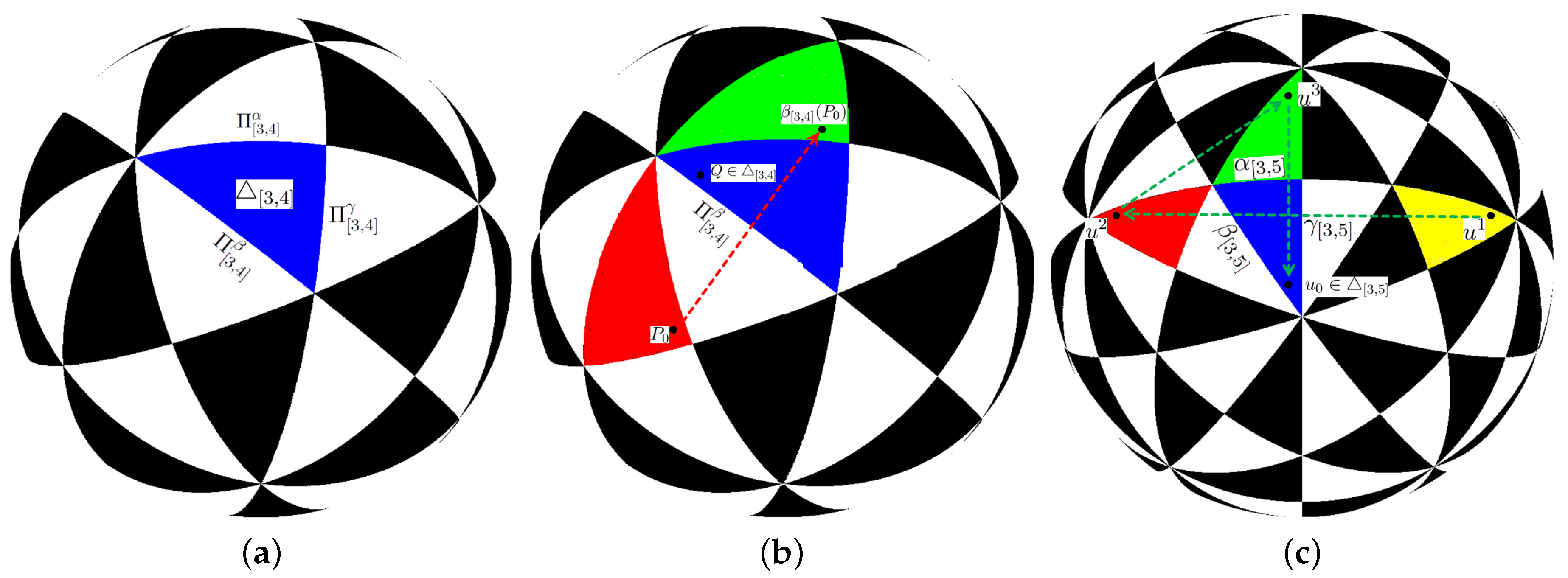
3. Transform Points of into Fundamental Region Symmetrically
4. Colorful Spherical Patterns with Symmetry
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Coxeter, H.S.M. Regular Polytopes; Dover: New York, NY, USA, 1973. [Google Scholar]
- Mcmulle, P.; Schulte, E. Abstract Regular Polytopes; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Conway, J.H.; Burgiel, H.; Goodman-Strauss, C. The Symmetries of Things; A K Peters Press: Natick, MA, USA, 2008. [Google Scholar]
- Armstrong, V.E. Groups and Symmetry; Springer: New York, NY, USA, 1987. [Google Scholar]
- Magnus, W. Noeuclidean Tessellation and Their Groups; Academic Press: New York, NY. USA, 1974. [Google Scholar]
- Rees, E.G. Notes on Geometry; Springer: Berlin/Heidelberg, Germany, 1983. [Google Scholar]
- Escher, M.C.; Ford, K.; Vermeulen, J.W. Escher on Escher: Exploring the Infinity; Harry N. Abrams: New York, NY, USA, 1989. [Google Scholar]
- Yen, J.; Séquin, C. Escher Sphere Construction Kit. In Proceedings of the 2001 Symposium on Interactive 3D Graphics, Research Triangle Park, NC, USA, 19–21 March 2001; pp. 95–98.
- Kaplan, C.S. Computer Graphics and Geometric Ornamental Design. Ph.D. Thesis, University of Washington, Washington, DC, USA, 2002. [Google Scholar]
- Field, M. Dynamics and Symmetry; Imperial College Press: London, UK, 2007. [Google Scholar]
- Humphreys, J.E.; Bollobas, B.; Fulton, W.; Katok, A.; Kirwan, F.; Sarnak, P.; Simon, B. Reflection Groups and Coxeter Groups; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Field, M.; Golubitsky, M. Symmetry in Chaos; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- Reiter, C.A. Chaotic Attractors with the Symmetry of the Tetrahedron. Comput. Graph. 1997, 6, 841–884. [Google Scholar] [CrossRef]
- Brisson, G.F.; Gartz, K.M.; McCune, B.J.; O’Brien, K.P.; Reiter, C.A. Symmetric Attractors in Three-dimensional Space. Chaos Soliton Fract. 1996, 7, 1033–1051. [Google Scholar] [CrossRef]
- Lu, J.; Zou, Y.R.; Liu, Z.Y. Colorful Symmetric Images in Three-dimensional Space from Dynamical Systems. Fractals 2012, 20, 53–60. [Google Scholar] [CrossRef]
- Benson, D.J.; Hitchin, N.J. Polynomial Invariant of Finite Groups; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Chung, K.W.; Chan, H.S.Y. Spherical Symmetries from Dynamics. Comput. Math. Appl. 1995, 7, 67–81. [Google Scholar] [CrossRef]
- Dumont, J.P.; Reiter, C.A. Chaotic Attractors Near Forbidden Symmetry. Chaos Soliton Fract. 2000, 11, 1287–1296. [Google Scholar] [CrossRef]
- Jones, K.C.; Reiter, C.A. Chaotic Attractors with Cyclic Symmetry Revisited. Comput. Graph. 2000, 24, 271–282. [Google Scholar] [CrossRef]
- Reiter, C.A. Chaotic Attractors with the Symmetry of the Dodecahedron. Vis. Comput. 1999, 4, 211–215. [Google Scholar] [CrossRef]
- Dumont, J.P.; Heiss, F.J.; Jones, K.C.; Reiter, C.A.; Vislocky, L.M. N-dimensional Chaotic Sttractors with Crystallographic Symmetry. Chaos Soliton Fract. 2001, 4, 761–784. [Google Scholar] [CrossRef]
- Coxeter, H.S.M.; Moser, W.O.J. Generators and Relations for Discrete Groups; Springer: New York, NY, USA, 1980. [Google Scholar]
- Lu, J.; Ye, Z.X.; Zou, Y.R. Colorful Patterns with Discrete Planar Symmetries from Dynamical Systems. Fractals 2012, 18, 35–43. [Google Scholar] [CrossRef]
- Ouyang, P.C.; Fathauer, R.W. Beautiful Math, Part 2, Aesthetic Patterns Based on Fractal Tilings. IEEE Comput. Graph. 2014, 1, 68–75. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, P.C.; Chung, K.W. Beautiful Math, Part 3, Hyperbolic Aesthetic Patterns Based on Conformal Mappings. IEEE Comput. Graph. 2014, 2, 72–79. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, P.C.; Cheng, D.S.; Cao, Y.H.; Zhan, X.G. The Visualization of Hyperbolic Patterns from Invariant Mapping Method. Comput. Graph. 2012, 2, 92–100. [Google Scholar] [CrossRef]



© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouyang, P.; Wang, L.; Yu, T.; Huang, X. Aesthetic Patterns with Symmetries of the Regular Polyhedron. Symmetry 2017, 9, 21. https://doi.org/10.3390/sym9020021
Ouyang P, Wang L, Yu T, Huang X. Aesthetic Patterns with Symmetries of the Regular Polyhedron. Symmetry. 2017; 9(2):21. https://doi.org/10.3390/sym9020021
Chicago/Turabian StyleOuyang, Peichang, Liying Wang, Tao Yu, and Xuan Huang. 2017. "Aesthetic Patterns with Symmetries of the Regular Polyhedron" Symmetry 9, no. 2: 21. https://doi.org/10.3390/sym9020021