1. Introduction
Nowadays, the research of complex networks has attracted many researchers. One interesting and important problem is to study the network structure by using different graph and network measures. Meanwhile, these graph and network measures have been widely applied in many different fields, such as chemistry, biology, ecology, sociology and computer science [
1,
2,
3,
4,
5,
6,
7]. From the viewpoint of information theory, the entropy of graphs was initiated to be applied by Mowshowitz [
8] and Trucco [
9]. Afterwards, Dehmer introduced graph entropies based on information functionals which capture structural information and studied their properties [
10,
11,
12]. The graph entropies have been used as the complexity measures of networks and measures for symmetry analysis. Recently, so-called generalized graph entropies have been investigated by Dehmer and Mowshowitz [
13] for better analysis and applications such as machine learning. The generalized graph entropies can characterize the topology of complex networks more effectively [
14].
The degree powers are extremely considerable invariants and studied extensively in graph theory and network science, so they are commonly used as the information functionals to explore the networks [
15,
16]. To study more properties of graph entropies based on the degree powers, Lu et al. obtained some upper and lower bounds which have different performances to bound the graph entropies in different kinds of graphs and showed their applications in structural complexity analysis [
17,
18]. Inspired by Dehmer and Mowshowitz [
13], we focus on the relationships between degree powers and the parametric complexity measures and then we construct generalized degree-based graph entropies by using the concept of the mentioned generalized graph entropies. The structure of this paper is as follows: In
Section 2, some definitions and notations of graph theory and the graph entropies we are going to study are reviewed. In
Section 3, we describe the definition of generalized degree-based graph entropies which are motivated by Dehmer and Mowshowitz [
13]. In
Section 4, we present some extremal properties of such entropies related to the degree powers. Moreover, we give some inequalities among the generalized degree-based graph entropies. In
Section 5, numerical results of an exemplary network are shown to demonstrate the new entropies. Finally, a short summary and conclusion are drawn in the last section.
2. Preliminaries to Degree-Based Graph Entropy
A
graph or
network G is an ordered pair
comprising a set
V of
vertices together with a set
E of
edges. In network science, vertices are called
nodes sometimes. The
order of a graph means the number of vertices. The
size of a graph means the number of edges. A graph of order
n and size
m is recorded as an
-graph. The
degree of a vertex
v denoted by
or in short
means the number of edges that connect to it, where an edge that connects a vertex to itself (a loop) is counted twice. The maximum and minimum degree in a graph are often denoted by
and
. If every vertex has the same degree (
), then
G is called a
regular graph, or is called a
d-regular graph with vertices of degree
d. An unordered pair of vertices
is called connected if a path leads from
u to
v. A
connected graph is a graph in which every unordered pair of vertices is connected. Otherwise, it is called a
disconnected graph. Obviously, in a connected graph,
. A
tree is a connected graph in which any two vertices are connected by exactly only one path. So tree is a connected
-graph.
is denoted a
path graph characterized as a tree in which the degree of all but two vertices is 2 and the degree of the two remaining vertices is 1.
is denoted a
star graph characterized as a tree in which the degree of all but one vertex is 1. More details can be seen in [
17,
18].
Next, we describe the concept of (Shannon’s) entropy [
19,
20]. The notation “log” means the logarithm is based 2, and the notation “ln” means the logarithm is based
.
Definition 1. Let be a probability distribution, namely, and . The (Shannon’s) entropy of the probability distribution is defined by In the above definition, we use for continuity of corresponding function.
Definition 2. Let be a graph of order n. For , we definewhere f is a meaningful information functional. According to the information functional f, the vertices are mapped to the non-negative real numbers. Because
, the quantities
can be seen as probability values. Then the graph entropy of
G has been defined as follows [
10,
12,
17,
18].
Definition 3. Let be a graph of order n and f be a meaningful information functional. The (Shannon’s) graph entropy of G is defined by Definition 4. Let be a graph of order n. For , if , then Therefore, the degree-based graph entropy of G is defined as 3. Generalized Degree-Based Graph Entropy
Many generalizations of entropy measure have been proposed based on the definition of Shannon’s entropy [
21,
22]. For example, Rényi entropy [
23], Daròczy’s entropy [
24] and quadratic entropy [
25] are representative generalized entropies. In [
13], Dehmer and Mowshowitz introduce a new class of generalized graph entropies that derive from the generalizations of entropy measure mentioned above and present two examples.
Definition 5. Let be a graph of order n. Then Definition 6. Let be a graph of order n and A its adjacency matrix. Denote by the eigenvalues of G. If , then the generalized graph entropies are as follows: Definition 7. Let be a graph of order n. Denote the collection of orbits by and their respective probabilities by , where k is the number of orbits. Then another class of generalized graph entropies are derived as Because it is difficult to obtain the eigenvalues or the collection of orbits of graph G for a large-scale graph, and they may not meet the requirements visually, we focus on the complexity of the graphs or networks determined by the vertices themselves and the relationship between them in this paper. For a given graph G, the vertex degree is a significant graph invariant, which is related to structural properties of the graph. Most other properties of the complex network are based on the degree distribution, such as the clustering coefficient, the community structure and so on. The vertex degree in a graph or network is also intuitional and noticeable. The vertices with varying values of degree chosen as the main construction of the graph or network may decide the complexity of the graph or network. Hence, we study the generalized graph entropies based on the vertex degree and degree powers.
According to the above definitions of generalized graph entropies, let for , then we obtain the generalized degree-based graph entropies as follows:
4. Properties of the Generalized Degree-Based Graph Entropies
In this section, we will show the relationships among the stated generalized degree-based graph entropies and the degree-based graph entropy. First we will present five simple propositions which can be inferred from the Rényi entropy and [
13].
Proof. Noticing that
we can obtain the Equations (
4) and (
5). Let
, we have
, then the Equation (
6) follows. ☐
Remark 1. Proposition 1 can be seen as a special case of (12) and (16) in [13] when the value of the information functional is the degree of every vertex. Proof. Using l’Hôspital’s rule, we can obtain the Equation (
7). ☐
Proposition 3. For , is monotonically decreasing with respect to α.
Proof. The derivative of the function
is
where
,
. Then
and
are also probability distributions. From the nonnegativity of Kullback-Leibler divergence, we obtain
. The inequality implies that
is monotonically decreasing with respect to
α. ☐
Proposition 4. For ,and for , Proof. Using Proposition 2 and Proposition 3, we can obtain the equalities above easily. ☐
Remark 2. Proposition 2, Proposition 3 and Proposition 4 can be seen as the special cases of the Rényi entropy’s properties.
Proof. Using the standard inequality
when
, we have
. Therefore,
Then the inequality (
10) follows. ☐
Next we define the sum of the α-th degree powers as , where α is an arbitrary real number.
Theorem 1. Let be an -graph. Then for , we have Proof. By substituting
into the Equations (
1)–(
3), we have
So the Equations (
11)–(
13) hold. ☐
From the above theorem, we know that the generalized degree-based graph entropies are closely related to the sum of the degree powers
. Obviously when
,
presents the sum of degrees. The sum of the degree powers as an invariant is called
zeroth order general Randić index [
26,
27,
28,
29]. For
,
is also called
first Zagreb index [
30,
31,
32,
33]. In [
34], Chen et al. have reviewed
for different values of
α and discussed the relationships with some indices such as Zagreb index, graph energies, HOMO-LUMO index, Estrada index [
35,
36,
37,
38,
39,
40,
41,
42,
43].
Corollary 1. Let be an -graph. Then we have Proof. Using Cauchy-Buniakowsky-Schwarz inequality, we obtain
In [
44] de Caen obtains the following inequality
So from Equation (
13), we have
or equivalently,
We can also find some conditions for the equalities: If G is a regular graph, then the equality holds; If G is a tree of order n, then the equality holds. ☐
Corollary 2. Let T be a tree of order n. Then we havewhere and denote the star graph and path graph of order n, respectively. Proof. In [
45], Li and Zhao present that among all trees of order
n, for
or
, the path graph and the star graph attain the minimum and maximum value of
respectively; while for
, the star graph and the path graph attain the minimum and maximum value of
respectively. Then using the Equation (
13), the result of the corollary is obtained. ☐
Theorem 2. When , we have ; and when , we have . Especially, when , we have .
Proof. First we define a new function on
α on the set of real numbers
as follows
Because straightforward derivative shows
we can claim that
is a strictly decreasing function on
α.
For
, we have
Using the standard inequality when , we find when .
Therefore, for
, we have
Especially, when , and . So holds in this case. ☐
Corollary 3. When , we have .
Proof. First we define a new function on
α on the set of real numbers
as follows
Because the second order derivative shows
we can claim that
is a convex function on
α. Since
, we find
for
, or equivalently
for
. Using Theorem 2, the inequality
holds. ☐
Theorem 3. When and , we have ; when , we have ; and when , we have .
Proof. First we have
and
is a strictly decreasing function on
α.
Therefore, for
,
and
are obtained. Then we have
This implies .
For
,
and
are obtained. Then we have
This implies .
For
, using (
6) we have
.
For
,
and
are obtained. Then we have
This implies . Thus we complete the proof. ☐
Corollary 4. When , we have .
Proof. For , we have the result by using Theorem 3. ☐
Theorem 4. When , we have ; when , we have ; and when , we have .
Proof. For
, using (
8) and (
10) we have
.
For
,
and
are obtained. Then we have
Using the standard inequality
when
, we find
. So
This implies .
For , using Theorem 2 and Theorem 3 we have and . This implies . Thus we complete the proof. ☐
5. Numerical Results
In order to illuminate the principle of generalized degree-based graph entropies, we show a network in
Figure 1 as an example.
The degree of each node of the example network is shown in
Table 1.
We can easily calculate
. The details of
and
with different
α are shown in
Table 2.
In
Table 2 that the value of
α is equal to
means
. Then
and
are degenerated to the degree-based graph entropy
.
It is clear that following the increase of the value of
α, the values of the generalized degree-based graph entropies
and
of the complex network are decrease. Based on the concept of the entropy, the bigger the value of the entropy is, the more complex of the network is. From the definitions of
and
, the value of the entropic index
α can be used to change the construction of the entropies. In other words, the value of
α represents the relationship among the nodes in the complex network. Combined with the complex network, the influence of each node’s degree on the entropies is changed by the value of
α. The relationship between the value of
α and the entropies of the complex network is shown as follows:
- (1)
When , the nodes with small value of degree play an important part in the construction of and , or they are chosen as the main construction of the complex networks. Especially when the value of , each node has the same influence on the whole network from the entropic point of view.
- (2)
When , the influence of each node on the network is based on the value of degree for each node. The generalized degree-based graph entropies and are degenerated to the degree-based graph entropy . So the structure property determined by the node’s degree decides the complexity of the complex network.
- (3)
When , the nodes with big value of degree play an important part in the construction of and , or they are chosen as the main construction of the complex networks. The values of the entropies tend to stabilization. The complex network is tended to orderly.
To sum up, according to the definition of the generalized degree-based graph entropies of the complex network, the value of the entropic index α is used to describe the different relationship among the nodes. When the value of α is smaller than 1, the nodes with small value of degree are more important than the nodes with big value of degree. The edges among those nodes with small value of degree become the main part of the complex network. As these nodes with small value of degree are the majority in the complex network, the whole network has greater complexity. When the value of α is equal to 0, the nodes in the network are equal to each other in terms of influence. When the value of α tends to 1, and are degenerated to , the level of complexity for the complex network is decided by the structure property. In other words, the complexity of the complex network is decided by the degree sequence and degree distribution. When the value of α is trended to ∞, the construction of the complex network is decided by the node which has a biggest value of degree, the values of and decrease to stable values, and the complex network is more orderly. The complexity of the complex network is not only decided by the structure of the complex network, but also influenced by the kind of the relationship between each node.
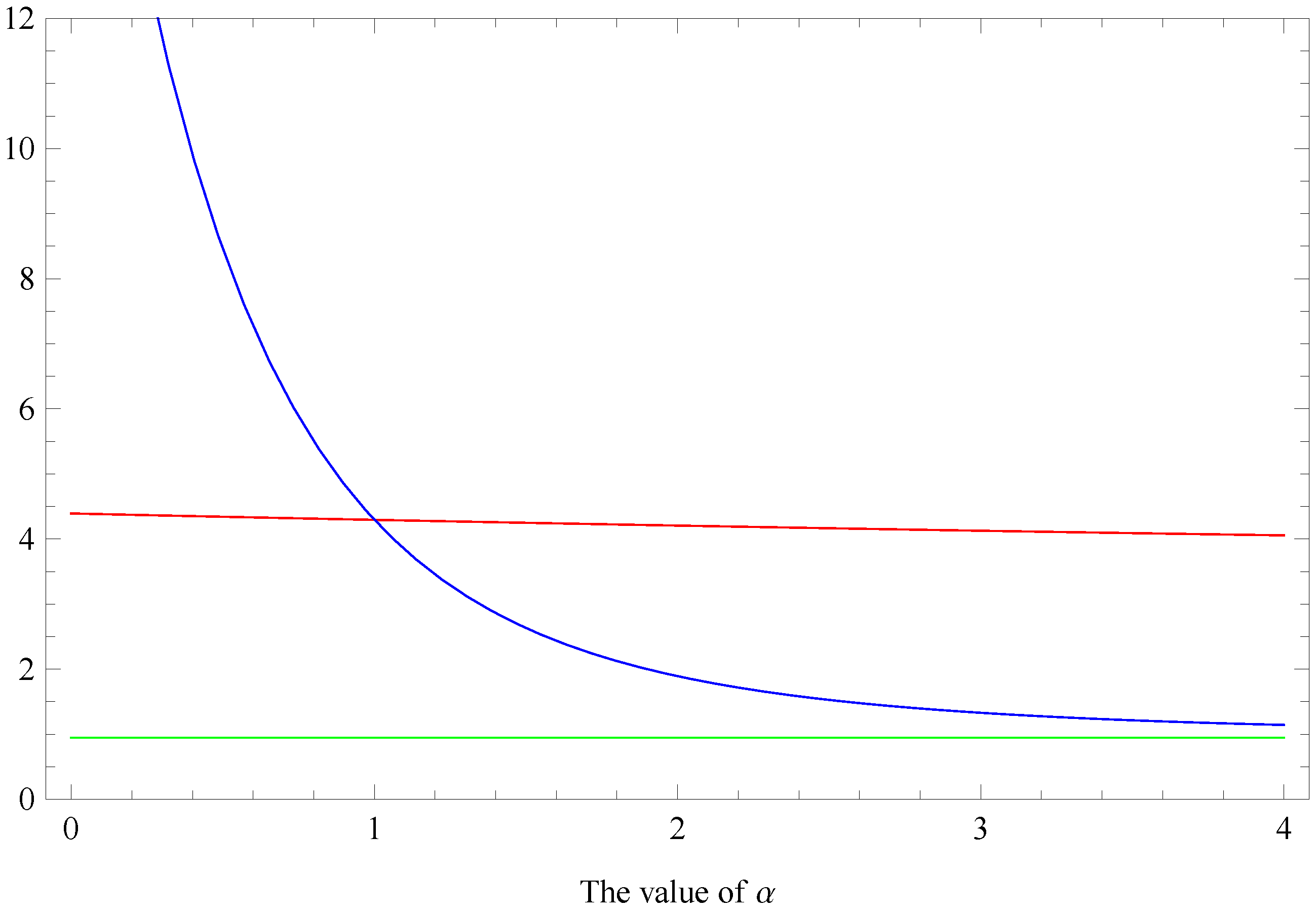
From
Figure 2, we can see the plotted values of the generalized degree-based graph entropies
,
and
relative to
α (
,
with a pole at
). The numerical results can be interpreted as follows: First we observe that the value of
is less than that of
for
, while the value of
is larger than that of
for
. Next, for
,
and
, we can have the values of
and
is always larger than that of
. Actually, using l’Hôspital’s rule we have that the value of
tends to 3.459 and the value of
tends to 1 when
α tends to
. At last, all the curves verify the inequalities in the
Section 4.
In addition, generalized graph entropy measures with parameters have been presented to be useful in studying the complexity associated with machine learning. For example, Dehmer et al. have described that the generalized graph entropies can be applied to the graph classification and clustering cases in machine learning. The applications involve optimizing particular parameters associated with graphs or networks in given sets [
4,
46]. So by applying supervised machine learning methods, the generalized degree-based entropies can be used for classifying the chemical structures, developing methods for characterizing predictive models according to optimal values of relevant parameters in bioinformatics, systems biology, and drug design.