Dual Hesitant Fuzzy Probability

Abstract

Intuitionistic fuzzy probabilities are an extension of the concept of probabilities with application in several practical problem solving tasks. The former are probabilities represented through intuitionistic fuzzy numbers, to indicate the uncertainty of the membership and nonmembership degrees in the value assigned to probabilities. Moreover, a dual hesitant fuzzy set (DHFS) is an extension of an intuitionistic fuzzy set, and its membership degrees and nonmembership degrees are represented by two sets of possible values; this new theory of fuzzy sets is known today as dual hesitant fuzzy set theory. This work will extend the notion of dual hesitant fuzzy probabilities by representing probabilities through the dual hesitant fuzzy numbers, in the sense of Zhu et al., instead of intuitionistic fuzzy numbers. We also give the concept of dual hesitant fuzzy probability, based on which we provide some main results including the properties of dual hesitant fuzzy probability, dual hesitant fuzzy conditional probability, and dual hesitant fuzzy total probability.

1. Introduction

After the introduction of the concept of fuzzy sets by Zadeh in [1], several surveys were conducted on possible extensions of the concept of fuzzy set. Among these extensions, one that has attracted the attention of much research in recent decades is dual hesitant fuzzy set theory, introduced by Zhu et al. [2]. In 2011, Xu and Xia [3] defined the concept of dual hesitant fuzzy element (DHFE), which can be considered as the basic unit of a DHFS, and is also a simple and effective tool used to express the decision makers’ hesitant preferences in the process of decision making. Since then, many scholars [4,5,6,7,8,9] have conducted much research work on aggregation, distance measures, correlation coefficient, and decision making with dual hesitant fuzzy information.

On the other hand, probability theory is an old uncertainty method which is appropriate to deal with another kind of uncertainty. However, since probabilities consider an absolute knowledge, and in many real situations this knowledge is partially known or uncertain, there were several ways to extend the notion of probabilities to deal with such situations. An original conception of connecting fuzzy set theory with probability theory was first introduced by Hirota and Wright [10]. For James Buckley [11], the probabilities of events, in practice, should be known exactly, however, these values are very often estimated or provided by experts, and therefore are of vague nature. He modeled this vagueness using fuzzy numbers. This approach has been applied in several subjects (see [11,12]), such as testing for HIV, and other blood type problems. Besides, according to fuzzy probability, James Buckley [11] also proposed fuzzy Markov chains, and joint fuzzy probability distributions, etc., then applied them to the fuzzy queuing decision problem, machine servicing problem, fuzzy decisions under risk and fuzzy reliability theory. In 2010, Costa et al. [13] introduced a generalization of the concept of fuzzy probabilities by using an original notion of intuitionistic fuzzy numbers instead of usual fuzzy numbers and gave some notions about intuitionistic fuzzy probabilities. In 2013, Costa et al. [14] investigated Atanassov’s intuitionistic fuzzy probability and Markov chains. Rashid et al. [15] introduced a convex hesitant fuzzy set and a quasi-convex hesitant fuzzy set with an example and investigated aggregation functions for convex hesitant fuzzy sets, which are available in the optimization problem.

As discussed above, a DHFS has its own desirable characteristics and advantages and appears to be a more flexible method—which is to be valued in multifold ways due to the practical demands—than the existing fuzzy sets, taking into account much more information given by decision makers, and at the same time, fuzzy probability and intuitionistic fuzzy probability play a crucial role in applications [11]; we urgently need to put forward dual hesitant fuzzy probability to satisfy the same problems. In this paper, we will introduce probabilities to a DHFS by using an original notion of dual hesitant fuzzy numbers instead of usual fuzzy numbers. Thus, we give an original generalization, in the context of a DHFS, to the intuitionistic fuzzy probability approach of Costa et al. in [13]; thus, we introduce a theory to deal with probabilities in a framework where it does not only model uncertainty in the probability of some events but also models the dual hesitation which is naturally present in the uncertainty.

Motivated by earlier research work, the remainder of the paper is organized as follows: In Section 2, some basic concepts of dual hesitant fuzzy sets are presented. In Section 3, we give some convexity for DHFSs, which contains a convex dual hesitant fuzzy set with respect to $(\alpha ,\beta )-cuts$ and a quasi-convex dual hesitant fuzzy set; we also introduce intuitionistic fuzzy numbers that are fundamental to the paper. In Section 4, we provide the main definitions and results of this work. Section 5 introduces a dual hesitant fuzzy extension of (fuzzy intuitionistic) conditional probability and it is proven that this extension satisfies more analogous properties than conditional probabilities. In Section 6, an example of the application of color blindness is given to show the actual need of dual hesitant fuzzy probability. A conclusion to the paper and further topics are given in Section 7.

2. Some Basic Concepts about DHFS

Zhu et al. [2] defined a DHFS—which is an extension of the hesitant fuzzy set, in terms of two functions that return two sets of membership values and nonmembership values, respectively, for each element in the domain—as follows.

Definition 1.

[2] Let X be a fixed set, then a DHFS D on X is defined as:

$$D=\{<x,h(x),g(x)>|x\in X\},$$

(1)

where $h\left(x\right)$ and $g\left(x\right)$ are two sets of some values in [0, 1], denoting the possible membership degrees and nonmembership degrees of the element $x\in X$ to the set D, respectively, with the conditions: $0\le \gamma ,\eta \le 1$ and $0\le {\gamma }^{+}+{\eta }^{+}\le 1$, where $\gamma \in h\left(x\right)$, $\eta \in g\left(x\right)$, ${\gamma }^{+}\in h^{+}\left(x\right)={\cup }_{\gamma \in h\left(x\right)}max\left\{\gamma \right\}$, and ${\eta }^{+}\in g^{+}\left(x\right)={\cup }_{\eta \in g\left(x\right)}max\left\{\eta \right\}$ for $x\in X$. For convenience, the pair $e\left(x\right)=\{<h(x),g(x)>\}$ is called a DHFE denoted by all $e=\{<h,g>\}$.

The support of the DHFS D is the crisp set $Supp\left(D\right)=\{t\in X:max$ $h\left(t\right)\ne 0$ and max $g\left(t\right)\ne 1\}\subseteq X$, whereas the kernel of the DHFS D is the crisp set $Ker\left(D\right)=\{t\in X:max$ $h\left(t\right)=1$ and $max$ $g\left(t\right)=0\}\subseteq X$. The DHFS D is said to be normal provided that it has a non-empty kernel.

From the above definition, we can see that it consists of two parts, that is, the membership hesitancy function and the nonmembership hesitancy function; this supports more exemplary and flexible access to assign values for each element in the domain, and two kinds of hesitancy can be handled in this situation. The existing sets, including fuzzy sets, intuitionistic fuzzy sets, hesitant fuzzy sets, and fuzzy multisets, can be regarded as special cases of DHFSs.

Example 1.

Let D be a dual hesitant fuzzy set in $X=\{x_1,x_2,x_3\}$, and we give three dual hesitant fuzzy elements to a set D as follows:

• $h_D\left(x_1\right)=\{\{0.7,0.5,0.3\},\{0.2,0.1\}\}$,
• $h_D\left(x_2\right)=\{\{0.4,0.3\},\{0.2,0.4\}\}$,
• $h_D\left(x_3\right)=\{\{0.6,0.3\},\{0.3,0.1,0.2\}\}$,

then $D=\{<x_1,\{0.7,0.5,0.3\},\{0.2,0.1\}>,$ $<x_2,\{0.4,0.3\},\{0.2,0.4\}>,$ $<x_3,\{0.6,0.3\},\{0.3,0.1,0.2\}\}$.

The following operations are also given by Zhu et al. [2], for any DHFEs, d, $d_1$ and $d_2$,

(1)

$\oplus -union$: $d_1\oplus d_2=$ ${\cup }_{{\gamma }_{d_1}\in h_{d_1},{\gamma }_{d_2}\in h_{d_2}}$ $\{\{{\gamma }_{d_1}+{\gamma }_{d_2}-{\gamma }_{d_1}{\gamma }_{d_2}\},\left\{{\eta }_{d_1}{\eta }_{d_2}\right\}\}$;

(2)

$\otimes -intersection$: $d_1\otimes d_2=$ ${\cup }_{{\gamma }_{d_1}\in h_{d_1},{\gamma }_{d_2}\in h_{d_2}}$ $\{\left\{{\gamma }_{d_1}{\gamma }_{d_2}\right\},\{{\eta }_{d_1}+{\eta }_{d_2}-{\eta }_{d_1}{\eta }_{d_2}\}\}$;

(3)

$nd={\cup }_{{\gamma }_d\in h_d,{\eta }_d\in g_d}\{1-{(1-{\gamma }_d)}^n,{\left({\eta }_d\right)}^n\}$;

(4)

$d^n={\cup }_{{\gamma }_d\in h_d,{\eta }_d\in g_d}\{{\left({\gamma }_d\right)}^n,1-{(1-{\eta }_d)}^n\}$, where n is a positive integral and all the results are also DHFEs.

Definition 2.

[2] Let $d_i=\{h_{d_i},g_{d_i}\}$ be any two DHFEs, $s\left(d_i\right)=\frac{1}{♯h}{\sum }_{\gamma \in h}\gamma -\frac{1}{♯g}{\sum }_{\eta \in g}\eta (i=1,2)$ the score function of $d_i(i=1,2)$, and $p\left(d_i\right)=\frac{1}{♯h}{\sum }_{\gamma \in h}\gamma +\frac{1}{♯g}$ ${\sum }_{\eta \in g}\eta (i=1,2)(i=1,2)$ the accuracy function of $d_i(i=1,2)$, where $♯h$ and $♯g$ are the numbers of the elements in h and g, respectively, then

 (i) 

if $s\left(d_1\right)>s\left(d_2\right)$, then $d_1$ is superior to $d_2$, denoted by $d_1\succ d_2$;

(ii) 

if $s\left(d_1\right)=s\left(d_2\right)$, then

(1) 

if $p\left(d_1\right)=p\left(d_2\right)$, then $d_1$ is equivalent to $d_2$, denoted by $d_1\sim d_2$;

(2)

if $p\left(d_1\right)>p\left(d_2\right)$, then $d_2$ is superior to $d_1$, denoted by $d_2\succ d_1$.

In order to give the level set of a DHFS, we give the following notion: Let $d=\{h,g\}$ be a DHFE. Then, $s\left(h\right)=\frac{1}{♯h}{\sum }_{\gamma \in h}\gamma$ and $s\left(g\right)=\frac{1}{♯g}{\sum }_{\eta \in g}\eta$ are the score function of the membership degrees and nonmembership degrees of DHFEs, respectively, where $♯h$ and $♯g$ are the numbers of elements in h and g, respectively.

3. Dual Hesitant Fuzzy Numbers

In this section, we carry out a brief introduction to some kinds of convexity for dual hesitant fuzzy sets, based on which we give some concepts about dual hesitant fuzzy numbers for a better understanding of the main body of the paper. Next, let us start by recalling a unit triangular lattice.

Definition 3.

[16,17] Let $T=\{(x_1,x_2)\in [0,1]\times [0,1]:x_1+x_2\le 1\}.$ Define on T a binary relation ${\le }_T$ given by $(x_1,x_2){\le }_T(y_1,y_2)$ provided that $x_1\le y_1$ and $y_2\le x_2$. Then, $(T,{\le }_T,0_T,1_T)$ is a bounded complete lattice, where $0_T$ stands for (0,1) and $1_T$ stands for (1, 0). This new lattice T is called the unit triangular lattice.

The unit triangular lattice T has been proven to be a helpful tool in the theory of representability of several ordered structures as total preorders, interval orders and semiorders (see [16,17] for further details).

Given a DHFS D, its supremum and infimum, with respect to ${\le }_T$, could be obtained as follows:

$$supD=(sup\left\{s\left(h_1\left(x\right)\right)\right|x\in D\},inf\left\{s\left(g_2\left(x\right)\right)\right|x\in X\}),$$

(2)

and

$$infD=(inf\left\{s\left(h_1\left(x\right)\right)\right|x\in D\},sup\left\{s\left(g_2\left(x\right)\right)\right|x\in X\}).$$

(3)

Given $(\alpha ,\beta )\in T$ and a DHFS D of universe X, the $(\alpha ,\beta )-cut$ of D is the set:

$$D_{(\alpha ,\beta )}=\{x\in X|s\left(h_D\left(x\right)\right)\ge \alpha ands\left(g_D\left(x\right)\right)\le \beta \}.$$

(4)

Notice that $D_{(\alpha ,\beta )}=(D_{\alpha },D^{\beta })$, where $D_{\alpha }=\{x\in X|s\left(h_D\left(x\right)\right)\ge \alpha \}$ and $D^{\beta }=\{x\in X|s\left(g_D\left(x\right)\right)\le \beta \}$. On the other hand, every DHFS can be recovered from its $(\alpha ,\beta )-cuts$. In fact, $(h_D\left(x\right),g_D\left(x\right))=sup\{(\alpha ,\beta )\in T|x\in A_{(\alpha ,\beta )}\}$, where the supremum is with respect to ${\le }_T$.

Definition 4.

Let D be a dual hesitant fuzzy set with universe R. D is convex if its cuts $D_{(\alpha ,\beta )}$ are convex subsets of X for all $\alpha ,\beta \in (0,1]$.

An equivalent statement is shown as follows:

Definition 5.

Let X be a vector space. A dual hesitant fuzzy set D of the universe X is said to be quasi-convex, if for all $x,y\in X$ and $\lambda \in [0,1]$ it holds that $(min\{s\left(h_D\left(x\right)\right),s\left(h_D\left(y\right)\right)\},$ $max\{s\left(g_D\left(x\right)\right),s\left(g_D\left(y\right)\right)\})$ ${\le }_T$ $\left(s\right(h_D(\lambda x+(1-\lambda )y),$ $s\left(g_D(\lambda x+(1-\lambda )y)\right)$.

Lemma 1.

If $D=\{<x,h_D\left(x\right),g_D\left(x\right)>\}$ is a DHFS and we denote by $D_1$ the hesitant fuzzy set defined by means of the membership function of D $(i.e.,D_1=h_D)$, then $D_{(\alpha ,\beta )}={\left(D_1\right)}_{\alpha }$ for any $\alpha \in (0,1]$. This means that $D_{(\alpha ,\beta )}=\{x\in X:h_D\left(x\right)\ge \alpha \}$.

Proof. 

It is trivial that $D_{\alpha ,\beta }\subseteq {\left(D_1\right)}_{\alpha }$. Let $x\in {\left(D_1\right)}_{\alpha }$, then $s\left(h_D\left(x\right)\right)\ge \alpha$. Since D is a DHFS, we have that $max\left\{h_D\left(x\right)\right\}+max\left\{g_D\left(x\right)\right\}\le 1$, then $s\left(g_D\left(x\right)\right)\le 1-max$ $s\left(h_D\left(x\right)\right)\le 1-\alpha$ and therefore $s\left(g_D\left(x\right)\right)\le \beta (\beta =1-\alpha )$. Then, $x\in D_{(\alpha ,\beta )}$. ☐

Remark 1.

${\left(D_1\right)}_{\alpha }$ and $\alpha -cut$ of the hesitant fuzzy set in Lemma 1 is given in [16].

Theorem 1.

Let X be a universe. The following statements are equivalent:

(1) 

D is a quasi-convex DHFS;

(2) 

any $(\alpha ,\beta )-cuts$ of DHFS D are convex crisp sets, for any $\alpha ,\beta \in (0,1]$;

(3) 

$h_D$ is the membership function of a convex hesitant fuzzy set with respect to $\alpha -cuts$ [16].

Proof. 

$\left(1\right)\iff \left(2\right)$: To prove the direct implication, given $(\alpha ,\beta )\in L$, for all $x,y\in X$ and $\lambda \in [0,1]$ such that $(\alpha ,\beta ){\le }_T$ $(min\{s\left(h_D\left(x\right)\right),s\left(h_D\left(y\right)\right)\}$ $,max\{s\left(g_D\left(x\right)\right),s\left(g_D\left(y\right)\right)\})$, if D is a quasi-convex DHFS, we have that $(\alpha ,\beta ){\le }_T(min\{s\left(h_D\left(x\right)\right),s\left(h_D\left(y\right)\right)\}$ $,max\{s\left(g_D\left(x\right)\right),s\left(g_D\left(y\right)\right)\})$ ${\le }_T\left(s\right(h_D(\lambda x+(1-\lambda )y),s(g_D(\lambda x+(1-\lambda )y)$. Then, any $(\alpha ,\beta )-cuts$ of a DHFS D are convex crisp sets, for any $\alpha \in (0,1]$.

On the contrary, given $x,y\in X$ and $(\alpha ,\beta )\in L$, if we call $\alpha =min\{s\left(h_D\left(x\right)\right),s\left(h_D\left(y\right)\right)\}$ and $\beta =min\{s\left(g_D\left(x\right)\right),s\left(g_D\left(y\right)\right)\}$, it is clear that $x,y$ belong to the $\alpha -cut$ of the dual hesitant fuzzy set defined by $D_{(\alpha ,\beta )}$. By hypothesis, $\lambda x+(1-\lambda )y$ also lies in this $(\alpha ,\beta )-cut$, so that $(\alpha ,\beta ){\le }_T(min\{s\left(h_D\left(x\right)\right),s\left(h_D\left(y\right)\right)\}$ $,min\{s\left(g_D\left(x\right)\right),s\left(g_D\left(y\right)\right)\})$ ${\le }_T(s\left(h_D(\lambda x+(1-\lambda )y)\right)$ $,s\left(g_D(\lambda x+(1-\lambda )y)\right))$. Thus, $(min\{s\left(h_D\left(x\right)\right),s\left(h_D\left(y\right)\right)\}$ $,max\{s\left(g_D\left(x\right)\right),s\left(g_D\left(y\right)\right)\})$ ${\le }_T$ $\left(s\right(h_D(\lambda x+(1-\lambda )y),$ $s\left(g_D(\lambda x+(1-\lambda )y)\right)$.

$\left(2\right)\iff \left(3\right)$: Based on Lemma 1, it is easy to prove that it holds. ☐

Definition 6.

Let D be a DHFS with universe R. D is continuous if $s\left(h_D\left(x\right)\right)$ and $s\left(g_D\left(x\right)\right)$ are continuous; D is normalized if there exists $x\in R$ such that $(s\left(h_D\left(x\right)\right),s\left(g_D\left(x\right)\right))=1_T$.

Thus, for the convex DHFS, its $(\alpha ,\beta )-cuts$ are closed intervals of real numbers, and so it is possible to represent them via their end points, which can be obtained as follows:

$$l\left(D(\alpha ,\beta )\right)=max(mins\left(h_D\right){\left(\alpha \right)}^{-1},mins\left(g_D\right){\left(\beta \right)}^{-1}),$$

(5)

and

$$r\left(D(\alpha ,\beta )\right)=min(maxs\left(h_D\right){\left(\alpha \right)}^{-1},maxs\left(g_D\right){\left(\beta \right)}^{-1}),$$

(6)

that is, $D(\alpha ,\beta )=\left[l\right(D(\alpha ,\beta )),r(D(\alpha ,\beta )\left)\right]$. Where $s\left(h_D\right){\left(\alpha \right)}^{-1}=\left\{x\right|s\left(h_D\left(x\right)\right)\ge \alpha \}$ and $s\left(g_D\right){\left(\alpha \right)}^{-1}=\left\{x\right|s\left(g_D\left(x\right)\right)\le \beta \}$.

Definition 7.

A DHFS D with the real universe is a dual hesitant fuzzy number (DHFN) if it is convex, normalized and continuous. Denote by ℑ the set of all DHFN.

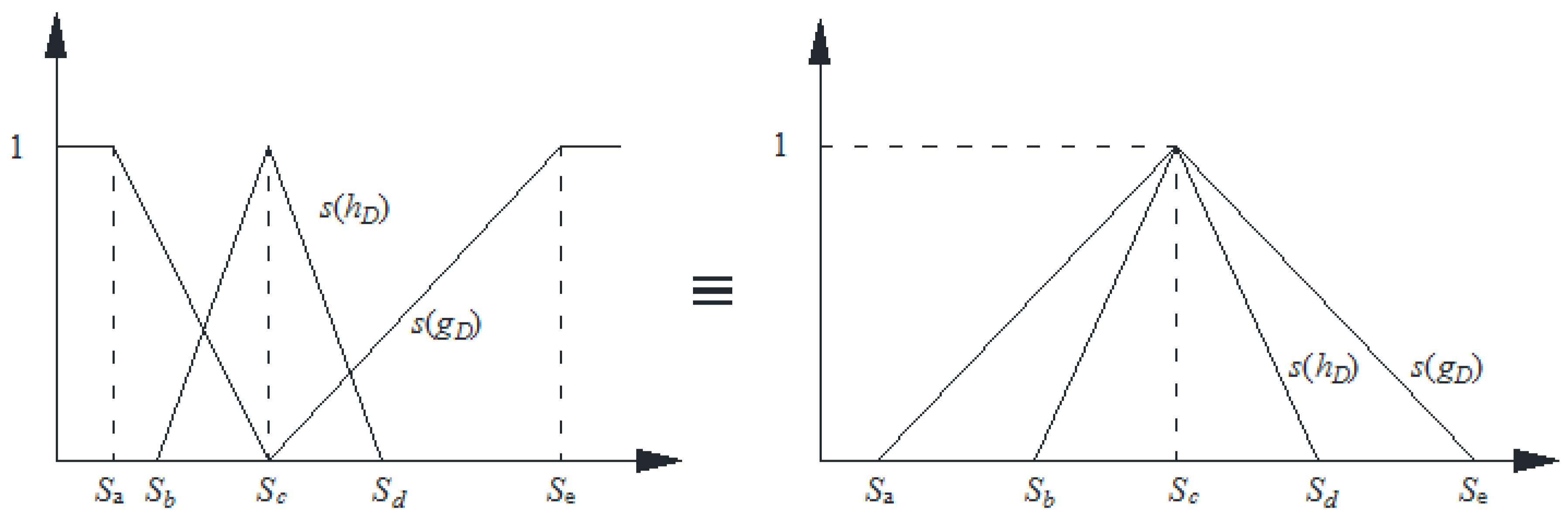
Important subclasses of a DHFN are those in which $s\left(h_D\right)$, as well as its complement $s\left(g_D\right)$, have a triangular shape, that is, they are triangular fuzzy numbers in the usual sense; then, we call the corresponding dual hesitant fuzzy number a dual hesitant triangular fuzzy number (DHTFN). Thus, as can be seen in Figure 1, the DHTFN is completely determined by the score functions of $s\left(h_D\right)$ and $s\left(g_D\right)$ in Figure 1. We can denote it by $(S_a,S_b/S_c/S_d,S_e)$; one advantage of the DHTFN is that its $(\alpha ,\beta )-cut$ can be expressed as follows:

$${(S_a,S_b/S_c/S_d,S_e)}_{(\alpha ,\beta )}=[max(S_a+(S_c-S_a)\alpha ,S_b+(S_c-S_b)\beta ),min(S_e+(S_e-S_c)\alpha ,S_d+(S_d-S_c)\beta )].$$

(7)

Remark 2.

If the DHFS reduces to a fuzzy set or an intuitionistic fuzzy set, then the DHFN reduces to a fuzzy number or an intuitionistic fuzzy number.

Let A and B be two DHFNs. Then, define the addition, subtraction, multiplication and division of A with B from the corresponding interval arithmetic operations on their $(\alpha ,\beta )-cuts$. Let $(\alpha ,\beta )\in L$,

$$\begin{array}{cc}{(A+B)}_{\alpha }\hfill & =\{x+y|x\in A_{(\alpha ,\beta )}andy\in B_{(\alpha ,\beta )}\}\hfill \\ & =[l\left(A_{(\alpha ,\beta )}\right)+l\left(B_{(\alpha ,\beta )}\right),r\left(A_{(\alpha ,\beta )}\right)+r\left(B_{(\alpha ,\beta )}\right)],\hfill \end{array}$$

(8)

$$\begin{array}{cc}{(A-B)}_{\alpha }\hfill & =\{x-y|x\in A_{(\alpha ,\beta )}andy\in B_{(\alpha ,\beta )}\}\hfill \\ & =[l\left(A_{(\alpha ,\beta )}\right)-r\left(B_{(\alpha ,\beta )}\right),r\left(A_{(\alpha ,\beta )}\right)-l\left(B_{(\alpha ,\beta )}\right)],\hfill \end{array}$$

(9)

$$\begin{array}{cc}{(A·B)}_{\alpha }\hfill & =\{x·y|x\in A_{(\alpha ,\beta )}andy\in B_{(\alpha ,\beta )}\}\hfill \\ & =[minS,maxS],\hfill \end{array}$$

(10)

$$\begin{array}{cc}{(A/B)}_{\alpha }\hfill & =\{x/y|x\in A_{(\alpha ,\beta )}andy\in B_{(\alpha ,\beta )}\}\hfill \\ & =[minT,maxT],\hfill \end{array}$$

(11)

where $S=\{l\left(A_{(\alpha ,\beta )}\right)·l\left(B_{(\alpha ,\beta )}\right),l\left(A_{(\alpha ,\beta )}\right)·r\left(B_{(\alpha ,\beta )}\right),$ $r\left(A_{(\alpha ,\beta )}\right)·l\left(B_{(\alpha ,\beta )}\right),r\left(A_{(\alpha ,\beta )}\right)·r\left(B_{(\alpha ,\beta )}\right)\}$ and $T=\{l\left(A_{(\alpha ,\beta )}\right)/l\left(B_{(\alpha ,\beta )}\right),l\left(A_{(\alpha ,\beta )}\right)/r\left(B_{(\alpha ,\beta )}\right),$ $r\left(A_{(\alpha ,\beta )}\right)/l\left(B_{(\alpha ,\beta )}\right),r\left(A_{(\alpha ,\beta )}\right)/r\left(B_{(\alpha ,\beta )}\right)\}$.

Notice that this method is equivalent to the extension principle method of fuzzy arithmetic [12] and intuitionistic fuzzy arithmetic [13]. Obviously, this procedure is more user friendly.

Theorem 2.

Let A and B be two DHFNs. Then, $A+B$, $A-B$, $A·B$ and $A/B(0\notin B)$ are DHFNs.

Proof. Straightforward.

It is possible to establish several orders on intuitionistic fuzzy numbers [11] which could be extended to DHFNs. Here, we give the following order on DHFNs:

$$A⪯B\iff A_{(\alpha ,\beta )}⊴B_{(\alpha ,\beta )}forall(\alpha ,\beta )\in L,$$

(12)

where,

$$\begin{array}{cc}\hfill A_{(\alpha ,\beta )}⊴B_{(\alpha ,\beta )}\iff & r\left(A_{(\alpha ,\beta )}\right)<r\left(B_{(\alpha ,\beta )}\right)or\hfill \\ & r\left(A_{(\alpha ,\beta )}\right)=r\left(B_{(\alpha ,\beta )}\right)andl\left(B_{(\alpha ,\beta )}\right)\le l\left(A_{(\alpha ,\beta )}\right).\hfill \end{array}$$

A DHFN D is strictly positive if for each $(\alpha ,\beta )-cut$, $D_{(\alpha ,\beta )}>0$. Then, we have

Lemma 2.

D is strictly positive if $D⪰0$.

Proof. Straightforward.

Lemma 3.

If A and B are strictly positive DHFNs, then

$${(A·B)}_{(\alpha ,\beta )}=[l\left(A_{(\alpha ,\beta )}\right)·l\left(B_{(\alpha ,\beta )}\right),r\left(A_{(\alpha ,\beta )}\right)·r\left(B_{(\alpha ,\beta )}\right)]=A_{(\alpha ,\beta )}·B_{(\alpha ,\beta )};$$

and

$${(A/B)}_{(\alpha ,\beta )}=[l\left(A_{(\alpha ,\beta )}\right)/r\left(B_{(\alpha ,\beta )}\right),r\left(A_{(\alpha ,\beta )}\right)/l\left(B_{(\alpha ,\beta )}\right)]=A_{(\alpha ,\beta )}/B_{(\alpha ,\beta )}.$$

Proof. Straightforward.

Theorem 3.

Let A, B and C be three strictly positive DHFNs. Then,

  (i) 

If $A⪯B$ then $\frac{A}{C}⪯\frac{B}{C}$;

 (ii) 

If $B\subseteq C$ then $\frac{A}{B}\subseteq \frac{A}{C}$;

(iii) 

$B\subseteq \frac{A·B}{A}$.

Proof. 

Let $(\alpha ,\beta )\in T$,

  (i)

If $A⪯B$, we have $r\left(A_{(\alpha ,\beta )}\right)<r\left(B_{(\alpha ,\beta )}\right)orr\left(A_{(\alpha ,\beta )}\right)=r\left(B_{(\alpha ,\beta )}\right)andl\left(B_{(\alpha ,\beta )}\right)<l\left(A_{(\alpha ,\beta )}\right)$, thus $\frac{r\left(A_{(\alpha ,\beta )}\right)}{l\left(C_{(\alpha ,\beta )}\right)}<\frac{r\left(B_{(\alpha ,\beta )}\right)}{l\left(C_{(\alpha ,\beta )}\right)}$ or $\frac{r\left(A_{(\alpha ,\beta )}\right)}{l\left(C_{(\alpha ,\beta )}\right)}=\frac{r\left(B_{(\alpha ,\beta )}\right)}{l\left(C_{(\alpha ,\beta )}\right)}$ and $\frac{l\left(A_{(\alpha ,\beta )}\right)}{r\left(C_{(\alpha ,\beta )}\right)}\le \frac{l\left(B_{(\alpha ,\beta )}\right)}{r\left(C_{(\alpha ,\beta )}\right)}$. Then $\frac{A}{C}⪯\frac{B}{C}$;

 (ii)

If $B\subseteq C$, we have $[l\left(B_{(\alpha ,\beta )}\right),r\left(B_{(\alpha ,\beta )}\right)]$ $\subseteq [l\left(C_{(\alpha ,\beta )}\right),r\left(C_{(\alpha ,\beta )}\right)]$, thus $[\frac{l\left(A_{(\alpha ,\beta )}\right)}{r\left(B_{(\alpha ,\beta )}\right)},\frac{r\left(A_{(\alpha ,\beta )}\right)}{l\left(B_{(\alpha ,\beta )}\right)}]$ $\subseteq [\frac{l\left(A_{(\alpha ,\beta )}\right)}{r\left(C_{(\alpha ,\beta )}\right)},\frac{r\left(A_{(\alpha ,\beta )}\right)}{l\left(C_{(\alpha ,\beta )}\right)}]$, namely, $\frac{A}{B}\subseteq \frac{A}{C}$;

(iii)

As $[l\left(B_{(\alpha ,\beta )}\right),r\left(B_{(\alpha ,\beta )}\right)]$ $\subseteq [\frac{l\left(A_{(\alpha ,\beta )}\right)l\left(B_{(\alpha ,\beta )}\right)}{r\left(A_{(\alpha ,\beta )}\right)},\frac{r\left(A_{(\alpha ,\beta )}\right)r\left(B_{(\alpha ,\beta )}\right)}{l\left(A_{(\alpha ,\beta )}\right)}]$, namely, $B\subseteq \frac{A·B}{A}$.

 ☐

4. Dual Hesitant Fuzzy Probability

Let $X=\{x_1,...,x_2\}$ be a finite set. Let ℑ be the set of all strictly positive DHFN and let ${\overline{d}}_i\in \Im$, $i=1,...,n,$ with ${\overline{d}}_i⪯\overline{1}$, for all $i=1,...,n$. A family of fixed DHFNs such that there are ${\overline{d}}_i\in {\left({\overline{d}}_i\right)}_{(\alpha ,\beta )}$ with ${\sum }_{i=1}^n{\overline{d}}_i=1$. For each $(\alpha ,\beta )\in T$, denote ${\left({\overline{d}}_1\right)}_{(\alpha ,\beta )}\times ...\times {\left({\overline{d}}_n\right)}_{(\alpha ,\beta )}$ by $S_{\alpha }^{\beta }$. Define also, for each $A\subseteq X$ and DHFS $(\alpha ,\beta )\in L$, the following set:

$${\left(\overline{P}\left(A\right)\right)}_{(\alpha ,\beta )}=\{\sum _{i\in I_A}{d}_i|(d_1,d_2,...,d_n)\in S_{\alpha }^{\beta }and\sum _{i=1}^{n}ma{x}_i{d}_i=1\},$$

(13)

where $I_A$ is the set of indexes of A, that is, $I_A=\{i\in \{1,...,n\}|x_i\in X\}$. Conventionally, ${\sum }_{i\in ⌀}{\overline{d}}_i=0$.

Theorem 4.

Let $A\subseteq X$, ${\left(\overline{P}\left(A\right)\right)}_{(\alpha ,\beta )}$ are the $(\alpha ,\beta )-cuts$ of a DHFN, $\overline{P}\left(A\right)$, that is, $\overline{P}:\wp \left(X\right)\to \Im$, where $\wp \left(X\right)$ is the powerset of X.

Proof. 

Let $S=\{y_1,y_2,...,y_n)\in {[0,1]}^{n}and{\sum }_{i=1}^{n}ma{x}_i{y}_i=1\}.$ For each $(\alpha ,\beta )\in L$, define $Dom[\alpha ,\beta ]=S\bigcap {\prod }_{i=1}^n{\left({\overline{d}}_i\right)}_{(\alpha ,\beta )}$ and $f:Dom[\alpha ,\beta ]\to [0,1]$ by:

$$f(d_1,d_2,...,d_n)=\sum _{i\in I_A}{d}_i.$$

(14)

We have that f is continuous and $Dom$ is bounded and closed. Then, the images of f are some bounded and closed intervals of R. For each $(\alpha ,\beta )\in L$, define $\mathsf{\Gamma }[\alpha ,\beta ]=f(Dom[\alpha ,\beta ])$.

By Equation (13), we have that, for each $\alpha ,\beta \in (0,1]$, ${\left(\overline{P}\left(A\right)\right)}_{(\alpha ,\beta )}={\bigcup }_j\mathsf{\Gamma }[\alpha ,\beta ]$. Therefore, $\left(\overline{P}\left(A\right)\right)$ is a DHFN.

$\overline{P}$ is called a dual hesitant fuzzy probability function. ☐

Remark 3.

If the DHFS reduces to a fuzzy set or an intuitionistic fuzzy set, then the dual hesitant fuzzy probability reduces to a fuzzy probability or an intuitionistic fuzzy probability.

Theorem 5.

Let $X=\{x_1,x_2,...,x_n\}$ and let $\overline{P}:\wp \left(X\right)\to \Im$ be a dual hesitant fuzzy probability function. Then, for each $A,B\subseteq X,$ the following properties hold:

  (i) 

If $A\cap B=⌀$ then $\overline{P}(A\cup B)\subseteq \overline{P}\left(A\right)+\overline{P}\left(B\right);$

 (ii) 

If $A\subseteq B$ then $\overline{P}\left(A\right)⪯\overline{P}\left(B\right);$

(iii) 

$\overline{P}(⌀)=\overline{0}⪯\overline{P}\left(A\right)⪯\overline{P}\left(X\right)=\overline{1};$

(iv) 

$\overline{1}⪯\overline{P}\left(A\right)+\overline{P}\left(A^c\right);$

 (v) 

If $A\cap B\ne ⌀$ then $\overline{P}(A\cup B)\subseteq \overline{P}\left(A\right)+\overline{P}\left(B\right)-\overline{P}(A\cap B).$

Proof. 

(i)

Notice that $A\cap B=⌀$ if and only if $I_A\cap I_B=⌀$. In order to prove (i), we only need to prove that:

$$\overline{P}{(A\cup B)}_{\alpha }\subseteq \overline{P}{\left(A\right)}_{\alpha }+\overline{P}{\left(B\right)}_{\alpha }.$$

(15)

Namely, for each $(\alpha ,\beta )\in L,$

$\{{\sum }_{i\in I_A}{d}_i+$ ${\sum }_{j\in I_B}{d}_j|(d_1,d_2,...,d_n)\in S_{\alpha }^{\beta }$ $and{\sum }_{l=1}^n{d}_l=1\}$ lies in

$\{{\sum }_{i\in I_A}{d}_i|(d_1,d_2,...,d_n)\in S_{\alpha }^{\beta }$ $and{\sum }_{l=1}^n{d}_l=1\}$ + $\{{\sum }_{j\in I_B}{d}_j|(d_1,d_2,...,d_n)$ $\in S_{\alpha }^{\beta }and{\sum }_{l=1}^n{d}_l=1\}$, which is obvious;

(ii)

If $A\subseteq B$, we have $\{{\sum }_{i\in I_A}{d}_i|(d_1,d_2,...,d_n)\in S_{\alpha }^{\beta }and{\sum }_{l=1}^n{d}_l=1\}\subseteq \{{\sum }_{i\in I_B}{d}_j|(d_1,d_2,...,d_n)\in S_{\alpha }^{\beta }and{\sum }_{l=1}^n{d}_l=1\}$, thus $\overline{P}\left(A\right)⪯\overline{P}\left(B\right);$

(iii)

If $\varnothing \subseteq A\subseteq X$, $\varnothing \subseteq \{{\sum }_{i\in I_A}{d}_i|(d_1,d_2,...,d_n)\in S_{\alpha }^{\beta }and{\sum }_{l=1}^n{d}_l=1\}\subseteq \{{\sum }_{i\in I_X}{d}_j|(d_1,d_2,...,d_n)\in S_{\alpha }^{\beta }and{\sum }_{l=1}^n{d}_l=1\}$, thus $\overline{P}(⌀)=\overline{0}⪯\overline{P}\left(A\right)⪯\overline{P}\left(X\right)=\overline{1}.$

(iv)

As (i), we donate $B=A^c$, then $\overline{P}\left(A\right)+\overline{P}\left(A^c\right)$ $⪰\overline{P}(A\cup A^c))=\overline{P}\left(X\right)=\overline{1}$;

(v)

If $A\cap B\ne ⌀$, for each $(\alpha ,\beta )\in L$, $\{{\sum }_{u\in I_A\cup I_B}{d}_u|(d_1,d_2,...,d_n)\in S_{\alpha }^{\beta }and{\sum }_{l=1}^n{d}_l=1\}$ lies in $\{{\sum }_{i\in I_A}{d}_i|(d_1,d_2,...,d_n)\in S_{\alpha }^{\beta }and{\sum }_{l=1}^n{d}_l=1\}$ + $\{{\sum }_{j\in I_B}{d}_j|(d_1,d_2,...,d_n)\in S_{\alpha }^{\beta }and{\sum }_{l=1}^n{d}_l=1\}$ − $\{{\sum }_{k\in I_A\cap I_B}{d}_k|(d_1,d_2,...,d_n)\in S_{\alpha }^{\beta }and{\sum }_{l=1}^n{d}_l=1\}$, which proves that $\overline{P}(A\cup B)\subseteq \overline{P}\left(A\right)+\overline{P}\left(B\right)-\overline{P}(A\cap B).$

 ☐

5. Dual Hesitant Fuzzy Conditional Probability

Let $A,B\subseteq X$ with $I_A$ and $I_B$ being their index sets, respectively. Define the dual hesitant fuzzy conditional probability of A with B as being the DHFS $\overline{P}\left(A\right|B)$ whose $(\alpha ,\beta )-cuts$ are:

$$\overline{P}{\left(A\right|B)}_{(\alpha ,\beta )}=\{\frac{{\sum }_{i\in I_A\cap I_B}{d}_i}{{\sum }_{j\in I_B}{d}_j}|(d_1,d_2,...,d_n)\in S_{\alpha }^{\beta }and\sum _{l=1}^n{d}_l=1\}.$$

(16)

Theorem 6.

$\overline{P}\left(A\right|B)\subseteq \frac{\overline{P}(A\cap B)}{\overline{P}\left(B\right)}.$

Proof. 

It is sufficient to prove that:

$$\overline{P}{\left(A\right|B)}_{(\alpha ,\beta )}\subseteq \frac{\overline{P}{(A\cap B)}_{(\alpha ,\beta )}}{\overline{P}{\left(B\right)}_{(\alpha ,\beta )}}.$$

(17)

Notice that $A\cap B=⌀$ if and only if $I_A\cap I_B=⌀$.

To prove Equation (17), it is sufficient to prove that for each $\alpha \in [0,1],$

$\{\frac{{\sum }_{i\in I_A\cap I_B}{d}_i}{{\sum }_{j\in I_B}{d}_j}|(d_1,d_2,...,d_n)\in S_{\alpha }^{\beta }and{\sum }_{l=1}^n{d}_l=1\}\subseteq \frac{\{{\sum }_{i\in I_A\cap I_B}{d}_i|(d_1,d_2,...,d_n)\in S_{\alpha }^{\beta }and{\sum }_{l=1}^n{d}_l=1\}}{\{{\sum }_{j\in I_B}{d}_j|(d_1,d_2,...,d_n)\in S_{\alpha }^{\beta }and{\sum }_{l=1}^n{d}_l=1\}},$ which is obvious. ☐

Theorem 7.

$\overline{P}\left(A\right|B)$ is a DHFN.

Proof. 

Analogous to the proof of Theorem 4 by replacing the function f in Equation (14) by $f(d_1,d_2,...,d_n)=\frac{{\sum }_{i\in I_A\cap I_B}{d}_i}{{\sum }_{j\in I_B}{d}_j}$. ☐

Theorem 8.

Let $X=\{x_1,x_2,...,x_n\}$ and let $\overline{P}:\wp \left(X\right)\to \Im$ be a dual hesitant fuzzy probability function. Then, for each $A,B\subseteq X,$ the following properties hold:

1.

If $A_1\cap A_2=⌀$ then $\overline{P}(A_1\cup A_2|B)\subseteq \overline{P}\left(A_1\right|B)+\overline{P}\left(A_2\right|B)$;

2.

$\overline{0}⪯\overline{P}\left(A\right|B)⪯\overline{1}$;

3.

$\overline{P}\left(A\right|A)=\overline{1}$, $\overline{P}\left(A\right|A^c)=\overline{0}$;

4.

If $B\subseteq A$ then $\overline{P}\left(A\right|B)=\overline{1}$;

5.

If $A\cap B=⌀$ then $\overline{P}\left(A\right|B)=\overline{0}$.

Proof. 

The proof of items 2–5, is trivial.

Notice that if $A_1\cap A_2=\varnothing$, then $I_{A_1}\cap I_{A_2}=\varnothing .$ To prove item 1, it is sufficient to prove that for each $(\alpha ,\beta )\in T$, $\overline{P}{(A_1\cup A_2|B)}_{(\alpha ,\beta )}$ $\subseteq \overline{P}{\left(A_1\right|B)}_{(\alpha ,\beta )}+\overline{P}{\left(A_2\right|B)}_{(\alpha ,\beta )}$.

However, this follows by the fact that $\overline{P}{(A_1\cup A_2|B)}_{\alpha }$ $=\{\frac{{\sum }_{i\in I_{A_1}\cap I_B}{d}_i+{\sum }_{j\in I_{A_2}\cap I_B}{d}_j}{{\sum }_{k\in I_B}{d}_k}|$ $(d_1,d_2,...,d_n)\in S_{\alpha }^{\beta }and{\sum }_{l=1}^n{d}_l=1\}$ lies in $\{\frac{{\sum }_{i\in I_{A_1}\cap I_B}{d}_i}{{\sum }_{k\in I_B}{d}_k}|(d_1,d_2,...,d_n)$ $\in S_{\alpha }^{\beta }and{\sum }_{l=1}^n{d}_l=1\}$ + $\{\frac{{\sum }_{i\in I_{A_2}\cap I_B}{d}_i}{{\sum }_{k\in I_B}{d}_k}|(d_1,d_2,...,d_n)$ $\in S_{\alpha }^{\beta }and{\sum }_{l=1}^n{d}_l=1\}$, which is obvious.

Notice that the last term in the above equality coincides with $\overline{P}{\left(A_1\right|B)}_{(\alpha ,\beta )}+\overline{P}{\left(A_2\right|B)}_{(\alpha ,\beta )}$. Then, $\overline{P}(A_1\cup A_2|B)\subseteq \overline{P}\left(A_1\right|B)+\overline{P}\left(A_2\right|B)$. ☐

Lemma 4.

Let $A,B,C\subseteq X$. Then, $\overline{P}(A\cap B|C)\subseteq \overline{P}\left(A\right|C)·\overline{P}\left(B\right|A\cap C).$

Proof. 

We only need to prove that for each $(\alpha ,\beta )\in T$, $\overline{P}{(A\cap B|C)}_{(\alpha ,\beta )}\subseteq \overline{P}{\left(A\right|C)}_{(\alpha ,\beta )}·\overline{P}{\left(B\right|A\cap C)}_{(\alpha ,\beta )}.$

Furthermore, by Equation (16), $\overline{P}{(A\cap B|C)}_{(\alpha ,\beta )}=\{\frac{{\sum }_{i\in I_A\cap I_B\cap I_C}{d}_i}{{\sum }_{j\in I_c}{d}_j}|(d_1,d_2,...,d_n)\in S_{(\alpha ,\beta )}and{\sum }_{l=1}^n{d}_l=1\}$ $\subseteq \{\frac{{\sum }_{i\in I_A\cap I_B\cap I_C}{d}_i}{{\sum }_{j\in I_A\cap I_C}{d}_j}|(d_1,d_2,...,d_n)\in S_{(\alpha ,\beta )}and{\sum }_{l=1}^n{d}_l=1\}$ $·\{\frac{{\sum }_{i\in I_A\cap I_C}{d}_i}{{\sum }_{j\in I_C}{d}_j}|(d_1,d_2,...,d_n)\in S_{(\alpha ,\beta )}and{\sum }_{l=1}^n{d}_l=1\}$ $=\overline{P}\left(A\right|C)·\overline{P}\left(B\right|A\cap C),$ which proves the Lemma. ☐

Theorem 9.

Let $A_1,A_2,...,A_k$ be subsets of X, i.e., $A_i\cap A_j=\varnothing$ when $i\ne j$ and $X={\cup }_{i=1}^k{A}_i$. Let $B,C\subseteq X$, then $\overline{P}\left(B\right|C)\subseteq {\sum }_{i=1}^k\overline{P}\left(A_j\right|C)·\overline{P}\left(B\right|A_j\cap C)$.

Proof. 

Since $B={\cup }_{i=1}^{k}B\cap A_i$, by Theorem 8 item 1, we have that $\overline{P}\left(B\right|C)\subseteq {\sum }_{i=1}^k\overline{P}(B\cap A_i|C)$. So, by Lemma 4, we have $\overline{P}(B\cap A_j|C)=\overline{P}\left(A_j\right|C)·\overline{P}\left(B\right|A_j\cap C)$, and therefore, $\overline{P}\left(B\right|C)\subseteq {\sum }_{i=1}^k\overline{P}\left(A_j\right|C)·\overline{P}\left(B\right|A_j\cap C)$. ☐

Lemma 5.

$\overline{P}(B\cap C)\subseteq \overline{P}\left(B\right|C)·\overline{P}\left(B\right)$.

Proof. 

Let $A=\{x_1,...,x_k\}$ and $B=\{x_l,...,x_m\}$ with $1\le l\le k\le m\le n.$ Then, $A\cap B=\{x_l,...,x_k\}$ and for any $(\alpha ,\beta )\in T,$ $\overline{P}{(B\cap C)}_{\alpha }=\{{\sum }_{i=l}^k{d}_i|(d_1,d_2,...,d_n)\in S_{\alpha }^{\beta }\}\subseteq$ $\{\frac{{\sum }_{i=l}^k{d}_i}{{\sum }_{i=l}^m{d}_i}|(d_{1j},d_2,...,d_n)\in S_{\alpha }^{\beta }\}·\{{\sum }_{i=l}^m{d}_i|(d_1,d_2,...,d_n)\in S_{\alpha }^{\beta }\}$ $=\overline{P}{(B/C)}_{(\alpha ,\beta )}·\overline{P}{\left(B\right)}_{(\alpha ,\beta )}$. ☐

Theorem 10.

Let $A_1,A_2,...,A_k$ be subsets of $X=\{x_1,x_2,...,x_n\}$ such that $A_i\cap A_j=\varnothing$ when $i\ne j$ and $X={\cup }_{i=1}^k{A}_i$. Let D by any event, then $\overline{P}\left(D\right)\subseteq \overline{P}\left(A_i\right)·\overline{P}\left(D\right|A_i)$.

Proof. 

Since $D={\cup }_{i=1}^{k}D\cap A_i$, then by Theorem 8 item 1, we have $\overline{P}\left(D\right)\subseteq {\sum }_{i=1}^k\overline{P}\left(A_i\right|D).$ Therefore, by Lemma 5, $\overline{P}\left(D\right)\subseteq \overline{P}\left(A_i\right)·\overline{P}\left(D\right|A_i)$.

Next, we give the dual hesitant fuzzy Bayes’ theorem. ☐

Theorem 11.

Let $A_1,A_2,...,A_k$ be subsets of $X=\{x_1,x_2,...,x_n\}$ such that $A_i\cap A_j=\varnothing$ when $i\ne j$ and $X={\cup }_{i=1}^k{A}_i$. Let D by any event, then $\overline{P}\left(A_i\right|D)\subseteq \frac{\overline{P}(A_i\cap D)}{{\sum }_{j=1}^k\overline{P}\left(A_j\right)\overline{P}\left(D\right|A_j)}$.

Proof. 

From Theorems 6 and 7, we have that $\overline{P}\left(A_i\right|D)\subseteq \frac{\overline{P}(A_i\cap D)}{\overline{P}\left(D\right)}\subseteq \frac{\overline{P}(A_i\cap D)}{{\sum }_{j=1}^k\overline{P}\left(A_j\right)\overline{P}\left(D\right|A_j)}$. ☐

6. Application of Color Blindness

Although fuzzy probabilities have been applied to the problem of color blindness by Buckley [11], sometimes they are not suitable for the practical environment. The following example is given to show the application of dual hesitant fuzzy probabilities.

Example 2.

Some people believe that red-green color blindness is more prevalent in males than in females. To test this hypothesis, we gather a random sample from the adult population. Let M be the event that a person is male, F is the event that a person is female, C is the event that a person has red-green color blindness and $C^{\prime }$ is the event that he/she does not have red-green color blindness.

Assume that researchers investigate three cities to reflect red-green color blindness in males and in females. As we cannot avoid information loss and some people do not participate in the survey, we can make it a DHFE. Thus, a dual hesitant fuzzy set of the point estimates of probabilities is given to indicate the results of the investigation:

• $p_1=\{\{p(M\cap C\},\{p(M\cap C^{\prime })\}\}$ $=\{<\{0.04,0.06,0.02\}$ $,\{0.4,0.35,0.45\}>\}$;
• $p_2=\{\{p(F\cap C\},\{p(F\cap C^{\prime })\}\}$ $=\{<\{0.08,0.06,0.07\},$ $\{0.3,0.4,0.2\}>\}$.

Then, we obtain that

• $p_1=\{s(p(M\cap C),s\left(p(M\cap C^{\prime })\right)\}$ $=\{<0.04,0.4>\}$;
• $p_2=\{s(p(F\cap C),s(p(F\cap C^{\prime })\}$ $=\{<0.07,0.3>\}$.

Assume that the uncertainty in these point estimates has been shown in their fuzzy values as follows:

We wish to calculate the dual hesitant fuzzy conditional probabilities $P\left(M\right|C)$ and $P\left(F\right|C)$. The $(\alpha ,\beta )-cuts$ of the first fuzzy probability are:

$$P{\left(M\right|C)}_{(\alpha ,\beta )}=\{\frac{p_1}{p_1+p_2}|S\},$$

(18)

for $(\alpha ,\beta )\in L$ and S donates "$p_i\in {\left(p_i\right)}_{(\alpha ,\beta )}(i=1,2,3)$ and $p_1+p_2+p_3=1$ ($p_3$ donates the information loss and some people not participating in the survey)". Let $H(p_1,p_2)=\frac{p_1}{p_1+p_2}$, then H is an increasing function of $p_1$ but decreasing in $p_2$. According to

Table 1. Dual hesitant triangular fuzzy number (DHTFN) of results.

	Uncertainty in Membership Degree h	Uncertainty in Nonmembership Degree g
$p_1$	(0.02/0.04/0.06)	(0.3/0.4/0.5)
$p_2$	(0.04/0.07/0.1)	(0.2/0.3/0.4)

, we obtain:

$$\begin{array}{cc}P{\left(M\right|C)}_{(\alpha ,\beta )}\hfill & =[l\left(H(p_{11},p_{22})\right),r\left(H(p_{12},p_{21})\right)]\hfill \\ & =[max\{{\displaystyle \frac{0.02+0.02\alpha }{0.16-0.05\alpha }},{\displaystyle \frac{0.3+0.1\beta }{0.9-0.2\beta }}\},min\{{\displaystyle \frac{0.06-0.02\alpha }{0.06+0.05\alpha }},{\displaystyle \frac{0.5-0.1\beta }{0.5+0.2\beta }}\}]\hfill \\ & \approx [max\{{\displaystyle \frac{1}{8}}+\frac{11}{40}\alpha ,{\displaystyle \frac{1}{3}}+{\displaystyle \frac{1}{6}}\beta \},min\{1-{\displaystyle \frac{3}{5}}\alpha ,1-{\displaystyle \frac{1}{2}}\beta \}]\hfill \end{array}$$

(19)

for all $(\alpha ,\beta )\in L$.

The $(\alpha ,\beta )-cuts$ of the second dual hesitant fuzzy probability are:

$$P{\left(F\right|C)}_{(\alpha ,\beta )}=\{\frac{p_2}{p_1+p_2}|S\},$$

(20)

for $(\alpha ,\beta )\in L$ and S donates "$p_i\in {\left(p_i\right)}_{(\alpha ,\beta )}(i=1,2,3)$ and $p_1+p_2+p_3=1$ ($p_3$ donates the information loss and some people not participating in the survey)". Let $G(p_1,p_2)=\frac{p_2}{p_1+p_2}$, then G is a decreasing function of $p_1$ but increasing in $p_2$. According to Table 1, we obtain:

$$\begin{array}{cc}P{\left(F\right|C)}_{(\alpha ,\beta )}\hfill & =[l\left(G(p_{12},p_{21})\right),r\left(G(p_{11},p_{22})\right)]\hfill \\ & =[max\{{\displaystyle \frac{0.04+0.03\alpha }{0.16-0.05\alpha }},{\displaystyle \frac{0.2+0.1\beta }{0.9-0.2\beta }}\},min\{{\displaystyle \frac{0.1-0.03\alpha }{0.06+0.05\alpha }},{\displaystyle \frac{0.4-0.1\beta }{0.5+0.2\beta }}\}]\hfill \\ & \approx [max\{{\displaystyle \frac{1}{4}}+{\displaystyle \frac{7}{20}}\alpha ,{\displaystyle \frac{2}{9}}+{\displaystyle \frac{5}{18}}\beta \},min\{1-{\displaystyle \frac{2}{5}}\alpha ,{\displaystyle \frac{4}{5}}-{\displaystyle \frac{3}{10}}\beta \}]\hfill \end{array}$$

(21)

for all $(\alpha ,\beta )\in L$.

Based on Equation (3.11), we obtain that, for $(\alpha ,\beta )\in L$, when $6\alpha -3\beta \ge 2$, $P\left(M\right|C)⪰P(F\left|C\right)$; when $6\alpha -3\beta <2$, $P\left(M\right|C)⪯P(F\left|C\right)$.

7. Conclusions and Further Study

This work extends the notion of dual hesitant fuzzy probabilities by representing probabilities through the dual hesitant fuzzy numbers, in the sense of Zhu et al., instead of intuitionistic fuzzy numbers. We also give the concept of dual hesitant fuzzy probability, based on which we provide some main results including the properties of dual hesitant fuzzy probability, dual hesitant fuzzy conditional probability, and dual hesitant fuzzy total probability. It is an extension of the approach of [13] to intuitionistic fuzzy probability, since all intuitionistic fuzzy sets (and thus intuitionistic fuzzy numbers and fuzzy probabilities) are a dual hesitant fuzzy set (with $h_D=u,g_D=v$).

This extension may be useful in some situations where some uncertain probabilities are hesitant, but where this uncertainty can be modeled using dual hesitant fuzzy numbers. As a future work, we intend, using this same approach, to generalize the notion of probability spaces as well as other concepts related to probability. We also expect to extend the notions of Markov chain, and the hidden Markov model, etc. Furthermore, DEHFSs are likely to play an important role in decision making with more studies on the theory and applications.