1. Introduction
K-means algorithm is one of the simplest clustering algorithm as unsupervised learning, so that is very widely used [
1]. As it is a partitioning-based clustering method in cluster analysis, a dataset is partitioned into several groups according to a similarity measure as a distance to the average of a group. A K-means algorithm minimizes the objective function known as squared error function iteratively by finding a new set of cluster centers. In each iteration, the value of the objective function becomes lower. In a k-means algorithm, the objective function is defined by the sum of square distances between an object and a cluster center.
The purpose of using k-means is to find clusters that minimize the sum of square distances between each cluster center and all objects in each cluster. Even though the number of clusters is small, the problem of finding an optimal k-means algorithm solution is NP-hard [
2,
3]. For this reason, a k-means algorithm adapts heuristics and finds local minimum as approximate optimal solutions. The time complexity of a k-means algorithm is
O(
i*
k*
n*
d), where
i iterations,
k centers, and
n points in
d dimensions.
K-means algorithm spends a lot of processing time for computing the distances between each of the k cluster centers and the n objects. So far, many researchers have worked on accelerating k-means algorithms by avoiding unnecessary distance computations between an object and cluster centers. Because objects usually remain in the same clusters after a certain number of iterations, much of the repetitive distance computation is unnecessary. So far, a number of studies on accelerating k-means algorithms to avoid unnecessary distance calculations have been carried out [
4,
5,
6].
The K-means algorithm is efficient for clustering large datasets, but it only works on numerical data. However, the real-world data is a mixture of both numerical and categorical features, so a k-means algorithm has a limitation of applying cluster analysis. To overcome this problem, several algorithms have been developed to cluster large datasets that contain both numerical and categorical values, and one well-known algorithm is the k-prototypes algorithm by Huang [
7]. The time complexity of the k-prototypes algorithm is also
O(
i*
k*
n*
d): one of the k-means. In case of large datasets, time cost of distance calculation between all data objects and the centers is high. To the best of our knowledge, however, there have been no studies that reduce the time complexity of the k-prototypes algorithm.
Recently, big data has become a big issue for academia and various industries. Therefore, there is a growing interest in the technology to process big data quickly from the viewpoint of computer science. The research on the fast processing of big data in clustering has been limited to numerical data. However, big data deals with numerical data as well as categorical data. Because numerical data and categorical data are processed differently, it is difficult to improve the performance of clustering algorithms that deal with categorical data in the existing way of improving performance.
In this paper, we propose a fast k-prototypes algorithm for mixed data (FKPT). The FKPT reduces distance calculation using partial distance computation. The contributions of this study are summarized as follows.
Reduction: computational cost is reduced without an additional data structure and memory spaces.
Simplicity: it is simple to implement because it does not require a complex data structure.
Convergence: it can be applied to other fast k-means algorithms to compute the distance between each cluster center and an object for numerical attributes.
Speed: it is faster than the conventional k-prototypes.
This study presents a new method of accelerating k-prototypes algorithm using partial distance computation by avoiding unnecessary distance computations between an object and cluster centers. As a result, we believe the algorithm proposed in this paper will become the algorithm of choice for fast k-prototypes clustering.
The organization of the rest of this paper is as follows. In
Section 2, various methods of accelerating k-means and traditional k-prototypes algorithm are described, for the proposed k-prototypes are defined. A fast k-prototypes algorithm proposed in this paper is explained and its time complexity is analyzed in
Section 3. In
Section 4, experimental results demonstrate the scalability and effectiveness of the FKPT using partial distance computation by comparison with traditional k-prototypes algorithm.
Section 5 concludes the paper.
3. K-prototypes Using Partial Distance Computation
The existing k-prototypes algorithm allocates objects to the cluster with the smallest distance by calculating the distance between each cluster center and a new object to be allocated to the cluster. Distance is calculated by comparing all attributes of an object with all attributes of each cluster center using the brute force method.
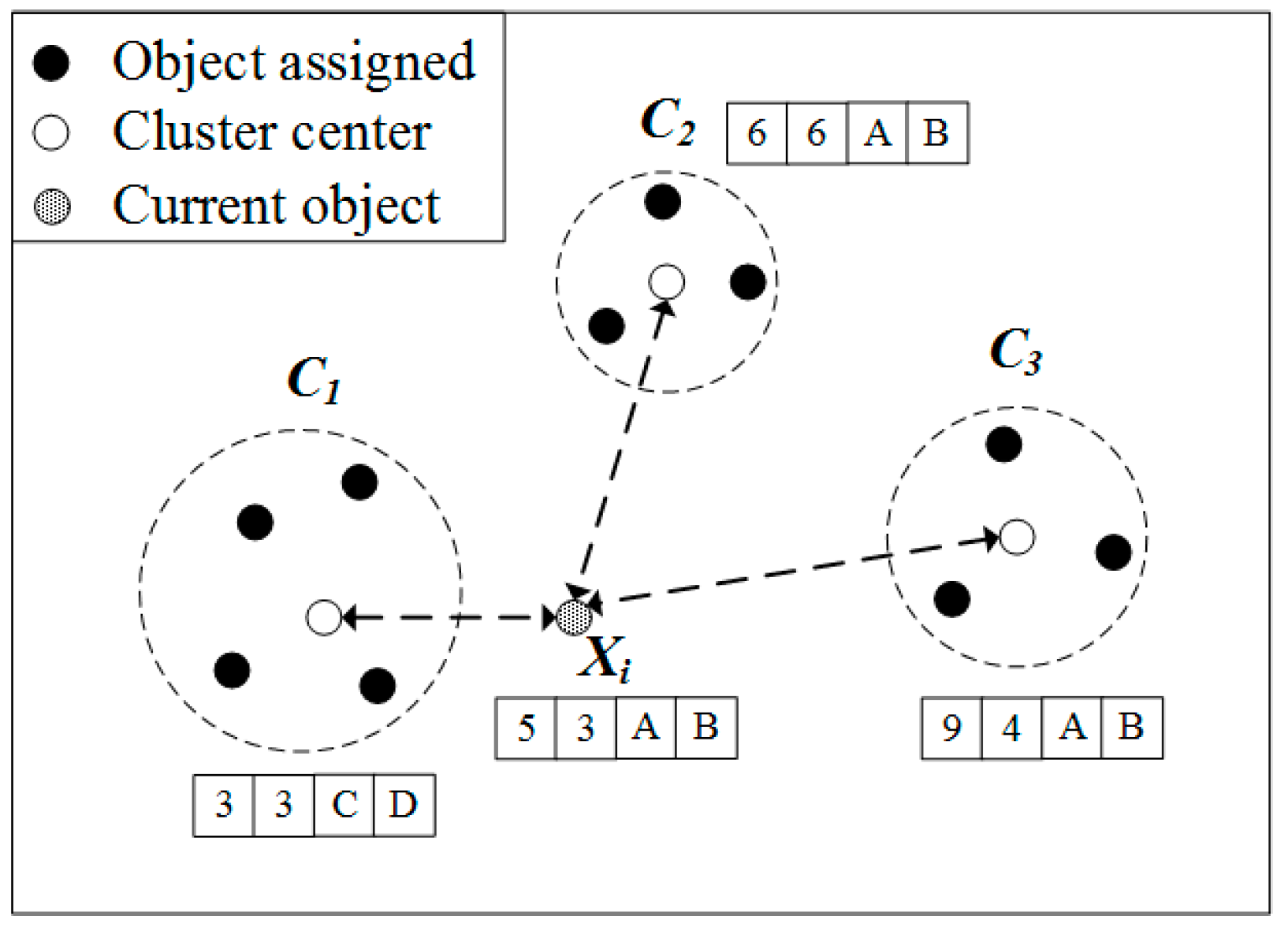
Figure 1 illustrates how k-prototypes algorithm organizes clusters with a target object. In this figure, an object consists of two numerical attributes and two categorical attributes. The entire dataset is divided into three clusters,
. The center of each cluster is
,
, and
. The traditional k-prototypes algorithm calculates distance with each cluster center to find the cluster to which
= (5, 3, A, B) is assigned. The distance about the numerical attribute of
and
is
,
,
, respectively. The distance about the categorical attribute of
and
is
,
respectively. The total distance of
and
,
, and
is 6, 10, and 17, respectively, and the cluster closest to
is
. Thus, the traditional k-prototypes algorithm computes the distance as a brute force method that compares both numerical and categorical properties.
The purpose of distance computation is to find a cluster center closest to an object. However, there is an unnecessary distance calculation in the traditional k-prototypes algorithm. According to Equation (4), the maximum value that can be obtained is 1 when comparing a single categorical attribute. In
Figure 1, an object has two categorical properties, so the maximum value that can be extracted from the distance comparing the categorical property is 2. In
Figure 1, when using a numerical attribute, the closest cluster with the object is
and a distance of 4, the second closest cluster is
, a distance of 4. Since the difference between these two values is greater than 2, comparing the numerical property, nevertheless the measured minimum distance, 4 added to the categorical property comparison maximum value 2, it does not exceed 10. In such a case, the cluster center closest to an object can be determined by calculating the numerical attribute value without calculating the category curl attribute in the distance calculation. Of course, the minimum distance cannot be obtained by comparing numerical properties for all cases only. In
Figure 1, at
, the distance of the numerical attribute of
and
is
,
,
, respectively.
This paper studies a method to find the closest center to an object without comparison for all attributes in a distance computation. We prove that the closest center to an object can be found without comparison for all attributes. For a proof, we define a computable max difference value as follows.
Definition 1. The computable max difference value means that the maximum difference value can be calculated in the distance measured between an object and cluster centers for one attribute.
According to Equation (4), the distance for a single categorical attribute between cluster centers and an object is either 0 or 1. Therefore, a computable max difference value for a categorical attribute, according to Definition 1, becomes 1 without taking the value of the attribute into account. If an object in the dataset consists of m categorical attributes, then a computable max difference value between a cluster and object is m. A computable max difference value of a numerical attribute is a difference of a maximum value and a minimum value of the attribute. Thus, to know a computable max difference value of a numerical attribute, we have to scan full datasets so that maximum and minimum values are obtained.
The proposed k-prototypes algorithm finds a minimum distance without distance computations of all attributes between an object and a cluster center using the computable max difference value of the object. The k-prototypes algorithm updates a cluster center after an object is assigned to the cluster of the closest center by the distance measure. By Equation (1), the distance between an object and a cluster center is computed by adding the distance of numerical attributes and the distance of categorical attributes. If a difference of the first and the second minimum distance on numerical attributes is higher than m, we can find a minimum distance between an object and a cluster center using only distance computation of numerical attributes without distance computations of categorical attributes.
Lemma 1. For a set of objects with m categorical attribute, if then .
Proof. By Equation (2),
.
According to Definition 1, the categorical distance between an object and a cluster center with m categorical attributes can be and . . .
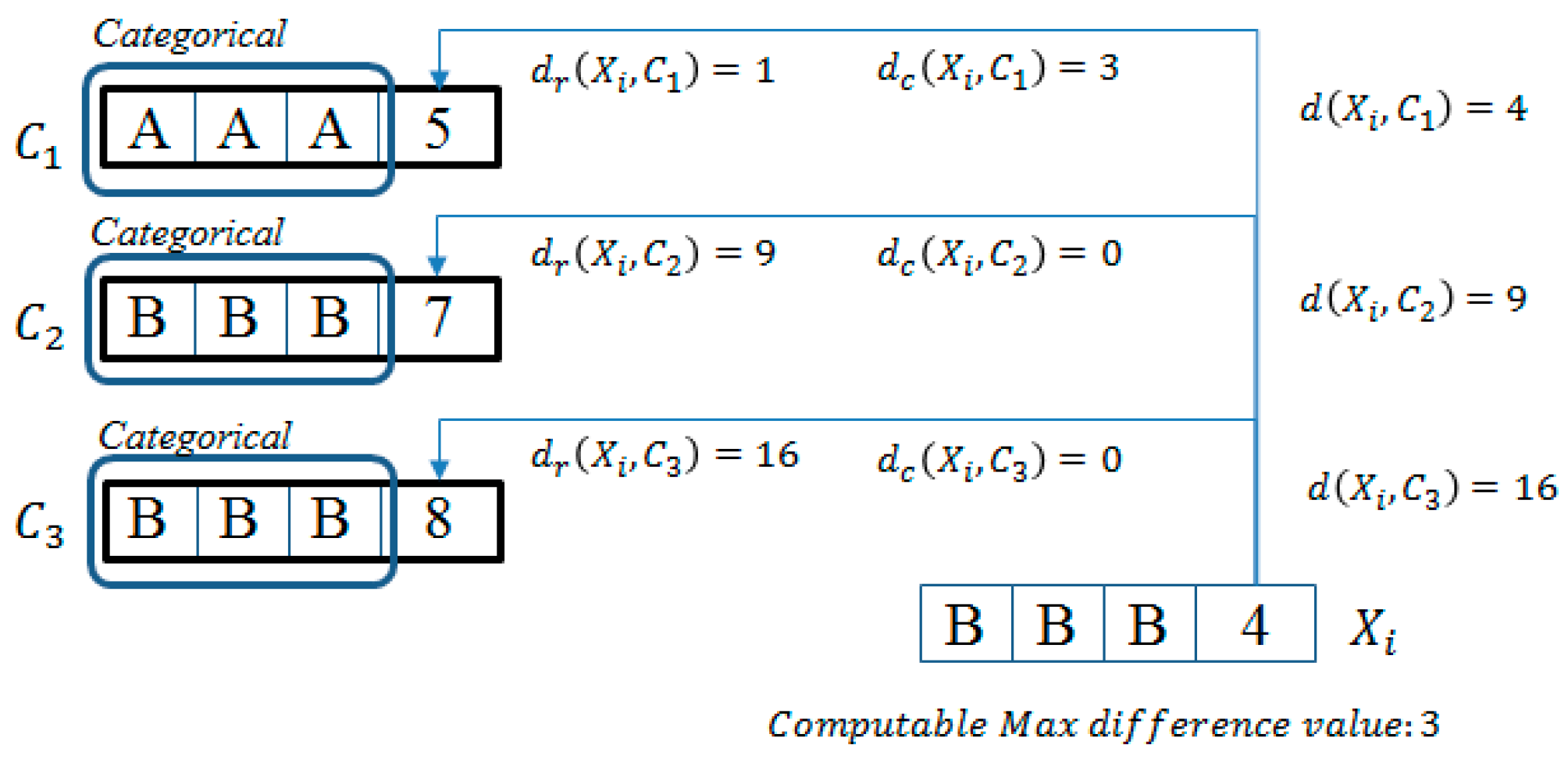
We introduce a way to determine the minimum distance between an object and each cluster center with only computation of numerical attribute by an example.
Example 1. We assume that
k = 3. Each current cluster center is as follows:
,
, and
. As shown by
Figure 2, we have to compute the distance between
and each of cluster centers (
,
, and
) for assigning
to the cluster of the closest center. Firstly, we compute the distance of numerical attributes,
is 1, 9, and 16, respectively.
is the closest to
only with numerical attributes. In this example, objects consisted of three categorical attributes; the minimum value of possible distance is 0, and the maximum value is 3. The difference of numerical distance between
and
is 8. Thus,
continues to be the closest to
, even if
is calculated by 3 as the computable max difference value.
3.1. Proposed Algorithm
In this section, we describe our proposed algorithm.
The proposed k-prototypes algorithm in this paper is similar to traditional k-prototypes. The difference between the proposed k-prototypes and traditional k-prototypes is that the distance between an object and cluster centers on the numerical attributes, , is calculated firstly.
In Line 4, firstly, you calculate the distance for a numerical attribute. You obtain the closest distance and the second closest distance value while calculating the distance. Using these two values and the number of the categorical attributes, m, the discriminant is performed. If the result of the discriminant is true, the distance to the categorical property is calculated, and then the result of the final distance is derived by adding the distance of the numerical property. If the result of the discriminant is false, the final distance is measured by the numerical attribute result only. By including in the cluster measured at the smallest distance, the value of the corresponding cluster center is updated.
Definition 1 is a function that determines whether to compare the categorical attribute with the algorithm that implements it. Returns the true value if the difference between the second smallest distance and the first smallest distance is less than m in the distance measured only by a numerical property comparison between an object and cluster center. If a true value is returned, Algorithm 1 calls a function that compares the distance of the categorical attribute to calculate the final distance. If a false value is returned, the distance measured by only the numerical property comparison is set as the final results value without comparing the categorical property. The larger the difference between the two distances, the greater the number of categorical attributes that need not be compared.
| Algorithm 1 Proposed k-prototypes algorithm |
| Input: n: the number of objects, k: the number of cluster, p: the number of numeric attribute, q: the number of categorical attribute |
| Output: k cluster |
| 01: INITIALIZE // Randomly choosing k object, and assigning it to . |
| 02: While not converged do |
| 03: for i = 1 to n do |
| 04: dist_n[] = DIST-COMPUTE-NUM(, k, p) // distance computation only numeric numerical attributes |
| 05: first_min = DIST-COMPUTE.first_min // first minimum value among |
| 06: second_min = DIST-COMPUTE.second_min // second minimum value among |
| 07: if (second_min − first_min < m) then |
| 08: dist[] = dist_n[] + DIST-COMPUTE-CATE(, k) |
| 09: else |
| 10: dist[] = dist_n[] |
| 11: num = |
| 12: is assigned to |
| 13: UPDATE-CENTER() |
In Algorithm 2, DIST-COMPUTE-NUM() calculates a distance between an object and cluster centers for numerical attributes and returns all distances for each cluster. In this algorithm, first_min and second_min is calculated to determine whether calculation of categorical data in a distance computation.
| Algorithm 2 DIST-COMPUTE-NUM() |
| Input: : an object vector, : a set of cluster center vectors, k: the number of clusters, p: the number of numeric attribute |
| Output: dist_n[], first_min, second_min |
| 01: for i = 1 to k do |
| 02: for j = 1 to p do |
| 03: dist_n[j] |
| 04: first_min = dist_n[0] |
| 05: second_min = dist_n[0] |
| 06: for i = 0 to k-1 do |
| 07: if (dist_n[i] < first_min) then |
| 08: second_min = first_min |
| 09: first_min = dist_n[i] |
| 10: else if (dist_n[i] < second_min) then |
| 11: second_min = dist_n[i] |
| 12: Return dist_n[] |
In Algorithm 3, a distance between an object and cluster centers is calculated for categorical attributes of each cluster.
| Algorithm 3 DIST-COMPUTE-CATE() |
| Input: : an object vector, : cluster center vectors, k: the number of clusters, p: the number of numeric attribute |
| Output: dist_c[] |
| 01: for i = 1 to k do |
| 02: for j = p + 1 to m do |
| 03: if () then |
| 04: dist_c[i] += 0 |
| 05: else |
| 06: dist_c[i] += 1 |
| 07: Return dist_c[] |
In Algorithm 4, the center vector of a cluster is assigned to new center vector. The center vectors consisted of two parts: numerical and categorical attributes. The numerical part of the center vector is calculated by an average value of each numerical attributes and the categorical part of the center vector is calculated by the value of the highest frequency in each categorical attribute.
| Algorithm 4 UPDATE-CENTER() |
| Input: : an i-th cluster center vectors |
| 01: foreach do |
| 02: for j = 1 to p do |
| 03: sum[j] += o[j] |
| 04: for j = 1 to p do |
| 05: C[j] = sum[j] / |
| 06: for j = p +1 to m do |
| 07: C[j] = argmax COUNT(o[j]) |
3.2. Time Complexity
The time complexity of traditional k-prototypes is , where I is the number of iterations, k is the number of clusters, n is the number of data objects, and m is the number of attributes. The best-case complexity of the proposed k-prototypes has a lower bound of , where p is the number of numerical attributes and The best case is that the difference of the first and the second minimum distance between an object and cluster centers for all objects in a given dataset on numerical attributes is less than m. The worst-case complexity has an upper bound of . The worst case is that the difference of the first and the second minimum distance between an object and cluster centers for all objects in a given dataset on numerical attributes is higher than m.
5. Conclusions
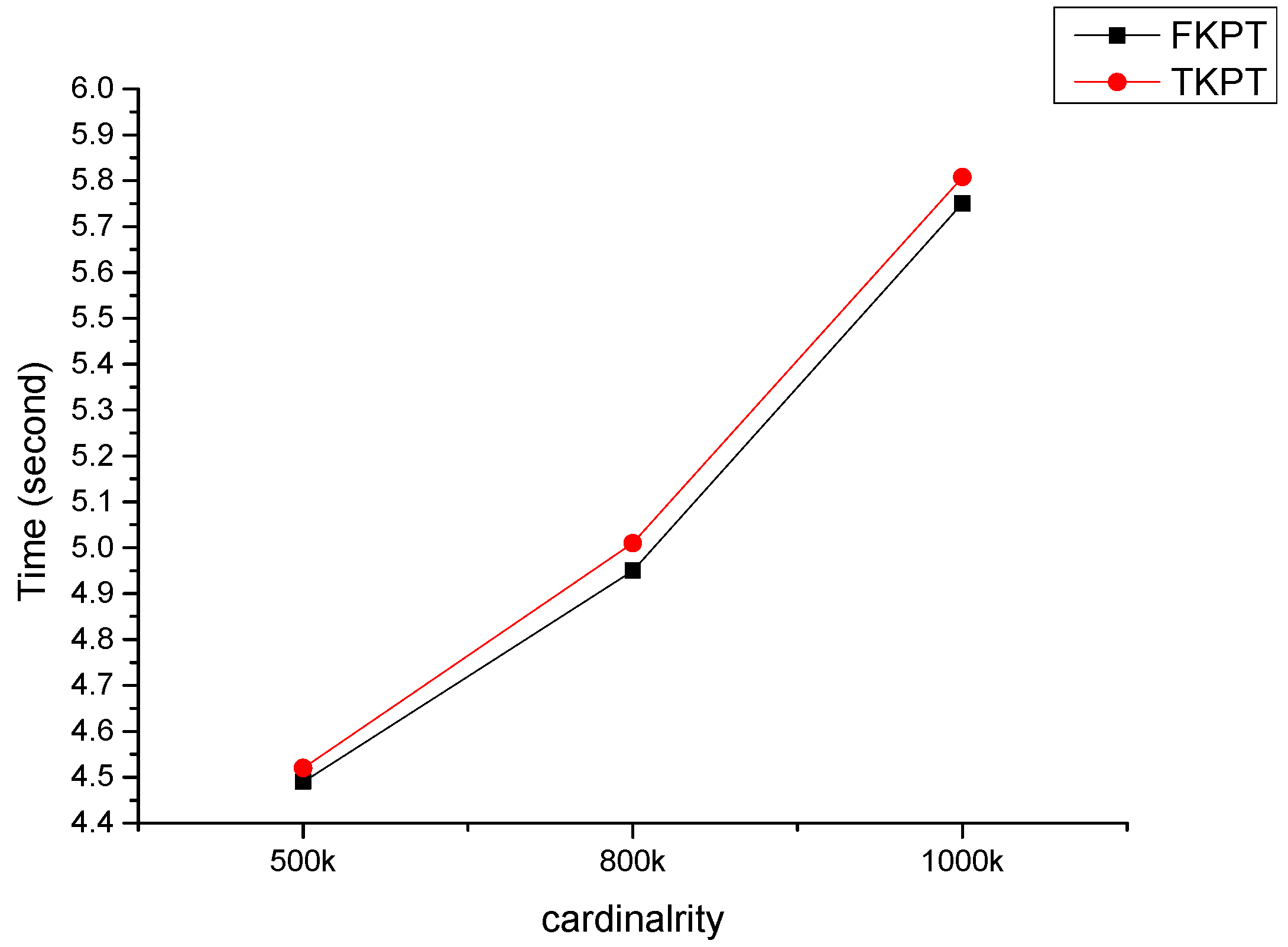
In this paper, we have proposed a fast k-prototypes algorithm for clustering mixed datasets. Experimental results show that our algorithm is fast than the original algorithm. Previous fast k-means algorithm focused on reducing candidate objects for computing distance to cluster centers. Our k-prototypes algorithm reduces unnecessary distance computation using partial distance computation without distance computations of all attributes between an object and a cluster center, which allows it to reduce time complexity. The experimental shows proposed k-prototypes algorithm improves computational performance than the original k-prototypes algorithm in our dataset.
However, our k-prototypes algorithm does not guarantee that the computational performance will be improved in all cases. If the difference of the first and the second minimum distance between an object and cluster centers for all objects in a given dataset on numerical attributes is less than m, then the performance of our k-prototypes is the same as the original k-prototypes. Our k-prototypes algorithm is influenced by the variance of the numerical data values. The larger variance of the numerical data values, the higher probability that the difference of the first and the second minimum distance between an object and cluster centers is large.
The k-prototypes algorithm proposed in this paper simply reduces the computational cost without using additional data structures and memories. Our algorithm is faster than the original k-prototypes algorithm. The goal of the existing k-means acceleration algorithm is to reduce the number of dimensions to be compared when calculating the distance between center and object, in order to reduce the number of objects compared with the center of the cluster. K-means, which deals only with numerical data, is the most widely used algorithm among clustering algorithms. Various acceleration algorithms have been developed to improve the speed of processing large data. However, real-world data is mostly a mixture of numerical data and categorical data. In this paper, we propose a method to speed up the k-prototypes algorithm for clustering mixed data. The method proposed in this paper is a method of reducing the number of objects compared with the center of existing clusters, and is not exclusive, and the existing methods and the methods proposed in this paper can be integrated with each other.
In this study, we considered only an effect of cardinality. However, the performance of the algorithm may be affected by dimensionality, the size of k, and data distributions. In future works, firstly we have a plan to measure performance of our proposed algorithm by dimensionality, the size of k, and data distributions. Secondly, we can prune more objects by using partitioning data points into grid. We will extend our fast k-prototypes algorithm to improve for better performance.