Some Single-Valued Neutrosophic Dombi Weighted Aggregation Operators for Multiple Attribute Decision-Making

Abstract

The Dombi operations of T-norm and T-conorm introduced by Dombi can have the advantage of good flexibility with the operational parameter. In existing studies, however, the Dombi operations have so far not yet been used for neutrosophic sets. To propose new aggregation operators for neutrosophic sets by the extension of the Dombi operations, this paper firstly presents the Dombi operations of single-valued neutrosophic numbers (SVNNs) based on the operations of the Dombi T-norm and T-conorm, and then proposes the single-valued neutrosophic Dombi weighted arithmetic average (SVNDWAA) operator and the single-valued neutrosophic Dombi weighted geometric average (SVNDWGA) operator to deal with the aggregation of SVNNs and investigates their properties. Because the SVNDWAA and SVNDWGA operators have the advantage of good flexibility with the operational parameter, we develop a multiple attribute decision-making (MADM) method based on the SVNWAA or SVNWGA operator under a SVNN environment. Finally, an illustrative example about the selection problem of investment alternatives is given to demonstrate the application and feasibility of the developed approach.

1. Introduction

In 1965, Zadeh [1] introduced a membership function between 0 and 1 instead of traditional crisp value of 0 and 1 and defined the fuzzy set (FS). Fuzzy theory is an important and interesting research topic in decision-making theory and science. However, FS is characterized only by its membership function between 0 and 1, but not a non-membership function. To overcome the insufficient of FS, Atanassov [2] introduced the concept of an intuitionistic fuzzy set (IFS), which is characterized by its membership function and non-membership function between 0 and 1. As a further generalization of an IFS, Atanassov and Gargov [3] further introduced the concept of an interval-valued intuitionistic fuzzy set (IVIFS), which is characterized by its interval membership function and interval non-membership function in the unit interval [0, 1]. Because IFSs and IVIFSs cannot represent indeterminate and inconsistent information, Smarandache [4] introduced a neutrosophic set (NS) from a philosophical point of view to express indeterminate and inconsistent information. In a NS A, its truth, falsity, and indeterminacy membership functions T_A(x), I_A(x) and F_A(x) are represented independently, which lie in real standard or nonstandard subsets of ]⁻0, 1⁺[, i.e., T_A(x): X → ]⁻0, 1⁺[, I_A(x): X → ]⁻0, 1⁺[, and F_A(x): X → ]⁻0, 1⁺[. Thus, the nonstandard interval ]⁻0, 1⁺[ may result in the difficulty of actual applications. Based on the real standard interval [0, 1], therefore, the concepts of a single-valued neutrosophic set (SVNS) [5] and an interval neutrosophic set (INS) [6] was presented as subclasses of NS to be easily used for actual applications, and then Ye [7] introduced a simplified neutrosophic set (SNS), including the concepts of SVNS and INS, which are the extension of IFS and IVIFS. Obviously, SNS is a subclass of NS, while SVNS and INS are subclasses of SNS. As mentioned in the literature [4,5,6,7], NS is the generalization of FS, IFS, and IVIFS. Thereby, Figure 1 shows the flow chart extended from FS to NS (SNS, SVNS, INS).

On the other hand, some researchers also introduced other fuzzy extensions, such as fuzzy soft sets, hesitant FSs, and hesitant fuzzy soft sets (see [8,9] for detail).

However, SNS (SVNS and INS) is very suitable for the expression of incomplete, indeterminate, and inconsistent information in actual applications. Recently, SNSs (INSs, and SVNSs) have been widely applied in many areas [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28], such as decision-making, image processing, medical diagnosis, fault diagnosis, and clustering analysis. Especially, many researchers [7,29,30,31,32,33,34,35,36] have developed various aggregation operators, like simplified neutrosophic weighted aggregation operators, simplified neutrosophic prioritized aggregation operators, single-valued neutrosophic normalized weighted Bonferroni mean operators, generalized neutrosophic Hamacher aggregation operators, generalized weighted aggregation operators, interval neutrosophic prioritized ordered weighted average operators, interval neutrosophic Choquet integral operators, interval neutrosophic exponential weighted aggregation operators, and so on, and applied them to decision-making problems with SNS/SVNS/INS information. Obviously, the aggregation operators give us powerful tools to deal with the aggregation of simplified (single-valued and interval) neutrosophic information in the decision making process.

In 1982, Dombi [37] developed the operations of the Dombi T-norm and T-conorm, which show the advantage of good flexibility with the operational parameter. Hence, Liu et al. [38] extended the Dombi operations to IFSs and proposed some intuitionistic fuzzy Dombi Bonferroni mean operators and applied them to multiple attribute group decision-making (MAGDM) problems with intuitionistic fuzzy information. From the existing studies, we can see that the Dombi operations are not extended to neutrosophic sets so far. To develop new aggregation operators for NSs based on the extension of the Dombi operations, the main purposes of this study are (1) to present some Dombi operations of single-valued neutrosophic numbers (SVNNs) (basic elements in SVNS), (2) to propose a single-valued neutrosophic Dombi weighted arithmetic average (SVNDWAA) operator and a single-valued neutrosophic Dombi weighted geometric average (SVNDWGA) operator for the aggregation of SVNN information and to investigate their properties, and (3) to develop a decision-making approach based on the SVNDWAA and SVNDWGA operators for solving multiple attribute decision-making (MADM) problems with SVNN information.

The rest of the paper is organized as follows. Section 2 briefly describes some concepts of SVNSs to be used for the study. Section 3 presents some new Dombi operations of SVNNs. In Section 4, we propose the SVNDWAA and SVNDWGA operators and investigate their properties. Section 5 develops a MADM approach based on the SVNDWAA and SVNDWGA operators. An illustrative example is presented in Section 6. Section 7 gives conclusions and future research directions.

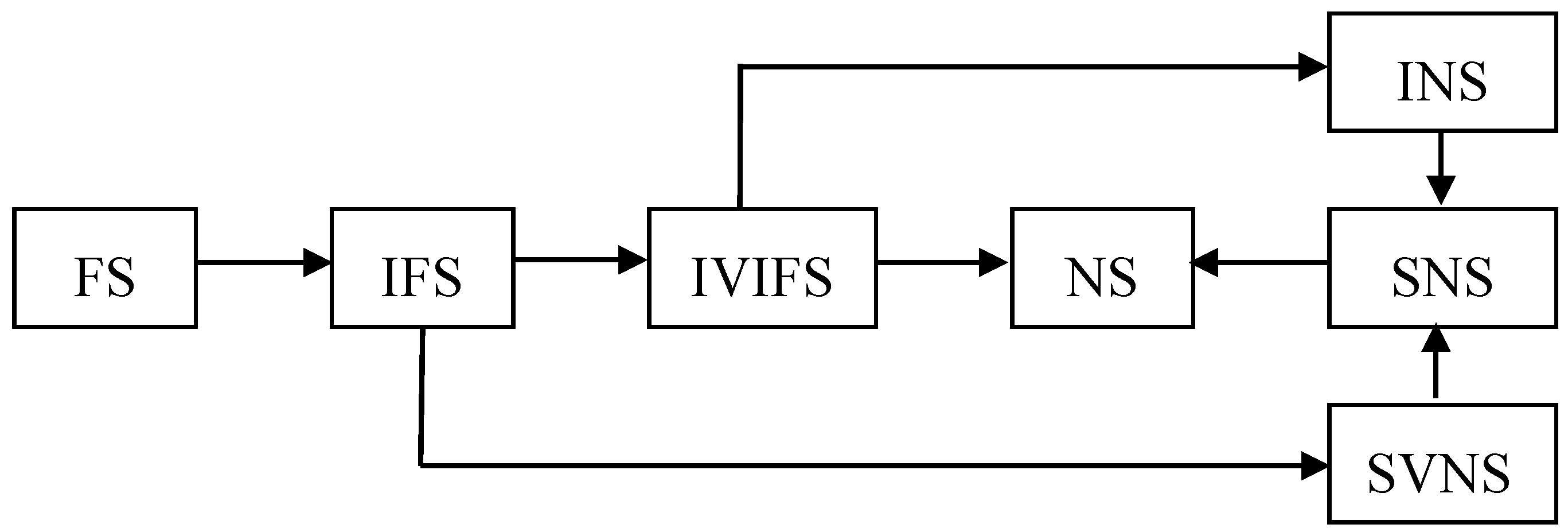
2. Some Concepts of SVNSs

As the extension of IFSs, Wang et al. [5] introduced the definition of a SVNS as a subclass of NS proposed by Smarandache [4] to easily apply in real scientific and engineering areas.

Definition  1.

[5] Let X be a universal set. A SVNS N in X is described by a truth-membership function t_N(x), an indeterminacy-membership function u_N(x), and a falsity-membership function v_N(x). Then, a SVNS N can be denoted as the following form:

$$N=\left\{\langle x,t_N(x),u_N(x),v_N(x)\rangle |x\in X\right\},$$

where the functions t_N(x), u_N(x), v_N(x) $\in$ [0, 1] satisfy the condition 0 ≤ t_N(x) + u_N(x) + v_N(x) ≤ 3 for x $\in$ X.

For convenient expression, a basic element <x, t_N(x), u_N(x), v_N(x)> in N is denoted by s = <t, u, v>, which is called a SVNN.

For any SVNN s = <t, u, v>, its score and accuracy functions [29] can be introduced, respectively, as follows:

$$E(s)=(2+t-u-v)/3,E(s)\in [0,1],$$

(1)

$$H(s)=t-v,H(s)\in [-1,1].$$

(2)

According to the two functions E(s) and H(s), the comparison and ranking of two SVNNs are introduced by the following definition [29].

Definition 2.

[29] Let s₁ = <t₁, u₁, v₁> and s₂ = <t₂, u₂, v₂> be two SVNNs. Then the ranking method for s₁ and s₂ is defined as follows:

(1) 

If E(s₁) > E(s₂), then s₁ $\succ$ s₂,

(2) 

If E(s₁) = E(s₂) and H(s₁) > H(s₂), then s₁ $\succ$ s₂,

(3) 

If E(s₁) = E(s₂) and H(s₁) = H(s₂), then s₁ = s₂.

3. Some Single-Valued Neutrosophic Dombi Operations

Definition 3.

[37]. Let p and q be any two real numbers. Then, the Dombi T-norm and T-conorm between p and q are defined as follows:

$$O_D(p,q)=\frac{1}{1+{\left\{{\left(\frac{1-p}{p}\right)}^{\rho }+{\left(\frac{1-q}{q}\right)}^{\rho }\right\}}^{1/\rho }},$$

(3)

$$O_D^c(p,q)=1-\frac{1}{1+{\left\{{\left(\frac{p}{1-p}\right)}^{\rho }+{\left(\frac{q}{1-q}\right)}^{\rho }\right\}}^{1/\rho }},$$

(4)

where ρ ≥ 1 and (p, q) $\in$ [0, 1] × [0, 1].

According to the Dombi T-norm and T-conorm, we define the Dombi operations of SVNNs.

Definition 4.

Let s₁ = <t₁, u₁, v₁> and s₂ = <t₂, u₂, v₂> be two SVNNs, ρ ≥ 1, and λ > 0. Then, the Dombi T-norm and T-conorm operations of SVNNs are defined below:

$$\begin{array}{c}(1)s_1\oplus s_2=\langle 1-\frac{1}{1+{\left\{{\left(\frac{t_1}{1-t_1}\right)}^{\rho }+{\left(\frac{t_2}{1-t_2}\right)}^{\rho }\right\}}^{1/\rho }},\frac{1}{1+{\left\{{\left(\frac{1-u_1}{u_1}\right)}^{\rho }+{\left(\frac{1-u_2}{u_2}\right)}^{\rho }\right\}}^{1/\rho }},\frac{1}{1+{\left\{{\left(\frac{1-v_1}{v_1}\right)}^{\rho }+{\left(\frac{1-v_2}{v_2}\right)}^{\rho }\right\}}^{1/\rho }}\rangle ;\\ (2)s_1\otimes s_2=\langle \frac{1}{1+{\left\{{\left(\frac{1-t_1}{t_1}\right)}^{\rho }+{\left(\frac{1-t_2}{t_2}\right)}^{\rho }\right\}}^{1/\rho }},1-\frac{1}{1+{\left\{{\left(\frac{u_1}{1-u_1}\right)}^{\rho }+{\left(\frac{u_2}{1-u_2}\right)}^{\rho }\right\}}^{1/\rho }},1-\frac{1}{1+{\left\{{\left(\frac{v_1}{1-v_1}\right)}^{\rho }+{\left(\frac{v_2}{1-v_2}\right)}^{\rho }\right\}}^{1/\rho }}\rangle ;\\ (3)\lambda s_1=\langle 1-\frac{1}{1+{\left\{\lambda {\left(\frac{t_1}{1-t_1}\right)}^{\rho }\right\}}^{1/\rho }},\frac{1}{1+{\left\{\lambda {\left(\frac{1-u_1}{u_1}\right)}^{\rho }\right\}}^{1/\rho }},\frac{1}{1+{\left\{\lambda {\left(\frac{1-v_1}{v_1}\right)}^{\rho }\right\}}^{1/\rho }}\rangle ;\\ (4)s_1^{\lambda }=\langle \frac{1}{1+{\left\{\lambda {\left(\frac{1-t_1}{t_1}\right)}^{\rho }\right\}}^{1/\rho }},1-\frac{1}{1+{\left\{\lambda {\left(\frac{u_1}{1-u_1}\right)}^{\rho }\right\}}^{1/\rho }},1-\frac{1}{1+{\left\{\lambda {\left(\frac{v_1}{1-v_1}\right)}^{\rho }\right\}}^{1/\rho }}\rangle .\end{array}$$

4. Dombi Weighted Aggregation Operators of SVNNs

Based on the Dombi operations of SVNNs in Definition 4, we propose the two Dombi weighted aggregation operators: the SVNDWAA and SVNDWGA operators, and then investigate their properties.

Definition 5.

Let s_j = <t_j, u_j, v_j> (j = 1, 2, …, n) be a collection of SVNNs and w = (w₁, w₂, …, w_n) be the weight vector for s_j with w_j $\in$ [0, 1] and ${\displaystyle {\sum }_{j=1}^n{w}_j}=1$. Then, the SVNDWAA and SVNDWGA operators are defined, respectively, as follows:

$$SVNDWAA(s_1,s_2,\dots ,s_n)=\underset{j=1}{\overset{n}{\oplus }}{w}_j{s}_j,$$

(5)

$$SVNDWGA(s_1,s_2,\dots ,s_n)=\underset{j=1}{\overset{n}{\otimes }}{s}_j^{w_j}.$$

(6)

Theorem 1.

Let s_j = <t_j, u_j, v_j> (j = 1, 2, …, n) be a collection of SVNNs and w = (w₁, w₂, …, w_n) be the weight vector for s_j with w_j $\in$ [0, 1] and ${\displaystyle {\sum }_{j=1}^n{w}_j}=1$. Then, the aggregated value of the SVNDWAA operator is still a SVNN, which is calculated by the following formula:

$$SVNDWAA(s_1,s_2,\dots ,s_n)=\langle 1-\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n{w}_j{\left(\frac{t_j}{1-t_j}\right)}^{\rho }}\right\}}^{1/\rho }},\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n{w}_j{\left(\frac{1-u_j}{u_j}\right)}^{\rho }}\right\}}^{1/\rho }},\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n{w}_j{\left(\frac{1-v_j}{v_j}\right)}^{\rho }}\right\}}^{1/\rho }}\rangle ,$$

(7)

By the mathematical induction, we can prove Theorem 1.

Proof. 

If n = 2, based on the Dombi operations of SVNNs in Definition 4 we can obtain the following result:

$$\begin{array}{l}SVNDWAA(s_1,s_2)=s_1\oplus s_2\\ =\langle 1-\frac{1}{1+{\left\{w_1{\left(\frac{t_1}{1-t_1}\right)}^{\rho }+w_2{\left(\frac{t_2}{1-t_2}\right)}^{\rho }\right\}}^{1/\rho }},\frac{1}{1+{\left\{w_1{\left(\frac{1-u_1}{u_1}\right)}^{\rho }+w_2{\left(\frac{1-u_2}{u_2}\right)}^{\rho }\right\}}^{1/\rho }},\frac{1}{1+{\left\{w_1{\left(\frac{1-v_1}{v_1}\right)}^{\rho }+w_2{\left(\frac{1-v_2}{v_2}\right)}^{\rho }\right\}}^{1/\rho }}\rangle \\ =\langle 1-\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^2{w}_j{\left(\frac{t_j}{1-t_j}\right)}^{\rho }}\right\}}^{1/\rho }},\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^2{w}_j{\left(\frac{1-u_j}{u_j}\right)}^{\rho }}\right\}}^{1/\rho }},\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^2{w}_j{\left(\frac{1-v_j}{v_j}\right)}^{\rho }}\right\}}^{1/\rho }}\rangle .\end{array}$$

If n = k, based on Equation (7), we have the following equation:

$$SVNDWAA(s_1,s_2,\dots ,s_k)=\langle 1-\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^k{w}_j{\left(\frac{t_j}{1-t_j}\right)}^{\rho }}\right\}}^{1/\rho }},\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^k{w}_j{\left(\frac{1-u_j}{u_j}\right)}^{\rho }}\right\}}^{1/\rho }},\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^k{w}_j{\left(\frac{1-v_j}{v_j}\right)}^{\rho }}\right\}}^{1/\rho }}\rangle .$$

If n = k + 1, there is the following result:

$$\begin{array}{l}SVNDWAA(s_1,s_2,\dots ,s_k,s_{k+1})\\ =\langle 1-\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^k{w}_j{\left(\frac{t_j}{1-t_j}\right)}^{\rho }}\right\}}^{1/\rho }},\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^k{w}_j{\left(\frac{1-u_j}{u_j}\right)}^{\rho }}\right\}}^{1/\rho }},\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^k{w}_j{\left(\frac{1-v_j}{v_j}\right)}^{\rho }}\right\}}^{1/\rho }}\rangle \oplus w_{k+1}{s}_{k+1}\\ =\langle 1-\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^{k+1}{w}_j{\left(\frac{t_j}{1-t_j}\right)}^{\rho }}\right\}}^{1/\rho }},\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^{k+1}{w}_j{\left(\frac{1-u_j}{u_j}\right)}^{\rho }}\right\}}^{1/\rho }},\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^{k+1}{w}_j{\left(\frac{1-v_j}{v_j}\right)}^{\rho }}\right\}}^{1/\rho }}\rangle \end{array}.$$

Hence, Theorem 1 is true for n = k + 1. Thus, Equation (7) holds for all n. □

Then, the SVNDWAA operator contains the following properties:

(1)

Reducibility: When w = (1/n, 1/n, …, 1/n), it is obvious that there exists

$$SVNDWAA(s_1,s_2,\dots ,s_n)=\langle 1-\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n\frac{1}{n}{\left(\frac{t_j}{1-t_j}\right)}^{\rho }}\right\}}^{1/\rho }},\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n\frac{1}{n}{\left(\frac{1-u_j}{u_j}\right)}^{\rho }}\right\}}^{1/\rho }},\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n\frac{1}{n}{\left(\frac{1-v_j}{v_j}\right)}^{\rho }}\right\}}^{1/\rho }}\rangle .$$

(2)

Idempotency: Let all the SVNNs be s_j = <t_j, u_j, v_j> = s (j = 1, 2, …, n). Then, SVNDWAA(s₁, s₂, …, s_n) = s.

(3)

Commutativity: Let the SVNS (s₁’, s₂’, …, s_n’) be any permutation of (s₁, s₂, …, s_n). Then, there is SVNDWAA(s₁’, s₂’, …, s_n’) = SVNDWAA(s₁, s₂, …, s_n).

(4)

Boundedness: Let s_min = min(s₁, s₂, …, s_n) and s_max = max(s₁, s₂, …, s_n). Then, s_min ≤ SVNDWAA(s₁, s₂, …, s_n) ≤ s_max.

Proof. 

(1) Based on Equation (7), the property is obvious.

(2) Since s_j = <t_j, u_j, v_j> = s (j = 1, 2, …, n). Then, by using Equation (7) we can obtain the following result:

$$\begin{array}{l}SVNDWAA(s_1,s_2,\dots ,s_n)=\langle 1-\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n{w}_j{\left(\frac{t_j}{1-t_j}\right)}^{\rho }}\right\}}^{1/\rho }},\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n{w}_j{\left(\frac{1-u_j}{u_j}\right)}^{\rho }}\right\}}^{1/\rho }},\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n{w}_j{\left(\frac{1-v_j}{v_j}\right)}^{\rho }}\right\}}^{1/\rho }}\rangle \\ =\langle 1-\frac{1}{1+{\left\{{\left(\frac{t}{1-t}\right)}^{\rho }\right\}}^{1/\rho }},\frac{1}{1+{\left\{{\left(\frac{1-u}{u}\right)}^{\rho }\right\}}^{1/\rho }},\frac{1}{1+{\left\{{\left(\frac{1-v}{v}\right)}^{\rho }\right\}}^{1/\rho }}\rangle =\langle 1-\frac{1}{1+\frac{t}{1-t}},\frac{1}{1+\frac{1-u}{u}},\frac{1}{1+\frac{1-v}{v}}\rangle =\langle t,u,v\rangle =s.\end{array}$$

Hence, SVNDWAA(s₁, s₂, …, s_n) = s holds.

(3) The property is obvious.

(4) Let s_min = min(s₁, s₂, …, s_n) = <t⁻, u⁻, v⁻> and s_max = max(s₁, s₂, …, s_n) = <t⁺, u⁺, v⁺>. Then, we have $t^{-}=\underset{j}{\min }(t_j)$, $u^{-}=\underset{j}{\max }(u_j)$, $v^{-}=\underset{j}{\max }(v_j)$, $t^{+}=\underset{j}{\max }(t_j)$, $u^{+}=\underset{j}{\min }(u_j)$, and $v^{+}=\underset{j}{\min }(v_j)$. Thus, there are the following inequalities:

$$1-\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n{w}_j{\left(\frac{t^{-}}{1-t^{-}}\right)}^{\rho }}\right\}}^{1/\rho }}\le 1-\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n{w}_j{\left(\frac{t_j}{1-t^j}\right)}^{\rho }}\right\}}^{1/\rho }}\le 1-\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n{w}_j{\left(\frac{t^{+}}{1-t^{+}}\right)}^{\rho }}\right\}}^{1/\rho }},$$

$$\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n{w}_j{\left(\frac{1-u^{+}}{u^{+}}\right)}^{\rho }}\right\}}^{1/\rho }}\le \frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n{w}_j{\left(\frac{1-u_j}{u_j}\right)}^{\rho }}\right\}}^{1/\rho }}\le \frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n{w}_j{\left(\frac{1-u^{-}}{u^{-}}\right)}^{\rho }}\right\}}^{1/\rho }},$$

$$\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n{w}_j{\left(\frac{1-v^{+}}{v^{+}}\right)}^{\rho }}\right\}}^{1/\rho }}\le \frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n{w}_j{\left(\frac{1-v_j}{v_j}\right)}^{\rho }}\right\}}^{1/\rho }}\le \frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n{w}_j{\left(\frac{1-v^{-}}{v^{-}}\right)}^{\rho }}\right\}}^{1/\rho }}.$$

Hence, s_min ≤ SVNDWAA(s₁, s₂, …, s_n) ≤ s_max holds. □

Theorem 2.

Let s_j = <t_j, u_j, v_j> (j = 1, 2, …, n) be a collection of SVNNs and w = (w₁, w₂, …, w_n) be the weight vector for s_j with w_j $\in$ [0, 1] and ${\displaystyle {\sum }_{j=1}^n{w}_j}=1$. Then, the aggregated value of the SVNDWGA operator is still a SVNN, which is calculated by the following formula:

$$SVNDWGA(s_1,s_2,\dots ,s_n)=\langle \frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n{w}_j{\left(\frac{1-t_j}{t_j}\right)}^{\rho }}\right\}}^{1/\rho }},1-\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n{w}_j{\left(\frac{u_j}{1-u_j}\right)}^{\rho }}\right\}}^{1/\rho }},1-\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n{w}_j{\left(\frac{v_j}{1-v_j}\right)}^{\rho }}\right\}}^{1/\rho }}\rangle .$$

(8)

The proof of Theorem 2 is the same as that of Theorem 1. Thus, it is omitted here.

Obviously, the SVNDWGA operator also contains the following properties:

(1)

Reducibility: When the weight vector is w = (1/n, 1/n, …, 1/n), it is obvious that there exists the following result:

$$SVNDWGA(s_1,s_2,\dots ,s_n)=\langle \frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n\frac{1}{n}{\left(\frac{1-t_j}{t_j}\right)}^{\rho }}\right\}}^{1/\rho }},1-\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n\frac{1}{n}{\left(\frac{u_j}{1-u_j}\right)}^{\rho }}\right\}}^{1/\rho }},1-\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n\frac{1}{n}{\left(\frac{v_j}{1-v_j}\right)}^{\rho }}\right\}}^{1/\rho }}\rangle .$$

(2)

Idempotency: Let all the SVNNs be s_j = <t_j, u_j, v_j> = s (j = 1, 2, …, n). Then, SVNDWGA(s₁, s₂, …, s_n) = s.

(3)

Commutativity: Let the SVNS (s₁’, s₂’, …, s_n’) be any permutation of (s₁, s₂, …, s_n). Then, there is SVNDWGA(s₁’, s₂’, …, s_n’) = SVNDWGA(s₁, s₂, …, s_n).

(4)

Boundedness: Let s_min = min(s₁, s₂, …, s_n) and s_max = max(s₁, s₂, …, s_n). Then, s_min ≤ SVNDWGA(s₁, s₂, …, s_n) ≤ s_max.

The proof processes of these properties are the same as the ones of the properties for the SVNDWAA operator. Hence, they are not repeated here.

5. MADM Method Using the SVNDWAA Operator or the SVNDWGA Operator

In this section, we propose a MADM method by using the SVNDWAA operator or the SVNDWGA operator to handle MADM problems with SVNN information.

For a MADM problem with SVNN information, let S = {S₁, S₂, …, S_m} be a discrete set of alternatives and G = {G₁, G₂, …, G_n} be a discrete set of attributes. Assume that the weight vector of the attributes is given as w = (w₁, w₂, …, w_n) such that w_j $\in$ [0, 1] and ${\displaystyle {\sum }_{j=1}^n{w}_j}=1$. If the decision makers are required to provide their suitability evaluation about the alternative S_i (i = 1, 2, …, m) under the attribute G_j (j = 1, 2, …, n) by the SVNN s_ij = <t_ij, u_ij, v_ij> (i = 1, 2, …, m; j = 1, 2, …, n), then, we can elicit a SVNN decision matrix D = (s_ij)_m×n.

Thus, we utilize the SVNDWAA operator or the SVNDWGA operator to develop a handling approach for MADM problems with SVNN information, which can be described by the following decision steps:

Step 1. Derive the collective SVNN s_i (i = 1, 2, …, m) for the alternative S_i (i = 1, 2, …, m) by using the SVNDWAA operator:

$$\begin{array}{l}{s}_i=SVNDWAA(s_{i1},s_{i2},\dots ,s_{in})\\ =\langle 1-\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n{w}_j{\left(\frac{t_{ij}}{1-t_{ij}}\right)}^{\rho }}\right\}}^{1/\rho }},\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n{w}_j{\left(\frac{1-u_{ij}}{u_{ij}}\right)}^{\rho }}\right\}}^{1/\rho }},\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n{w}_j{\left(\frac{1-v_{ij}}{v_{ij}}\right)}^{\rho }}\right\}}^{1/\rho }}\rangle \end{array},$$

(9)

or by using the SVNDWGA operator:

$$\begin{array}{l}{s}_i=SVNDWGA(s_{i1},s_{i2},\dots ,s_{in})\\ =\langle \frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n{w}_j{\left(\frac{1-t_{ij}}{t_{ij}}\right)}^{\rho }}\right\}}^{1/\rho }},1-\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n{w}_j{\left(\frac{u_{ij}}{1-u_{ij}}\right)}^{\rho }}\right\}}^{1/\rho }},1-\frac{1}{1+{\left\{{\displaystyle \sum _{j=1}^n{w}_j{\left(\frac{v_{ij}}{1-v_{ij}}\right)}^{\rho }}\right\}}^{1/\rho }}\rangle \end{array},$$

(10)

where w = (w₁, w₂, …, w_n) is the weight vector such that w_j $\in$ [0, 1] and ${\displaystyle {\sum }_{j=1}^n{w}_j}=1$.

Step 2. Calculate the score values of E(s_i) (the accuracy degrees of H(s_i) if necessary) of the collective SVNN s_i (i = 1, 2, …, m) by using Equations (1) and (2).

Step 3. Rank the alternatives and select the best one(s).

Step 4. End.

6. Illustrative Example

An illustrative example about investment alternatives for a MADM problem adapted from Ye [10] is used for the applications of the proposed decision-making method under a SVNN environment. An investment company wants to invest a sum of money in the best option. To invest the money, a panel provides four possible alternatives: (1) S₁ is a car company; (2) S₂ is a food company; (3) S₃ is a computer company; (4) S₄ is an arms company. The investment company must take a decision corresponding to the requirements of the three attributes: (1) G₁ is the risk; (2) G₂ is the growth; (3) G₃ is the environmental impact. The suitability evaluations of the alternative S_i (i = 1, 2, 3, 4) corresponding to the three attributes of G_j (j = 1, 2, 3) are given by some decision makers or experts and expressed by the form of SVNNs. Thus, when the four possible alternatives corresponding to the above three attributes are evaluated by the decision makers, we can give the single-valued neutrosophic decision matrix D(s_ij)_m×n, where s_ij = <t_ij, u_ij, v_ij> (i = 1, 2, 3, 4; j = 1, 2, 3) is SVNN, as follows:

$$D{(s_{ij})}_{4\times 3}=\left[\begin{array}{ccc}\langle 0.4,0.2,0.3\rangle & \langle 0.4,0.2,0.3\rangle & \langle 0.8,0.2,0.5\rangle \\ \langle 0.6,0.1,0.2\rangle & \langle 0.6,0.1,0.2\rangle & \langle 0.5,0.2,0.8\rangle \\ \langle 0.3,0.2,0.3\rangle & \langle 0.5,0.2,0.3\rangle & \langle 0.5,0.3,0.8\rangle \\ \langle 0.7,0.0,0.1\rangle & \langle 0.6,0.1,0.2\rangle & \langle 0.6,0.3,0.8\rangle \end{array}\right].$$

The weight vector of the three attributes is given as w = (0.35, 0.25, 0.4).

Then, we utilize the SVNDWAA operator or the SVNDWGA operator to handle the MADM problem with SVNN information.

In this decision-making problem, the MADM steps based on the SVNDWAA operator can be described as follows:

Step 1. Derive the collective SVNNs of s_i for the alternative S_i (i = 1, 2, 3, 4) by using Equation (9) for ρ = 1 as follows:

s₁ = <0.6667, 0.2000, 0.3571>, s₂ = <0.5652, 0.1250, 0.2857>, s₃ = <0.4444, 0.2308, 0.4000>, and s₄ = <0.6418, 0, 0.1905>.

Step 2. Calculate the score values of E(s_i) of the collective SVNN s_i (i = 1, 2, 3, 4) for the alternatives S_i (i = 1, 2, 3, 4) by using Equation (1) as the following results:

E(s₁) = 0.7032, E(s₂) = 0.7182, E(s₃) = 0.6046, and E(s₄) = 0.8171.

Step 3. Based on the obtained score values, the ranking order of the alternatives is S₄ $\succ$ S₂ $\succ$ S₁ $\succ$ S₃ and the best one is S₄.

Or we use the SVNDWGA operator for the MADM problem, which can be described as the following steps:

Step 1’. Derive the collective SVNNs of s_i for the alternative S_i (i = 1, 2, 3, 4) by using Equation (10) for ρ = 1 as follows:

s₁ = <0.5000, 0.2000, 0.3966>, s₂ = <0.5556, 0.1429, 0.6364>, s₃ = <0.4054, 0.2432, 0.6500>, and s₄ = <0.6316, 0.1661, 0.6298>.

Step 2’. Calculate the score values of E(s_i) of the collective SVNN s_i (i = 1, 2, 3, 4) for the alternatives S_i (i = 1, 2, 3, 4) by using Equation (1) as the following results:

E(s₁) = 0.6345, E(s₂) = 0.5921, E(s₃) = 0.5041, and E(s₄) = 0.6119.

Step 3’. Based on the obtained score values, the ranking order of the alternatives is S₁ $\succ$ S₄ $\succ$ S₂ $\succ$ S₃ and the best one is S₁.

In order to ascertain the effects on the ranking alternatives by changing parameters of ρ $\in$ [1, 10] in the SVNDWAA and SVNDWGA operators, all the results are depicted in

Table 1. Ranking results for different operational parameters of the single-valued neutrosophic Dombi weighted arithmetic average (SVNDWAA) operator.

ρ	E(s1), E(s2), E(s3), E(s4)	Ranking Order
1	0.7032, 0.7182, 0.6046, 0.8171	S4 $\succ$ S2 $\succ$ S1 $\succ$ S3
2	0.7259, 0.7356, 0.6257, 0.8326	S4 $\succ$ S2 $\succ$ S1 $\succ$ S3
3	0.7380, 0.7434, 0.6364, 0.8396	S4 $\succ$ S2 $\succ$ S1 $\succ$ S3
4	0.7449, 0.7480, 0.6429, 0.8441	S4 $\succ$ S2 $\succ$ S1 $\succ$ S3
5	0.7492, 0.7511, 0.6472, 0.8474	S4 $\succ$ S2 $\succ$ S1 $\succ$ S3
6	0.7521, 0.7533, 0.6503, 0.8499	S4 $\succ$ S2 $\succ$ S1 $\succ$ S3
7	0.7542, 0.7550, 0.6525, 0.8520	S4 $\succ$ S2 $\succ$ S1 $\succ$ S3
8	0.7558, 0.7564, 0.6543, 0.8536	S4 $\succ$ S2 $\succ$ S1 $\succ$ S3
9	0.7571, 0.7574, 0.6556, 0.8549	S4 $\succ$ S2 $\succ$ S1 $\succ$ S3
10	0.7580, 0.7583, 0.6567, 0.8560	S4 $\succ$ S2 $\succ$ S1 $\succ$ S3

and

Table 2. Ranking results for different operational parameters of the single-valued neutrosophic Dombi weighted geometric average (SVNDWGA) operator.

ρ	E(s1), E(s2), E(s3), E(s4)	Ranking Order
1	0.6345, 0.5921, 0.5041, 0.6119	S1 $\succ$ S4 $\succ$ S2 $\succ$ S3
2	0.6145, 0.5602, 0.4722, 0.5645	S1 $\succ$ S4 $\succ$ S2 $\succ$ S3
3	0.6026, 0.5460, 0.4549, 0.5454	S1 $\succ$ S2 $\succ$ S4 $\succ$ S3
4	0.5950, 0.5374, 0.4439, 0.5351	S1 $\succ$ S2 $\succ$ S4 $\succ$ S3
5	0.5898, 0.5316, 0.4363, 0.5286	S1 $\succ$ S2 $\succ$ S4 $\succ$ S3
6	0.5861, 0.5272, 0.4308, 0.5241	S1 $\succ$ S2 $\succ$ S4 $\succ$ S3
7	0.5834, 0.5238, 0.4266, 0.5208	S1 $\succ$ S2 $\succ$ S4 $\succ$ S3
8	0.5813, 0.5211, 0.4234, 0.5183	S1 $\succ$ S2 $\succ$ S4 $\succ$ S3
9	0.5797, 0.5190, 0.4208, 0.5163	S1 $\succ$ S2 $\succ$ S4 $\succ$ S3
10	0.5784, 0.5172, 0.4188, 0.5147	S1 $\succ$ S2 $\succ$ S4 $\succ$ S3

.

From Table 1 and Table 2, we see that the ranking orders based on the SVNDWAA and SVNDWGA operators indicate their obvious difference due to using different aggregation operators. Then, the different operational parameters of ρ can change the ranking orders corresponding to the SVNDWGA operator, which is more sensitive to ρ in this decision-making problem; while the different operation parameters of ρ show the same ranking orders corresponding to the SVNDWAA operator, which is not sensitive to ρ in this decision-making problem.

Compared with existing related method [38], the decision-making method developed in this paper can deal with single-valued neutrosophic or intuitionistic fuzzy MADM problems, while existing method [38] cannot handle single-valued neutrosophic MADM problems.

However, this MADM method based on the SVNDWAA and SVNDWGA operators indicates the advantage of its flexibility in actual applications. Therefore, the developed MADM method provides a new effective way for decision makers to handle single-valued neutrosophic MADM problems.

7. Conclusions

This paper presented some Dombi operations of SVNNs based on the Dombi T-norm and T-conorm operations, and then proposed the SVNDWAA and SVNDWGA operators and investigated their properties. Further, we developed to a MADM method by using the SVNDWAA operator or the SVNDWGA operator to deal with MADM problems under a SVNN environment, in which attribute values with respect to alternatives are evaluated by the form of SVNNs and the attribute weights are known information. We utilized the SVNDWAA operator or the SVNDWGA operator and the score (accuracy) function to rank the alternatives and to determine the best one(s) according to the score (accuracy) values in the different operational parameters. Finally, an illustrative example about the decision-making problem of investment alternatives was provided to demonstrate the application and feasibility of the developed approach. The decision-making results of the illustrative example demonstrated the main highlights of the proposed MADM method: (1) different operational parameters of ρ in the SVNDWGA and SVNDWAA operators can affect the ranking orders; (2) the decision-making process is more flexible corresponding to some operational parameter ρ specified by decision makers’ preference and/or actual requirements; (3) the SVNDWGA and SVNDWAA operators provide new aggregation methods of SVNNs to solve MADM problems under an SVNN environment.

In the future work, we shall further develop new Dombi aggregation operators for simplified neutrosophic sets (including SVNSs and INSs) and apply them to solve practical applications in these areas like group decision-making in [39,40], expert system, information fusion system, fault diagnosis, medical diagnosis, and so on.