Planning of Knotting Based on Manipulation Skills with Consideration of Robot Mechanism/Motion and Its Realization by a Robot Hand System
Abstract
:1. Introduction
- We define a problem setting for knotting manipulation (Section 2).
- We extract several basic manipulation skills for knotting (Section 3.1).
- We propose a knot description based on knot theory (Section 3.2), and we identify the characteristics of manipulation skills using the knot description (Section 3.3).
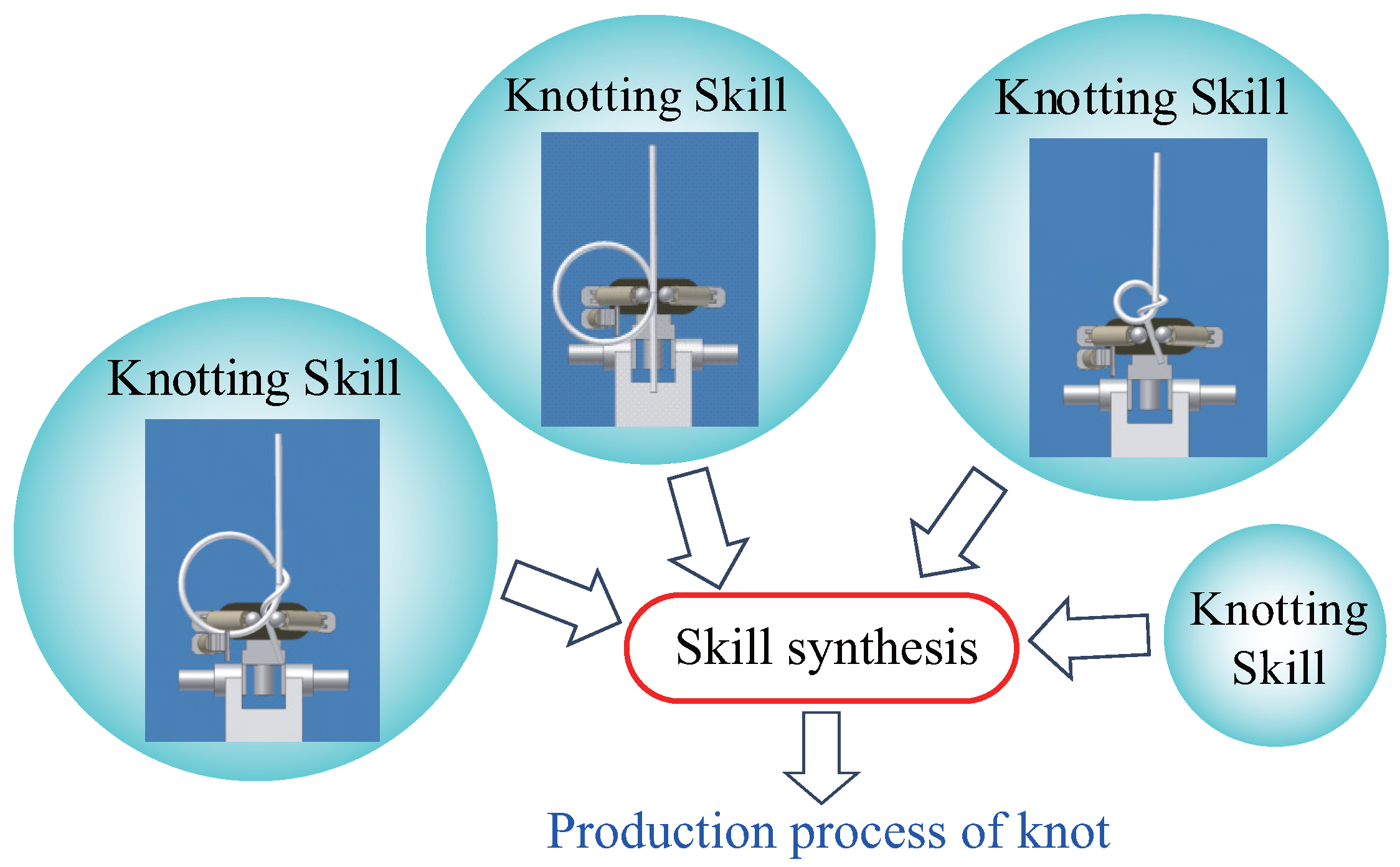
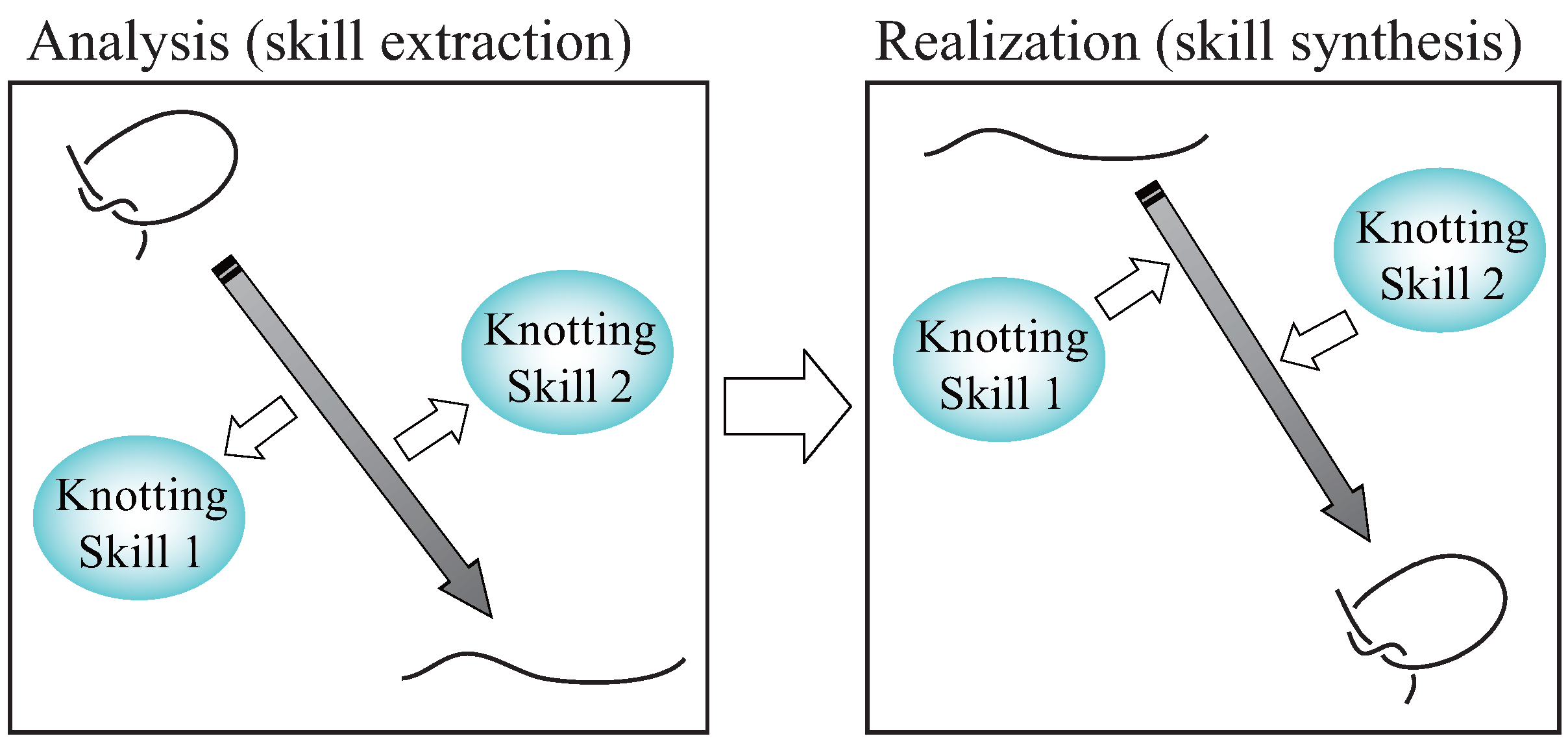
- We also suggest a method for obtaining a knotting procedure in which several knots can be achieved by synthesizing these skills (Section 4.1).
- We analyzed several types of knots using the proposed method (Section 4.2, Section 4.3 and Section 4.4).
- We realized two kinds of knots (overhand knot and half hitch) using a robot hand system (Section 5).
- We finally conclude this article and discuss future work (Section 6).
1.1. Related Work
1.2. Contribution
2. Problem Setting
- a knot formed with a single rope,
- a knot formed with two ropes and
- a knot formed with a single rope and an object.
- As shown in Figure 3, a rope is manipulated by an end-effector with two fingers and a robot arm, where the two fingers perform grasping and manipulation of the rope.
- The knot shape during manipulation can be held at multiple fixation points.
- The knot is produced on the knot production plane, and the robot can approach the knot production plane from only one direction, such as from above.
- Given a reference knot,
- Describe the knot and analyze the knot while unraveling it,
- Develop a plan to tie the knot based on the analysis result and
- Produce the knot with a robot system.
3. Manipulation Skills and Knot Description
3.1. Extraction of Manipulation Skills
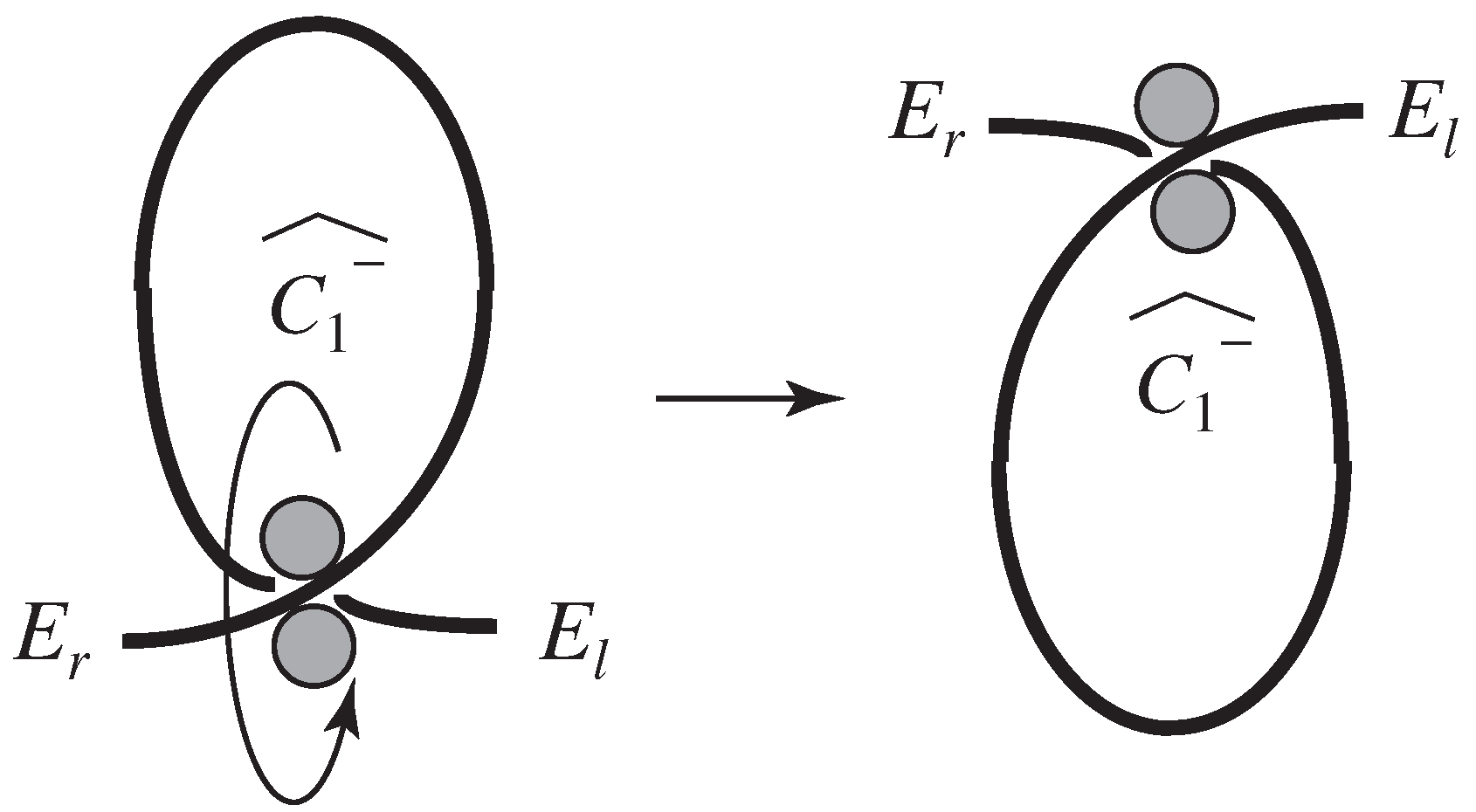
3.2. Knot Description
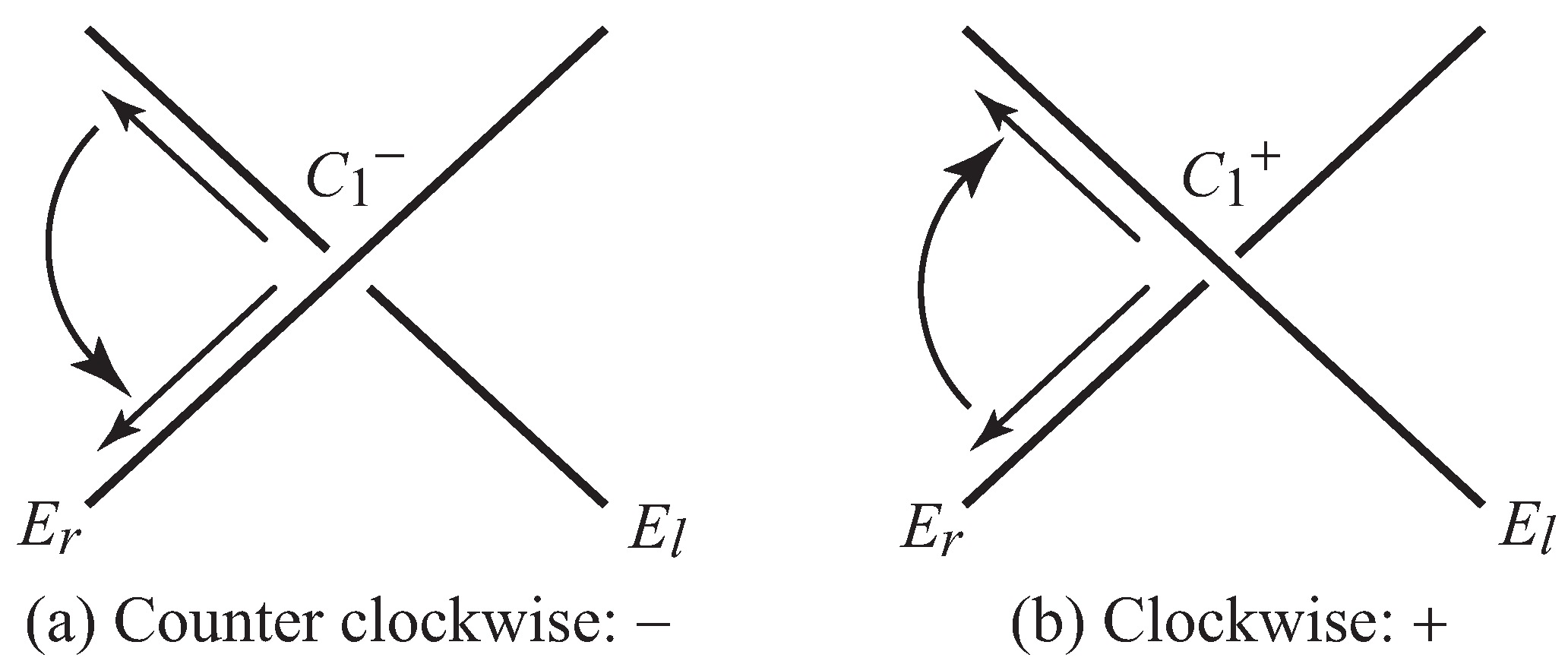
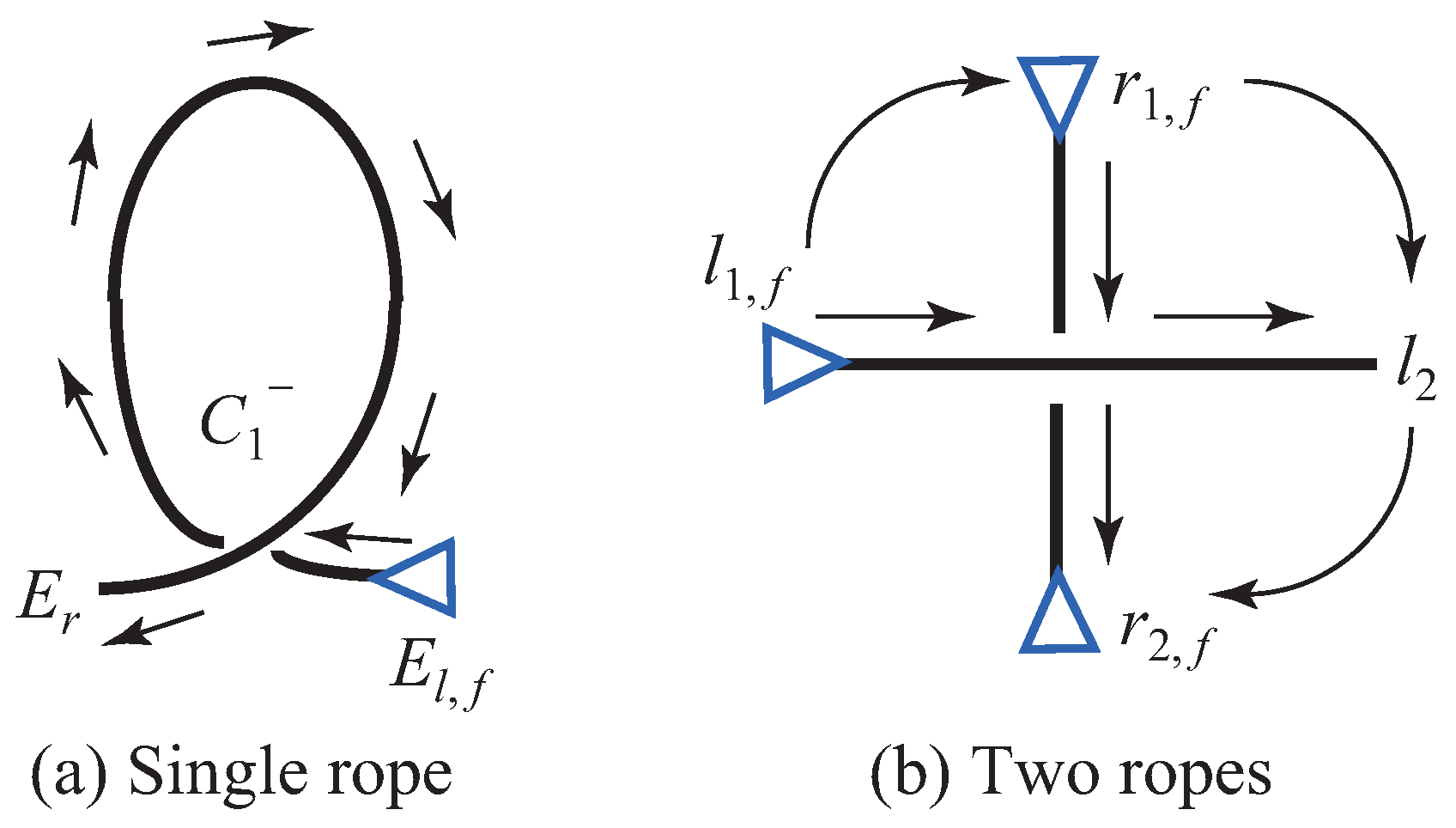
3.2.1. Description of Intersections
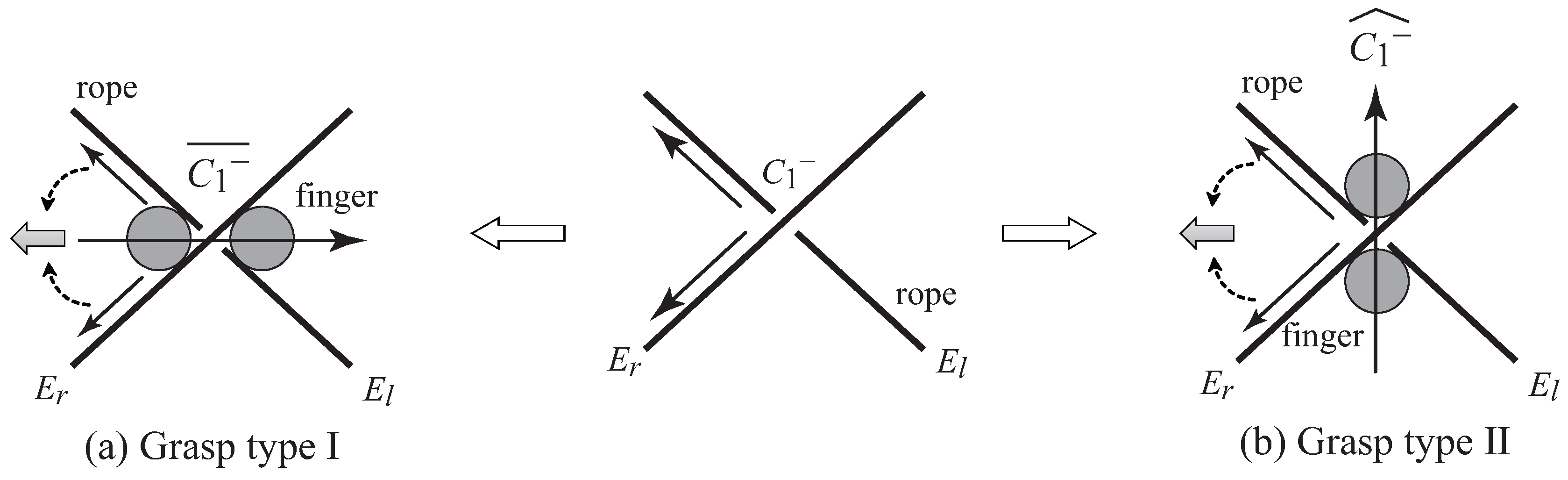
3.2.2. Description of Grasp Types of Intersections
3.2.3. Description of Fixation Locations of Rope
3.3. Characteristics of Manipulation Skills
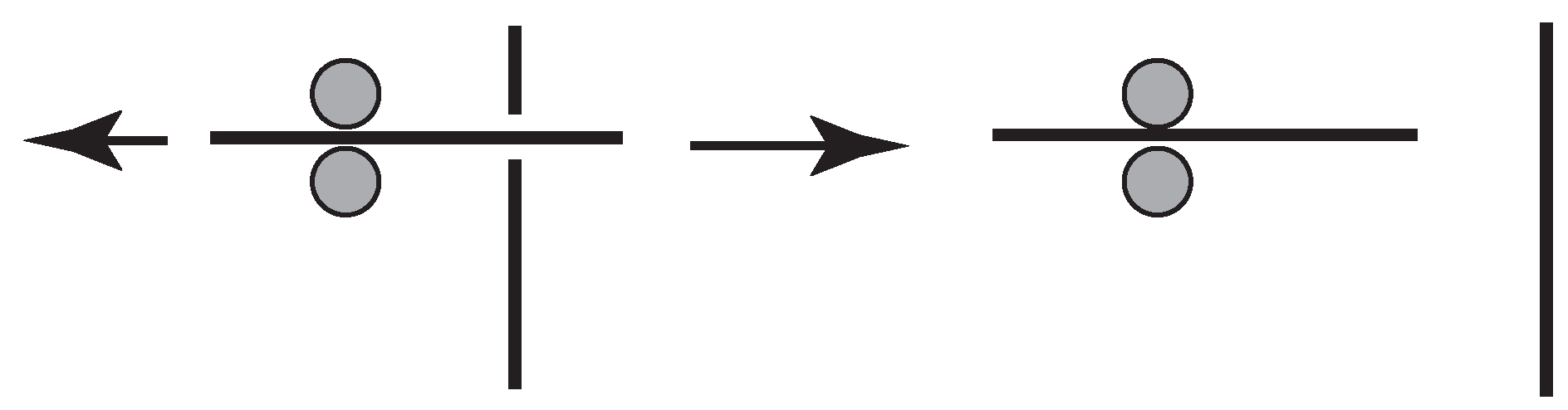
3.3.1. Rope Moving
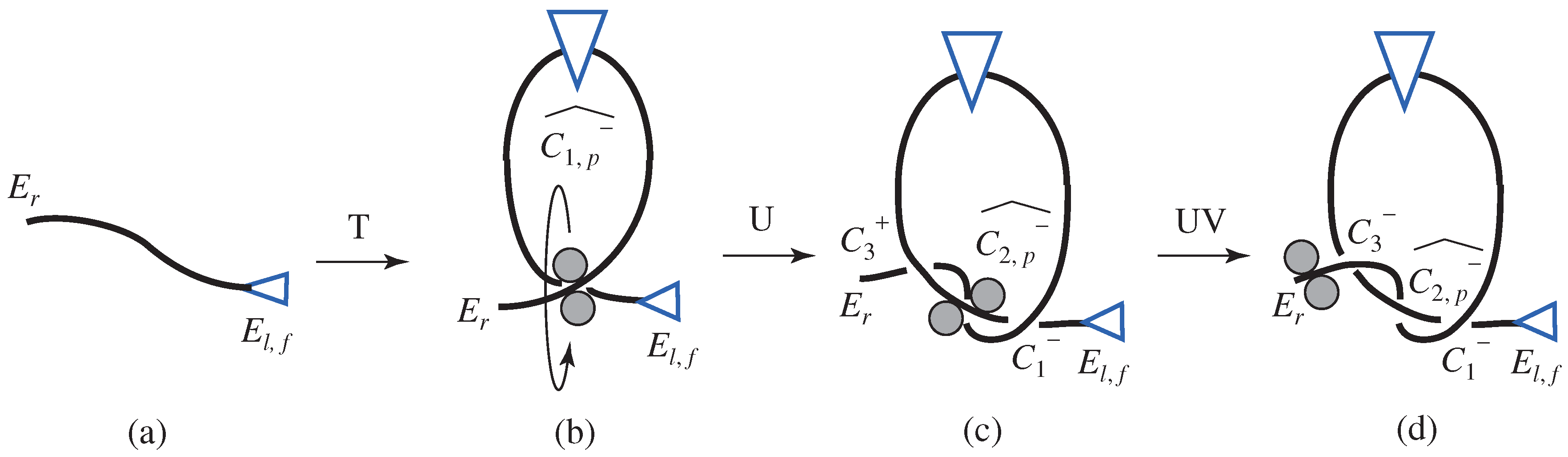
3.3.2. Loop Production
3.3.3. Rope Permutation
3.3.4. Rope Pulling
Rope Permutation and Rope Pulling
4. Knot Analysis
- a knot formed with a single rope,
- a knot formed with two ropes, and
- a knot formed with a single rope and an object.
4.1. Analysis Method
4.1.1. Constraint Condition for Knotting Manipulation
- is fixed (), and is freely moved by the robot.
- The first intersection is produced so as to change the rope direction clockwise from to .
- passes over the rest of the string.
- , and are fixed (, , ), and is freely moved by the robot.
- The first intersection is produced so as to assign the direction () clockwise.
- passes over the rest of the string.
4.1.2. Rules for Manipulation Skills
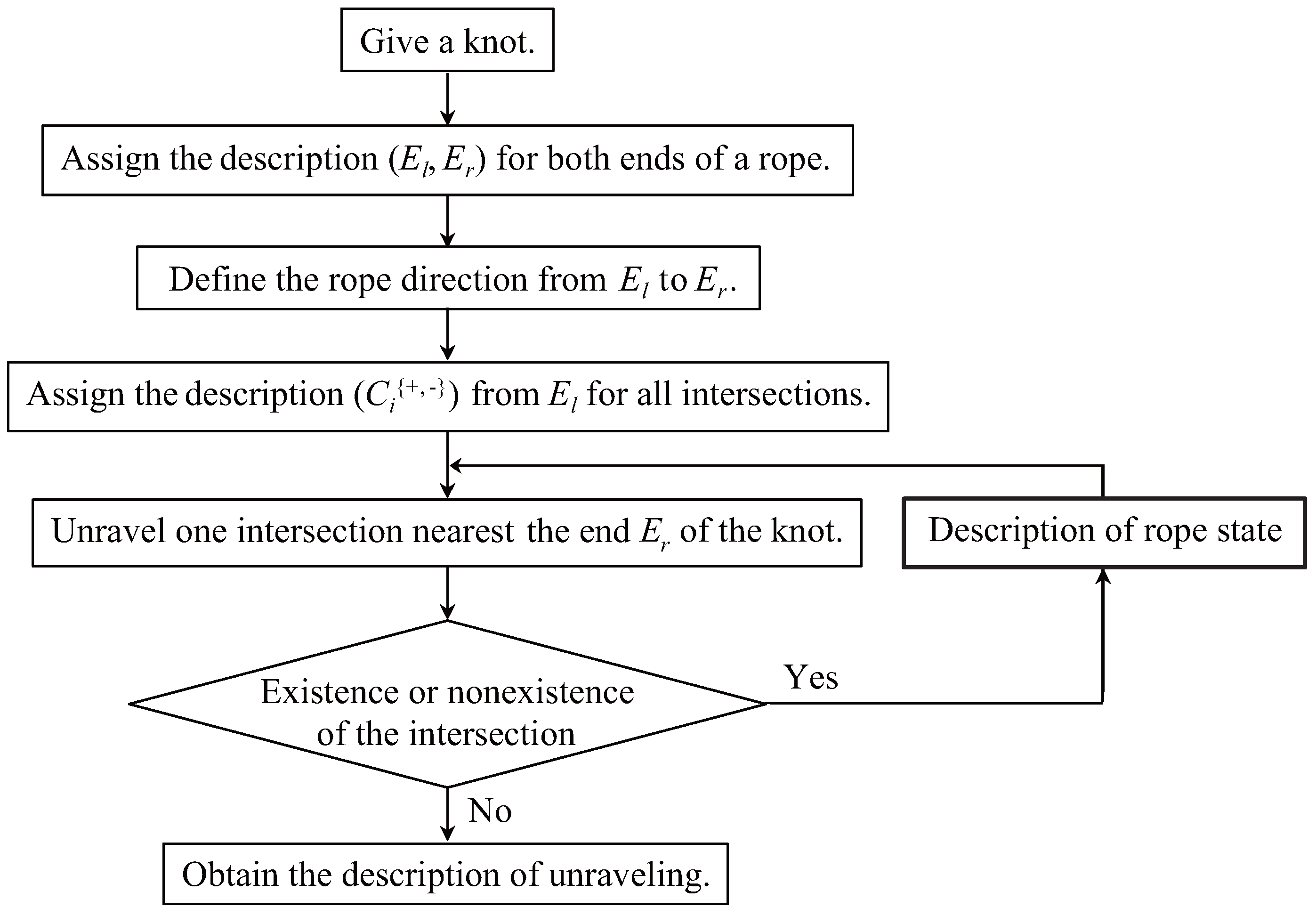
4.1.3. Overall Procedure
- Represent a knot based on the knot description explained in the previous section.
- Unravel one intersection of the knot, starting from the intersection nearest the end of the rope.
- Iterate Step 2 until all intersections disappear. As a result, a sequence of operations for removing the intersections is obtained.
- Apply appropriate manipulation skills to the sequence, while following the sequence obtained in Step 3 in reverse.
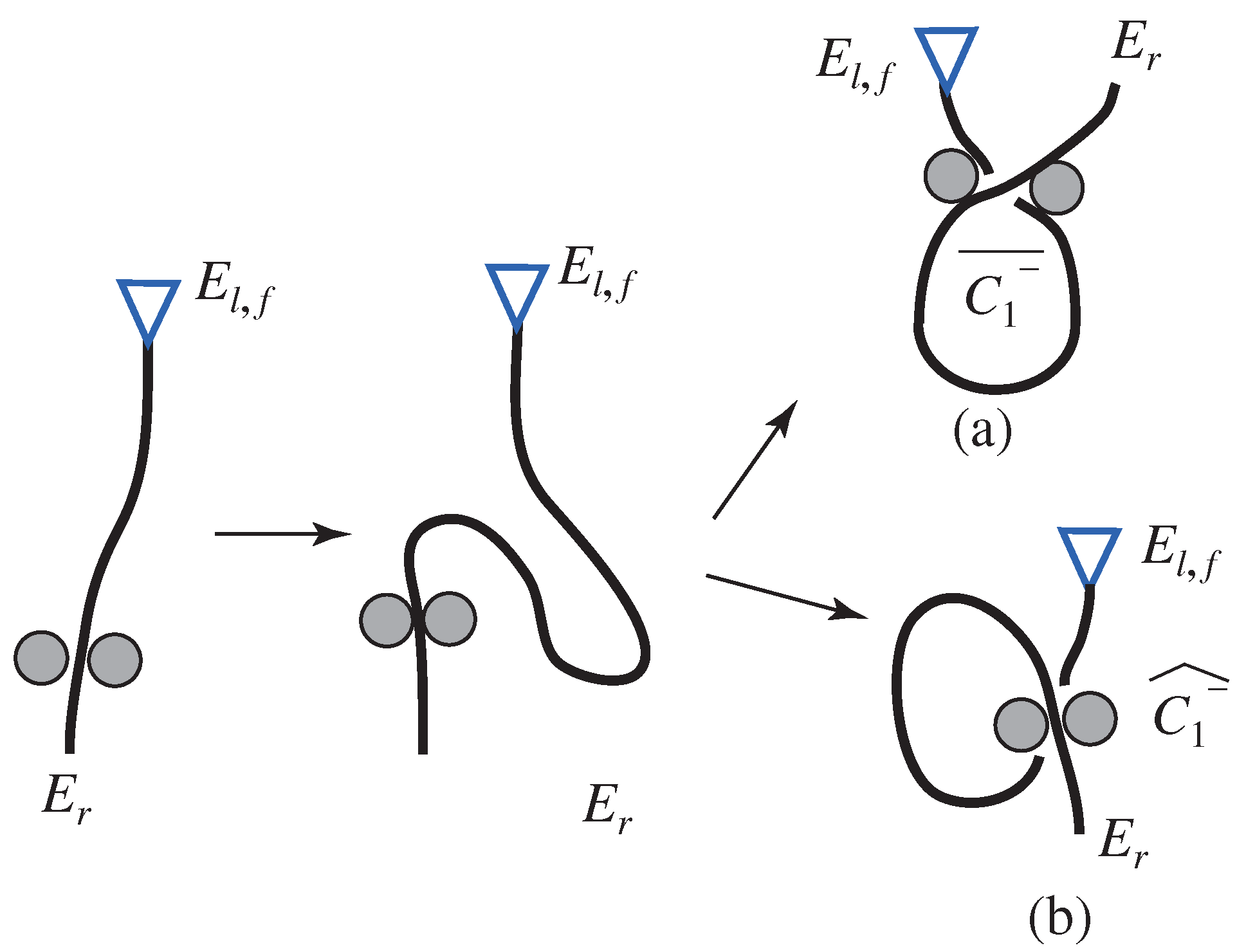
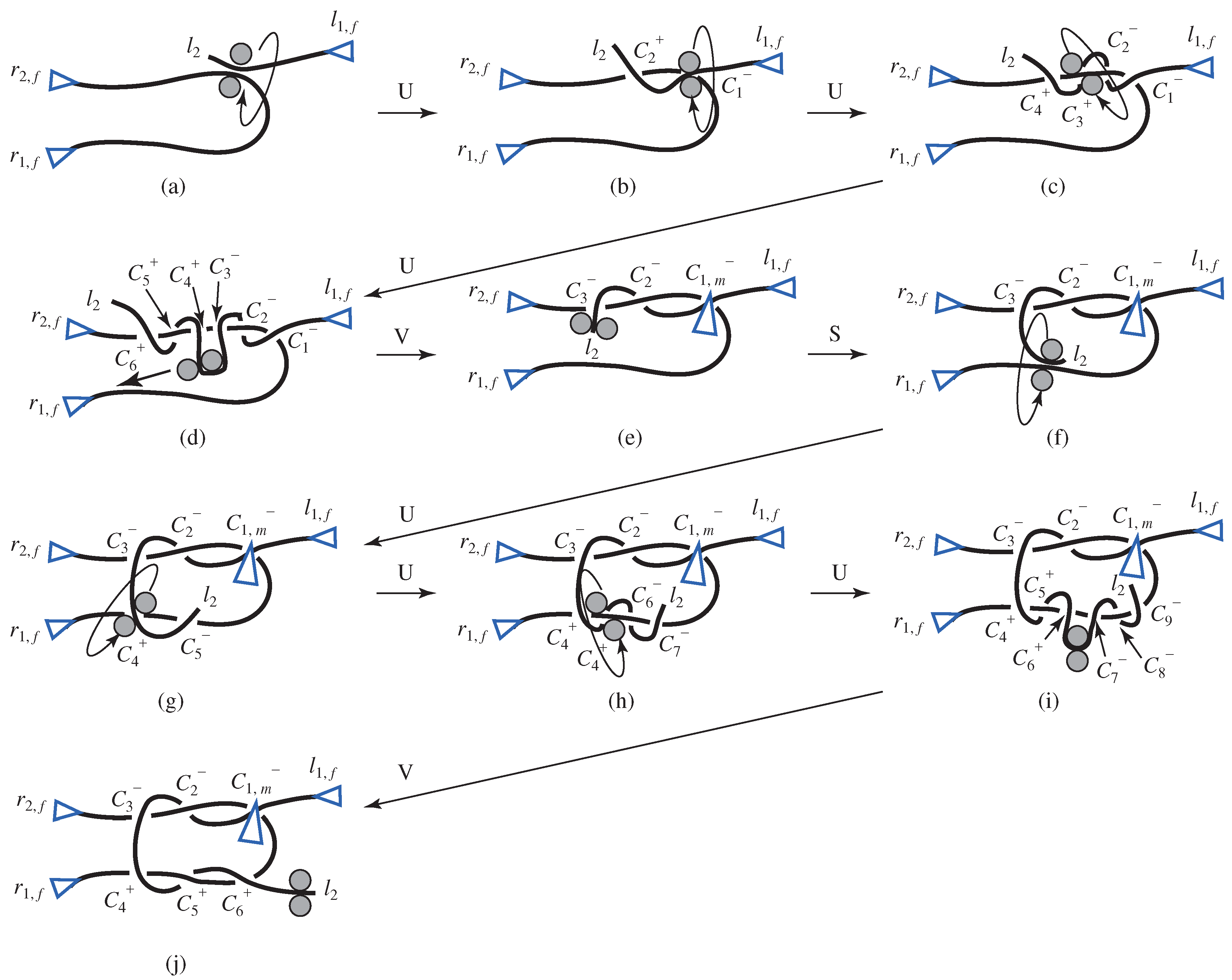
4.2. Knots with a Single Rope
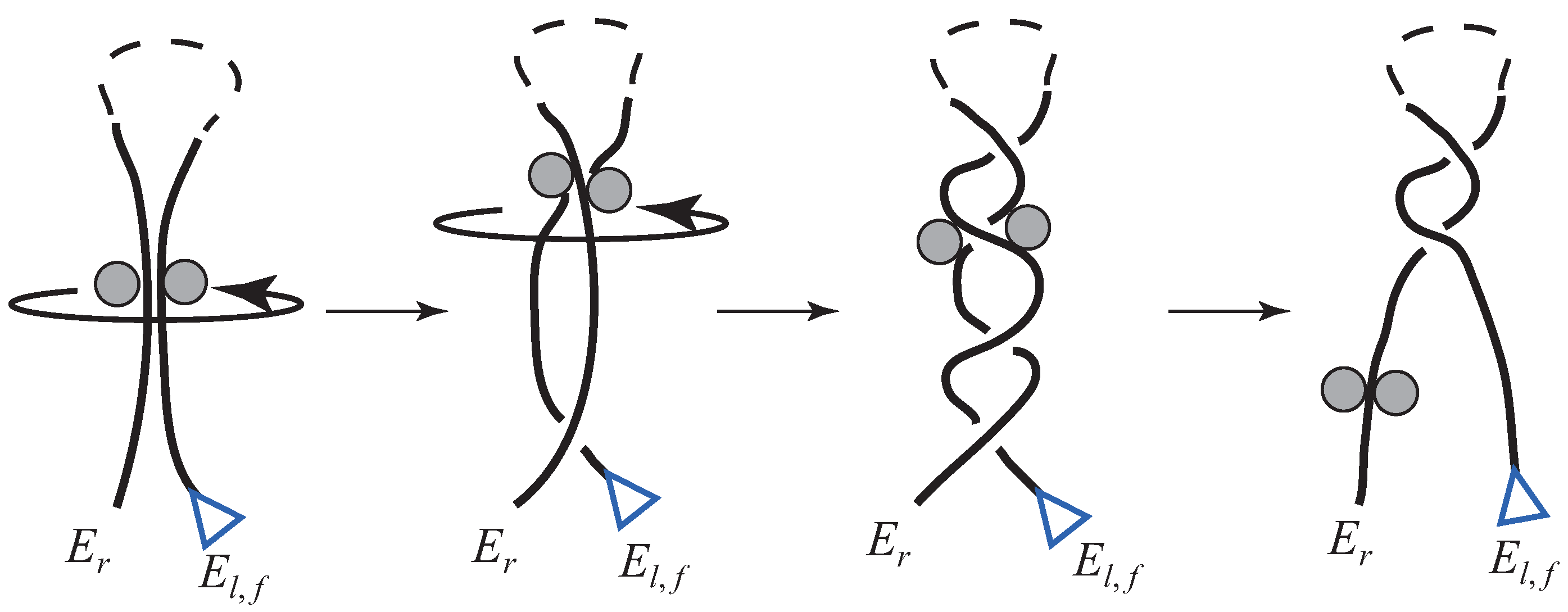
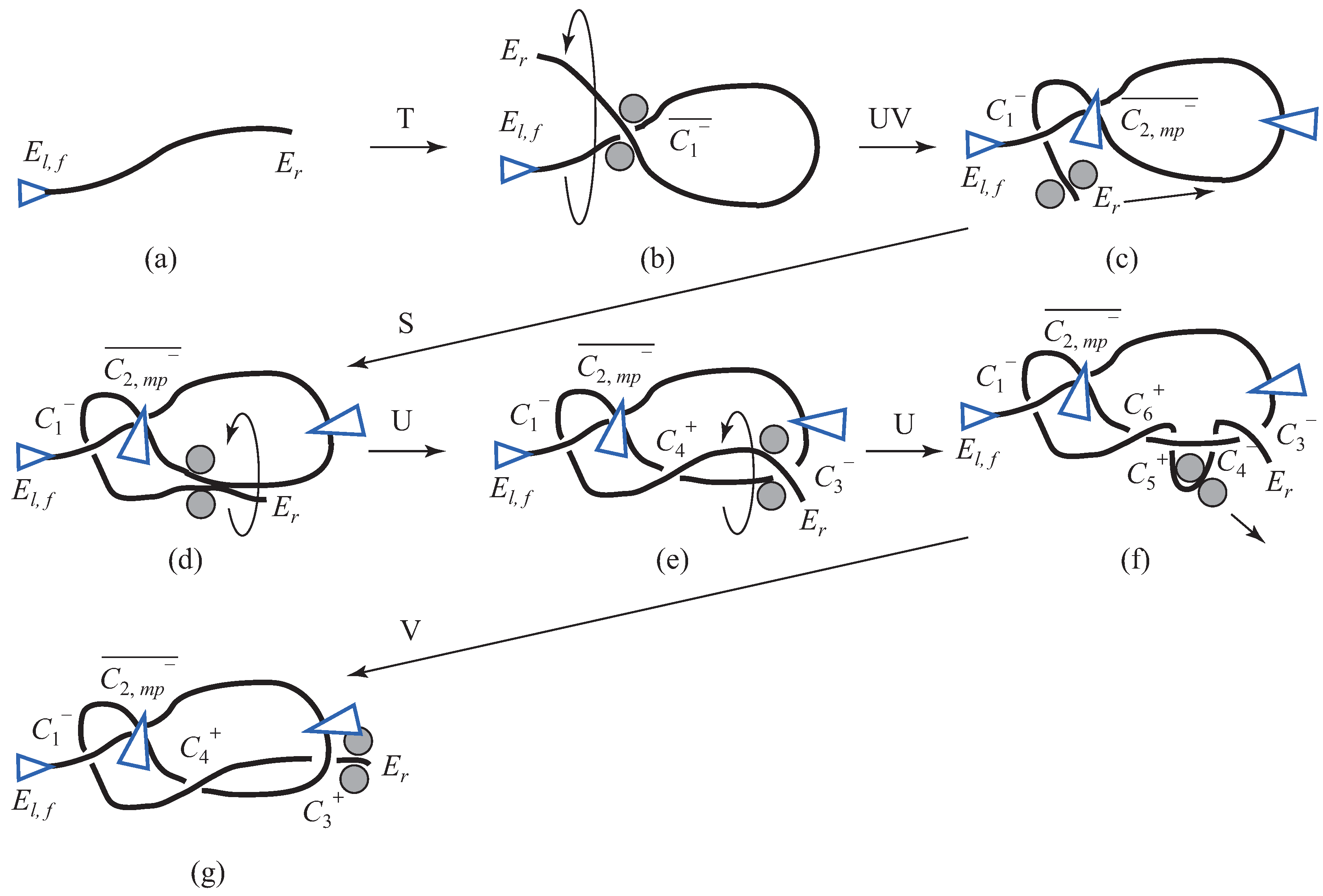
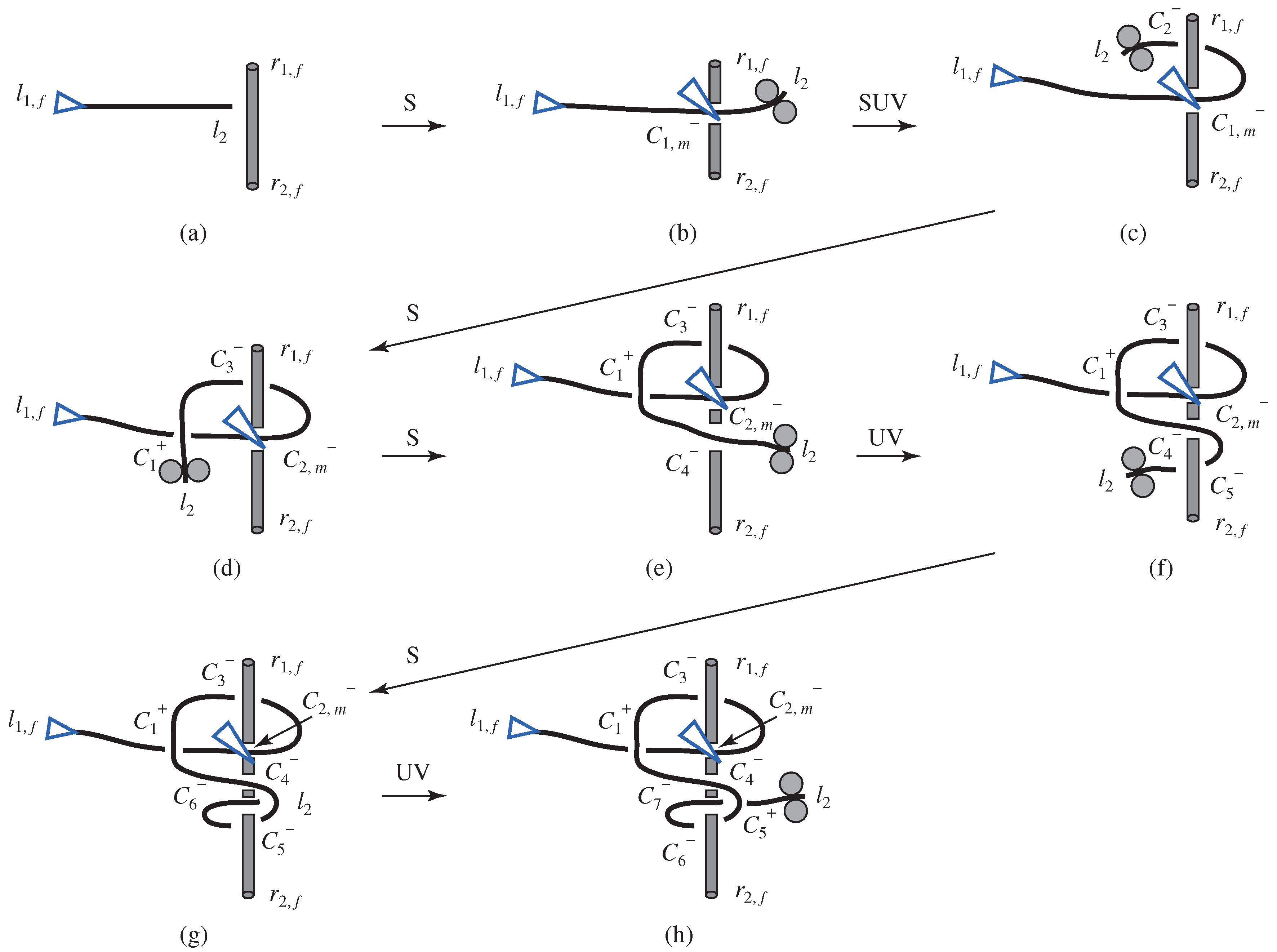
4.2.1. Overhand Knot
Unraveling of Overhand Knot
Knotting of Overhand Knot
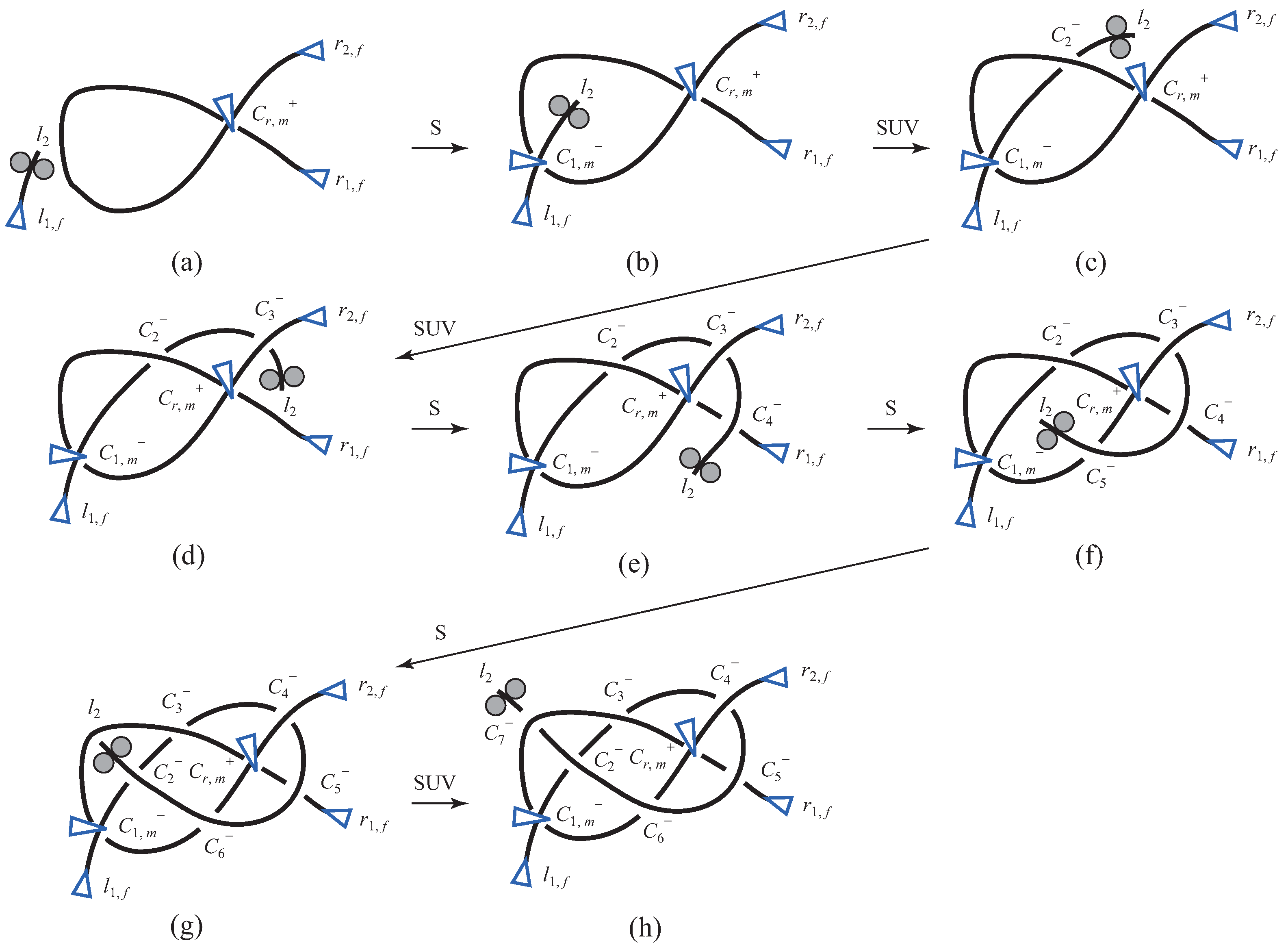
4.2.2. Figure-Eight Knot
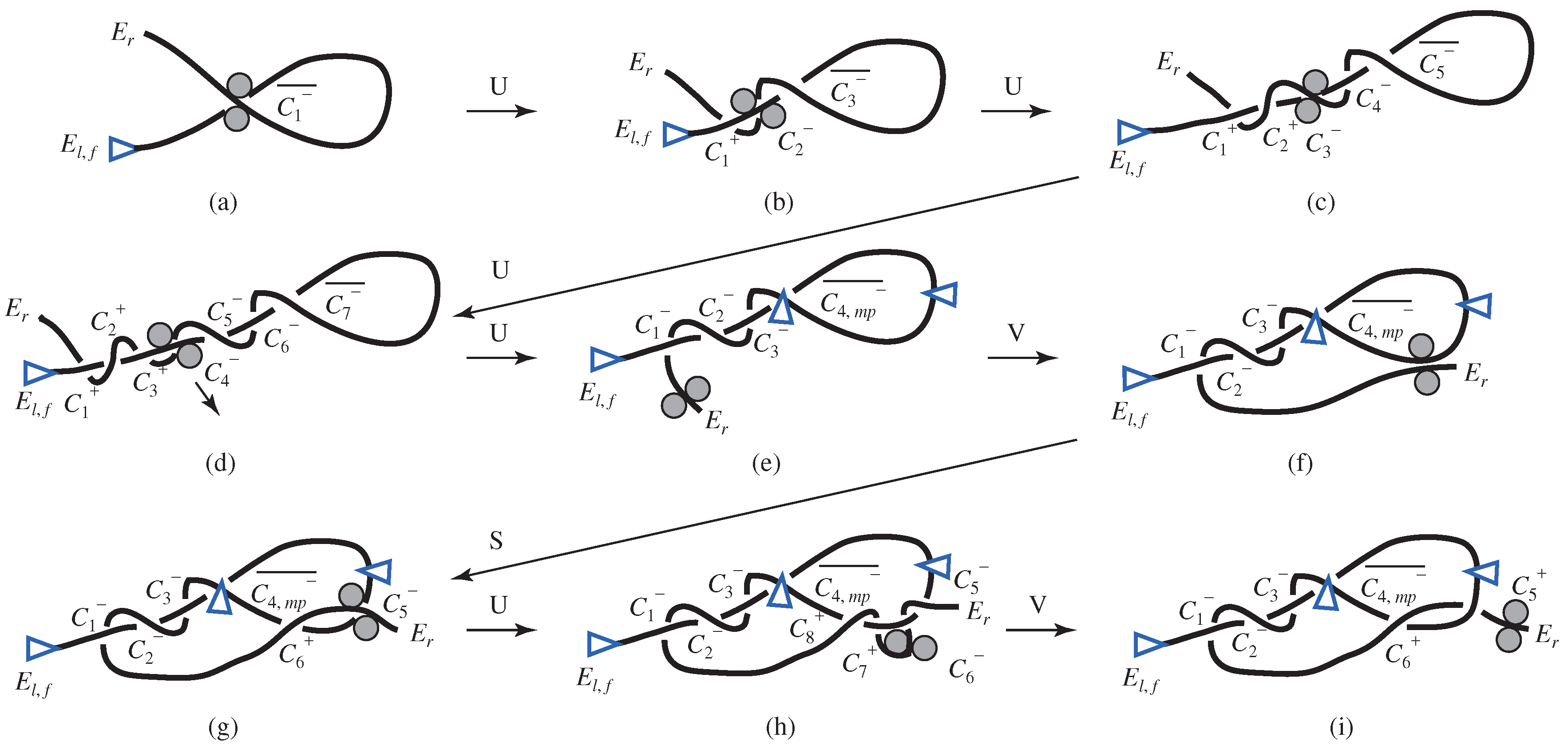
4.2.3. Stevedore’s Knot
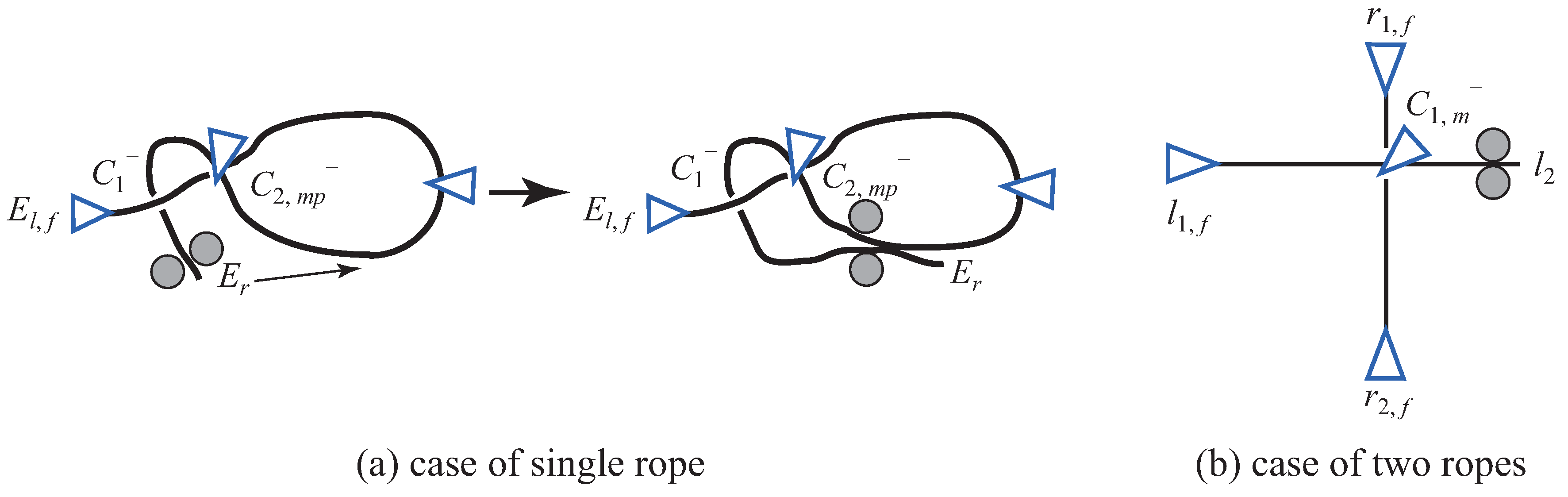
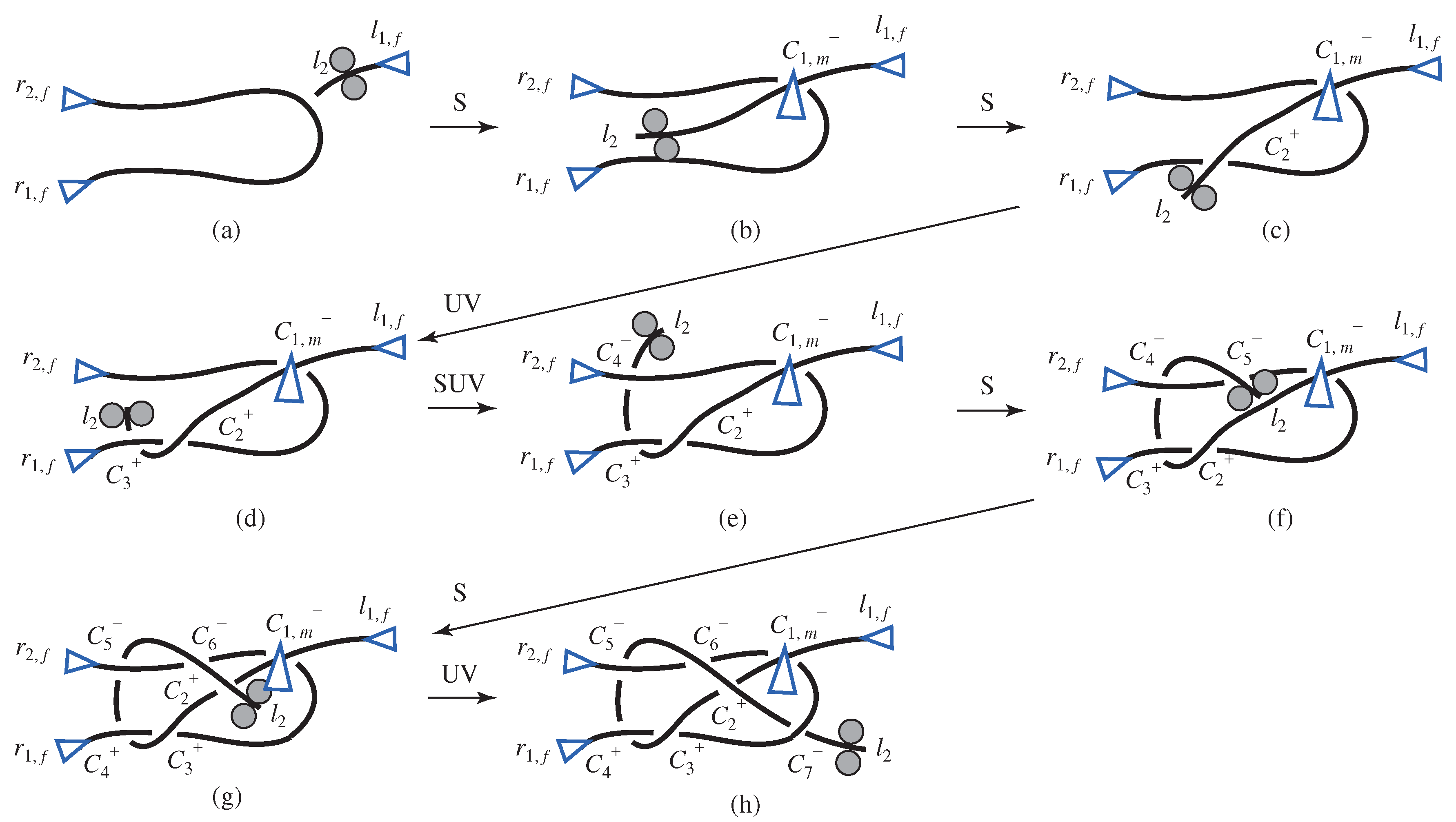
4.3. Knots with Two Ropes
4.3.1. Sheet Bend
4.3.2. Square Knot
4.3.3. Granny Knot
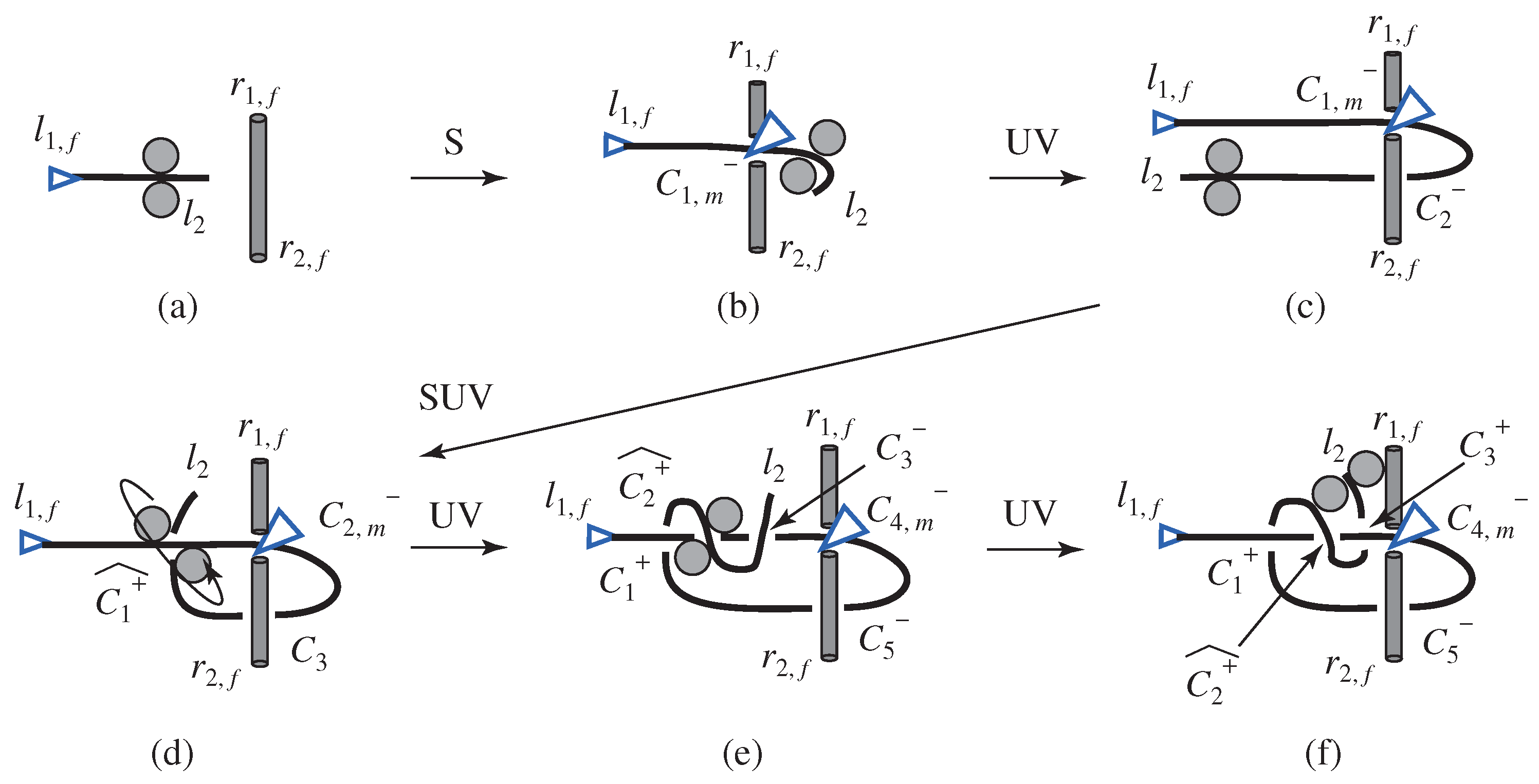
4.4. Knot with Single Rope and Object
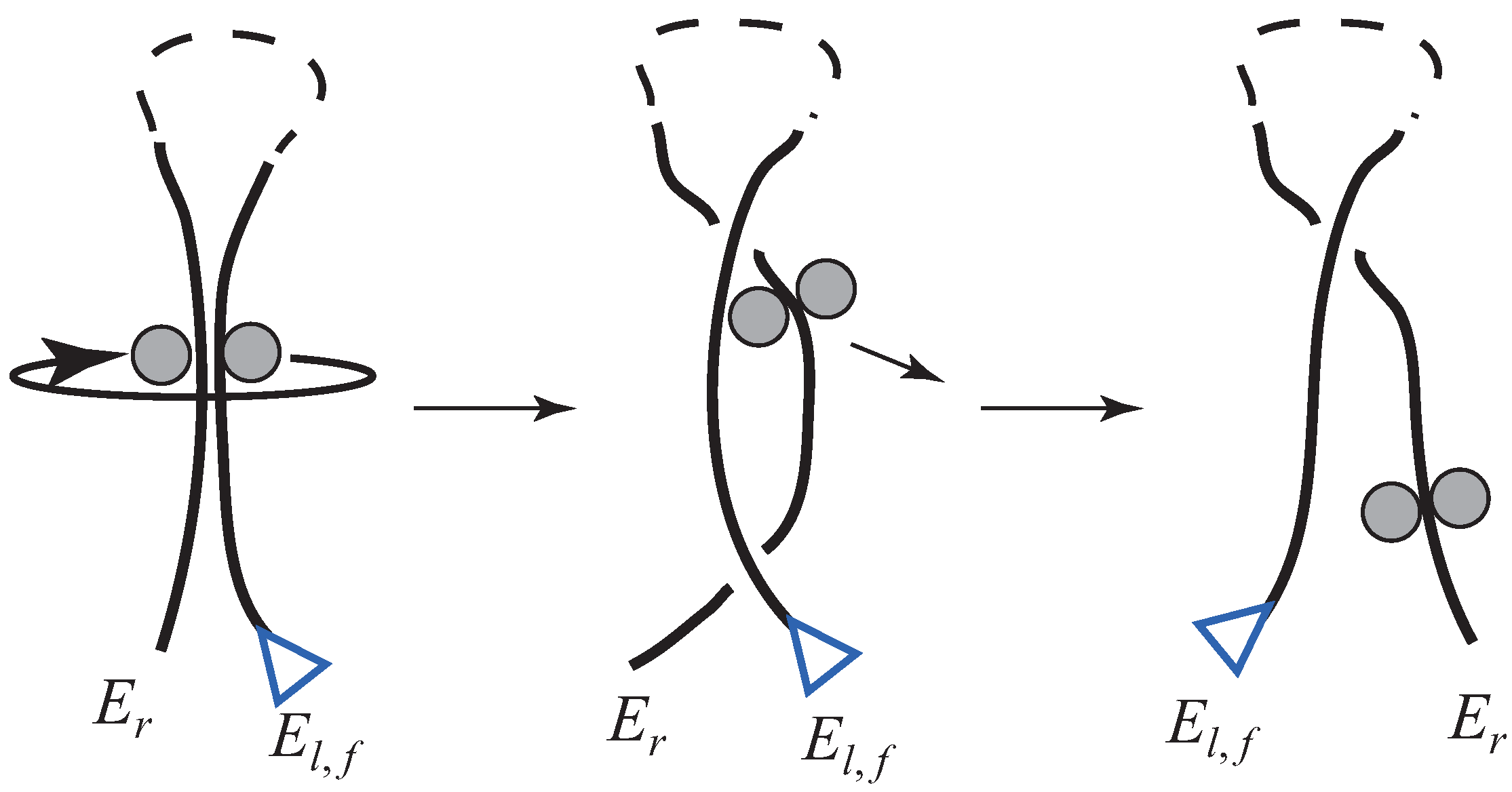
4.4.1. Half Hitch
4.4.2. Clove Hitch
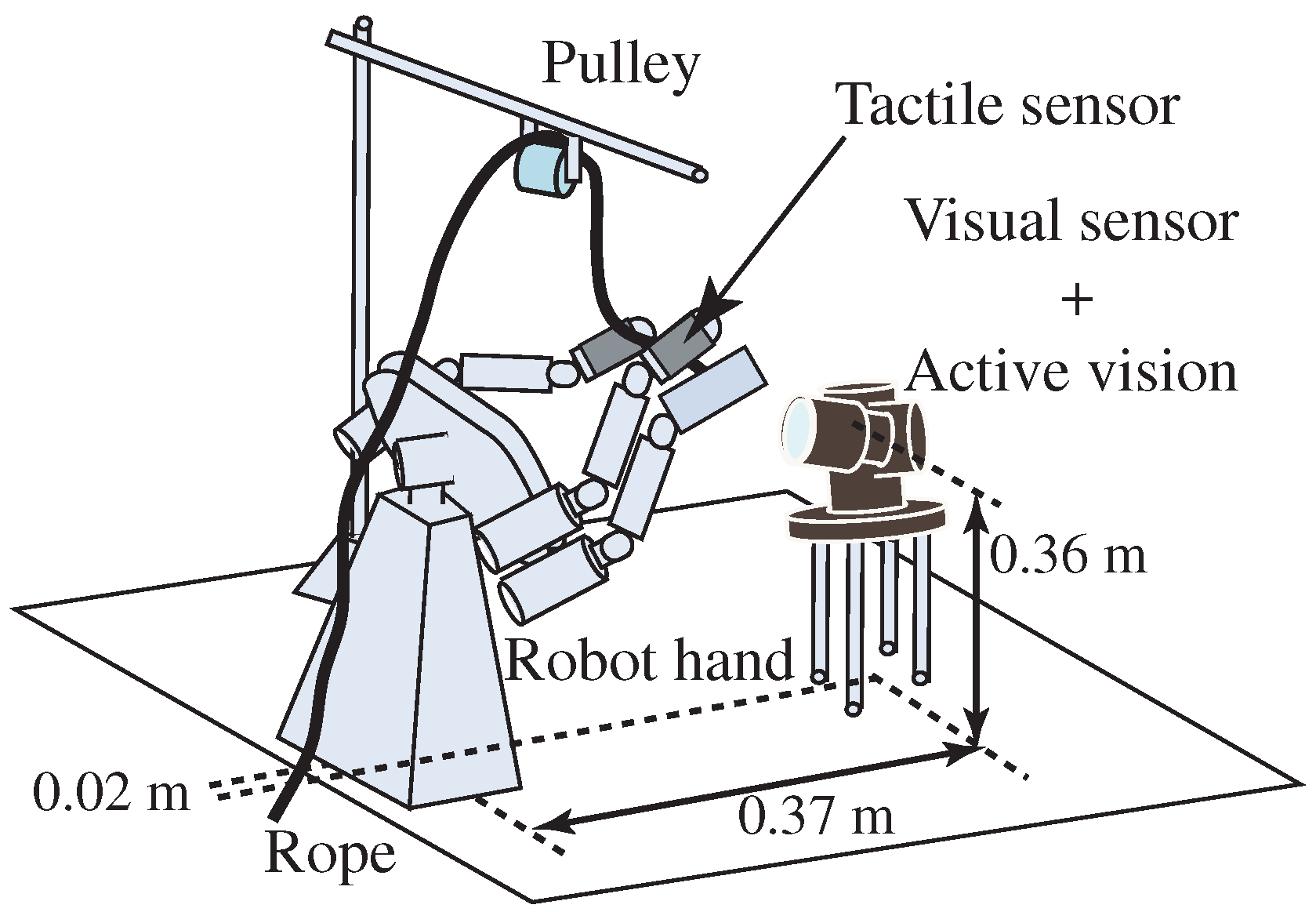
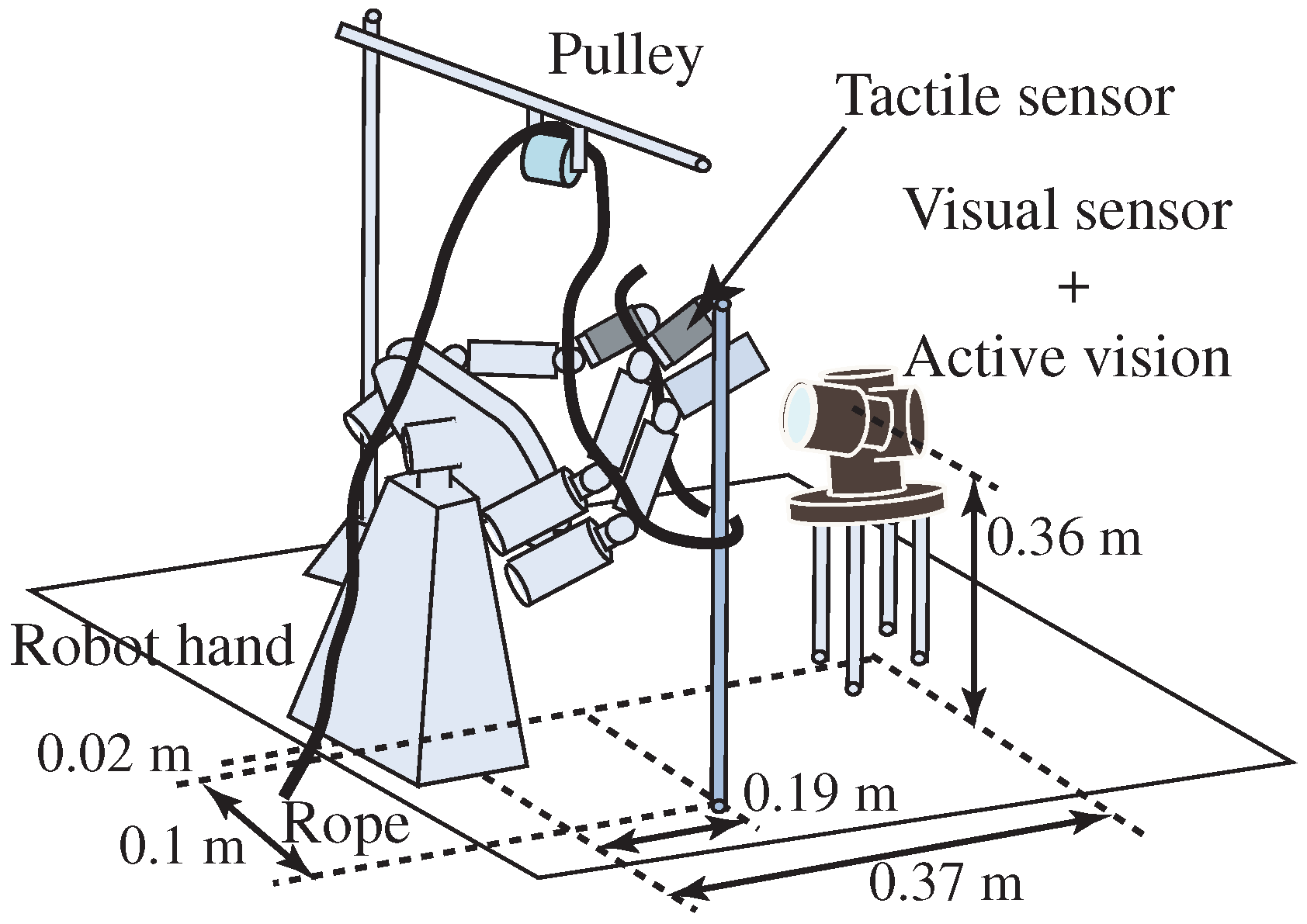
5. Knotting Manipulation by a High-Speed Robot System
5.1. Experimental Result for Overhand Knot
5.2. Experimental Result of Half Hitch
6. Conclusions
- We analyzed the knotting motion of a human hand to identify the necessary knotting skills. Then, we proposed a knot description methodology and a method of obtaining the production process of a knot based on combinations of these skills.
- We suggested a knotting strategy that does not depend on the flexible characteristics of the rope. A real-time tactile and visual sensory feedback control method was proposed to improve the success rate and robustness for various ropes.
- We demonstrated experimental results achieved by a high-speed multi-fingered hand system.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yamakawa, Y.; Namiki, A.; Ishikawa, M.; Shimojo, M. One-handed Knotting of a Flexible Rope with a High-speed Multifingered Hand having Tactile Sensors. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 703–708. [Google Scholar]
- Inoue, H.; Inaba, M. Hand-Eye Coordination in Rope Handling; Robotics Research: The First International Symposium; MIT Press: Cambridge, MA, USA, 1984; pp. 163–174. [Google Scholar]
- Matsuno, T.; Fukuda, T.; Arai, F. Flexible Rope Manipulation by Dual Manipulator System Using Vision Sensor. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Como, Italy, 8–12 July 2001; pp. 677–682. [Google Scholar]
- Saha, M.; Isto, P. Motion Planning for Robotic Manipulation of Deformable Linear Object. In Proceedings of the IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006; pp. 2478–2484. [Google Scholar]
- Morita, T.; Takamatsu, J.; Ogawara, K.; Kimura, H.; Ikeuchi, K. Knot Planning from Observation. In Proceedings of the IEEE International Conference on Robotics and Automation, Taipei, Taiwan, 14–19 September 2003; pp. 3887–3892. [Google Scholar]
- Wakamatsu, H.; Arai, E.; Hirai, S. Knotting/Unknotting Manipulation of Deformable Linear Objects. Int. J. Robot. Res. 2006, 25, 371–395. [Google Scholar] [CrossRef]
- Onda, H.; Kudoh, S.; Suehiro, T. Handling and Describing String-Tying Operations Based on Metrics Using Segments between Crossing Sections. IEEE Robot. Autom. Lett. 2016, 1, 375–382. [Google Scholar] [CrossRef]
- Vinh, T.V.; Tomizawa, T.; Kudoh, S.; Suehiro, T. Knotting task execution based a hand-rope relation. Adv. Robot. 2017, 31, 570–579. [Google Scholar] [CrossRef]
- Wang, W.; Balkcom, D. Towards Arranging and Tightening Knots and Unknots with Fixtures. IEEE Trans. Autom. Sci. Eng. 2015, 12, 1318–1331. [Google Scholar] [CrossRef]
- Wang, W.; Balkcom, D. Towards tying knots precisely. In Proceedings of the IEEE International Conference on Robotics and Automation, Stockholm, Sweden, 16–21 May 2016; pp. 3639–3646. [Google Scholar]
- Yamakawa, Y.; Namiki, A.; Ishikawa, M.; Shimojo, M. Knotting Manipulation of a Flexible Rope with a High-speed Multifingered Hand System based on Skill Synthesis. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 2691–2696. [Google Scholar]
- Yamakawa, Y.; Namiki, A.; Ishikawa, M.; Shimojo, M. One-handed Knotting of a Linear Flexible Object based on Reconfigurable Skill Synthesis Strategy. In Proceedings of the ASME/IFToMM International Conference on Reconfigurable Mechanisms and Robots, London, UK, 22–24 June 2009; pp. 486–493. [Google Scholar]
- Yamakawa, Y.; Namiki, A.; Ishikawa, M.; Shimojo, M. Knotting a Flexible Rope using a High-speed Multifingered Hand System based on Synthesis of Knotting Manipulation Skills. In Robotics 2010 Current and Future Challenges; InTech: Rijeka, Croatia, 2010; pp. 149–166. [Google Scholar]
- Adams, C.C. The Knot Book—An Elementary Introduction to the Mathematical Theory of Knots; American Mathematical Society: Providence, RI, USA, 2004. [Google Scholar]
- Namiki, A.; Imai, Y.; Ishikawa, M.; Kaneko, M. Development of a High-speed Multifingered Hand System and Its Application to Catching. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Las Vegas, NV, USA, 27–31 October 2003; pp. 2666–2671. [Google Scholar]
- Ishikawa, M.; Shimojo, M. A Method for Measuring the Center Position of a Two Dimensional Distributed Load Using Pressure-Conductive Rubber. Trans. Soc. Instrum. Control Eng. 1982, 18, 730–735. (In Japanese) [Google Scholar] [CrossRef]
- Nakabo, Y.; Ishikawa, M.; Toyoda, H.; Mizuno, S. 1 ms column parallel vision system and its application of high speed target tracking. In Proceedings of the International Conference on Robotics and Automation, San Francisco, CA, USA, 24–28 April 2000; pp. 650–655. [Google Scholar]
- Ishikawa Watanabe Laboratory, One Handed Knotting of flexible rope using a High-speed Multifingered Hand. Available online: http://www.k2.t.u-tokyo.ac.jp/fusion/Knotting/index-e.html (accessed on 20 August 2017).
- Ishikawa Watanabe Laboratory, Knotting manipulation based on skill synthesis. Available online: http://www.k2.t.u-tokyo.ac.jp/fusion/SkillSynthesis/index-e.html (accessed on 20 August 2017).







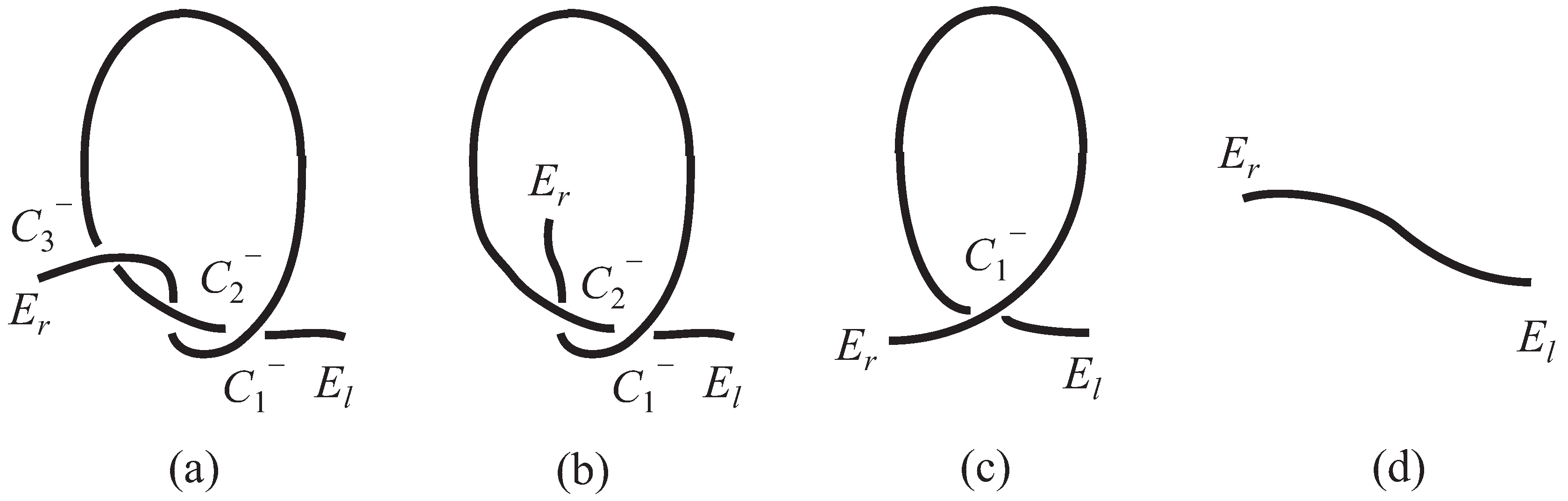


| Production of Intersection | ⟶ | Manipulation Skill |
|---|---|---|
| Add an intersection ‘−’ in case that | ||
| there is no intersection in a single rope | ⟶ | Loop production (T) |
| Add an intersection ‘−’ : intersection of odd number | ⟶ | Rope moving (S) |
| : intersection of even number | ⟶ | Rope permutation + Rope pulling (UV) |
| Add an intersection ‘+’ : intersection of odd number | ⟶ | Rope permutation + Rope pulling (UV) |
| : intersection of even number | ⟶ | Rope moving (S) |
| Add two intersections | ⟶ | Rope permutation (U) |
| Change cross sign of intersection | ⟶ | Rope permutation + Rope pulling (UV) |
| Delete intersections from one intersection to or | ⟶ | Rope pulling (V) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamakawa, Y.; Namiki, A.; Ishikawa, M.; Shimojo, M. Planning of Knotting Based on Manipulation Skills with Consideration of Robot Mechanism/Motion and Its Realization by a Robot Hand System. Symmetry 2017, 9, 194. https://doi.org/10.3390/sym9090194
Yamakawa Y, Namiki A, Ishikawa M, Shimojo M. Planning of Knotting Based on Manipulation Skills with Consideration of Robot Mechanism/Motion and Its Realization by a Robot Hand System. Symmetry. 2017; 9(9):194. https://doi.org/10.3390/sym9090194
Chicago/Turabian StyleYamakawa, Yuji, Akio Namiki, Masatoshi Ishikawa, and Makoto Shimojo. 2017. "Planning of Knotting Based on Manipulation Skills with Consideration of Robot Mechanism/Motion and Its Realization by a Robot Hand System" Symmetry 9, no. 9: 194. https://doi.org/10.3390/sym9090194




