Online Estimation and Correction of Systematic Encoder Line Errors
Abstract
:1. Introduction
2. Systematic Errors on the Encoder Signals
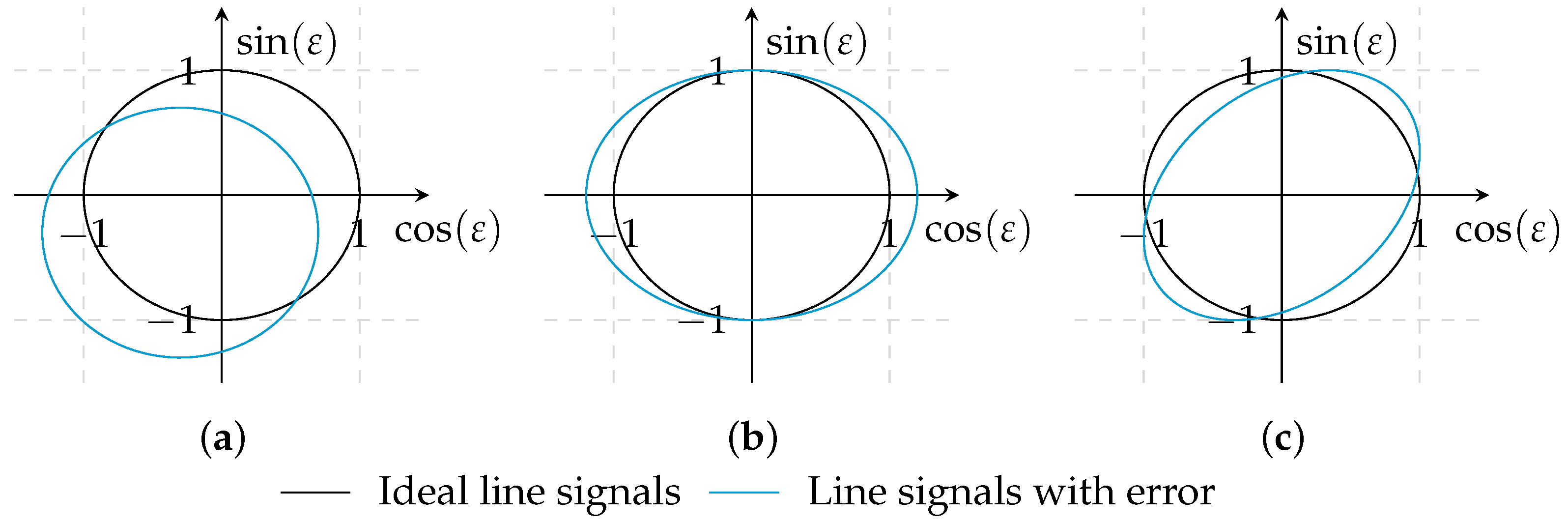
 ) illustrates the ideal line signals without any errors, and it corresponds to a circle with radius 1 and a center in the origin. The resulting courses for individual error parameters are depicted in blue (
) illustrates the ideal line signals without any errors, and it corresponds to a circle with radius 1 and a center in the origin. The resulting courses for individual error parameters are depicted in blue (  ). Offset errors shift the origin as shown in Figure 1a. A deviation in amplitude deforms the circle into an ellipse parallel to one of the axes as shown in Figure 1b. The distortion in Figure 1c is caused by phase-shifted line signals.
). Offset errors shift the origin as shown in Figure 1a. A deviation in amplitude deforms the circle into an ellipse parallel to one of the axes as shown in Figure 1b. The distortion in Figure 1c is caused by phase-shifted line signals.3. The Harmonic Error Correction
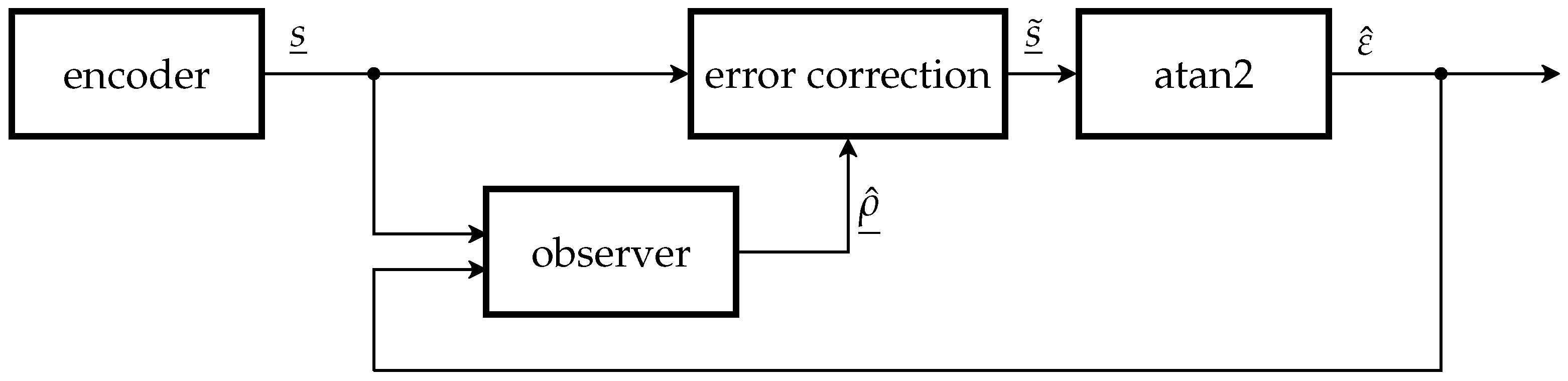
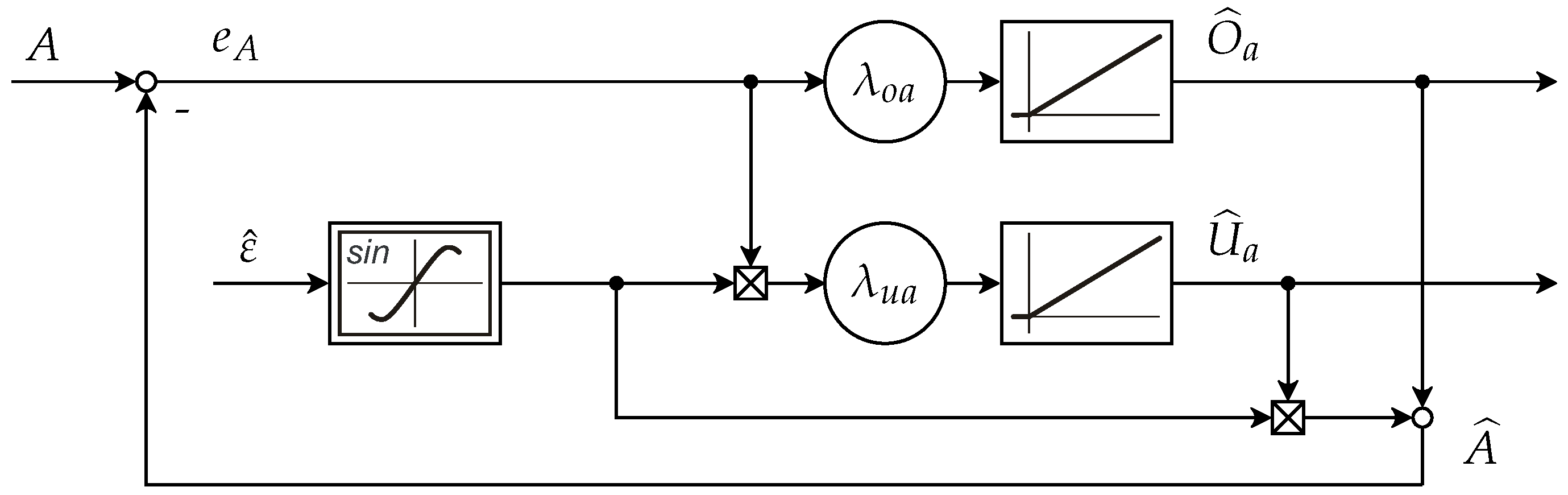
3.1. Theoretical Structure
3.2. Stability
3.3. Simulation
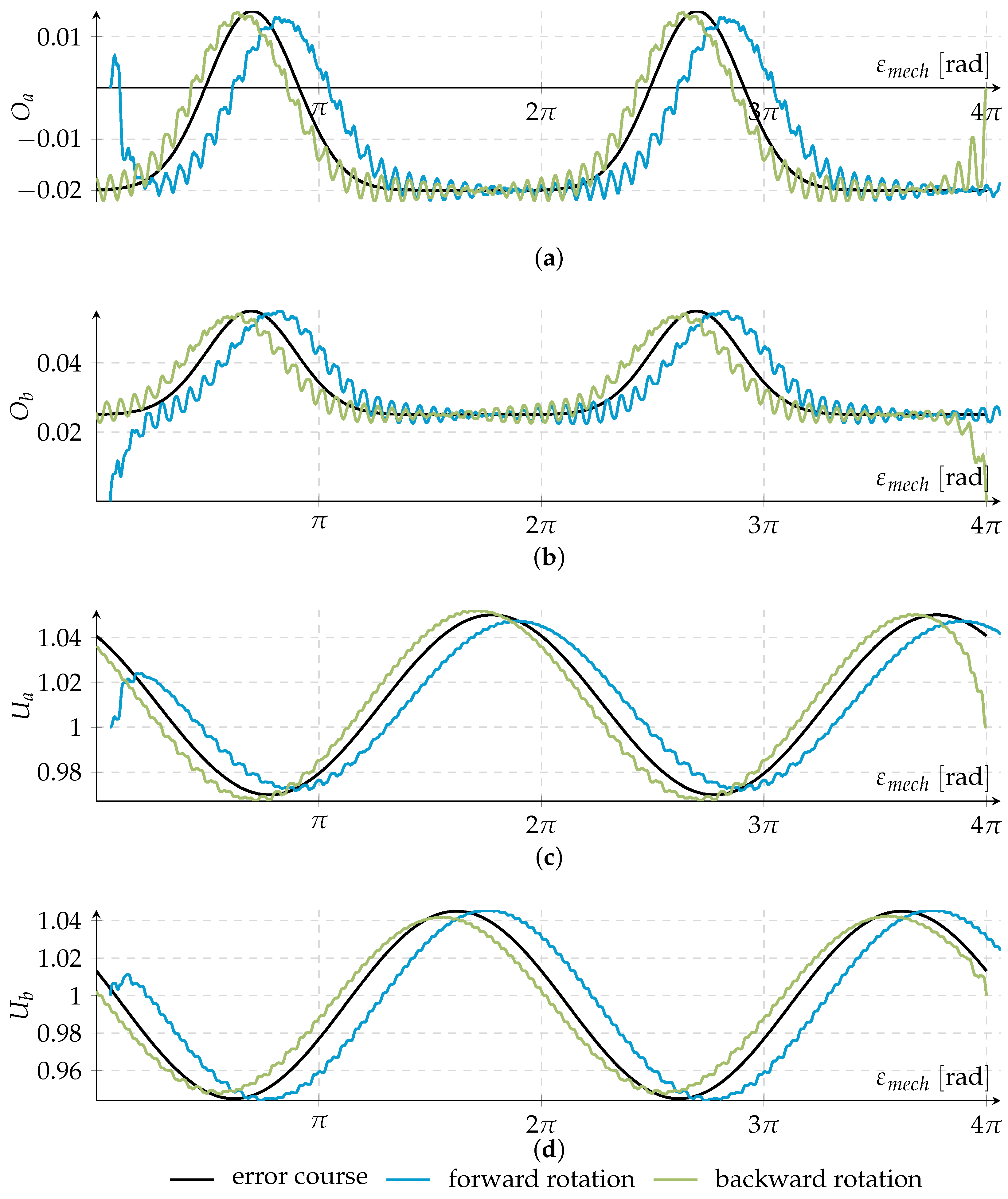
 ) represents the chosen error curve for each parameter. The blue (
) represents the chosen error curve for each parameter. The blue (  ) and the green curve (
) and the green curve (  ) depict the estimated parameter course if the encoder turns forward or backward.
) depict the estimated parameter course if the encoder turns forward or backward.3.4. Experimental Results
4. The Iterative Harmonic Error Correction
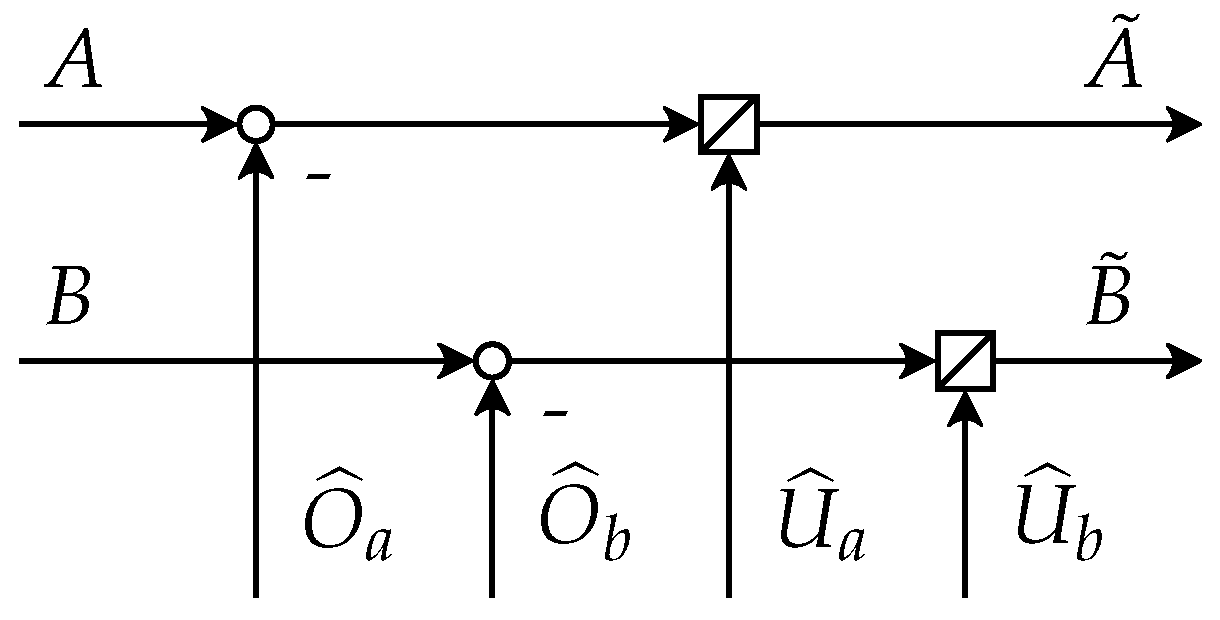
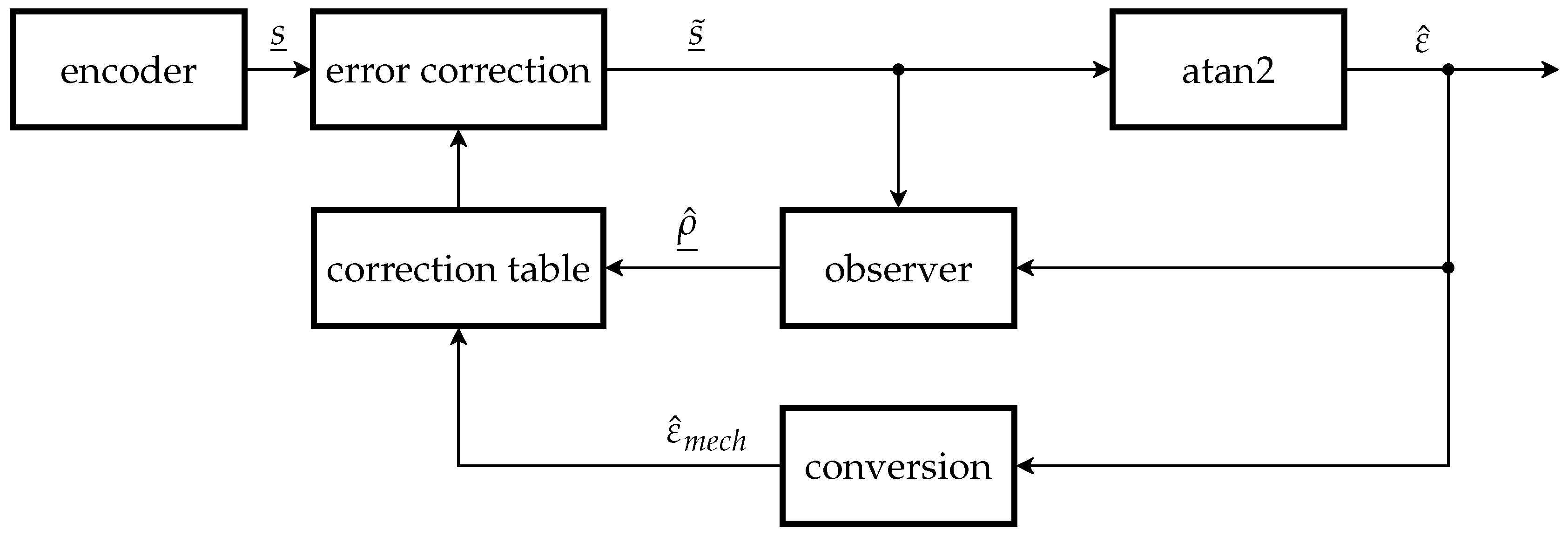
4.1. Theoretical Structure
4.2. Comparison
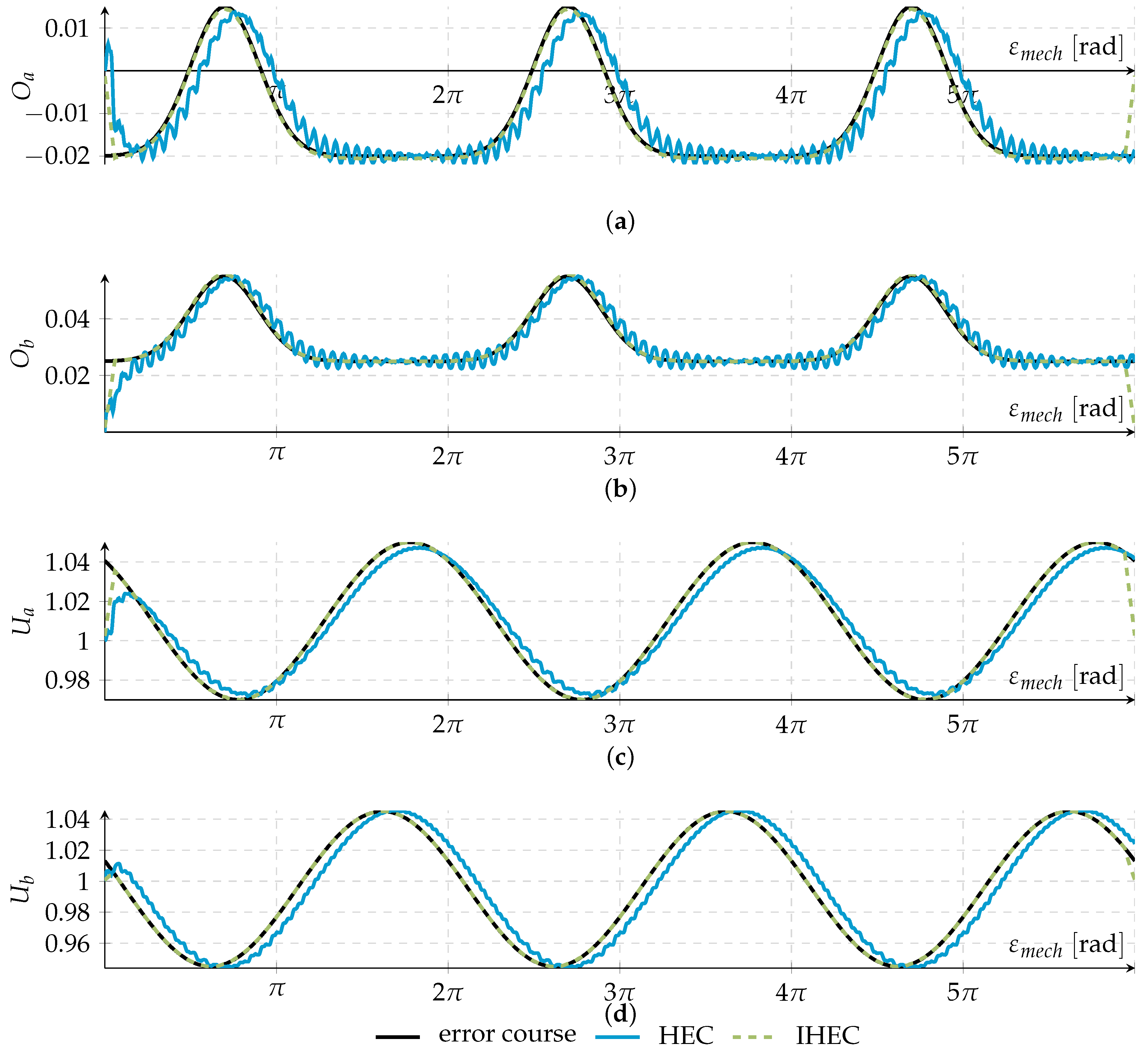
 ) shows the erroneous parameter course, the blue line (
) shows the erroneous parameter course, the blue line (  ) the estimated course obtained by the HEC and the dotted green line (
) the estimated course obtained by the HEC and the dotted green line (  ) the same by IHEC, which is depicted after six iterations. As described in Section 4.1, the courses of the IHEC increase ramp-shaped at the right and left end of the estimation, but in the center part of the graphic, the curves track the chosen parameter course. Moreover, it must be noted that this performance is achieved after just a few iterations.
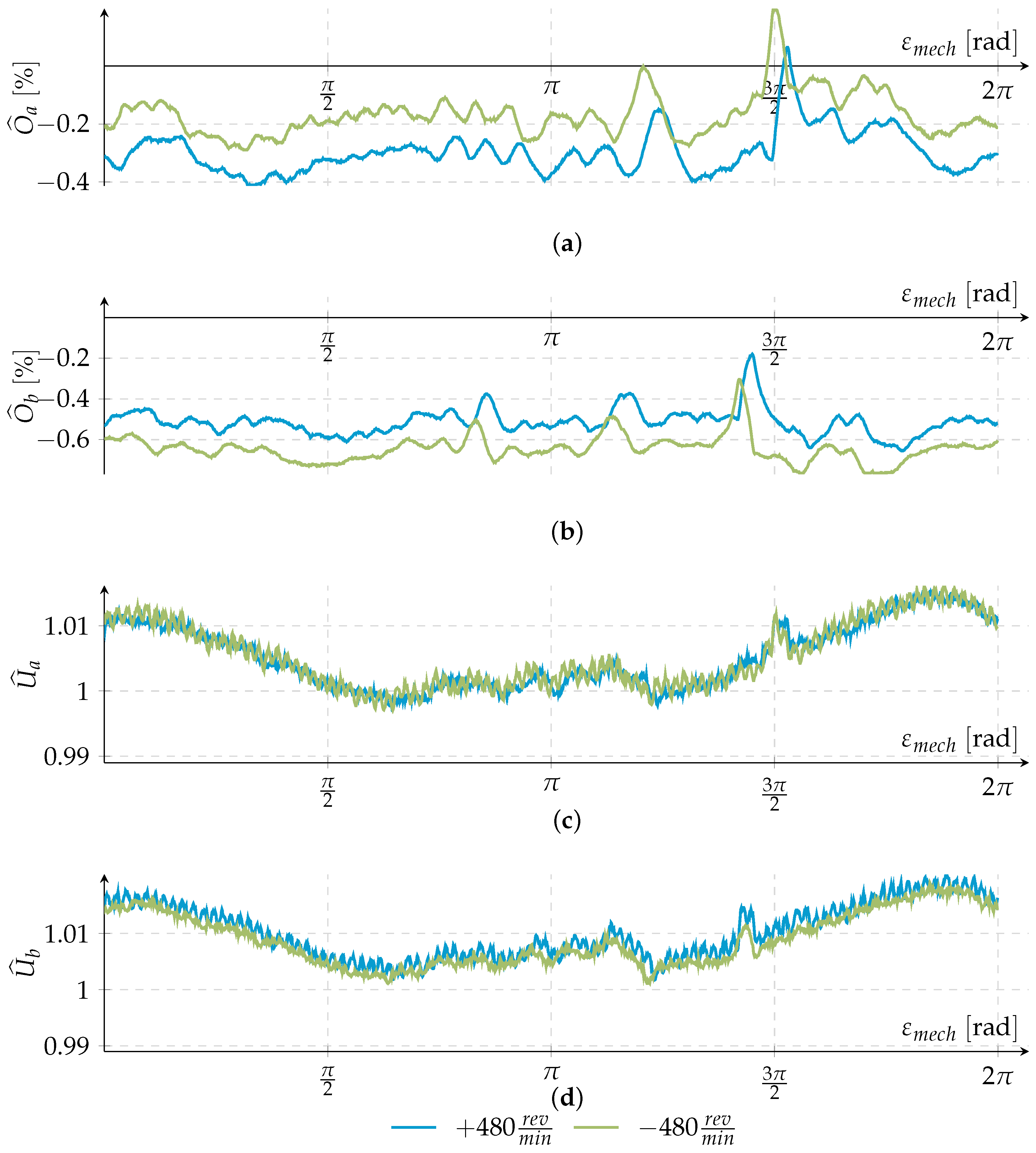
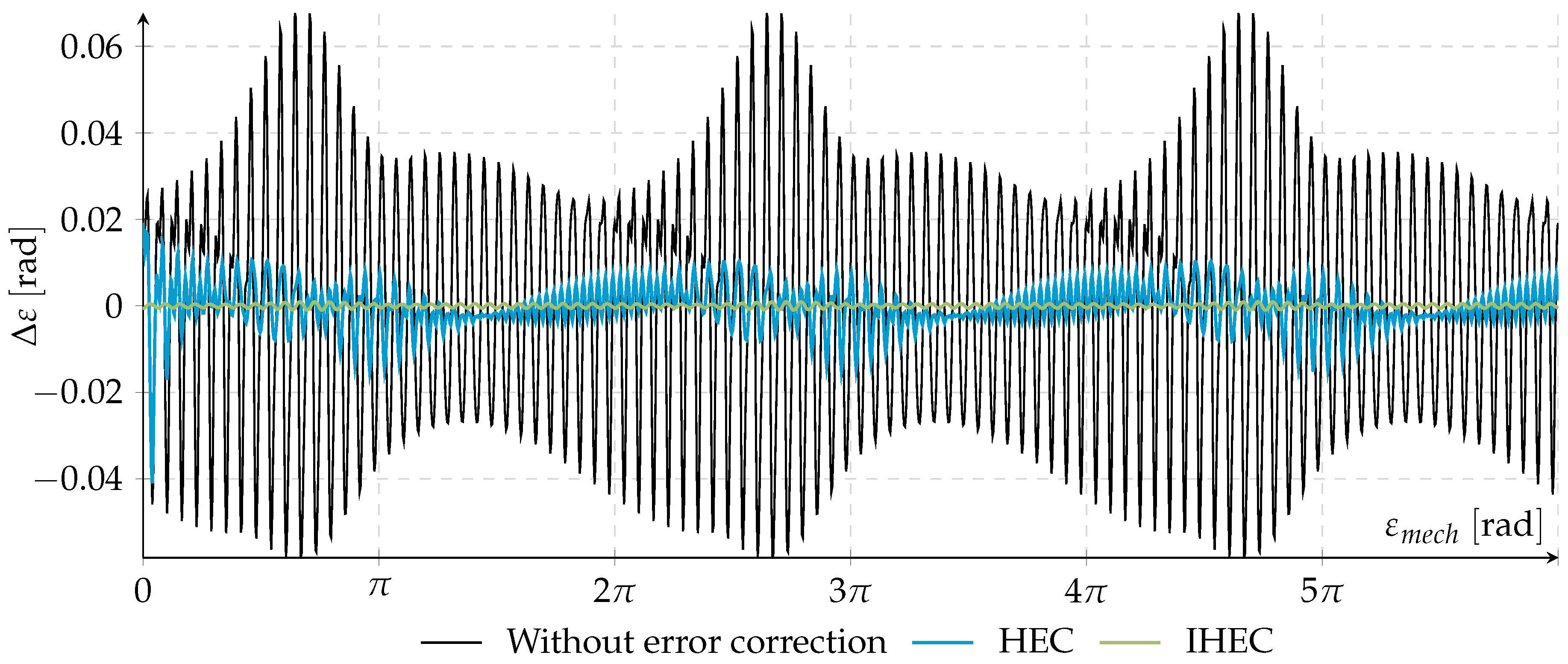
) the same by IHEC, which is depicted after six iterations. As described in Section 4.1, the courses of the IHEC increase ramp-shaped at the right and left end of the estimation, but in the center part of the graphic, the curves track the chosen parameter course. Moreover, it must be noted that this performance is achieved after just a few iterations. ) shows the angle difference, if the angle is determined without correcting the erroneous line signals. The blue (
) shows the angle difference, if the angle is determined without correcting the erroneous line signals. The blue (  ) and the green line (
) and the green line (  ) show the difference if the HEC and the IHEC is applied. The improvement by the two correction methods is obvious. The IHEC provides the best compensation at the price, and several revolutions are needed to adapt to the error course.
) show the difference if the HEC and the IHEC is applied. The improvement by the two correction methods is obvious. The IHEC provides the best compensation at the price, and several revolutions are needed to adapt to the error course.5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| HEC | Harmonic Error Correction |
| IHEC | Iterative Harmonic Error Correction |
| ENDAT | Digital encoder communications protocol, proprietary Dr. Johannes Heidenhain GmbH |
| HIPERFACE® | Digital encoder communications protocol, proprietary SICK STEGMANN GmbH |
| BiSS | Open digital encoder communications protocol, iC-Haus GmbH |
| FPGA | Field Programmable Gate Array |
| HANN | Harmonic Activated Neural Network |
References
- EnDat 2.2—Bidirektionales Interface für Positionsmessgeräte. Technische Information company brochure from Dr. Johannes Heidenhain GmbH. Available online: http://www.endat.de (accessed on 19 December 2016).
- Specification Hiperface®: Motor Feedback Protocol. Company brochure from Sick Stegmann GmbH. Available online: https://www.sick.com (accessed on 19 December 2016).
- BiSS Interface. Protocol Description (C-Mode). Available online: http://biss-interface.com (accessed on 8 December 2016).
- Hwang, S.; Kim, D.; Kim, J.; Jang, D. Signal Compensation for Analog Rotor Position Errors due to Nonideal Sinusoidal Encoder Signals. J. Power Electron. 2014, 14, 82–91. [Google Scholar] [CrossRef]
- Gröling, C. Systematische Abweichungen auf dem Winkelistwert. Optimierungspotential bei Servoumrichtern für Permanenterregte Synchronmaschinen. Ph.D. Thesis, TU Braunschweig, Braunschweig, Germany, 2009; pp. 82–85. [Google Scholar]
- Höschler, B.; Számel, L. Innovative technique for easy high-resolution position acquisition with sinusoidal incremental encoders. In Proceedings of the PCIM Power Conversion & Intelligent Motion Conference, Nürnberg, Germany, 10–12 June 1997; pp. 407–415.
- Peterson, R. Quadrature Error Correction. U.S. Patent 5,134,404, 28 July 1992. [Google Scholar]
- Tan, K.; Tang, K. Adaptive Online Correction and Interpolation of Quadrature Encoder Signals Using Radial Basis Function. IEEE Trans. Control Syst. Technol. 2005, 13, 370–377. [Google Scholar]
- Kirchberger, R.; Hiller, B. Oversamplingverfahren zur Verbesserung der Erfassung von Lage und Drehzahl an elektrischen Antrieben mit inkrementellen Gebersystemen. In Proceedings of the SPS/IPC/Drives, Nürnberg, Germany, 23–25 November 1999; pp. 598–606.
- Daaboul, Y.; Schumacher, W. High-performance position evaluation for high speed drives via systematic error correction methods of optical encoders. In Proceedings of the 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013.
- Bünte, A.; Beineke, S. High-Performance Speed Measurement by Suppression of Systematic Resolver and Encoder Errors. IEEE Trans. Ind. Electron. 2004, 51, 49–53. [Google Scholar] [CrossRef]
- Tan, K.; Zhou, H.; Lee, T. New Interpolation Method for Quadrature Encoder Signals. IEEE Trans. Instrum. Meas. 2002, 51, 1073–1079. [Google Scholar] [CrossRef]
- Schröder, D. Harmonisch Aktiviertes Neuronales Netz (HANN). In Intelligente Verfahren; Springer: Berlin, Germany, 2010; pp. 58–60. [Google Scholar]
- Adamy, J. Die Stabilitätstheorie von Ljapunov. In Nichtlineare Regelungstechnik; Springer: Berlin, Germany, 2009; pp. 95–99. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albrecht, C.; Klöck, J.; Martens, O.; Schumacher, W. Online Estimation and Correction of Systematic Encoder Line Errors. Machines 2017, 5, 1. https://doi.org/10.3390/machines5010001
Albrecht C, Klöck J, Martens O, Schumacher W. Online Estimation and Correction of Systematic Encoder Line Errors. Machines. 2017; 5(1):1. https://doi.org/10.3390/machines5010001
Chicago/Turabian StyleAlbrecht, Carla, Jan Klöck, Onno Martens, and Walter Schumacher. 2017. "Online Estimation and Correction of Systematic Encoder Line Errors" Machines 5, no. 1: 1. https://doi.org/10.3390/machines5010001




