Modal Coupling in Presence of Dry Friction
Abstract
:1. Introduction
1.1. Automotive Brake Squeal
1.2. Modal Coupling Effects on Brake Squeal
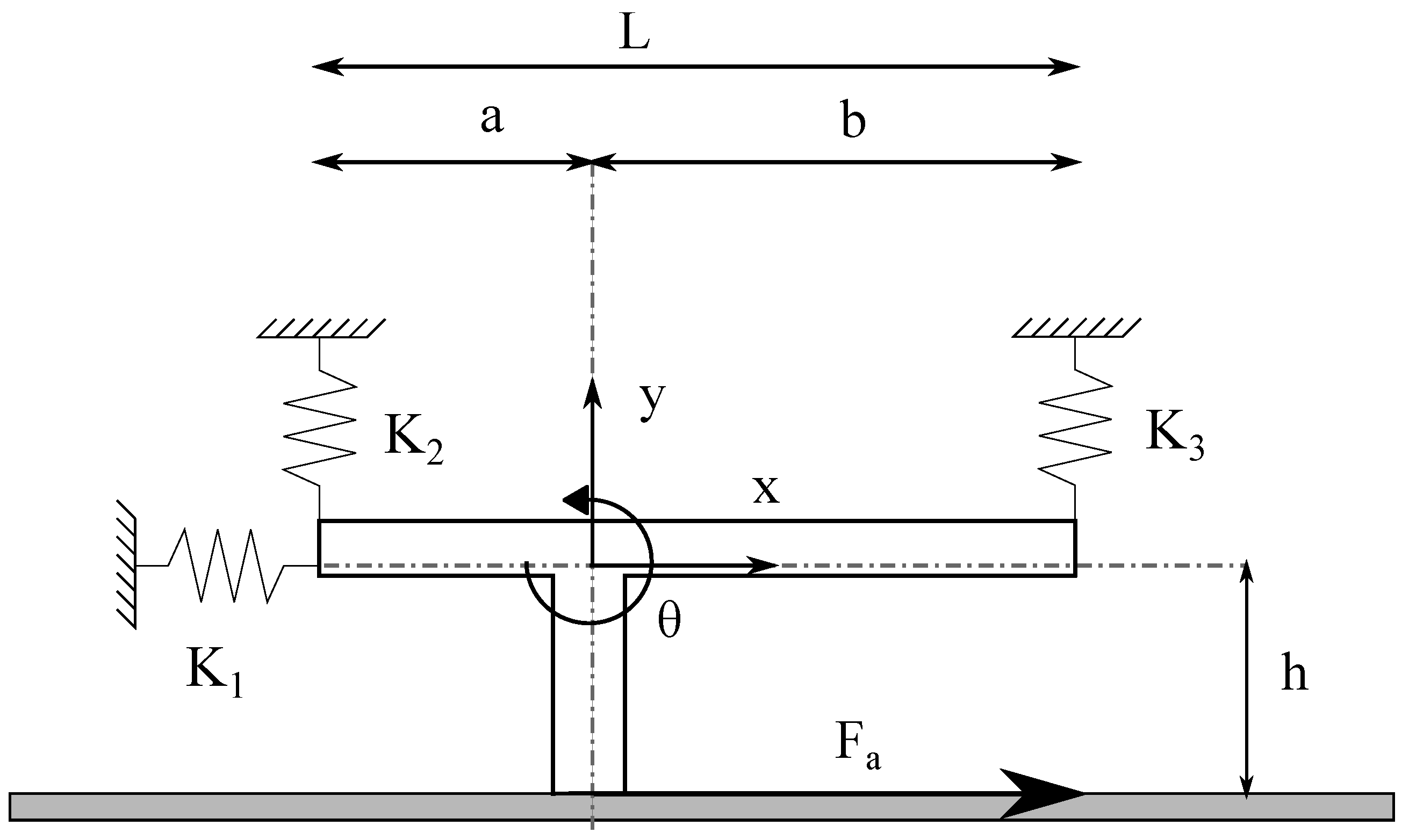
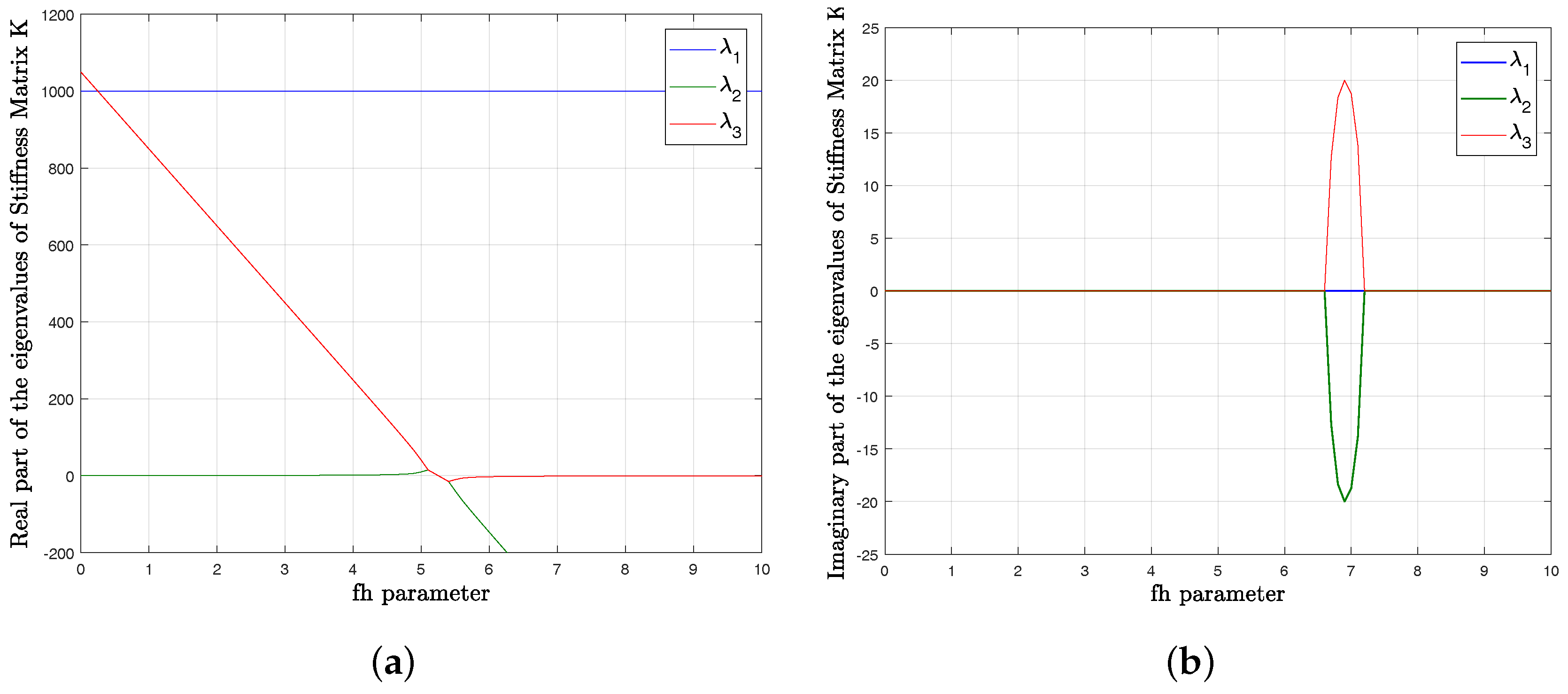
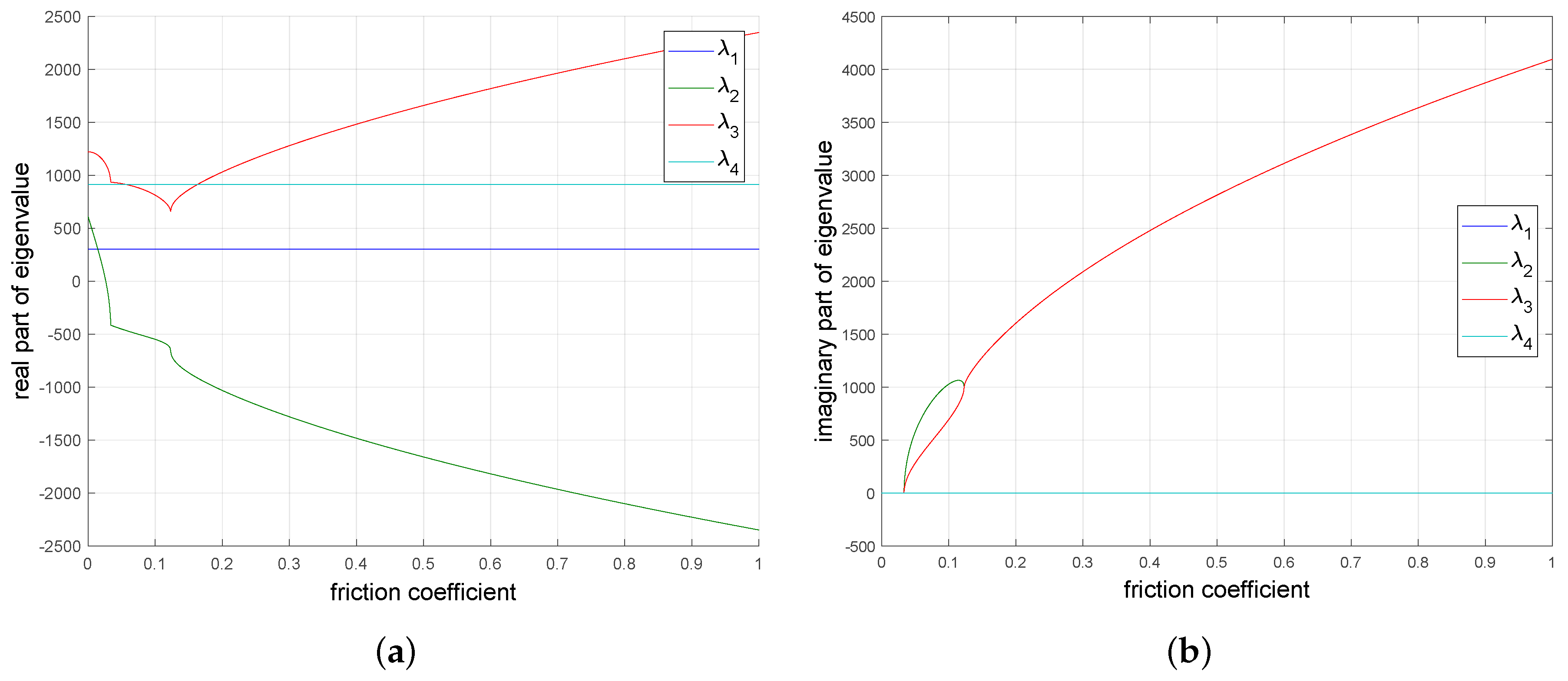
2. Discrete Model Behavior in the Presence of Dry Friction
3. Continuous Model Behavior in the Presence of Dry Friction
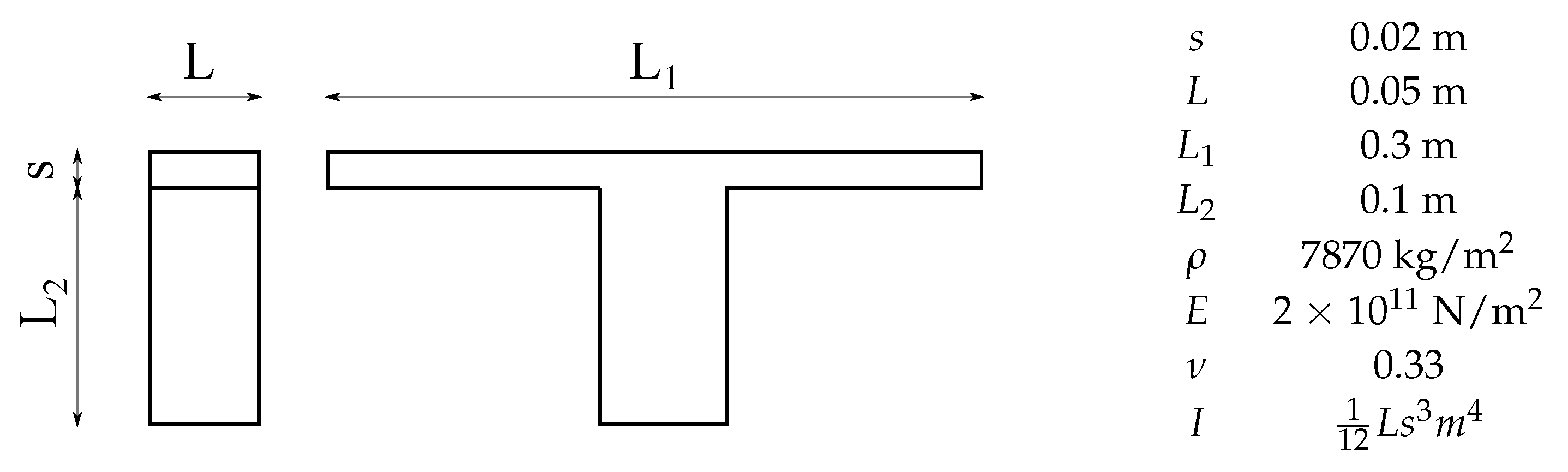
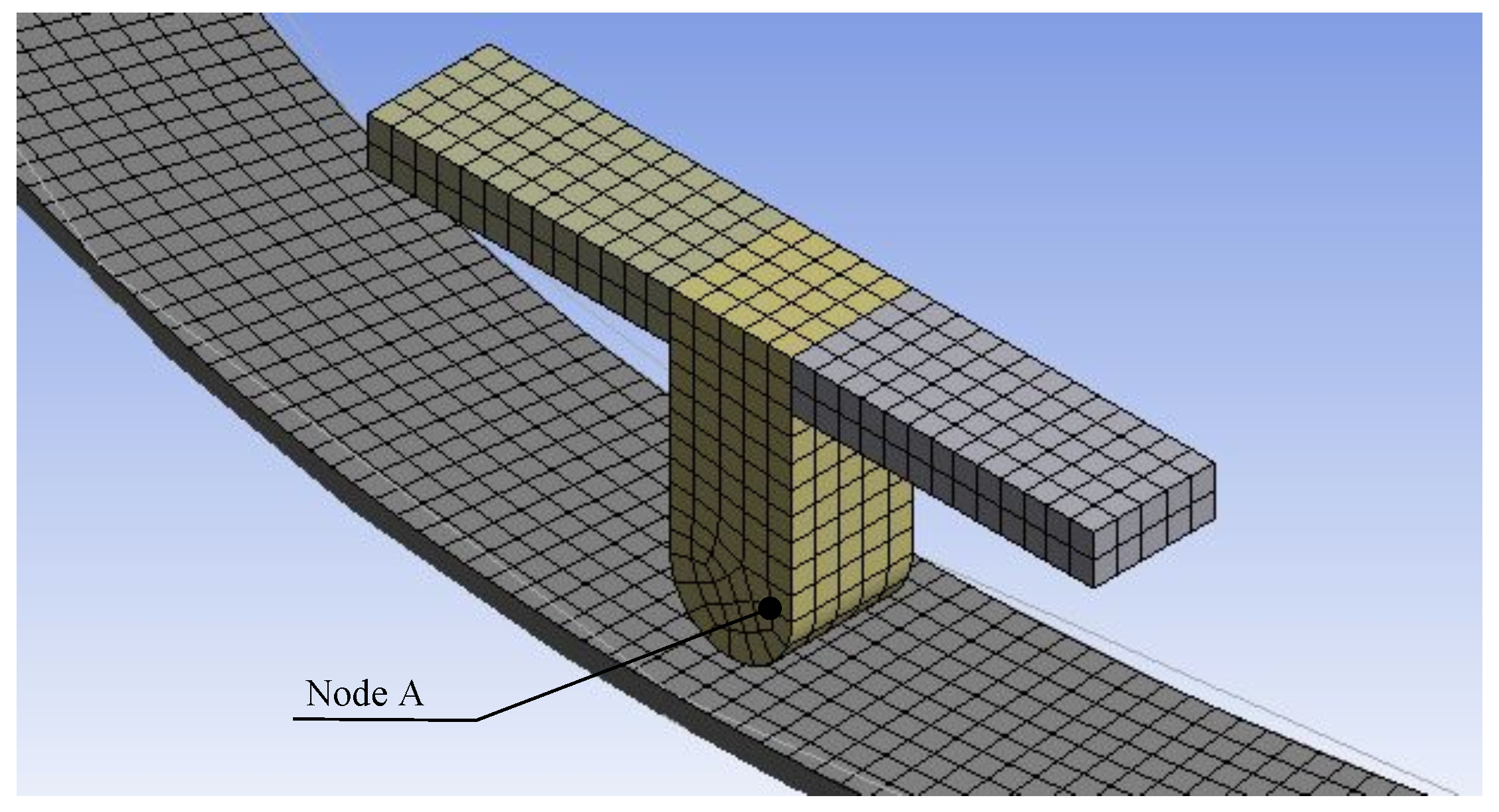
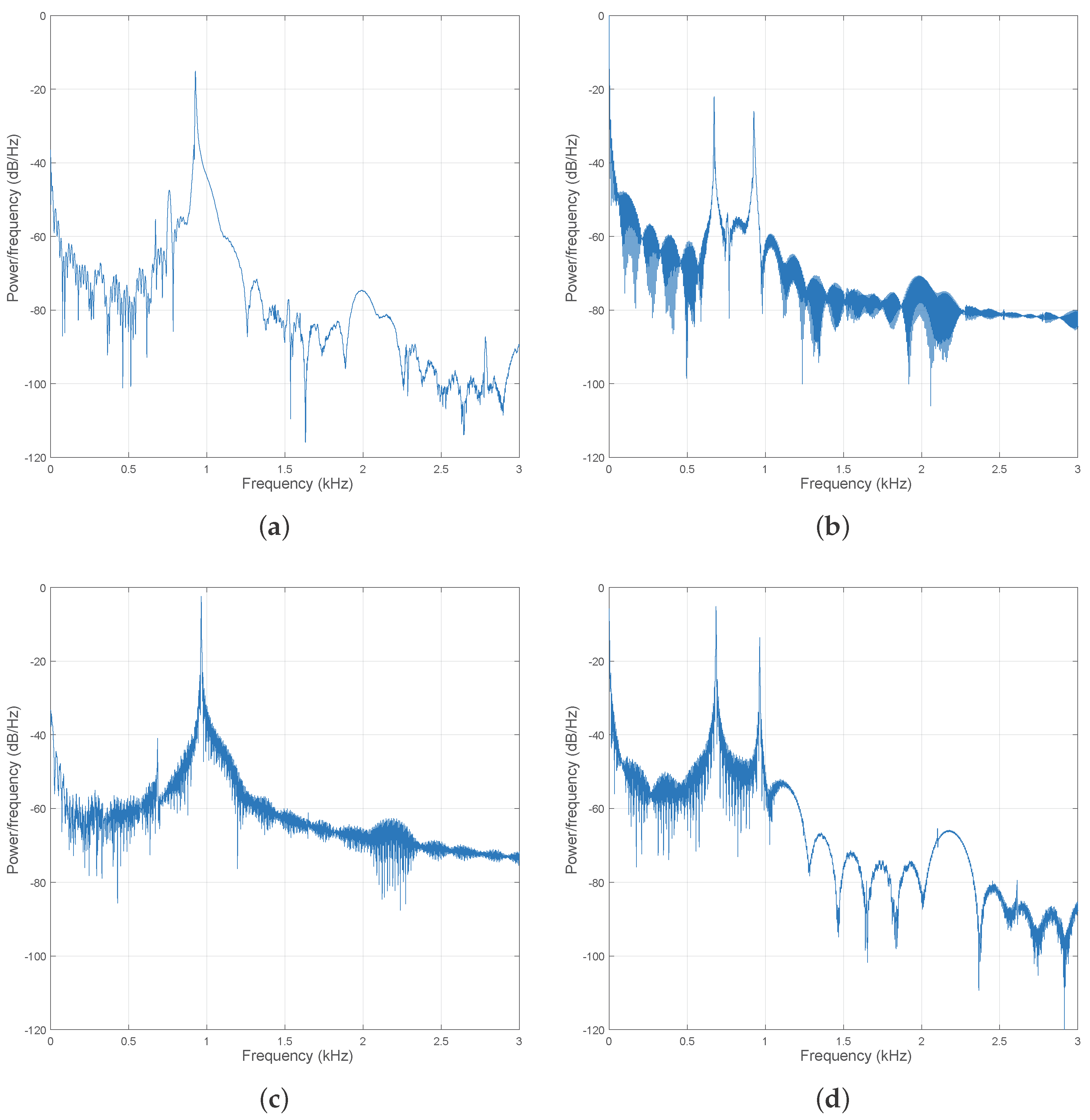
4. Analysis of the Finite Element Model
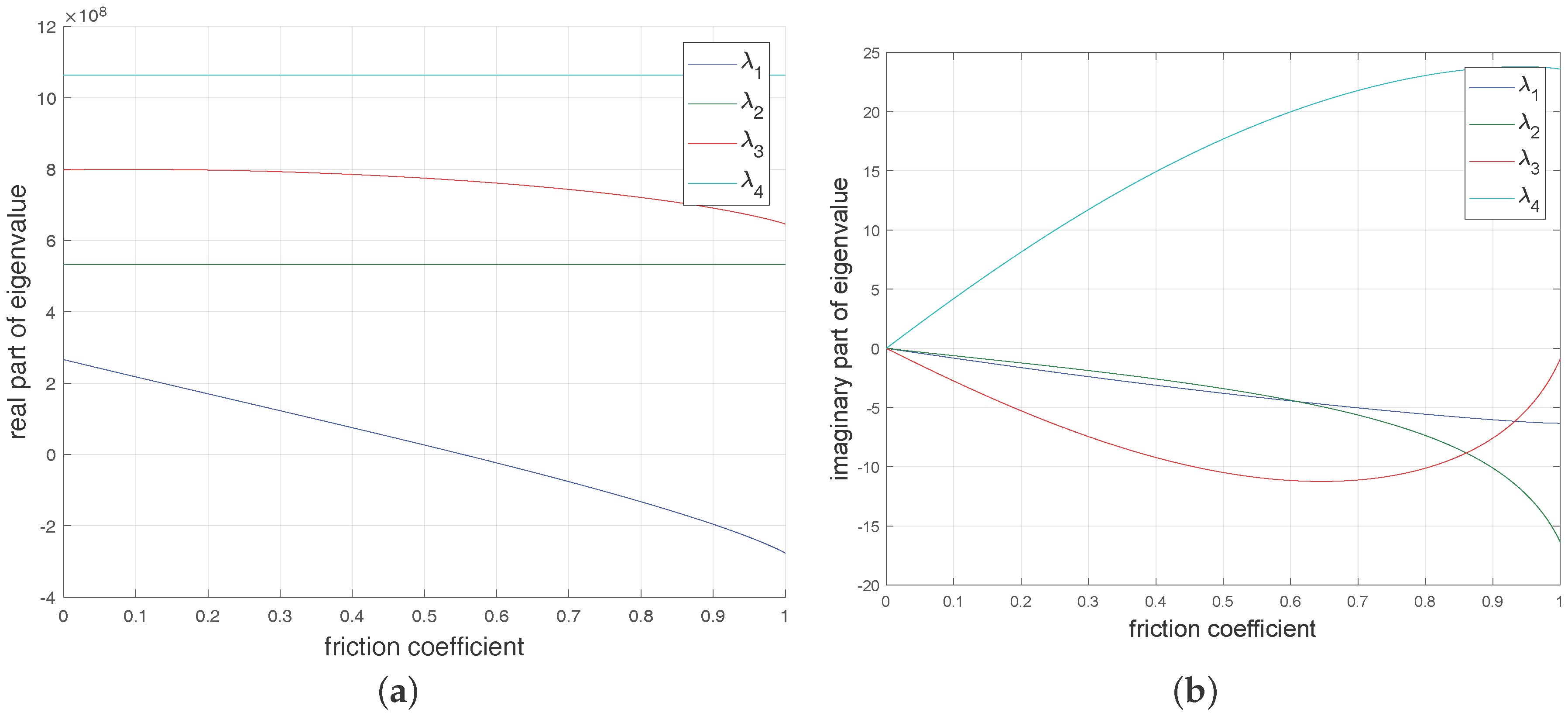
4.1. Modal Analysis
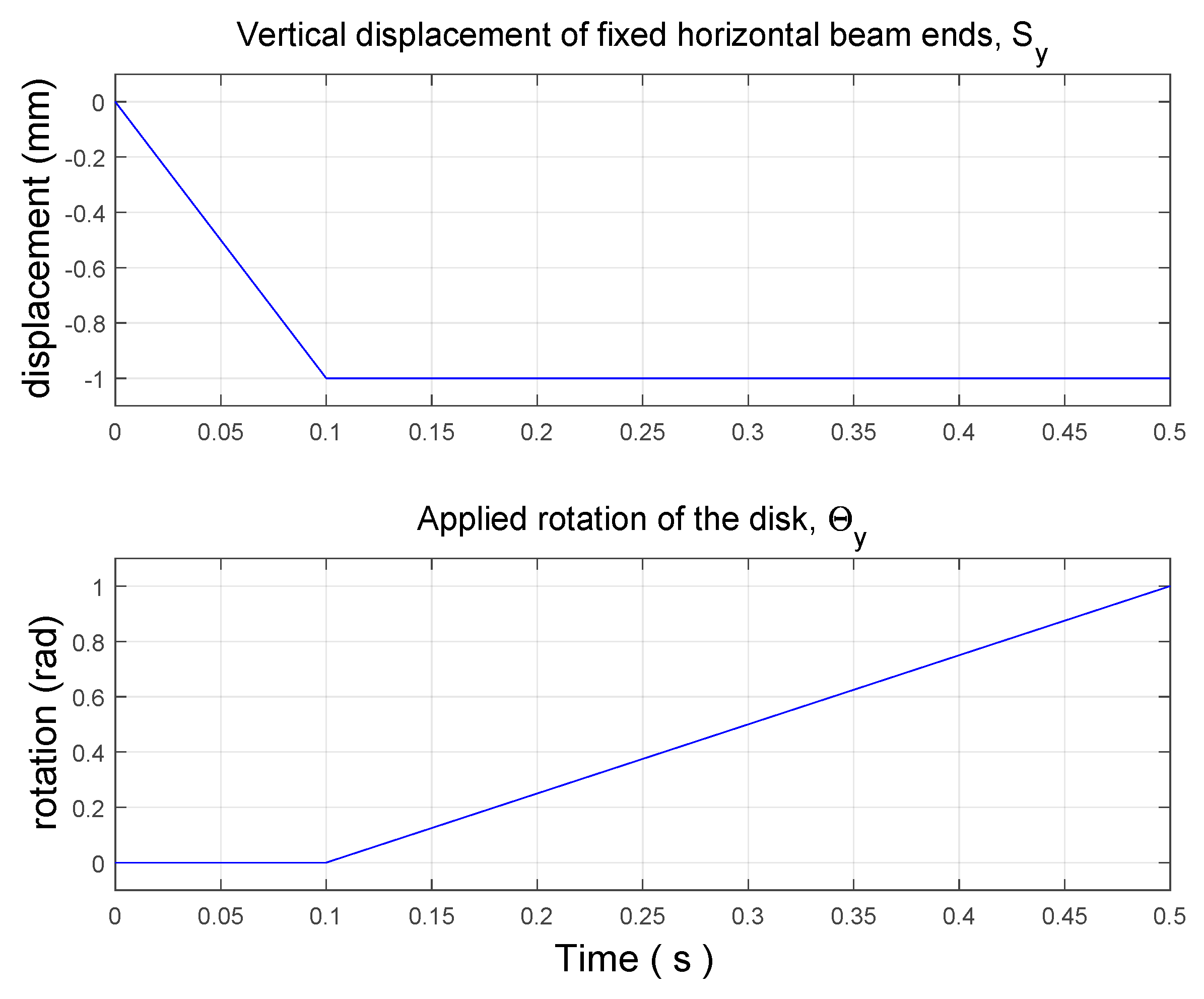
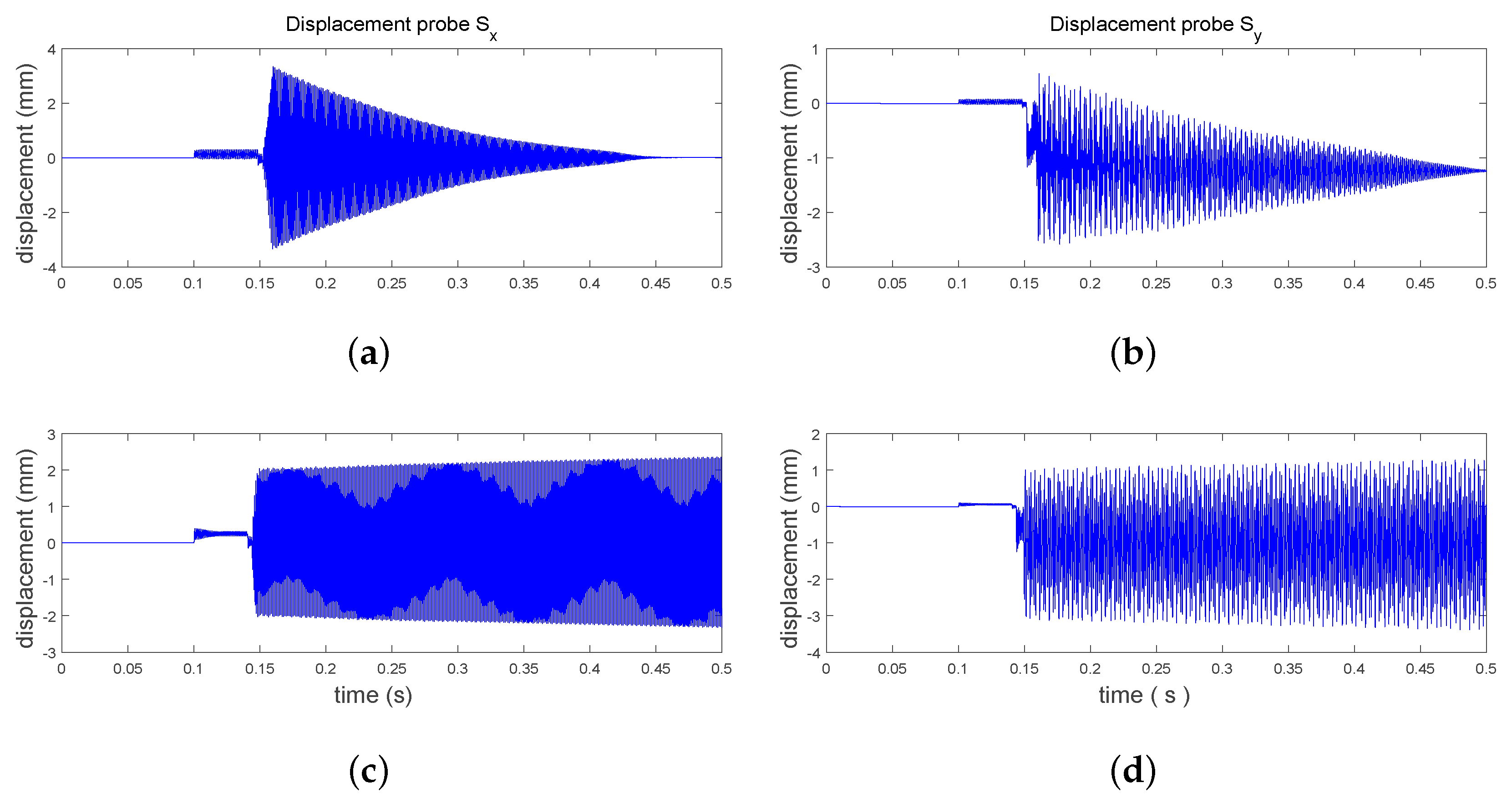
4.2. Transient Analysis
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Kinkaid, N.M.; O’Reilly, O.M.; Papadopoulos, P. Automotive disc brake squeal. J. Sound Vib. 2008, 267, 105–166. [Google Scholar] [CrossRef]
- Budinsky, T.; Brooks, P.; Barton, D. The influence of disc geometry on the center of pressure and squeal propensity for an automotive disc brake. In Proceedings of the EuroBrake 2017 Conference, Dresden, Germany, 2–4 May 2017. [Google Scholar]
- Sriwiboon, M.; Tiempan, N.; Kaewlob, K.; Rhee, S.K.; Yuhas, D. Disc Pad Physical Properties vs. Porosity: The Question of Compressibility as an Intrinsic Physical Property. SAE Inte. J. Mater. Manuf. 2017, 11. [Google Scholar] [CrossRef]
- Jeong, B.; Kwak, S.D.; Kim, C.K. Optimization for Brake Feeling in Vehicle without Brake Noise; SAE Technical Papers: Warrendale, PA, USA, 2016. [Google Scholar]
- Kanehira, Y.; Aoki, Y.; Nishizawa, Y. Evaluation of an Energy Dissipation Mechanism by Friction for Brake Shims; SAE Technical Papers: Warrendale, PA, USA, 2017. [Google Scholar]
- Festjens, H.; Gaël, C.; Franck, R.; Jean-Luc, D.; Remy, L. Effectiveness of multilayer viscoelastic insulators to prevent occurrences of brake squeal: A numerical study. Appl. Acoust. 2012, 73, 1121–1128. [Google Scholar] [CrossRef]
- Fulco, E.R.; Tonet, G.; Matozo, L.T.; Varante, P.E.D. Influence of the Shim Contact Stiffness on Disc Brakes Squeal Noise; SAE Technical Papers: Warrendale, PA, USA, 2013. [Google Scholar]
- Spelsberg-Korspeter, G. Eigenvalue optimization against brake squeal: Symmetry, mathematical background and experiments. J. Sound Vib. 2012, 331, 4259–4268. [Google Scholar] [CrossRef]
- Lakkam, S.; Koetniyom, S. Optimization of constrained layer damping for strain energy minimization of vibrating pads. Songklanakarin J. Sci. Technol. 2012, 34, 179–187. [Google Scholar]
- Esgandari, M.; Olatunbosun, O. Computer aided engineering prediction of brake noise: Modeling of brake shims. J. Vibr. Control 2016, 22, 2347–2355. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z.; Gao, J.; Hong, J.; Villecco, F.; Li, Y. A method for designing assembly tolerance networks of mechanical assemblies. Math. Probl. Eng. 2012. [Google Scholar] [CrossRef]
- Pellegrino, A.; Villecco, F. Design Optimization of a Natural Gas Substation with Intensification of the Energy Cycle. Math. Probl. Eng. 2010. [Google Scholar] [CrossRef]
- Formato, A.; Ianniello, D.; Villecco, F.; Lenza, T.L.L.; Guida, D. Design optimization of the plough working surface by computerized mathematical model. Emir. J. Food Agric. 2017, 29, 36–44. [Google Scholar] [CrossRef]
- Villecco, F.; Pellegrino, A. Entropic measure of epistemic uncertainties in multibody system models by axiomatic design. Entropy 2017, 19, 291. [Google Scholar] [CrossRef]
- Bonnay, K.; Magnier, V.; Brunel, J.F.; Dufrénoy, P.; De Saxcé, G. Influence of geometry imperfections on squeal noise linked to mode lock-in. Inter. J. Sol. Struct. 2015, 75, 99–108. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.-H.; Fang, J.; Zhao, W.-Z. Research on squeal noise of tread brake system in rail freight vehicle. IOP Conf. Ser. Mater. Sci. Eng. 2017, 220. [Google Scholar] [CrossRef]
- Zainudin, M.A.; Abu Bakar, A.R. Preventing disc brake squeal using a thin plate shim. Int. J. Veh. Struct. Syst. 2012, 4, 23–27. [Google Scholar]
- Shimizu, H.; Oura, Y.; Suzuki, T.; Sano, Y. The Effect of Grease on Brake Squeal; SAE Technical Papers: Warrendale, PA, USA, 2014. [Google Scholar]
- Wagner, A.; Spelsberg-Korspeter, G.; Hagedorn, P. Structural optimization of an asymmetric automotive brake disc with cooling channels to avoid squeal. J. Sound Vib. 2014, 333, 1888–1898. [Google Scholar] [CrossRef]
- Lv, H.-M.; Zhang, L.-J.; Yu, Z.-P. Influence of surface run-out on disc brake squeal. J. Vibroeng. 2013, 15, 520–531. [Google Scholar]
- Sriwiboon, L.; Wu, J.; Meng, D. Transient Analysis of a Flexible Pin-on-Disk System and Its Application to the Research into Time-Varying Squeal. J. Vib. Acoust. Trans. ASME 2018, 140. [Google Scholar] [CrossRef]
- Charroyer, L.; Chiello, O.; Sinou, J.-J. Parametric study of the mode coupling instability for a simple system with planar or rectilinear friction. J. Sound Vib. 2016, 384, 94–112. [Google Scholar] [CrossRef]
- Du, Y.; Wang, Y. Squeal analysis of a modal-parameter-based rotating disc brake model. Int. J. Mech. Sci. 2017, 131–132, 1049–1060. [Google Scholar] [CrossRef]
- Jaeyoung, K. Automotive brake squeal analysis with rotating finite elements of asymmetric disc in time. J. Sound Vib. 2017, 393, 388–400. [Google Scholar]
- De Simone, M.C.; Rivera, Z.B.; Guida, D. Finite Element Analysis on Squeal-Noise in Railway Applications. FME Trans. 2018, 46, 93–100. [Google Scholar]
- Pappalardo, C.M. A Natural Absolute Coordinate Formulation for the Kinematic and Dynamic Analysis of Rigid Multibody Systems. Nonlinear Dyn. 2015, 81, 1841–1869. [Google Scholar] [CrossRef]
- Kulkarni, S.; Pappalardo, C.M.; Shabana, A.A. Pantograph/Catenary Contact Formulations. ASME J. Vib. Acoust. 2017, 139, 1–12. [Google Scholar] [CrossRef]
- Guida, D.; Pappalardo, C.M. On the use of Two-dimensional Euler Parameters for the Dynamic Simulation of Planar Rigid Multibody Systems. Arch. Appl. Mech. 2017, 1–19. [Google Scholar] [CrossRef]
- Guida, D.; Pappalardo, C.M. Forward and Inverse Dynamics of Nonholonomic Mechanical Systems. Meccanica 2014, 49, 1547–1559. [Google Scholar] [CrossRef]
- Guida, D.; Nilvetti, F.; Pappalardo, C.M. Mass, Stiffness and Damping Identification of a Two-story Building Model. In Proceedings of the 3rd ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering (COMPDYN 2011), Corfu, Greece, 25–28 May 2011; pp. 25–28. [Google Scholar]
- Pappalardo, C.M.; Guida, D. Experimental Identification and Control of a Frame Structure using an Actively Controlled Inertial-based Vibration Absorber. In Proceedings of the International Conference on Control, Artificial Intelligence, Robotics and Optimization (ICCAIRO 2017), Prague, Czech Republic, 20–22 May 2017; pp. 99–104. [Google Scholar]
- Guida, D.; Nilvetti, F.; Pappalardo, C.M. On Parameter Identification of Linear Mechanical Systems. In Proceedings of the 3rd International Conference on Applied Mathematics, Simulation, Modelling, Circuits, Systems and Signals, (WSEAS), Vouliagmeni Beach, Athens, Greece, 29–31 December 2009; pp. 55–60. [Google Scholar]
- Guida, D.; Nilvetti, F.; Pappalardo, C.M. Parameter Identification of a Two Degrees of Freedom Mechanical System. Int. J. Mech. 2009, 3, 23–30. [Google Scholar]
- Guida, D.; Pappalardo, C.M. Sommerfeld and Mass Parameter Identification of Lubricated Journal Bearing. WSEAS Trans. Appl. Theor. Mech. 2009, 4, 205–214. [Google Scholar]
- Guida, D.; Nilvetti, F.; Pappalardo, C.M. Experimental Investigation on a New Hybrid Mass Damper. In Proceedings of the 8th International Conference on Structural Dynamics (EURODYN 2011), Leuven, Belgium, 4–6 July 2011; pp. 1644–1649. [Google Scholar]
- De Simone, M.C.; Guida, D. Dry Friction Influence on Structure Dynamics. In Proceedings of the 5th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering (COMPDYN 2015), Crete Island, Greece, 25–27 May 2015; pp. 4483–4491. [Google Scholar]
- Guida, D.; Nilvetti, F.; Pappalardo, C.M. Instability Induced by Dry Friction. Int. J. Mech. 2009, 3, 44–51. [Google Scholar]
- Guida, D.; Nilvetti, F.; Pappalardo, C.M. Dry Friction Influence on Cart Pendulum Dynamics. Int. J. Mech. 2009, 3, 31–38. [Google Scholar]
- Guida, D.; Nilvetti, F.; Pappalardo, C.M. Dry Friction Influence on Inverted Pendulum Control. In Proceedings of the 3rd International Conference on Applied Mathematics, Simulation, Modelling (ASM’09), Vouliagmeni Beach, Athens, Greece, 29–31 December 2009; pp. 49–54. [Google Scholar]
- Guida, D.; Nilvetti, F.; Pappalardo, C.M. Friction Induced Vibrations of a Two Degrees of Freedom System. In Proceedings of the 10th WSEAS International Conference on Robotics, Control and Manufacturing Technology (ROCOM ’10), Hangzhou, China, 11–13 April 2010; pp. 133–136. [Google Scholar]
- Ruggiero, A.; Affatato, S.; Merola, M.; De Simone, M.C. FEM analysis of metal on UHMWPE total hip prosthesis during normal walking cycle. In Proceedings of the XXIII Conference of the Italian Association of Theoretical and Applied Mechanics (AIMETA 2017), Salerno, Italy, 4–7 September 2017. [Google Scholar]
- Pappalardo, C.M.; Yu, Z.; Zhang, X.; Shabana, A.A. Rational ANCF Thin Plate Finite Element. ASME J. Comput. Nonlinear Dyn. 2016, 11, 1–15. [Google Scholar] [CrossRef]
- Pappalardo, C.M.; Wallin, M.; Shabana, A.A. A New ANCF/CRBF Fully Parametrized Plate Finite Element. ASME J. Comput. Nonlinear Dyn. 2017, 12, 1–13. [Google Scholar]
- Pappalardo, C.M.; Wang, T.; Shabana, A.A. Development of ANCF Tetrahedral Finite Elements for the Nonlinear Dynamics of Flexible Structures. Nonlinear Dyn. 2017, 89, 2905–2932. [Google Scholar] [CrossRef]
- Pappalardo, C.M.; Wang, T.; Shabana, A.A. On the Formulation of the Planar ANCF Triangular Finite Elements. Nonlinear Dyn. 2017, 89, 1019–1045. [Google Scholar] [CrossRef]
- De Simone, M.C.; Russo, S.; Rivera, Z.B.; Guida, D. Multibody Model of a UAV in Presence of Wind Fields. In Proceedings of the 2017 International Conference on Control, Artificial Intelligence, Robotics & Optimization (ICCAIRO), Prague, Czech Republic, 20–22 May 2017; pp. 83–88. [Google Scholar]
- De Simone, M.C.; Guida, D. Identification and Control of a Unmanned Ground Vehicle by Using Arduino. UPB Sci. Bull. Ser. D 2018. accepted. [Google Scholar]
- Concilio, A.; De Simone, M.C.; Rivera, Z.B.; Guida, D. A New Semi-Active Suspension System for Racing Vehicles. FME Transactions. 2017, 45, 565–571. [Google Scholar] [CrossRef]
- Sharifzadeh, M.; Timpone, F.; Farnam, A.; Senatore, A.; Akbari, A. Tyre-Road Adherence Conditions Estimation for Intelligent Vehicle Safety Applications. In Advances in Italian Mechanism Science; Springer: New York, NY, USA, 2017; pp. 389–398. [Google Scholar]
- Guida, D.; Nilvetti, F.; Pappalardo, C.M. Optimal Control Design by Adjoint-Based Optimization for Active Mass Damper with Dry Friction. In Proceedings of the 4th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering COMPDYN 2013, Kos Island, Greece, 12–14 June 2013; pp. 1–19. [Google Scholar]
- Pappalardo, C.M.; Patel, M.D.; Tinsley, B.; Shabana, A.A. Contact Force Control in Multibody Pantograph/ Catenary Systems. Proc. Inst. Mech. Eng. Part K J. Multibody Dyn. 2016, 230, 307–328. [Google Scholar] [CrossRef]
- Pappalardo, C.M.; Patel, M.D.; Tinsley, B.; Shabana, A.A. Pantograph/Catenary Contact Force Control. In Proceedings of the ASME 2015 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference IDETC/CIE 2015, Boston, MA, USA, 2–5 August 2015. [Google Scholar]
- Pappalardo, C.M.; Guida, D. Adjoint-based Optimization Procedure for Active Vibration Control of Nonlinear Mechanical Systems. ASME J. Dyn. Syst. Meas. Control 2017, 139, 1–11. [Google Scholar] [CrossRef]
- Pappalardo, C.M.; Guida, D. Control of Nonlinear Vibrations using the Adjoint Method. Meccanica 2017, 52, 2503–2526. [Google Scholar] [CrossRef]
- Quatrano, A.; De Simone, M.C.; Rivera, Z.B.; Guida, D. Development and Implementation of a Control System for a retrofitted CNC Machine by using Arduino. FME Trans. 2017, 45, 578–584. [Google Scholar] [CrossRef]
- Guida, D.; Pappalardo, C.M. Control Design of an Active Suspension System for a Quarter-Car Model with Hysteresis. J. Vib. Eng. Technol. 2015, 3, 277–299. [Google Scholar]
- Guida, D.; Pappalardo, C.M. A New Control Algorithm for Active Suspension Systems Featuring Hysteresis. FME Trans. 2013, 41, 285–290. [Google Scholar]
- Guida, D.; Nilvetti, F.; Pappalardo, C.M. Adjoint-based Optimal Control Design for a Cart Pendulum System with Dry Friction. In Proceedings of the ECCOMAS Thematic Conference on Multibody Dynamics, Zagreb, Croatia, 1–4 July 2013; pp. 269–285. [Google Scholar]
- De Simone, M.C.; Guida, D. On the Development of a Low Cost Device for Retrofitting Tracked Vehicles for Autonomous Navigation. In Proceedings of the XXIII Conference of the Italian Association of Theoretical and Applied Mechanics (AIMETA 2017), Salerno, Italy, 4–7 September 2017. [Google Scholar]
- Ruggiero, A.; De Simone, M.C.; Russo, D.; Guida, D. Sound pressure measurement of orchestral instruments in the concert hall of a public school. Int. J. Circuits Syst. Signal Process. 2016, 10, 75–812. [Google Scholar]

| = 0.01 | −5.3 | −6.9 | −10.3 | −20.9 | 505.2 |
| = 1 | −10.2 | −20.2 | ⋯ | 20.3 | 10.2 |
| = 100 | −505.2 | 20.9 | 10.3 | 6.9 | 5.3 |
| Stable Case () | Unstable Case () | |||
|---|---|---|---|---|
| Mode | Frequency (Hz) | Stability | Frequency (Hz) | Stability |
| 1 | 1080.4 | 0 | 1080.4 | 0 |
| 2 | 1572 | 0 | 1574.8 | 0 |
| 3 | 2729.5 | 0 | 2729.7 | 0 |
| 4 | 4390,7 | 0 | 4389.8 | 0 |
| 5 | 4582.7 | 0 | 4582.6 | 0 |
| 6 | 4745.9 | 0 | 4747.2 | 0 |
| 7 | 6618.8 | 0 | 6624.9 | 12.684 |
| 8 | 6631.9 | 0 | 6624.9 | −12.684 |
| 9 | 7536.5 | 0 | 7536.5 | 0 |
| 10 | 7943.2 | 0 | 7943.1 | 0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Simone, M.C.; Guida, D. Modal Coupling in Presence of Dry Friction. Machines 2018, 6, 8. https://doi.org/10.3390/machines6010008
De Simone MC, Guida D. Modal Coupling in Presence of Dry Friction. Machines. 2018; 6(1):8. https://doi.org/10.3390/machines6010008
Chicago/Turabian StyleDe Simone, Marco Claudio, and Domenico Guida. 2018. "Modal Coupling in Presence of Dry Friction" Machines 6, no. 1: 8. https://doi.org/10.3390/machines6010008






