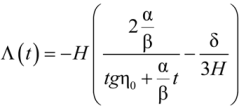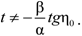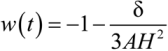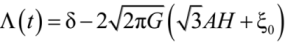Rip Cosmology via Inhomogeneous Fluid
Abstract
:1. Introduction
2. Dark Fluid Inhomogeneous Equation of State in the Some Cosmological Models
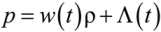
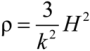
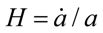 is the Hubble parameter, a(t) is the scale factor, k2 = 8πG with Newton’s gravitational constant G.
is the Hubble parameter, a(t) is the scale factor, k2 = 8πG with Newton’s gravitational constant G.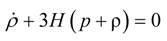
2.1. The Little Rip Case
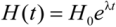
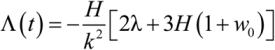
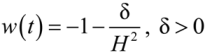
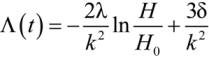
2.2. The Pseudo Rip Case
 the Hubble ratio tends to a constant value H0 and the universe asymptotically approaches the de Sitter space. It may correspond to a PR model.
the Hubble ratio tends to a constant value H0 and the universe asymptotically approaches the de Sitter space. It may correspond to a PR model.
 is the dimensionless parameter,
is the dimensionless parameter, 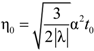 , where t0 is the present time and λ is a negative tension (λ < 0). If
, where t0 is the present time and λ is a negative tension (λ < 0). If 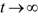 , then the Hubble parameter.
, then the Hubble parameter. 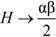 This situation corresponds to the universe expands in a quasi-de Sitter regime.
This situation corresponds to the universe expands in a quasi-de Sitter regime.2.3. The Quasi Rip Case
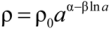
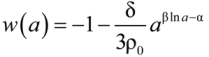
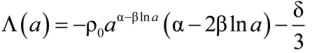
3. Examples of the Viscous Little Rip Cosmology
3.1. Dark Fluid with Bulk Viscosity
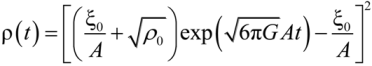
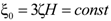 , where ζ is the bulk viscosity and A is a positive constant. Now we consider the viscous LR cosmology from the point of view of 4d FRW non-viscous cosmology, analogous to Section 2.
, where ζ is the bulk viscosity and A is a positive constant. Now we consider the viscous LR cosmology from the point of view of 4d FRW non-viscous cosmology, analogous to Section 2.3.2. The Turbulent Description
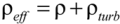
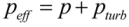
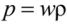
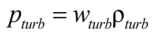
4. Conclusions
Acknowledgements
Conflict of Interest
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of omega and lambda from 42 high-redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Bamba, K.; Capozzielo, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to lorentz non-invariant models. Phys. Rept. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Kamionkowski, M.; Weinberg, N.N. Phantom energy and cosmic doomsday. Phys. Rev. Lett. 2003, 91, 071301:1–071301:4. [Google Scholar]
- Nojiri, S.; Odintsov, S.D. Introduction to modified gravity and gravitational alternative for dark energy. Int. J. Geom. Methods Mod. Phys. 2007, 4, 115–145. [Google Scholar] [CrossRef]
- Frampton, H.F.; Ludwick, K.J.; Scherrer, R.J. The little rip. Phys. Rev. D 2011, 84, 063003:1–063003:5. [Google Scholar]
- Brevik, I.; Elizalde, E.; Nojiri, S.; Odintsov, S.D. Viscous little rip cosmology. Phys. Rev. D 2011, 84, 103508:1–103508:6. [Google Scholar]
- Frampton, P.H.; Ludwick, K.J.; Nojiri, S.; Odintsov, S.D.; Scherrer, R.J. Models for little rip dark energy. Phys. Lett. B 2012, 708, 204–211. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Nojiri, S.; Odintsov, S.D.; Yurov, A.V. Phantom cosmology without big rip singularity. Phys. Lett. B 2012, 709, 396–403. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Nojiri, S.; Odintsov, S.D.; Scherrer, R.J. Scalar dark energy models mimicking ΛCDM with arbitrary future evolution. Phys. Lett. B 2012, 713, 145–153. [Google Scholar] [CrossRef]
- stashenok, A.V.; Elizalde, E.; Odintsov, S.D.; Yurov, A.V. Equation-of-State formalism for dark energy models on the brane and the future of brane universes. Eur. Phys. J. C 2012, 72, 2260:1–2260:10. [Google Scholar]
- Nojiri, S.; Odintsov, S.D.; Saez-Gomez, D. Cyclic, ekpyrotic and little rip universe in modified gravity. ArXiv E-Prints 2012. arXiv:1108.0767. [Google Scholar]
- Makarenko, A.N.; Obukhov, V.V.; Kirnos, I.V. From big to little rip in modified F(R, G) gravity. 2013, 343, 481–488. [Google Scholar]
- Frampton, P.H.; Ludwick, K.J.; Scherrer, R.J. Pseudo-rip: Cosmological models intermediate between the cosmological constant and the little rip. Phys. Rev. D 2012, 85, 083001:1–083001:5. [Google Scholar]
- Wei, H.; Wang, L.F.; Guo, X.J. Quasi-rip: A new type of rip model without cosmic doomsday. Phys. Rev. D 2012, 86, 083003:1–083003:7. [Google Scholar]
- Nojiri, S.; Odintsov, S.D. Inhomogeneous equation of state of the universe: Phantom era, future singularity and crossing the phantom barrier. Phys. Rev. D 2005, 72, 023003:1–023003:12. [Google Scholar]
- Brevik, I.; Obukhov, V.V.; Osetrin, K.E.; Timoshkin, A.V. Little rip cosmological models with time-dependent equation of state. Mod. Phys. Lett. A 2012, 27, 1250210:1–1250210:8. [Google Scholar]
- Brevik, I.; Obukhov, V.V.; Timoshkin, A.V.; Rabochaya, Y. Rip brane cosmology from 4d inhomogeneous dark fluid universe. Astrophys. Space Sci. 2013, 346, 267–271. [Google Scholar] [CrossRef]
- Brevik, I.; Obukhov, V.V.; Timoshkin, A.V. Quasi-Rip and Pseudo-Rip universes induced by the fluid inhomogeneous equation of state. Astrophys. Space Sci. 2013, 344, 275–279. [Google Scholar]
- Brevik, I.; Myrzakulov, R.; Nojiri, S.; Odintsov, S.D. Turbulence and little rip cosmology. Phys. Rev. D 2012, 86, 063007:1–063007:8. [Google Scholar]
- Brevik, I.; Timoshkin, A.V.; Rabochaya, Y.; Zerbini, S. Turbulence accelerating cosmology from an inhomogeneous dark fluid. Astrophys. Space Sci. 2013, 347, 203–208. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Obukhov, V.V.; Timoshkin, A.V.; Savushkin, E.V. Rip Cosmology via Inhomogeneous Fluid. Galaxies 2013, 1, 107-113. https://doi.org/10.3390/galaxies1020107
Obukhov VV, Timoshkin AV, Savushkin EV. Rip Cosmology via Inhomogeneous Fluid. Galaxies. 2013; 1(2):107-113. https://doi.org/10.3390/galaxies1020107
Chicago/Turabian StyleObukhov, Valerii V., Alexander V. Timoshkin, and Evgenii V. Savushkin. 2013. "Rip Cosmology via Inhomogeneous Fluid" Galaxies 1, no. 2: 107-113. https://doi.org/10.3390/galaxies1020107