Constraints on Non-Standard Gravitomagnetism by the Anomalous Perihelion Precession of the Planets
Abstract
:1. Introduction
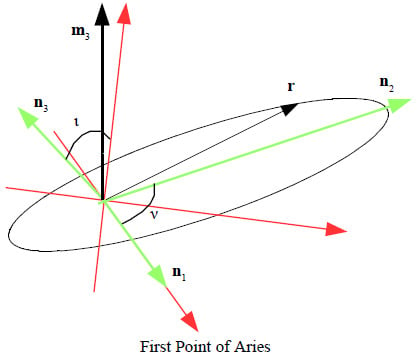
2. Definitions and Orbital Data

2.1. Components of the Perturbation Force
3. Results and Discussion
| Planet | a (km) | ϵ | ω | Ω | ι |
|---|---|---|---|---|---|
| Mercury | 57,909,100 | 0.205630 | 29.124° | 48.331° | 7.005° |
| Venus | 108,208,000 | 0.00677323 | 55.186° | 76.678° | 3.394° |
| Earth | 149,598,261 | 0.01671123 | 114.208° | −11.260° | 1.579° |
| Mars | 227,939,100 | 0.093315 | 286.537° | 49.562° | 1.850° |
| Jupiter | 778,547,200 | 0.048775 | 275.066° | 100.492° | 1.305° |
| Saturn | 1,433,449,370 | 0.055723219 | 336.014° | 113.643° | 2.485° |

3.1. Precession of the Longitude of the Ascending Node
| (n,m) | ercury | enus | arth | ars | upiter | aturn | β |
|---|---|---|---|---|---|---|---|
| (1,0) | 6.402 | −57.82 | −579.0 | 36.45 | −18.0 | −6.0 | −0.00061 |
| (2,0) | 6.63 | −61.44 | −522.96 | 37.968 | −19.2 | −6.0 | 0.00065 |
| (1,1) | 50.97 | −0.786 | −156.96 | −10.95 | 0.6 | −6.0 | −0.019 |
| (2,1) | 53.628 | −0.87 | −117.96 | −11.676 | 0.66 | −6.0 | 0.021 |
| (3,1) | 56.298 | −0.966 | −96.78 | −12. | −0.678 | −6.0 | 0.023 |
| (2,3) | 28.2 | −0.012 | −279. | −5.028 | 0.258 | −6.0 | 0.116 |
| (4,5) | 3.216 | −3.33 × 10−5 | −56.46 | −0.42 | 0.018 | −6.0 | 0.6824 |
| (4,5) | -0.0804 | 8.325 × 10−7 | 1.4115 | 0.0105 | −0.00045 | 0.15 | −0.017 |
| EPM2008 | −3.6 ± 5.0 | −0.4 ± 0.5 | −0.2 ± 0.4 | 0.1 ± 0.5 | - | −6 ± 2 | - |
| INPOP10a | 0.4 ± 0.6 | 0.2 ± 1.5 | −0.2 ± 0.9 | −0.04 ± 0.15 | −41 ± 42 | 0.15 ± 0.68 | - |
| EPM2011 | −2 ± 3 | 2.6 ± 1.6 | 0.19± 0.19 | −0.02± 0.037 | 58.7 ± 28.3 | −0.32 ± 0.47 | - |
| Parameters | ercury | enus | arth | ars | upiter | aturn |
|---|---|---|---|---|---|---|
| , | −0.970 | −0.025 | 0.0038 | −0.137 | −0.0093 | −0.0274 |
| , | 1.003 | 0.027 | −0.0039 | 0.147 | 0.0083 | 0.0274 |
| , | −0.811 | 0.000275 | 0.001375 | 0.2205 | −0.034 | 0.0087 |
| , | 0.849 | −0.0003 | −0.0009 | −0.228 | 0.0361 | −0.0086 |
| , | 0.885 | −0.0003 | −0.0007 | −0.236 | 0.0379 | −0.0083 |
| , | 0.509 | −7.1 × 10−6 | −0.0024 | −0.158 | 0.019 | −0.0108 |
| , | 0.347 | −1.8 × 10−7 | −0.0026 | −0.117 | 0.012 | −0.0123 |
| INPOP10a | 1.4 ± 1.8 | 0.2± 1.5 | 0.0± 0.9 | -0.05± 0.13 | −41 ± 43 | −0.1 ± 0.4 |
3.2. Contributions to the Gravity Probe B Experiment

4. Conclusions
Conflicts of Interest
References
- Will, C.M. The Confrontation between General Relativity and Experiment. Living Rev. Relativ. 2006, 9. [Google Scholar] [CrossRef]
- Williams, J.G.; Turyshev, S.G.; Boggs, D.H. The past and present Earth-Moon system: The speed of light stays steady as tides evolve. Planet. Sci. 2014, 3. [Google Scholar] [CrossRef]
- Iorio, L. On the anomalous secular increase of the eccentricity of the orbit of the moon. Mon. Not. R. Astron. Soc. 2011, 415, 1266–1275. [Google Scholar] [CrossRef]
- Iorio, L. An empirical explanation of the anomalous increases in the astronomical unit and the lunar eccentricity. Astron. J. 2011, 142. [Google Scholar] [CrossRef]
- Acedo, L. Anomalous post-Newtonian terms and the secular increase of the astronomical unit. Adv. Space Res. 2013, 52, 1297–1303. [Google Scholar] [CrossRef]
- Acedo, L. A phenomenological variable speed of light theory and the secular increase of the astronomical unit. Phys. Essays 2013, 26, 567–573. [Google Scholar] [CrossRef]
- Anderson, J.D.; Nieto, M.M. Astrometric solar-system anomalies. Proc. Int. Astron. Union 2010, 5, 189–197. [Google Scholar] [CrossRef]
- Williams, J.G.; Boggs, D.H. Lunar Core and Mantle. What Does LLR See? In Proceedings of the 16th International Workshop on Laser Ranging, Poznan, Poland, 13–17 October 2008.
- Williams, J.G.; Boggs, D.H.; Folkner, W.M. DE421 Lunar Orbit, Physical Librations, and Surface Coordinates. Available online: ftp://ssd.jpl.nasa.gov/pub/eph/planets/ioms/de421_moon_coord_iom.pdf (accessed on 18 May 2014).
- Iorio, L. The Lingering Anomalous Secular Increase of the Eccentricity of the Orbit of the Moon: Further Attempts of Explanations of Cosmological Origin. Galaxies 2014, 2, 259–262. [Google Scholar] [CrossRef]
- Pitjev, N.P.; Pitjeva, E.V. Constraints on dark matter in the solar system. Astron. Lett. 2013, 39, 141–149. [Google Scholar] [CrossRef]
- Pitjeva, E.V. Updated IAA RAS planetary ephemerides EPM-2011 and their use in scientific research. Solar Syst. Res. 2013, 47, 386–402. [Google Scholar] [CrossRef]
- Pitjeva, E.V.; Pitjev, N.P. Relativistic effects and dark matter in the Solar system from observations of planets and spacecraft. Mon. Not. R. Astron. Soc. 2013, 432, 3431–3437. [Google Scholar] [CrossRef]
- Pitjeva, E.V.; Pitjev, N.P. Development of a planetary ephemerides EPM and their applications. Celest. Mech. Dyn. Astron. 2014, 119, 237–256. [Google Scholar] [CrossRef]
- Iorio, L. The recently determined anomalous perihelion precession of Saturn. Astron. J. 2009, 137, 3615–3618. [Google Scholar] [CrossRef]
- Iorio, L. The perihelion precession of Saturn, planet X/Nemesis and MOND. Open Astron. J. 2010, 3, 1–6. [Google Scholar] [CrossRef]
- Pitjeva, E.V. Ephemerides EPM2008: The Updated Models, Constants, Data, Paper Presented at Journées “Systémes de Référence Spatio-temporels” and X Lohrmann-Kolloquium, Dresden, Germany, 2010. Available online: http://syrte.obspm.fr/jsr/journees2008/pdf/ (accessed on 23 September 2014).
- Fienga, A.; Laskar, J.; Kuchynka, P.; Manche, H.; Desvignes, G.; Gastineau, M.; Cognard, I.; Theureau, G. The INPOP10a planetary ephemeris and its applications in fundamental physics. Celest. Mech. Dyn. Astron. 2011, 111, 363–385. [Google Scholar] [CrossRef] [Green Version]
- Dvali, G.; Gabadadze, G.; Porrati, M. 4D Gravity on a Brane in 5D Minkowski Space. Phys. Lett. B 2000, 485, 208–214. [Google Scholar] [CrossRef]
- Iorio, L. On the effects of Dvali Gabadadze Porrati braneworld gravity on the orbital motion of a test particle Class. Quantum Gravity 2005, 22, 5271–5281. [Google Scholar] [CrossRef]
- Lue, A.; Starkman, G. Gravitational leakage into extra dimensions: Probing dark energy using local gravity. Phys. Rev. D 2003, 67. [Google Scholar] [CrossRef]
- Khriplovich, I.B.; Pitjeva, E.V. Upper limits on density of dark matter in Solar System. Int. J. Mod. Phys. D 2006, 15, 615–618. [Google Scholar] [CrossRef]
- Iorio, L. Solar system planetary orbital motions and dark matter J. Cosmol. Astropart. Phys. 2006, 2006. [Google Scholar] [CrossRef]
- Sereno, M.; Jetzer, Ph. Dark matter versus modifications of the gravitational inverse-square law: Results from planetary motion in the Solar system. Mon. Not. R. Astron. Soc. 2006, 371, 626–632. [Google Scholar] [CrossRef]
- Iorio, L. Solar System planetary tests of ċ/c. Gen. Relativ. Grav. 2010, 42, 199–208. [Google Scholar] [CrossRef]
- Hees, A.; Folkner, W.M.; Jacobson, R.A.; Park, R.S. Constraints on modified Newtonian dynamics theories from radio tracking of the Cassini spacecraft. Phys. Rev. D. 2014, 89, 102002. [Google Scholar] [CrossRef]
- Blanchet, L.; Novak, J. External field effect of modified Newtonian dynamics in the Solar System. Mon. Not. R. Astron. Soc. 2011, 412, 2530–2542. [Google Scholar] [CrossRef] [Green Version]
- De la Fuente Marcos, C.; de la Fuente Marcos, R. Extreme trans-Neptunian objects and the Kozai mechanism: Signalling the presence of trans-Plutonian planets. Mon. Not. R. Astron. Soc. 2014, 443, L59–L63. [Google Scholar] [CrossRef]
- Fernández, J.A. On the existence of a distant Solar companion and its possible effects on the Oort cloud and the observed comet population. Astroph. J. 2011, 726, 33. [Google Scholar] [CrossRef]
- Trujillo, C.A.; Sheppard, S.S. A Sedna-like body with a perihelion of 80 astronomical units. Nature 2014, 507, 471–474. [Google Scholar] [CrossRef] [PubMed]
- Iorio, L. Constraints on planet X/Nemesis from Solar System’s inner dynamics. Mon. Not. R. Astron. Soc. 2009, 400, 346–353. [Google Scholar] [CrossRef]
- Iorio, L. Planet X revamped after the discovery of the Sedna-like object 2013 VP113. Mon. Not. R. Astron. Soc. Lett. 2014, 444, L78–L79. [Google Scholar] [CrossRef]
- Iorio, L. Constraints on the location of a putative distant massive body in the Solar system planetary data. Celest. Mech. Dyn. Astron. 2012, 112, 117–130. [Google Scholar] [CrossRef]
- Iorio, L. Perspectives of effectively constraining the location of a massive trans-Plutonian object with the New Horizons spacecraft: Trans-Plutonian object with the New Horizons spacecraft: A sensitivity analysis. Celest. Mech. Dyn. Astron. 2013, 116, 357–366. [Google Scholar] [CrossRef]
- Lense, J.; Thirring, H. On the Influence of the Proper Rotation of Central Bodies on the Motions of Planets and Moons According to Einstein’s Theory of Gravitation. Phys. Z. 1918, 19, 156–163. [Google Scholar]
- De Sitter, W. Einstein’s theory of gravitation and its astronomical consequences. Mon. Not. R. Astron. Soc. 1916, 76, 699–728. [Google Scholar] [CrossRef]
- Iorio, L. Constraining the Angular Momentum of the Sun with Planetary Orbital Motions and General Relativity. Sol. Phys. 2012, 281, 815–826. [Google Scholar] [CrossRef]
- Rindler, W. Relativity: Special, General, and Cosmological, 2nd ed.; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Acedo, L. The flyby anomaly: A case for strong gravitomagnetism? Adv. Space Res. 2014, 54, 788–796. [Google Scholar] [CrossRef]
- Hehl, F.W.; von der Heyde, P.; David Kerlick, G.; Nester, J.M. General Relativity with Spin and Torsion: Foundations and Prospects. Rev. Mod. Phys. 1976, 48, 393–416. [Google Scholar] [CrossRef]
- Hammond, R.T. Torsion Gravity. Rep. Prog. Phys. 2002, 65, 599–649. [Google Scholar] [CrossRef]
- Giles, P. Time-Distance Measurements of Large-Scale Flows in the Solar Convection Zone. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1999. [Google Scholar]
- Danby, J.M.A. Fundamentals of Celestial Mechanics, 2nd ed.; Willmann-Bell, Inc.: Richmond, VA, USA, 1988. [Google Scholar]
- Pollard, H. Mathematical Introduction to Celestial Mechanics; Prentice-Hall Inc.: Englewood Cliffs, NJ, USA, 1966. [Google Scholar]
- Arfken, G. Mathematical Methods for Physicists, 3rd ed.; Academic Press: Orlando, FL, USA, 1985. [Google Scholar]
- NASA’s Planetary Factsheet. Available online: http://nssdc.gsfc.nasa.gov/planetary/factsheet/ (accessed on 23 September 2014).
- Iorio, L.; Lichtenegger, H.I.M.; Ruggiero, M.L.; Corda, C. Phenomenology of the Lense-Thirring effect in the Solar System. Astrophys. Space Sci. 2011, 331, 351–395. [Google Scholar] [CrossRef]
- Everitt, C.W.F.; DeBra, D.B.; Parkinson, B.W.; Turneaure, J.P.; Conklin, J.W.; Heifetz, M.I.; Keiser, G.M.; Silbergleit, A.S.; Holmes, T.; Kolodziejczak, J.; et al. Gravity Probe B: Final Results of a Space Experiment to Test General Relativity. Phys. Rev. Lett. 2011, 106, 221101. [Google Scholar] [CrossRef] [PubMed]
- Everitt, C.W.F.; Adams, M.; Bencze, W.; Buchman, S.; Clarke, B.; Conklin, J.; DeBra, D.B.; Dolphin, M.; Heifetz, M.; Hipkins, D.; et al. Gravity Probe B Data Analysis: Status and Potential for Improved Accuracy of Scientific Results. Space Sci. Rev. 2009, 148, 53–69. [Google Scholar] [CrossRef]
- Renzetti, G. History of the attempts to measure orbital frame-dragging with artificial satellites. Cent. Eur. J. Phys. 2013, 11, 531–544. [Google Scholar] [CrossRef]
- Ciufolini, I.; Paolozzi, A.; Koenig, R.; Pavlis, E.C.; Ries, J.; Matzner, R.; Gurzadyan, V.; Penrose, R.; Sindoni, G.; Paris, C. Fundamental Physics and General Relativity with the LARES and LAGEOS satellites. Nucl. Phys. B (Proc. Suppl.) 2013, 243–244, 180–193. [Google Scholar] [CrossRef]
- Ciufolini, I.; Paolozzi, A.; Pavlis, E.; Ries, J.; Gurzadyan, V.; Koenig, R.; Matzner, R.; Penrose, R.; Sindoni, G. Testing general relativity and gravitational physics using LARES satellite. Eur. Phys. J. Plus 2012, 127, 133:1–133:7. [Google Scholar] [CrossRef]
- Renzetti, G. Are higher degree even zonals really harmful for the LARES/LAGEOS frame-dragging experiment? Can. J. Phys. 2012, 90, 883–888. [Google Scholar] [CrossRef]
- Renzetti, G. First results from LARES: An analysis. N. Astron. 2013, 23, 63–66. [Google Scholar] [CrossRef]
- Renzetti, G. Some reflections on the Lageos frame-dragging experiment in view of recent data analyzes. N. Astron. 2014, 29, 25–27. [Google Scholar] [CrossRef]
- Iorio, L. An Assessment of the Systematic Uncertainty in Present and Future Tests of the Lense-Thirring Effect with Satellite Laser Ranging. Space Sci. Rev. 2009, 148, 363–381. [Google Scholar] [CrossRef]
- Iorio, L.; Ruggiero, M.L.; Corda, C. Novel considerations about the error budget of the LAGEOS-based tests of frame-dragging with GRACE geopotential models. Acta Astronaut. 2013, 91, 141–148. [Google Scholar] [CrossRef]
- Iorio, L. Preliminary bounds of the gravitational local position invariance from Solar system planetary precessions. Mon. Not. R. Astron. Soc. 2014, 437, 3482–3489. [Google Scholar] [CrossRef]
- Bel, L. Earth and Moon orbital anomalies. 2014. [Google Scholar]
© 2014 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acedo, L. Constraints on Non-Standard Gravitomagnetism by the Anomalous Perihelion Precession of the Planets. Galaxies 2014, 2, 466-481. https://doi.org/10.3390/galaxies2040466
Acedo L. Constraints on Non-Standard Gravitomagnetism by the Anomalous Perihelion Precession of the Planets. Galaxies. 2014; 2(4):466-481. https://doi.org/10.3390/galaxies2040466
Chicago/Turabian StyleAcedo, Luis. 2014. "Constraints on Non-Standard Gravitomagnetism by the Anomalous Perihelion Precession of the Planets" Galaxies 2, no. 4: 466-481. https://doi.org/10.3390/galaxies2040466