Nonparametric Reconstruction of the O_m Diagnostic to Test ΛCDM

Abstract

In this work, we consider an O_m diagnostic using a non-parametric reconstruction by employing the Loess–Simex factory. This procedure allows us to perform a model-independent comparison for w(z) with the astrophysical data. The concordance model can be tested with the advantage that our approach represents an alternative and efficient way to relax the use of priors and find a possible w that reliably describes the data with no previous knowledge of a cosmological model.

1. Introduction

At present, numerous projects and surveys are either underway or being proposed [1,2,3,4,5] to discover the underlying cause of the accelerated expansion of the universe, which is well established by present observations such as: Supernovae Type Ia (SNIa) [6,7], Baryon Acoustic Oscillations (BAO) [8], Cosmic Microwave Background Radiation (CMBR) anisotropies [9], Large Scale Structure formation [10] and Weak Lensing [11]. The current standard cosmological model, consistent with these vast observations, is the ΛCDM or concordance model, in which this accelerated behaviour is driven by a cosmological constant Λ and filled with Cold Dark Matter (CDM). This Λ is usually related to an extra component in the Universe, the so-called Dark Energy (DE) with $w=-1$. Despite its simplicity, the ΛCDM model has a couple of theoretical loopholes (e.g., the fine tuning and coincidence problems [12]) which had led to alternative proposals that either modified the General Relativity or considered a scenario with a dynamic DE. In this way, DE can be described by an equation of state (EoS) written in terms of the redshift, $w\left(z\right)$, but until now, we did not have precise evidence and/or evolution of this quantity. Since its properties are still being researched, a wide variety of reconstructions of DE parameterizations have been proposed to help discern the dynamics of this component [13,14,15,16,17,18,19,20,21,22,23,24].

In spite of the efforts to solve the theoretical loopholes of the concordance model, there has been no strong alternative yet. In this situation, it may be useful to test the consistency of the ΛCDM model with cosmological observations and compare it with alternatives models or parameterizations. However, this mainstream idea is unlikely to yield any new physics beyond this scenario, but revealing such possible new physics is essential to avoiding prior knowledge of a cosmological model in order to find an adequate EoS that reliably describes the astrophysical data available. An important goal along the same lines is to differentiate the ΛCDM model from other DE models in a scenario that has as few priors as possible because, as we have experienced over the years, incorrect priors of $w\left(z\right)$ or values of the density quantities can lead us to incorrect cosmological results. An interesting null test of DE, called the $O_m$ diagnostic, was proposed in [25]. The elegance of this proposal lies in its theoretical form, which is constructed using only the Hubble parameter $H\left(z\right)$, a quantity that can be measured directly from the observations. This procedure allows us to differentiate between the cosmological constant (flat ΛCDM) and a dynamical model (curved ΛCDM) only by considering as a prior the value of ${\Omega }_m$. Even if the value of ${\Omega }_m$ is not accurately known, Reference [26] presented some interesting insights using an extension of the $O_m$ diagnostic called two-points difference. As a step forward, Reference [27] analyzed a curved ΛCDM, in which the diagnostic function $O_m^{\left(2\right)}$ includes first derivatives of $H\left(z\right)$, and a new parameter related to the curvature, $O_k$, enters the scene. These tests are quite helpful because we have a scenario in which the diagnostic function can tell if the previous DE assumptions are in agreement with the ΛCDM model or deviate from it towards an alternative DE or a modified gravity model.

One of the most direct ways to reconstruct $w\left(z\right)$ is via the luminosity distance $d_L$ of SNIa observations. The derivative of this quantity leads indirectly to $H\left(z\right)$. Then, we need the second derivative of $d_L$ to reconstruct $w\left(z\right)$. So far, there are two astrophysical samples that directly reflect measures of it: first, the Cosmic Chronometers (C-C), which gives a compilation of $H\left(z\right)$ measurements estimated with the differential evolution of passively evolving early-type galaxies [28,29,30,31,32,33]; second, the radial BAO scale in the galaxy distribution, a relic of the pre-recombination universe [34,35]. The aforementioned diagnostic has been tested with these astrophysical samples and provides a solution of the cosmic acceleration based in a smoothed model-independent via Gaussian processes [36,37], but the price that we pay for using this are the strong constraints over the statistical process and the assumption of an initial guess cosmological model.

In light of these issues, Reference [38] proposed the use of two statistical techniques: the Locally Weighted Scatterplot Smoothing (Loess) [39] and the Simulation and Extrapolation methods (Simex) [40] in order to address a nonparametric scenario with the fewest number of priors, a smooth reconstruction of the parameter $H\left(z\right)$, and, of course, obtain the well established cosmic acceleration. Two novel achievements using these statistical techniques are: (1) we do not need any DE parameterization as a prior, and we instead we directly apply the full astrophysical sample in the code structure, and the evolution of the cosmological parameters will be issued by the smooth curve given by the observations; (2) we do not require any functional distribution for the analysis. There are only a couple of restrictions that are related to the statistical analysis: (a) the size of the window data where we are going to develop a fitting routine based on a specific degree of the polynomial [41,42]; and (b) we require a weight function that will give to each data point some importance with respect to the other observations around them. We clarify that this factory is a cosmological-model-independent method due to the relaxed use of information concerning cosmological parameters in comparison to Gaussian processes, where the use of strong constraints on spatial flatness is required [36]. In order to proceed with this research, we will follow these ideas to constrain even more the use of priors via the Loess–Simex factory and reconstruct $h\left(z\right)$ and its derivative to test the ΛCDM model. Our final results demonstrate that the Loess–Simex factory applied to the dynamical $O_m$ diagnostic finds a preference for a DE model with an equation of state $w=-2/3$, which corresponds to a static domain wall network.

This paper is organised as follows: in Section 2, we give an overview of the quantities used to test the ΛCDM model. In Section 3 and Section 4, we derive the equations for the $O_m$ diagnostic by considering a constant EoS and presenting the cases for a flat and curved universe. In Section 5, we describe the astrophysical samples for $H\left(z\right)$. In the following two sections, we describe our methodology with the Loess–Simex factory to reconstruct $h\left(z\right)$ and the $O_m$ diagnostic. In Section 7, we present a discussion of the results obtained.

2. ΛCDM Background

The dark energy reconstruction starts underlying the validity of the FLRW metric that gives the Friedmann equation

$${\left(\frac{H\left(z\right)}{H_0}\right)}^2\equiv h^2\left(z\right)={\Omega }_{0m}{(1+z)}^3+{\Omega }_{0k}{(1+z)}^2+(1-{\Omega }_{0m}-{\Omega }_{0k})f\left(z\right),$$

(1)

where

$$f\left(z\right)=exp\left[3{\int }_0^{z}d\tilde{z}\left(\frac{1+w\left(\tilde{z}\right)}{1+\tilde{z}}\right)\right],$$

(2)

and ${\Omega }_{0m}$, ${\Omega }_{0k}$ are the matter and curvature densities at present epoch, respectively. The EoS that characterizes DE can be obtained by introducing Equation (2) in Equation (1) and deriving to obtain its characteristic expression

$$w\left(z\right)=\frac{2(1+z)h{h}^{\prime }-3h^2+{\Omega }_{0k}{(1+z)}^2}{3\left[h^2-{\Omega }_{0m}{(1+z)}^3-{\Omega }_{0k}{(1+z)}^2\right]},$$

(3)

where $h^{\prime }\left(z\right)$ is the first derivative of the normalized Hubble parameter with respect to the redshift z. Here, we can notice that, depending on the values of the density parameters, there is a strong restriction over $w\left(z\right)$. The simplest explanation for DE is when this parameter acquires the value $w=-1$, which is related to a cosmological constant Λ. Other interesting cases emerge when $w>-1$ ($w<-1$), which points to the quintessence (phantom) scenario, respectively. Furthermore, the models are still restricted to the values of the density parameters, and a distinction between them is quite difficult at this point. However, $w\left(z\right)$ degenerates with the density parameters and the current data are not accurate enough to distinguish between these parameters, making the need for model-independent methods and experimental tests an important issue. One way to alleviate this problem is via an approach of cosmography [43,44,45], which does not take into account any model a priori and can derive cosmological bounds directly from the astrophysical data. Nevertheless, since this cosmography relates cosmological parameters to Taylor-like expansions, this approach goes through truncated series problems.

All of the issues mentioned above were the pattern to propose a diagnostic to differentiate between DE models in scenarios where w could be a constant (and flat) and dynamical (and non-flat). The $O_m$ diagnostic outlines a test where we can fathom between DE models in the cases when the value of $O_m$ is a constant or not. Following these lines, let us start our study by describing a $O_m$ diagnostic with a flat ΛCDM model as an example. Afterwards, we will proceed with the presentation of the dynamical (non-flat) diagnostic.

3. The O_m Diagnostic Background

Let us begin with the distance-redshift relation

$$D\left(z\right)=\frac{H_0}{c}\frac{d_L\left(z\right)}{(1+z)},$$

(4)

where

$$d_L\left(z\right)=\frac{c(1+z)}{H_0\sqrt{-{\Omega }_{0k}}}sin\left[\sqrt{-{\Omega }_{0k}}{\int }_0^{z}d\tilde{z}\frac{H_0}{H\left(\tilde{z}\right)}\right]$$

(5)

is the luminosity distance. Deriving Equations (4) and (5) and considering a flat universe (${\Omega }_{0k}=0$), it can be found that $D^{\prime }\left(z\right)=H_0/H\equiv h^{-1}$. In this flat background with a constant DE EoS, $w=w_0$, the Equation (1) can be expressed as:

$$h^2\left(z\right)={\Omega }_{0m}{(1+z)}^3+(1-{\Omega }_{0m}){(1+z)}^{3(1+w_0)},$$

(6)

from where we can define a function that characterizes this diagnostic

$$O_{m_0}^{\left(1\right)}\left(z\right)\equiv \frac{h^2-{(1+z)}^{3(1+w_0)}}{{(1+z)}^3\left[1-{(1+z)}^{3w_0}\right]},$$

(7)

where the upper index ‘(1)’ indicates the existence of a first derivative of the luminosity distance $d_L$.

To test the ΛCDM model using direct observations of the Hubble rate $H\left(z\right)$, we require a set in Equation (7) $w_0=-1$ [25]

$$O_m^{\left(1\right)}\left(z\right)=\frac{h^2-1}{z(3+3z+z^2)}.$$

(8)

At this point, we can distinguish a ΛCDM model from any DE models by rewriting Equation (8) using Equation (6), obtaining

$$O_m^{\left(1\right)}\left(z\right)={\Omega }_{0m}+(1-{\Omega }_{0m})\left[\frac{{(1+z)}^{3(1+w_0)}-1}{{(1+z)}^3-1}\right],$$

(9)

where, on one hand, $w_0=-1$ implies ΛCDM with $O_m^{\left(1\right)}={\Omega }_{0m}$. On the other hand, $w_0>-1$ (or $w_0<-1$) implies quintessence (or phantom) scenarios with $O_m^{\left(1\right)}>{\Omega }_{0m}$ (or $O_m^{\left(1\right)}<{\Omega }_{0m}$), respectively. These descriptions are detailed in

Table 1. Features in the $O_m$ diagnostic with respect to the value of ${\Omega }_{0m}$, which can be taken from recent Planck results [46] and a constant EoS $w=w_0$.

EoS	Om Diagnostic	Model
$w_0=-1$	$O_m^{\left(1\right)}={\Omega }_{0m}$	Flat ΛCDM.
$w_0>-1$	$O_m^{\left(1\right)}>{\Omega }_{0m}$	Quintessence.
$w_0<-1$	$O_m^{\left(1\right)}<{\Omega }_{0m}$	Phantom.

.

Once we consider a Hubble rate $h\left(z\right)$ sample, it is possible to estimate confidence values of $O_m^{\left(1\right)}$. If the test does not give a constant behaviour, then the ΛCDM model is ruled out and the existence of DE models or a curved ΛCDM scenario are considered. In the first option, several DE candidates can be related to $O_m^{\left(1\right)}$ (see Figure 1) by considering a specific value for $w_0$, e.g., non-interacting cosmic strings with $w_0=-1/3$ [47], static domain walls with $w_0=-2/3$ [48,49] and phantom models with $w_0<-1$ [13,14,15,16,17,18,19]. To distinguish between these models, we require the introduction of the $O_m$ diagnostic at the first-order in h, which is related to the dynamical test.

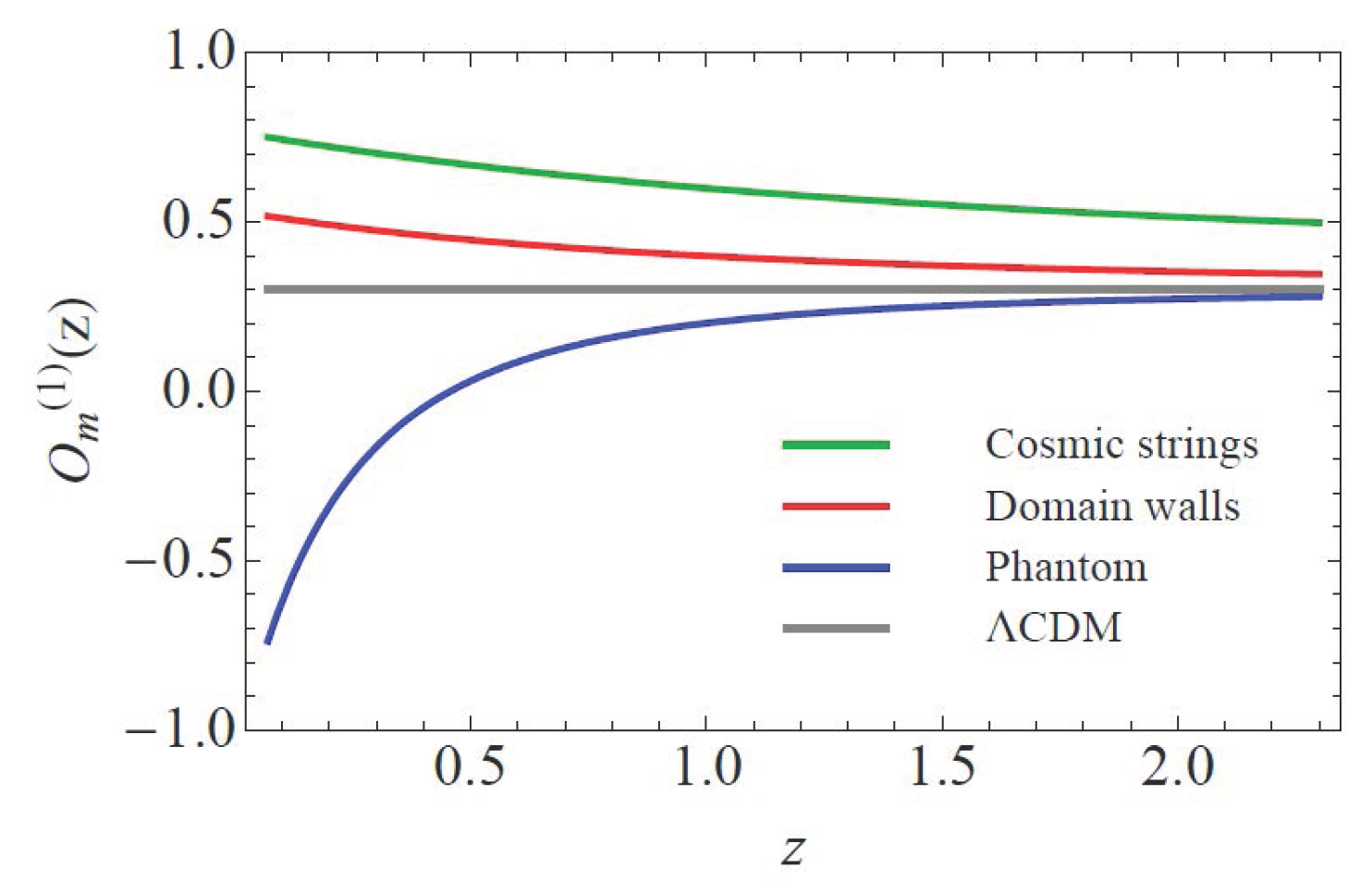
4. The Dynamical O_m Diagnostic

A more meticulous analysis based on the abovementioned features takes into account a curved model, where the first derivatives of $h\left(z\right)$ come on to the scene. Expressions for this case can be obtained by considering ${\Omega }_{0k}\ne 0$ and $w=w_0$ in Equation (1):

$$h^2\left(z\right)={\Omega }_{0m}{(1+z)}^3+{\Omega }_{0k}{(1+z)}^2+(1-{\Omega }_{0m}-{\Omega }_{0k}){(1+z)}^{3(1+w_0)},$$

(10)

from where we can find two expressions:

$$\begin{array}{cc}\hfill O_{m_0}^{\left(2\right)}\left(z\right)=& \frac{h^2\left[3w_0{(1+z)}^{3w_0+1}+3z{(1+z)}^{3w_0}+3{(1+z)}^{3w_0}-2\right]-(1+3w_0){(1+z)}^{3(1+w_0)}}{{(1+z)}^3\left[1-{(1+z)}^{3w_0}+3w_{0}z{(1+z)}^{3w_0}\right]}\hfill \\ & -\frac{2h{h}^{\prime }(1+z)\left[z{(1+z)}^{3w_0}+{(1+z)}^{3w_0}-1\right]}{{(1+z)}^3\left[1-{(1+z)}^{3w_0}+3w_{0}z{(1+z)}^{3w_0}\right]},\hfill \end{array}$$

(11)

$$O_{k_0}\left(z\right)=\frac{3\left\{w_0{(1+z)}^{3(1+w_0)}-h^2\left[w_0{(1+z)}^{3w_0}+{(1+z)}^{3w_0}-1\right]\right\}+2h{h}^{\prime }(1+z)\left[{(1+z)}^{3w_0}-1\right]}{{(1+z)}^2\left[3w_{0}z{(1+z)}^{3w_0}-{(1+z)}^{3w_0}+1\right]},$$

(12)

where the upper index ‘(2)’ indicates the existence of a second derivative of the luminosity distance. The calculations are explained in Appendix A.

We can obtain the curved ΛCDM case when we consider $w_0=-1$ in the systems (11) and (12), which gives [27]

$$\begin{array}{ccc}\hfill O_m^{\left(2\right)}\left(z\right)& =& \frac{2\left[(1+z)(1-h^2)+z(2+z)h{h}^{\prime }\right]}{z^2(1+z)(3+z)},\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill O_k\left(z\right)& =& \frac{3{(1+z)}^2(h^2-1)-2z(3+3z+z^2)h{h}^{\prime }}{z^2(1+z)(3+z)}.\hfill \end{array}$$

(14)

To perform the distinctions between DE models, we can rewrite Equation (11) using Equation (10) and its derivative, which gives $O_{m_0}^{\left(2\right)}={\Omega }_{0m}$ and $O_{k_0}={\Omega }_{0k}$, implying a ΛCDM model.

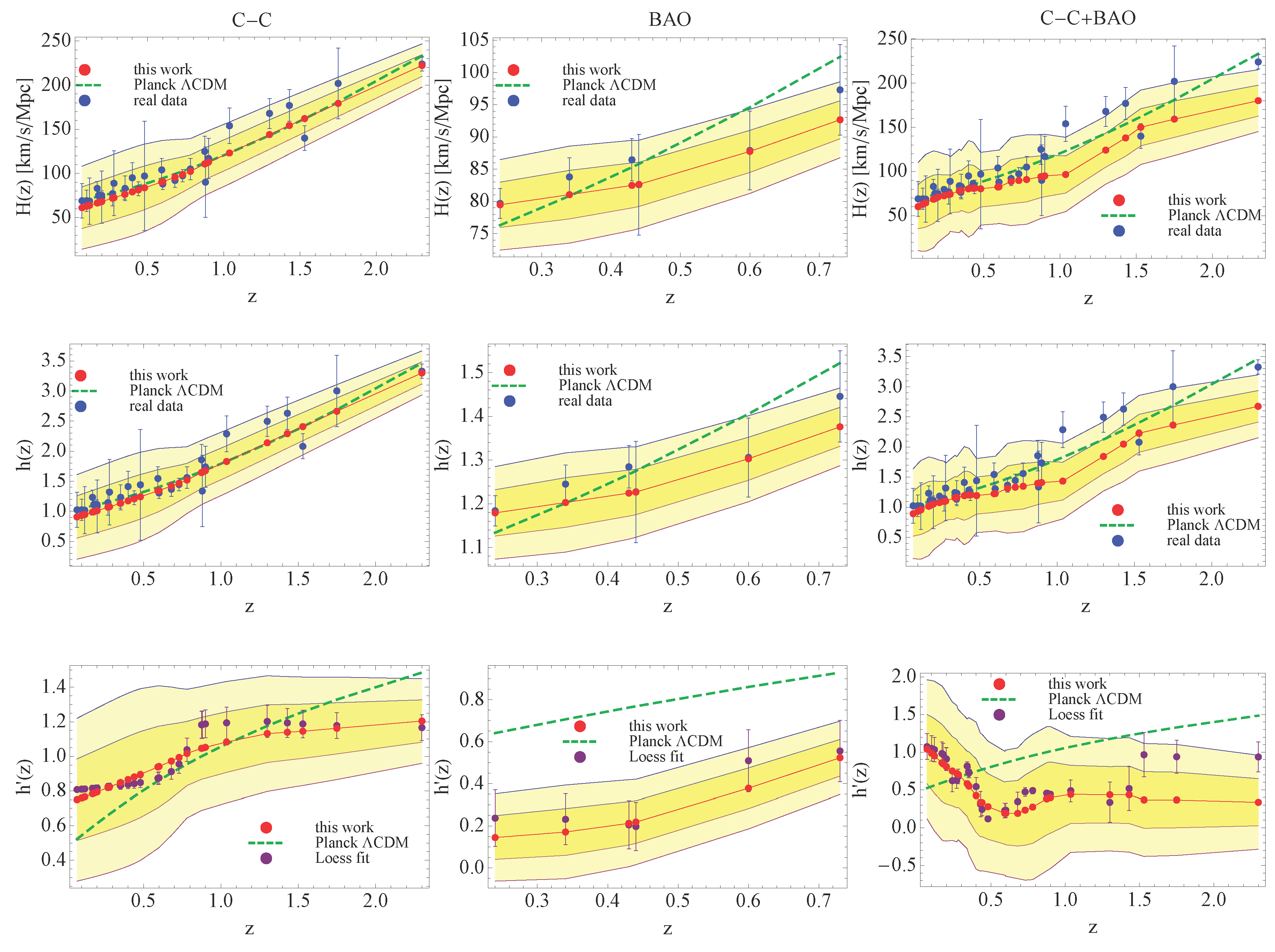
5. Observations of the Hubble Rate

To perform the diagnostic analysis, we require having at hand the observed $H\left(z\right)$ data. This parameter has become an effective probe in cosmology comparison with SNIa, BAO and CMB data. In fact, it is more rewarding to study the observational $H\left(z\right)$ data directly due to the fact that all these tests use the distance scale (e.g., the luminosity distance $d_L$, the shift parameter R, or the distance parameter A) measurement to determine the values of the cosmological parameters, which needs the integral of $H\left(z\right)$ and therefore loses some important information of this quantity.

$H\left(z\right)$ depends on the differential age as a function of redshift z in the form: $H\left(z\right)=-{(1+z)}^{-1}dz/dt$, which gives a direct measurement of $H\left(z\right)$ through the change of redshift in cosmic time. As an independent approach of this measure, we provide two samples:

(1)

Cosmic Chronometers (C-C) data. This kind of sample gives a measurement of the expansion rate without relying on the nature of the metric between the chronometer and us. We are going to employ several data sets presented in [28]. A full compilation of the latter, which includes 28 measurements of $H\left(z\right)$ in the range $0.07<z<2.3$, are reported in [50]. The normalized parameter $h\left(z\right)$ can be easily determined by considering the value $H_0=67.31\pm 0.96$ km s⁻¹ M pc⁻¹ [46].

(2)

Data from BAO. Unlike the angular diameter $d_A$ measures given by the transverse BAO scale, the $H\left(z\right)$ data can be extracted from the measurements of the line-of-sight of this BAO scale. Because the BAO distance scale is embodied in the CMB, its measurements on DE parameters are strongest at low redshift. The samples that we are going to consider consist of three data points from [34] and three more from [35] measured at six redshifts in the range $0.24<z<0.73$. This data set is shown in

Table 2. BAO sample data from [34,35].

z	H(z) [km s−1 M pc−1]	σH2
0.24	79.69	2.32
0.34	83.80	2.96
0.43	86.45	3.27
0.44	82.6	7.8
0.6	87.9	6.1
0.73	97.3	7.0

.

6. Nonparametric Reconstructions

Following the same methodology proposed in [38], we are going to reconstruct the normalized Hubble parameter h using the Loess–Simex factory.

6.1. Reconstruction of $h\left(z\right)$

Step A1. Windows and subsample selection. We are going to select the proportion of observations fitting in a specific window. Each selection consists of some percentage of the total number of observations and to each subsample will be assigned a specific weighted least square local polynomial fit. We use a subsample via one quantity that is usually known in the statistical jargon as the smoothing parameter or span s, and we use $k=ns$, where k is the number of observations per window and rounded to the next largest integer, n is the total number of observations and s typically takes values that oscillate between 0 and 1. The election of the optimal value of s can be done by using cross-validation [51], which basically consists of omitting the ith observation from the local regression at the focal value $x_{i,0}$. The cross-validation function is given by the expression

$$CV\left(s\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^n}{({\widehat{y}}_{-i}\left(s\right)-y_i)}^2,$$

(15)

where ${\widehat{y}}_{-i}\left(s\right)$ is ${\widehat{y}}_{-i}$ for span s. Using Equation (15), we calculated the values: $s=0.9$ for the C-C sample, $s=0.85$ for the BAO sample and $s=0.4$ for the C-C+BAO total sample, which correspond to 90, 85 and 40 percent of the data in each window, respectively. A detailed process can be found in [38].

Step A2. Weighted subsamples. Having already selected the amount of data in each window, consider a certain amount of data points near which are more related between them than others that are significantly far away and receive a null weight. This idea is encoded in the weight function described by a tricube kernel:

$$W\left({\overline{z}}_i\right)=\left\{\begin{array}{lll}{\left(1-{\left|{\overline{z}}_i\right|}^3\right)}^3& \text{for}& \left|{\overline{z}}_i\right|<1,\\ \\ 0& \text{for}& \left|{\overline{z}}_i\right|\ge 1,\end{array}\right.$$

(16)

where ${\overline{z}}_i=(z_i-z_0)/d$, indicates the distance between the predictor redshift value for the i-th observation and the focal redshift $z_0$. d is the maximum distance between the point of interest and elements inside the window.

Step A3. Regression analysis. Following the Loess technique, we consider a low-degree polynomial to perform a local fit of the subsample in each window:

$$H\left(z\right)=a_0+a_{1}z.$$

(17)

A similar fit routine proposal was presented in [42]. The right hand side second term is related to $H^{\prime }$, parameter that we will reconstruct in Section 6.2. As we can see from Equation (17), we shall consider a linear polynomial appropriate to fit each subset of data. Higher-degree polynomials are possible, and would work in theory, but it would result in models that are not really compliant with the spirit of Loess, which looks for a low-order polynomial and a simple model that can fit data easily. The reconstructed quantity is a weighted sum of the observations $H\left(z\right)$ represented as:

$$\widehat{H}\left(z\right)={\displaystyle \sum _{i=1}^n}{W}_{ij}{H}_i,$$

(18)

where the weights in this regression are $W_{ij}=W[(x_i-x_0)/d]$ and $j=1,\dots ,k$.

Step A4. Simulated data sample. Simex is a simple simulation algorithm that allows for displaying the effect of measurement errors on parameter estimates. It consists of adding to the data sets an additional measurement error as follows:

$${\eta }_i\left(\lambda \right)=H_i+\sqrt{\beta }{\sigma }_{H_i},$$

(19)

where ${\eta }_i\left(\lambda \right)$ denotes the simulated data points and ${\sigma }_{H_i}$ is the measurement error variance of each $H\left(z\right)$ observation. The resulting measurement error is $\beta =(1+\lambda )$, in which we can extrapolate the data sample to an error free zone if $\lambda =-1$. This zone is achieved after performing a standard regression, using a quadratic polynomial, of the data set computed for different values of λ. Specifically, we are going to consider as a starting value $\lambda =0.5$ until $\lambda =2$ increasing in steps of 0.1.

Step A5. Starting the reconstruction. After performing the latter extrapolation step, the data set will be simplified to the same length of the initial data, and, finally, these simulated data sets are normalized by $H_0$, given as a result the reconstruction of $h\left(z\right)$. All of the above steps are repeated for all the data points in the astrophysical sample. The connection of the Loess–Simex reconstructed data points are represented by a curve due to the lack of parameter estimates. The reconstructed normalized Hubble parameter $h\left(z\right)$ gives a general trend of the model.

Step A6. About the confidence regions. To design the confidence regions of the reconstructed parameter $h\left(z\right)$, we require the transfer uncertainties via error propagation given by

$$\begin{array}{ccc}\hfill {{\sigma }_h}^2& =& {\left(\frac{{\sigma }_H}{H_0}\right)}^2+\left(\frac{H^2}{{H_0}^4}\right){\sigma }_{H_0}^2.\hfill \end{array}$$

(20)

With this expression, we can calculate the uncertainties for the $O_m$ diagnostic

$$\begin{array}{ccc}\hfill {\sigma }_{O_m^{\left(1\right)}}^2& =& {\left[\frac{2h}{z(3+3z+z^2)}\right]}^2{{\sigma }_h}^2.\hfill \end{array}$$

(21)

For the dynamical $O_m$ diagnostic, we have the following uncertainties:

$$\begin{array}{ccc}\hfill {\sigma }_{O_m^{\left(2\right)}}^2& =& {\left[\frac{-4h(1+z)+2z(2+z)h^{\prime }}{z^2(1+z)(3+z)}\right]}^2{\sigma }_h^2+{\left[\frac{2(2+z)h}{z(1+z)(3+z)}\right]}^2{\sigma }_{h^{\prime }}^2,\hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill {\sigma }_{O_k}^2& =& {\left[\frac{6h{(1+z)}^2-2z(3+3z+z^2)h^{\prime }}{z^2(1+z)(3+z)}\right]}^2{\sigma }_h^2+{\left[\frac{-2(3+3z+z^2)h}{z(1+z)(3+z)}\right]}^2{\sigma }_{h^{\prime }}^2.\hfill \end{array}$$

(23)

As the set implies, we need to find the value of the variable ${\sigma }_H$. Let us start with the fitted value $\widehat{H}\left(z\right)$ obtained in the Step A3. For nonparametric regression models, we estimate the error variance as

$$S^2=\frac{1}{n-d{f}_{mod}}{\displaystyle \sum _{i=1}^n}{r}_i^2,$$

(24)

where $r_i=H_i-{\widehat{H}}_i$ is the residual for the i-th observation and $d{f}_{mod}$ is the equivalent degrees of freedom for the model, which, in our case, is equal to two. With this, we are capable of computing the variance of the fitted value $\widehat{H}\left(z\right)$ at $z=z_i$ as:

$$\widehat{V}\left({\widehat{H}}_i\right)\equiv {\sigma }_{{\widehat{H}}_i}^2=S^2{\displaystyle \sum _{j=1}^n}{W}_{ij}^2.$$

(25)

The results of the latter are considered to compute the propagation values ${\sigma }_h$ in Equation (20). Finally, the 68% confidence interval and the 95% confidence interval are given by $h_i\pm \sqrt{\widehat{V}\left({\widehat{H}}_i\right)}$ and $h_i\pm 2\sqrt{\widehat{V}\left({\widehat{H}}_i\right)}$, respectively, and $h_i=\widehat{H_i}/H_0$.

6.2. Reconstruction of $h^{\prime }\left(z\right)$

The logistics in this issue remains in the steps explained above. Nonetheless, we are going to proceed with a data set that only includes the coefficients related to the first derivative of $H\left(z\right)$.

Step B1. Reconstruction of $h^{\prime }\left(z\right)$. Let us proceed as in Step A1 until Step A3, where in the latter we performed a linear fit for these points using Equation (17). The fitting coefficients of our interest are determined by the evaluation of the polynomial in $z=0$ as $H^{\prime }\left(0\right)=a_1$, where the prime denotes differentiation with respect to z. The new data set will consist of these $a_1$ coefficients for the 28 simulated data points, to which we apply a least squares fit and then extrapolate to $\lambda =-1$, giving us the data set that we normalize to obtain the values of $h^{\prime }\left(z\right)$ and its respective curve as in Step A5.

Step B2. About the error propagation. Estimating the errors of $h^{\prime }\left(z\right)$ and constructing a similar step as was developed with Equations (24) and (25) can be a little tricky, and it is necessary to be careful in the following methodology. This can be seen from the form of Equation (19), an expression that can be used similarly for $h^{\prime }\left(z\right)$ if we have at hand the values of $H^{\prime }\left(z\right)$ (already obtained in the linear fit performance in Step B1). The next question is: how we can compute the uncertainties of $H^{\prime }\left(z\right)$? We need to start from Step A4, where we perform a least squares fit and the polynomial that we need to propagate now is

$${{\sigma }_{H^{\prime }}}^2={\sigma }_{a_0}^2+z^2{\sigma }_{a_1}^2+z^4{\sigma }_{a_2}^2,$$

(26)

where the σ-values are the diagonal elements of the covariance matrix obtained from $H^{\prime }\left(z\right)$ data set.

With the new set $[H^{\prime }\left(z\right),{\sigma }_{H^{\prime }}]$, we are ready to reproduce the same steps starting in Equation (19) and computing its error and matrix variance Equations (24) and (25). Until now, we have not taken yet into account any normalization of $H^{\prime }\left(z\right)$, an aspect that is implicit in the following propagation of errors

$$\begin{array}{ccc}\hfill {{\sigma }_{h^{\prime }}}^2& =& {\left(\frac{{\sigma }_{H^{\prime }}}{H_0}\right)}^2+\left(\frac{H^{\prime 2}}{{H_0}^4}\right){\sigma }_{H_0}^2.\hfill \end{array}$$

(27)

Finally, using this error propagation and its respective $h^{\prime }\left(z\right)$ value, we can construct the confidence regions as in Step A6.

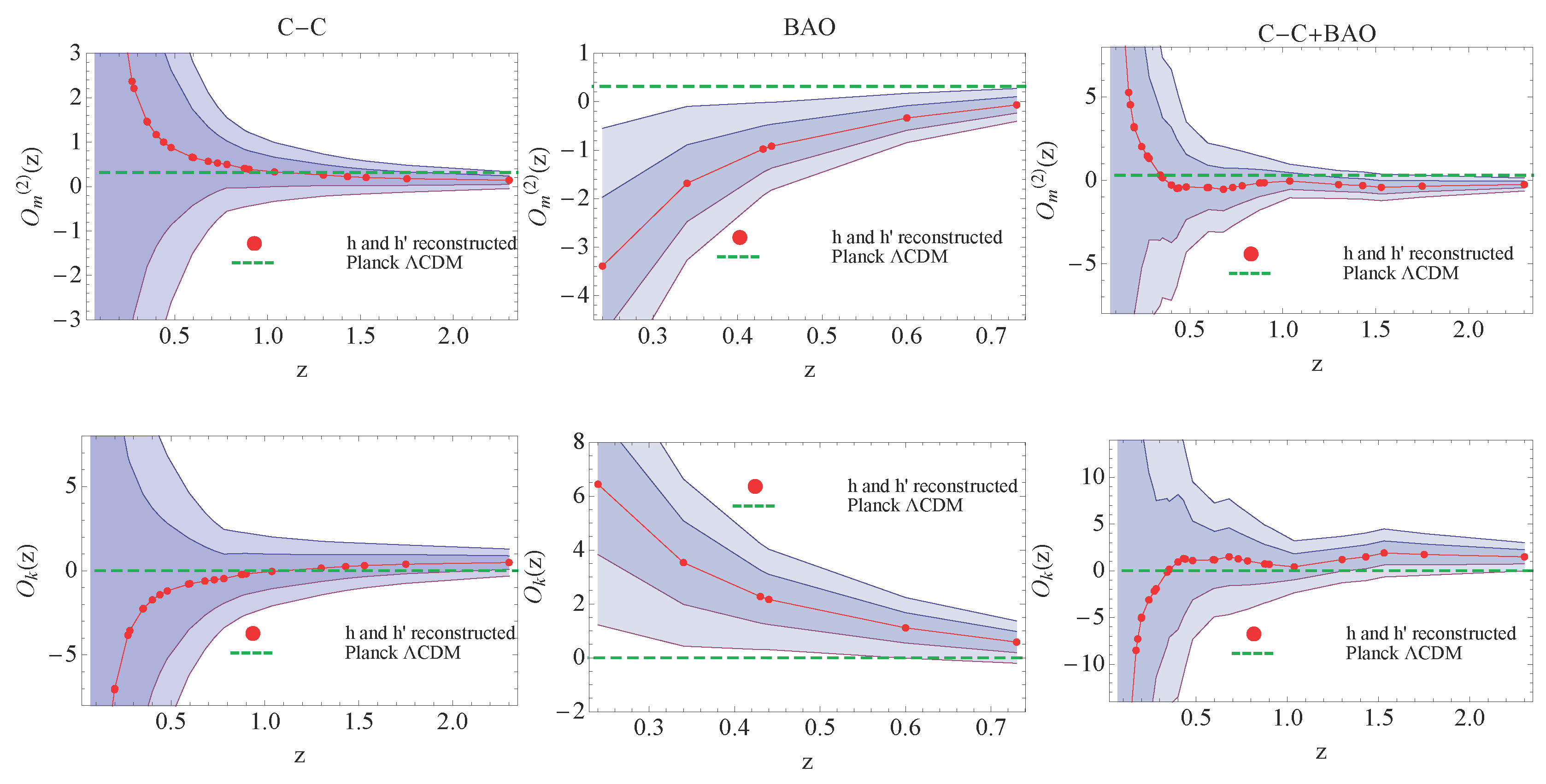
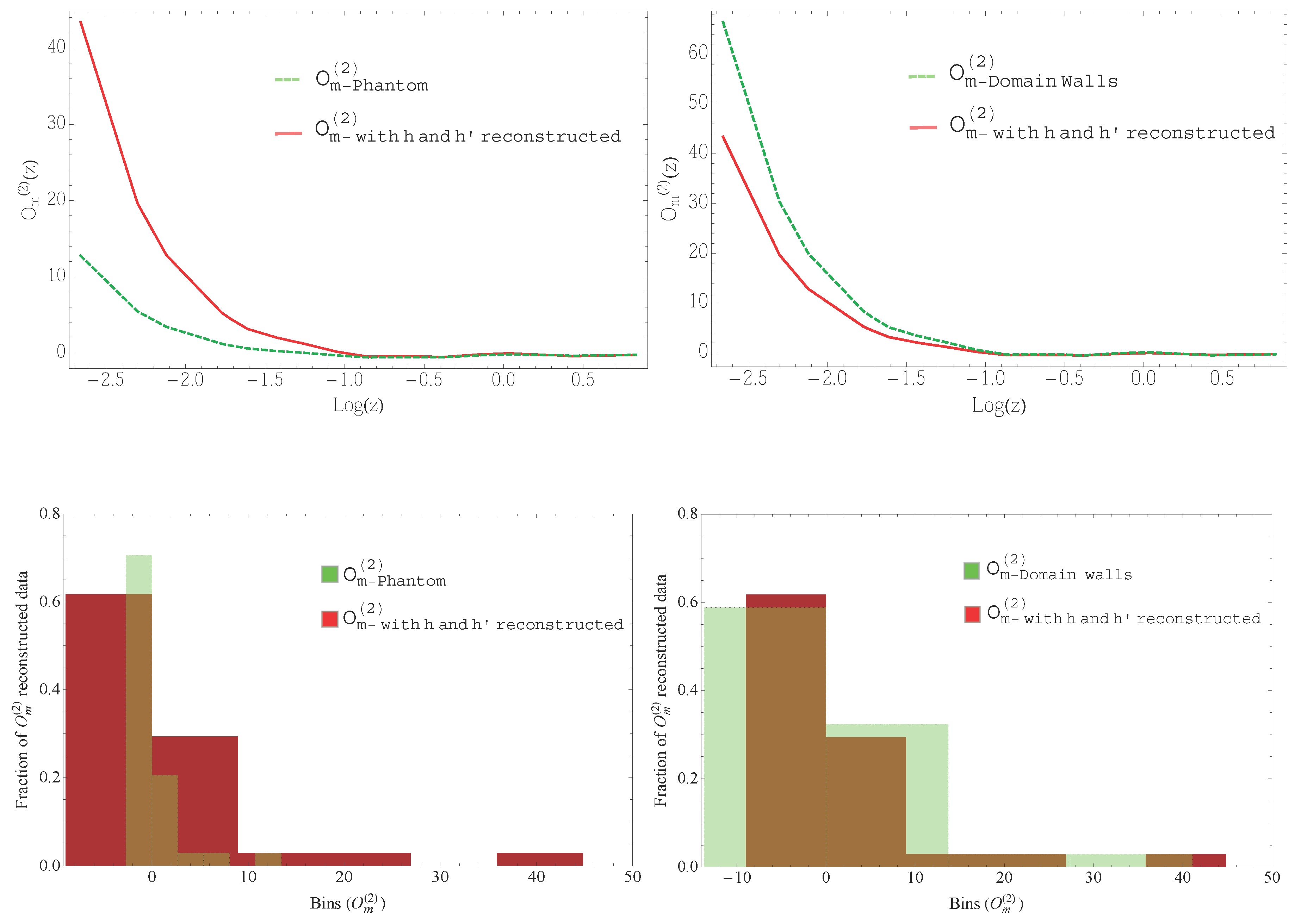
6.3. Nonparametric Reconstruction of the $O_m$ Diagnostic

On one hand, regarding the $O_m$ diagnostic for ΛCDM flat model (8), it is straightforward to compute the $O_m$ data set using the Loess–Simex estimate values $h\left(z\right)$ calculated in Section 6. The values of $O_m$ are given directly from the new data set $\widehat{h}\left(z\right)$.

On the other hand, the uncertainty calculations are easily performed via Equation (21). Thereupon, we constructed the 68% and the 95% confidence intervals using the expressions: ${\widehat{O}}_m\pm {\sigma }_{{\widehat{O}}_m}$ and ${\widehat{O}}_m\pm 2{\sigma }_{{\widehat{O}}_m}$, respectively.

As we discussed, the existence of a non-flat universe brings to the scene $h^{\prime }\left(z\right)$ and $O_k$. In this case, the system is given by Equations (13) and (14), which are independent of the values of the cosmological parameters ${\Omega }_m$ and ${\Omega }_k$ and imply a model that only relies on the values of our reconstructed $h\left(z\right)$ and $h^{\prime }\left(z\right)$.

The confidence regions will be computed using the error propagation Equations (21) and (22) and the expressions: ${\widehat{O}}_m^{\left(2\right)}\pm {\sigma }_{{\widehat{O}}_m^{\left(2\right)}}$, ${\widehat{O}}_m^{\left(2\right)}\pm 2{\sigma }_{{\widehat{O}}_m^{\left(2\right)}}$ and ${\widehat{O}}_k\pm {\sigma }_{{\widehat{O}}_k}$, ${\widehat{O}}_k\pm 2{\sigma }_{{\widehat{O}}_k}$.

7. Discussion and Conclusions

We developed the Loess–Simex factory to achieve two interesting goals. First, we performed the reconstruction of the normalized Hubble parameter $h\left(z\right)$, results that are represented by red dots (red line) in Figure 2, Figure 3 and Figure 4. In addition, in the upper plots of Figure 2, we illustrated the original $H\left(z\right)$ data set represented by blue dots with its respective error values and its nonparametric reconstruction (red dots/line). It is interesting to note the comparison between these reconstructed points and the ΛCDM model, which is represented by a dotted green line.

Our second goal was the reconstruction of the $O_m$ diagnostic and the $O_m^{\left(2\right)}$ and $O_k$ parameters using two astrophysical samples (C-C and BAO) for $H\left(z\right)$ and the combination of them. The reconstruction of the $O_m$ diagnostic was made by considering two options: (I) using the already reconstructed h values (top of Figure 3) and (II) performing directly its reconstruction (bottom of Figure 3).

Let us discuss the results for each case.

For the C-C sample, the nonparametric reconstruction has the same trend as the one reported in [38]. However, in our case, we worked with the normalized Hubble parameter h, the behaviour of which is analogous to the previous case, as it is expected. The direct reconstruction of the $O_m$ diagnostic appears to be in good agreement with ΛCDM at $z>1$. It is interesting to notice that, in this case, the confidence regions look smaller than in the case when we use the reconstructed h data.

For the BAO sample, unlike other proposals mentioned above, our results show a ΛCDM model that lies in our $O_m$ confidence contour reconstructions at 2-σ, even by performing the reconstruction with a few values of this data set. As in the previous sample, the direct reconstruction of this diagnostic gave a concordance model between 1 up to 2-σ. The reconstructions of $O_m^{\left(2\right)}$ and $O_k$ imply the reconstruction of $h^{\prime }$, and the analysis shows large uncertainties. Even so, the reconstructions at high redshifts show a trend that possibly can loiter to ΛCDM at $z>0.7$ (see Figure 4, middle row).

For the C-C+BAO sample, we observe that the reconstruction is almost similar to the C-C case, clearly due to the amount of data of the first sample in comparison to the second sample. The concentration of data points at $z<0.5$ is related to the effects of the evaluation of the reconstructed data in Equation (8). We observed in the $O_m^{\left(2\right)}$ analysis a pull of the reconstructed curve up at $z<0.3$, which probably shows the important relationship between derivatives of the data and the model itself. The direct reconstruction at zero-order loiters to ΛCDM up to $z=1$, but because this is not a constant in the entire redshift range, we need to consider a dynamical test.

In order to find the adequate DE model in agreement with the reconstructions, we have performed a $O_m^{\left(2\right)}$ diagnostic (first-order in h, i.e., $h^{\prime }$), determining that even when the $O_m^{\left(1\right)}$ diagnostic hints to a phantom behaviour, when we enter in the region $w>-1$, the reconstructions have a preference for a EoS with known physical meaning $w=-2/3$, which corresponds to a static domain wall network in the entire redshift range. This EoS value is also able to reproduce the current cosmic acceleration in unified dark energy models [52,53,54,55,56,57]. At the top of Figure 5, we compare the dynamical $O_m^{\left(2\right)}$ diagnostics reconstructed (red curves) with $O_m^{\left(2\right)}$ diagnostics Equation (11) (green dashed curves) using two specific DE EoS models. How much is the fraction of the reconstructed data that make one DE model better than the other? To answer this, we calculated the probability of this fraction for each DE model in terms of the $O_m^{\left(2\right)}$ bins. The results are represented by the histograms at the bottom of Figure 5. The green bars represent DE models (phantom and static domain walls) and the red bars represent the amount of the reconstructed data. The bin widths for the $O_m^{\left(2\right)}$ reconstructed values are calculated by using [58]. We have that 62% of the reconstructed data lie in $O_m^{\left(2\right)}<0$. Then, in this range, we observe that the amount of $O_m^{\left(2\right)}$ deviation between this data and each DE model corresponds to 8% for a phantom model and 3% for a static domain wall, making the latter a better model in agreement with the reconstructed data.

In addition, we notice the existence of poles in both analyses (see, for instance, Equations (8), (11) and (12)) only for the case when $w=-1$, which can be related with the problem of the phantom divide line. However, at least at this point in the diagnostic, this kind of divergence is an intrinsic problem that is not relevant since the current data available do not include $z=0$. Forthcoming studies along the lines of these analyses promise to greatly improve with the use of high quality observations to make this nonparametric $O_m$ diagnostic more accurate and a very useful tool for testing alternative DE parameterizations and modify gravity proposals.