The Evaluation of Linear Complementarity Problem Method in Modeling the Fluid Cavitation for Squeeze Film Damper with Off-Centered Whirling Motion

Abstract

For the application of squeeze film damper (SFD) in aero-engine, a cavitation model is evaluated by means of linear complementarity problem (LCP) method. Different from the conventional SFD study that employs circular-center orbits (CCOs), a realistic condition is explored where the shaft whirling center and bearing center are misaligned. Taking into account the fluid as incompressible and compressible, the governing equations, including film cavitation, are respectively solved by developing an algorithm using the LCP method. The numerical results are compared with experimental data and the effectiveness of the model is verified. The proposed model can provide some references to investigate the competency of this cavitation method in SFDs.

1. Introduction

Squeeze film dampers (SFDs) have been widely used in modern aircraft engines to attenuate the structure vibration and reduce the cabin noise. SFDs are lubricating elements that provide mechanical support and viscous damping in a rotordynamic system. The application of SFDs on aircraft engines reduces the vibration amplitudes of the rotor at critical speeds and increases the onset of the rotor instability speed [1]. However, current analytical SFD models are often simplified and have not been calibrated for engine applications. Very little test data are available in the literature for realistic engine conditions. Therefore, it is essential to advance the modeling technology in this field and provide references for its industrial applications.

The competence of an SFD involves several nonlinear components, such as lubricant cavitation, fluid inertia, damper geometry, seal presence, and oil feeding and draining configurations. These elements play key roles in affecting the behavior of an SFD and they have undergone investigation for many years [1,2]. Despite a large quantity of work in this field, cavitation is still not fully understood to accurately evaluate its impact on the performance of SFD. Cavitation is a phenomenon of film rupture when the fluid pressure drops to the vapor pressure or even below, which is characterized by a complex process of bubble nucleation, growth, and implosion. The occurrence of film cavitation leads to a two-phase flow problem in SFD, which drastically reduces the damper capability [3].

Direct observation of cavitation in SFD is achieved through capturing high-speed photographic images and recording stroboscopic videos [3,4]. The measurement of absolute pressure in a cavitated region is attained by applying specific strain-gauge sensors [5,6,7] or pressure transducers [8,9,10]. These experiments also offer the guidelines for understanding the consequence of cavitation in a squeezed film.

The theoretical approaches to address the cavitation problem diverge on the detection of the cavitation boundary. Conventional models apply the Jakobsson-Floberg-Olsson (JFO) theory [11,12] to numerically solve the cavitation onset and the reformation boundary through extensive iterations. The Elrod cavitation algorithm [13] accelerates the computation by introducing a technique that transforms the governing equation from the elliptic form to a parabolic form. The concept of mass conserving in the cavitated film is recently interpreted as a linear complementarity problem (LCP) and a reformulated model is illustrated for an incompressible liquid [14]. For the compressible flow, two mathematical models are presented in references [15,16] for a thin film flow between two surfaces in relative motion. Although the LCP method demonstrates general agreement with analytical results in several specific bearing configurations [14,15,16], little effort has been devoted on this manner to addressing the cavitation phenomenon in SFD and comparing it with the experiment data.

A new LCP algorithm is proposed in this paper for modeling the cavitation in SFD. The developed cavitation model includes a complementarity pair that is different from previous work [14,15,16]. The paper is organized as follows: firstly, the governing equation is presented for the flow in SFD with open-ended condition; accordingly, two mathematical models are introduced to investigate the cavitation, where the flow is treated as incompressible and compressible, respectively. The formulated equations contain complementarity variables and the equations can be numerically solved. Moreover, the cavitation algorithm is applied to simulate off-centered whirling motion with no oil feeding, fully degassed lubricant, and open-end SFD application. Finally, the predictions are compared with existing experimental data [17] to verify the model accuracy.

2. Mathamatical Model

The flow equation in a hydrodynamic bearing system is usually governed by the Reynolds equation [18]. When considering an SFD that has a small length-to-diameter ratio (i.e., $L/D\to 0$) with open-ended configuration, the circumferential flow in the film can be regarded as effectively small [2]. Accordingly, the Reynolds equation is reduced to

$$\frac{\partial }{\partial z}(\frac{\rho h^3}{12\mu }\frac{\partial p}{\partial z})=\frac{\partial \rho h}{\partial t}$$

(1)

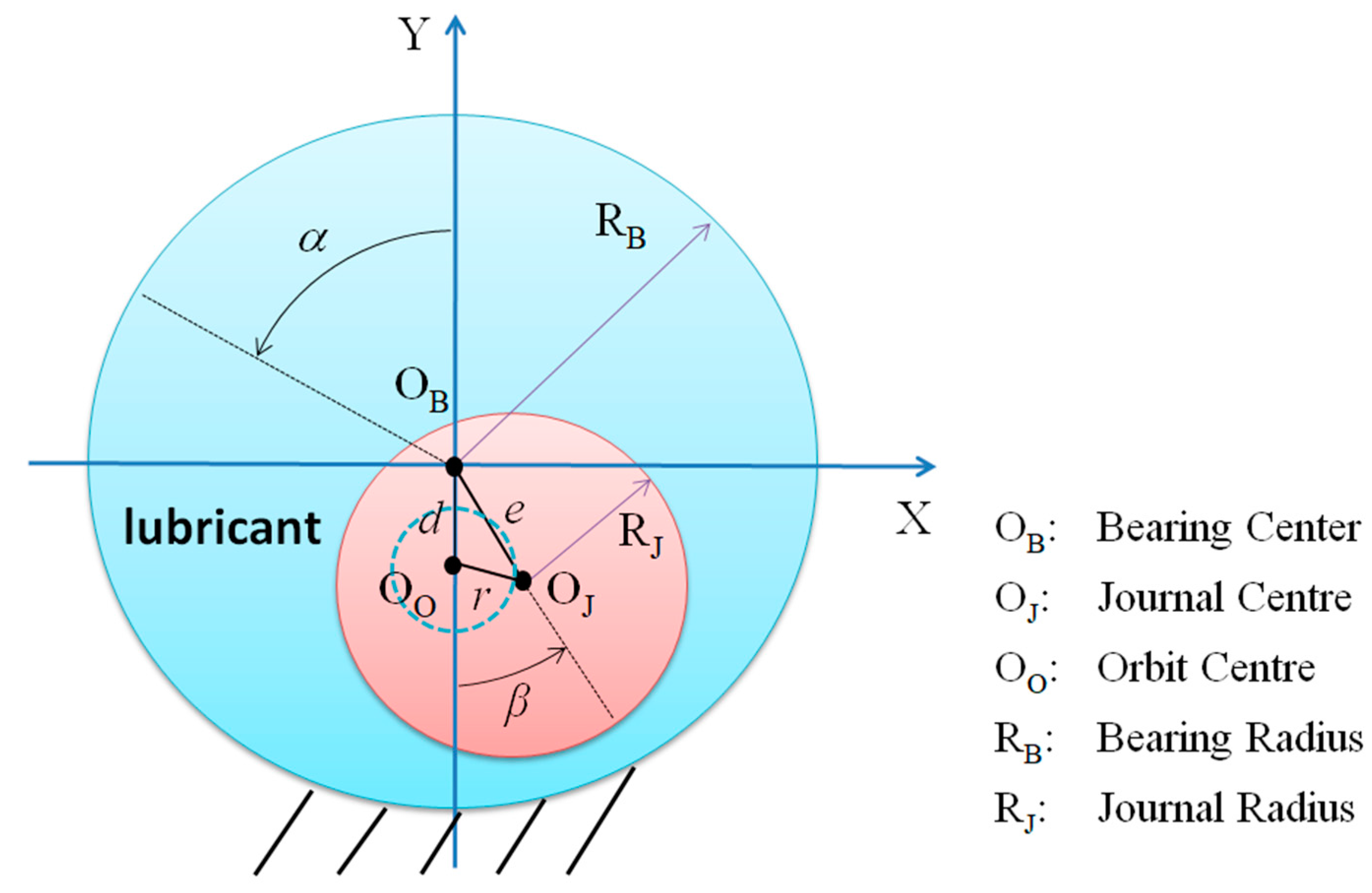
For SFD executing offset circular orbits, the film thickness at a specific time is determined by parameters including the radial clearance, the orbit ratio, the offset ratio, and the whirling frequency. Based on the coordinate relationship shown in Figure 1, the mathematical expression of film thickness is given by [19]

$$h=c(1-\delta \cos \alpha -\lambda \cos (\beta -\alpha ))$$

(2)

$$\beta =\omega t$$

(3)

The solution to Equation (1) provides the general dynamic response of SFD. To solve this equation with the occurrence of film cavitation, the following method is proposed.

2.1. Incompressible Flow

The LCP method for incompressible flow was introduced in [14], where the author considered cavitation only at absolute zero pressure. In this paper, the LCP method is extended to a model where the film can be ruptured at any prescribed pressure. This new incompressible flow model is more general in cavitation conditions and it follows the principle of mass conservation.

2.1.1. Governing Equation

The lubricant density is assumed to be a constant in the full-film region, namely ${\rho }_0$, and the pressure is considered unchanged in the cavitation zone, namely $p_c$. Instead of solving the pressure and density directly, one can solve for the relative pressure $\Delta p$ and the relative density $\Delta \rho$ first, where

$$\begin{array}{l}\Delta p=p-p_c\\ \Delta \rho ={\rho }_0-\rho \end{array}$$

(4)

In the full-film region, the pressure is above the cavitation pressure (i.e., $p>p_c$) while the density is equal to the lubricant density (i.e., $\rho ={\rho }_0$). One can get the following relation accordingly

$$\{\begin{array}{l}\Delta p>0\\ \Delta \rho =0\\ \Delta p\cdot \Delta \rho =0\\ \frac{\partial \Delta p}{\partial z}\cdot \Delta \rho =0\end{array}$$

(5)

In the cavitation zone, the pressure is equal to the cavitation pressure (i.e., $p=p_c$), while the density is below the lubricant density (i.e., $\rho <{\rho }_0$), rendering that

$$\{\begin{array}{l}\Delta p=0\\ \Delta \rho >0\\ \Delta p\cdot \Delta \rho =0\\ \frac{\partial \Delta p}{\partial z}\cdot \Delta \rho =0\end{array}$$

(6)

If the Swift-Stieber boundary condition [18] is applied for the cavitation interface and we assume that the mass transfer is null between the full-film and the cavity regions, the following equation is derived

$$\{\begin{array}{l}\Delta p=0\\ \Delta \rho =0\\ \Delta p\cdot \Delta \rho =0\\ \frac{\partial \Delta p}{\partial z}\cdot \Delta \rho =0\end{array}$$

(7)

Consequently, the relative pressure and relative density are complementary to each other everywhere within the lubricant film. In other words, the following condition is valid regardless of film rupture

$$\{\begin{array}{l}\Delta p\ge 0\\ \Delta \rho \ge 0\\ \Delta p\cdot \Delta \rho =0\\ \frac{\partial \Delta p}{\partial z}\cdot \Delta \rho =0\end{array}$$

(8)

Since $\Delta p$ and $\Delta \rho$ are complementarity pairs, the governing equation is proposed to be interpreted into a linear complementarity equation.

Substitution of Equation (4) into Equation (1) gives

$$\frac{\partial }{\partial z}\left[\frac{({\rho }_0-\Delta \rho )h^3}{12\mu }\frac{\partial (\Delta p+p_c)}{\partial z}\right]=\frac{\partial ({\rho }_0-\Delta \rho )h}{\partial t}$$

(9)

As the cavitation pressure is assumed to be constant, the above equation can be reduced to

$$\frac{\partial }{\partial z}\left[\frac{({\rho }_0-\Delta \rho )h^3}{12\mu }\frac{\partial \Delta p}{\partial z}\right]=\frac{\partial ({\rho }_0-\Delta \rho )h}{\partial t}$$

(10)

Application of the complementarity condition (i.e., Equation (8)) to Equation (10) yields

$$\frac{\partial }{\partial z}\left(\frac{{\rho }_0{h}^3}{12\mu }\frac{\partial \Delta p}{\partial z}\right)=\frac{\partial ({\rho }_0-\Delta \rho )h}{\partial t}$$

(11)

Provided that the pressure and density at the initial state, i.e., $t=0$, one can incrementally solve the above equation at any time and find the dynamic response of the system. The backward difference scheme is used to approximate the time derivations in this study.

To formulate an LCP equation, the finite difference method is applied to discretize the physical domain (which is the axial length in this case) into a uniform grid with N elements of size $\Delta z$($\Delta z=L/N$). A central difference scheme is used to approximate the derivatives on the left side of Equation (11), and a backward difference scheme is applied on the right side. The discretized equation is given as follows

$$\frac{{\rho }_0{(h_{}^k)}^3}{12\mu }\frac{\Delta p_{i+1}^k-2\Delta p_i^k+\Delta p_{i-1}^k}{{(\Delta z)}^2}=\frac{({\rho }_0-\Delta {\rho }_i^k)h_{}^k-({\rho }_0-\Delta {\rho }_i^{k-1})h_{}^{k-1}}{\Delta t}$$

(12)

where $i$ denotes the node in the axial location, while $k$ denotes the step in the time frame.

Equation (12) can be further organized into a standard LCP form as

$$\{\begin{array}{l}\left\{\Delta p\right\}=\left[M\right]\left\{\Delta \rho \right\}+\left\{q\right\}\\ \left\{\Delta p\right\}\ge 0\\ \left\{\Delta \rho \right\}\ge 0\\ \left\{\Delta p\right\}{\left\{\Delta \rho \right\}}^T=0\end{array}$$

(13)

where the detailed description is provided in Appendix A.

2.1.2. Boundary Condition

The boundary condition is also constructed with complementarity variables. Given the pressure condition at specific locations where the film is unruptured, e.g., $p=p_{in}>p_c$ at inlet, we have

$$\{\begin{array}{l}\Delta p_{in}=p_{in}-p_c\\ \Delta {\rho }_{in}=0\end{array}$$

(14)

Furthermore, the above condition can be represented in the form of a linear equation as

$$\Delta p_{in}=\Delta {\rho }_{in}+p_{in}-p_c$$

(15)

A similar equation for the flow at the outlet boundary can also be derived. The complete LCP equation for the flow response in an SFD is formulated by these boundary equations and the governing equation for the interior points (i.e., Equation (13)).

An LCP solver would assist in providing the solution with respect to time given the initial flow state. The solution of the system in the current time step is determined by the flow status at the previous time step, and this solution will be subsequently implemented to find the fluid response for the next time step.

2.1.3. Initial Condition

The fluid at initial status can be solved through Equation (11) by neglecting the time variation for the density variables. Accordingly, a discretized form of such equation is shown as follows, and its solution is used as the input for the first time step.

$$\frac{{\rho }_0{(h_{}^0)}^3}{12\mu }\frac{\Delta p_{i+1}^0-2\Delta p_i^0+\Delta p_{i-1}^0}{{(\Delta z)}^2}=({\rho }_0-\Delta {\rho }_i^0)\frac{\partial h_{}^0}{\partial t}$$

(16)

Similarly, one can apply the introduced LCP method to solve the above equation.

2.2. Compressible Flow

The fluid bulk modulus is a material property that is characterizing the compressibility of a fluid. It is employed by reference [13,15] when developing the cavitation algorithms. Our work continues to use this parameter to address the compressibility of the fluid in the liquid phase, and integrate it with the LCP method to find the boundaries for both the leading and trailing edges of the cavitation.

2.2.1. Governing Equation

The fluid bulk modulus $B$ is given in Equation (17), and it shows the relationship between the density and pressure

$$B=\rho \frac{\partial p}{\partial \rho }$$

(17)

Assuming that the fluid bulk modulus is a constant for the flow in the liquid phase, one obtains the following after a direct integration of Equation (17)

$$\rho ={\rho }_c{e}^{\left(p-p_c\right)/B}$$

(18)

Equation (18) can be used to describe the fluid density in the full-film domain; however, it is not compatible for the density in the cavitated region. To address this issue, a modification is proposed by adding a variable to the above equation

$$\rho ={\rho }_c{e}^{\left(p-p_c\right)/B}-\xi$$

(19)

where $\xi$ is defined as a saturation function and it satisfies the following conditions

$$\begin{array}{cccc}\xi =0& in& full-film& region\\ 0<\xi <{\rho }_c& in& cavitation& region\end{array}$$

(20)

However, the unknown variables $p$ and $\xi$ are not in a linear combination. In order to form an LCP equation, Equation (19) is further modified as

$$\rho ={\rho }_c+\eta -\xi$$

(21)

where $\eta$ is a new variable defined as

$$\eta ={\rho }_c\left[e^{\left(p-p_c\right)/B}-1\right]$$

(22)

Equation (21) provides a linear combination of the complementarity pairs $\eta$ and $\xi$, which is in the ideal form to be implemented into the governing equation.

Since the variable $\eta$ connects the unknown pressure $p$ in the film, which is of fundamental interest in an SFD, $\frac{\partial p}{\partial z}$ in Equation (1) needs to be transformed in terms of $\eta$. Equation (22) yields

$$p=p_c+B\ln \left(1+\frac{\eta }{{\rho }_c}\right)$$

(23)

Accordingly, the following relation is derived

$$\frac{\partial p}{\partial z}=\frac{\partial p}{\partial \eta }\frac{\partial \eta }{\partial z}=\frac{B}{{\rho }_c+\eta }\frac{\partial \eta }{\partial z}$$

(24)

In the full-film region, where $p-p_c>0$, the introduced variables follow the condition as

$$\{\begin{array}{l}\xi =0\\ \eta >0\\ \xi \eta =0\\ \xi \frac{\partial \eta }{\partial z}=0\end{array}$$

(25)

In the cavitation region, where $p-p_c=0$, the following equation is derived

$$\{\begin{array}{l}\xi >0\\ \eta =0\\ \xi \eta =0\\ \xi \frac{\partial \eta }{\partial z}=0\end{array}$$

(26)

At the cavitation interface, if the Swift-Stieber condition is considered and the nil mass transfer is assumed, one renders the following

$$\{\begin{array}{l}\xi =0\\ \eta =0\\ \xi \eta =0\\ \xi \frac{\partial \eta }{\partial z}=0\end{array}$$

(27)

Therefore, the introduced variables $\eta$ and $\xi$ are non-negative and complementarity to each other within the squeezed film, i.e.,

$$\{\begin{array}{l}\xi \ge 0\\ \eta \ge 0\\ \xi \eta =0\\ \xi \frac{\partial \eta }{\partial z}=0\end{array}$$

(28)

Substitution of Equations (21) and (24) into Equation (1) gives

$$\frac{\partial }{\partial z}\left[\frac{B{h}^3({\rho }_c+\eta -\xi )}{12\mu \left({\rho }_c+\eta \right)}\frac{\partial \eta }{\partial z}\right]=\frac{\partial ({\rho }_c+\eta -\xi )h}{\partial t}$$

(29)

Applying Equation (28) to the above equation, a reduced form is obtained as

$$\frac{\partial }{\partial z}\left[\frac{B{h}^3}{12\mu }\frac{\partial \eta }{\partial z}\right]=\frac{\partial (\eta -\xi )h}{\partial t}+{\rho }_c\frac{\partial h}{\partial t}$$

(30)

Subsequently, the finite difference method is employed to numerically solve the above equation. After discretizing, the following equation is achieved

$$\frac{B{(h_{}^k)}^3}{12\mu }\frac{{\eta }_{i+1}^k-2{\eta }_i^k+{\eta }_{i-1}^k}{{(\Delta z)}^2}=\frac{({\eta }_i^k-{\xi }_i^k)h_{}^k-({\eta }_i^{k-1}-{\xi }_i^{k-1})h_{}^{k-1}}{\Delta t}+{\rho }_c\frac{h^k-h^{k-1}}{\Delta t}$$

(31)

Consequently, an LCP equation is formulated with respect to the complementarity pairs. The organized LCP equation is

$$\{\begin{array}{l}\left\{\eta \right\}=\left[M\right]\left\{\xi \right\}+\left\{q\right\}\\ \left\{\eta \right\}\ge 0\\ \left\{\xi \right\}\ge 0\\ \left\{\eta \right\}{\left\{\xi \right\}}^T=0\end{array}$$

(32)

where the detailed description is provided in Appendix B.

2.2.2. Boundary Condition

If the full-film flow is considered for the flow at the boundary, one can obtain the following equation for a compressible liquid flow

$$\{\begin{array}{l}{\eta }_{in}={\rho }_c\left[e^{\left(p_{in}-p_c\right)/B}-1\right]\\ {\xi }_{in}=0\end{array}$$

(33)

Hence, Equation (33) is organized into an LCP equation form as

$${\eta }_{in}={\xi }_{in}+{\rho }_c\left[e^{\left(p_{in}-p_c\right)/B}-1\right]$$

(34)

The integration of the LCP equation for the boundary and the interior points formulates the complete equation set that needs to be solved using the existing solver.

2.2.3. Initial Condition

Similarly, the equation for the initial condition can be obtained through neglecting the time variation of unknown variables in Equation (30), i.e.,

$$\frac{B{(h_{}^0)}^3}{12\mu }\frac{{\eta }_{i+1}^0-2{\eta }_i^0+{\eta }_{i-1}^0}{{(\Delta z)}^2}=({\eta }_i^0-{\xi }_i^0)\frac{\partial h^0}{\partial t}+{\rho }_c\frac{\partial h^0}{\partial t}$$

(35)

The solution of Equation (43) is regarded as the flow at the initial state, and it is used as the input value to solve the flow status for a dynamic response.

The simulation result and comparison are discussed in the next section.

3. Case Study

In this section, simulation results under different running conditions are presented. The simulation scenario is simplified by disregarding the thermo-hydrodynamics and air-ingestion effects. Some results from the numerical model are validated against the experiment [17]. The experiment is conducted on an SFD executing offset circular whirls, in the absence of fluid inertia and end-seals. Pressure signals at three locations that are evenly spaced around the squeeze film at the mid-plane are simultaneously recorded in the test.

Table 1. Parameters tested in the experiment.

Parameter	Case I	Case II	Case III
c [mm]	0.385	0.385	0.385
D [mm]	140	140	140
L [mm]	30	30	30
pin [barg]	2→0.2	0.5	1
pout [barg]	0	0	0
δ	0.042	0.23	0.23
λ	0.5	0.46	0.46
ρ0 [kg/m3]	877	877	877
μ [pa·s]	0.06→0.066	0.098	0.077
ω [rad/s]	314	178	209
α1 [rad]	1.44	3.36	3.36
α2 [rad]	5.63	1.27	1.27
α3 [rad]	3.53	5.45	5.45

summarizes the main characteristics of three cases corresponding to the experiment at ‘II run’, ‘IV run’, and ‘V run’ [17]. These cases are selected in the presence of fluid cavitation without the effect of entrained air. The squeeze film Reynolds number at these conditions is less than 0.68 so that the effect of fluid inertia is neglected [2]. The inlet and outlet pressure are considered as approximately equal to the mean pressure of the inlet and outlet grooves in the test rig, respectively. Furthermore, in the simulation model, a linear variation for the fluid viscosity is assumed in Case I. This viscosity function is given as Equation (40), which is developed based on the test condition in order to provide an accurate lubricant property for scenarios under varying inlet pressure

$$\mu =\frac{-p_{in}+20}{300}$$

(36)

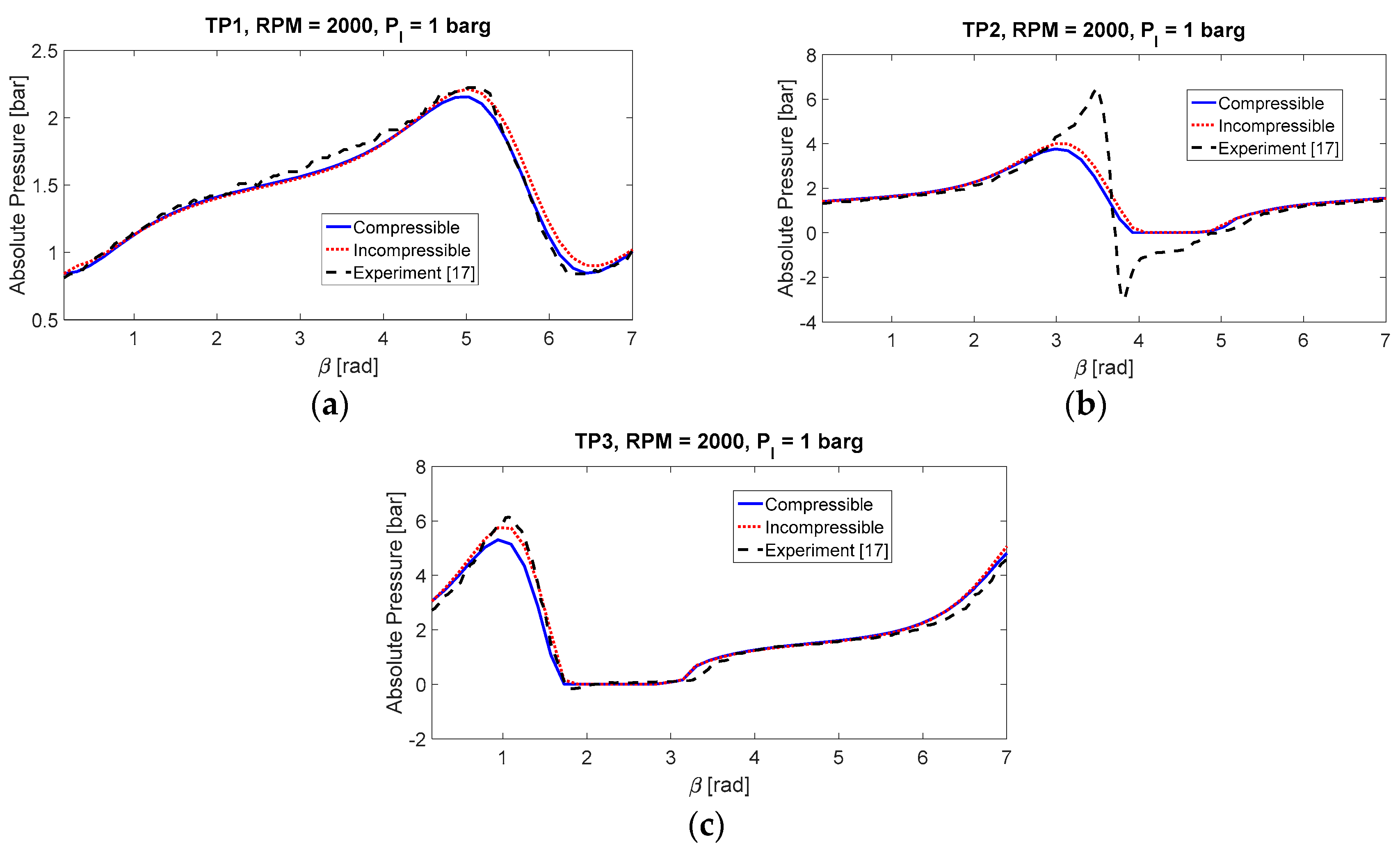
The cavitation pressure is prescribed to be 0.01 bar in all three cases, and the fluid bulk modulus is tested on a value of 10MPa. Simulation results at three different locations, i.e., α_1, α_2, and α_3, are shown in a motion of one whirling cycle.

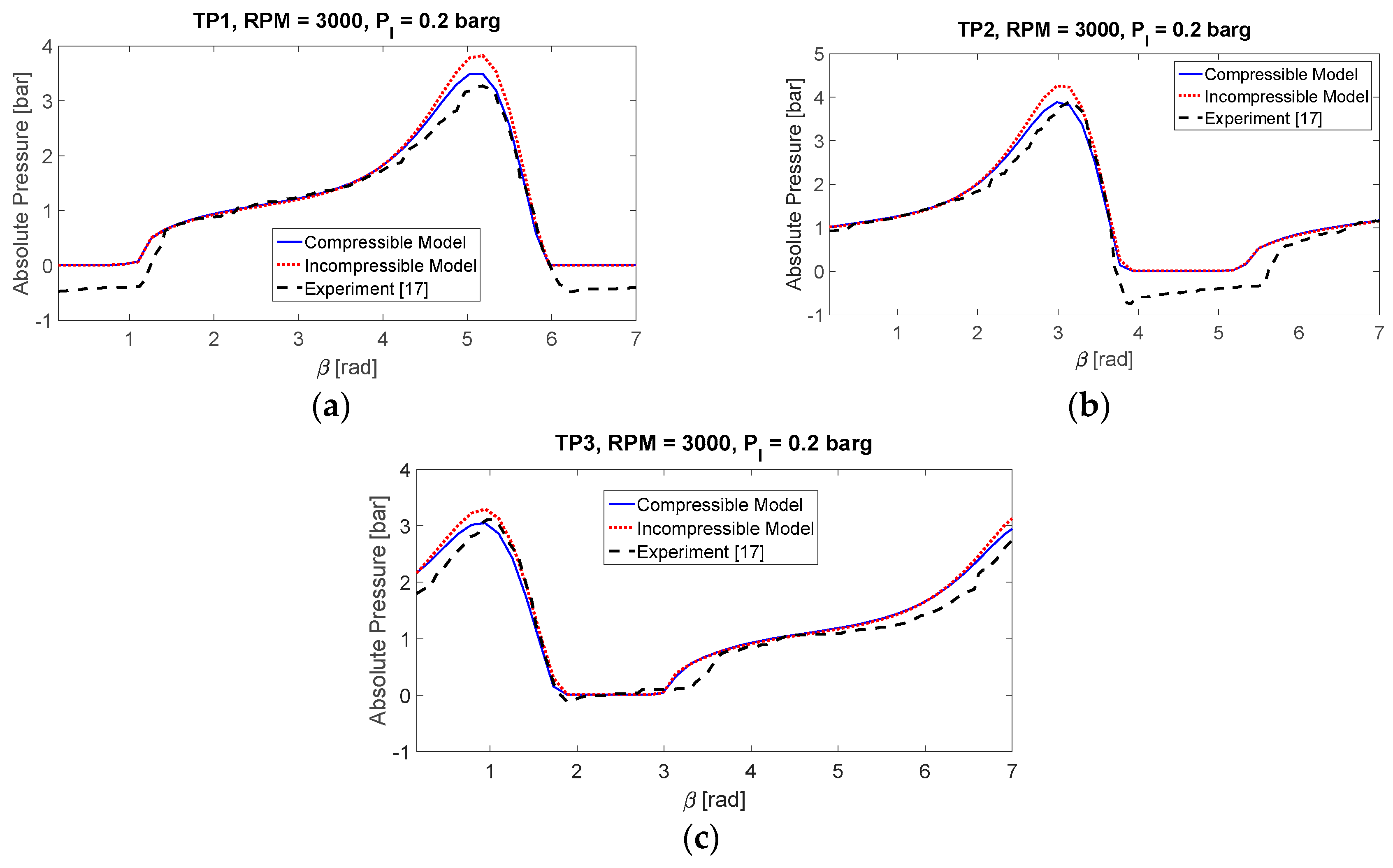
Figure 2 and Figure 3 show the result comparison of Case I between the developed models and the experiment. Figure 2a–c illustrate the pressure for the measured position at α_1, α_2, and α₃, respectively, under the gauge pressure of 0.2 bars. In the positive pressure ranges, the compressible model provides excellent results that are closer to the experiment, while the incompressible model over-predicts the peak pressure. In the cavitation zones, the developed models slightly underestimate the extent of cavitation, with both the incompressible model and compressible model having the same edges for the film rupture and formation boundaries. A deviation of the simulation results from the experiment is that the developed models are not capable of providing any pressure data under the cavitation pressure. This limitation is the result of the assumed cavitation boundary, where a prescribed value is applied to define the pressure in the cavitation zone and the cavitation interface is modeled using the Swift-Stieber condition. In other words, the model implies a condition that the fluid is unable to reach any subcavity pressure without considering the tensile strength of the fluid; while in the actual operation where the SFD is whirling at high speeds, the fluid pressure rapidly oscillates and it reaches negative as a result of the tensile strength. 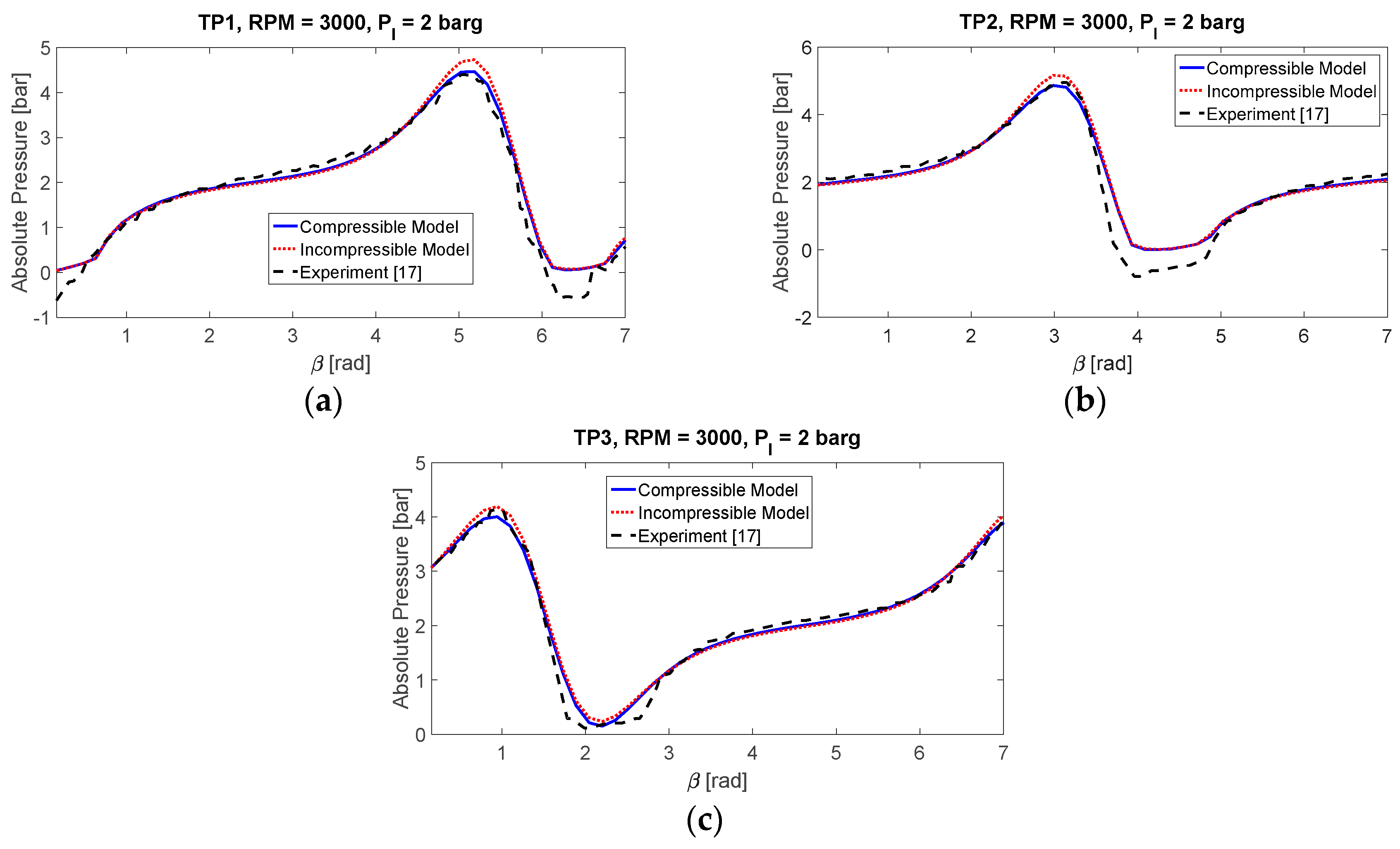Figure 3a–c showed the comparison of pressure at three locations under the gauge pressure of 2.0 bars. It is clear that with the increase of the gauge pressure, cavitation is reduced significantly. The compressible model appears to offer better results than the incompressible model at all of the different positions.

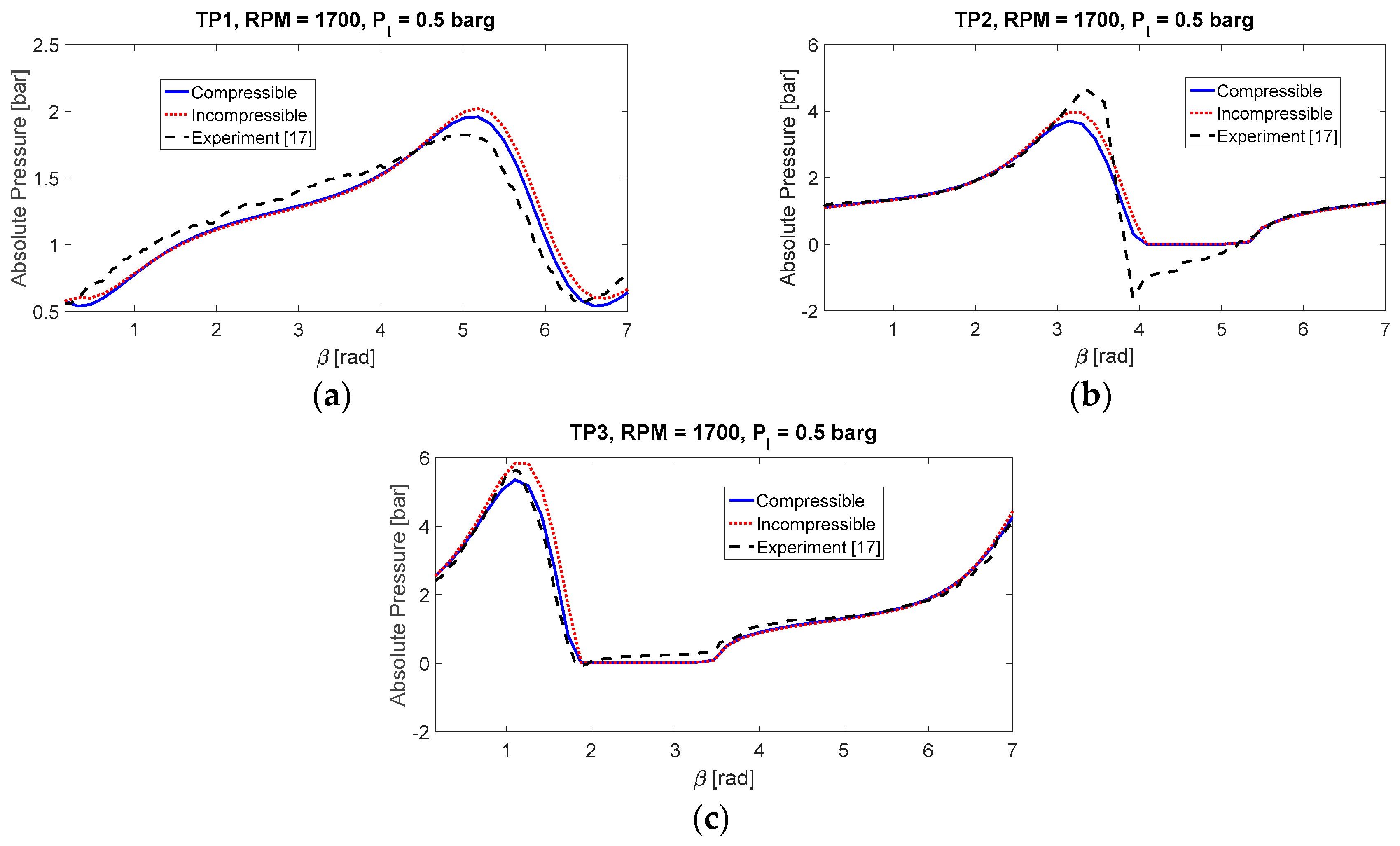
Figure 4 and Figure 5 plot the results for Case II and Case III, respectively. It detects quite clearly some distinctive features in the behavior of the fluid film at high offset ratio. As shown in Figure 4a and Figure 5a, the films remain unruptured at measured position 1 with the smallest pressure fluctuations under both operating conditions. At position 3, where the pressure is theoretically the highest, the simulation provides an accurate prediction of the pressure profile and the extent of the cavitation region, shown in Figure 4c and Figure 5c. A deviance is recorded on position 2, where the maximum pressure is higher than predicted, especially in Case III.

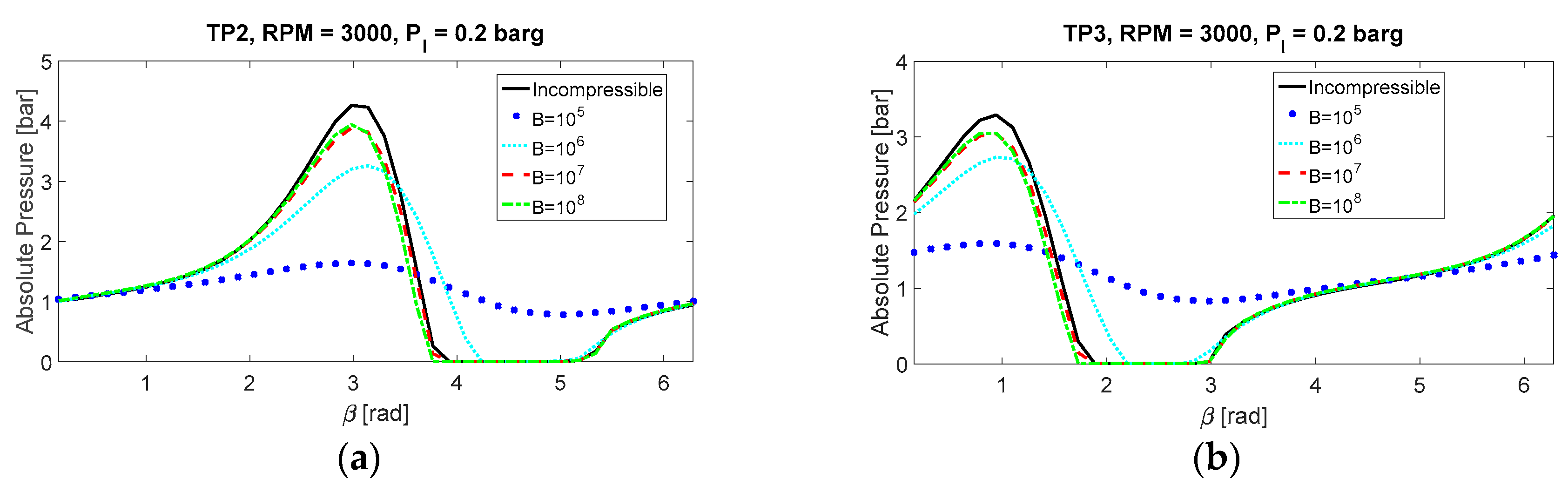
Figure 6 reports a further investigation of the model sensibility by exploring the effect of fluid compressibility. To be specific, a series of the fluid bulk modulus is implemented in the compressible model to produce comparable results. The simulation is conducted under the operating condition of Case I. Figure 6a,b demonstrate the pressure profile at one cycle for position 2 and position 3, respectively. With small fluid bulk modulus, i.e., B = 10⁵, the fluid film is predicted to be in a status with the absence of cavitation. However, as this number increases, the peak film pressure increases; meanwhile, the cavitation zone is expanded as an accompanied phenomenon. The prediction of peak pressure has a limit level for the compressible model, regardless of the magnitude of the fluid bulk modulus. If compared with the incompressible flow model, the simulation from the compressible model presents a lower maximum pressure but a larger cavitation area, and a higher bulk modulus provides closer predictions to the ones from the incompressible model.

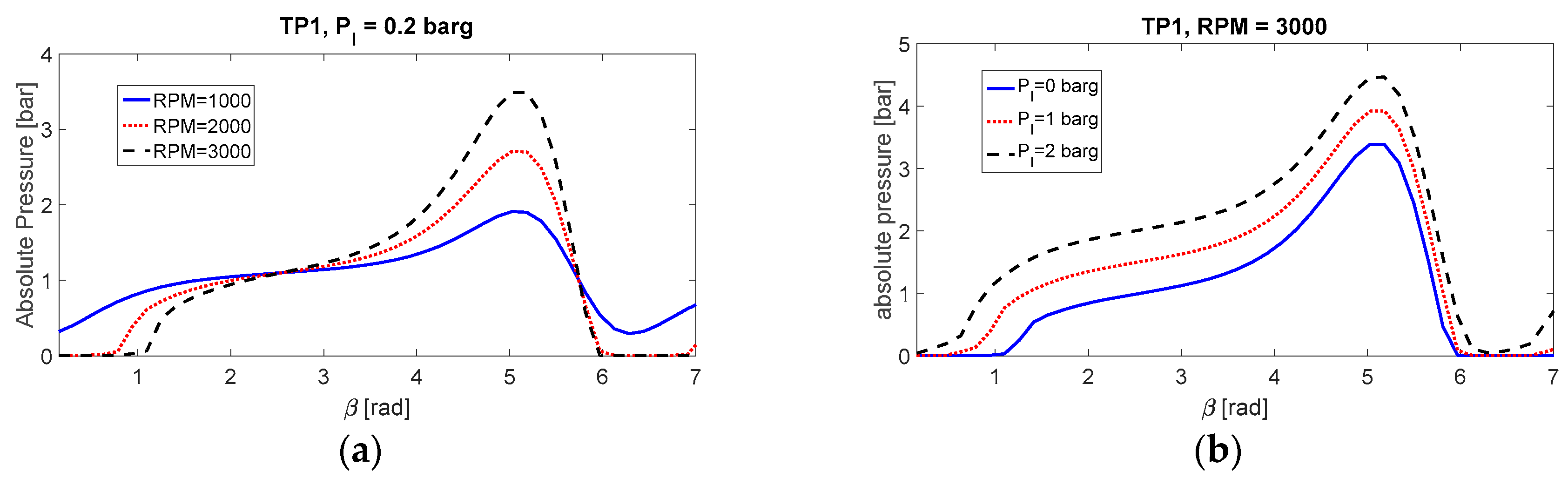
Figure 7 examines the model competence by adjusting the operating speed and oil supply pressure, following the scenario from the Case I study. The whirling speed is carried out at low, medium, and high speeds, i.e., 1000 RPM, 2000 RPM, and 3000 RPM, respectively. Figure 7a shows the film behavior of position α₁ under difference running speeds. The pressure is fairly regular, with small amplitude at low speed, in the absence of film cavitation. As the speed increases to a higher level, the maximum pressure raises and cavitation starts to occur. A large operating speed tends to cause an increased amount of cavitation and larger pressure variations. Figure 7b plots the mid-plane pressure of the film under different oil feeding conditions, with the supply pressure studied at 0, 1, and 2 bars. At small gauge pressure, the developed film pressure is relatively low, while the region of cavitation is fairly large. As the inlet pressure increases, the film pressure increases simultaneously, and the size of cavitation shrinks. It is very likely that if the inlet pressure reaches a certain level, cavitation would disappear.

4. Conclusions

This research demonstrates a new approach to address the cavitation phenomenon in SFD. The model is developed based on the LCP method for both incompressible and compressible flow assumptions. To determine the pressure distribution in the fluid system, the finite difference method is applied. The resulting equation is efficiently solved by the LCP solver. The cavitation model is validated against the experimental data that is reported in the literature under three different operating conditions. Both incompressible and compressible flow models present overall agreement with the test data. The results show that the compressible fluid model has the advantage of predicting the pressure in the positive range. Both models give excellent performance on the prediction of the cavitation extent.

The model sensitivity is studied by evaluating the value of fluid bulk modulus. Higher fluid bulk modulus provides closer predictions to that from the incompressible flow model. The computational speeds for both models are similarly fast without facing any convergence issues. Given the lubricant bulk modulus, the compressible model is suggested for application due to its advantage on the pressure prediction in the active film section.

Furthermore, simulation is performed at different operating speeds and different conditions for oil supply pressure. The predicted results shows that high speeds and low feeding pressure are contributors in the development of film cavitation, and high supply pressure would prevent the occurrence of cavitation.

Overall, the developed model is reliable to predict vibration response in SFD applications.