1. Introduction
This article presents an experimental characterization of the mechanical properties of a hollow sphere steel foam manufactured by the Fraunhofer Institute in Dresden, Germany. Following experimental results, computational models of hollow sphere steel foam are introduced. The characterization of the hollow sphere foam encompasses more material properties than do most reports in the open literature, which focus on the compressive yield stress and densification strains [
1,
2,
3]. The additional material properties, which include compressive plastic Poisson’s ratio, compressive unloading modulus, tensile elastic modulus, tensile unloading modulus, tensile yield stress, and tensile fracture strain, as well as shear properties, provide sufficient information to allow calibration of a macroscopic, continuum, constitutive model for the material.
2. Experimentally Measured Properties of Hollow Sphere Foam
Fifty bars of 15% relative density hollow sphere (HS) steel foam were acquired from the Fraunhofer Institute in Dresden, Germany. Each bar measures approximately 270 mm by 52 mm by 55 mm and is composed of a mild steel of between 0.3% and 0.5% carbon. Each sphere has average 1.85 mm diameter, and 0.08 mm thickness.
2.1. Compressive Properties
Four types of uniaxial compressive tests were performed in order to evaluate the mechanical properties of the foam. All tests were displacement-controlled and used an Instron 3369 testing machine with one extensometer. Tests were based upon standard ISO/DIS 13314(E) (“Compression Test for Porous and Cellular Metals”). The displacement rate was between 0.5 mm/min and 1.0 mm/min (0.3%/min and 1.3%/min) and platens were lubricated with automobile axle grease, and at least three tests of each type were performed:
(i) No unloadings, transverse extensometer (dimensions: 52 mm by 55 mm by 75 mm ± 3%).
(ii) Single unloading in inelastic region, longitudinal extensometer (dimensions: 52 mm by 55 mm by 80 mm ± 2%) (see
Figure 1).
(iii) Unloadings every 0.5% to 1.0% strain, longitudinal extensometer (dimensions: 52 mm by 55mm by either 80 mm ± 2% or 140 mm ± 2%).
(iv) No unloadings, reduced cross-section, no extensometer (dimensions: 25 mm ± 5% by 25 mm ± 5% by 55 mm ± 3%).
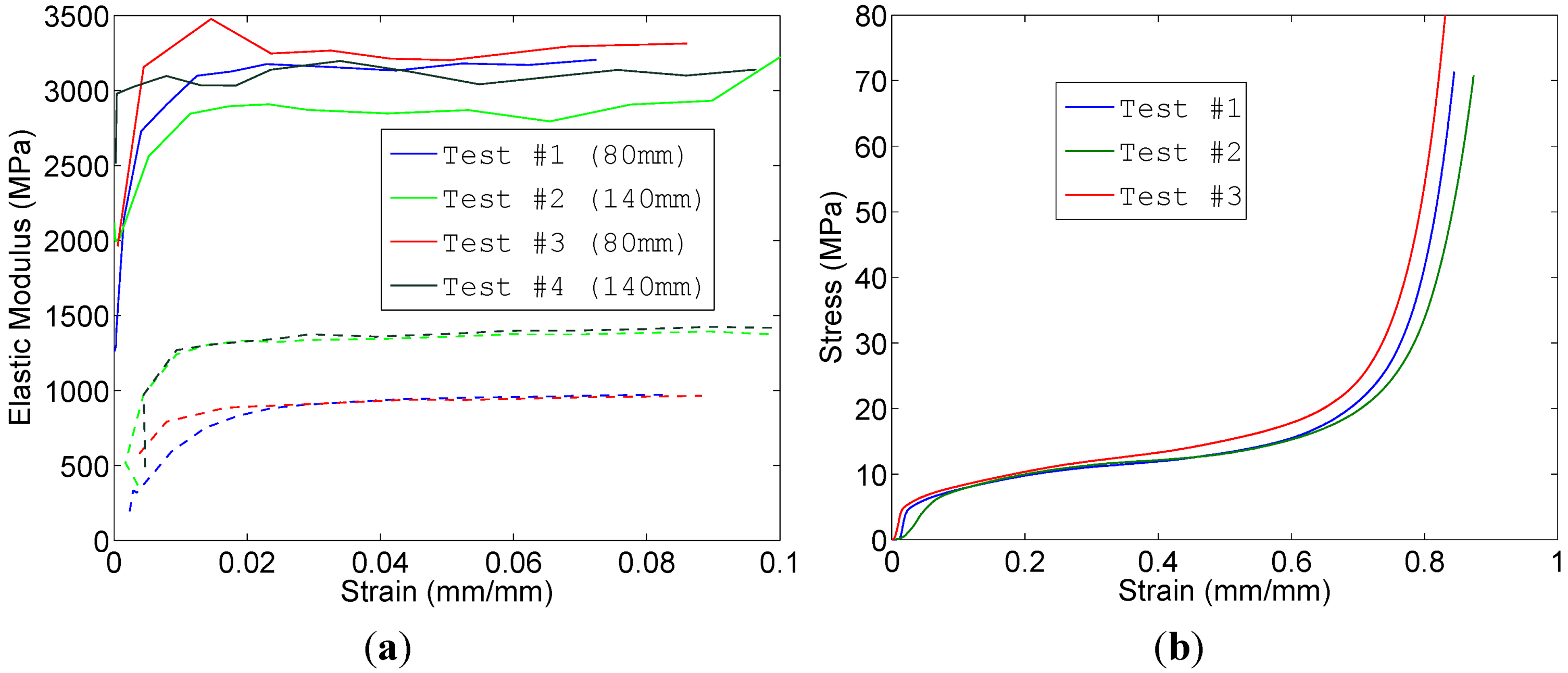
Tests #2 and #3 showed that there is a significant difference between the apparent stiffnesses calculated from extensometer data and crosshead displacement data (3150 MPa
vs. 700 MPa), suggesting that hollow sphere steel foam experiences strong localized strain near the platens. Engineering Poisson’s ratio (test type 1) increased from approximately 0.0 to about 0.2 in the inelastic range, where the Poisson’s ratio appeared to level off between 20% and 50% applied axial strain. Unloading moduli (test type 3) began around 2000 MPa in the elastic range, and rapidly increased to approximately 3150 MPa, a value from which there is minimal deviation with increasing strain (see
Figure 2). Compressive stress-strain curves can be divided into three regimes: linear-elastic, yield plateau with approximately constant slope, and a final portion of steeply rising stress. The strain corresponding to the onset of the rapidly rising portion of the stress-strain curve is labeled as the densification strain [
4].
Figure 1.
Photo of compression test with longitudinal extensometer.
Figure 2.
(a) Elastic modulus vs. strain, as measured from unloadings (test type 3). Upper solid lines represent measurements from the extensometer, lower dashed lines are from crosshead displacement; (b) stress-strain curves for tests up to densification (test type 4).
No established definition exists for the onset of densification, and the following definition was adopted. Let
Et,0.05(ɛ) be the tangent modulus of the material determined by performing a linear regression on the stress-strain curve over the range (ɛ − 0.05, ɛ + 0.05), and define
Et,0.05(ɛ
proof) to be the value of this tangent modulus in the window immediately following the 0.01 proof stress (essentially a 0.01 offset version of the yield stress). Thus, the densification strain is defined as:
In essence, the densification is assumed to begin when the tangent modulus exceeds for the first time the post-yield tangent modulus. Densification begins approximately at a strain of 65% for our hollow sphere foam, at a stress of 17 MPa (test type 4, see
Figure 2). Full results are summarized in
Table 1.
Table 1.
Mechanical properties of steel foam in compression.
| Statistic | Initial Loading Modulus (MPa) | Inelastic Unloading Modulus (MPa) | Yield Stress (MPa) | Densification Strain (mm/mm) | Densification Stress (MPa) | Elastic Poisson’s Ratio | Poisson’s Ratio 50% Strain |
|---|
| Average | 1900 | 3150 | 3.6 | 65% | 17 | ~0.0 | 0.2 |
| Range | ±600 | ±100 | ±0.4 | ±5% | ±3 | ±0.05 | ±0.01 |
2.2. Tensile Properties
Tensile testing was based upon the ASTM E8-08 (“Tension Testing of Metallic Materials”) standard, and specifically the “plate-like” specimen described therein. Modified grips consisting of 25 mm slots cut into both ends of the sample with solid plates epoxied into these two slots were used. Tension was applied at 0.5 mm/min (1.0%/min), and an extensometer was attached to the test section of the specimen (see
Figure 3). Three samples were tested in this manner, plus a fourth one that was tested with repeated unloadings.
Figure 3.
(a) Photo of mounted tension specimen and dimensioned drawing (in mm); (b) Photo of fracture in test #1; (c) Macro photo of tensile fracture surface. Arrows mark examples of where welds pulled out.
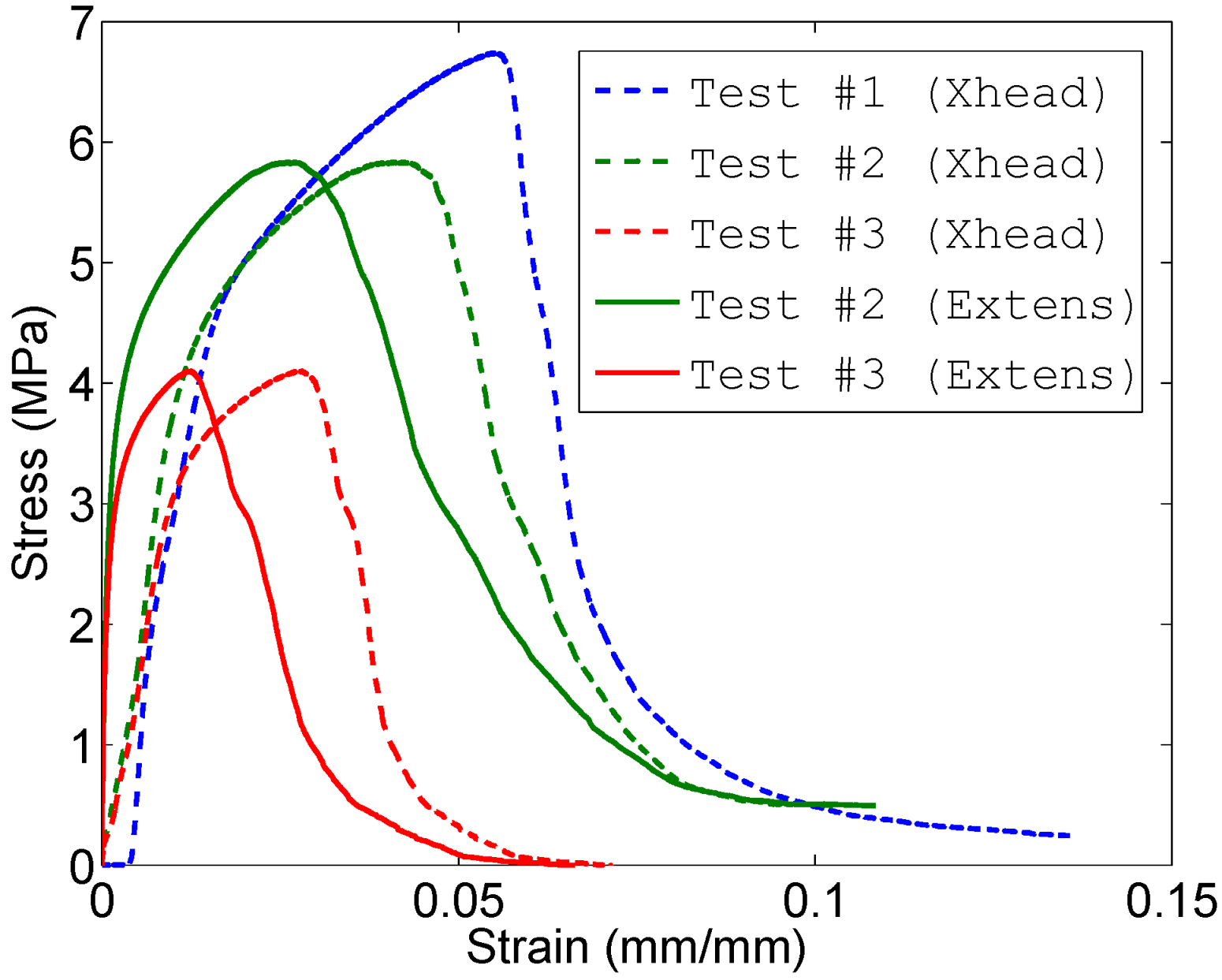
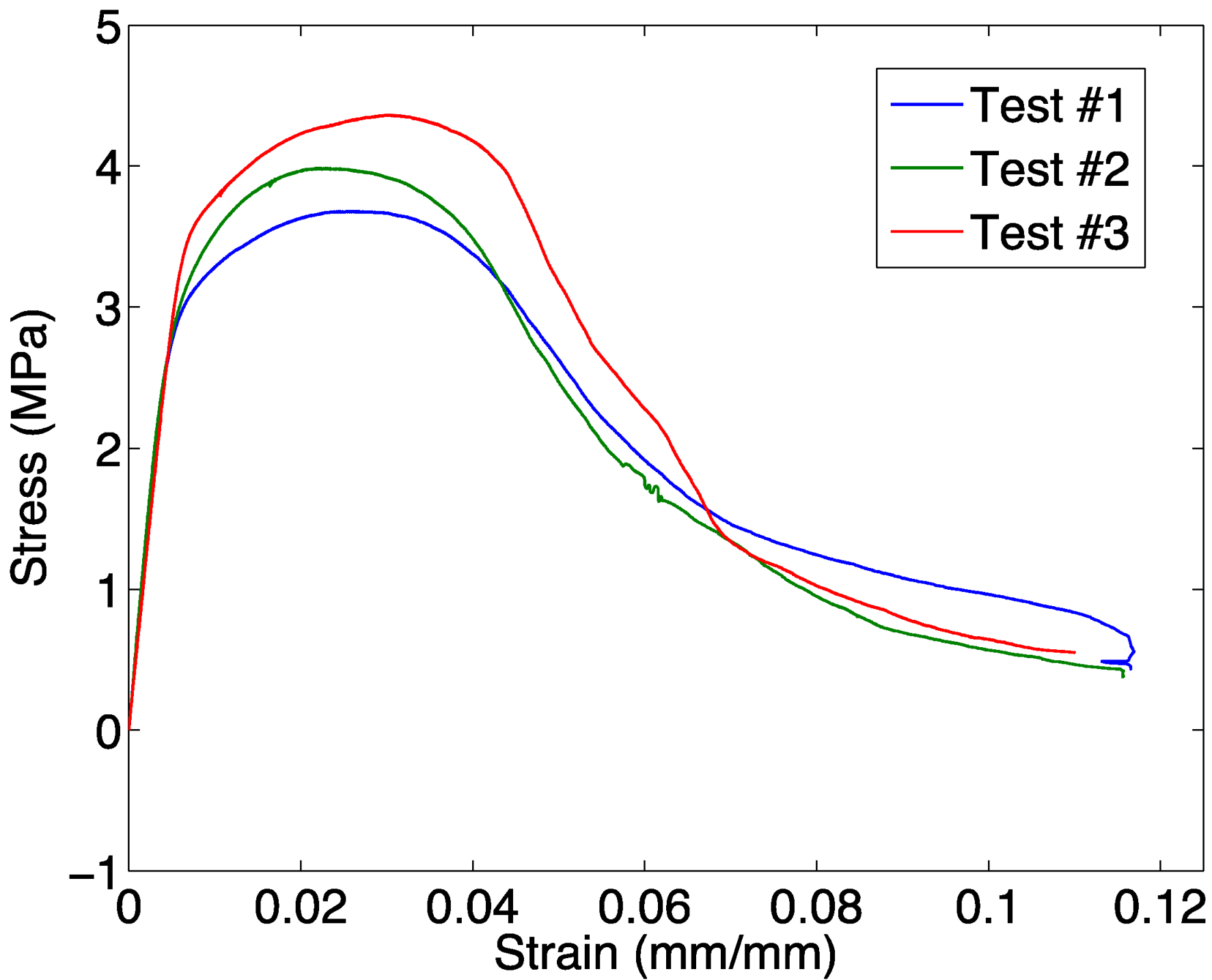
Tension tests showed a wide variation in results (see
Figure 4). Fracture occurred at strains between 1.5% and 4.0%, and ultimate stresses were between 4 and 6 MPa. In tests #1 and #2, the fracture occurred along two distinct cracks (see
Figure 3), while in test #3, the entire cross-section fractured across a single dominant crack. On a mesostructural level, fracture surfaces were characterized by pullout of the sphere-to-sphere welds (see
Figure 3). Unloading moduli were nearly identical to those observed in compression, at approximately 3100 MPa, and only once fracture began did the moduli begin to drop rapidly.
Figure 4.
Tensile stress-strain graph showing crosshead and extensometer measurements.
2.3. Shear Properties
Shear tests were performed upon hollow sphere foam (
Figure 5). Tests showed remarkable consistency, with elastic modulus and ultimate stress varying by less than ±10% (see
Figure 6 and
Table 2). Some ductility is evident in that the material yields before it reaches its ultimate strength. There are also two distinct slopes in the post-yield behavior. The second, smaller slope, beginning at about 0.07 shear strain, is likely where friction between the heterogeneous fracture surfaces begins.
Figure 5.
(a) The full shear test setup;(b) shear specimens #1;(c) and #2 (right) at about 0.08 strain, clearly showing shear cracks.
Figure 6.
Stress vs. shear strain graph for hollow sphere shear tests.
Table 2.
Summary of hollow sphere shear properties.
| Statistic | Shear Modulus (MPa) | Yield Stress (MPa) | Yield Shear Strain (mm/mm) | Ultimate Stress (MPa) | Ultimate Shear Strain (mm/mm) |
|---|
| Average | 648 | 3.3 | 0.007 | 4.0 | 0.026 |
| Range | ±40 | ±0.3 | ±0.001 | ±0.4 | ±0.004 |
2.4. Discussion
Comparing to Friedl
et al. [
5] tests on 8% foams, a similar yield stress (4.6 MPa) but an elastic modulus (640 MPa), nearly 5 times greater than their tests, was observed in compression. In tension, similar values for yield stress (3.3 MPa), fracture strain (3.3%), and fracture stress (5.3 MPa) were observed. This similarity, despite higher relative density of our foam (14.5%), may be explained by Friedl’s use of a stronger base metal (316 L stainless).
Gibson and Ashby [
6] developed mathematical models for predicting the effective properties of metal foams. Comparing all of their available “open-cell” equations to experimental results, the results are within the predicted range with the exception of Poisson’s ratio, which is predicted to be approximately 0.3, differing substantially from our experimental values given in
Table 1.
3. Computational Models
Computational models have been developed using MATLAB and ADINA to simulate the behavior of hollow sphere foam. The model is meshed with either 10-node or 11-node tetrahedral elements, with the maximum element size of approximately 5 mm. Each simulation takes approximately 4–6 h to run on a 6-core, 2.2 GHz per core, 16 GB RAM machine.
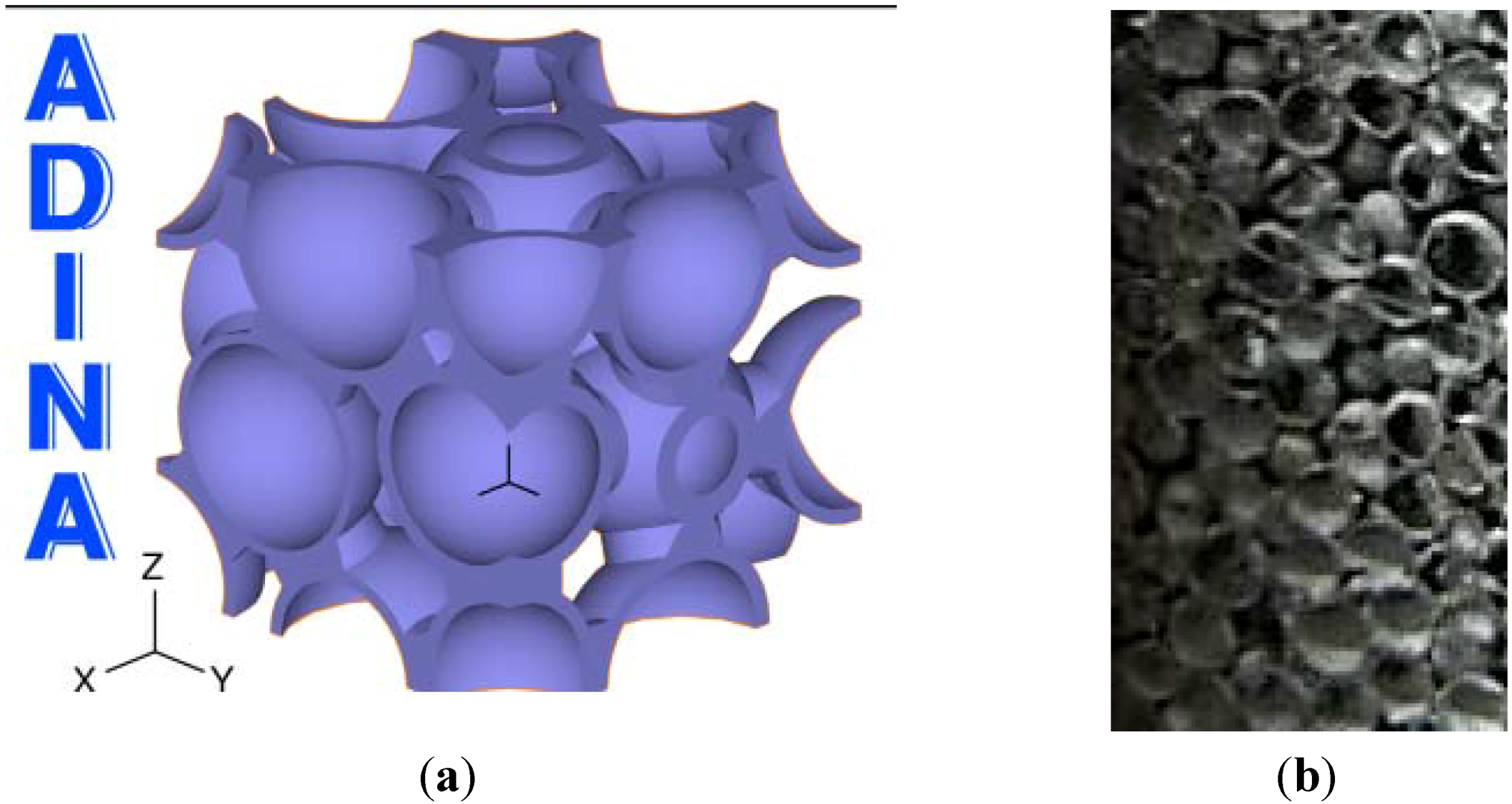
3.1. Hollow Spheres
The mesostructure of sintered hollow sphere foam consist of the spheres and the welds between those spheres. The spheres have been shown to be random close-packed (RCP) [
7]. Wouterse and Philipse [
8] tested five RCP algorithms, and showed that two different variations of the “Mechanical Contraction Method” resulted in RCP stackings that were most similar to an experimental stacking. The simpler of those two algorithms, the “Modified Mechanical Contraction Method”, was selected [
8,
9] for our study. After sphere locations were determined, the cylindrical welds were inserted to connect spheres, or overlapping walls were merged. Sphere size, wall thickness, weld diameter, and sphere location were allowed to vary randomly in order to capture variation in foam mesostructure (
Figure 7).
Figure 7.
(a) Sample geometry generated by hollow sphere algorithm;(b) Steel foam surface.
3.2. Validation
Several simulations were performed in order to validate the full stress-strain curve of the simulations with those obtained experimentally. The study also investigated size effects within the simulations. One 7 mm cube, two 6.25 mm cubes, and several 5.5 mm cubes were simulated. All inputs were based upon microscopy studies when possible. The base metal yield stress 172 MPa was based upon the experimental test performed on compacted samples, and the elastic modulus was initially assumed to be the standard 200,000 MPa. However, based upon microscopy studies of intact foam samples, a microporosity (that is, porosity within the sphere walls themselves) of 20% was estimated and therefore the initial base elastic modulus was reduced by this value. The validation simulations showed increasing accuracy as model size increased from 5.5 to 7 mm (see
Figure 8a,b).
Similarly to experimental tests by Andrews [
10], smaller samples have lower apparent strengths and stiffnesses. No known, published research has attempted to study the effect of model size upon Poisson’s ratio. The simulated Poisson’s ration decreased with the sample size. The simulations of 7 mm models match experimental engineering Poisson’s ratio with reasonable accuracy. While the experimental data is noisy, Poisson’s ratio rises with compressive strains, which indicates a gradual increase in foam incompressibility.
Figure 8.
Validation of lotus-type simulations against experimental stress-strain curve. (a) Compressive stress-strain;(b) Poisson’s ratio.
4. Macroscopic Constitutive Models
Structural models usually employ continuum material properties such as elastic modulus, yield stress, and other macroscopic mechanical properties. Classical von Mises plasticity, utilizing associated flow rules, typically assume incompressibility in the plastic regime [
11] and that yield properties are dependent only on shear stress (distortional energy). However, steel foam is compressible in the plastic regime and thus mean stress is important (dilatational energy).
Miller [
12] and Deshpande and Fleck [
13] generalized von Mises plasticity by accounting for pressure dependence in their effective stress formulation. The model was expanded and validated for aluminum foams by Hanssen [
14] to include nonlinear hardening, and later to also account for tensile fracture by Reyes
et al. [
15]. Our experiments provided data for calibration of Deshpande-Fleck plasticity and enabled simulations of structural components discussed elsewhere [
16]. The continuum level plasticity requires parameters from uni-axial compressive test. Also, tensile fracture strain is needed to calibrate the element erosion criterion in order to account for relatively weak tensile behavior of steel foams. Deshpande and Fleck (D-F) [
13] yield criterion depends on deviatoric stress (von Mises), and on pressure stress σ
m:
where σ
VM = von Mises effective stress:
and σ
m = trσ, and σ
dev deviatoric stress:
The shape of D-F yield surface is controlled by α:
where
vp = plastic Poisson’s ratio at 20% engineering strain [
13].
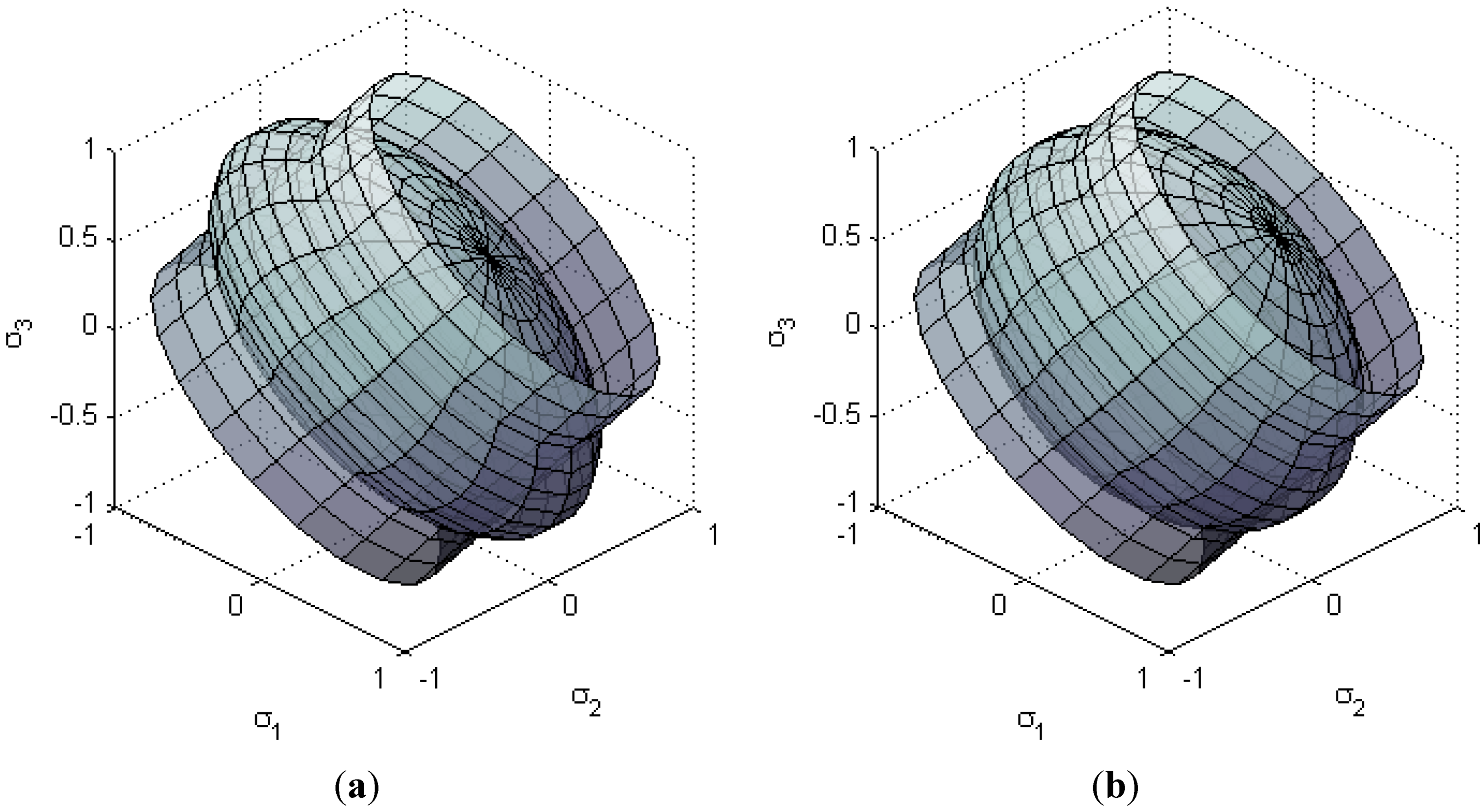
Calibration of D-F plasticity requires measurement of plastic Poisson’s ratio in order to determine the shape of the yield surface. Compressible foam may have plastic Poisson’s ratio as lows as
vp = 0. In such a case, the yield surface is a shallow ellipsoid (
Figure 9a). As foam becomes less compressible, its plastic Poisson’s ratio increases (e.g.,
vp= 0.2), and the yield surface converges toward the von Mises cylinder (
Figure 9b). Plastic hardening parameters are calibrated against uniaxial compressive experiment. Hanssen [
14] proposed an analytical hardening expression in order to enhance numerical stability, and his material subroutine is implemented in LS-DYNA software [
17]:
where ɛ
D = −lnρ = measure of compaction, ρ = foam relative density, and
![Metals 02 00399 i007]()
= D-F effective plastic strain [
13]. Here, σ
p, γ, α
2,βare material parameters, which are obtained by curve-fitting to experimental results (
Figure 10). Calibrated input parameters for our foam are listed in
Table 3.
Figure 9.
Foam plasticity: Deshpande-Fleck ellipsoid, and von Mises cylinder for comparison. (a) vp = 0.0 (α = 2.12); (b) vp = 0.2 (α = 1.5).
Figure 10.
Calibration of foam plastic hardening.
Table 3.
Summary of steel foam material properties.
| Material properties | Model Parameters |
|---|
| Relative density,ρ | 0.145 |
| Elastic modulus | 3150 MPa |
| Poisson’s ratio (elastic) | 0.05 |
| Yield surface | |
| Curve-fitted plateau stress,σp | 7.4 MPa |
| Shape parameter, α | 1.75 |
| Hardening | |
| Curve-fitted, γ | 10.9 |
| Curve-fitted, α2 | 33.2 |
| Curve-fitted, β | 5.5 |
| Failure | |
| Tensile fracture strain | 0.02 |
5. Conclusions
This paper contains three sets of results: experimental characterization of the compressive and tensile properties of hollow sphere steel foams; simulation of the compressive stress-strain response with meso-scale model; and calibration of continuum foam plasticity. Elastic modulus is 3150 MPa in tension and compression for hollow sphere foams, and the elastic Poisson’s ratio is close to 0.0, and engineering plastic Poisson’s ratio at 20% compressive strain is 0.2. Yield stresses of 3.6 MPa are found in compression, and in tension a fracture strain of between 1% and 3% is observed. Shear modulus of 650 MPa, yield stress of 3.3 MPa are observed.
The potential for use of meso-scale simulations was demonstrated. Deterministic models were randomly perturbed in order to enhance the realism of the simulations. The analyzed model needs to be sufficiently large to obtain reasonable estimates of macroscopic material properties. Overly small sample size may result in incorrect estimates of strength and stiffness.
Foam plasticity was calibrated against our experimental results. Continuum foam model is necessary for modeling of structural components, because meso-scale representations become computational prohibitive for components encompassing millions of spheres. D-F plasticity accounts for foam compressibility, in contrast to classical plasticity, which assumes tri-axial incompressibility of metals after initial yield. Also, in order to account for weak tensile strength of hollow sphere foams, fracture criterion needs to supplement the plasticity description.
Future advancements of meso-scale models are needed to enable calibration of continuum foam plasticity for virtual prototyping of structural components. Such progress requires better understanding of base material hardening, inclusion of internal contacts, as well as local imperfections to enable shell buckling initiations, among other computational challenges.

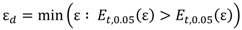



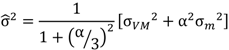
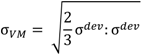
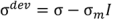
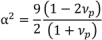
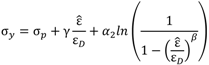
 = D-F effective plastic strain [13]. Here, σp, γ, α2,βare material parameters, which are obtained by curve-fitting to experimental results (Figure 10). Calibrated input parameters for our foam are listed in Table 3.
= D-F effective plastic strain [13]. Here, σp, γ, α2,βare material parameters, which are obtained by curve-fitting to experimental results (Figure 10). Calibrated input parameters for our foam are listed in Table 3.