Mechanical Properties of Metallic Glasses
Abstract
:1. Introduction
2. Elastic Properties
2.1. Simulation of Elastic Deformation
2.1.1. Effect of Heterogeneity in Local Elasticity
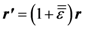
 is the strain tensor and follows the Hook’s law. However, at the atomic level a solid is not a continuum body. As an approximation we may use the von Kármán model of spheres connected by springs [10]. Then Equation (1) could be extended to describe the deformation of the atomic system as
is the strain tensor and follows the Hook’s law. However, at the atomic level a solid is not a continuum body. As an approximation we may use the von Kármán model of spheres connected by springs [10]. Then Equation (1) could be extended to describe the deformation of the atomic system as
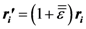
 is uniform, or affine, only for homogeneous deformation of a Bravais lattice with only one atom in the unit cell. If the unit cell contains more than one atom, even for macroscopically uniform strain the local strain is not necessarily the same for each non-equivalent atom,
is uniform, or affine, only for homogeneous deformation of a Bravais lattice with only one atom in the unit cell. If the unit cell contains more than one atom, even for macroscopically uniform strain the local strain is not necessarily the same for each non-equivalent atom,
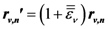

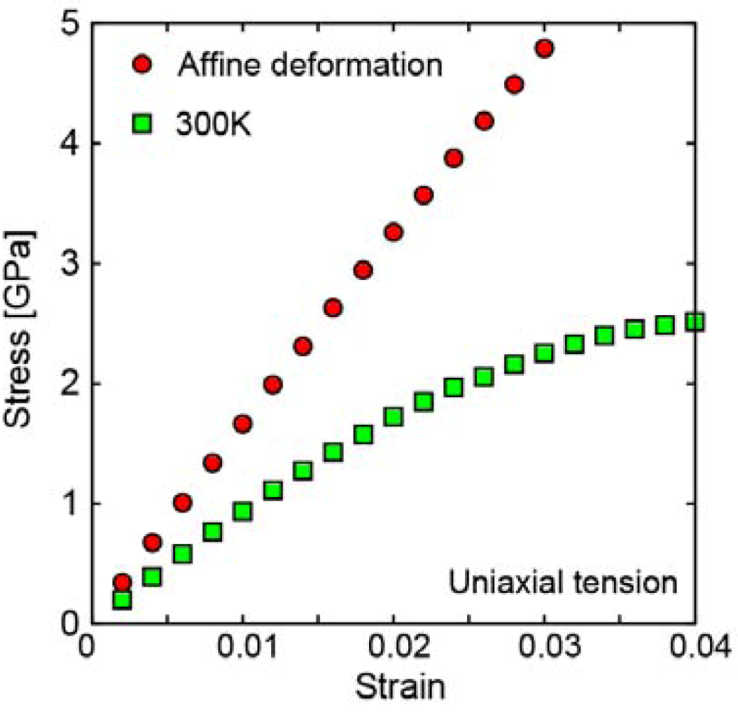

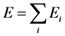
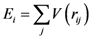
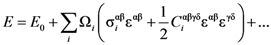
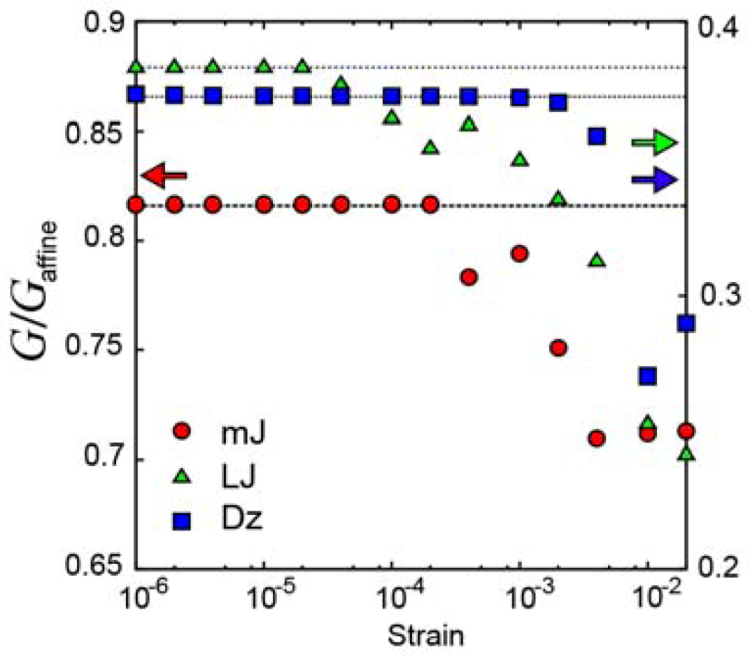
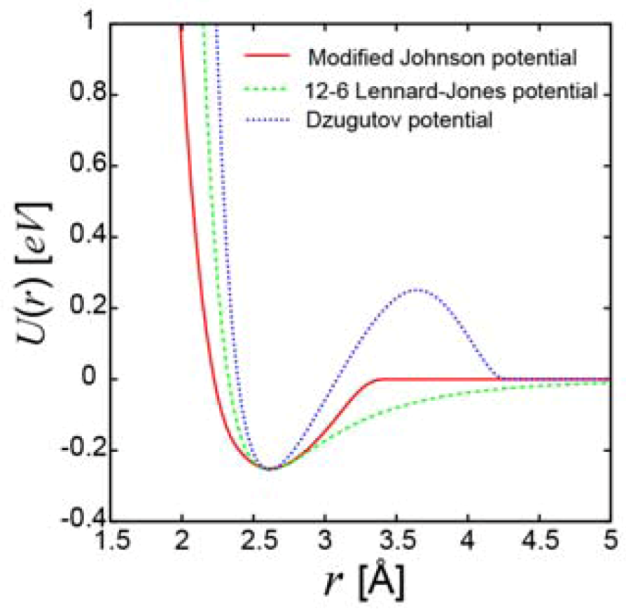
2.1.2. Local plastic deformation
 ), Lennard-Jones glass (
), Lennard-Jones glass (  ), and glass with the Dzugutov potential (
), and glass with the Dzugutov potential (  ).
).
 ), Lennard-Jones glass (
), Lennard-Jones glass (  ), and glass with the Dzugutov potential (
), and glass with the Dzugutov potential (  ).
).
2.2. Diffraction Experiments
2.2.1. Anisotropic PDF
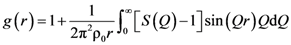
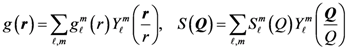

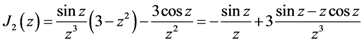
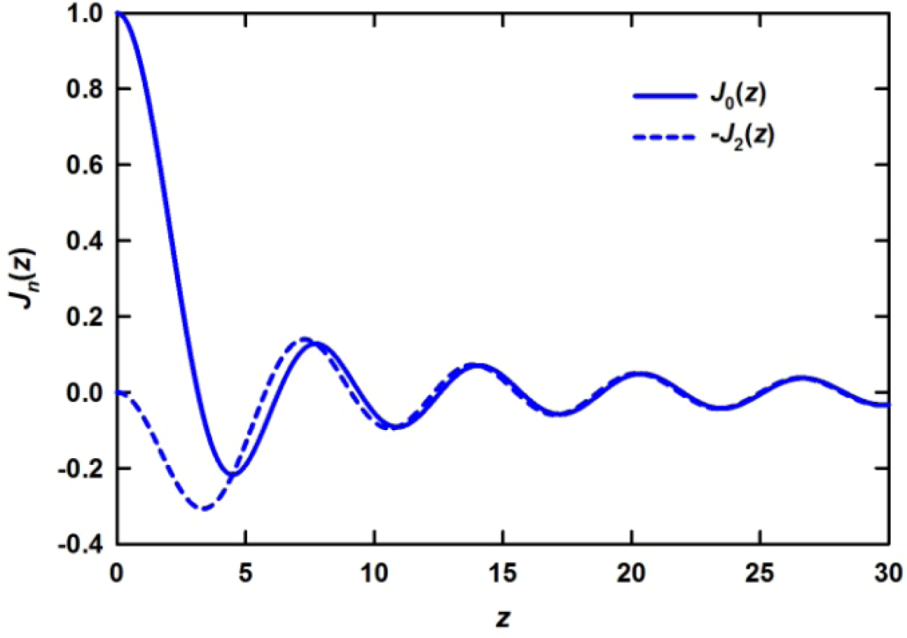
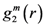 is proportional to the derivative of the isotropic term,
is proportional to the derivative of the isotropic term, 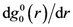 [21]. For uniaxial compression or tension [42],
[21]. For uniaxial compression or tension [42],

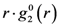 is close to the derivative as shown in Figure 5 [42], particularly at large distances, and the magnitude of the strain thus determined agrees with the macroscopic strain. However, there are small but significant deviations at short distances. The interpretation of these deviations is still an open question as discussed below. It should also be noted that in order to discuss such small deviations it becomes important to use the Bessel transformation, Equation (11), rather than the Fourier-transformation, Equation (9).
is close to the derivative as shown in Figure 5 [42], particularly at large distances, and the magnitude of the strain thus determined agrees with the macroscopic strain. However, there are small but significant deviations at short distances. The interpretation of these deviations is still an open question as discussed below. It should also be noted that in order to discuss such small deviations it becomes important to use the Bessel transformation, Equation (11), rather than the Fourier-transformation, Equation (9).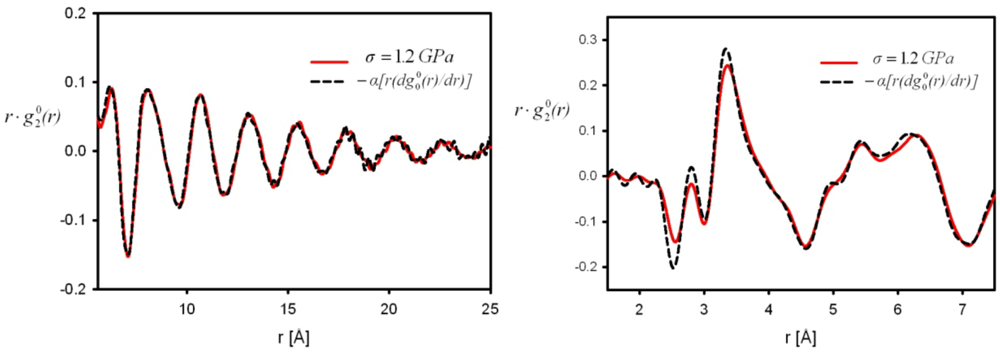
2.2.2. Interpretation of the Results
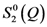 (~∆S(Q)) compared to Q
(~∆S(Q)) compared to Q  . The measurement was made for Zr52.5Cu17.9Ni14.6Al10Ti5 glass under tension at 1.2 GPa. Note that they do not decay even beyond 6 Å−1, and Q
. The measurement was made for Zr52.5Cu17.9Ni14.6Al10Ti5 glass under tension at 1.2 GPa. Note that they do not decay even beyond 6 Å−1, and Q 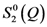 is proportional to Q
is proportional to Q  as expected.
as expected.
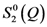 (~∆S(Q)) compared to Q
(~∆S(Q)) compared to Q  . The measurement was made for Zr52.5Cu17.9Ni14.6Al10Ti5 glass under tension at 1.2 GPa. Note that they do not decay even beyond 6 Å−1, and Q
. The measurement was made for Zr52.5Cu17.9Ni14.6Al10Ti5 glass under tension at 1.2 GPa. Note that they do not decay even beyond 6 Å−1, and Q 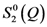 is proportional to Q
is proportional to Q  as expected.
as expected. 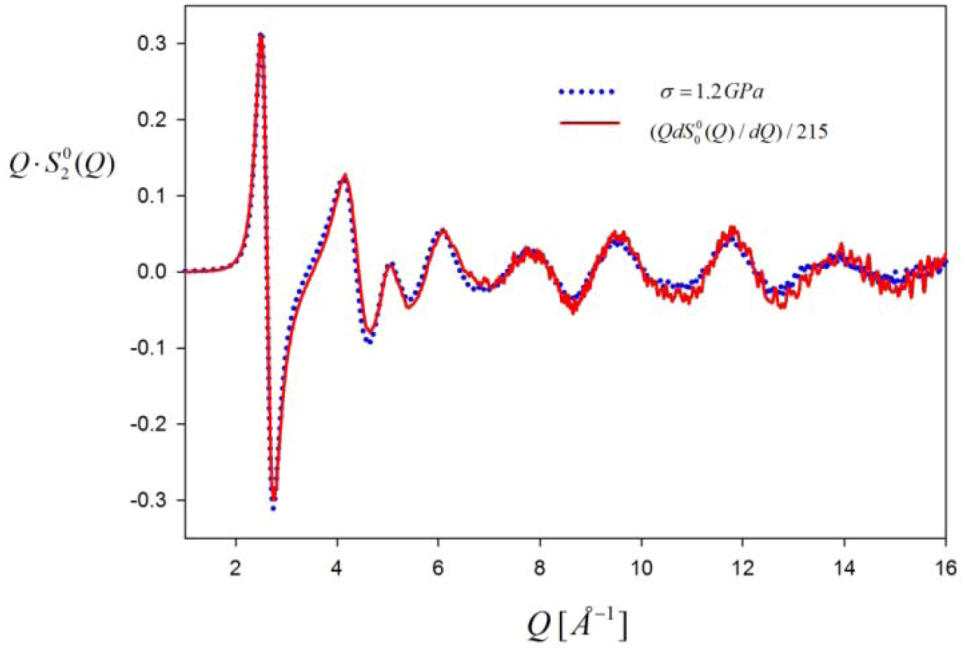
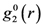 and what is expected for affine deformation, Equation (13), is very similar to that for anelastic (creep) deformation discussed below. For this reason [42] assigns the shear softening to anelastic deformation. They found that the observed
and what is expected for affine deformation, Equation (13), is very similar to that for anelastic (creep) deformation discussed below. For this reason [42] assigns the shear softening to anelastic deformation. They found that the observed 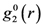 can be fit nicely with
can be fit nicely with
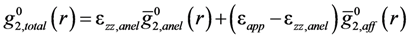
 is the anisotropic PDF for anelastic deformation shown below in Figure 7. The fraction of the affine strain to the total strain, z = εzz,aff/εapp, was found to be about 0.76, implying as much as 24% of the strain originates from the anelastic effect. As it turns out this fraction is exactly what has been assumed in the theory of glass transition [43] to be the fraction of the liquid-like atomic sites at the glass transition.
is the anisotropic PDF for anelastic deformation shown below in Figure 7. The fraction of the affine strain to the total strain, z = εzz,aff/εapp, was found to be about 0.76, implying as much as 24% of the strain originates from the anelastic effect. As it turns out this fraction is exactly what has been assumed in the theory of glass transition [43] to be the fraction of the liquid-like atomic sites at the glass transition. 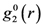 of glassy Zr52.5Cu17.9Ni14.6Al10Ti5 after creep deformation at 300 °C for 30 min. under the stress of 1.2 GPa, compared to
of glassy Zr52.5Cu17.9Ni14.6Al10Ti5 after creep deformation at 300 °C for 30 min. under the stress of 1.2 GPa, compared to 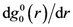 [42].
[42].
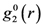 of glassy Zr52.5Cu17.9Ni14.6Al10Ti5 after creep deformation at 300 °C for 30 min. under the stress of 1.2 GPa, compared to
of glassy Zr52.5Cu17.9Ni14.6Al10Ti5 after creep deformation at 300 °C for 30 min. under the stress of 1.2 GPa, compared to 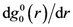 [42].
[42].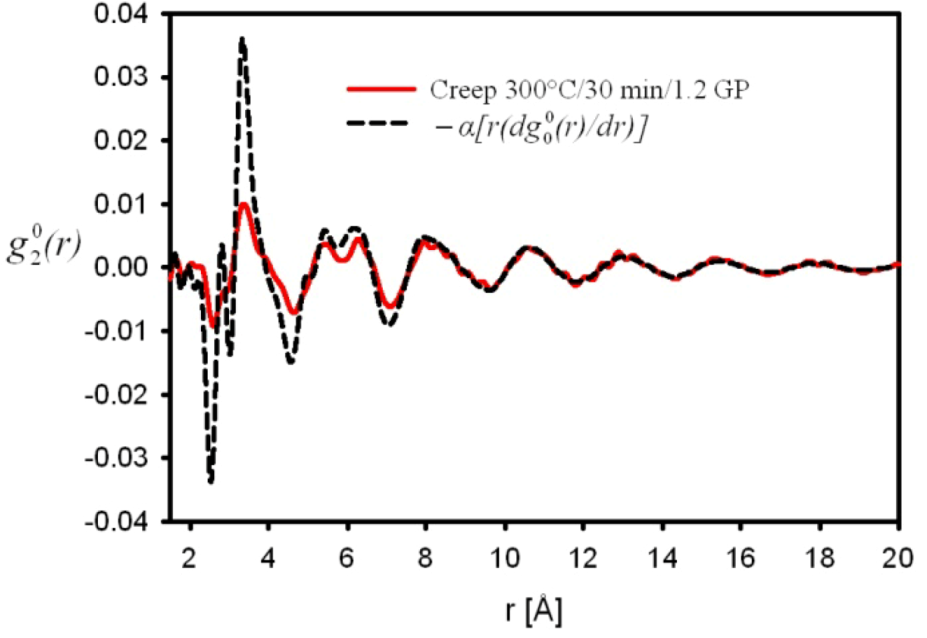
3. Creep and Anelastic Deformation
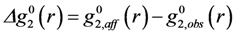
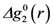 for elastic deformation (blue line). The two curves in Figure 9 are similar, suggesting that the apparent elastic deformation contains significant anelastic component [42]. However, there are some differences in detail, which deserve further studies.
for elastic deformation (blue line). The two curves in Figure 9 are similar, suggesting that the apparent elastic deformation contains significant anelastic component [42]. However, there are some differences in detail, which deserve further studies.
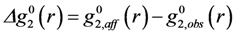 , reflecting structural re-arrangement, for anelastic deformation (red) and for elastic deformation (blue) [42].
, reflecting structural re-arrangement, for anelastic deformation (red) and for elastic deformation (blue) [42].
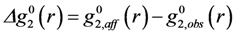 , reflecting structural re-arrangement, for anelastic deformation (red) and for elastic deformation (blue) [42].
, reflecting structural re-arrangement, for anelastic deformation (red) and for elastic deformation (blue) [42].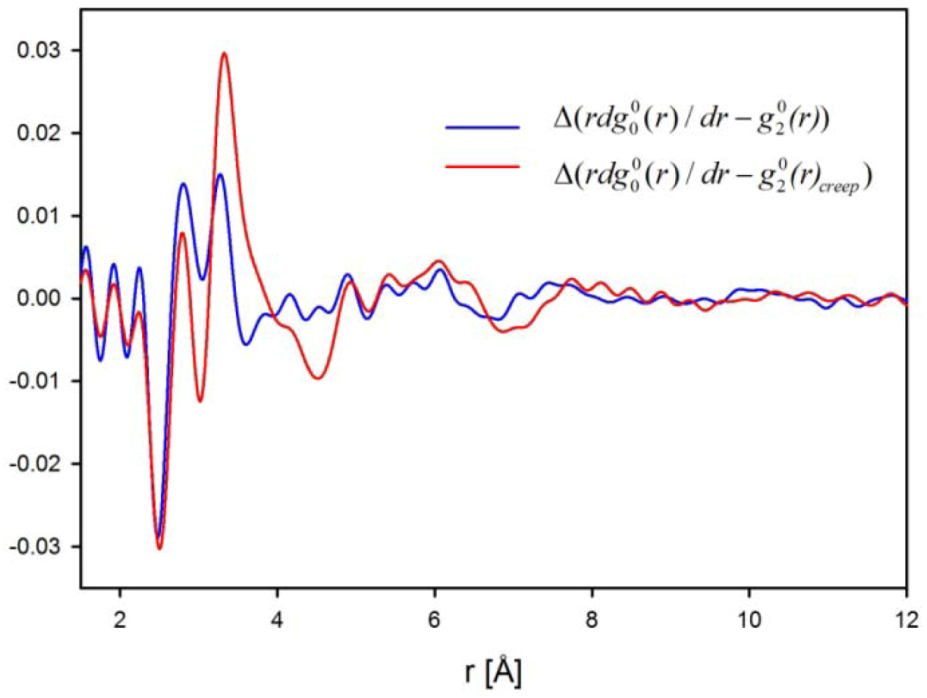
4. Plastic Deformation
4.1. Macroscopic Behavior
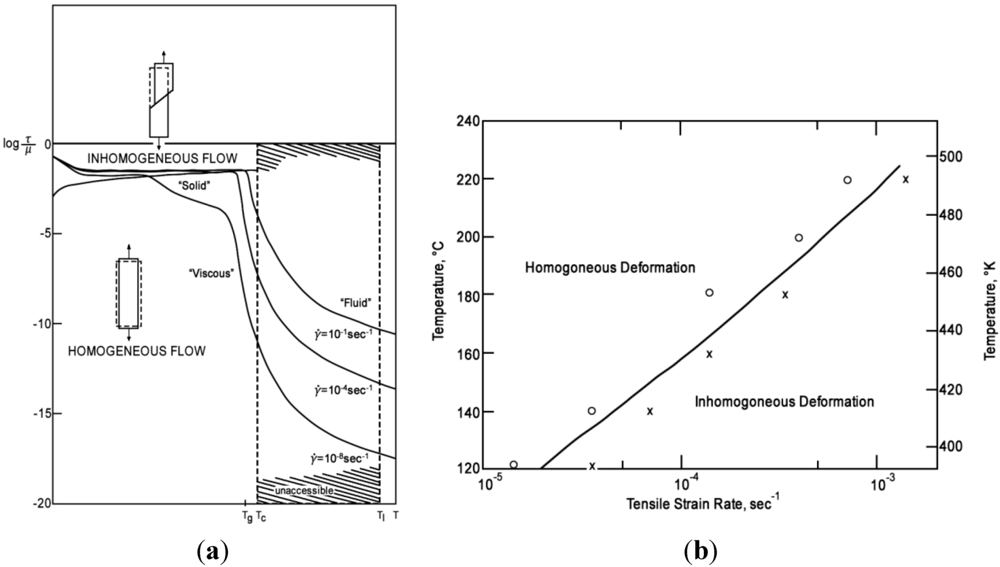
4.1.1. Shear Band Formation and Non-Linear Viscosity
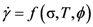
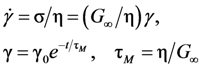
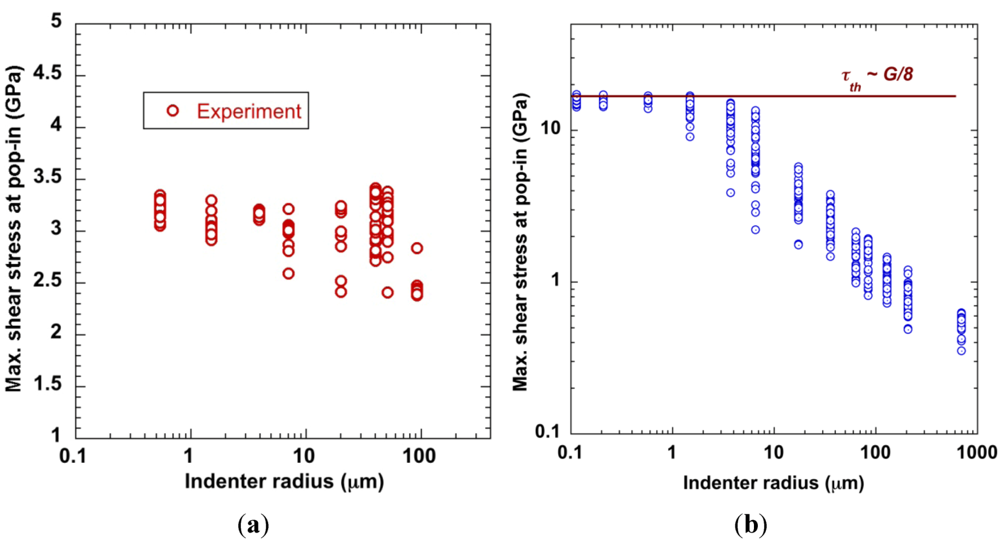
4.1.2. Size Effect and Extrinsic Defects
4.1.3. Feedback Effect of Structural Parameter
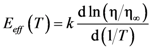
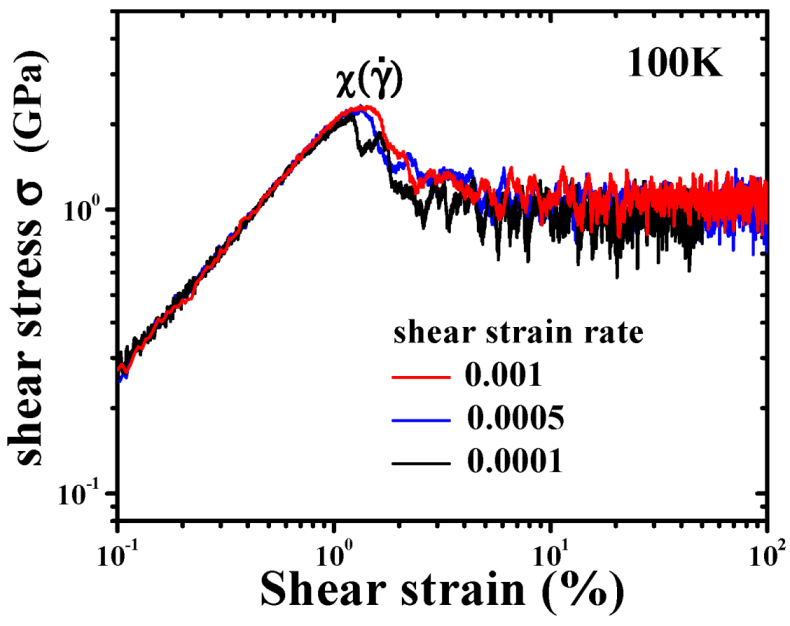
4.1.4. Effect of Structural Relaxation
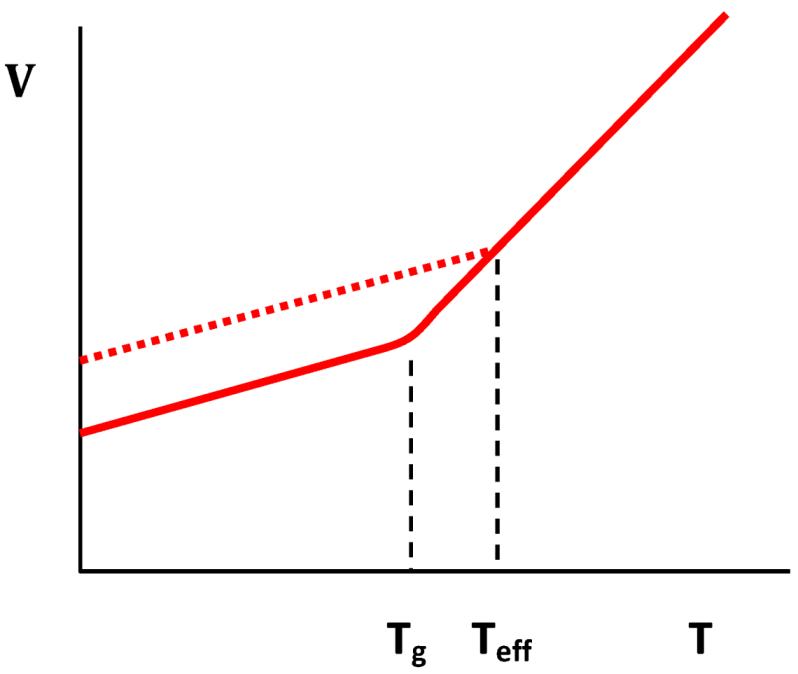
4.1.5. Ductility
4.2. Computer Simulation
4.2.1. Earlier Simulations
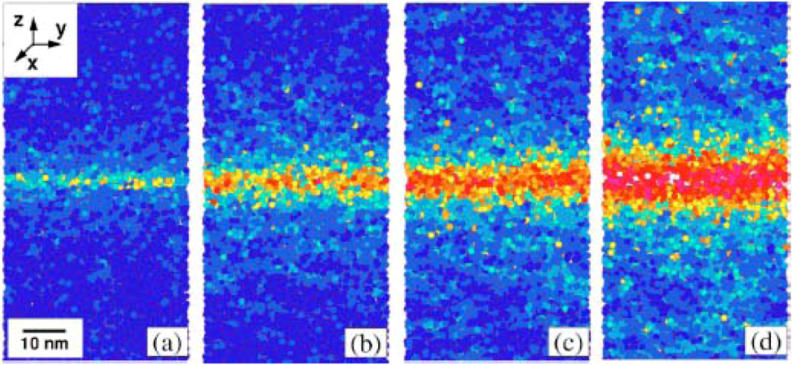
4.2.2. Equivalence of Stress and Temperature

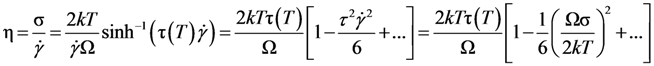
 . Thus viscosity decreases with stress, a phenomenon known as shear-thinning. In general applying the stress has a similar effect as increasing the temperature. In that sense stress and temperature are equivalent [84].
. Thus viscosity decreases with stress, a phenomenon known as shear-thinning. In general applying the stress has a similar effect as increasing the temperature. In that sense stress and temperature are equivalent [84]. 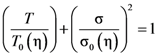
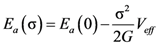
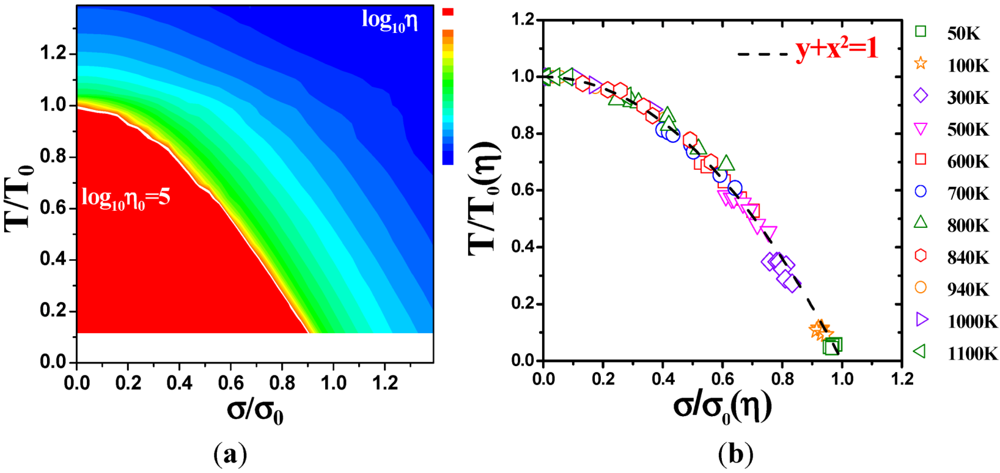
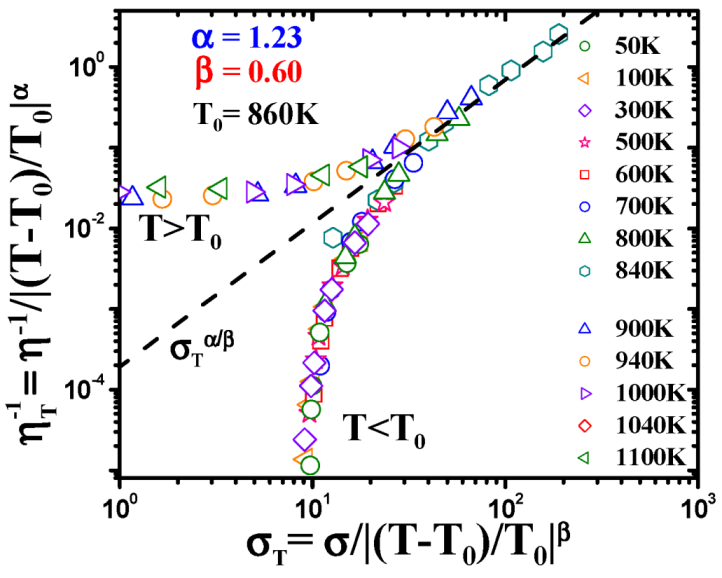
4.2.3. Non-Linear Constitutive Law and Scaling Behavior
 , a Newtonian liquid behavior. Because viscosity is given by
, a Newtonian liquid behavior. Because viscosity is given by  , the result can be re-plotted as η against σ, as in Figure 16b. In high-temperature liquids η is only weakly dependent on σ, whereas it is very strongly dependent on σ in glasses, becoming almost vertical at low temperatures.
, the result can be re-plotted as η against σ, as in Figure 16b. In high-temperature liquids η is only weakly dependent on σ, whereas it is very strongly dependent on σ in glasses, becoming almost vertical at low temperatures. , simulated for Zr50Cu40Al10 at various temperatures [60]. Tg = 860 K for this system. (b) The same data plotted as viscosity, η, against σ.
, simulated for Zr50Cu40Al10 at various temperatures [60]. Tg = 860 K for this system. (b) The same data plotted as viscosity, η, against σ.
 , simulated for Zr50Cu40Al10 at various temperatures [60]. Tg = 860 K for this system. (b) The same data plotted as viscosity, η, against σ.
, simulated for Zr50Cu40Al10 at various temperatures [60]. Tg = 860 K for this system. (b) The same data plotted as viscosity, η, against σ.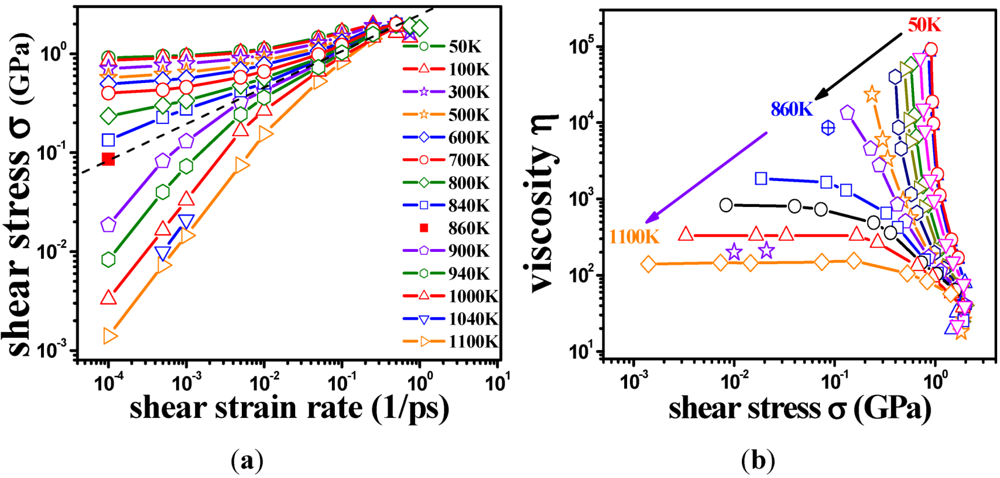
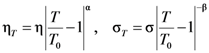
 (Figure 16a), thus η is a very strong function of σ, as shown in Figure 16b. Because G∞ does not depend strongly on temperature τM (η/G∞) is also a strong function of σ, and diverges at small σ, which makes sense in the glassy state. τM becomes quickly reduced with increasing σ. Yielding occurs when
(Figure 16a), thus η is a very strong function of σ, as shown in Figure 16b. Because G∞ does not depend strongly on temperature τM (η/G∞) is also a strong function of σ, and diverges at small σ, which makes sense in the glassy state. τM becomes quickly reduced with increasing σ. Yielding occurs when  . But τM is not necessarily the same as τα. Of interest here is the competition between the strain rate
. But τM is not necessarily the same as τα. Of interest here is the competition between the strain rate  , thus τM, and the structural relaxation rate τα. At low temperatures τα is longer than τM, so that the structure cannot follow the stress, and overshooting becomes necessary. At high temperatures τα is comparable to τM, so that the “structure” can follow the stress without overshooting. In fact the same happens if the temperature is kept constant and the strain rate is varied. Strain localization and stress overshoot happens when
, thus τM, and the structural relaxation rate τα. At low temperatures τα is longer than τM, so that the structure cannot follow the stress, and overshooting becomes necessary. At high temperatures τα is comparable to τM, so that the “structure” can follow the stress without overshooting. In fact the same happens if the temperature is kept constant and the strain rate is varied. Strain localization and stress overshoot happens when  is high enough. So the strain localization and the formation of shear band, even though it has a huge impact on the performance of a metallic glass as a structural material, is not an essential feature of deformation of metallic glasses. It simply depends on the experimental condition.
is high enough. So the strain localization and the formation of shear band, even though it has a huge impact on the performance of a metallic glass as a structural material, is not an essential feature of deformation of metallic glasses. It simply depends on the experimental condition. 5. Atomistic Mechanism of Deformation
5.1. Theories of Mechanical Deformation
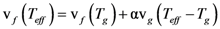
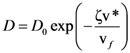
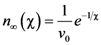
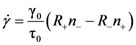

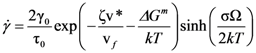
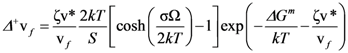

 is the attempt frequency, and is given by
is the attempt frequency, and is given by
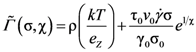
 , and the structural relaxation rate, 1/τα., to change ϕ, in this case the STZ density n(χ). At low temperatures 1/τα is slower than
, and the structural relaxation rate, 1/τα., to change ϕ, in this case the STZ density n(χ). At low temperatures 1/τα is slower than  , so that ϕ cannot follow the stress, and overshooting occurs. After the yield stress is reached, however, n(χ) quickly increases and softening takes place. The steady-state flow is achieved with a newly stabilized effective temperature χ, which is much higher than the initial real temperature. At high temperatures 1/τα is faster than
, so that ϕ cannot follow the stress, and overshooting occurs. After the yield stress is reached, however, n(χ) quickly increases and softening takes place. The steady-state flow is achieved with a newly stabilized effective temperature χ, which is much higher than the initial real temperature. At high temperatures 1/τα is faster than  , so that n(χ) can follow the stress without overshooting. In fact the same happens if the temperature is kept constant and the strain rate is varied. Strain localization and stress overshoot happens when
, so that n(χ) can follow the stress without overshooting. In fact the same happens if the temperature is kept constant and the strain rate is varied. Strain localization and stress overshoot happens when  is high enough [90]. In this sense the strain localization and the formation of shear band depends on the experimental condition.
is high enough [90]. In this sense the strain localization and the formation of shear band depends on the experimental condition.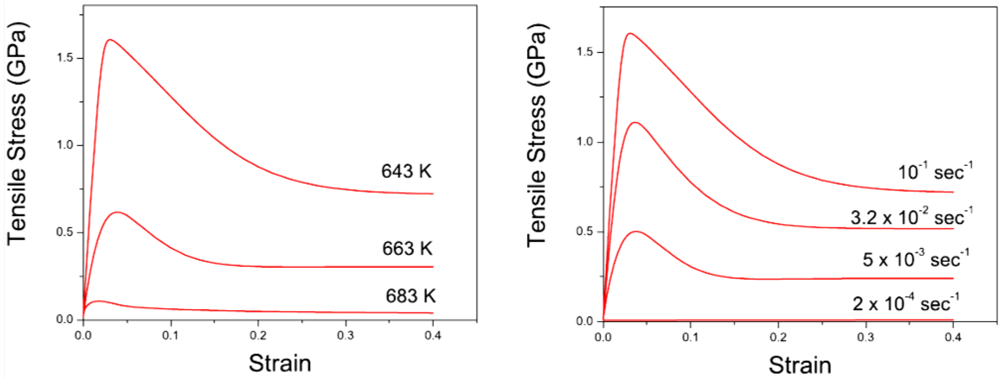
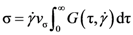
 ) is the time-dependent transient dynamical shear modulus, and vσ is a coupling constant [91,92]. G(τ,
) is the time-dependent transient dynamical shear modulus, and vσ is a coupling constant [91,92]. G(τ,  ) is approximated by ψ2(t), where ψ(t) is the density correlation function,
) is approximated by ψ2(t), where ψ(t) is the density correlation function,

5.2. Atomistic Models of Mechanical Deformation
5.2.1. Nature of “Structural Defects” in Glasses
5.2.2. Free-Volume Mechanism
5.2.3. Shear-Transformation-Zones (STZ) Theory
 ) [107], and theoretical fit by the STZ theory (lines) [105]. (b) Flow stress s, plotted against the strain rate, q, at various temperatures. Circles are by simulation (Figure 16a [60]), and lines are by the STZ theory [108].
) [107], and theoretical fit by the STZ theory (lines) [105]. (b) Flow stress s, plotted against the strain rate, q, at various temperatures. Circles are by simulation (Figure 16a [60]), and lines are by the STZ theory [108].
 ) [107], and theoretical fit by the STZ theory (lines) [105]. (b) Flow stress s, plotted against the strain rate, q, at various temperatures. Circles are by simulation (Figure 16a [60]), and lines are by the STZ theory [108].
) [107], and theoretical fit by the STZ theory (lines) [105]. (b) Flow stress s, plotted against the strain rate, q, at various temperatures. Circles are by simulation (Figure 16a [60]), and lines are by the STZ theory [108].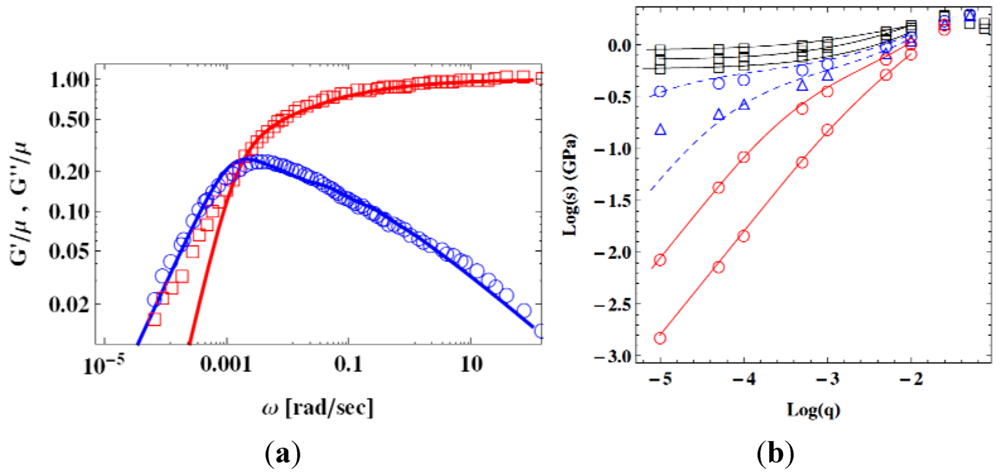
5.2.4. Mode-Coupling Theory
5.2.5. Local Configurational Excitations
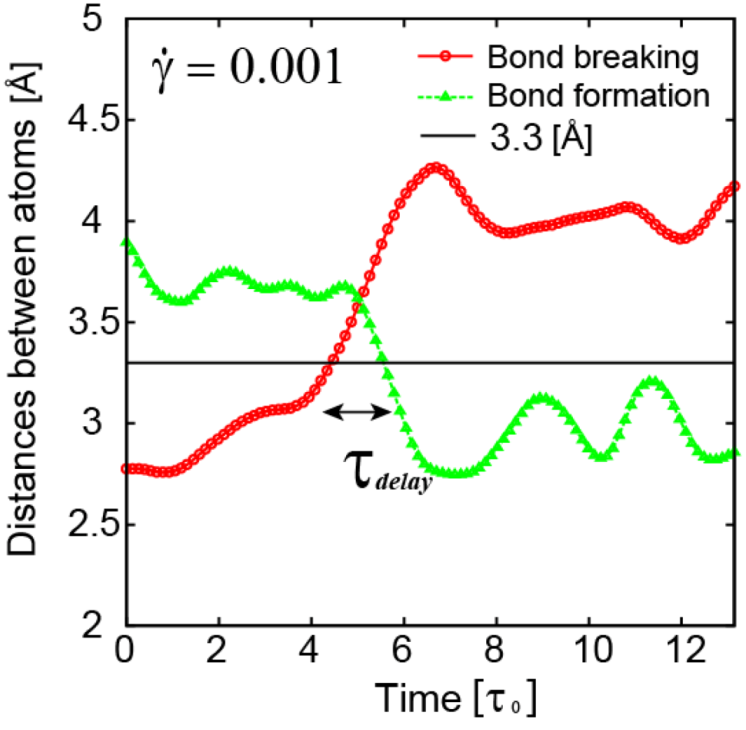
 . Because
. Because  , this means connected to the lifetime of local topology, a microscopic quantity. The factor of 1/2 reflects the fact that two topology actions, bond cutting and bond creation, are coupled. This shows that the bond exchange shown in Figure 8 is indeed the elementary atomistic mechanism of deformation.
, this means connected to the lifetime of local topology, a microscopic quantity. The factor of 1/2 reflects the fact that two topology actions, bond cutting and bond creation, are coupled. This shows that the bond exchange shown in Figure 8 is indeed the elementary atomistic mechanism of deformation. (nearest neighbor strain) and
(nearest neighbor strain) and  (strain due to local topology) [24]. See [24] and text for the meaning.
(strain due to local topology) [24]. See [24] and text for the meaning.
 = 0.001 τ0−1 at 300 K, within two intervals of 250 fs (= 3.29 τ0, τ0 = 0.761 × 10−13 s). The progress in time is shown by color. The cut bonds are clustered suggesting cascade chain reactions. Here the bond lifetime is 81 τ0. The size of the box is 59.34 × 10 × 59.34 Å3. This figure was generated from the model used in [24].
= 0.001 τ0−1 at 300 K, within two intervals of 250 fs (= 3.29 τ0, τ0 = 0.761 × 10−13 s). The progress in time is shown by color. The cut bonds are clustered suggesting cascade chain reactions. Here the bond lifetime is 81 τ0. The size of the box is 59.34 × 10 × 59.34 Å3. This figure was generated from the model used in [24].
 = 0.001 τ0−1 at 300 K, within two intervals of 250 fs (= 3.29 τ0, τ0 = 0.761 × 10−13 s). The progress in time is shown by color. The cut bonds are clustered suggesting cascade chain reactions. Here the bond lifetime is 81 τ0. The size of the box is 59.34 × 10 × 59.34 Å3. This figure was generated from the model used in [24].
= 0.001 τ0−1 at 300 K, within two intervals of 250 fs (= 3.29 τ0, τ0 = 0.761 × 10−13 s). The progress in time is shown by color. The cut bonds are clustered suggesting cascade chain reactions. Here the bond lifetime is 81 τ0. The size of the box is 59.34 × 10 × 59.34 Å3. This figure was generated from the model used in [24].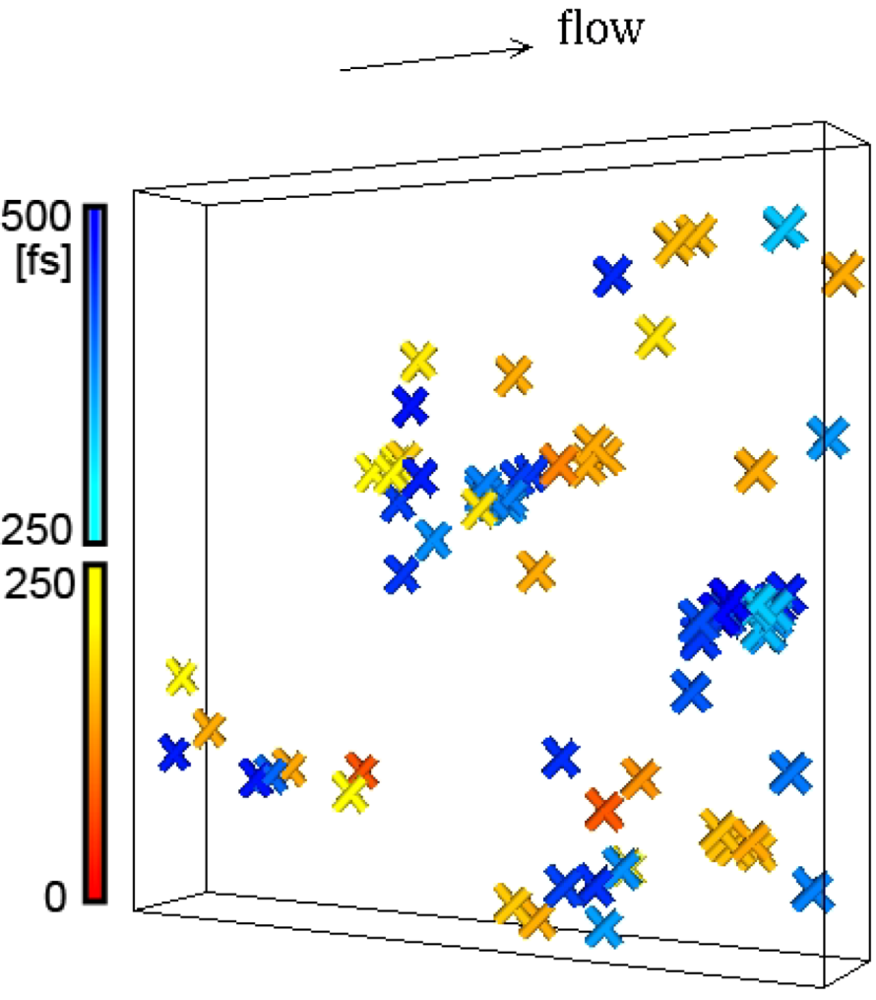
5.2.6. Atomic Structure during the Flow
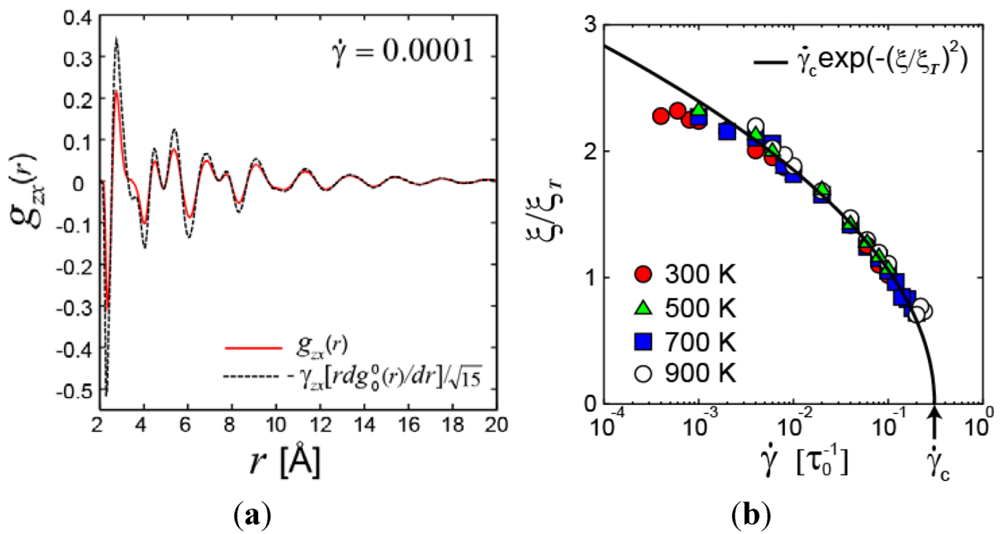
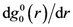 , as is the case for elastic deformation. A liquid, however, respond elastically only within the time-scale of τM. Accordingly the elastic structural change cannot be long-range, but is limited to a finite lengthscale [24]. The spatial extension of the elastically deformed region ζ, depends on both temperature and shear rate. The temperature dependence is weak; ζT = 10.56 Å at 300 K, 10.85 Å at 500 K, 11.06 Å at 700 K, and 11.12 Å at 900 K. But ζ, depends significantly on the shear rate at high rates, and ζ extrapolates to zero at a critical shear rate,
, as is the case for elastic deformation. A liquid, however, respond elastically only within the time-scale of τM. Accordingly the elastic structural change cannot be long-range, but is limited to a finite lengthscale [24]. The spatial extension of the elastically deformed region ζ, depends on both temperature and shear rate. The temperature dependence is weak; ζT = 10.56 Å at 300 K, 10.85 Å at 500 K, 11.06 Å at 700 K, and 11.12 Å at 900 K. But ζ, depends significantly on the shear rate at high rates, and ζ extrapolates to zero at a critical shear rate,  . This is also related to the communication via the sound waves. At very high shear rates the local structure changes faster than the time for a sound wave to travel from one atom to another, so communication cannot be achieved, and elastic correlation does not have time to develop.
. This is also related to the communication via the sound waves. At very high shear rates the local structure changes faster than the time for a sound wave to travel from one atom to another, so communication cannot be achieved, and elastic correlation does not have time to develop.6. Conclusions
Acknowledgments
Conflict of Interest
References
- Chen, H.S.; Wang, T.T. Mechanical properties of metallic glasses of PdSi based alloys. J. Appl. Phys. 1970, 41, 5338–5339. [Google Scholar]
- Masumoto, T.; Maddin, R. The mechanical properties of palladium 20 a/o silicon alloy quenched from the liquid state. Acta Metall. 1971, 19, 725–741. [Google Scholar] [CrossRef]
- Chen, H.H. Glassy metals. Rep. Prog. Phys. 1980, 43, 353–432. [Google Scholar] [CrossRef]
- Ashby, M.F.; Greer, A.L. Metallic glasses as structural materials. Scr. Mater. 2006, 54, 321–326. [Google Scholar] [CrossRef]
- Anderson, P.W. Through the glass lightly. Science 1995, 267, 1615. [Google Scholar]
- Weaire, D.; Ashby, M.F.; Logan, J.; Weins, M.J. On the use of pair potentials to calculate the properties of amorphous metals. Acta Metall. 1971, 19, 779–788. [Google Scholar]
- Spaepen, F. A microscopic mechanism for steady state inhomogeneous flow in metallic glasses. Acta Metall. 1977, 25, 407–415. [Google Scholar] [CrossRef]
- Inoue, A.; Zhang, T.; Masumoto, T. Al-La-Ni amorphous alloys with a wide supercooled liquid region. Mater. Trans. JIM 1989, 30, 965–972. [Google Scholar]
- Peker, A.; Johnson, W.L. A highly processable metallic glass: Zr41.2Ti13.8Cu12.5Ni10.0Be22.5. Appl. Phys. Lett. 1993, 63, 2342–2344. [Google Scholar] [CrossRef]
- Born, M.; Huang, K. Dynamical Theory of Crystal Lattices; Clarendon Press: Oxford, UK, 1954. [Google Scholar]
- Davis, L.A. Mechanics of Metallic Glasses. In Rapidly Quenched Metals; Giessen, G., Ed.; MIT: Cambridge, MA, USA, 1976; pp. 369–391. [Google Scholar]
- Hashin, Z.; Shtrikman, S. A variational approach to the theory of the elastic behavior of multiphase materials. J. Mech. Phys. Solids 1963, 11, 127–140. [Google Scholar] [CrossRef]
- Egami, T.; Maeda, K.; Vitek, V. Structural defects in amorphous solids: A computer simulation study. Philos. Mag. A 1980, 41, 883–901. [Google Scholar] [CrossRef]
- Egami, T.; Srolovitz, D. Local fluctuations in amorphous and liquid metals: A simple theory of glass transition. J. Phys. F 1982, 12, 2141–2163. [Google Scholar] [CrossRef]
- Egami, T.; Ojha, M.; Nicholson, D.M.; Louzguine-Luzgin, D.; Chen, N.; Inoue, A. Glass formability and Al-Au system. Philos. Mag. A 2012, 92, 655–665. [Google Scholar] [CrossRef]
- Kröner, E. Continuum Theory of Defects. In Les Houches, Session XXXV, 1980—Physics of Defects; Balian, R., Kléman, M., Poirier, J.-P., Eds.; North-Holland: Dordrecht, The Netherland, 1981; pp. 215–315. [Google Scholar]
- Maloney, C.E.; Robbins, M.O. Evolution of displacements and strains in sheared amorphous solids. J. Phys. Cond. Mat. 2008, 20, 244128. [Google Scholar] [CrossRef]
- Tsamados, M.; Tanguy, A.; Goldenberg, C.; Barrat, J.-L. Local elasticity map and plasticity in a model Lennard-Jones glass. Phys. Rev. E 2009, 80, 026112. [Google Scholar] [CrossRef]
- Suzuki, Y.; Egami, T. Shear deformation of glassy metals: Breakdown of cauchy relationship and anelasticity. J. Non-Cryst. Solids 1985, 75, 361–366. [Google Scholar]
- Papakonstantopoulos, G.J.; Riggleman, R.A.; Barrat, J.-L.; de Pablo, J.J. Molecular plasticity of polymeric glasses in the elastic regime. Phys. Rev. E 2008, 77, 041502. [Google Scholar] [CrossRef]
- Suzuki, Y.; Haimovich, J.; Egami, T. Bond-orientational anisotropy in metallic glasses observed by X-ray diffraction. Phys. Rev. B 1987, 35, 2162–2168. [Google Scholar] [CrossRef]
- Tomida, T.; Egami, T. Molecular-dynamics study of structural anisotropy and anelasticity in metallic glasses. Phys. Rev. B 1993, 48, 3048–3057. [Google Scholar] [CrossRef]
- Dmowski, W.; Egami, T. Observation of structural anisotropy in metallic glasses induced by mechanical deformation. J. Mater. Res. 2007, 22, 412–418. [Google Scholar] [CrossRef]
- Iwashita, T.; Egami, T. Atomic mechanism of flow in simple liquids under shear. Phys. Rev. Lett. 2012, 108, 196001. [Google Scholar] [CrossRef]
- Srolovitz, D.; Maeda, K.; Vitek, V.; Egami, T. Structural defects in amorphous solids; Statistical analysis of a computer model. Phil. Mag. A 1981, 44, 847–866. [Google Scholar] [CrossRef]
- Dzugutov, M. Glass-formation in a simple monoatomic liquid with icosahedral inherent local order. Phys. Rev. A 1992, 46, R2984–R2987. [Google Scholar] [CrossRef]
- Hafner, J. From Hamiltonian to Phase Diagrams; Springer-Verlag: Berlin, Germany, 1987. [Google Scholar]
- Poulsen, H.F.; Wert, J.A.; Neuefeind, J.; Honkimäki, V. Measuring strain distributions in amorphous materials. Nat. Mater. 2004, 4, 33–36. [Google Scholar]
- Hufnagel, T.C.; Ott, R.T.; Almer, J. Structural aspects of elastic deformation of a metallic glass. Phys. Rev. B 2006, 73, 064204. [Google Scholar]
- Wang, X.D.; Bednarcik, J.; Saksl, K.; Franz, H.; Cao, Q.P.; Jiang, J.Z. Tensile behavior of bulk metallic glasses by in situ Z-ray diffraction. Appl. Phys. Lett. 2007, 91, 081913. [Google Scholar]
- Das, J.; Bostrom, M.; Mattern, N.; Kvick, A.; Yavari, A.R.; Greer, A.L.; Eckert, J. Plasticity in bulk metallic glasses investigated via the strain distribution. Phys. Rev. B 2007, 76, 092203. [Google Scholar]
- Stoica, M.; Das, J.; Bednarcik, J.; Franz, H.; Mattern, N.; Wang, W.H.; Eckert, J. Strain distribution in Zr64.13Cu15.75Ni10.12Al10 bulk metallic glass investigated by in situ tensile tests under synchrotron radiation. J. Appl. Phys. 2008, 104, 013522. [Google Scholar]
- Wilson, T.; Clausen, B.; Proffen, T.; Elle, J.; Brown, D. In situ neutron scattering measurement of stress-strain behavior of a bulk metallic glass. Metall. Mater. Trans. A 2008, 39A, 1942–1946. [Google Scholar]
- Mattern, N.; Bednarcik, J.; Pauly, S.; Wang, G.; Das, J.; Eckert, J. Structural evolution of Cu–Zr metallic glasses under tension. Acta Mater. 2009, 57, 4133–4139. [Google Scholar] [CrossRef]
- Wang, D.; Bednarcik, J.; Franz, H.; Lou, H.B.; He, Z.H.; Cao, Q.P.; Jiang, J.Z. Local strain behavior of bulk metallic glasses under tension studied by in situ x-ray diffraction. Appl. Phys. Lett. 2009, 94, 011911. [Google Scholar]
- Sato, S.; Suzuki, H.; Shobu, T.; Imafuku, M.; Tsuchiya, Y.; Wagatsuma, K.; Kato, H.; Setyawan, A.D.; Saida, J. Atomic-scale characterization of elastic deformation of Zr-based metallic glass under tensile stress. Mater. Trans. 2010, 51, 1381–1385. [Google Scholar] [CrossRef]
- Stoica, M.; Das, J.; Bednarcik, J.; Wang, G.; Vaughan, G.; Wang, W.H.; Eckert, J. Mechanical response of metallic glasses: Insights from in situ high energy X-ray diffraction. JOM 2010, 62, 76–82. [Google Scholar]
- Vempati, U.K.; Valavala, P.K.; Falk, M.L.; Almer, J.; Hufnagel, T.C. Length-scale dependence of elastic strain from scattering measurements in metallic glasses. Phys. Rev. B 2012, 85, 214201. [Google Scholar]
- Ma, D.; Stoica, A.D.; Wang, X.-L.; Lu, Z.P.; Clausen, B.; Brown, D.W. Elastic moduli inheritance and the weakest link in bulk metallic glasses. Phys. Rev. Lett. 2012, 108, 085501. [Google Scholar] [CrossRef]
- Warren, B.E. X-Ray Diffraction; Dover: New York, NY, USA, 1969. [Google Scholar]
- Egami, T.; Billinge, S.J.L. Underneath the Bragg Peaks: Structural Analysis of Complex Materials; Elsevier Ltd.: Oxford, UK, 2003. [Google Scholar]
- Dmowski, W.; Iwashita, T.; Chuang, C.-P.; Almer, J.; Egami, T. Elastic heterogeneity in metallic glasses. Phys. Rev. Lett. 2010, 105, 205502. [Google Scholar] [CrossRef]
- Egami, T.; Poon, S.J.; Zhang, Z.; Keppens, V. Glass transition in metallic glasses: A microscopic model of topological fluctuations in the bonding network. Phys. Rev. B 2007, 76, 024203. [Google Scholar]
- Maddin, R.; Masumoto, T. The deformation of amorphous palladium-20 at % silicon. Mater. Sci. Eng. 1972, 9, 153–162. [Google Scholar] [CrossRef]
- Berry, B.S.; Pritchet, W.C. Magnetic annealing and directional ordering of an amorphous ferromagnetic alloy. Phys. Rev. Lett. 1975, 34, 1022–1025. [Google Scholar] [CrossRef]
- Egami, T.; Dmowski, W.; Kosmetatos, P.; Boord, M.; Tomida, T.; Oikawa, E.; Inoue, A. Deformation induced bond orientational order in metallic glasses. J. Non-Cryst. Solids 1995, 192–193, 591–594. [Google Scholar]
- Schuh, C.A.; Huffnagel, T.C.; Ramamurty, U. Mechanical behavior of amorphous alloys. Acta Matall. 2007, 55, 4067–4109. [Google Scholar] [CrossRef]
- Trexler, M.M.; Thadhani, N.N. Mechanical properties of bulk metallic glasses. Prog. Mater. Sci. 2010, 55, 759–839. [Google Scholar] [CrossRef]
- Suryanarayana, C.; Inoue, A. Bulk Metallic Glasses; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Ashby, M.F. A first report on deformation-mechanism maps. Acta Metall. 1972, 20, 887–897. [Google Scholar] [CrossRef]
- Argon, A.S. Mechanisms of inelastic deformation in metallic glasses. J. Phys. Chem. Solids 1982, 43, 945–961. [Google Scholar] [CrossRef]
- Volkert, C.A.; Donohue, A.; Spaepen, F. Effect of sample size on deformation in amorphous metals. J. Appl. Phys. 2008, 103, 083539. [Google Scholar] [CrossRef]
- Schuster, B.E.; Wei, Q.; Hufnagel, T.C.; Ramesh, K.T. Size-independent strength and deformation mode in compression of a Pd-based metallic glass. Acta Matall. 2008, 56, 5091–5100. [Google Scholar] [CrossRef]
- Bei, H.; Lu, Z.P.; Shim, S.; Chen, G.; George, E.P. Specimen size effects on Zr-based bulk metallic glasses investigated by uniaxial compression and spherical nanoindentation. Met. Matall. Trans. A 2010, 41, 1735–1742. [Google Scholar] [CrossRef]
- Morris, J.R.; Bei, H.; Pharr, G.M.; George, E.P. Size effects and stochastic behavior of nanoindentation pop in. Phys. Rev. Lett. 2011, 106, 165502. [Google Scholar] [CrossRef]
- Tian, L.; Cheng, Y.-Q.; Shan, Z.-W.; Li, J.; Wang, C.-C.; Han, X.-D.; Sun, J.; Ma, E. Approaching the ideal elastic limit of metallic glasses. Nat. Commun. 2011, 3. [Google Scholar] [CrossRef] [Green Version]
- Kivelson, D.; Kivelson, S.A.; Zhao, X.; Nussinov, Z.; Torjus, G. A thermodynamic theory of supercooled liquids. Physica A 1995, 219, 27–38. [Google Scholar] [CrossRef]
- Debenedetti, P.; Stillinger, F.H. Supercooled liquids and the glass transition. Nature 2001, 410, 259–267. [Google Scholar]
- Sastry, S.; Debenedetti, P.; Stillinger, F.H. Signatures of distinct dynamical regimes in the energy landscape of a glass-forming liquid. Nature 1998, 393, 554–557. [Google Scholar]
- Guan, P.; Chen, M.W.; Egami, T. On the stress-temperature scaling for steady-state flow in metallic glasses. Phys. Rev. Lett. 2010, 104, 187002. [Google Scholar]
- Egami, T. Structural relaxation in metallic glasses. Ann. N. Y. Acad. Sci. 1981, 37, 238–251. [Google Scholar]
- Dmowski, D.; Yokoyama, Y.; Chuang, A.; Ren, Y.; Umemoto, M.; Tuchiya, K.; Inoue, A.; Egami, T. Structural rejuvenation in a bulk metallic glass induced by severe plastic deformation. Acta Mater. 2010, 58, 429–438. [Google Scholar]
- Egami, T. Structural relaxation in amorphous alloys—Compositional short range ordering. Mat. Res. Bull. 1978, 13, 557–562. [Google Scholar] [CrossRef]
- Morito, N.; Egami, T. Internal friction and reversible structural relaxation in metallic glass Fe32Ni36Cr14P12B6. Acta Metall. 1984, 32, 603–613. [Google Scholar]
- Egami, T. Structural relaxation in amorphous Fe40Ni40P14B6 studied by energy-dispersive X-ray diffraction. J. Mater. Sci. 1978, 13, 2587–2599. [Google Scholar] [CrossRef]
- Egami, T.; Maeda, K.; Srolovitz, D.; Vitek, V. Local atomic structure of amorphous metals. J. de Phys. (Paris) 41, C8-272–C8-274.
- Srolovitz, D.; Egami, T.; Vitek, V. Radial distribution function and structural relaxation in amorphous solids. Phys. Rev. B 1981, 24, 6936–6944. [Google Scholar] [CrossRef]
- Cohen, M.H.; Turnbull, D. Molecular transport in liquids and glasses. J. Chem. Phys. 1959, 31, 1164–1169. [Google Scholar] [CrossRef]
- Kohda, M.; Haruyama, O.; Egami, T. Kinetics of volume and enthalpy relaxation in Pt60Ni15P25 bulk metallic glass. Phys. Rev. B 2010, 81, 092203. [Google Scholar]
- Lewandowski, J.J.; Wnag, W.H.; Greer, A.L. Intrinsic plasticity or brittleness of metallic glasses. Philos. Mag. Lett. 2005, 85, 77–87. [Google Scholar] [CrossRef]
- Gu, X.J.; McDermott, A.G.; Poon, J.; Shiflet, G.J. Critical Poisson’s ratio for plasticity in Fe-Mo-C-B-Ln bulk amorphous steel. Appl. Phys. Lett. 2006, 88, 211905. [Google Scholar]
- Schroers, J.; Johnson, W.L. Ductile bulk metallic glass. Phys. Rev. Lett. 2004, 93, 255506. [Google Scholar] [CrossRef]
- Demetriou, M.D.; Launey, M.E.; Garrett, G.; Schramm, J.P.; Hofmann, D.C.; Johnson, W.L.; Ritchie, R.O. A damage-tolerant glass. Nat. Mater. 2011, 10, 123–128. [Google Scholar]
- Zhang, B.; Zhao, D.Q.; Pan, M.X.; Wnag, W.H.; Greer, A.L. Amorphous metallic plastic. Phys. Rev. Lett. 2005, 94, 205502. [Google Scholar] [CrossRef]
- Yokoyama, Y.; Fujita, K.; Yavari, A.R.; Inoue, A. Malleable hypoeutectic Zr-Ni-Cu-Al bulk glassy alloys with tensile plastic elongation at room temperature. Philos. Mag. Lett. 2009, 89, 322–334. [Google Scholar] [CrossRef]
- Williams, R.S.; Egami, T. Temper Embrittlement of Amorphous Alloys. In Rapidly Quenched Metals III; Cantor, B., Ed.; The Metals Society: London, UK, 1978; Volume 1, pp. 214–220. [Google Scholar]
- Inoue, A.; Fan, C.; Saida, J.; Zhang, T. High-strength Zr-based bulk amorphous alloys containing nanocrystalline and quasicrystalline particles. Sci. Technol. Adv. Mater. 2000, 1, 73–86. [Google Scholar] [CrossRef]
- Pauly, S.; Gorantla, S.; Wang, G.; Kühn, U.; Eckert, J. Transformatio-mediated ductility in CuZr-based bulk metallic glass. Nat. Mater. 2010, 9, 473–477. [Google Scholar]
- Kobayashi, S.; Maeda, K.; Takeuchi, S. Computer simulation of deformation of amorphous Cu57Zr43. Acta Metall. 1980, 28, 1641–1652. [Google Scholar] [CrossRef]
- Srolovitz, D.; Vitek, V.; Egami, T. An atomist study of deformation in amorphous metals. Acta Metall. 1983, 31, 335–352. [Google Scholar] [CrossRef]
- Shi, Y.; Falk, M.L. Stress-induced structural transformation and shear banding during simulated nanoindentation of a metallic glass. Acta Matall. 2007, 55, 4317–4324. [Google Scholar] [CrossRef]
- Li, Q.-K.; Li, M. Atomistic simulations of correlations between volumetric change and shear softening in amorphous metals. Phys. Rev. B 2007, 75, 094101. [Google Scholar] [CrossRef]
- Eyring, H. Viscosity, plasticity, and diffusion as examples of absolute reaction rates. J. Chem. Phys. 1936, 4, 283–291. [Google Scholar] [CrossRef]
- Barrat, J.-L.; Berthier, L. Fluctuation-dissipation relation in a sheared fluid. Phys. Rev. E 2000, 63, 012503. [Google Scholar]
- Berthier, L.; Barrat, J.-L. Shearing a glassy material: Numerical test of nonequilibrium mode-coupling approaches and experimental proposals. Phys. Rev. Lett. 2002, 89, 095702. [Google Scholar] [CrossRef]
- Argon, A.S. Plastic deformation in metallic glasses. Acta Metall. 1979, 27, 47–58. [Google Scholar] [CrossRef]
- Olsson, P.; Teitel, S. Critical scaling of shear viscosity at the jamming transition. Phys. Rev. Lett. 2007, 99, 178001. [Google Scholar] [CrossRef]
- Adam, G.; Gibbs, J.H. On the temperature dependence of cooperative relaxation properties in glass-forming liquids. J. Chem. Phys. 1965, 43, 139–146. [Google Scholar] [CrossRef]
- Falk, M.L.; Langer, J.S. Dynamics of viscoplastic deformation in amorphous solids. Phys. Rev. E 1998, 57, 7192–7205. [Google Scholar] [CrossRef]
- Langer, J.S. Shear-transformation-zone theory of plastic deformation near the glass transition. Phys. Rev. E 2008, 77, 021502. [Google Scholar] [CrossRef]
- Götze, W. Complex Dynamics of Glass-Forming Liquids: Mode-Coupling Theory; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Fuchs, M.; Cates, M.E. Theory of nonlinear rheology and yielding of dense colloidal suspensions. Phys. Rev. Lett. 2002, 89, 248304. [Google Scholar] [CrossRef]
- Voigtmann, Th. Yield stresses and flow curves in metallic glass formers and granular systems. Eur. Phys. J. 2011, 34, 106. [Google Scholar]
- Batschinski, A.J. Examination of the inner friction of liquids. I. Z. Physik. Chem. 1913, 84, 643–706. [Google Scholar]
- Doolittle, A.K. Studies of newtonian flow. II. The dependence of the viscosity of liquids on free space. J. Appl. Phys. 1951, 22, 1471–1415. [Google Scholar] [CrossRef]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. Mechanical properties of substances of high molecular weight. 19. The temperature dependence of relaxation mechanisms in amorphous polymers and other glass-forming liquids. J. Am. Chem. Soc. 1955, 77, 3701–3707. [Google Scholar]
- Turnbull, D.; Cohen, M.H. Free-volume model of the amorphous phase: Glass transition. J. Chem. Phys. 1961, 34, 120–125. [Google Scholar] [CrossRef]
- Turnbull, D.; Cohen, M.H. On the free-volume model of the liquid-glass transition. J. Chem. Phys. 1970, 52, 3038–3041. [Google Scholar] [CrossRef]
- Egami, T. Understanding the properties and structure of metallic glasses at the atomic level. J. Metals 2010, 62, 70–75. [Google Scholar]
- Caris, J.; Lewandowski, J.J. Pressure effects on metallic glasses. Acta Matall. 2010, 58, 1026–1036. [Google Scholar] [CrossRef]
- Nachtrieb, N.H.; Petit, J. Self-diffusion in liquid mercury. J. Chem. Phys. 1956, 24, 746–750. [Google Scholar] [CrossRef]
- Klugkist, P.; Rätzke, K.; Rehders, S.; Troche, P.; Faupel, F. Activation volume of Co-57 diffusion in amorphous Co81Zr19. Phys. Rev. Lett. 1998, 80, 3288–3291. [Google Scholar] [CrossRef]
- Bennett, C.H.; Chaudhari, P.; Moruzzi, P.; Steinhardt, P. Stability of vacancy and vacancy clusters in amorphous solids. Philos. Mag. A 1979, 40, 485–495. [Google Scholar] [CrossRef]
- Argon, A.S.; Shi, L.T. Development of visco-plastic deformation in metallic glasses. Acta Metall. 1983, 31, 499–507. [Google Scholar] [CrossRef]
- Johnson, W.L.; Samwer, K. A universal criterion for plastic yielding of metallic glasses with a (T/Tg)2/3 temperature dependence. Phys. Rev. Lett. 2005, 95, 195501. [Google Scholar] [CrossRef]
- Stillinger, F.H. Topographic view of supercooled liquids and glass-formation. Science 1995, 267, 1935–1939. [Google Scholar]
- Bouchbinder, E.; Langer, J.S. Linear response theory for hard and soft glassy materials. Phys. Rev. Lett. 2011, 106, 148301. [Google Scholar] [CrossRef]
- Langer, J.S.; Egami, T. Glass dynamics at high strain rates. Phys. Rev. E 2012, 86, 011502. [Google Scholar] [CrossRef]
- Gauthier, C.; Pelletier, J.M.; Wang, Q.; Blandin, J.J. Viscoelastic and viscoplastic properties of bulk metallic glasses: Comparison with oxide glasses and amorphous polymers. J. Non-Cryst. Solids 2004, 345–346, 469–472. [Google Scholar]
- Percus, J.K.; Yevick, G.J. Analysis of classical statistical mechanics by means of collective coordinates. Phys. Rev. 1958, 110, 1–13. [Google Scholar] [CrossRef]
- Bernal, J.D. A geometrical approach to the structure of liquids. Nature 1959, 183, 141–147. [Google Scholar]
- Finney, J.L. Random packings and the structure of simple liquids. I. The geometry of random close packing. Proc. Roy. Soc. Lond. A 1970, 319, 479–493. [Google Scholar] [CrossRef]
- Honeycutt, J.D.; Andersen, H.C. Molecular dynamics study of melting and freezing of small Lennard-Jones clusters. J. Phys. Chem. 1987, 91, 4950–4963. [Google Scholar] [CrossRef]
- Steinhardt, P.; Alben, R.; Weaire, D. Relaxed continuous random network models. I. Structural characteristics. J. Non-Cryst. Solids 1974, 15, 199–214. [Google Scholar]
- Rivier, N. Disclination lines in glasses. Philos. Mag. A 1979, 40, 859–868. [Google Scholar] [CrossRef]
- Egami, T.; Aur, S. Local atomic structure of amorphous and crystalline alloys: Computer simulation. J. Non-Cryst. Solids 1987, 89, 60–74. [Google Scholar]
- Donati, C.; Douglas, J.F.; Kob, W.; Plimpton, S.J.; Poole, P.H.; Glotzer, S.C. Stringlike cooperative motion in a supercooled liquid. Phys. Rev. Lett. 1998, 80, 2338–2341. [Google Scholar] [CrossRef]
- Yamamoto, R.; Onuki, A. Dynamics of highly supercooled liquids: Heterogeneity, rheology, and diffusion. Phys. Rev. E 1998, 58, 3515–3529. [Google Scholar] [CrossRef]
- Widmer-Cooper, A.; Harrowell, P. Predicting the long-time dynamic heterogeneity in a supercooled liquid on the basis of short-time heterogeneities. Phys. Rev. Lett. 2006, 96, 185701. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Egami, T.; Iwashita, T.; Dmowski, W. Mechanical Properties of Metallic Glasses. Metals 2013, 3, 77-113. https://doi.org/10.3390/met3010077
Egami T, Iwashita T, Dmowski W. Mechanical Properties of Metallic Glasses. Metals. 2013; 3(1):77-113. https://doi.org/10.3390/met3010077
Chicago/Turabian StyleEgami, Takeshi, Takuya Iwashita, and Wojciech Dmowski. 2013. "Mechanical Properties of Metallic Glasses" Metals 3, no. 1: 77-113. https://doi.org/10.3390/met3010077