A Meso-Mechanical Constitutive Model of Particle-Reinforced Titanium Matrix Composites at High Temperatures
Abstract
:1. Introduction
2. Experimental Procedure
2.1. Materials
2.2. Specimen Preparation
2.3. Quasi-Static Tensile Tests
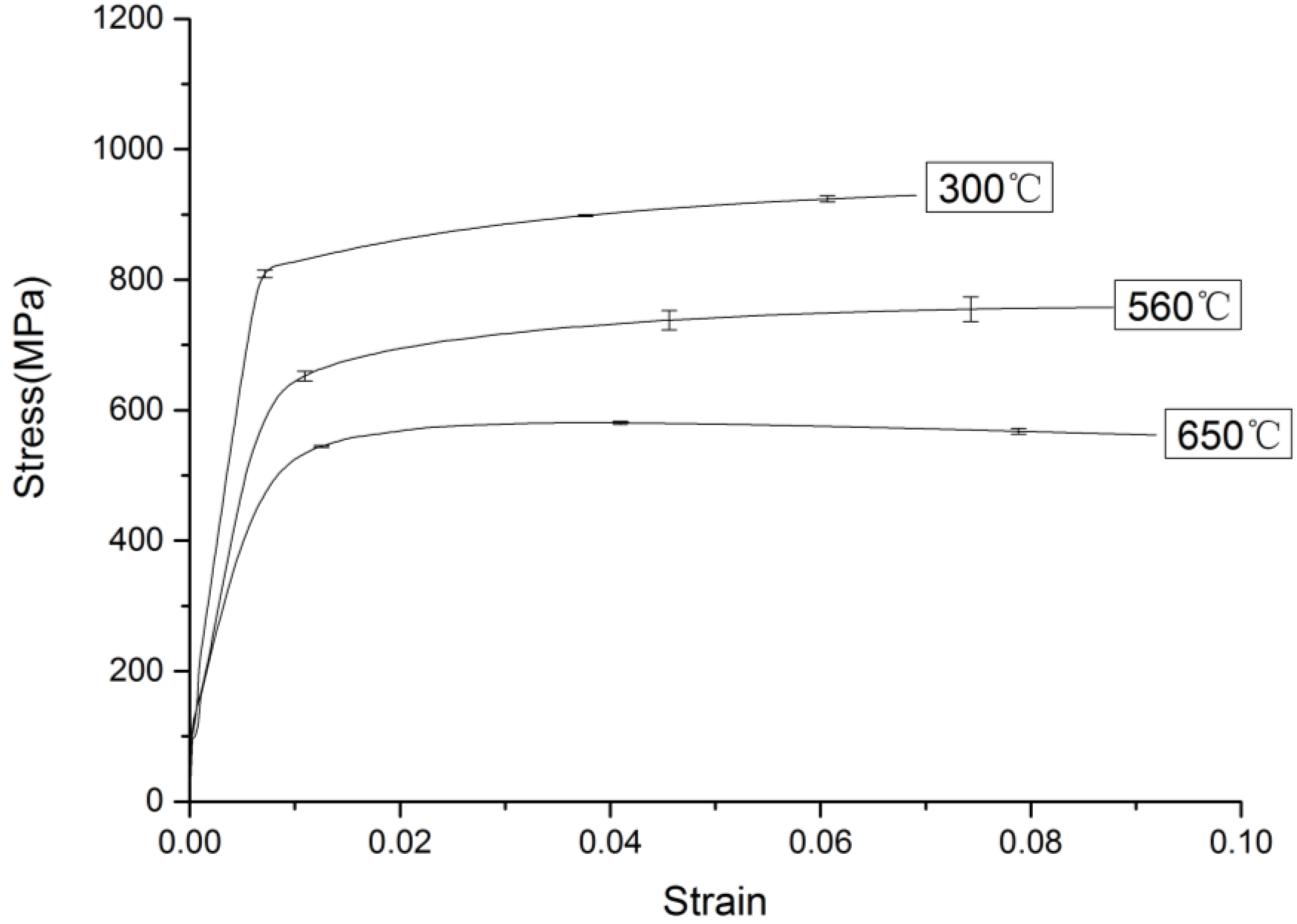
2.4. Experimental Results
2.4.1. Microstructure
2.4.2. Stress-Strain Relationship
3. Meso-Mechanical Theory for Multiphase Composite
3.1. Average Stress of the Reinforcement and the Matrix
3.2. Effective Stiffness Tensor of the Composite
4. Elastoplastic Analysis of the Composite
4.1. Constitutive Model of the Matrix
4.2. Stress for the Reinforcement and the Matrix and the Secant Tensor of the Composite under Force Boundary Conditions
4.3. Interfacial Debonding Model
4.4. Elastoplastic Stress-Strain Relationship
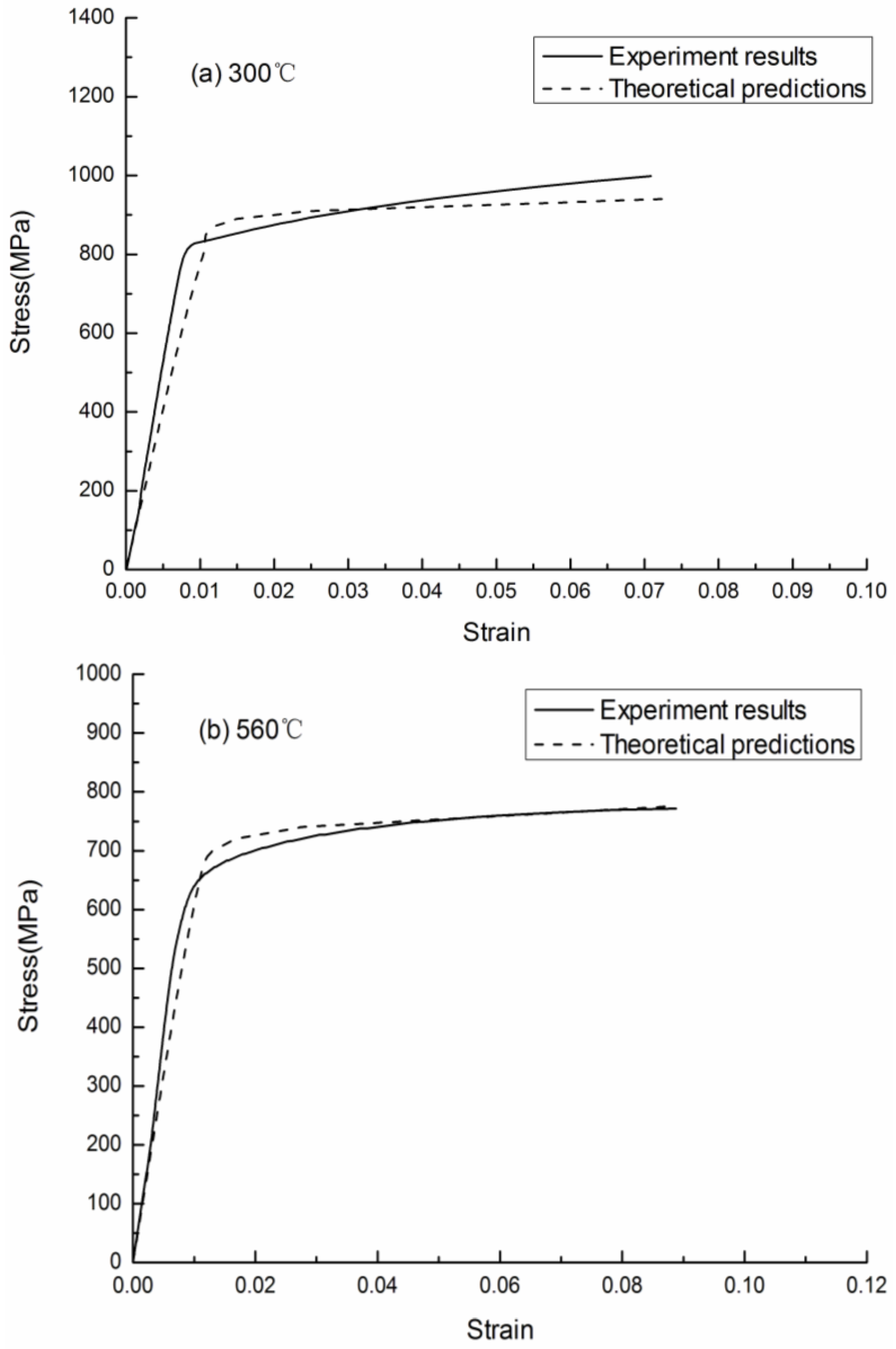
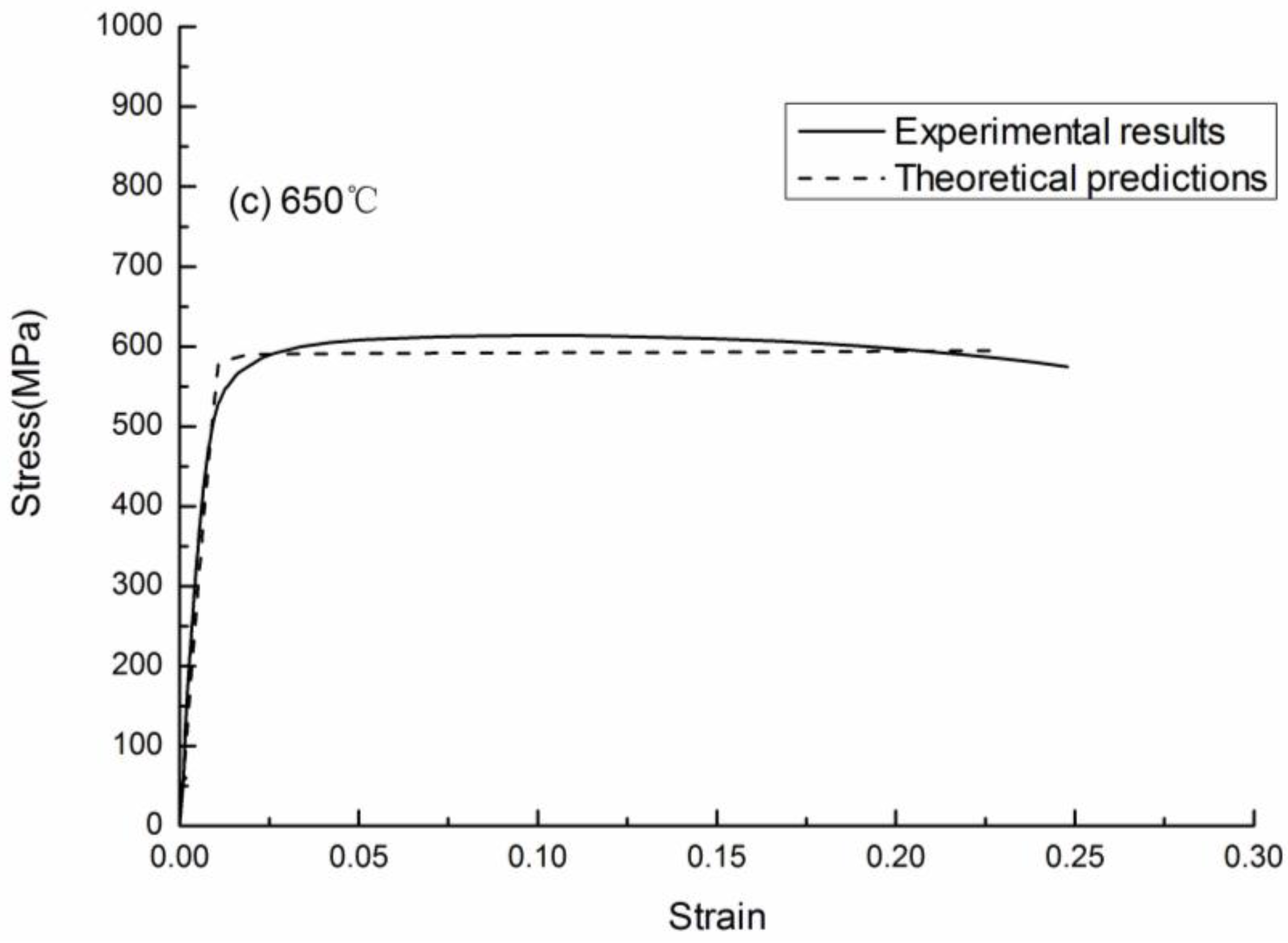
5. Comparison of Numerical Predictions with Experimental Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hunt, M. MMCs for exotic needs. Compos. Mater. Sci. 1992, 104, 53–62. [Google Scholar]
- Gorynin, I.V. Titanium alloys for marine application. Mater. Sci. Eng. A 1999, 263, 112–116. [Google Scholar] [CrossRef]
- Schutz, R.W.; Scaturro, M.R. An overview of current and candidate titanium alloy applications on U.S. navy surface ships. Nav. Eng. J. 1991, 175–191. [Google Scholar] [CrossRef]
- Luo, Y.Z. Recent development of titanium metallic matrix composites. Rare Met. Mater. Eng. 1997, 26, 1–7. [Google Scholar]
- Vallauri, D.; Adrian, I.C.A.; Chrysanthou, A. TiC-TiB2 composites: A review of phase relationships, processing and properties. J. Eur. Ceram. Soc. 2008, 28, 1697–1713. [Google Scholar] [CrossRef]
- Leyens, C.; Peters, M. Titanium and Titanium Alloys; Wiley-VCH: Cologne, Germany, 2003. [Google Scholar]
- Tjong, S.C.; Ma, Z.Y. Microstructural and mechanical characteristics of in-situ metal matrix composites. Mater. Sci. Eng. R 2000, 29, 49–113. [Google Scholar] [CrossRef]
- Tjong, S.C.; Mai, Y.W. Processing-structure-property aspects of particulate- and whisker-reinforced titanium matrix composites. Compos. Sci. Technol. 2008, 68, 583–660. [Google Scholar] [CrossRef]
- Wang, X.H.; Zou, Z.D.; Qu, S.Y.; Song, S.L. Microstructure and wear properties of Fe-based hardfacing coating reinforced by TiC particles. J. Mater. Process. Technol. 2005, 168, 89–94. [Google Scholar] [CrossRef]
- Akhtar, F.; Guo, S.J. Microstructure, mechanical and fretting wear properties of TiC-stainless steel composites. Mater. Charact. 2008, 59, 84–90. [Google Scholar] [CrossRef]
- Gu, D.D.; Hagedorn, Y.C.; Meiners, W.; Wissenbach, K.; Poprawe, R. Nanocrystalline TiC reinforced Ti matrix bulk-form nanocomposites by Selective Laser Melting (SLM): Densification, growth mechanism and wear behavior. Compos. Sci. Technol. 2011, 71, 1612–1620. [Google Scholar] [CrossRef]
- Gu, D.D.; Meng, G.B.; Li, C.; Meiners, W.; Poprawe, R. Selective laser melting of TiC/Ti bulk nanocomposites: Influence of nanoscale reinforcement. Scr. Mater. 2012, 67, 185–188. [Google Scholar] [CrossRef]
- Tohgo, K.; Weng, G.J. A Progressive Damage Mechanics in Particle-reinforced Metal-Matrix Composites under High Triaxial Tension, Trans. of ASME. J. Eng. Mater. Technol. 1994, 116, 414–420. [Google Scholar] [CrossRef]
- Tohgo, K.; Chou, T.W. Incremental Theory of Particulate-Reinforced Composites Including Debonding Damage. JSME Int. J. Ser. A 1996, 39, 389–397. [Google Scholar] [CrossRef]
- Tohgo, K.; Itoh, Y.; Shimamura, Y. A Constitutive Model of Particulate-Reinforced Composites Taking Account of Particle Size Effects and Damage Evolution. Compos. A 2010, 41, 313–321. [Google Scholar] [CrossRef]
- Tohgo, K.; Fujii, T.; Shimamura, D.K.Y. Influence of Particle Size and Debonding Damage on an Elastic-Plastic Singular Field around a Crack-Tip in Particulate-Reinforced Composites. Acta Mech. 2014, 225, 1373–1389. [Google Scholar] [CrossRef]
- Li, W.; Song, W.D.; Ning, J.G.; Mao, X.N. Effects of strain rate and temperature on mechanical properties of TP-650 composite. Rare Mater. Eng. 2010, 39, 1195–1199. [Google Scholar]
- Song, W.D.; Ning, J.G.; Mao, X.N.; Tang, H.P. A modified Johnson-Cook model for titanium matrix composites reinforced with titanium carbide particles at elevated temperatures. Mater. Sci. Eng. A 2013, 576, 280–289. [Google Scholar] [CrossRef]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion and related problems. Proc. R. Soc. Lond. 1957, 241A, 376–396. [Google Scholar] [CrossRef]
- Eshelby, J.D. The elastic field outside an ellipsoidal inclusion. Proc. R. Soc. Lond. 1959, 252A, 561–569. [Google Scholar] [CrossRef]
- Hill, R. A self-consistent mechanics of composite materials. J. Mech. Phys. Solids 1965, 13, 213–222. [Google Scholar] [CrossRef]
- Budiansky, B. On the elastic model of some heterogeneous materials. J. Mech. Phys. Solids 1976, 12, 81–97. [Google Scholar]
- Morit, T.; Tanaka, K. Average stress in matrix and average energy of materials with misfitting inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Roscoe, R.A. The Viscosity of suspensions of rigid spheres. Br. J. Appl. Phys. 1952, 3, 267–269. [Google Scholar] [CrossRef]
- Hashin, Z.; Shtrikman, S. A variational approach to the theory of the elastic behaviour of multiphase materials. J. Mech. Phys. Solids 1963, 11, 127–140. [Google Scholar] [CrossRef]
- Hashin, Z.; Shtrikman, S. A variational approach to the theory of the effective magnetic permeability of multi- phase materials. J. Mech. Phys. Solids 1962, 10, 335–342. [Google Scholar] [CrossRef]
- Buryachenko, V. Elastic-plastic behavior of elastically homogeneous materials with a random field of inclusions. Int. J. Plast. 1999, 15, 687–720. [Google Scholar] [CrossRef]
- Hu, G.K. Composite plasticity based on matrix average second order stress moment. Int. J. Plast. 1997, 12, 1007–1015. [Google Scholar] [CrossRef]
- Tandon, P.; Weng, G.J. A theory of particle-reinforced plasticity. ASME J. Appl. Mech. 1991, 55, 126–135. [Google Scholar] [CrossRef]
- Song, W.; Yang, Y.; Ning, J. A Meso-Mechanical Constitutive Model of Particle Reinforced Titanium Matrix Composites Subjected to Impact Loading. J. Nano Res. 2013, 23, 104–107. [Google Scholar] [CrossRef]
- Lissenden, C.J. Fiber-matrix interfacial constitutive relations for metal matrix composites. Compos. B 1999, 30, 267–278. [Google Scholar] [CrossRef]
- Lee, H.K.; Pyo, S.H. An elastoplastic multi-level damage model for ductile matrix composites considering evolutionary weakened interface. Int. J. Solid Struct. 2008, 45, 1614–1631. [Google Scholar] [CrossRef]
- Xia, S.H.; Wang, J.T. A micromechanical model of toughening behavior in the dual-phase composite. Int. J. Plast. 2010, 26, 1442–1460. [Google Scholar] [CrossRef]
- Song, W.D.; Ning, J.G.; Wang, J. Mechanical Behavior of Titanium Carbide Particle-Reinforced Titanium Matrix Composite under Quasi-Static and Dynamic Tension. Adi. Sci. Lett. 2011, 4, 635–640. [Google Scholar] [CrossRef]
- Weibull, W. A statistical distribution function of side applicability. J. Appl. Mech. 1951, 18, 293–297. [Google Scholar]
- Zhao, Y.H.; Weng, G.J. Plasticity of a two-phase composite with partially debonded inclusions. Int. J. Plast. 1996, 12, 781–804. [Google Scholar] [CrossRef]


| Temperature | R.T. | 300 °C | 600 °C | 650 °C | 700 °C |
|---|---|---|---|---|---|
| E0/GPa | 113 | 71 | 25 | 20 | 15 |
| /MPa | 1050 | 670 | 590 | 540 | 420 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, W.; Dai, L.; Xiao, L.; Wang, C.; Mao, X.; Tang, H. A Meso-Mechanical Constitutive Model of Particle-Reinforced Titanium Matrix Composites at High Temperatures. Metals 2017, 7, 15. https://doi.org/10.3390/met7010015
Song W, Dai L, Xiao L, Wang C, Mao X, Tang H. A Meso-Mechanical Constitutive Model of Particle-Reinforced Titanium Matrix Composites at High Temperatures. Metals. 2017; 7(1):15. https://doi.org/10.3390/met7010015
Chicago/Turabian StyleSong, Weidong, Liansong Dai, Lijun Xiao, Cheng Wang, Xiaonan Mao, and Huiping Tang. 2017. "A Meso-Mechanical Constitutive Model of Particle-Reinforced Titanium Matrix Composites at High Temperatures" Metals 7, no. 1: 15. https://doi.org/10.3390/met7010015





