Numerical Predictions of the Occurrence of Necking in Deep Drawing Processes
Abstract
:1. Introduction
2. Constitutive Equations of the Ductile Damage Model
3. Numerical Integration of the Model and Its Validation
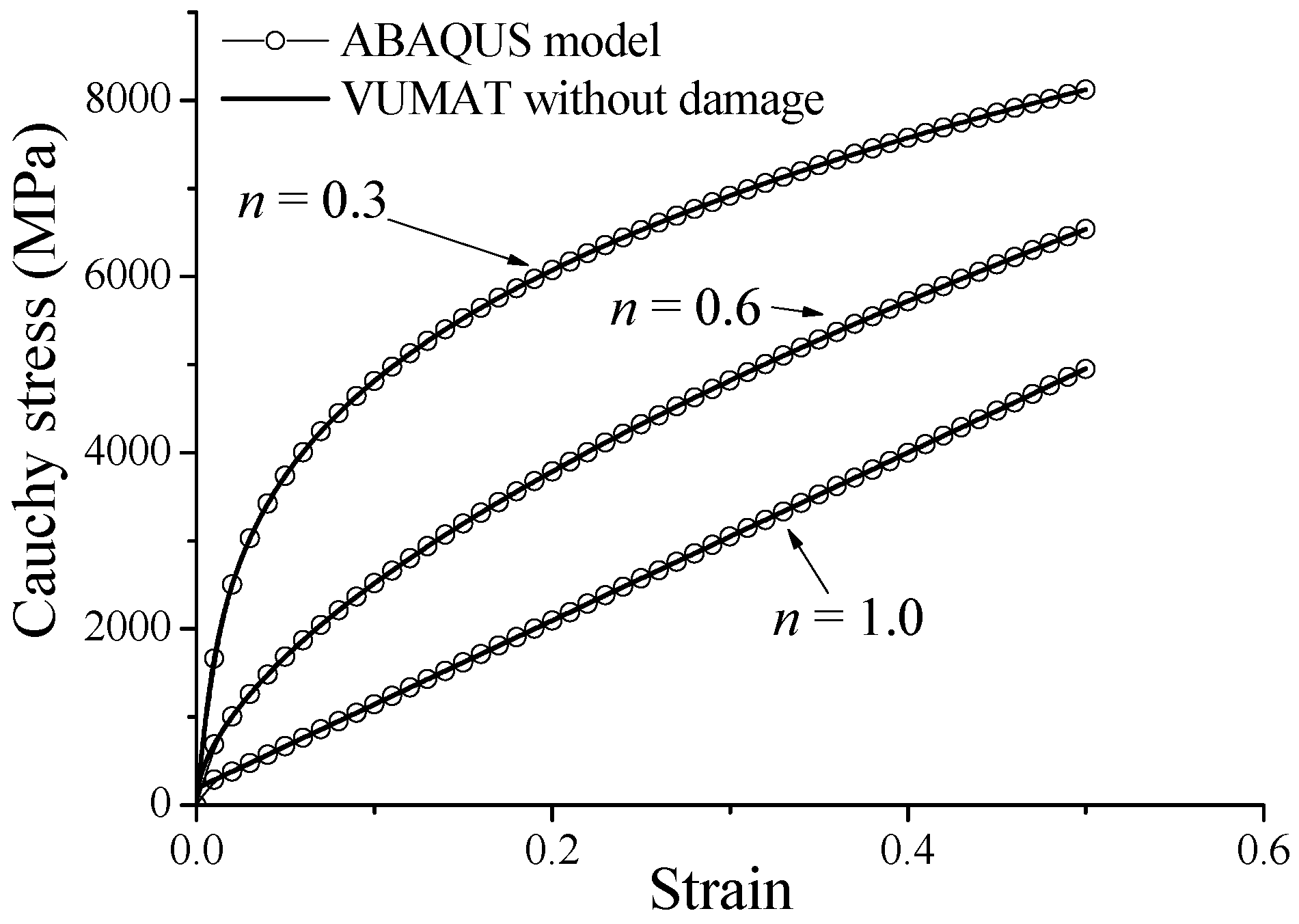
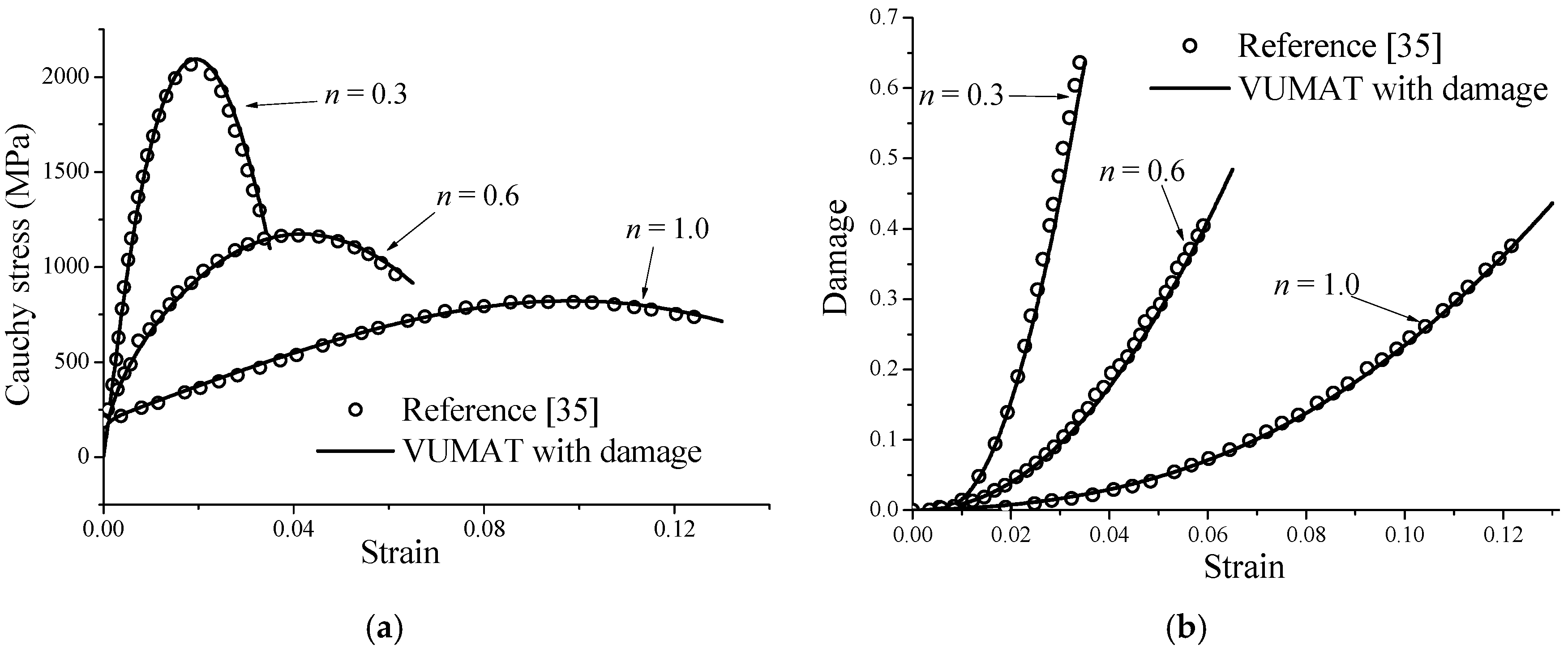
3.1. Time Integration Scheme
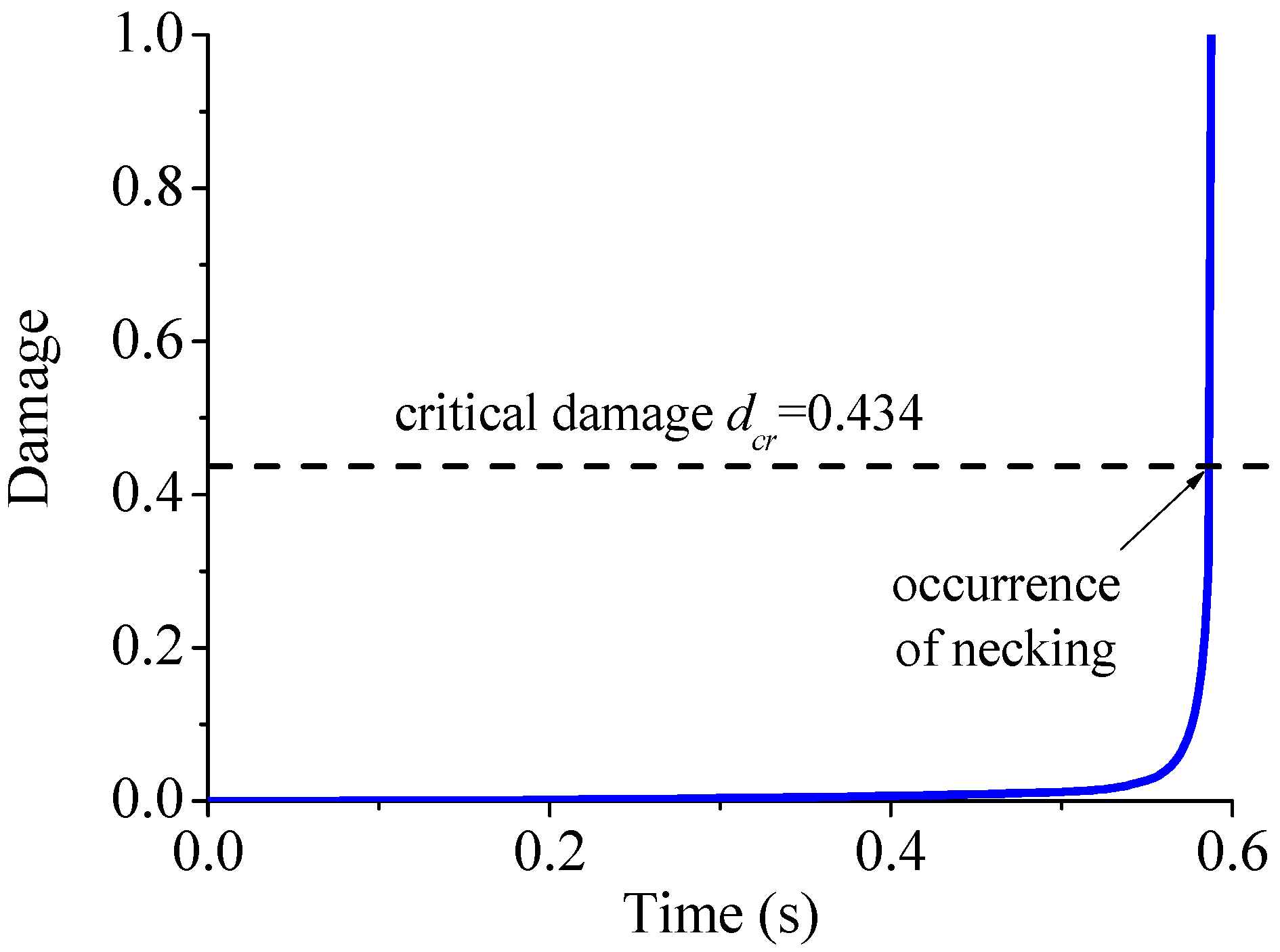
3.2. Numerical Validation
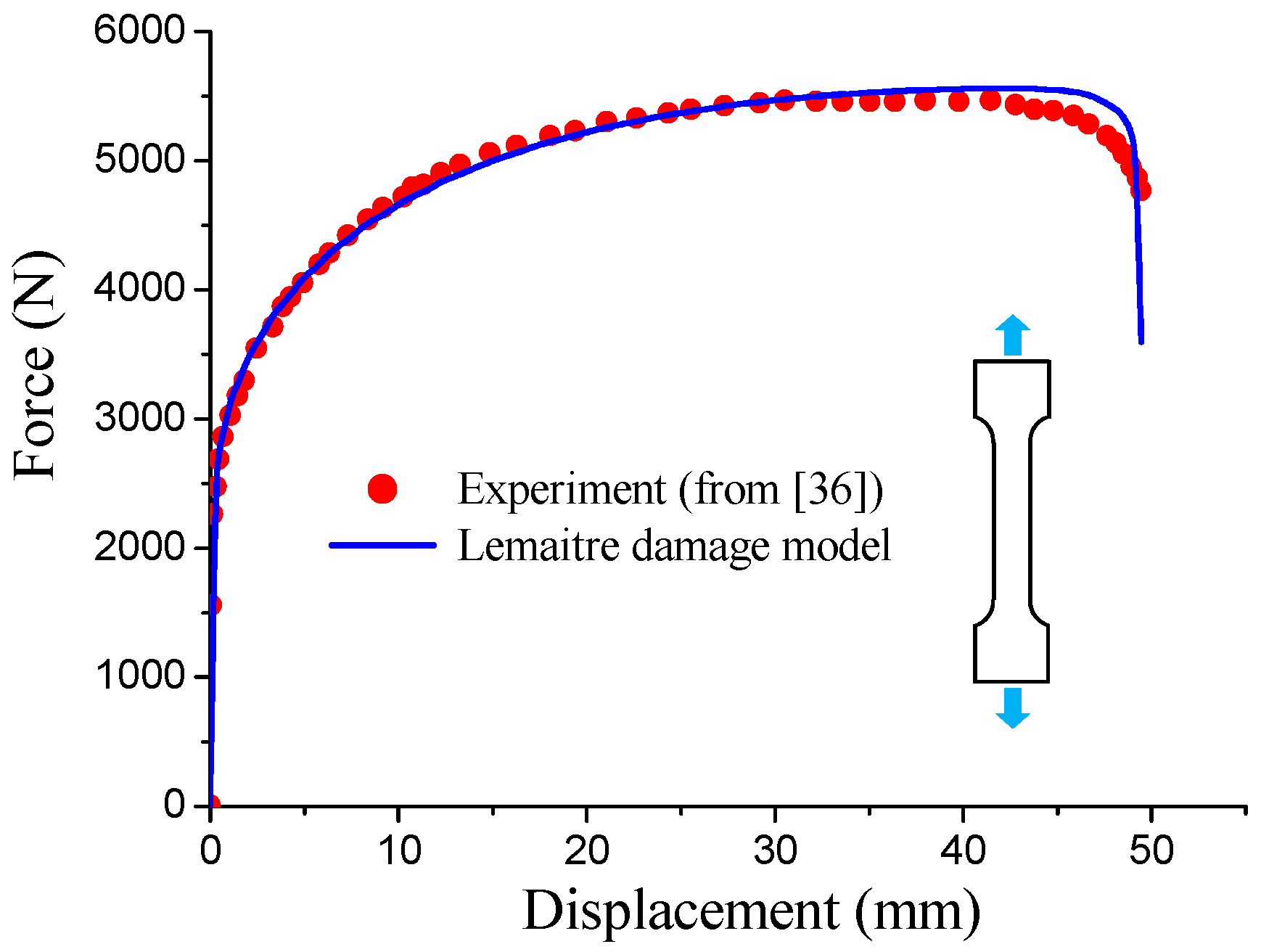
4. Identification of the St14 Steel Material Parameters
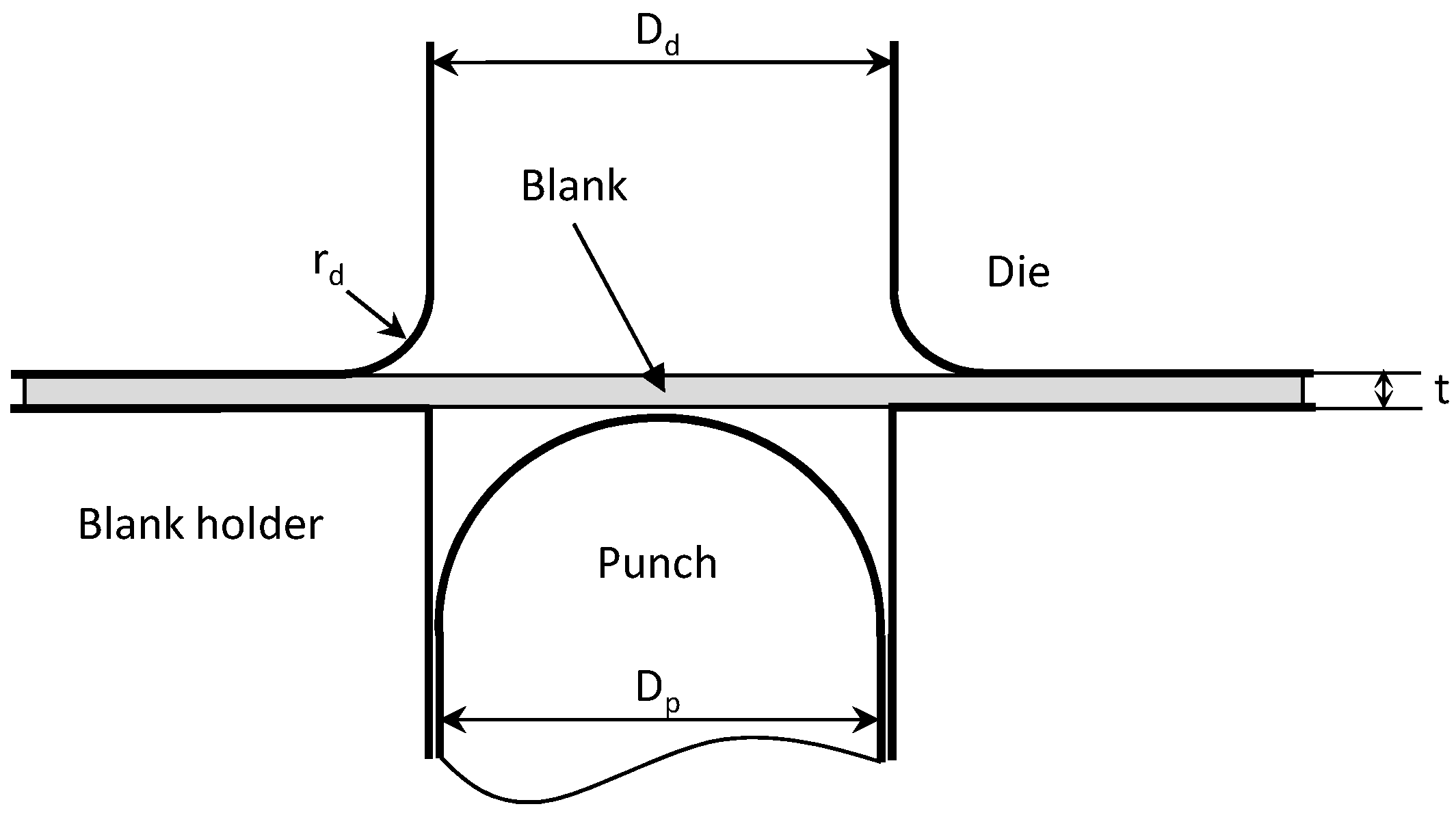
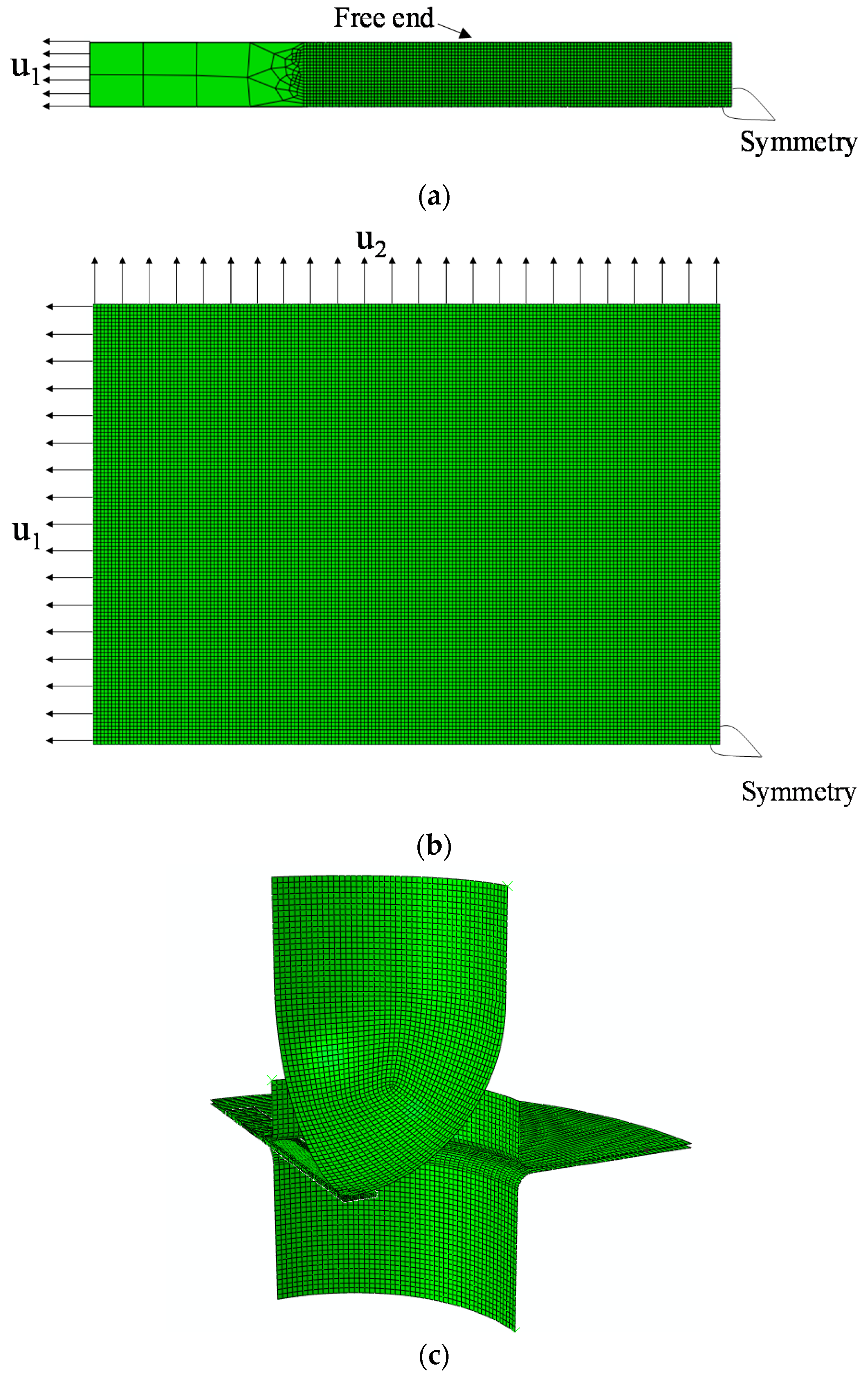
5. Description of the Finite Element Models
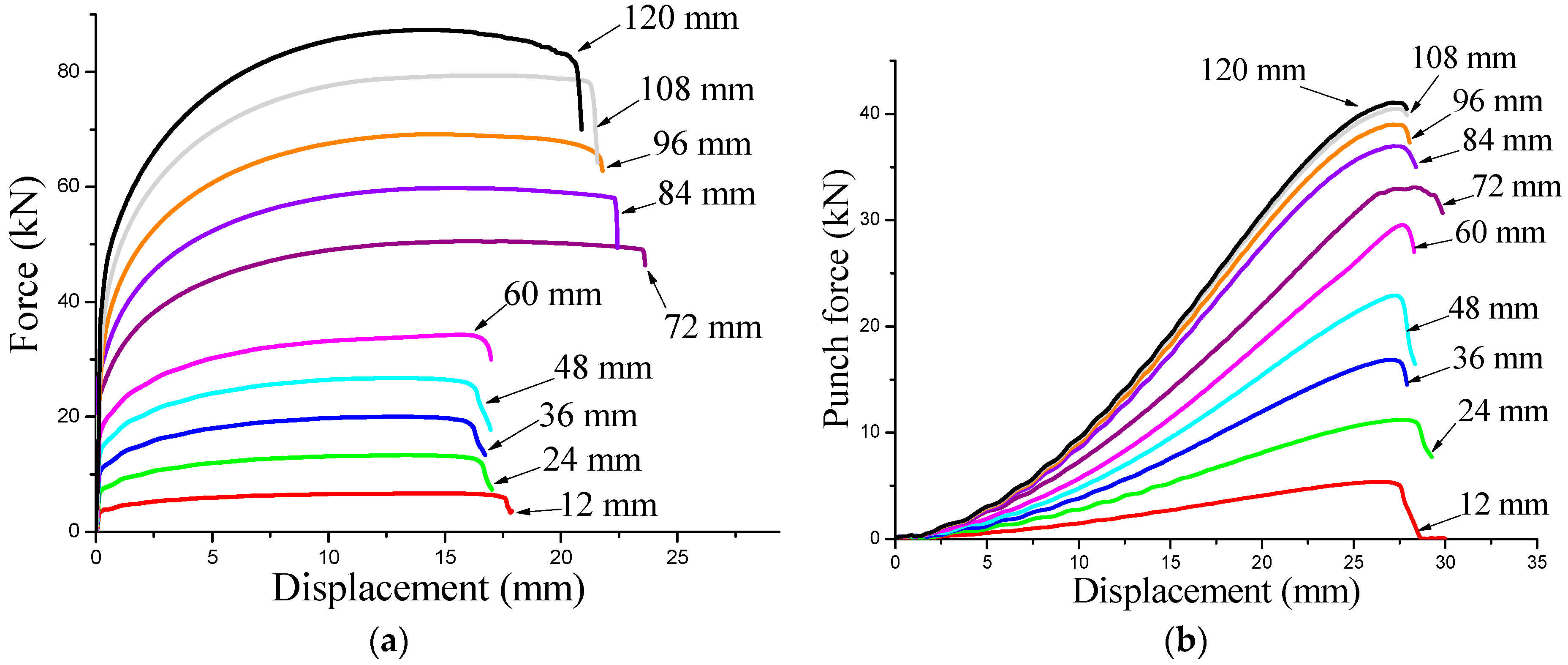
5.1. Finite Element Simulations
- Punch diameter Dp = 60 mm;
- Initial sheet thickness t = 0.8 mm;
- Die radius rd = 3 mm;
- Die opening diameter Dd = 66 mm.
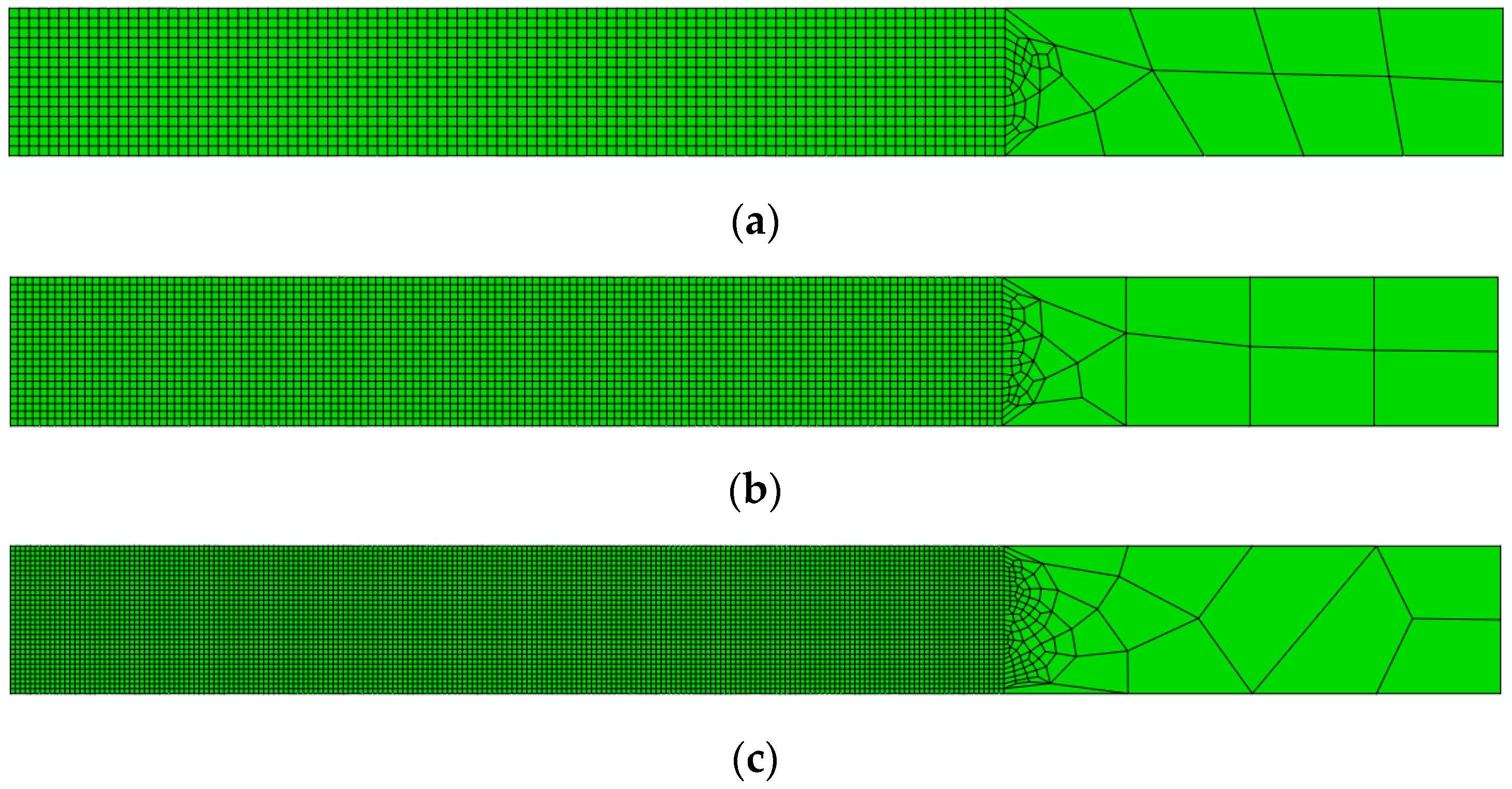
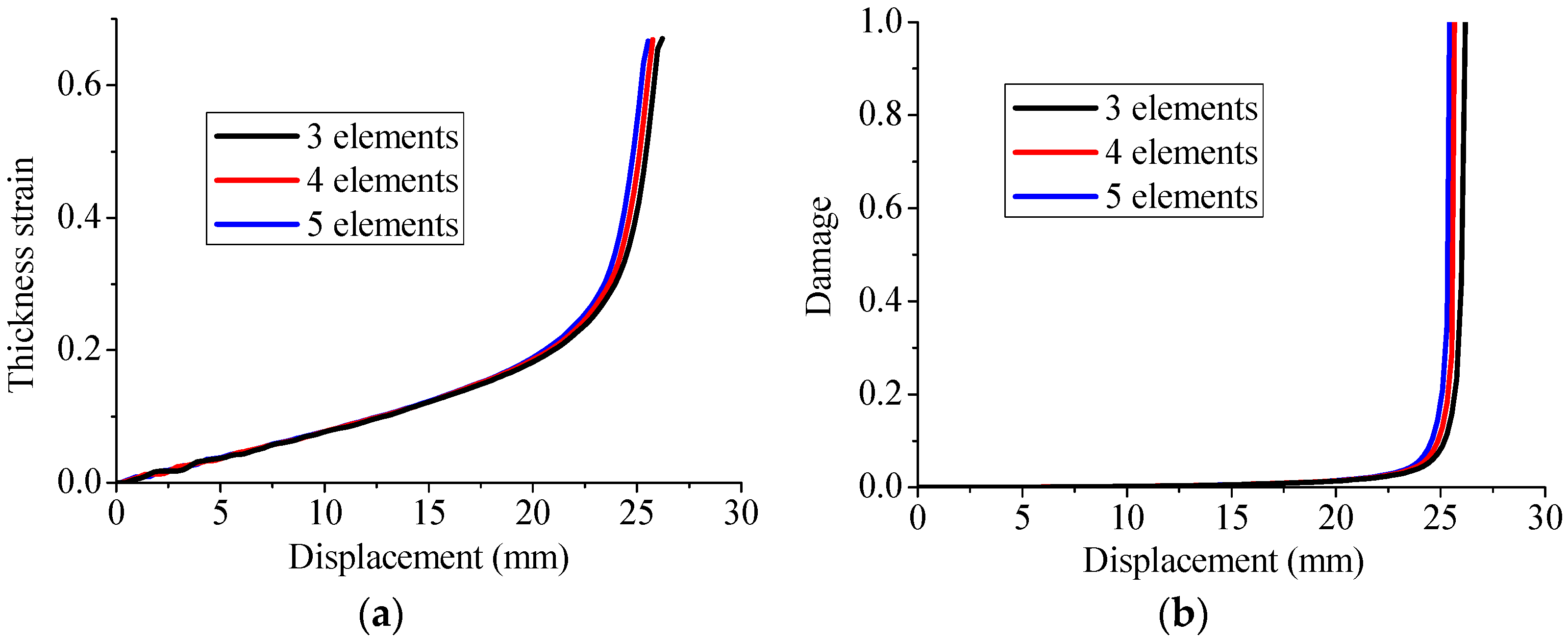
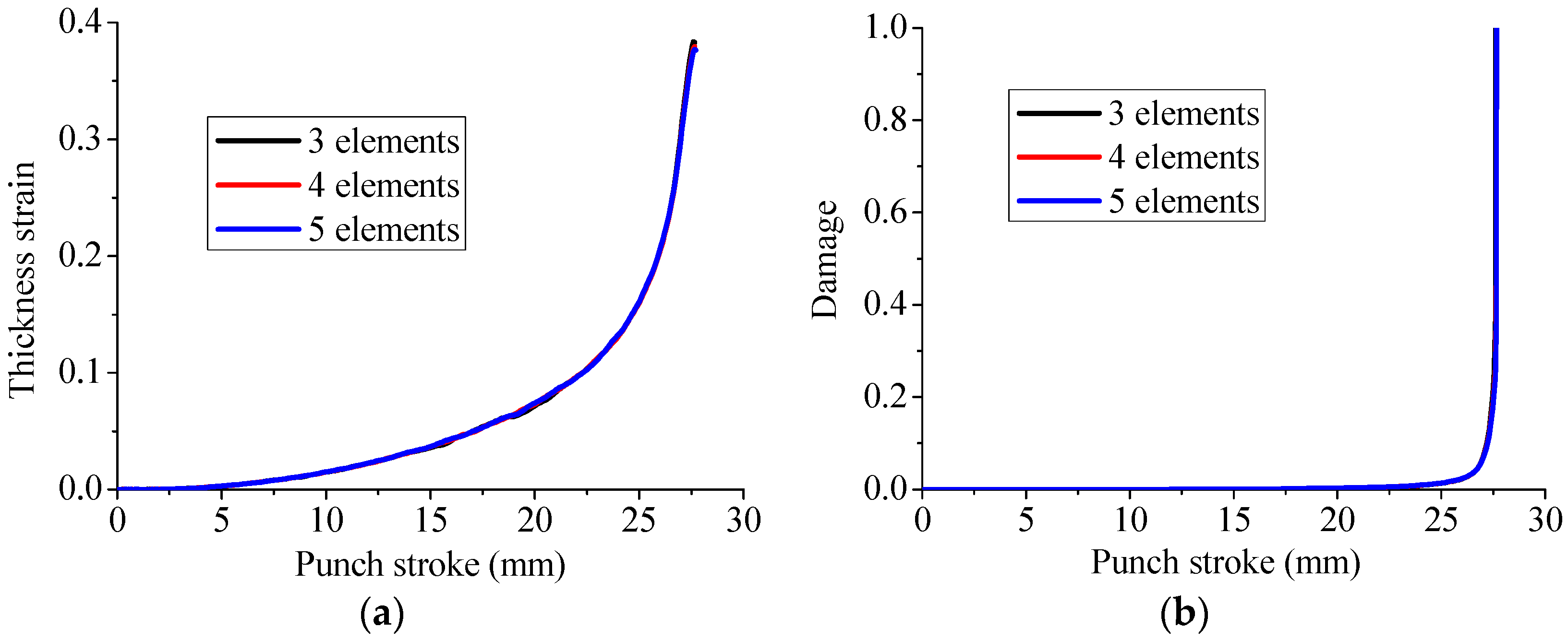
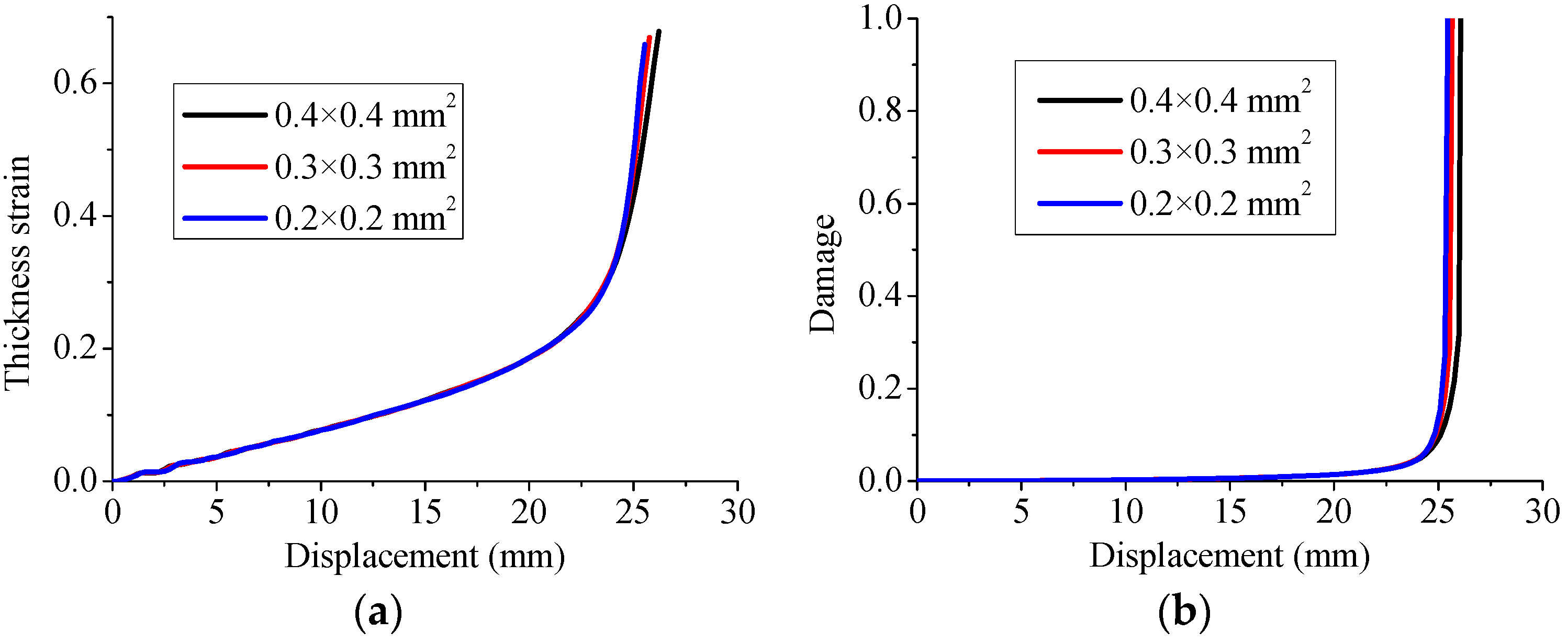
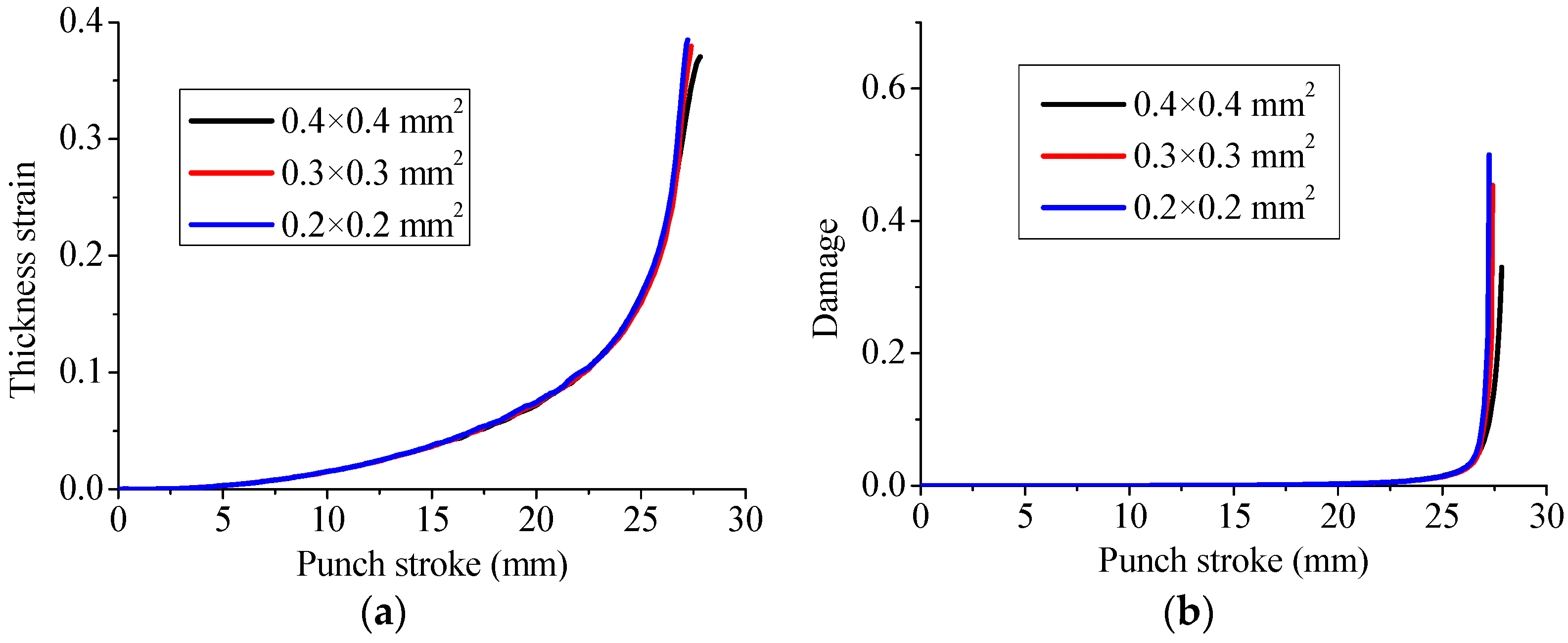
5.2. Mesh Sensitivity
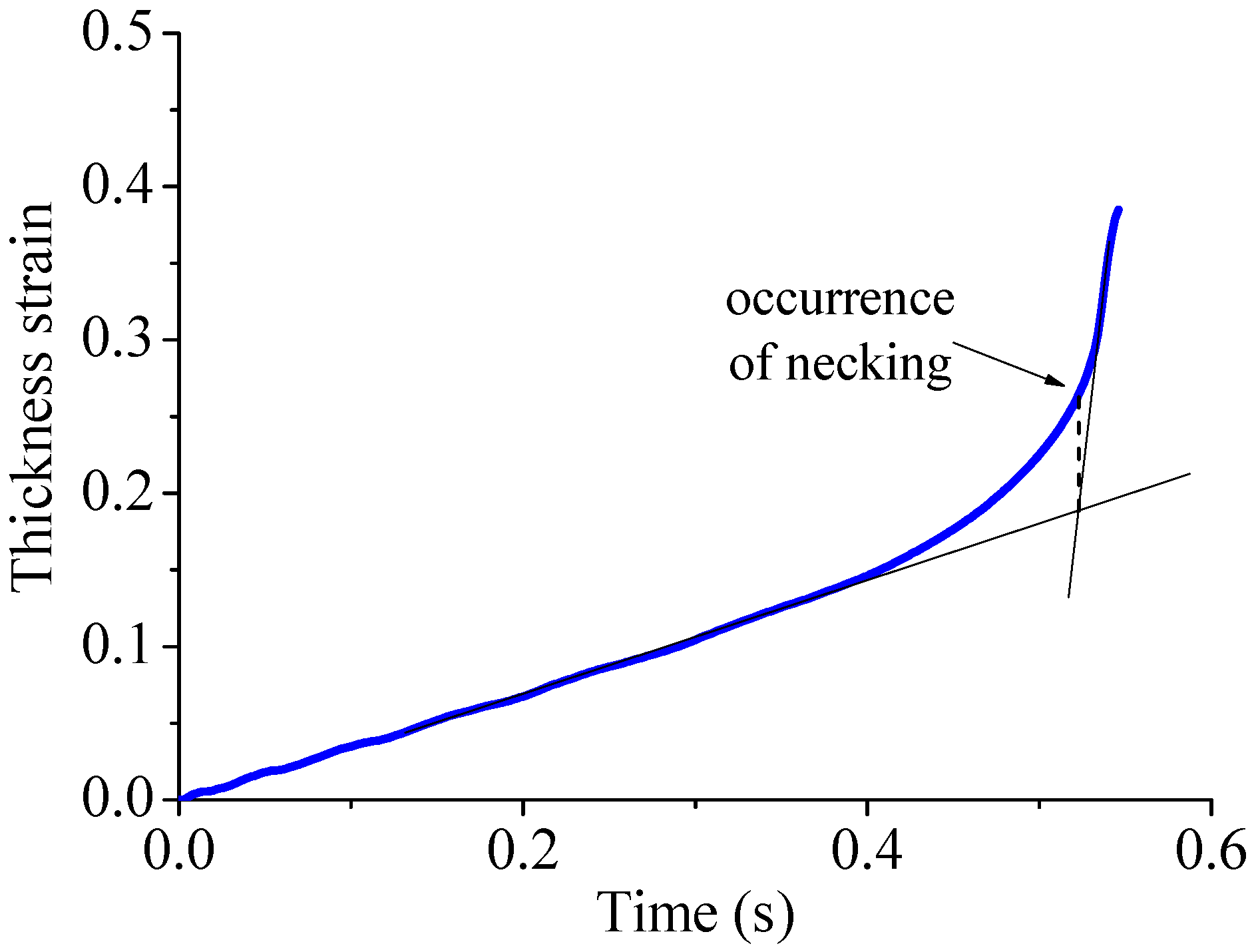
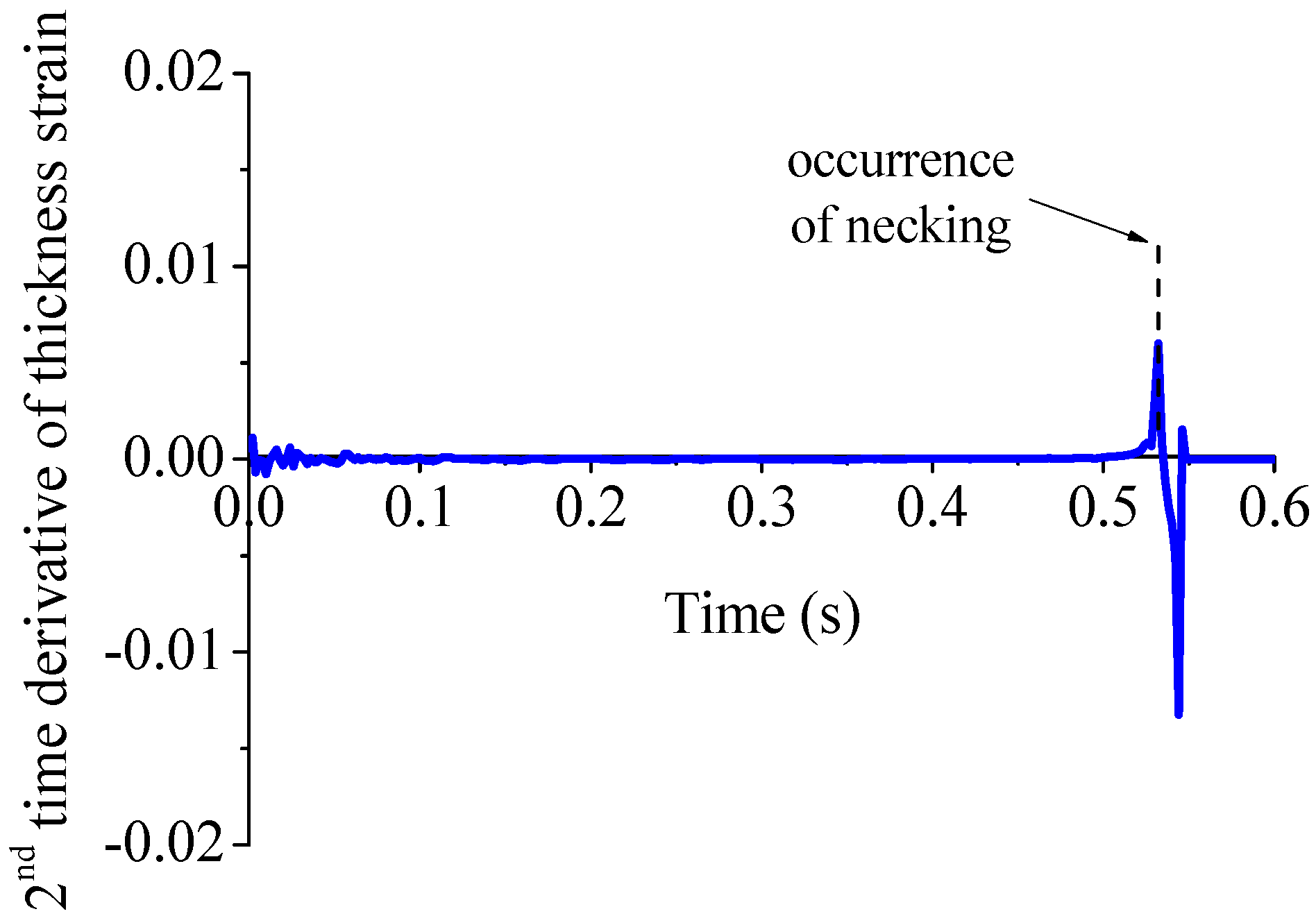
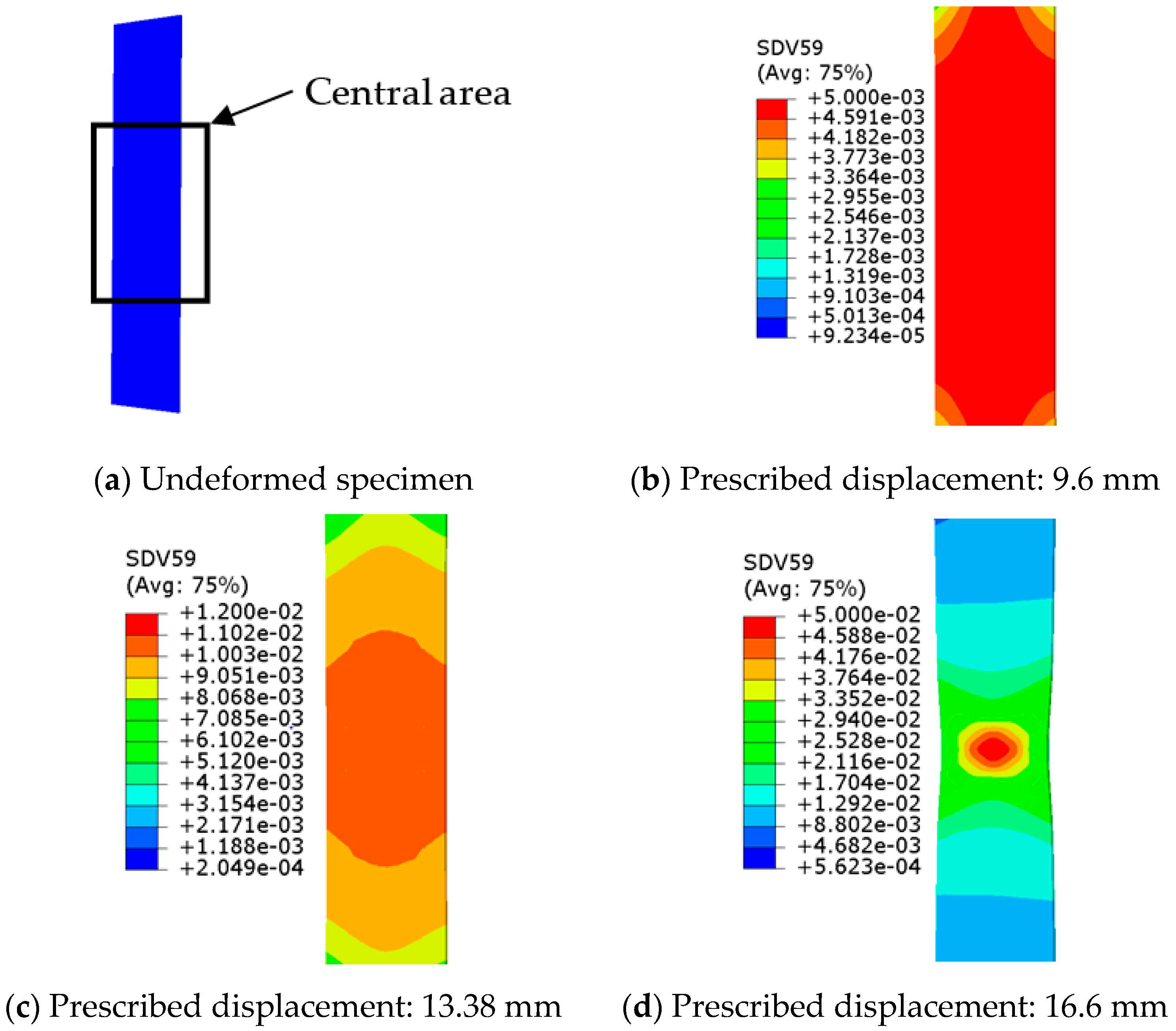
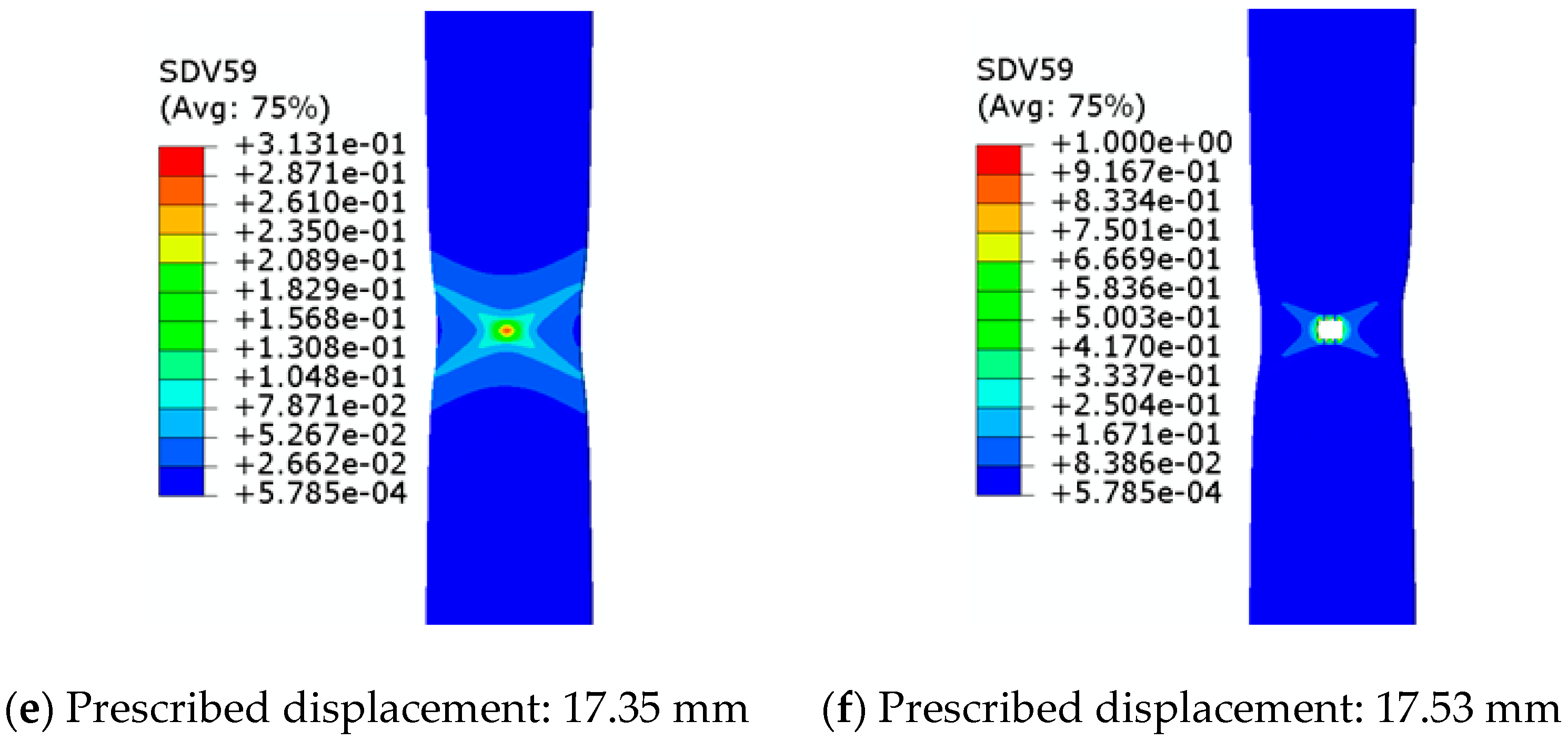
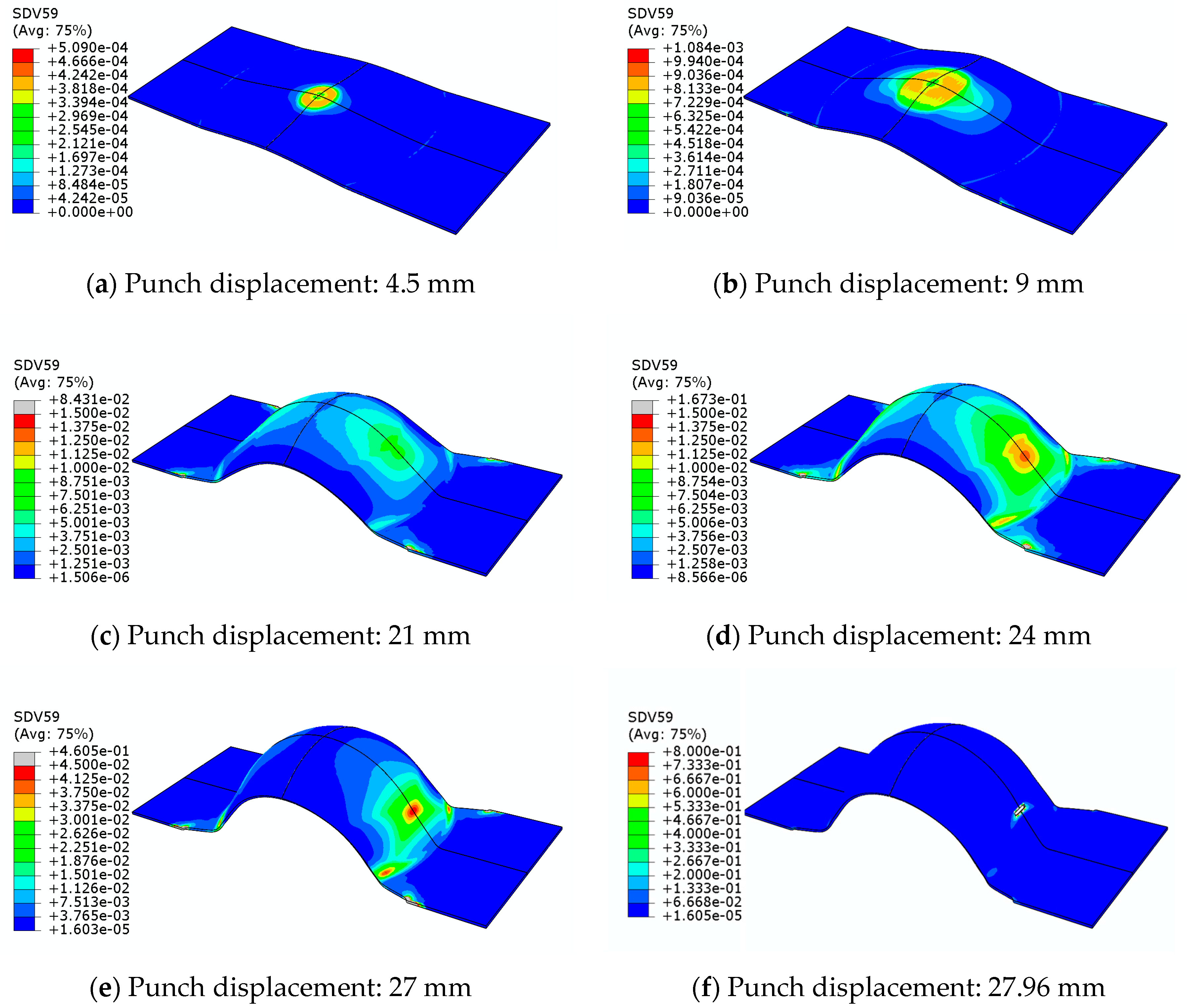
6. Numerical Criteria for the Prediction of the Occurrence of Necking
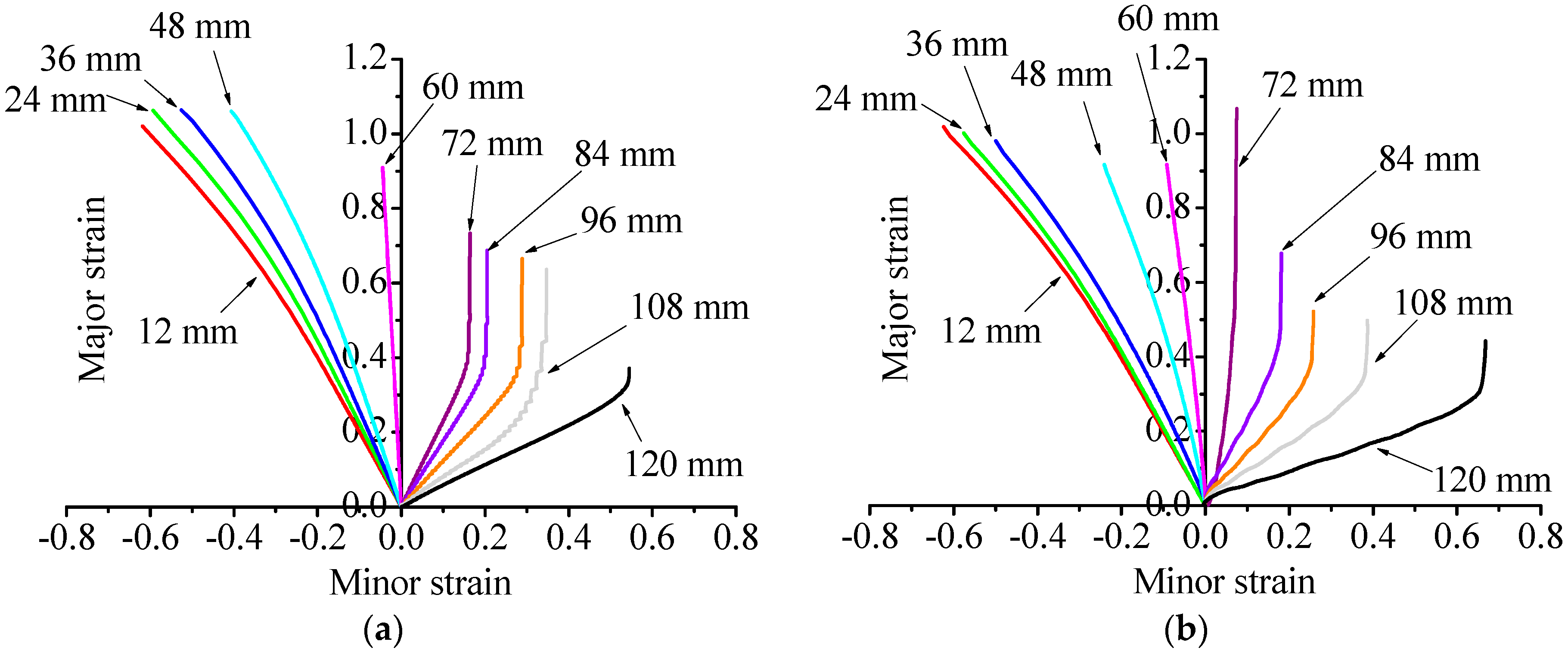
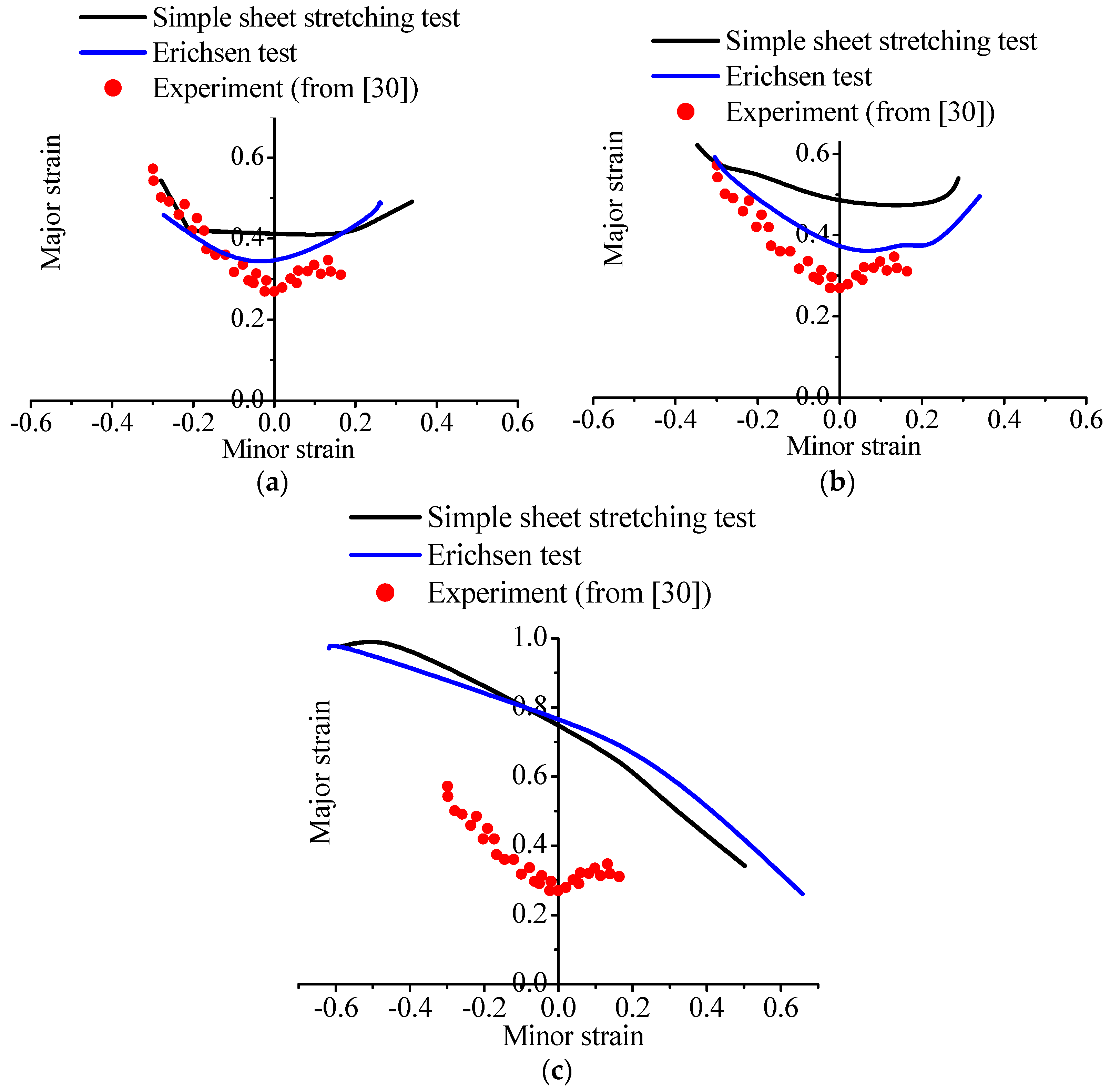
7. Application to the Determination of FLDs
8. Conclusions
Author Contributions
Conflicts of Interest
References
- Keeler, S.; Backofen, W.A. Plastic instability and fracture in sheets stretched over rigid punches. ASM Trans. Q. 1963, 56, 25–48. [Google Scholar]
- Goodwin, G. Application of strain analysis to sheet metal forming problems in the press shop. SAE Tech. Pap. 1968. [Google Scholar] [CrossRef]
- Swift, H.W. Plastic instability under plane stress. J. Mech. Phys. Solids 1952, 1, 1–18. [Google Scholar] [CrossRef]
- Considère, A. Mémoire sur l’emploi du fer et de l’acier dans les constructions. Annals Ponts Chaussées 1885, 9, 574. [Google Scholar]
- Hill, R. On discontinuous plastic states, with special reference to localized necking in thin sheets. J. Mech. Phys. Solids 1952, 1, 19–30. [Google Scholar] [CrossRef]
- Marciniak, Z.; Kuczyński, K. Limit strains in the processes of stretch-forming sheet metal. Int. J. Mech. Sci. 1967, 9, 609–620. [Google Scholar] [CrossRef]
- Brun, R.; Chambard, A.; Lai, M.; De Luca, P. Actual and virtual testing techniques for a numerical definition of materials. In Proceedings of the 4th International Conference and Workshop NUMISHEET ’99, Besançon, France, 13–17 September 1999; pp. 393–398. [Google Scholar]
- Petek, A.; Pepelnjak, T.; Kuzman, K. An improved method for determining forming limit diagram in the digital environment. J. Mech. Eng. 2005, 51, 330–345. [Google Scholar]
- Situ, Q.; Jain, M.K.; Bruhis, M. A suitable criterion for precise determination of incipient necking in sheet materials. Mater. Sci. Forum 2006, 519–521, 111–116. [Google Scholar] [CrossRef]
- Situ, Q.; Jain, M.K.; Bruhis, M. Further experimental verification of a proposed localized necking criterion. In Proceedings of the 9th International Conference on Numerical Methods in Industrial Forming Processes, Porto, Portugal, 17–21 June 2007; pp. 907–912. [Google Scholar]
- Situ, Q.; Jain, M.K.; Bruhis, M.; Metzger, D.R. Determination of forming limit diagrams of sheet materials with a hybrid experimental-numerical approach. Int. J. Mech. Sci. 2011, 53, 707–719. [Google Scholar] [CrossRef]
- Clift, S.E.; Hartley, P.; Sturgess, C.E.N.; Rowe, G.W. Fracture prediction in plastic deformation processes. Int. J. Mech. Sci. 1990, 32, 1–17. [Google Scholar] [CrossRef]
- Wierzbicki, T.; Bao, Y.; Lee, Y.-W.; Bai, Y. Calibration and evaluation of seven fracture models. Int. J. Mech. Sci. 2005, 47, 719–743. [Google Scholar] [CrossRef]
- Bao, Y.; Wierzbicki, T. On fracture locus in the equivalent strain and stress triaxiality space. Int. J. Mech. Sci. 2004, 46, 81–98. [Google Scholar] [CrossRef]
- Han, H.N.; Kim, K.-H. A ductile fracture criterion in sheet metal forming process. J. Mater. Process. Technol. 2003, 142, 231–238. [Google Scholar] [CrossRef]
- Jain, M.; Allin, J.; Lloyd, D.J. Fracture limit prediction using ductile fracture criteria for forming of an automotive aluminum sheet. Int. J. Mech. Sci. 1999, 41, 1273–1288. [Google Scholar] [CrossRef]
- Gurson, A.L. Continuum theory of ductile rupture by void nucleation and growth: Part I—Yield criteria and flow rules for porous ductile media. J. Eng. Mater. Technol. 1977, 99, 2–15. [Google Scholar] [CrossRef]
- Tvergaard, V.; Needleman, A. Analysis of the cup-cone fracture in a round tensile bar. Acta Metall. Mater. 1984, 32, 157–169. [Google Scholar] [CrossRef]
- Rousselier, G. Ductile fracture models and their potential in local approach of fracture. Nucl. Eng. Des. 1987, 105, 97–111. [Google Scholar] [CrossRef]
- Pardoen, T.; Doghri, I.; Delannay, F. Experimental and numerical comparison of void growth models and void coalescence criteria for the prediction of ductile fracture in copper bars. Acta Mater. 1998, 46, 541–552. [Google Scholar] [CrossRef]
- Benzerga, A.A.; Besson, J. Plastic potentials for anisotropic porous solids. Eur. J. Mech. A/Solids 2001, 20, 397–434. [Google Scholar] [CrossRef]
- Monchiet, V.; Cazacu, O.; Charkaluk, E.; Kondo, D. Macroscopic yield criteria for plastic anisotropic materials containing spheroidal voids. Int. J. Plast. 2008, 24, 1158–1189. [Google Scholar] [CrossRef]
- Lemaitre, J. A continuous damage mechanics model for ductile fracture. J. Eng. Mater. Technol. ASME 1985, 107, 83–89. [Google Scholar] [CrossRef]
- Chaboche, J.L. Thermodynamically founded CDM models for creep and other conditions. In Creep and Damage in Materials and Structures; CISM Courses and Lectures No 399, International Centre for Mechanical Sciences; Springer: Vienna, Austria, 1999; Volume 399, pp. 209–283. [Google Scholar]
- Lemaitre, J. A Course on Damage Mechanics; Springer: Berlin, Germany, 1992. [Google Scholar]
- Chow, C.L.; Lu, T.J. On evolution laws of anisotropic damage. Eng. Fract. Mech. 1989, 34, 679–701. [Google Scholar] [CrossRef]
- Chaboche, J.L. Development of continuum damage mechanics for elastic solids sustaining anisotropic and unilateral damage. Int. J. Damage Mech. 1993, 2, 311–329. [Google Scholar] [CrossRef]
- Abu Al-Rub, R.K.; Voyiadjis, G.Z. On the coupling of anisotropic damage and plasticity models for ductile materials. Int. J. Solids Struct. 2003, 40, 2611–2643. [Google Scholar] [CrossRef]
- Takuda, H.; Yoshii, T.; Hatta, N. Finite-element analysis of the formability of a magnesium-based alloy AZ31 sheet. J. Mater. Process. Technol. 1999, 89–90, 135–140. [Google Scholar] [CrossRef]
- Aboutalebi, F.H.; Farzin, M.; Mashayekhi, M. Numerical prediction and experimental validations of ductile damage evolution in sheet metal forming processes. Acta Mech. Solida Sin. 2012, 25, 638–650. [Google Scholar] [CrossRef]
- Hill, R. A theory of the yielding and plastic flow of anisotropic metals. Proc. R. Soc. A 1948, 193, 281–297. [Google Scholar] [CrossRef]
- Lemaitre, J.; Desmorat, R.; Sauzay, M. Anisotropic damage law of evolution. Eur. J. Mech. A Solids 2000, 9, 187–208. [Google Scholar] [CrossRef]
- Li, Y.-F.; Nemat-Nasser, S. An explicit integration scheme for finite deformation plasticity in finite-element methods. Finite Elem. Anal. Des. 1993, 15, 93–102. [Google Scholar] [CrossRef]
- Kojic, M. Stress integration procedures for inelastic material models within finite element method. ASME Appl. Mech. Rev. 2002, 55, 389–414. [Google Scholar] [CrossRef]
- Doghri, I.; Billardon, R. Investigation of localization due to damage in elasto-plastic materials. Mech. Mater. 1995, 19, 129–149. [Google Scholar] [CrossRef]
- Aboutalebi, F.H.; Farzin, M.; Poursina, M. Numerical simulation and experimental validation of a ductile damage model for DIN 1623 St14 steel. Int. J. Adv. Manuf. Technol. 2011, 53, 157–165. [Google Scholar] [CrossRef]
- Aboutalebi, F.H.; Banihashemi, A. Numerical estimation and practical validation of Hooputra’s ductile damage parameters. Int. J. Adv. Manuf. Technol. 2014, 75, 1701–1710. [Google Scholar] [CrossRef]
- Besson, J.; Steglich, D.; Brocks, W. Modeling of crack growth in round bars and plane strain specimens. Int. J. Solids Struct. 2001, 38, 8259–8284. [Google Scholar] [CrossRef]
- Peerlings, R.H.G.; Geers, M.G.D.; de Borst, R.; Brekelmans, W.A.M. A critical comparison of nonlocal and gradient-enhanced softening continua. Int. J. Solids Struct. 2001, 38, 7723–7746. [Google Scholar] [CrossRef]
- Zhang, C.; Leotoing, L.; Zhao, G.; Guines, D.; Ragneau, E. A comparative study of different necking criteria for numerical and experimental prediction of FLCs. J. Mater. Eng. Perform. 2011, 20, 1036–1042. [Google Scholar] [CrossRef]
- Kami, A.; Dariani, B.M.; Vanini, A.S.; Comsa, D.S.; Banabic, D. Numerical determination of the forming limit curves of anisotropic sheet metals using GTN damage model. J. Mater. Process. Technol. 2015, 216, 472–483. [Google Scholar] [CrossRef]
- Volk, W.; Hora, P. New algorithm for a robust user-independent evaluation of beginning instability for the experimental FLC determination. Int. J. Mater. Form. 2011, 4, 339–346. [Google Scholar] [CrossRef]
- Liewald, M.; Drotleff, K. Novel punch design for nonlinear strain path generation and evaluation methods. Key Eng. Mater. 2015, 639, 317–324. [Google Scholar] [CrossRef]
- Silva, M.B.; Martínez-Donaireb, A.J.; Centenob, G.; Morales-Palmab, D.; Vallellanob, C.; Martinsa, P.A.F. Recent approaches for the determination of forming limits by necking and fracture in sheet metal forming. Procedia Eng. 2015, 132, 342–349. [Google Scholar] [CrossRef]
- Soyarslan, C.; Richter, H.; Bargmann, S. Variants of Lemaitre’s damage model and their use in formability prediction of metallic materials. Mech. Mater. 2016, 92, 58–79. [Google Scholar] [CrossRef]
| Material | E (MPa) | ν | σ0 (MPa) | K (MPa) | n |
|---|---|---|---|---|---|
| Steel | 0.3 | 200 | 0.3–0.6–1.0 |
| Material | β | S (MPa) | s | Yei (MPa) |
|---|---|---|---|---|
| Steel | 1 | 0.5 | 1 | 0 |
| Material | E (MPa) | ν | σ0 (MPa) | K (MPa) | n |
|---|---|---|---|---|---|
| St14 | 0.3 | 130 | 585 | 0.44 |
| Material | β | S (MPa) | s | Yei (MPa) |
|---|---|---|---|---|
| Steel | 4.251 | 2.648 | 1.831 | 0.001 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chalal, H.; Abed-Meraim, F. Numerical Predictions of the Occurrence of Necking in Deep Drawing Processes. Metals 2017, 7, 455. https://doi.org/10.3390/met7110455
Chalal H, Abed-Meraim F. Numerical Predictions of the Occurrence of Necking in Deep Drawing Processes. Metals. 2017; 7(11):455. https://doi.org/10.3390/met7110455
Chicago/Turabian StyleChalal, Hocine, and Farid Abed-Meraim. 2017. "Numerical Predictions of the Occurrence of Necking in Deep Drawing Processes" Metals 7, no. 11: 455. https://doi.org/10.3390/met7110455





