A Numerical Study on the Excitation of Guided Waves in Rectangular Plates Using Multiple Point Sources
Abstract
:1. Introduction
2. Semi-Analytical Finite-Element Method
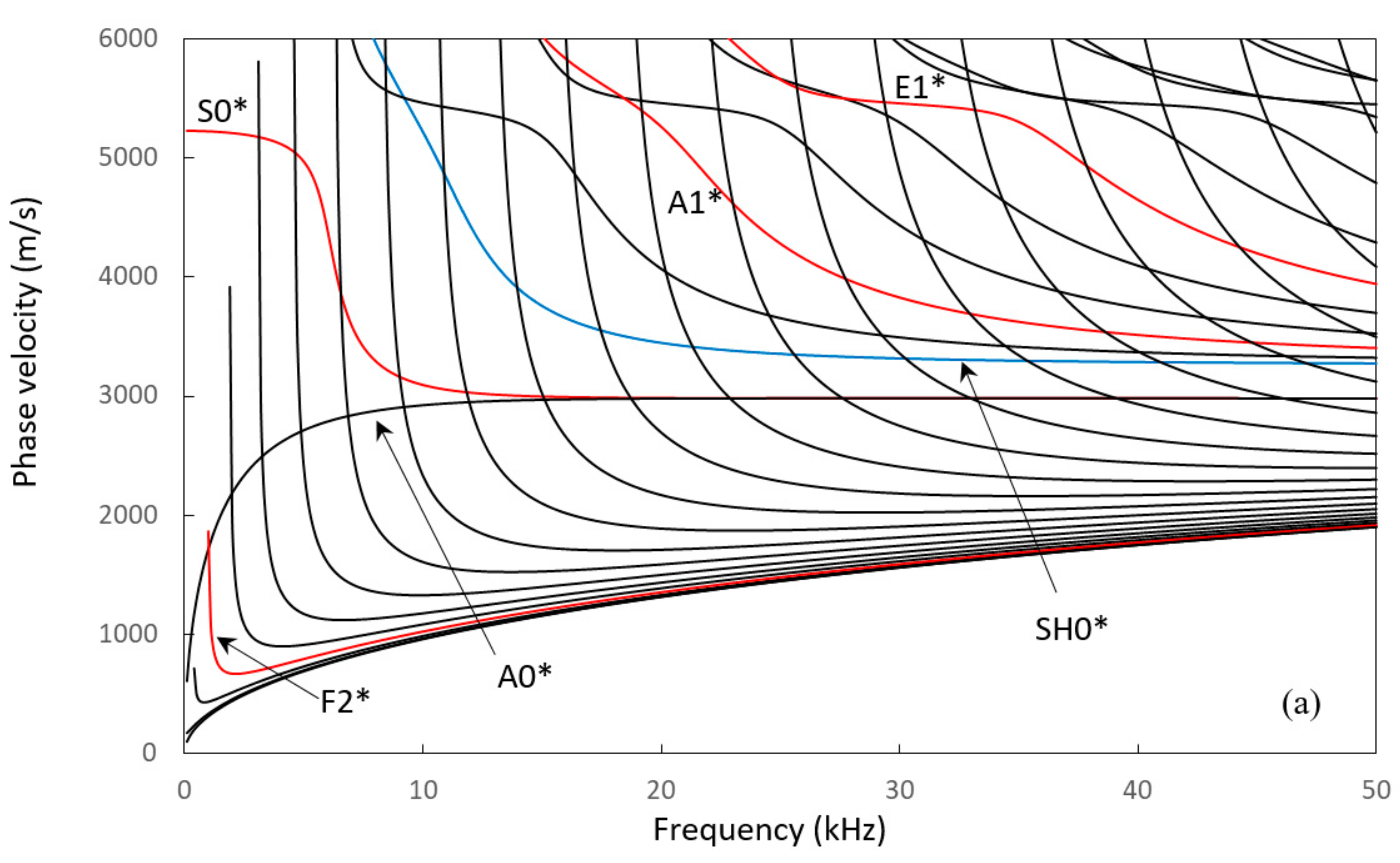
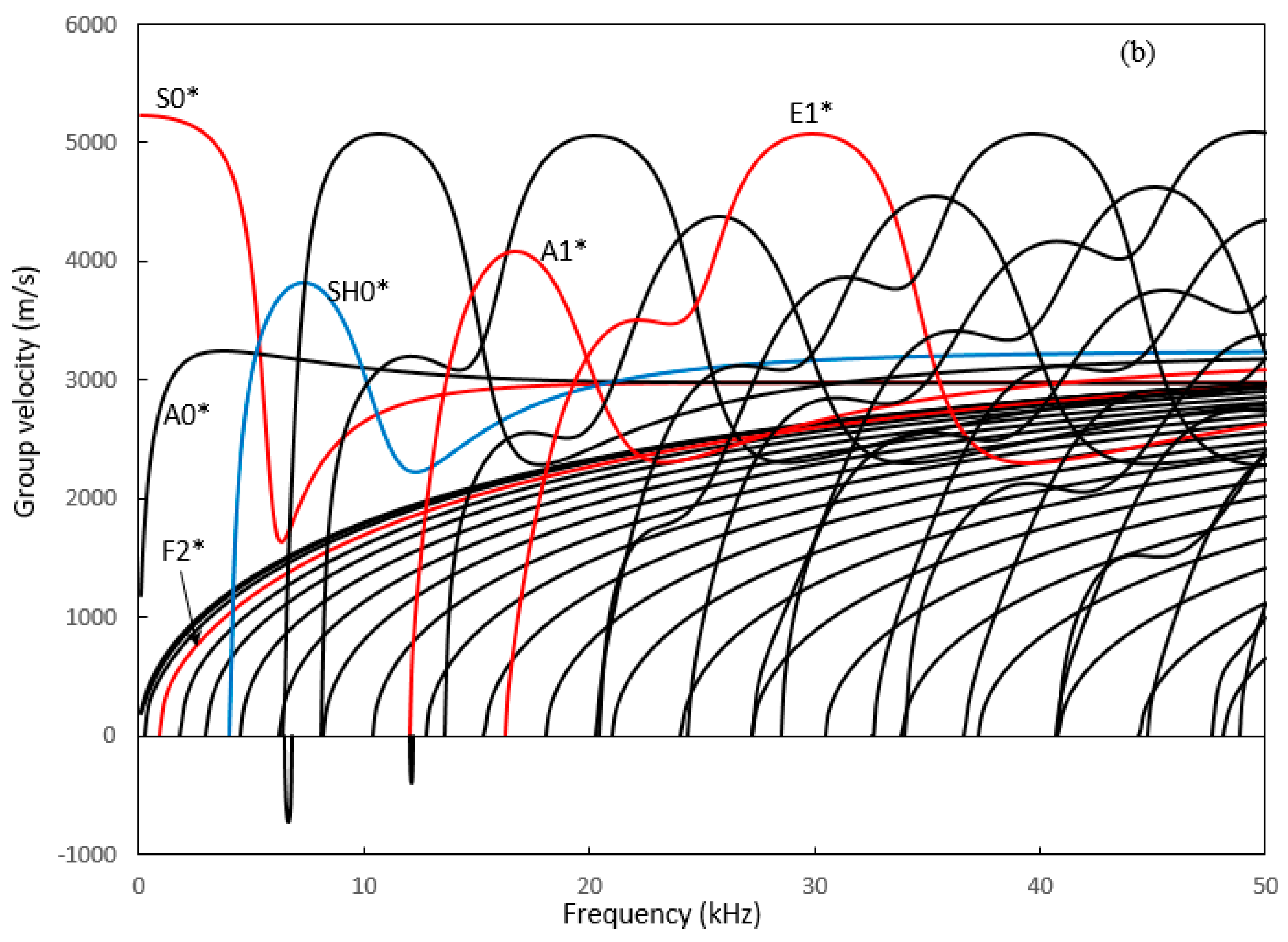
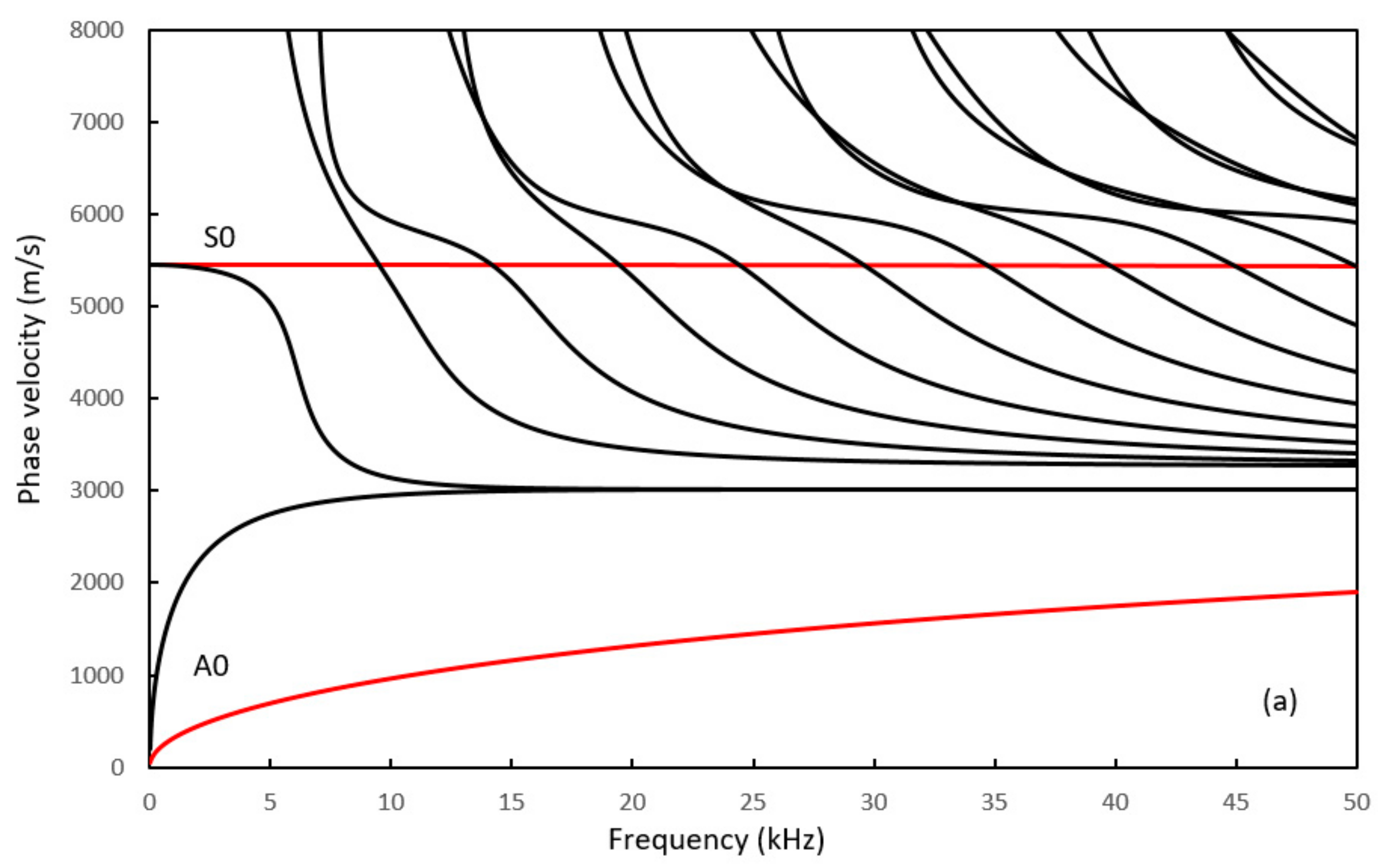
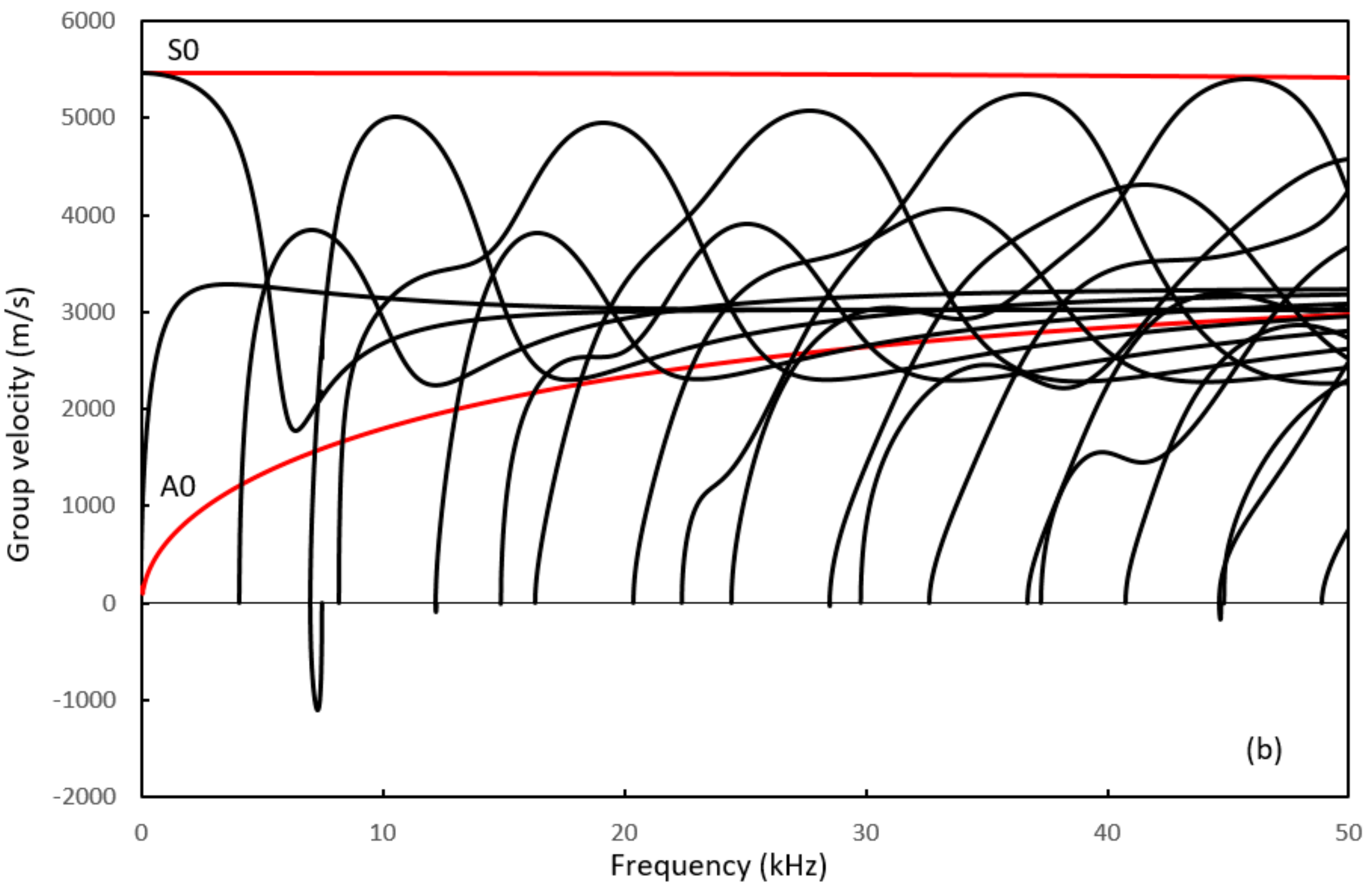
3. Dispersion Curves and Modal Analysis
4. Excitation of Guided Wave Modes
4.1. Excitation of Rayleigh Modes
4.2. Excitation of Shear Type Modes
4.3. Excitation of Extensional Type Modes
4.4. Excitation of Flexural Type Modes
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Lamb, H. On Waves in an Elastic Plate. Proc. R. Soc. Lond. Ser. A 1917, 93, 114–128. [Google Scholar] [CrossRef]
- Rayleigh, L. On the free vibrations of an infinite plate of homogeneous isotropic elastic matter. Proc. Lond. Math. Soc. 1889, 20, 225–234. [Google Scholar] [CrossRef]
- Meleshko, V.V.; Bondarenko, A.A.; Dovgiy, S.A.; Trofimchuk, A.N.; van Heijst, G.J.F. Elastic waveguides: History and the state of the art. I. J. Math. Sci. 2009, 162, 99–120. [Google Scholar] [CrossRef]
- Diligent, O. Interaction between Fundamental Lamb Modes and Defects in Plates. Ph.D. Thesis, Mechanical Engineering Department, Imperial College London, London, UK, 2003. [Google Scholar]
- Lee, B.C.; Staszewski, W.J. Lamb Wave Propagation modelling for damage detection: I. Two-dimensional analysis. Smart Mater. Struct. 2007, 16, 249–259. [Google Scholar] [CrossRef]
- Burrows, S.E.; Dutton, B.; Dixon, S. Laser generation of Lamb waves for defect detection: Experimental methods and finite element modelling. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 82–89. [Google Scholar] [CrossRef] [PubMed]
- Mindlin, R.D.; Fox, E.A. Vibrations and waves in elastic bars of rectangular cross section. Trans. ASME J. Appl. Mech. 1960, 27, 152–158. [Google Scholar] [CrossRef]
- Medick, M.A. Extensional waves in elastic bars of rectangular cross section. J. Acoust. Soc. Am. 1968, 43, 152–161. [Google Scholar] [CrossRef]
- Kastrzhitskaya, E.V.; Meleshko, V.V. Propagation of harmonic waves in an elastic rectangular waveguide. Sov. Appl. Mech. 1990, 26, 773–781. [Google Scholar] [CrossRef]
- Lowe, M.J.S. Matrix techniques for modelling ultrasonic waves in multi-layered media. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1995, 47, 525–542. [Google Scholar] [CrossRef]
- Krushynska, A.A.; Meleshko, V.V. Normal waves in elastic bars of rectangular cross section. J. Acoust. Soc. Am. 2011, 129, 1324–1335. [Google Scholar] [CrossRef] [PubMed]
- Kuo, C.W.; Suh, C.S. On the dispersion and attenuation of guided waves in tubular section with multi-layered viscoelastic coating—Part I: Axial wave propagation. Int. J. Appl. Mech. 2017, 9, 1750001. [Google Scholar] [CrossRef]
- Mukdadi, O.M.; Desai, Y.M.; Datta, S.K.; Shah, A.H.; Niklasson, A.J. Elastic guided waves in a layered plate with rectangular cross section. J. Acoust. Soc. Am. 2002, 112, 1766–1779. [Google Scholar] [CrossRef] [PubMed]
- Hayashi, T.; Song, W.J.; Rose, J.L. Guided wave dispersion curves for a bar with an arbitrary cross-section, a rod and rail example. Ultrasonics 2003, 41, 175–183. [Google Scholar] [CrossRef]
- Bartoli, I.; Marzani, A.; Lanza di Scalea, F.; Viola, E. Modeling wave propagation in damped waveguides of arbitrary cross-section. J. Sound Vib. 2006, 295, 685–707. [Google Scholar] [CrossRef]
- Mu, J.; Rose, J.L. Guided wave propagation and mode differentiation in hollow cylinders with viscoelastic coatings. J. Acoust. Soc. Am. 2008, 124, 866–874. [Google Scholar] [CrossRef] [PubMed]
- Treyssède, F. Elastic waves in helical waveguides. Wave Motion 2008, 45, 457–470. [Google Scholar] [CrossRef]
- Treyssède, F.; Laguerre, L. Investigation of elastic modes propagating in multi-wire helical waveguides. J. Sound Vib. 2010, 329, 1702–1716. [Google Scholar] [CrossRef]
- Mazzotti, M.; Marzani, A.; Bartoli, I.; Viola, E. Guided waves dispersion analysis for prestressed viscoelastic waveguides by means of the SAFE method. Int. J. Solids Struct. 2012, 49, 2359–2372. [Google Scholar] [CrossRef]
- Treyssède, F. Dispersion curve veering of longitudinal guided waves propagating inside prestressed seven-wire strands. J. Sound Vib. 2016, 367, 56–68. [Google Scholar] [CrossRef]
- Nguyen, K.L.; Treyssède, F.; Hazard, C. Numerical modeling of three-dimensional open elastic waveguides combining semi-analytical finite element and perfectly matched layer methods. J. Sound Vib. 2015, 344, 158–178. [Google Scholar] [CrossRef]
- Duan, W.; Kirby, R.; Mudge, P.; Gan, T.-H. A one dimensional numerical approach for computing the eigenmodes of elastic waves in buried pipelines. J. Sound Vib. 2016, 384, 177–193. [Google Scholar] [CrossRef]
- Zuo, P.; Fan, Z. SAFE-PML approach for modal study of waveguides with arbitrary cross sections immersed in inviscid fluid. J. Sound Vib. 2017, 406, 181–196. [Google Scholar] [CrossRef]
- Mazzotti, M.; Bartoli, I.; Marzani, A.; Viola, E. A coupled SAFE-2.5D BEM approach for the dispersion analysis of damped leaky guided waves in embedded waveguides of arbitrary cross-section. Ultrasonics 2013, 53, 1227–1241. [Google Scholar] [CrossRef] [PubMed]
- Hua, J.; Mu, J.; Rose, J.L. Guided wave propagation in single and double layer hollow cylinders embedded in infinite media. J. Acoust. Soc. Am. 2011, 129, 691–700. [Google Scholar]
- Castaings, M.; Lowe, M. Finite element model for waves guided along solid systems of arbitrary section coupled to infinite solid media. J. Acoust. Soc. Am. 2008, 123, 696–708. [Google Scholar] [CrossRef] [PubMed]
- Gunawan, A.; Hirose, S. Boundary element analysis of guided waves in a bar with an arbitrary cross-section. Eng. Anal. Bound. Elem. 2005, 29, 913–924. [Google Scholar] [CrossRef]
- Mazzotti, M.; Bartoli, I.; Marzani, A.; Viola, E. A 2.5D boundary element formulation for modeling damped waves in arbitrary cross-section waveguides and cavities. J. Comput. Phys. 2013, 248, 363–382. [Google Scholar] [CrossRef]
- Mace, B.R.; Duhamel, D.; Brennan, M.J.; Hinke, L. Finite element prediction of wave motion in structural waveguides. J. Acoust. Soc. Am. 2005, 117, 2835–2843. [Google Scholar] [CrossRef] [PubMed]
- Mace, B.R.; Manconi, E. Modelling Wave Propagation in Two-Dimensional Structures Using Finite Element Analysis. J. Sound Vib. 2008, 318, 884–902. [Google Scholar] [CrossRef]
- Maki, Y.; Mace, B.R.; Brennan, M.J. Numerical issues concerning the wave and finite element method for free and forced vibrations of waveguides. J. Sound Vib. 2009, 327, 92–108. [Google Scholar]
- Søe-Knudesn, A.; Sorokin, S. On accuracy of the wave finite element predictions of wavenumbers and power flow: A benchmark problem. J. Sound Vib. 2011, 330, 2694–2700. [Google Scholar] [CrossRef]
- Song, C. The scaled boundary finite element method in structural dynamics. Int. J. Numer. Methods Eng. 2009, 77, 1139–1171. [Google Scholar] [CrossRef]
- Gravenkamp, H.; Man, H.; Song, C.; Prager, J. The computation of dispersion relations for three-dimensional elastic waveguides using the Scaled Boundary Finite Element Method. J. Sound Vib. 2013, 332, 3756–3771. [Google Scholar] [CrossRef]
- Gravenkamp, H.; Birk, C.; Song, C. Computation of dispersion curves for embedded waveguides using dashpot boundary condition. J. Acoust. Soc. Am. 2014, 135, 1127–1138. [Google Scholar] [CrossRef] [PubMed]
- Gravenkamp, H.; Birk, C.; Van, J. Modeling ultrasonic waves in elastic waveguides of arbitrary cross-section embedded in infinite solid medium. Comput. Struct. 2015, 149, 61–71. [Google Scholar] [CrossRef]
- Moser, F.; Jacobs, L.; Qu, J. Modelling elastic wave propagation in waveguides with finite element method. NDT E Int. 1999, 32, 225–234. [Google Scholar] [CrossRef]
- Benmeddour, F.; Treyssède, F.; Laguerre, L. Numerical modeling of guided wave interaction with non-axisymmetric cracks in elastic cylinders. Int. J. Solids Struct. 2011, 48, 764–774. [Google Scholar] [CrossRef]
- Duan, W.; Kirby, R. A numerical model for the scattering of elastic waves from a non-axisymmetric defect in a pipe. Finite Elem. Anal. Des. 2015, 100, 28–40. [Google Scholar] [CrossRef]
- Duan, W.; Kirby, R.; Mudge, P. On the scattering of elastic waves from a non-axisymmetric defect in a coated pipe. Ultrasonics 2016, 65, 228–241. [Google Scholar] [CrossRef] [PubMed]
- Duan, W.; Kirby, R.; Mudge, P. On the scattering of torsional waves from axisymmetric defects in buried pipelines. J. Acoust. Soc. Am. 2017, 141, 3250–3261. [Google Scholar] [CrossRef] [PubMed]
- Gravenkamp, H.; Birk, C.; Song, C.M. Simulation of elastic guided waves interacting with defects in arbitrarily long structures using the scaled boundary finite element method. J. Comput. Phys. 2015, 295, 438–455. [Google Scholar] [CrossRef]
- Morse, R.W. Dispersion of compressional waves in isotropic rods of rectangular cross section. J. Acoust. Soc. Am. 1948, 20, 833–838. [Google Scholar] [CrossRef]
- Cegla, F.B. Energy concentration at the center of large aspect ratio rectangular waveguides at high frequencies. J. Acoust. Soc. Am. 2008, 123, 4218–4226. [Google Scholar] [CrossRef] [PubMed]
- Cui, H.; Lin, W.; Zhang, H.; Wang, X.; Trevelyan, J. Characteristics of group velocities of backward waves in a hollow cylinder. J. Acoust. Soc. Am. 2014, 135, 3398–3408. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bjurstrom, H.; Ryden, N. Detecting the thickness mode frequency in a concrete plate using backward wave propagation. J. Acoust. Soc. Am. 2016, 139, 649–657. [Google Scholar] [CrossRef] [PubMed]
- Palacios, J.; Smith, E.; Rose, J.; Royer, R. Instantaneous de-icing of freezer ice via ultrasonic actuation. AIAA J. 2011, 49, 1158–1167. [Google Scholar] [CrossRef]
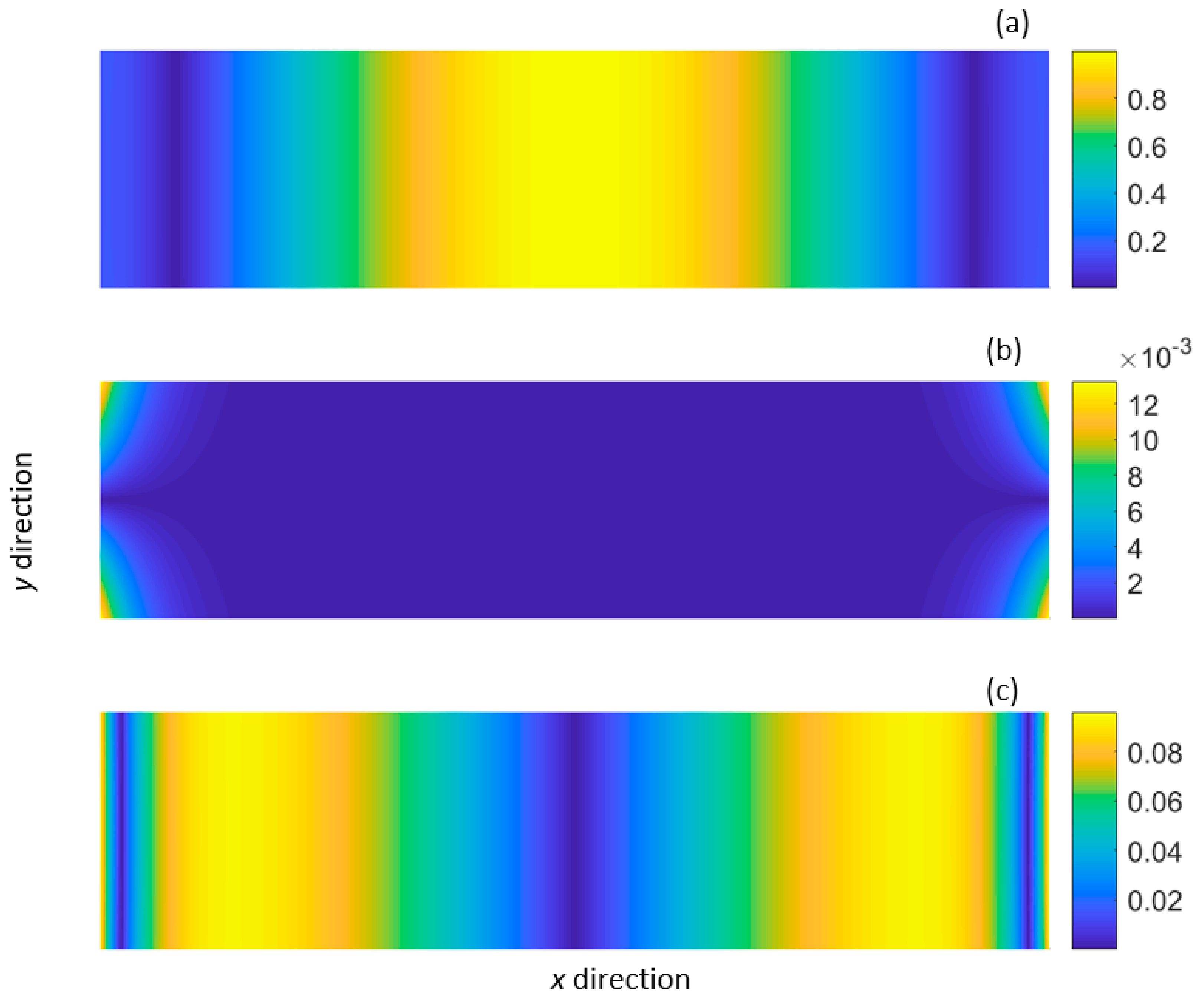
 , Current semi-analytical finite-element (SAFE) solutions;
, Current semi-analytical finite-element (SAFE) solutions;  , numerical solutions given by Mukdadi et al. [13].
, numerical solutions given by Mukdadi et al. [13].
 , Current semi-analytical finite-element (SAFE) solutions;
, Current semi-analytical finite-element (SAFE) solutions;  , numerical solutions given by Mukdadi et al. [13].
, numerical solutions given by Mukdadi et al. [13].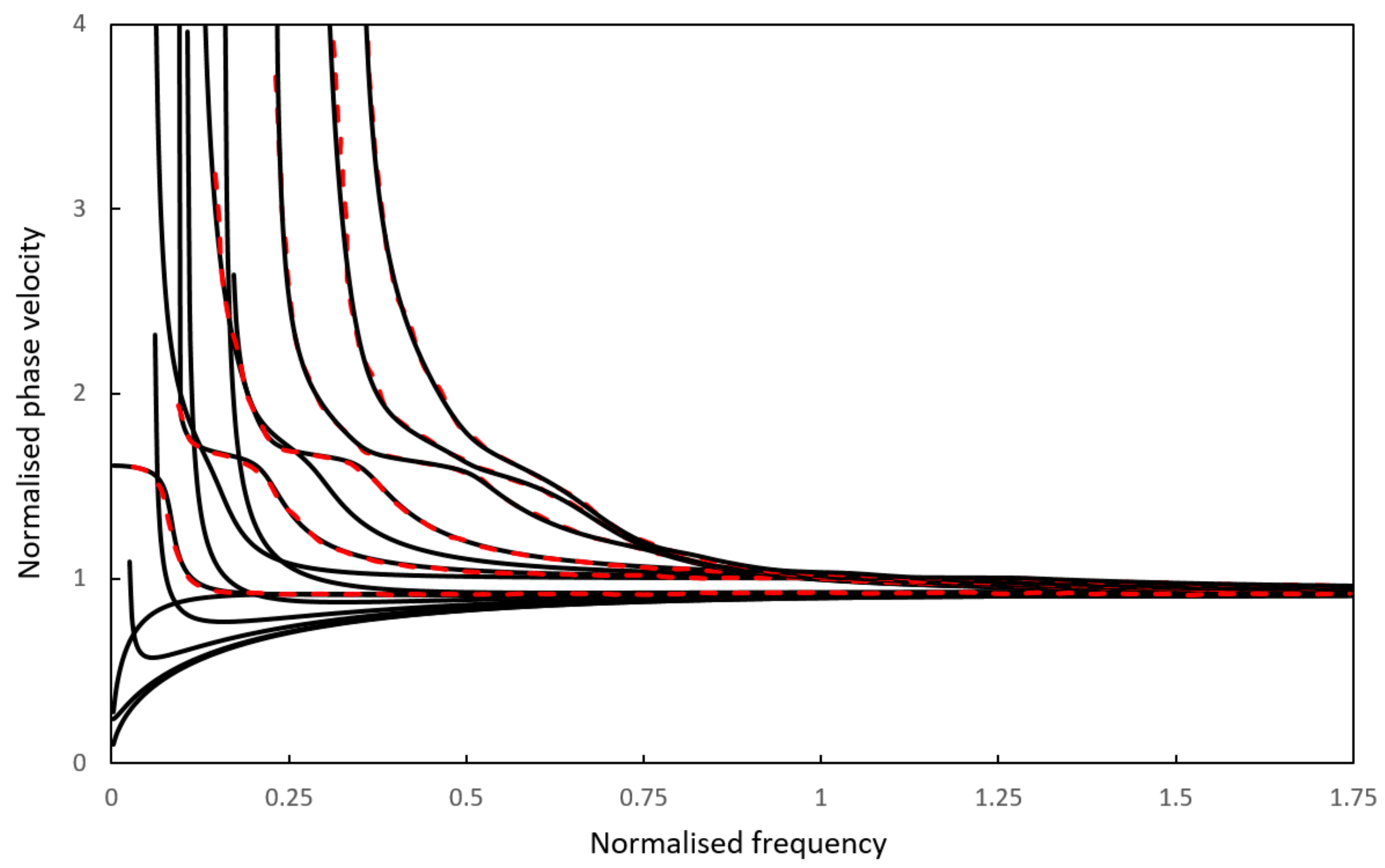
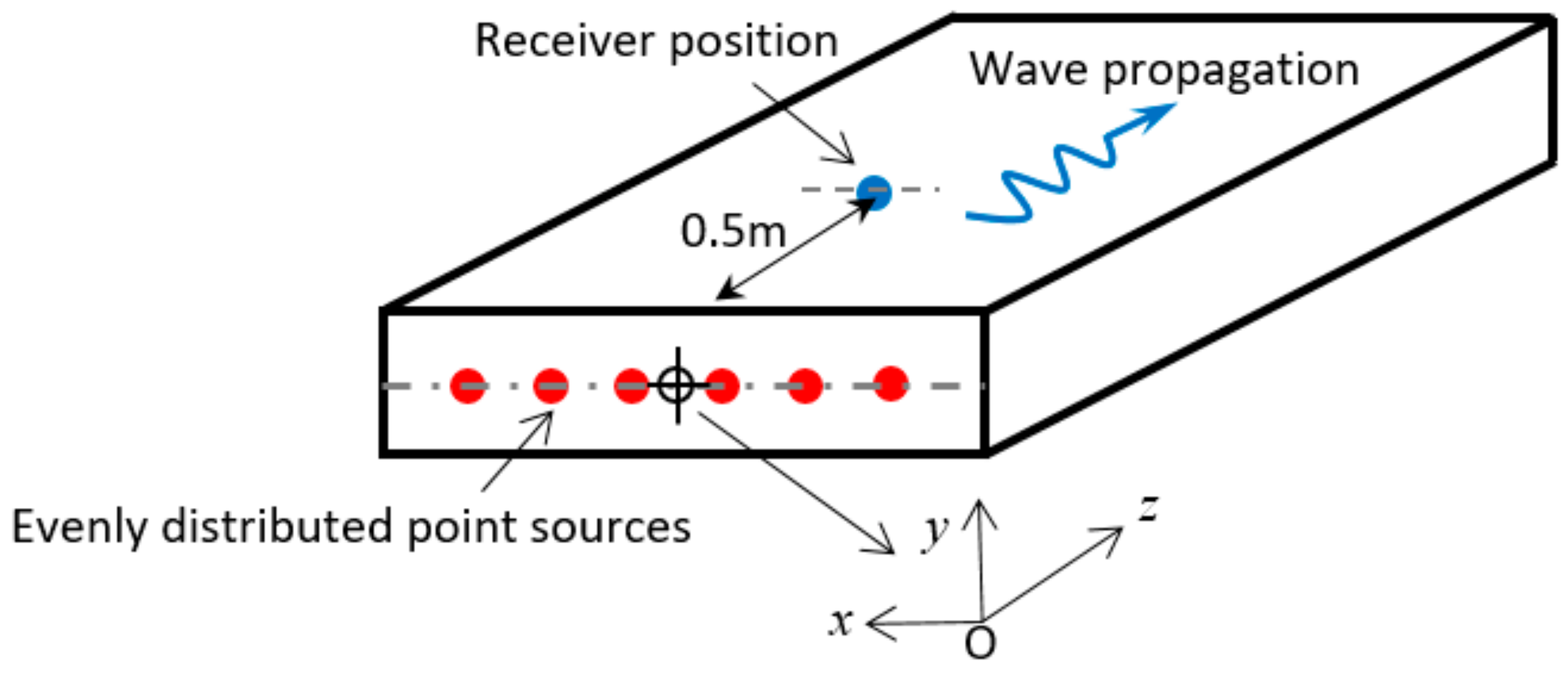
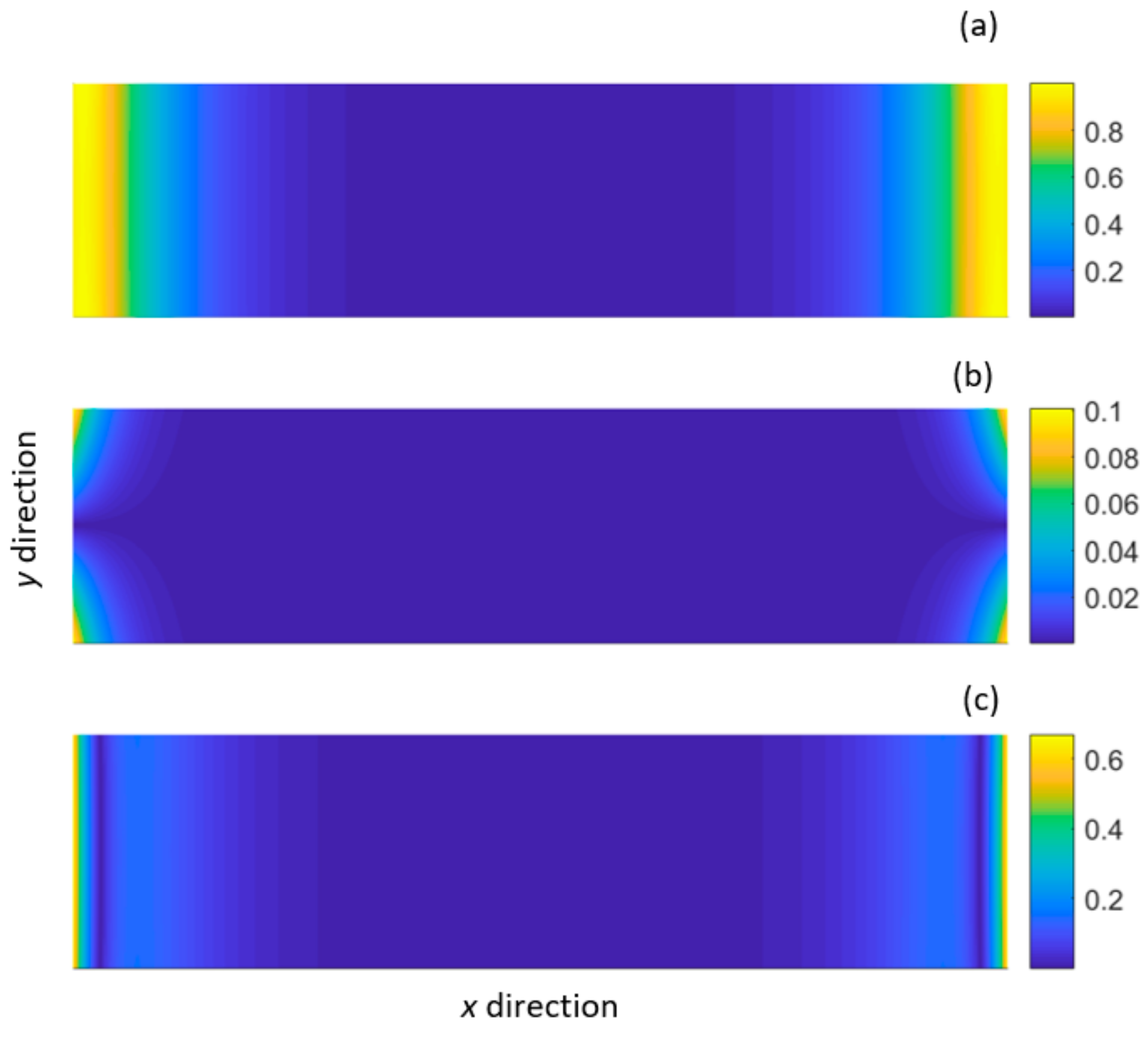
 , 79 point sources;
, 79 point sources;  , 39 point sources;
, 39 point sources;  , 19 point sources;
, 19 point sources;  , 15 point sources.
, 15 point sources.
 , 79 point sources;
, 79 point sources;  , 39 point sources;
, 39 point sources;  , 19 point sources;
, 19 point sources;  , 15 point sources.
, 15 point sources.
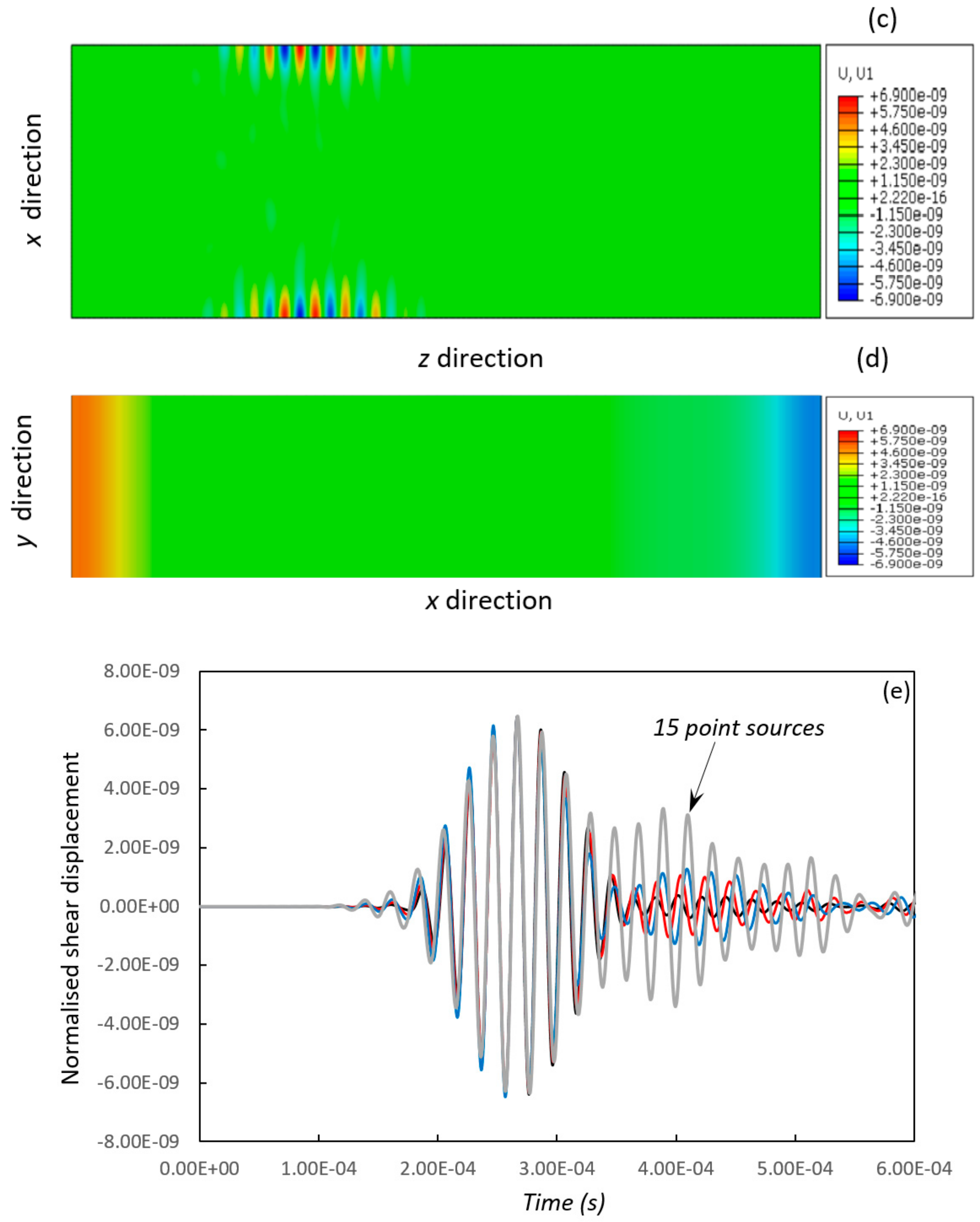
 , 19 point sources;
, 19 point sources;  , 15 point sources;
, 15 point sources;  , 9 point sources;
, 9 point sources;  , 7 point sources.
, 7 point sources.
 , 19 point sources;
, 19 point sources;  , 15 point sources;
, 15 point sources;  , 9 point sources;
, 9 point sources;  , 7 point sources.
, 7 point sources.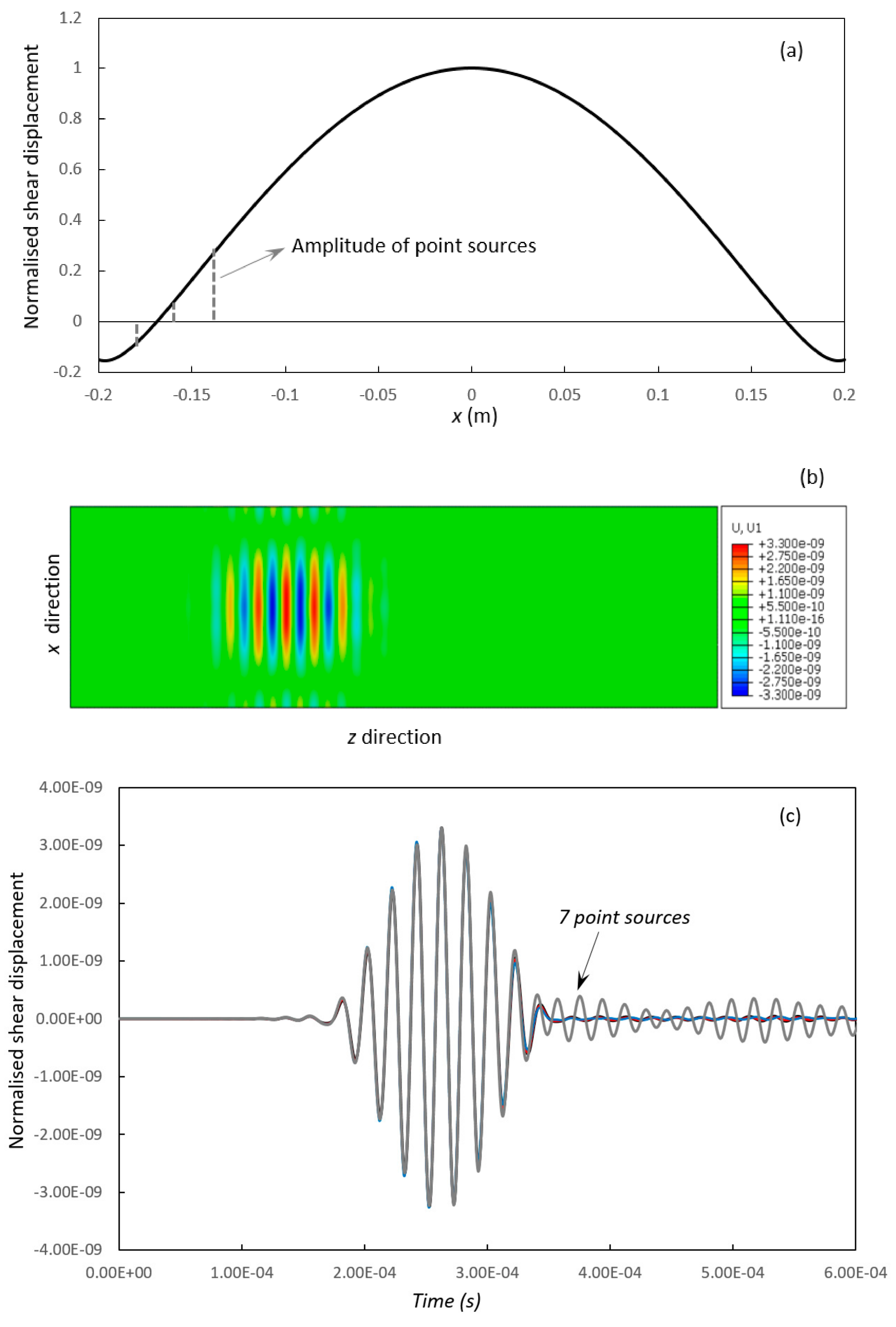
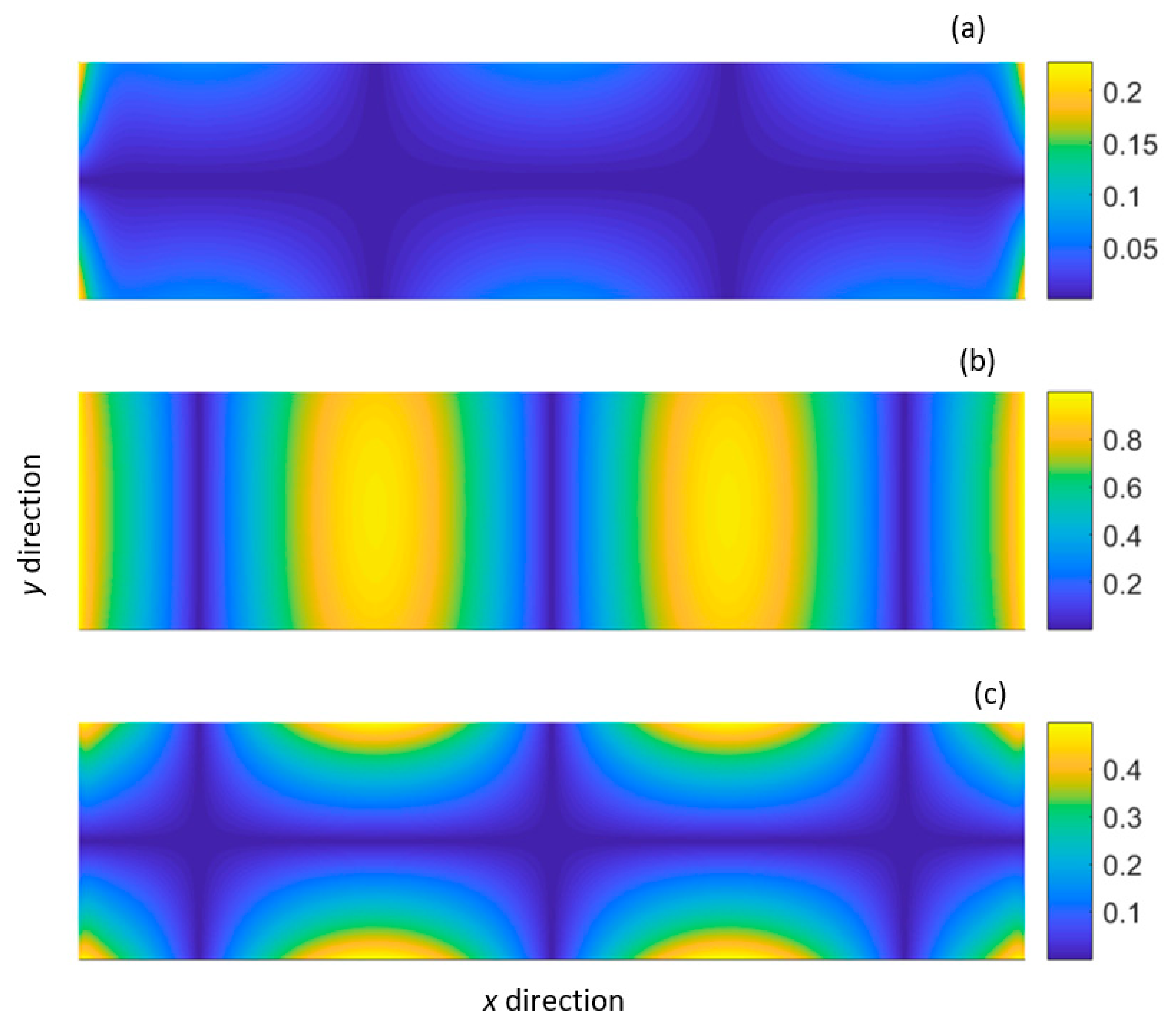
 , 19 point sources;
, 19 point sources;  , 15 point sources;
, 15 point sources;  , 9 point sources;
, 9 point sources;  , 7 point sources.
, 7 point sources.
 , 19 point sources;
, 19 point sources;  , 15 point sources;
, 15 point sources;  , 9 point sources;
, 9 point sources;  , 7 point sources.
, 7 point sources.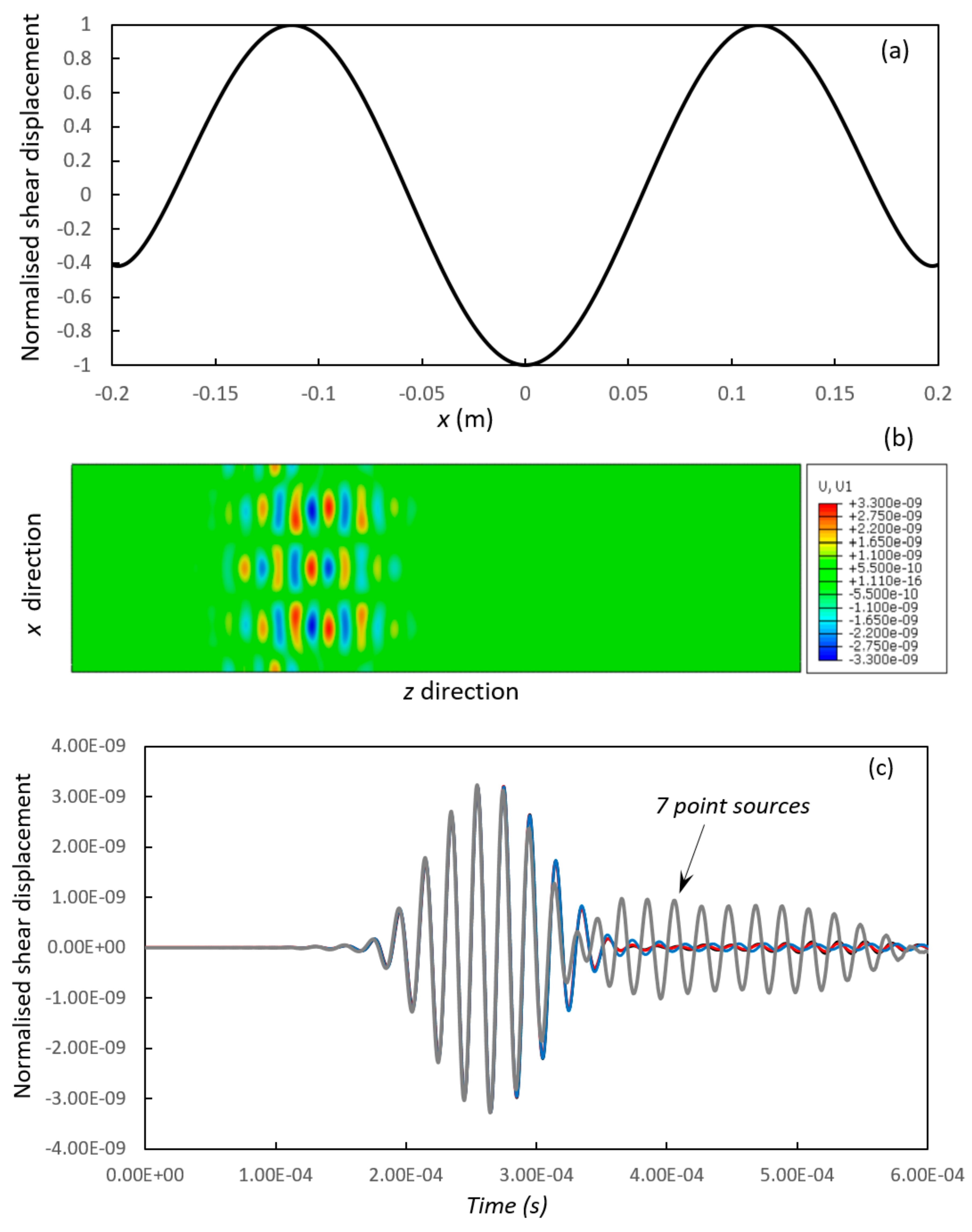

 , 19 point sources;
, 19 point sources;  , 15 point sources;
, 15 point sources;  , 7 point sources;
, 7 point sources;  , 3 point sources.
, 3 point sources.
 , 19 point sources;
, 19 point sources;  , 15 point sources;
, 15 point sources;  , 7 point sources;
, 7 point sources;  , 3 point sources.
, 3 point sources.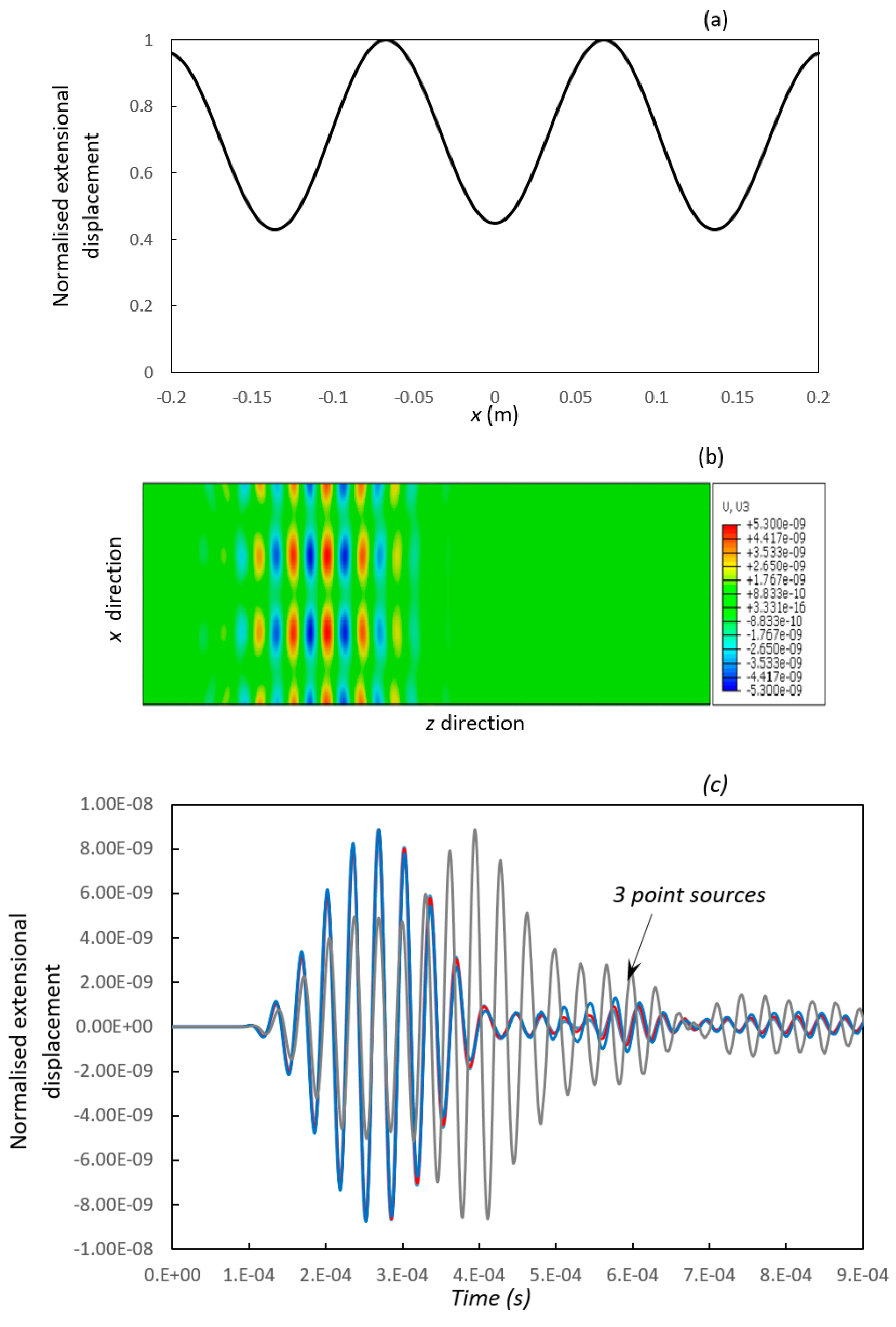
 , 39 point sources;
, 39 point sources;  , 19 point sources;
, 19 point sources;  , 15 point sources;
, 15 point sources;  , 9 point sources.
, 9 point sources.
 , 39 point sources;
, 39 point sources;  , 19 point sources;
, 19 point sources;  , 15 point sources;
, 15 point sources;  , 9 point sources.
, 9 point sources.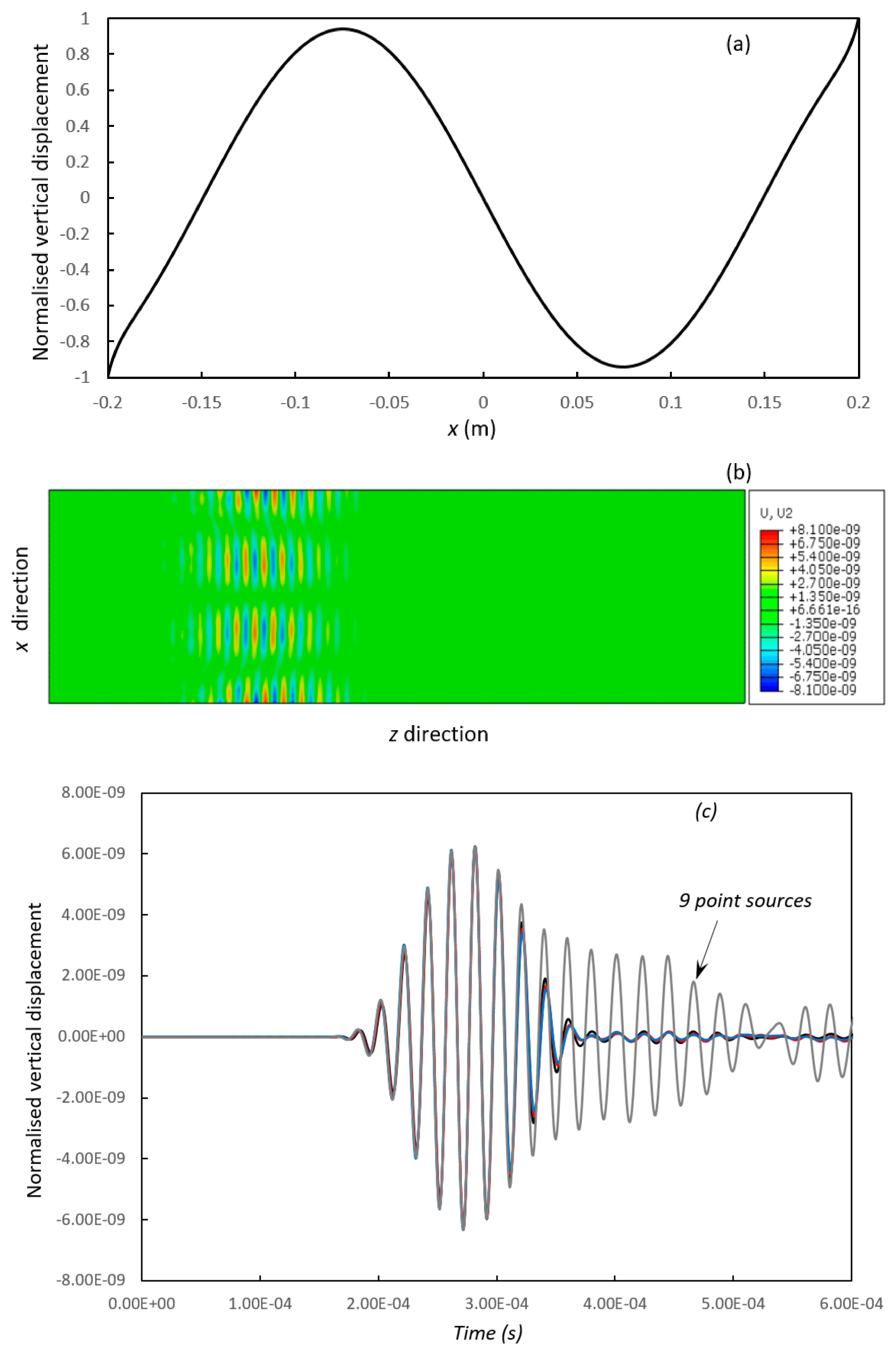
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, W.; Niu, X.; Gan, T.-H.; Kanfoud, J.; Chen, H.-P. A Numerical Study on the Excitation of Guided Waves in Rectangular Plates Using Multiple Point Sources. Metals 2017, 7, 552. https://doi.org/10.3390/met7120552
Duan W, Niu X, Gan T-H, Kanfoud J, Chen H-P. A Numerical Study on the Excitation of Guided Waves in Rectangular Plates Using Multiple Point Sources. Metals. 2017; 7(12):552. https://doi.org/10.3390/met7120552
Chicago/Turabian StyleDuan, Wenbo, Xudong Niu, Tat-Hean Gan, Jamil Kanfoud, and Hua-Peng Chen. 2017. "A Numerical Study on the Excitation of Guided Waves in Rectangular Plates Using Multiple Point Sources" Metals 7, no. 12: 552. https://doi.org/10.3390/met7120552




