Estimation of Fracture Loads in AL7075-T651 Notched Specimens Using the Equivalent Material Concept Combined with the Strain Energy Density Criterion and with the Theory of Critical Distances
Abstract
:1. Introduction
2. Theoretical Background
2.1. Theory of Critical Distances
2.2. Strain Energy Density Criteron
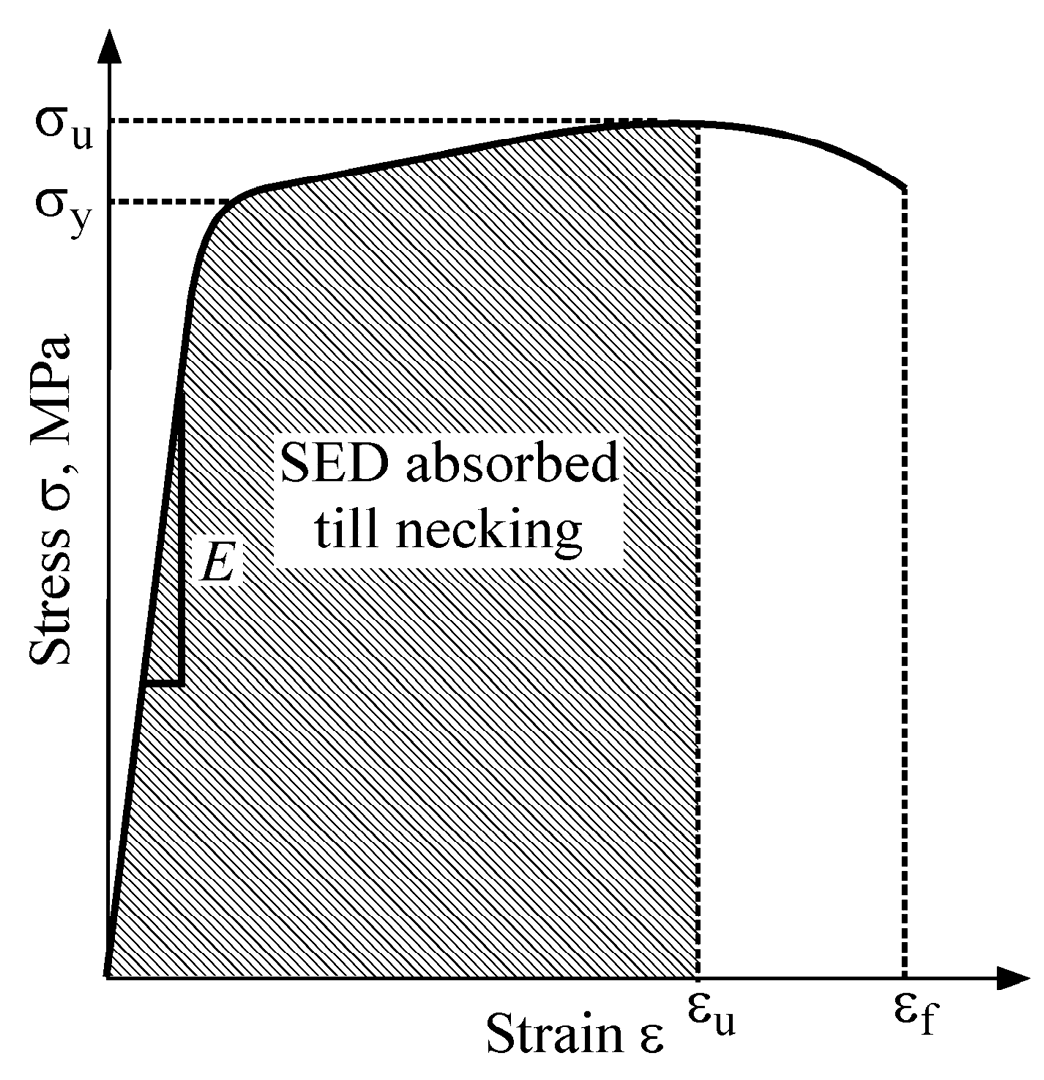
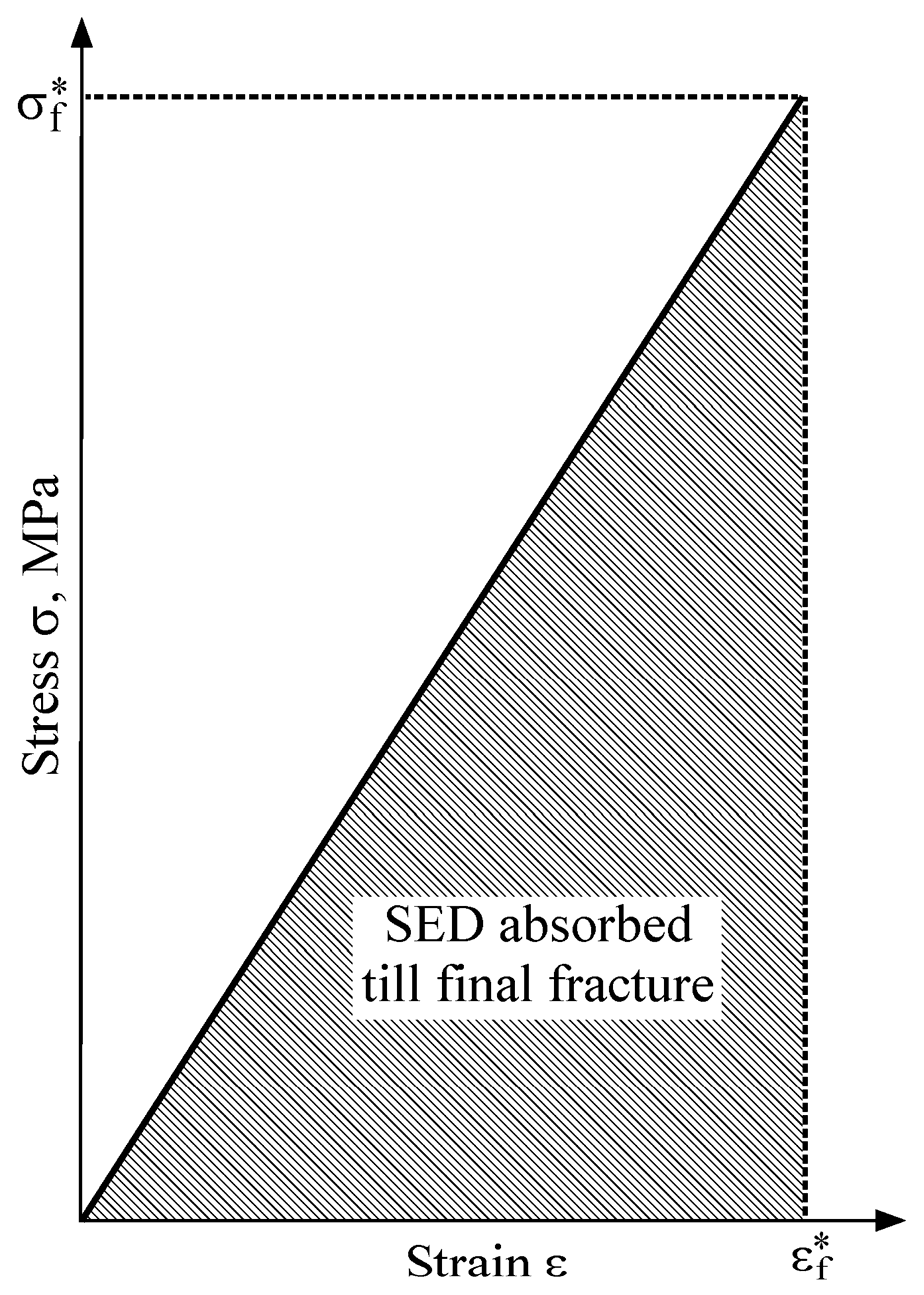
2.3. Equivalent Material Concept
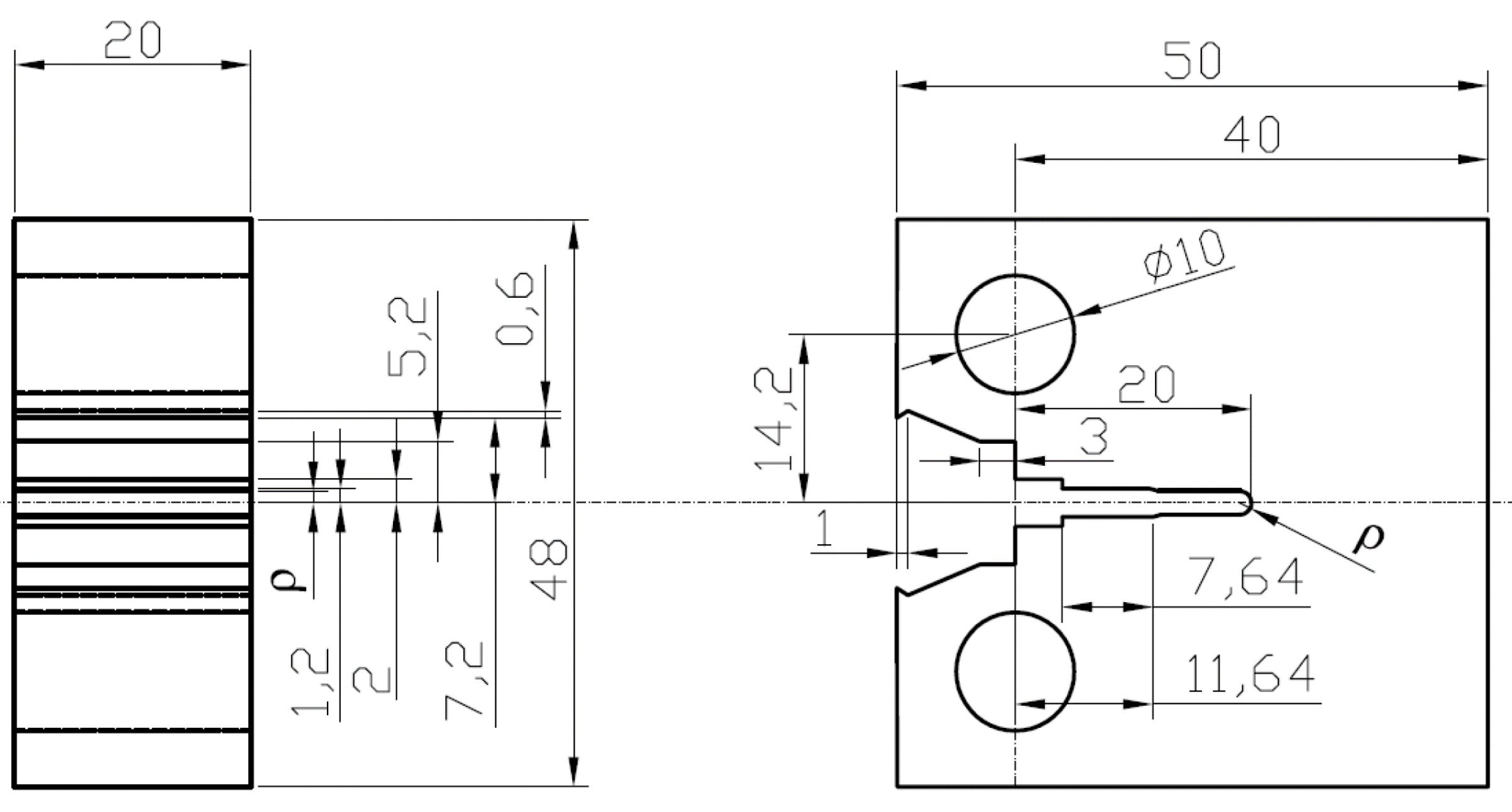
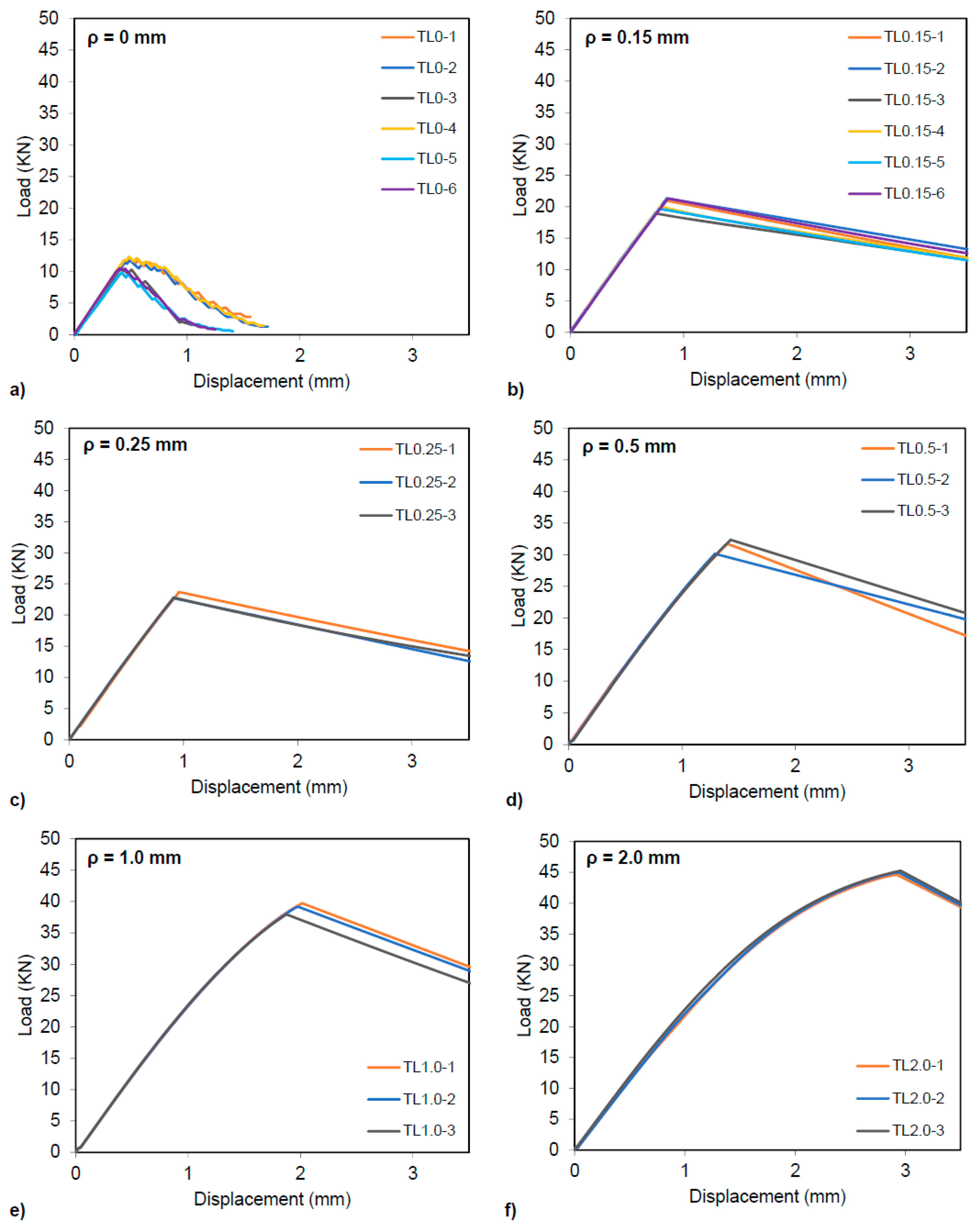
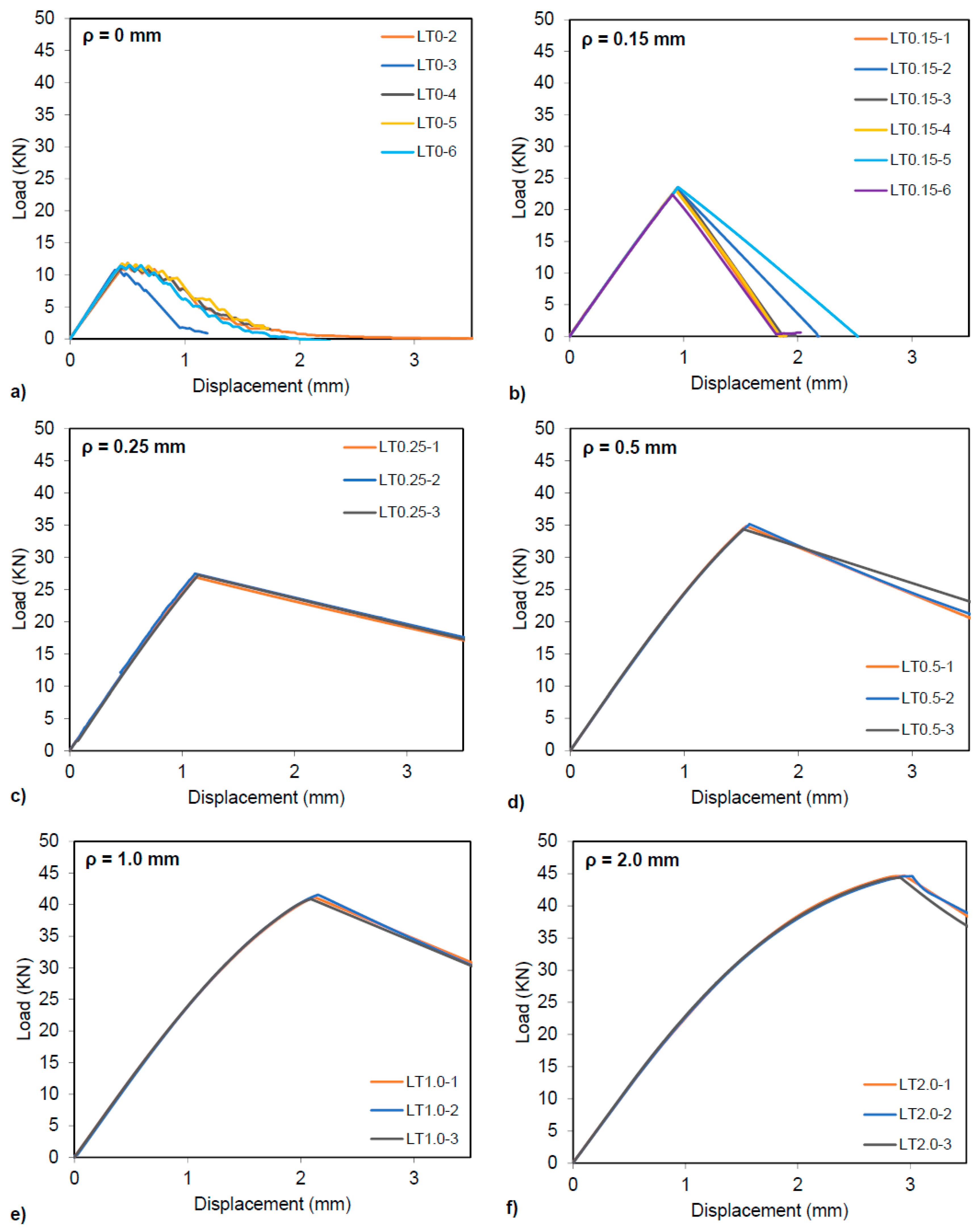
3. Materials and Methods
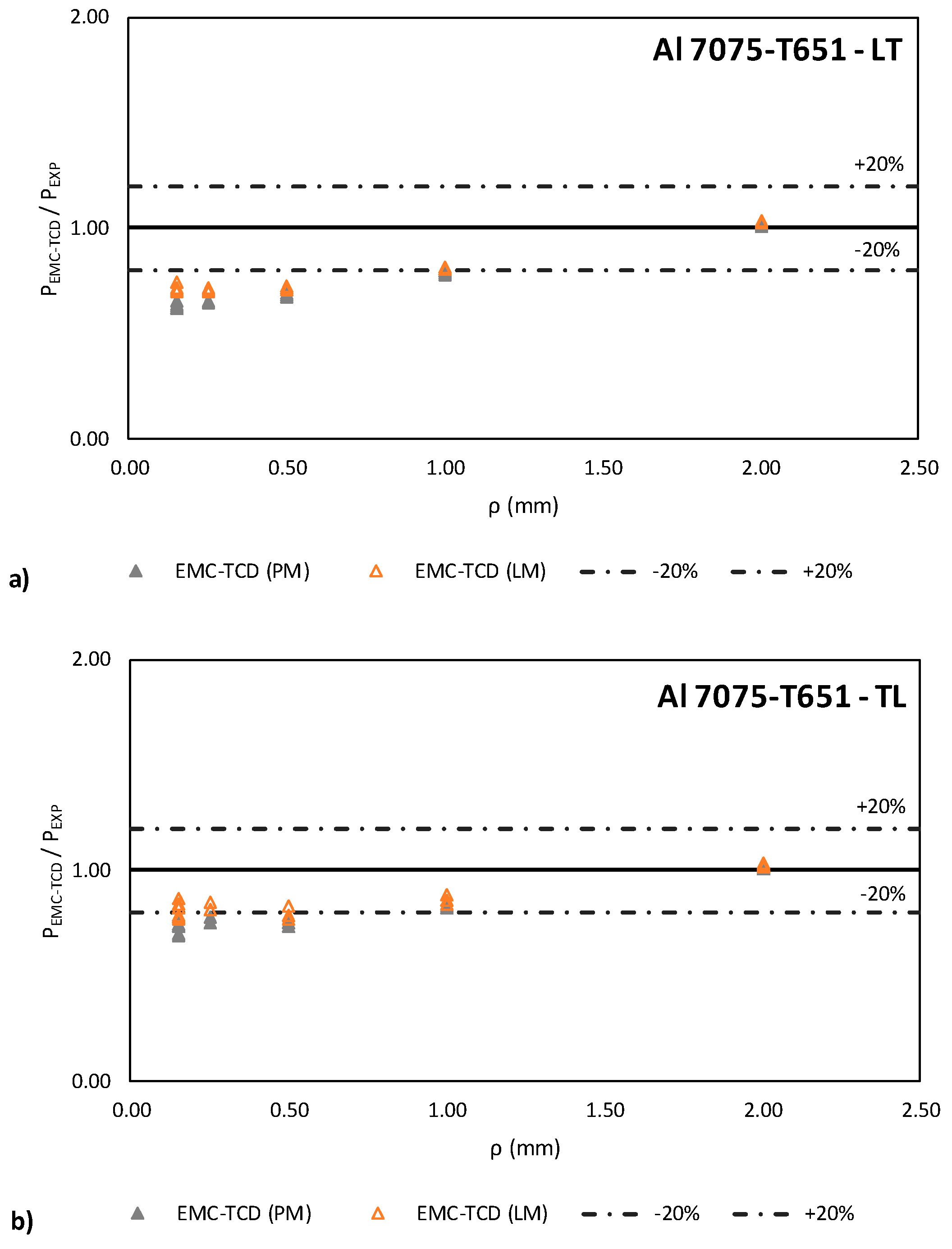
4. Results and Discussion
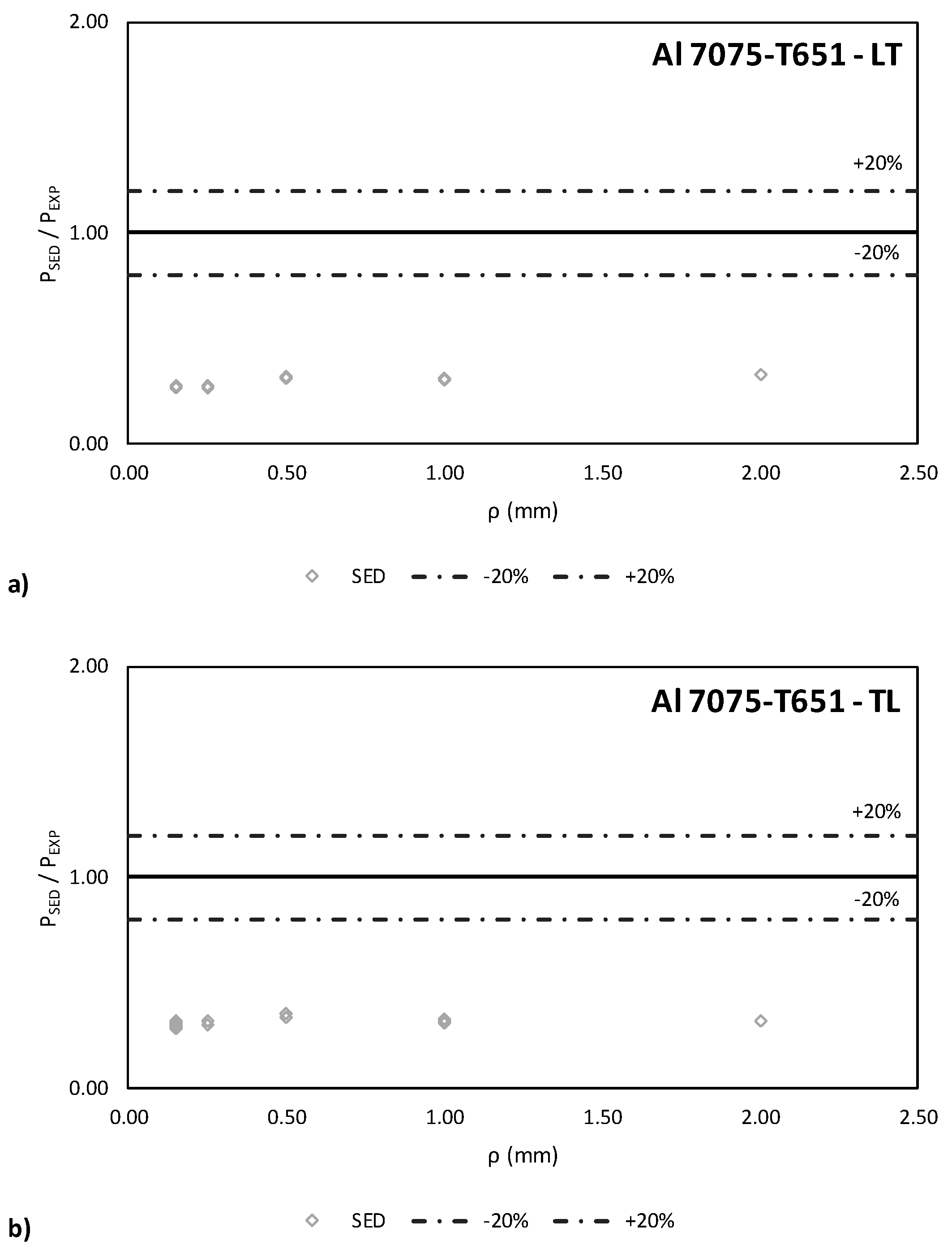
4.1. SED Fracture Load Predictions
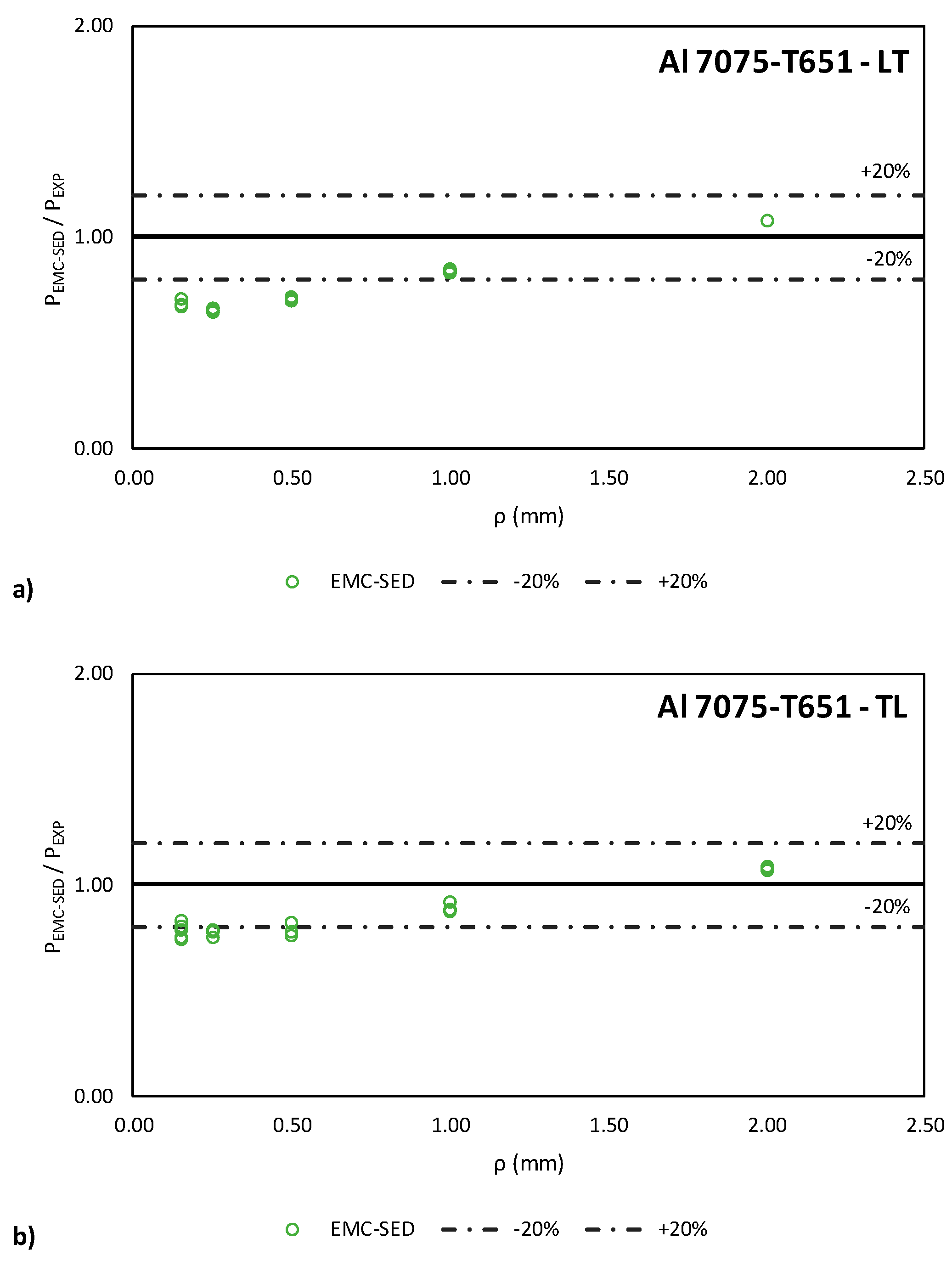
4.2. Equivalent Material Concept-Strain Energy Density (EMC-SED) Fracture Load Predictions
4.3. Theory of Critical Distances-Strain Energy Density (TCD-SED) Fracture Load Predictions
5. Conclusions
- The strict formulation of the Strain Energy Density criterion can only be employed to analyze brittle materials that have linear elastic behavior. Its application on materials that exhibit non-linear elastic behavior results in poor predictions, since a significant part of the stress-strain curve has not been taken into account.
- The combination of the Strain Energy Density criterion with the Equivalent Material Concept provides accurate results for large notch radii while for small notch radii the degree of approximation of the model is noticeably conservative.
- When the Theory of Critical Distances is combined with the Equivalent Material Concept to predict fracture loads, good agreement has been found between the predicted values and the experimental fracture loads for large notch radii whereas for small notch radii the fracture loads are, again, conservative.
- The use of the EMC combined with either of SED or TCD, allows accurate predictions of the fracture loads to be obtained without any previous calibration of the model. Only the material stress-strain curve, which can be easily obtained, is required for the application of these methods.
- The applicability of the combination of EMC-SED and EMC-TCD in real engineering applications is recommendable since it does not require time-consuming elastoplastic analysis.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cicero, S.; Madrazo, V.; Carrascal, I.A. Analysis of notch effect in PMMA using the Theory of Critical Distances. Eng. Fract. Mech. 2012, 86, 56–72. [Google Scholar] [CrossRef]
- Cicero, S.; García, T.; Madrazo, V. On the Line Method apparent fracture toughness evaluations: Experimental overview, validation and some consequences on fracture assessments. Theor. Appl. Fract. Mech. 2015, 78, 15–19. [Google Scholar] [CrossRef]
- Madrazo, V.; Cicero, S.; Carrascal, I.A. On the Point Method and the Line Method notch effect predictions in Al7075-T651. Eng. Fract. Mech. 2012, 79, 363–379. [Google Scholar] [CrossRef]
- Cicero, S.; Madrazo, V.; Carrascal, I.A. On the Point Method load-bearing capacity predictions in Al7075-T651 structural components containing stress risers. Eng. Fail. Anal. 2012, 26, 129–138. [Google Scholar] [CrossRef]
- Ibáñez-Gutiérrez, F.T.; Cicero, S.; Carrascal, I.A.; Procopio, I. Effect of fibre content and notch radius in the fracture behaviour of short glass fibre reinforced polyamide 6: An approach from the Theory of Critical Distances. Compos. Part B Eng. 2016, 94, 299–311. [Google Scholar] [CrossRef]
- Cicero, S.; García, T.; Castro, J.; Madrazo, V.; Andrés, D. Analysis of notch effect on the fracture behaviour of granite and limestone; an approach from the Theory of Critical Distances. Eng. Geol. 2014, 177, 1–9. [Google Scholar] [CrossRef]
- Cicero, S.; Madrazo, V.; Carrascal, I.A.; Cicero, R. Assessment of notched structural components using Failure Assessment Diagrams and the Theory of Critical Distances. Eng. Fract. Mech. 2011, 78, 2809–2825. [Google Scholar] [CrossRef]
- Taylor, D. The Theory of Critical Distances: A New Perspective in Fracture Mechanics; Elseiver: Oxford, UK, 2007. [Google Scholar]
- Sih, G.C. Strain-energy-density factor applied to mixed mode crack problems. Int. J. Fract. 1974, 10, 305–321. [Google Scholar] [CrossRef]
- Kipp, M.E.; Sih, G.C. The strain energy density failure criterion applied to notched elastic solids. Int. J. Solids Struct. 1975, 11, 153–173. [Google Scholar] [CrossRef]
- Gillemot, L.F. Criterion of crack initiation and spreading. Eng. Fract. Mech. 1975, 8, 239–253. [Google Scholar] [CrossRef]
- Molski, K.; Glinka, G. A method of elastic-plastic stress and strain calculation at a notch root. Mater. Sci. Eng. 1981, 50, 93–100. [Google Scholar] [CrossRef]
- Lazzarin, P.; Campagnolo, A.; Berto, F. A comparison among some recent energy-and stress-based criteria for the fracture assessment of sharp V-notched components under Mode I loading. Theor. Appl. Fract. Mech. 2014, 71, 21–30. [Google Scholar] [CrossRef]
- Campagnolo, A.; Berto, F.; Leguillon, D. Fracture assessment of sharp V-notched components under Mode II loading: A comparison among some recent criteria. Theor. Appl. Fract. Mech. 2016, 85, 217–226. [Google Scholar] [CrossRef]
- Berto, F.; Lazzarin, P. A review of the volume-based strain energy density approach applied to V-notches and welded structures. Theor. Appl. Fract. Mech. 2009, 52, 183–194. [Google Scholar] [CrossRef]
- Berto, F.; Lazzarin, P. Recent developments in brittle and quasi-brittle failure assessment of engineering materials by means of local approaches. Mater. Sci. Eng. R 2014, 75, 1–48. [Google Scholar] [CrossRef]
- Lazzarin, P.; Berto, F. Some expressions for the strain energy in a finite volume surrounding the root of blunt V-notches. Int. J. Fract. 2005, 135, 161–185. [Google Scholar] [CrossRef]
- Niu, L.S.; Chehimi, C.; Pluvinage, G. Stress field near a large blunted V notch and application of the concept of notch stress intensity factor to the fracture of very brittle materials. Eng. Fract. Mech. 1994, 49, 325–335. [Google Scholar] [CrossRef]
- Pluvinage, G. Fatigue and fracture emanating from notch; the use of the notch stress intensity factor. Nucl. Eng. Des. 1998, 185, 173–184. [Google Scholar] [CrossRef]
- Dugdale, D.S. Yielding of steel sheets containing slits. J. Mech. Phys. Solids 1960, 8, 100–108. [Google Scholar] [CrossRef]
- Barenblatt, G.I. The formation of equilibrium cracks during brittle fracture. General ideas and hypothesis. Axially symmetric cracks. J. Appl. Math. Mech. 1959, 23, 622–636. [Google Scholar] [CrossRef]
- Hilleborg, A.; Modeer, M.; Petersson, P.E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem. Concr. Res. 1976, 6, 777–782. [Google Scholar] [CrossRef]
- Gómez, F.J.; Elices, M.; Valiente, A. Cracking in PMMA containing U-shaped notches. Fatigue Fract. Eng. Mater. Struct. 2000, 23, 795–803. [Google Scholar] [CrossRef]
- Lawn, B. Fracture of Brittle Solids; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Weibull, W. The Phenomenon of Rupture in Solids; Generalstabens litografiska anstalts foÌrlag: Stockholm, Sweden, 1939; Volume 153, 55p. [Google Scholar]
- Beremin, F.M.; Pineau, A.; Mudry, F.; Devaux, J.C.; D’Escatha, Y.; Ledermann, P. A local criterion for cleavage fracture of a nuclear pressure vessel steel. Metall. Trans. A 1983, 14, 2277–2287. [Google Scholar] [CrossRef]
- Ritchie, R.O.; Knott, J.F.; Rice, J.R. On the relationship between critical tensile stress and fracture toughness in mild steel. J. Mech. Phys. Solids 1973, 21, 395–410. [Google Scholar] [CrossRef]
- Torabi, A.R.; Berto, F.; Campagono, A. Elastic-plastic fracture analysis of notched Al 7075-T6 plates by means of the local energy combined with the equivalent material concept. Phys. Mesomech. 2016, 19, 204–214. [Google Scholar] [CrossRef]
- Torabi, A.R.; Campagono, A.; Berto, F. A successful combination of the equivalent material concept and the averaged strain energy density criterion for predicting crack initiation from blunt V-notches in ductile aluminium plates under mixed mode loading. Phys. Mesomech. 2016, 19, 382–391. [Google Scholar] [CrossRef]
- Torabi, A.R. Estimation of tensile load-bearing capacity of ductile metallic materials weakened by a V-notch: The equivalent material concept. Mater. Sci. Eng. A 2012, 536, 249–255. [Google Scholar] [CrossRef]
- Torabi, A.R.; Alaei, M. Mixed-mode ductile failure analysis of V-notched Al 7075-T6 thin sheets. Eng. Fract. Mech. 2015, 150, 70–75. [Google Scholar] [CrossRef]
- Torabi, A.R.; Habibi, R.; Mohammad Hosseini, B. On the Ability of the Equivalent Material Concept in Predicting Ductile Failure of U-Notches under Moderate- and Large-Scale Yielding Conditions. Phys. Mesomech. 2015, 18, 337–347. [Google Scholar] [CrossRef]
- Neuber, H. Theory of Notch Stresses: Principles for Exact Calculation of Strength with Reference to Structural form and Material; Springer: Berlin, Germany, 1958. [Google Scholar]
- Peterson, R.E. Notch sensitivity. In Metal Fatigue; McGraw Hill: New York, NY, USA, 1959; pp. 293–306. [Google Scholar]
- Creager, M.; Paris, C. Elastic Field Equations for Blunt Cracks with Reference to Stress Corrosion Cracking. Int. J. Fract. 1967, 3, 247–252. [Google Scholar] [CrossRef]
- Knott, J.F. Fundamentals of Fracture Mechanics; Butterworths: London, UK, 1973. [Google Scholar]

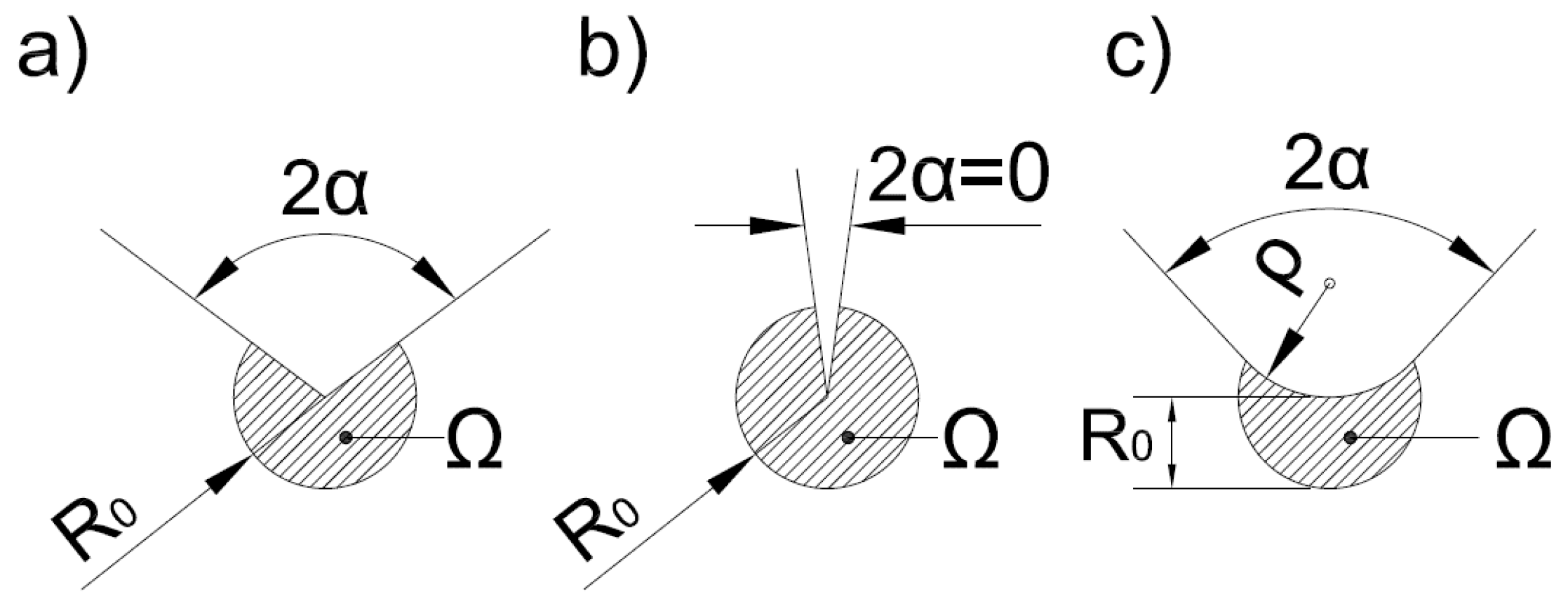
| 2α (rad) | 0 | π/6 | π/4 | π/3 | π/2 | 2π/3 | 3π/4 | 5π/6 |
|---|---|---|---|---|---|---|---|---|
| F(2α) | 0.785 | 0.6917 | 0.6692 | 0.662 | 0.7049 | 0.8779 | 1.0717 | 1.4417 |
| Rc/ρ | ν = 0.20 | ν = 0.25 | ν = 0.30 | ν = 0.35 | ν = 0.40 |
|---|---|---|---|---|---|
| 0.01 | 0.5956 | 0.5813 | 0.5638 | 0.5432 | 0.5194 |
| 0.05 | 0.5401 | 0.5258 | 0.5086 | 0.4884 | 0.4652 |
| 0.1 | 0.4828 | 0.4687 | 0.4518 | 0.4322 | 0.4099 |
| 0.3 | 0.3341 | 0.3216 | 0.3069 | 0.2902 | 0.2713 |
| 0.5 | 0.2508 | 0.2401 | 0.2276 | 0.2135 | 0.1976 |
| 1 | 0.1473 | 0.1399 | 0.1314 | 0.1217 | 0.111 |
| Zn | Mg | Cu | Cr | Fe | Si | Al | |
|---|---|---|---|---|---|---|---|
| Al7075-T651 | 5.41 | 2.84 | 1.47 | 0.19 | 0.17 | 0.15 | Rest |
| Test | E (GPa) | σy (MPa) | σu (MPa) | emax (%) |
|---|---|---|---|---|
| TL-1 | 74.8 | 537.4 | 601.6 | 8.09 |
| TL-2 | 73.9 | 541.0 | 602.8 | 9.95 |
| LT-1 | 71.0 | 550.8 | 607.8 | 9.13 |
| LT-2 | 72.3 | 557.3 | 616.2 | 9.02 |
| Specimen | Notch Radius (mm) | Experimental Fracture Load (KN) | Specimen | Notch Radius (mm) | Experimental Fracture Load (KN) |
|---|---|---|---|---|---|
| TL0-1 | 0 | 11.78 | - | 0 | - |
| TL0-2 | 11.32 | LT0-2 | 10.96 | ||
| TL0-3 | 10.51 | LT0-3 | 10.76 | ||
| TL0-4 | 12.30 | LT0-4 | 11.35 | ||
| TL0-5 | 9.81 | LT0-5 | 11.72 | ||
| TL0-6 | 10.46 | LT0-6 | 11.40 | ||
| TL0.15-2 | 0.15 | 20.95 | LT0.15-1 | 0.15 | 23.09 |
| TL0.15-3 | 21.31 | LT0.15-2 | 23.36 | ||
| TL0.15-4 | 18.95 | LT0.15-3 | 23.12 | ||
| TL0.15-5 | 20.03 | LT0.15-4 | 23.13 | ||
| TL0.15-6 | 19.66 | LT0.15-5 | 23.54 | ||
| TL0.15-7 | 21.32 | LT0.15-6 | 22.35 | ||
| TL0.25-1 | 0.25 | 23.68 | LT0.25-1 | 0.25 | 26.95 |
| TL0.25-2 | 22.68 | LT0.25-2 | 27.47 | ||
| TL0.25-3 | 22.79 | LT0.25-3 | 27.25 | ||
| TL0.5-1 | 0.5 | 31.71 | LT0.5-1 | 0.5 | 34.83 |
| TL0.5-2 | 30.14 | LT0.5-2 | 35.14 | ||
| TL0.5-3 | 32.33 | LT0.5-3 | 34.36 | ||
| TL1.0-1 | 1 | 39.71 | LT1.0-1 | 1 | 41.12 |
| TL1.0-2 | 39.17 | LT1.0-2 | 41.54 | ||
| TL1.0-3 | 37.95 | LT1.0-3 | 40.85 | ||
| TL2.0-1 | 2 | 44.58 | LT2.0-1 | 2 | 44.66 |
| TL2.0-2 | 44.96 | LT2.0-2 | 44.60 | ||
| TL2.0-3 | 45.23 | LT2.0-3 | 44.39 |
| Specimen | PSED (KN) | Specimen | PSED (KN) |
|---|---|---|---|
| TL0.15-2 | 6.09 | LT0.15-1 | 6.19 |
| TL0.15-3 | LT0.15-2 | ||
| TL0.15-4 | LT0.15-3 | ||
| TL0.15-5 | LT0.15-4 | ||
| TL0.15-6 | LT0.15-5 | ||
| TL0.15-7 | LT0.15-6 | ||
| TL0.25-1 | 7.20 | LT0.25-1 | 7.32 |
| TL0.25-2 | LT0.25-2 | ||
| TL0.25-3 | LT0.25-3 | ||
| TL0.5-1 | 10.78 | LT0.5-1 | 10.95 |
| TL0.5-2 | LT0.5-2 | ||
| TL0.5-3 | LT0.5-3 | ||
| TL1.0-1 | 12.47 | LT1.0-1 | 12.67 |
| TL1.0-2 | LT1.0-2 | ||
| TL1.0-3 | LT1.0-3 | ||
| TL2.0-1 | 14.36 | LT2.0-1 | 14.53 |
| TL2.0-2 | LT2.0-2 | ||
| TL2.0-3 | LT2.0-3 |
| Material | E (GPa) | σf* (MPa) |
|---|---|---|
| Al 7075-T651 LT | 71.6 | 2709 |
| Al 7075-T651 TL | 74.4 | 2727 |
| Specimen | PEMC-SED (KN) | Specimen | PEMC-SED (KN) |
|---|---|---|---|
| TL0.15-2 | 15.75 | LT0.15-1 | 15.78 |
| TL0.15-3 | LT0.15-2 | ||
| TL0.15-4 | LT0.15-3 | ||
| TL0.15-5 | LT0.15-4 | ||
| TL0.15-6 | LT0.15-5 | ||
| TL0.15-7 | LT0.15-6 | ||
| TL0.25-1 | 17.75 | LT0.25-1 | 17.80 |
| TL0.25-2 | LT0.25-2 | ||
| TL0.25-3 | LT0.25-3 | ||
| TL0.5-1 | 24.70 | LT0.5-1 | 24.64 |
| TL0.5-2 | LT0.5-2 | ||
| TL0.5-3 | LT0.5-3 | ||
| TL1.0-1 | 34.77 | LT1.0-1 | 34.59 |
| TL1.0-2 | LT1.0-2 | ||
| TL1.0-3 | LT1.0-3 | ||
| TL2.0-1 | 48.32 | LT2.0-1 | 48.03 |
| TL2.0-2 | LT2.0-2 | ||
| TL2.0-3 | LT2.0-3 |
| Specimen | PEMC-PM (KN) | PEMC-LM (KN) | Specimen | PEMC-PM (KN) | PEMC-LM (KN) |
|---|---|---|---|---|---|
| TL0.15-2 | 14.68 | 16.49 | LT0.15-1 | 14.68 | 16.54 |
| TL0.15-3 | LT0.15-2 | ||||
| TL0.15-4 | LT0.15-3 | ||||
| TL0.15-5 | LT0.15-4 | ||||
| TL0.15-6 | LT0.15-5 | ||||
| TL0.15-7 | LT0.15-6 | ||||
| TL0.25-1 | 17.72 | 19.29 | LT0.25-1 | 17.68 | 19.30 |
| TL0.25-2 | LT0.25-2 | ||||
| TL0.25-3 | LT0.25-3 | ||||
| TL0.5-1 | 23.73 | 24.96 | LT0.5-1 | 23.63 | 24.89 |
| TL0.5-2 | LT0.5-2 | ||||
| TL0.5-3 | LT0.5-3 | ||||
| TL1.0-1 | 32.61 | 33.52 | LT1.0-1 | 32.43 | 33.37 |
| TL1.0-2 | LT1.0-2 | ||||
| TL1.0-3 | LT1.0-3 | ||||
| TL2.0-1 | 45.44 | 46.11 | LT2.0-1 | 45.17 | 45.85 |
| TL2.0-2 | LT2.0-2 | ||||
| TL2.0-3 | LT2.0-3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fuentes, J.D.; Cicero, S.; Berto, F.; Torabi, A.R.; Madrazo, V.; Azizi, P. Estimation of Fracture Loads in AL7075-T651 Notched Specimens Using the Equivalent Material Concept Combined with the Strain Energy Density Criterion and with the Theory of Critical Distances. Metals 2018, 8, 87. https://doi.org/10.3390/met8020087
Fuentes JD, Cicero S, Berto F, Torabi AR, Madrazo V, Azizi P. Estimation of Fracture Loads in AL7075-T651 Notched Specimens Using the Equivalent Material Concept Combined with the Strain Energy Density Criterion and with the Theory of Critical Distances. Metals. 2018; 8(2):87. https://doi.org/10.3390/met8020087
Chicago/Turabian StyleFuentes, Juan Diego, Sergio Cicero, Filippo Berto, Ali Reza Torabi, Virginia Madrazo, and Payman Azizi. 2018. "Estimation of Fracture Loads in AL7075-T651 Notched Specimens Using the Equivalent Material Concept Combined with the Strain Energy Density Criterion and with the Theory of Critical Distances" Metals 8, no. 2: 87. https://doi.org/10.3390/met8020087






