Modeling a Pull-In Instability in Micro-Machined Hybrid Contactless Suspension
Abstract
:1. Introduction
2. Hybrid Suspension
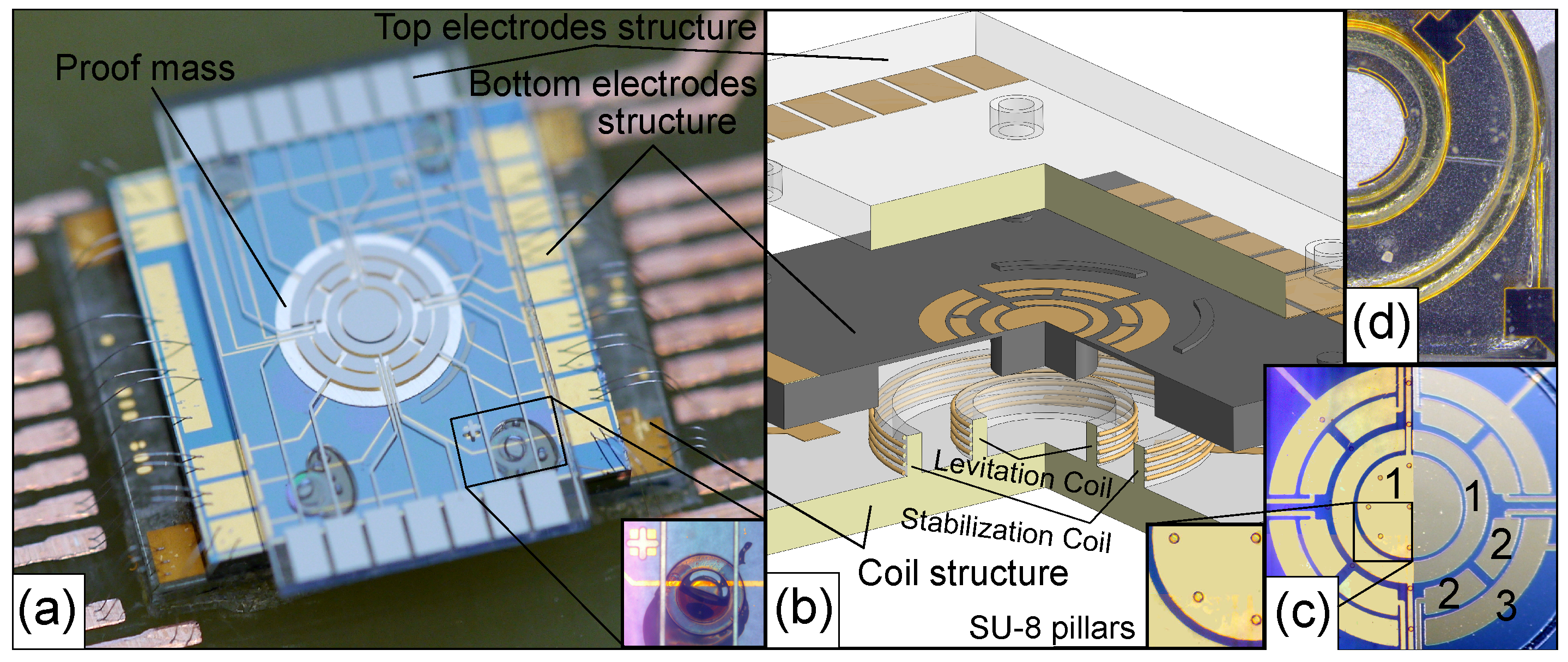
2.1. Fabrication
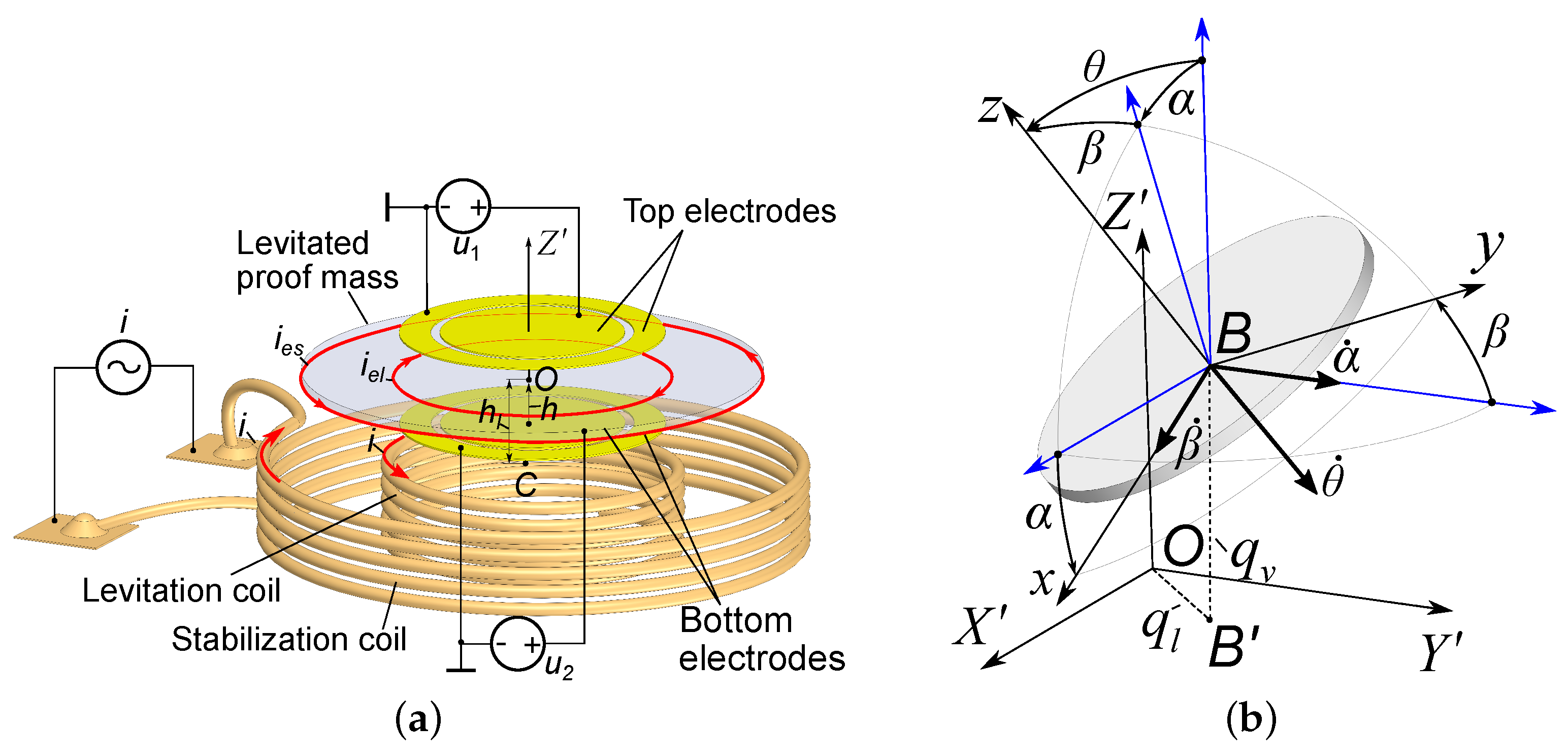
2.2. Operating Principle
2.3. Preliminary Experimental Results
3. Analytical Model
The Accelerometer Equation of Motion
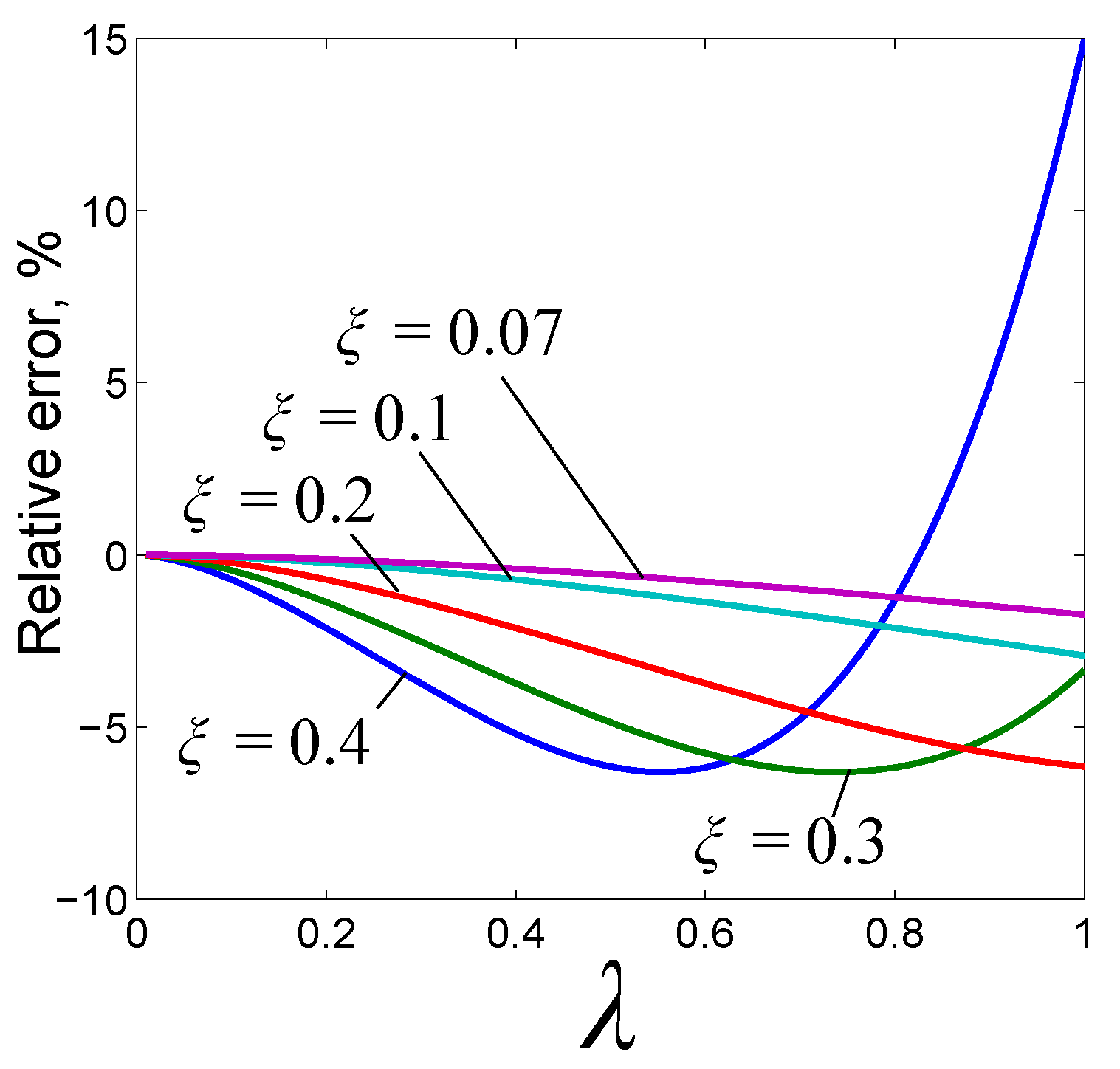
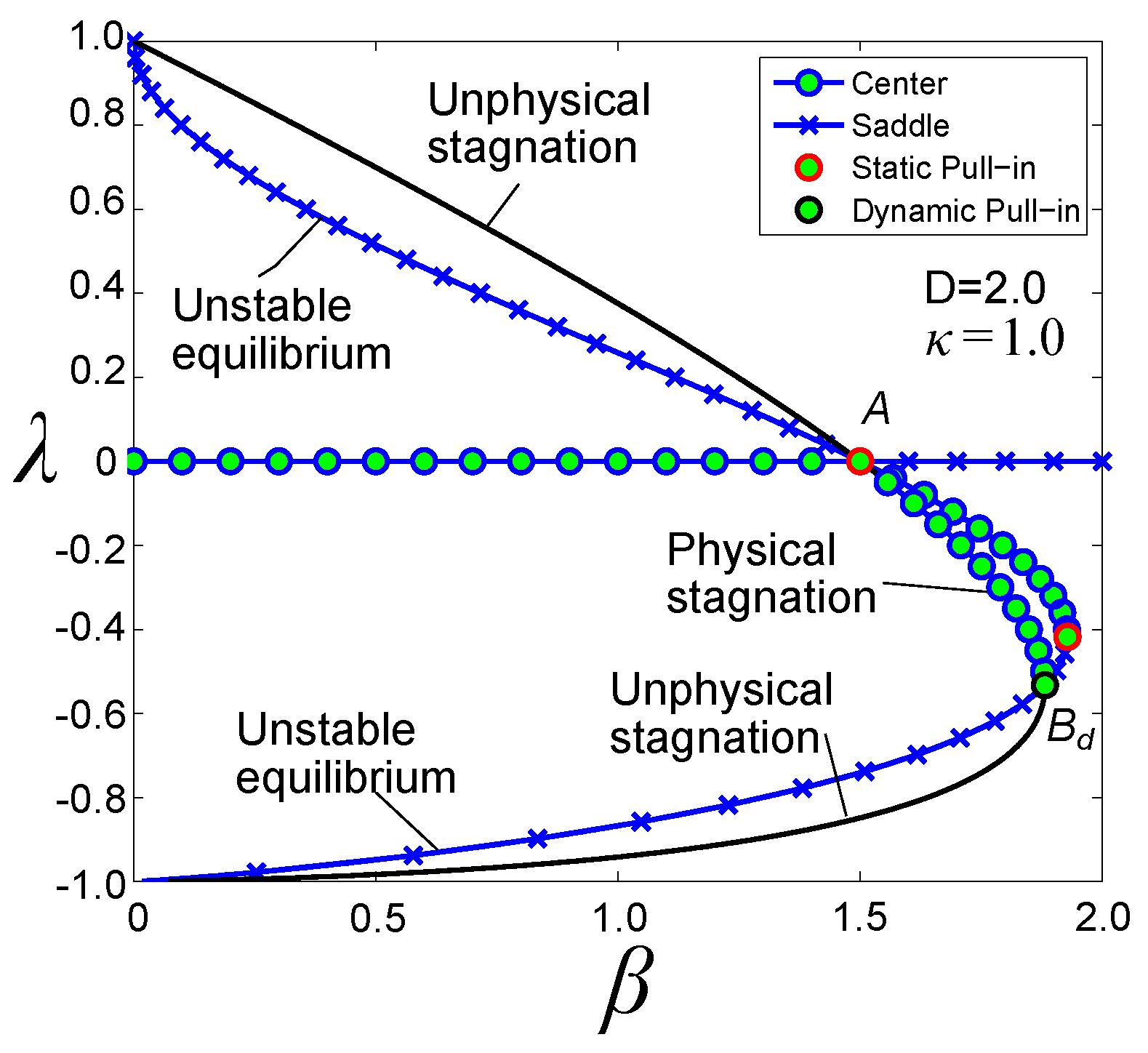
4. Static Pull-In Instability
5. Dynamic Pull-In Instability
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| Amplitude modulator | |
| Deep reactive-ion etching | |
| Negative stiffness | |
| Silicon-on-Insulator | |
| -CS | Micro-machined Contactless Suspensions |
| -ECS | Micro-machined Electrostatic Suspensions |
| -MCS | Micro-machined Magnetic Suspensions |
| -HCS | Micro-machined Hybrid Suspensions |
Appendix A
References
- Post, E.R.; Popescu, G.A.; Gershenfeld, N. Inertial measurement with trapped particles: A microdynamical system. Appl. Phys. Lett. 2010, 96, 143501. [Google Scholar] [CrossRef]
- Poletkin, K.V. Thermal Noise in Ideal Micro-machined Levitated Gyroscope. In Proceedings of the MikroSystemTechnik Congress 2017, Munich, Germany, 23–25 October 2017; VDE Verlag: München, Germany, 2017; pp. 789–792. [Google Scholar]
- Poletkin, K.V.; Korvink, J.G.; Badilita, V. Mechanical Thermal Noise in Micro-Machined Levitated Two-Axis Rate Gyroscopes. IEEE Sens. J. 2018, 18, 1390–1402. [Google Scholar] [CrossRef]
- Poletkin, K.V.; Badilita, V.; Lu, Z.; Wallrabe, U.; Shearwood, C. Magnetic Sensors and Devices: Technologies and Applications; CRC Press: Boca Raton, FL, USA, 2017; pp. 101–131. [Google Scholar]
- Toda, R.; Takeda, N.; Murakoshi, T.; Nakamura, S.; Esashi, M. Electrostatically levitated spherical 3-axis accelerometer. Technical Digest. In Proceedings of the Fifteenth IEEE International Conference on Micro Electro Mechanical Systems (Cat. No. 02CH37266), Las Vegas, NV, USA, 24 January 2002; pp. 710–713. [Google Scholar]
- Murakoshi, T.; Endo, Y.; Fukatsu, K.; Nakamura, S.; Esashi, M. Electrostatically levitated ring-shaped rotational gyro/accelerometer. Jpn. J. Appl. Phys. 2003, 42, 2468–2472. [Google Scholar] [CrossRef]
- Cui, F.; Liu, W.; Chen, W.; Zhang, W.; Wu, X. Design, Fabrication and Levitation Experiments of a Micromachined Electrostatically Suspended Six-Axis Accelerometer. Sensors 2011, 11, 11206–11234. [Google Scholar] [CrossRef] [PubMed]
- Han, F.; Liu, Y.; Wang, L.; Ma, G. Micromachined electrostatically suspended gyroscope with a spinning ring-shaped rotor. J. Micromech. Microeng. 2012, 22, 105032. [Google Scholar] [CrossRef]
- Han, F.; Sun, B.; Li, L.; Wu, Q. Performance of a sensitive micromachined accelerometer with an electrostatically suspended proof mass. IEEE Sens. J. 2015, 15, 209–217. [Google Scholar]
- Coombs, T.; Samad, I.; Ruiz-Alonso, D.; Tadinada, K. Superconducting micro-bearings. IEEE Trans. Appl. Supercond. 2005, 15, 2312–2315. [Google Scholar] [CrossRef]
- Lu, Z.; Poletkin, K.; Hartogh, B.d.; Wallrabe, U.; Badilita, V. 3D micro-machined inductive contactless suspension: Testing and Modeling. Sens. Actuators A Phys. 2014, 220, 134–143. [Google Scholar] [CrossRef]
- Poletkin, K.; Moazenzadeh, A.; Mariappan, S.G.; Lu, Z.; Wallrabe, U.; Korvink, J.G.; Badilita, V. Polymer Magnetic Composite Core Boosts Performance of 3D Micromachined Inductive Contactless Suspension. IEEE Magn. Lett. 2016, 7, 1–3. [Google Scholar] [CrossRef]
- Poletkin, K.V.; Lu, Z.; Maozenzadeh, A.; Mariappan, S.G.; Korvink, J.G.; Wallrabe, U.; Badilita, V. 3D Micro-machined Inductive Suspensions with the Lowest Energy Consumption. In Proceedings of the MikroSystemTechnik Congress 2017, Munich, Germany, 23–25 October 2017; VDE Verlag: München, Germany, 2017; pp. 500–502. [Google Scholar]
- Shearwood, C.; Ho, K.; Williams, C.; Gong, H. Development of a levitated micromotor for application as a gyroscope. Sens. Actuators A Phys. 2000, 83, 85–92. [Google Scholar] [CrossRef]
- Su, Y.; Xiao, Z.; Ye, Z.; Takahata, K. Micromachined Graphite Rotor Based on Diamagnetic Levitation. IEEE Electron Device Lett. 2015, 36, 393–395. [Google Scholar] [CrossRef]
- Su, Y.; Zhang, K.; Ye, Z.; Xiao, Z.; Takahata, K. Exploration of micro-diamagnetic levitation rotor. Jpn. J. Appl. Phys. 2017, 56, 126702. [Google Scholar] [CrossRef]
- Garmire, D.; Choo, H.; Kant, R.; Govindjee, S.; Sequin, C.; Muller, R.; Demmel, J. Diamagnetically levitated MEMS accelerometers. In Proceedings of the International IEEE Solid-State Sensors, Actuators and Microsystems Conference, Lyon, France, 10–14 June 2007; pp. 1203–1206. [Google Scholar]
- Ando, B.; Baglio, S.; Marletta, V.; Valastro, A. A Short-Range Inertial Sensor Exploiting Magnetic Levitation and an Inductive Readout Strategy. IEEE Trans. Instrum. Meas. 2018, PP, 1–8. [Google Scholar] [CrossRef]
- Dieppedale, C.; Desloges, B.; Rostaing, H.; Delamare, J.; Cugat, O.; Meunier-Carus, J. Magnetic bistable micro-actuator with integrated permanent magnets. In Proceedings of the IEEE Sensors, Vienna, Austria, 24–27 October 2004; Volume 1, pp. 493–496. [Google Scholar]
- Boukallel, M.; Piat, E.; Abadie, J. Passive diamagnetic levitation: theoretical foundations and application to the design of a micro-nano force sensor. In Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003) (Cat. No.03CH37453), Las Vegas, NV, USA, 27–31 October 2003; Volume 2, pp. 1062–1067. [Google Scholar]
- Abadie, J.; Piat, E.; Oster, S.; Boukallel, M. Modeling and experimentation of a passive low frequency nanoforce sensor based on diamagnetic levitation. Sens. Actuators A Phys. 2012, 173, 227–237. [Google Scholar] [CrossRef] [Green Version]
- Lyuksyutov, I.F.; Naugle, D.G.; Rathnayaka, K.D.D. On-chip manipulation of levitated femtodroplets. Appl. Phys. Lett. 2004, 85, 1817–1819. [Google Scholar] [CrossRef]
- Chetouani, H.; Jeandey, C.; Haguet, V.; Rostaing, H.; Dieppedale, C.; Reyne, G. Diamagnetic Levitation With Permanent Magnets for Contactless Guiding and Trapping of Microdroplets and Particles in Air and Liquids. IEEE Trans. Magn. 2006, 42, 3557–3559. [Google Scholar] [CrossRef]
- Lu, Z.; Chen, P.C.Y.; Lin, W. Force Sensing and Control in Micromanipulation. IEEE Trans. Syst. Man Cyberne. Part C 2006, 36, 713–724. [Google Scholar] [CrossRef]
- Liu, W.; Chen, W.Y.; Zhang, W.P.; Huang, X.G.; Zhang, Z.R. Variable-capacitance micromotor with levitated diamagnetic rotor. Electron. Lett. 2008, 44, 681–683. [Google Scholar] [CrossRef]
- Sari, I.; Kraft, M. A MEMS Linear Accelerator for Levitated Micro-objects. Sens. Actuators A Phys. 2015, 222, 15–23. [Google Scholar] [CrossRef]
- Liu, K.; Zhang, W.; Liu, W.; Chen, W.; Li, K.; Cui, F.; Li, S. An innovative micro-diamagnetic levitation system with coils applied in micro-gyroscope. Microsyst. Technol. 2010, 16, 431–439. [Google Scholar] [CrossRef]
- Xu, Y.; Cui, Q.; Kan, R.; Bleuler, H.; Zhou, J. Realization of a Diamagnetically Levitating Rotor Driven by Electrostatic Field. IEEE/ASME Trans. Mechatron. 2017, 22, 2387–2391. [Google Scholar] [CrossRef]
- Poletkin, K.; Lu, Z.; Wallrabe, U.; Badilita, V. A New Hybrid Micromachined Contactless Suspension With Linear and Angular Positioning and Adjustable Dynamics. J. Microelectromech. Syst. 2015, 24, 1248–1250. [Google Scholar] [CrossRef]
- Poletkin, K.V.; Chernomorsky, A.I.; Shearwood, C. A Proposal for Micromachined Accelerometer, base on a Contactless Suspension with Zero Spring Constant. IEEE Sens. J. 2012, 12, 2407–2413. [Google Scholar] [CrossRef]
- Poletkin, K. A novel hybrid contactless suspension with adjustable spring constant. In Proceedings of the 19th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Kaohsiung, Taiwan, 18–22 June 2017; pp. 934–937. [Google Scholar]
- Poletkin, K.; Shalati, R.; Korvink, J.G.; Badilita, V. Pull-in Actuation in Micro-machined Hybrid Contactless Suspension. In Proceedings of the 17th International Conference on Micro and Nanotechnology for Power Generation and Energy Conversion Applications (Power MEMS 2017), Kanazawa, Japan, 14–17 November 2017; pp. 150–153. [Google Scholar]
- Elata, D.; Bamberger, H. On the dynamic pull-in of electrostatic actuators with multiple degrees of freedom and multiple voltage sources. J. Microelectromech. Syst. 2006, 15, 131–140. [Google Scholar] [CrossRef]
- Poletkin, K.; Chernomorsky, A.; Shearwood, C.; Wallrabe, U. A qualitative analysis of designs of micromachined electromagnetic inductive contactless suspension. Int. J. Mech. Sci. 2014, 82, 110–121. [Google Scholar] [CrossRef]
- Poletkin, K.V.; Lu, Z.; Wallrabe, U.; Korvink, J.G.; Badilita, V. A qualitative technique to study stability and dynamics of micro-machined inductive contactless suspensions. In Proceedings of the 19th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Kaohsiung, Taiwan, 18–22 June 2017; pp. 528–531. [Google Scholar]
- Poletkin, K.; Lu, Z.; Wallrabe, U.; Korvink, J.G.; Badilita, V. Stable dynamics of micro-machined inductive contactless suspensions. Int. J. Mech. Sci. 2017, 131–132, 753–766. [Google Scholar] [CrossRef]
- Poletkin, K.V.; Chernomorsky, A.I.; Shearwood, C. A Proposal for Micromachined Dynamically Tuned Gyroscope, Based on Contactless Suspension. IEEE Sens. J. 2012, 12, 2164–2171. [Google Scholar] [CrossRef]
- Merkin, D.R. Introduction to the Theory of Stability; Springer Science & Business Media: Berlin, Germany, 2012; Volume 24. [Google Scholar]
- Poletkin, K.; Chernomorsky, A.I.; Shearwood, C.; Wallrabe, U. An analytical model of micromachined electromagnetic inductive contactless suspension. In Proceedings of the ASME 2013 International Mechanical Engineering Congress & Exposition, San Diego, CA, USA, 15–21 November 2013; ASME: San Diego, CA, USA, 2013; p. V010T11A072. [Google Scholar]
- Lu, Z.; Poletkin, K.; Wallrabe, U.; Badilita, V. Performance characterization of micromachined inductive suspensions based on 3D wirebonded microcoils. Micromachines 2014, 5, 1469–1484. [Google Scholar] [CrossRef]
- Rosa, E.; Grover, F. Formulas and tables for the calculation of mutual and self-inductance. J. Wash. Acad. Sci. 1911, 1, 14–16. [Google Scholar] [CrossRef]
- Dwight, H.B. Tables of Integrals and Other Mathematical Data, 4th ed.; The MacMillan Company: New York, NY, USA, 1961. [Google Scholar]



| Parameters of the Prototype | ||
| Diameter of the proof mass | () | 3.2 |
| Thickness of the proof mass | () | 30 |
| Levitation height | () | 150 |
| Spacing | () | 50 |
| Results of Measurements | ||
| Stiffness () | () | 0.043 |
| Stiffness ( V) | () | 0.03 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poletkin, K.V.; Korvink, J.G. Modeling a Pull-In Instability in Micro-Machined Hybrid Contactless Suspension. Actuators 2018, 7, 11. https://doi.org/10.3390/act7010011
Poletkin KV, Korvink JG. Modeling a Pull-In Instability in Micro-Machined Hybrid Contactless Suspension. Actuators. 2018; 7(1):11. https://doi.org/10.3390/act7010011
Chicago/Turabian StylePoletkin, Kirill V., and Jan G. Korvink. 2018. "Modeling a Pull-In Instability in Micro-Machined Hybrid Contactless Suspension" Actuators 7, no. 1: 11. https://doi.org/10.3390/act7010011