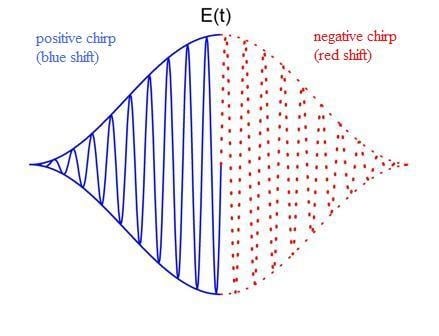
Spectral Shifts of Nonadiabatic High-Order Harmonic Generation
Abstract
:1. Introduction
 is the ponderomotive energy of the electrons oscillating in the laser field, E and ω are the amplitude and frequency of the laser field, respectively (atomic units e = me = ћ = 1 are used throughout the paper unless otherwise specified). As a consequence, the cutoff energy of HHG, i.e., maximal kinetic energy Ek plus ionization potential Ip, is:
is the ponderomotive energy of the electrons oscillating in the laser field, E and ω are the amplitude and frequency of the laser field, respectively (atomic units e = me = ћ = 1 are used throughout the paper unless otherwise specified). As a consequence, the cutoff energy of HHG, i.e., maximal kinetic energy Ek plus ionization potential Ip, is:
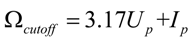
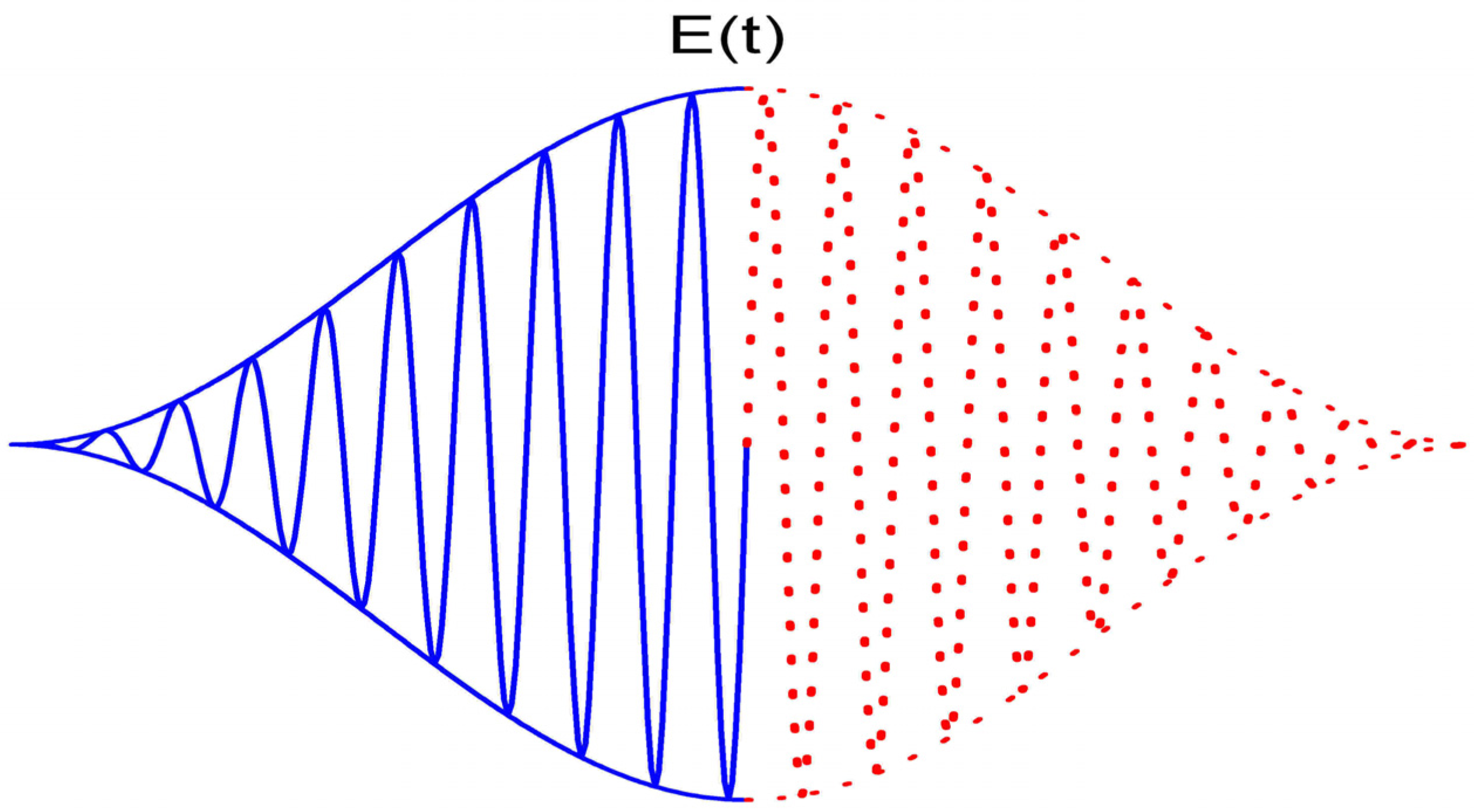
 of the HHG spectrum. In short laser fields with very high intensity, the depletion of the ground state and rapid change of intensity I(t) will lead to nonadiabatic effects in HHG, such as red [11] and blue [12] shifts of HHG. We review the recent progress in these nonadiabatic spectral shifts of HHG and in particular MHOHG in this article.
of the HHG spectrum. In short laser fields with very high intensity, the depletion of the ground state and rapid change of intensity I(t) will lead to nonadiabatic effects in HHG, such as red [11] and blue [12] shifts of HHG. We review the recent progress in these nonadiabatic spectral shifts of HHG and in particular MHOHG in this article.2. Blue Shift in HHG
2.1. Blue Shift by Propagating Effect
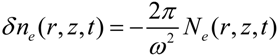
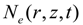 denotes the electron density. The variation of the refractive index leads to a blue shift of the fundamental laser field. The shift can be estimated by the following expression (CGS units) [18],
denotes the electron density. The variation of the refractive index leads to a blue shift of the fundamental laser field. The shift can be estimated by the following expression (CGS units) [18],
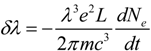
2.2. Nonadiabatic Blue Shift in HHG
3. Red Shift of HHG in Resonant Systems
3.1. Four-Step Model of MHOHG in Resonant Systems
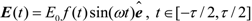
 , τ is the total duration of the laser pulses.
, τ is the total duration of the laser pulses.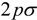 (the life time is around 4 ns [23].) resonant with the ground state. The MHOHG spectra of HeH2+ are obtained by numerically solving the TDSE. For the computational details of this one-electron system, we refer to reference [21]. The internuclear distance R is fixed at 4 a.u. (near the excited state minimum R =3.89 a.u.). The energy of the first excited state
(the life time is around 4 ns [23].) resonant with the ground state. The MHOHG spectra of HeH2+ are obtained by numerically solving the TDSE. For the computational details of this one-electron system, we refer to reference [21]. The internuclear distance R is fixed at 4 a.u. (near the excited state minimum R =3.89 a.u.). The energy of the first excited state 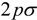 is −1.03 a.u. (28 eV). The initial state for time evolution is the ground state
is −1.03 a.u. (28 eV). The initial state for time evolution is the ground state 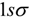 . The laser polarization is along the z molecular axis. The power spectra of MHOHG is calculated by a Fourier transformation of the dipole momentum in the acceleration form
. The laser polarization is along the z molecular axis. The power spectra of MHOHG is calculated by a Fourier transformation of the dipole momentum in the acceleration form  , as it is the most reliable numerical method for strong field interactions avoiding after pulse transient effects such as in the dipole form [24]. To further probe the temporal structures of MHOHG, we perform a time profile analysis of the harmonic spectra. The time profile of harmonic ωq is obtained by a wavelet analysis as in signal processing [25,26,27]:
, as it is the most reliable numerical method for strong field interactions avoiding after pulse transient effects such as in the dipole form [24]. To further probe the temporal structures of MHOHG, we perform a time profile analysis of the harmonic spectra. The time profile of harmonic ωq is obtained by a wavelet analysis as in signal processing [25,26,27]:
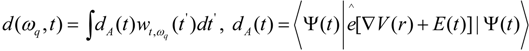
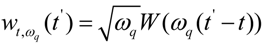 . The mother wavelet we use is a Morlet wavelet:
. The mother wavelet we use is a Morlet wavelet:
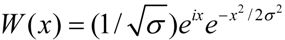
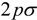 state and the total ionization rate Г(t) as a function of time in Figure 4, from which one concludes that EE and EI are not synchronous. For laser intensity below the saturation threshold, the excitation to the localized resonant state
state and the total ionization rate Г(t) as a function of time in Figure 4, from which one concludes that EE and EI are not synchronous. For laser intensity below the saturation threshold, the excitation to the localized resonant state 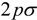 on the RLE will strongly enhance the ionization rate of the system on the FLE. In this way, the red shift generated on the FLE will be larger than the blue shift on the RLE. An overall noticeable red shift can be observed in the MHOHG process. The time delay between EE and subsequent EI plays an important role in producing a noticeable “redshift” in MHOHG for very short pulses.
on the RLE will strongly enhance the ionization rate of the system on the FLE. In this way, the red shift generated on the FLE will be larger than the blue shift on the RLE. An overall noticeable red shift can be observed in the MHOHG process. The time delay between EE and subsequent EI plays an important role in producing a noticeable “redshift” in MHOHG for very short pulses. state. The laser polarization is along the z axis, i.e., the orientation angle χ = 0°. The peak laser intensity is I = 3.5 × 1015 W/cm2. The wavelength is 400 nm. The pulse has a cos2(πt / τ) shape ƒ(t) with a duration of 15 optical cycles as illustrated in (b).
state. The laser polarization is along the z axis, i.e., the orientation angle χ = 0°. The peak laser intensity is I = 3.5 × 1015 W/cm2. The wavelength is 400 nm. The pulse has a cos2(πt / τ) shape ƒ(t) with a duration of 15 optical cycles as illustrated in (b).
 state. The laser polarization is along the z axis, i.e., the orientation angle χ = 0°. The peak laser intensity is I = 3.5 × 1015 W/cm2. The wavelength is 400 nm. The pulse has a cos2(πt / τ) shape ƒ(t) with a duration of 15 optical cycles as illustrated in (b).
state. The laser polarization is along the z axis, i.e., the orientation angle χ = 0°. The peak laser intensity is I = 3.5 × 1015 W/cm2. The wavelength is 400 nm. The pulse has a cos2(πt / τ) shape ƒ(t) with a duration of 15 optical cycles as illustrated in (b).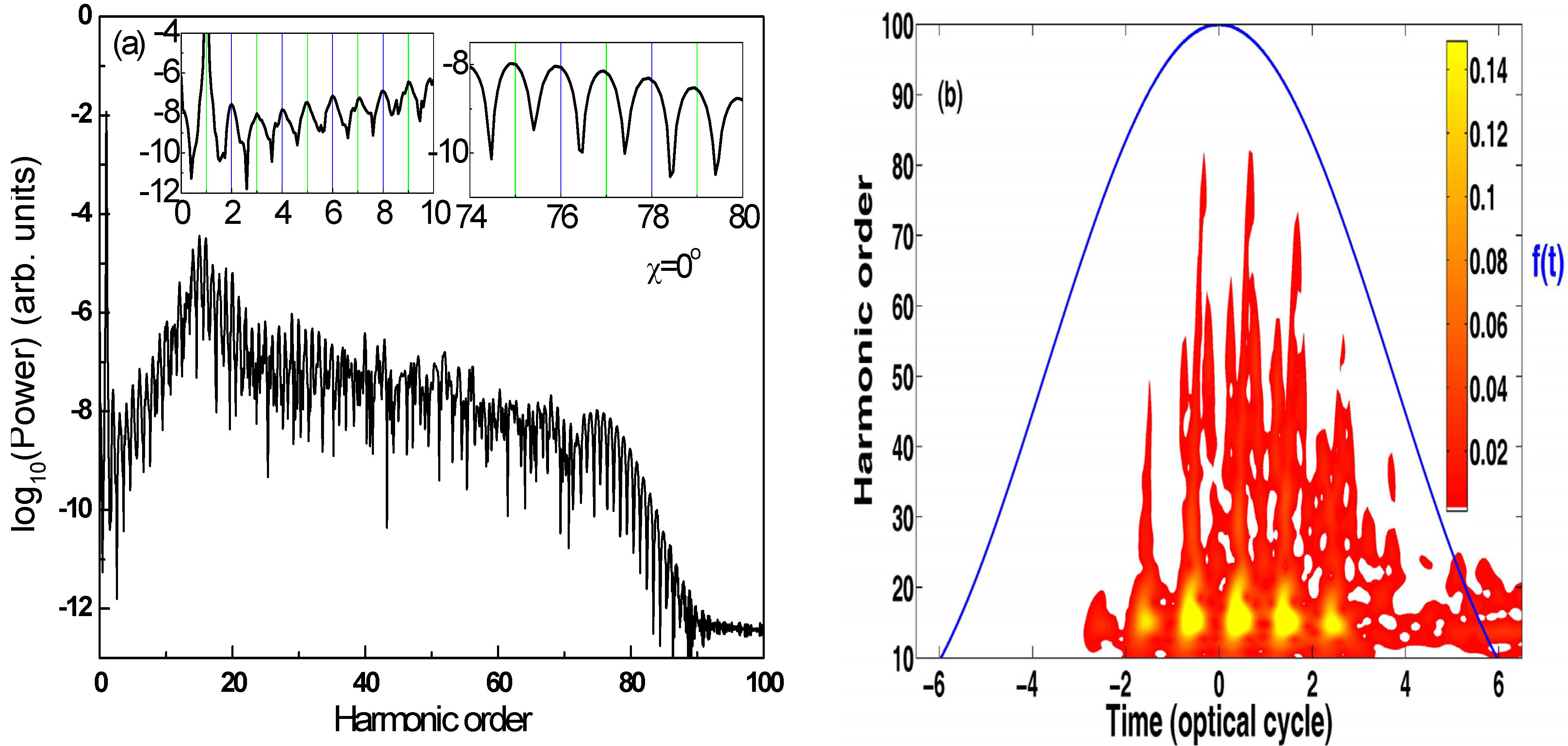
 state to the localized long lifetime
state to the localized long lifetime 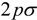 excited state; part of the electron is ionized from the excited state in step (2), then accelerated by the laser field in step (3), and then transits back to the ground state to emit photons in step (4) when the laser field changes its direction. Part of the electron in the excited state will directly transit to the ground state in step (2*) when the laser field changes its phase. This leads to a strong resonance in the harmonic spectra. The Stark shift of the energy levels E1 and E2 is included [11]. E+1 and E+2 refer to the dressed energies with the field along +z direction, while E-1 and E-2 refer to the dressed energies with the field along −z direction.
excited state; part of the electron is ionized from the excited state in step (2), then accelerated by the laser field in step (3), and then transits back to the ground state to emit photons in step (4) when the laser field changes its direction. Part of the electron in the excited state will directly transit to the ground state in step (2*) when the laser field changes its phase. This leads to a strong resonance in the harmonic spectra. The Stark shift of the energy levels E1 and E2 is included [11]. E+1 and E+2 refer to the dressed energies with the field along +z direction, while E-1 and E-2 refer to the dressed energies with the field along −z direction.
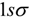 state to the localized long lifetime
state to the localized long lifetime 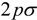 excited state; part of the electron is ionized from the excited state in step (2), then accelerated by the laser field in step (3), and then transits back to the ground state to emit photons in step (4) when the laser field changes its direction. Part of the electron in the excited state will directly transit to the ground state in step (2*) when the laser field changes its phase. This leads to a strong resonance in the harmonic spectra. The Stark shift of the energy levels E1 and E2 is included [11]. E+1 and E+2 refer to the dressed energies with the field along +z direction, while E-1 and E-2 refer to the dressed energies with the field along −z direction.
excited state; part of the electron is ionized from the excited state in step (2), then accelerated by the laser field in step (3), and then transits back to the ground state to emit photons in step (4) when the laser field changes its direction. Part of the electron in the excited state will directly transit to the ground state in step (2*) when the laser field changes its phase. This leads to a strong resonance in the harmonic spectra. The Stark shift of the energy levels E1 and E2 is included [11]. E+1 and E+2 refer to the dressed energies with the field along +z direction, while E-1 and E-2 refer to the dressed energies with the field along −z direction.
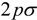 (solid black line) and the total ionization rate (dotted red line) as a function of time. The laser parameters are the same as those in Figure 2.
(solid black line) and the total ionization rate (dotted red line) as a function of time. The laser parameters are the same as those in Figure 2.
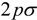 (solid black line) and the total ionization rate (dotted red line) as a function of time. The laser parameters are the same as those in Figure 2.
(solid black line) and the total ionization rate (dotted red line) as a function of time. The laser parameters are the same as those in Figure 2.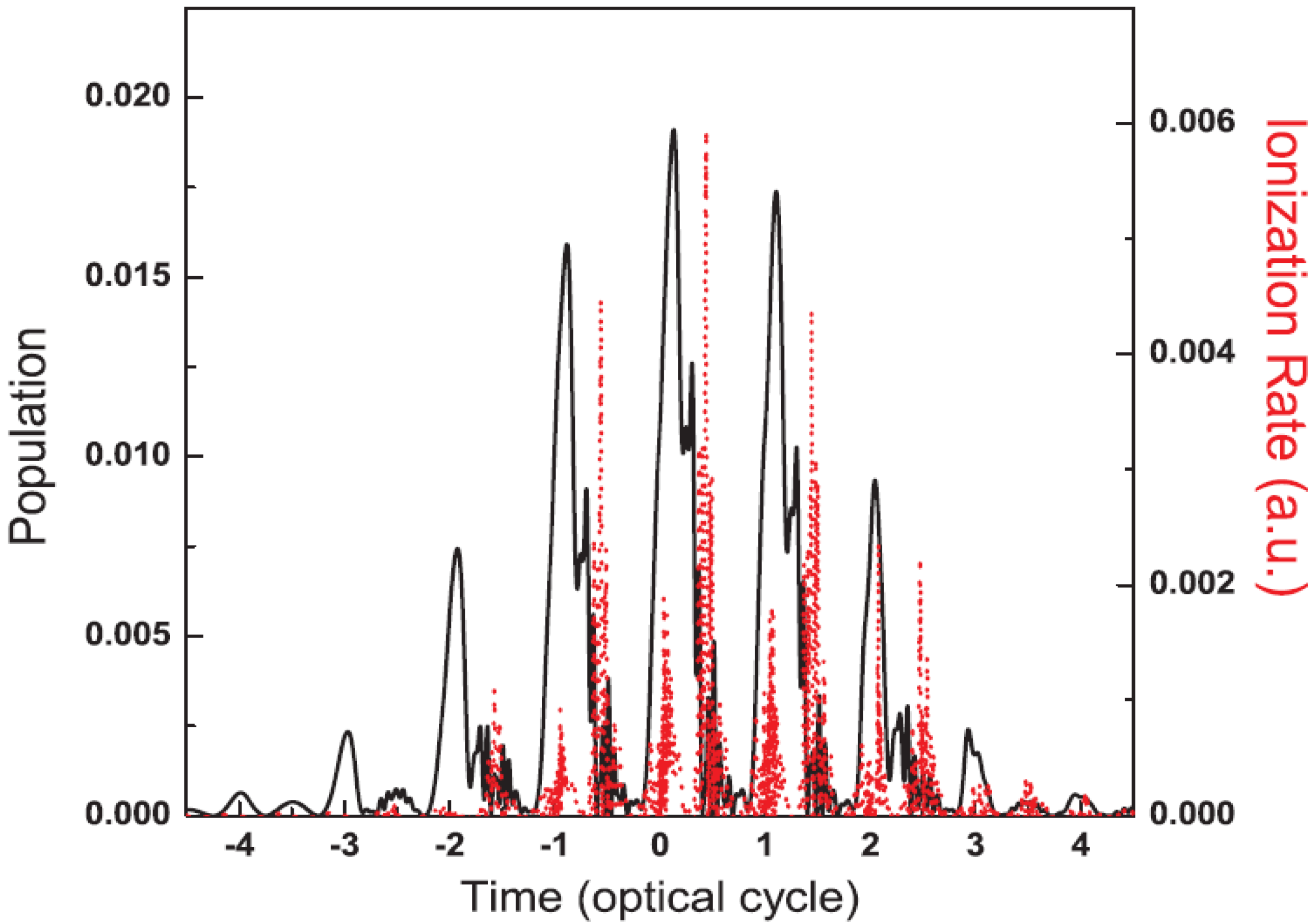
3.2. Pulse Duration Dependence of Red Shift in MHOHG
 . Shorter pulses enhance this effect, while this nonadiabatic effect will be less noticeable for longer pulses. To emphasize this effect, MHOHG spectra for harmonic order 40 to 42 in the plateau produced by different duration of laser pulses are illustrated in Figure 5a. The laser intensity and wavelength are kept the same as those in Figure 2. The corresponding time profiles of harmonic with order 40 are presented in Figure 5b. The nonadiabatic spectral red shift of MHOHG gradually decreases as the laser-pulse duration increases from 10 to 20 optical cycles. From the time profile analysis, the harmonic generation process is gradually shifted from the falling part of the pulse to the rising part in agreement with the above prediction.
. Shorter pulses enhance this effect, while this nonadiabatic effect will be less noticeable for longer pulses. To emphasize this effect, MHOHG spectra for harmonic order 40 to 42 in the plateau produced by different duration of laser pulses are illustrated in Figure 5a. The laser intensity and wavelength are kept the same as those in Figure 2. The corresponding time profiles of harmonic with order 40 are presented in Figure 5b. The nonadiabatic spectral red shift of MHOHG gradually decreases as the laser-pulse duration increases from 10 to 20 optical cycles. From the time profile analysis, the harmonic generation process is gradually shifted from the falling part of the pulse to the rising part in agreement with the above prediction.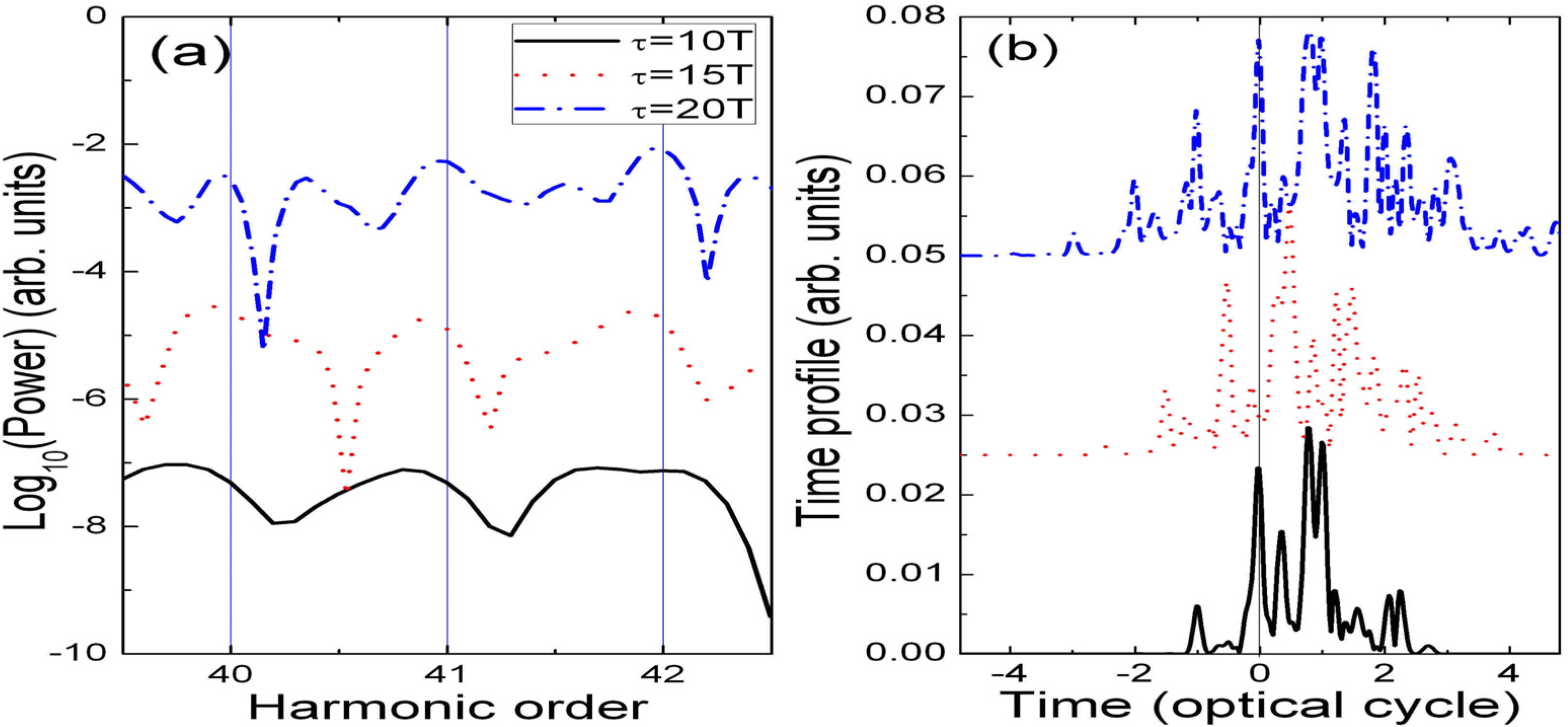
3.3. Orientation Dependence of Red Shift in MHOHG
 state with long life time plays a key role in the red shift of MHOHG. The radiative transition from the ground
state with long life time plays a key role in the red shift of MHOHG. The radiative transition from the ground 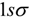 state to the resonant
state to the resonant 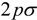 state is however restricted to the parallel component of the laser field. In this subsection, we explore the orientation dependence of the red shift in MHOHG [22]. The numerical results of MHOHG spectra with different orientation angles χ and the corresponding time profiles are presented in Figure 6a,b, respectively.
state is however restricted to the parallel component of the laser field. In this subsection, we explore the orientation dependence of the red shift in MHOHG [22]. The numerical results of MHOHG spectra with different orientation angles χ and the corresponding time profiles are presented in Figure 6a,b, respectively.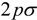 . The intensity of MHOHG in the plateau with orientation angle χ=0° (parallel) is more than two orders higher than that with orientation angle χ=90° (perpendicular). The reason is that the direct ionization rate from the ground state
. The intensity of MHOHG in the plateau with orientation angle χ=0° (parallel) is more than two orders higher than that with orientation angle χ=90° (perpendicular). The reason is that the direct ionization rate from the ground state 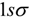 is very low due to the large ionization potential. However, the EE to the resonant excited state
is very low due to the large ionization potential. However, the EE to the resonant excited state 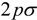 will lead to EI, which greatly increases the ionization rate of the system. For the parallel orientation, the amplitude of radiative transition to the
will lead to EI, which greatly increases the ionization rate of the system. For the parallel orientation, the amplitude of radiative transition to the 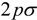 state is maximal. This corresponds to an efficient laser-induced electron transfer (LIET) in a nonsymmetric system [20]. One can observe a strong resonance in the MHOHG spectra. When we gradually increase the orientation angle χ between the molecular axis and laser polarization, the transition amplitude along the molecular axis direction diminishes, and the intensity of the resonance and the plateau in MHOHG decreases. It can be observed in the corresponding time profiles in Figure 6b. For perpendicular orientation with χ=90°, the transition from the
state is maximal. This corresponds to an efficient laser-induced electron transfer (LIET) in a nonsymmetric system [20]. One can observe a strong resonance in the MHOHG spectra. When we gradually increase the orientation angle χ between the molecular axis and laser polarization, the transition amplitude along the molecular axis direction diminishes, and the intensity of the resonance and the plateau in MHOHG decreases. It can be observed in the corresponding time profiles in Figure 6b. For perpendicular orientation with χ=90°, the transition from the 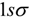 state to
state to 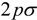 state is forbidden by selection rules. The electron may transit from the
state is forbidden by selection rules. The electron may transit from the 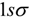 state to 2pπ state (−0.7388 a.u. (20.1 eV)). However, the 2pπ state is not a resonant state with long life time. Its role in the MHOHG is therefore negligible. As a consequence, the above four-step model gradually changes to a three-step model with increasing angle χ, and the time profiles of higher-order harmonics illustrated in Figure 6b becomes more symmetric with respect to the time when the laser pulse reaches its peak intensity, i.e., t = 0. The red shift of MHOHG decreases with the increase of the orientation angle χ. No noticeable red shift occurs in the MHOHG spectra when χ=90° as illustrated in the calculations presented in Figure 6a for the intensities and in Figure 6b for the time profiles. One may expect only odd-order harmonic generation due to the symmetry of the system with χ=90°. However, a little population on the 2pπ state will break the symmetry of the system, which will lead to even-order harmonic generation [22].
state to 2pπ state (−0.7388 a.u. (20.1 eV)). However, the 2pπ state is not a resonant state with long life time. Its role in the MHOHG is therefore negligible. As a consequence, the above four-step model gradually changes to a three-step model with increasing angle χ, and the time profiles of higher-order harmonics illustrated in Figure 6b becomes more symmetric with respect to the time when the laser pulse reaches its peak intensity, i.e., t = 0. The red shift of MHOHG decreases with the increase of the orientation angle χ. No noticeable red shift occurs in the MHOHG spectra when χ=90° as illustrated in the calculations presented in Figure 6a for the intensities and in Figure 6b for the time profiles. One may expect only odd-order harmonic generation due to the symmetry of the system with χ=90°. However, a little population on the 2pπ state will break the symmetry of the system, which will lead to even-order harmonic generation [22].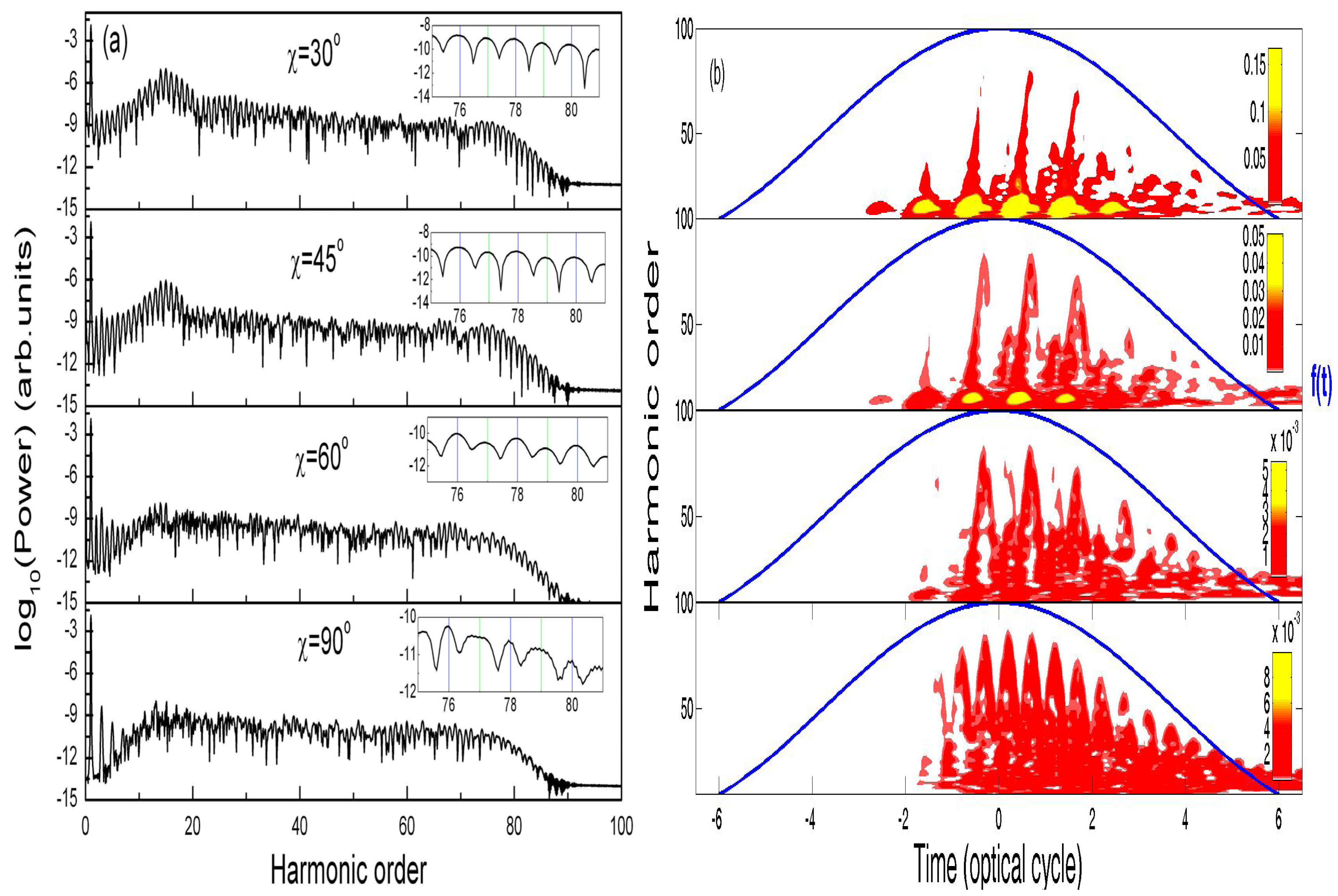
4. Conclusions
Acknowledgments
Conflict of Interest
References
- McPherson, A.; Gibson, G.; Jara, H.; Johann, U.; Luk, T.S.; McIntyre, I.A.; Boyer, K.; Rhodes, C.K. Studies of multiphoton production of vacuum-ultraviolet radiation in the rare gases. J. Opt. Soc. Am. B 1987, 4, 595–601. [Google Scholar]
- Ferray, M.; Huillier, A.L.; Li, X.F.; Lompre, L.A.; Mainfray, G.; Manus, C. Multiple-harmonic conversion of 1064 nm radiation in rare gases. J. Phys. B 1988, 21, L31–L35. [Google Scholar] [CrossRef]
- Corkum, P.B.; Krausz, F. Attosecond science. Nat. Phys. 2007, 3, 381–387. [Google Scholar] [CrossRef]
- Krausz, F.; Ivanov, M. Attosecond physics. Rev. Mod. Phys. 2009, 81, 163–234. [Google Scholar]
- Corkum, P.B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 1993, 71, 1994–1997. [Google Scholar] [CrossRef]
- Lewenstein, M.; Balcou, P.; Ivanov, M.Y.; L’Huillier, A.; Corkum, P.B. Theory of high-harmonic generation by low-frequency laser fields. Phys. Rev. A 1994, 49, 2117–2132. [Google Scholar]
- Bandrauk, A.D.; Chelkowski, S.; Goudreau, S. Control of harmonic generation using two-colour femtosecond-attosecond laser fields: Quantum and classical perspectives. J. Mod. Opt. 2005, 52, 411–428. [Google Scholar]
- Bandrauk, A.D.; Barmaki, S.; Kamta, G.L. Laser phase control of high-order harmonic generation at large internuclear distance: the h+-h2+ system. Phys. Rev. Lett. 2007, 98, 013001–1. [Google Scholar]
- Bandrauk, A.D.; Barmaki, S.; Cheklowski, S.; Kamta, G.L. Progress in Ultrafast Intense Laser Science III; Yamanouchi, K., Chin, S.L., Agostini, P., Ferrante, G., Eds.; Springer: Berlin, Germany, 2008; Volume 3, p. 171. [Google Scholar]
- Moreno, P.; Plaja, L.; Roso, L. Ultrahigh harmonic generation from diatomic molecular ions in highly excited vibrational states. Phys. Rev. A 1997, 55, R1593–R1596. [Google Scholar] [CrossRef]
- Bian, X.B.; Bandrauk, A.D. Nonadiabatic molecular high-order harmonic generation from polar molecules: Spectral redshift. Phys. Rev. A 2011, 83, 041403:1–041403:4. [Google Scholar]
- Shin, H.J.; Lee, D.G.; Cha, Y.H.; Hong, K.H.; Nam, C.H. Generation of nonadiabatic blueshift of high harmonics in an intense femtosecond laser field. Phys. Rev. Lett. 1999, 83, 2544–2547. [Google Scholar]
- Wahlström, C.G.; Larsson, J.; Persson, A.; Starczewski, T.; Svanberg, S.; Salières, P.; Balcou, P.; L’Huillier, A. High-order harmonic generation in rare gases with an intense short-pulse laser. Phys. Rev. A 1993, 48, 4709–4720. [Google Scholar] [CrossRef]
- Singhal, H.; Arora, V.; Naik, P.A.; Gupta, P.D. Spectral blueshifts in laser light scattered from argon-gas-cluster plasmas. Phys. Rev. A 2005, 72, 043201:1–043201:7. [Google Scholar]
- Geissler, M.; Tempea, G.; Brabec, T. Phase-matched high-order harmonic generation in the nonadiabatic limit. Phys. Rev. A 2000, 62, 033817:1–033817:8. [Google Scholar]
- Watson, J.B.; Sanpera, A.; Burnett, K. Pulse-shape effects and blueshifting in the single-atom harmonic generation from neutral species and ions. Phys. Rev. A 1995, 51, 1458–1463. [Google Scholar] [CrossRef]
- Kan, C.; Capjack, C.E.; Rankin, R.; Burnett, N.H. Spectral and temporal structure in high harmonic emission from ionizing atomic gases. Phys. Rev. A 1995, 52, R4336–R4339. [Google Scholar]
- Rae, S.C.; Burnett, K. Detailed simulations of plasma-induced spectral blueshifting. Phys. Rev. A 1992, 46, 1084–1090. [Google Scholar]
- Shin, H.J.; Lee, D.G.; Cha, Y.H.; Kim, J.H.; Hong, K.H.; Nam, C.H. Nonadiabatic blueshift of high-order harmonics from Ar and Ne atoms in an intense femtosecond laser field. Phys. Rev. A 2001, 63, 053407:1–053407:9. [Google Scholar]
- Bian, X.B.; Bandrauk, A.D. Multichannel molecular high-order harmonic generation from asymmetric diatomic molecules. Phys. Rev. Lett. 2010, 105, 093903:1–093903:4. [Google Scholar]
- Bian, X.B.; Bandrauk, A.D. Phase control of multichannel molecular high-order harmonic generation by the asymmetric diatomic molecule HeH2+ in two-color laser fields. Phys. Rev. A 2011, 83, 023414:1–023414:7. [Google Scholar]
- Bian, X.-B.; Bandrauk, A.D. Orientation dependence of nonadiabatic molecular high-order-harmonic generation from resonant polar molecules. Phys. Rev. A 2012, 86, 053417:1–053417:5. [Google Scholar]
- Ben-Itzhak, I.; Gertner, I.; Heber, O.; Rosner, B. Experimental evidence for the existence of the 2pσ bound state of HeH2+ and its decay mechanism. Phys. Rev. Lett. 1993, 71, 1347–1350. [Google Scholar] [CrossRef]
- Bandrauk, A.D.; Chelkowski, S.; Diestler, D.J.; Manz, J.; Yuan, K.J. Quantum simulation of high-order harmonic spectra of the hydrogen atom. Phys. Rev. A 2009, 79, 023403:1–023403:14. [Google Scholar]
- Antoine, P.; Piraux, B.; Maquet, A. Time profile of harmonics generated by a single atom in a strong electromagnetic field. Phys. Rev. A 1995, 51, R1750–R1753. [Google Scholar]
- Chandre, C.; Wiggins, S.; Uzer, T. Time–frequency analysis of chaotic systems. Physica D 2003, 181, 171–196. [Google Scholar] [CrossRef]
- Ganeev, R.A.; Witting, T.; Hutchison, C.; Frank, F.; Tudorovskaya, M.; Lein, M.; Okell, W.A.; Zaïr, A.; Marangos, J.P.; Tisch, J.W.G. Isolated sub-fs XUV pulse generation in Mn plasma ablation. Opt. Express 2012, 20, 25239–25248. [Google Scholar] [CrossRef]
- Strelkov, V. Role of autoionizing state in resonant high-order harmonic generation and attosecond pulse production. Phys. Rev. Lett. 2010, 104, 123901:1–123901:4. [Google Scholar] [CrossRef]
- Hostetter, J.A.; Tate, J.L.; Schafer, K.J.; Gaarde, M.B. Semiclassical approaches to below-threshold harmonics. Phys. Rev. A 2010, 82, 023401:1–023401:8. [Google Scholar]
- Kamta, G.L.; Bandrauk, A.D. Effects of molecular symmetry on enhanced ionization by intense laser pulses. Phys. Rev. A 2007, 75, 041401:1–041401:4. [Google Scholar]
- Kamta, G.L.; Bandrauk, A.D. Nonsymmetric molecules driven by intense few-cycle laser pulses: Phase and orientation dependence of enhanced ionization. Phys. Rev. A 2007, 76, 053409:1–053409:15. [Google Scholar]
- Milošević, D.B. Resonant high-order harmonic generation from plasma ablation: Laser intensity dependence of the harmonic intensity and phase. Phys. Rev. A 2010, 81, 023802:1–023802:7. [Google Scholar]
- Ganeev, R.A.; Suzuki, M.; Baba, M.; Kuroda, H.; Ozaki, T. Strong resonance enhancement of a single harmonic generated in the extreme ultraviolet range. Opt. Lett. 2006, 31, 1699–1701. [Google Scholar]
- Schultze, M.; Fieß, M.; Karpowicz, N.; Gagnon, J.; Korbman, M.; Hofstetter, M.; Neppl, S.; Cavalieri, A.L.; Komninos, Y.; Mercouris, T.; et al. Delay in photoemission. Science 2010, 328, 1658–1662. [Google Scholar] [CrossRef]
- Klünder, K.; Dahlström, J.M.; Gisselbrecht, M.; Fordell, T.; Swoboda, M.; Guénot, D.; Johnsson, P.; Caillat, J.; Mauritsson, J.; Maquet, A.; et al. Probing single-photon ionization on the attosecond time scale. Phys. Rev. Lett. 2011, 106, 143002:1–143002:4. [Google Scholar]
- Neppl, S.; Ernstorfer, R.; Bothschafter, E.M.; Cavalieri, A.L.; Menzel, D.; Barth, J.V.; Krausz, F.; Kienberger, R.; Feulner, P. Attosecond time-resolved photoemission from core and valence states of magnesium. Phys. Rev. Lett. 2012, 109, 087401:1–087401:5. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Bian, X.-B.; Bandrauk, A.D. Spectral Shifts of Nonadiabatic High-Order Harmonic Generation. Appl. Sci. 2013, 3, 267-277. https://doi.org/10.3390/app3010267
Bian X-B, Bandrauk AD. Spectral Shifts of Nonadiabatic High-Order Harmonic Generation. Applied Sciences. 2013; 3(1):267-277. https://doi.org/10.3390/app3010267
Chicago/Turabian StyleBian, Xue-Bin, and André D. Bandrauk. 2013. "Spectral Shifts of Nonadiabatic High-Order Harmonic Generation" Applied Sciences 3, no. 1: 267-277. https://doi.org/10.3390/app3010267