Intra- and Interlayer Electron-Phonon Interactions in 12/12C and 12/13C BiLayer Graphene
Abstract
:1. Introduction
2. Interlayer Interactions
2.1. AB Stacked Bilayer Graphene
2.2. Twisted Systems
3. Electron-Phonon Interactions: Theoretical Background
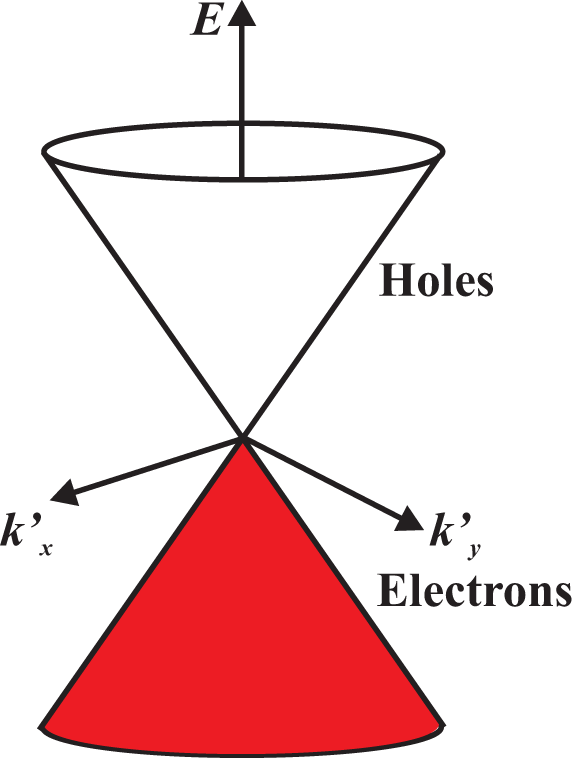
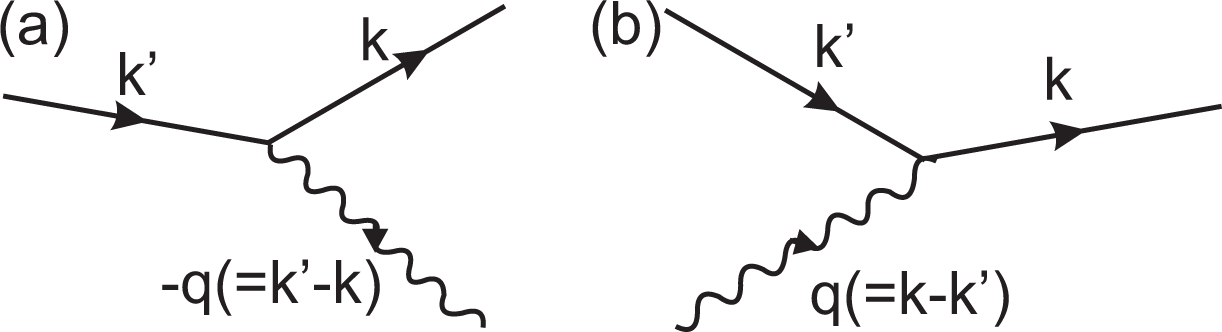
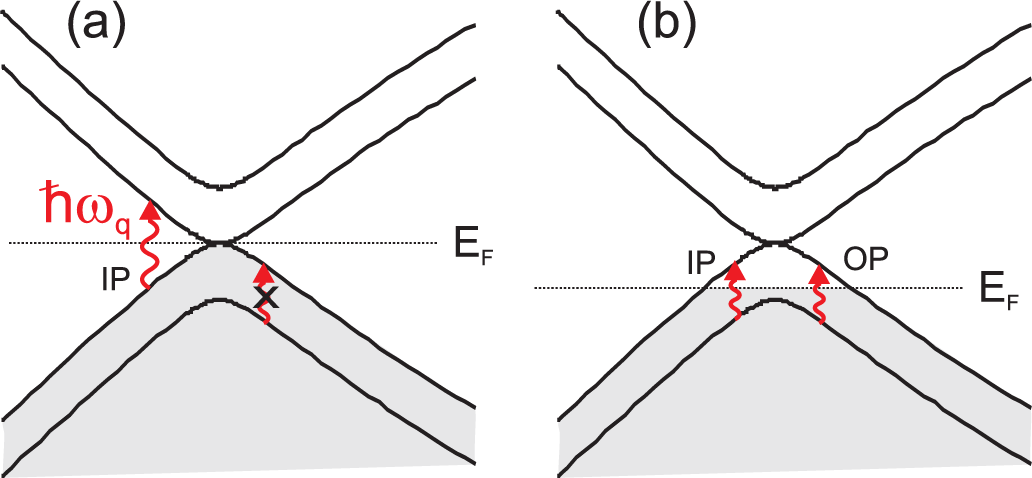
3.1. The Fröhlich Hamiltonian
3.2. Phonon Frequencies and the Kohn Anomaly
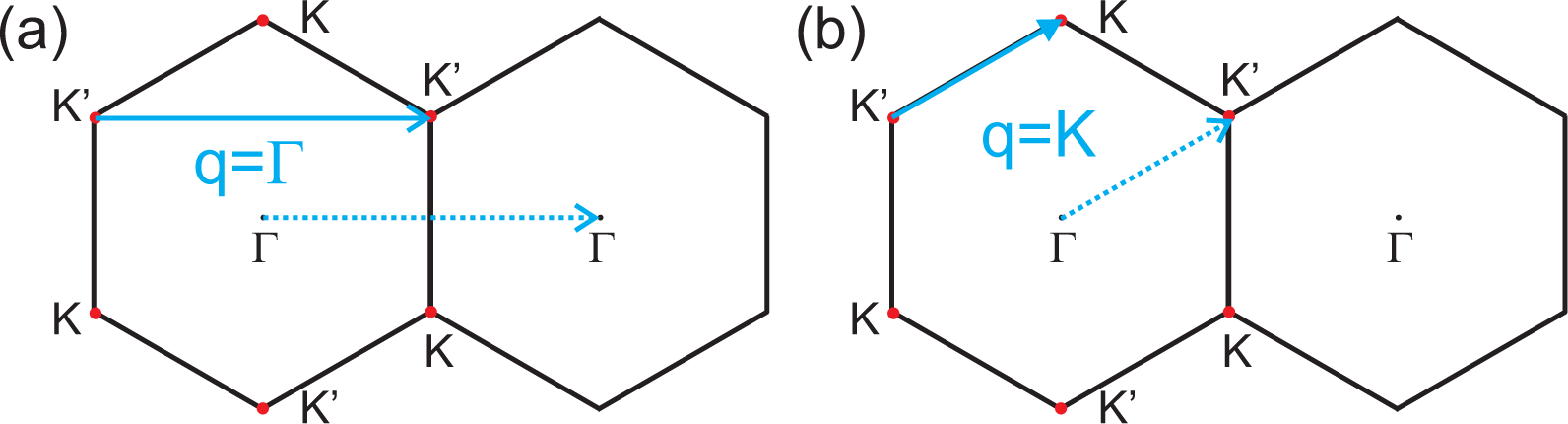
3.3. Consequences of the Kohn Anomaly in Graphene
4. Inversion Symmetry in 2LG Systems
5. Intra- and Inter-Layer Phonon Energy Renormalizations
5.1. Interlayer-Related Phonons in 2LG
5.2. Isotopes
6. Final Remarks
Acknowledgments
Conflicts of Interest
References
- Heinonen, O.; Taylor, P.L. A Quantum Approach to Condensed Matter Physics; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Bonaccorso, F.; Sun, Z.; Hasan, T.; Ferrari, A.C. Graphene photonics and optoelectronics. Nat. Photon. 2010, 4, 611. [Google Scholar]
- Neto, A.H.C.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar]
- Stankovich, S.; Dikin, D.A.; Dommett, G.H.B.; Kohlhaas, K.M.; Zimney, E.J.; Stach, E.A.; Piner, R.D.; Nguyen, S.T.; Ruoff, R.S. Graphene-based composite materials. Nature 2006, 442, 282. [Google Scholar]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197. [Google Scholar]
- Zhang, Y.; Tan, Y.W.; Stormer, H.L.; Kim, P. Experimental observation of the quantum hall effect and Berry’s phase in graphene. Nature 2005, 438, 201. [Google Scholar]
- Kim, K.S.; Zhao, Y.; Jang, H.; Lee, S.Y.; Kim, J.M.; Ahn, J.H.; Kim, P.; Choi, J.Y.; Hong, B.H. Large-scale pattern growth of graphene films for stretchable transparent electrodes. Nature 2009, 457, 706. [Google Scholar]
- Bae, S.; Kim, H.; Lee, Y.; Xu, X.; Park, J.S.; Zheng, Y.; Balakrishnan, J.; Lei, T.; Kim, H.R.; Song, Y.I.; et al. Roll-to-roll production of 30-inch graphene films for transparent electrodes. Nat. Nanotechnol. 2010, 5, 574. [Google Scholar]
- Kuzmenko, A.B.; van Heumen, E.; van der Marel, D.; Lerch, P.; Blake, P.; Novoselov, K.S.; Geim, A.K. Infrared spectroscopy of electronic bands in bilayer graphene. Phys. Rev. B. 2009, 79, 115441. [Google Scholar]
- Gava, P.; Lazzeri, M.; Saitta, A.M.; Mauri, F. Ab initio study of gap opening and screening effects in gated bilayer graphene. Phys. Rev. B. 2009, 79, 165431. [Google Scholar]
- Fang, W.J.; Hsu, A.L.; Caudillo, R.; Song, Y.; Birdwell, A.G.; Zakar, E.; Kalbac, M.; Dubey, M.; Palacios, T.; Dresselhaus, M.S.; et al. Rapid identification of stacking orientation in isotopically labeled chemical-vapor grown bilayer graphene by Raman spectroscopy. Nano Lett 2013, 13, 1541–1548. [Google Scholar]
- Lemme, M.C.; Koppens, F.H.L.; Falk, A.L.; Rudner, M.S.; Park, H.; Levitov, L.S.; Marcus, C.M. Gate-activated photoresponse in a graphene p-n junction. Nano Lett 2011, 11, 4134–4137. [Google Scholar]
- Lui, C.H.; Li, Z.; Mak, K.F.; Cappelluti, E.; Heinz, T.F. Observation of an electrically tunable band gap in trilayer graphene. Nat. Phys. 2011, 7, 944–947. [Google Scholar]
- Lui, C.H.; Malard, L.M.; Kim, S.; Lantz, G.; Laverge, F.E.; Saito, R.; Heinz, T.F. Observation of out-of-plane vibrations in few-layer graphene. Nano Lett 2012, 12, 5539–5544. [Google Scholar]
- Tunable Phonon-Induced Transparency in Bilayer Graphene Nanoribbons. Available online: http://arxiv.org/abs/1310.4394 accessed on 14 April 2014.
- Tang, T.; Zhang, Y.; Park, C.; Geng, B.; Girit, C.; Hao, Z.; Martin, M.C.; Zettl, A.; Crommie, M.F.; Louie, S.G.; et al. A tunable phonon-exciton Fano system in bilayer graphene. Nat. Nanotechnol. 2010, 5, 32–36. [Google Scholar]
- Kuzmenko, A.B.; Benfatto, L.; Cappelluti, E.; Crassee, I.; van der Marel, D.; Blake, P.; Novoselov, K.S.; Geim, A.K. Gate tunable infrared phonon anomalies in bilayer graphene. Phys. Rev. Lett. 2009, 103, 116804. [Google Scholar]
- Low, T.; Guinea, F.; Yan, H.; Xia, F.; Avouris, P. Novel midinfrared plasmonic properties of bilayer graphene. Phys. Rev. Lett. 2014, 112, 116801. [Google Scholar]
- Zhang, L.M.; Li, Z.Q.; Basov, D.N.; Fogler, M.M.; Hao, Z.; Martin, M.C. Determination of the electronic structure of bilayer graphene from infrared spectroscopy. Phys. Rev. B. 2008, 78, 235408. [Google Scholar]
- Kuzmenko, A.B.; Crassee, I.; van der Marel, D.; Blake, P.; Novoselov, K.S. Determination of the gate-tunable band gap and tight-binding parameters in bilayer graphene using infrared spectroscopy. Phys. Rev. B. 2009, 80, 165406. [Google Scholar]
- Sato, K.; Park, J.S.; Saito, R.; Cong, C.; Yu, T.; Lui, C.H.; Heinz, T.; Dresselhaus, G.; Dresselhaus, M.S. Raman spectra of out-of-plane phonons in bilayer graphene. Phys. Rev. B. 2011, 84, 035419. [Google Scholar]
- Kitipornchai, S.; He, X.Q.; Liew, K.M. Continuum model for the vibration of multilayered graphene sheets. Phys. Rev. B. 2005, 72, 075443. [Google Scholar]
- Saha, S.K.; Waghmare, U.V.; Krishnamurthy, H.R.; Sood, A.K. Phonons in few-layer graphene and interplanar interaction: A first-principles study. Phys. Rev. B. 2008, 78, 165421. [Google Scholar]
- Yan, J.-A.; Ruan, W.Y.; Chou, M.Y. Phonon dispersions and vibrational properties of monolayer, bilayer, and trilayer graphene: Density-functional perturbation theory. Phys. Rev. B. 2008, 77, 125401. [Google Scholar]
- Jiang, J.-W.; Tang, H.; Wang, B.-S.; Su, Z.-B. Raman and infrared properties and layer dependence of the phonon dispersions in multilayered graphene. Phys. Rev. B. 2008, 77, 235421. [Google Scholar]
- Zhao, Y.; Luo, X.; Li, H.; Zhang, J.; Araujo, P.T.; Gan, C.K.; Wu, J.; Zhang, H.; Quek, S.Y.; Dresselhaus, M.S.; et al. Interlayer breathing and shear modes in few-trilayer MoS2 and WSe2. Nano Lett. 2013, 13, 1007. [Google Scholar]
- Osada, M.; Sasaki, T. Two-dimensional dielectric nanosheets: Novel nanoelectronics from nanocrystal building blocks. Adv. Mater. 2012, 24, 210. [Google Scholar]
- Geim, A.K.; Grigorieva, I.V. van der Waals heterostructures. Nature 2013, 499, 419. [Google Scholar]
- Chakraborty, B.; Bera, A.; Muthu, D.V.S.; Bhowmick, S.; Waghmare, U.V.; Sood, A.K. Symmetry-dependent phonon renormalization in monolayer MoS2 transistor. Phys. Rev. B. 2012, 85, 161403(R). [Google Scholar]
- Lazzeri, M.; Mauri, F. Nonadiabatic Kohn anomaly in a doped graphene monolayer. Phys. Rev. Lett. 2006, 97, 266407. [Google Scholar]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183. [Google Scholar]
- Dresselhaus, M.S.; Saito, R.; Dresselhaus, G. Physical Properties of Carbon Nanotubes; Imperial College Press: London, UK, 1998. [Google Scholar]
- Yan, J.; Ruan, W.Y.; Chou, M.Y. Phonon dispersions and vibrational properties of monolayer, bilayer, and trilayer graphene: Density-functional perturbation theory. Phys. Rev. B. 2008, 77, 125401. [Google Scholar]
- Michel, K.H.; Verberck, B. Theory of the evolution of phonon spectra and elastic constants from graphene to graphite. Phys. Rev. B. 2008, 78, 085424. [Google Scholar]
- Wallace, P.R. The band theory of graphite. Phys. Rev. 1947, 71, 622. [Google Scholar]
- McClure, J.W. Band structure of graphite and de haas-van alphen effect. Phys. Rev. 1957, 108, 612. [Google Scholar]
- Slonczewski, J.C.; Weiss, P.R. Band structure of graphite. Phys. Rev. 1958, 109, 272. [Google Scholar]
- Partoens, B.; Peeters, F.M. From graphene to graphite: Electronic structure around the K point. Phys. Rev. B. 2006, 74, 075404. [Google Scholar]
- McCann, E. Asymmetry gap in the electronic band structure of bilayer graphene. Phys. Rev. B. 2006, 74, 161403. [Google Scholar]
- Malard, L.M.; Nilsson, J.; Elias, D.C.; Brant, J.C.; Plentz, F.; Alves, E.S.; Neto, A.H.C.; Pimenta, M.A. Probing the electronic structure of bilayer graphene by Raman scattering. Phys. Rev. B. 2007, 76, 201401(R). [Google Scholar]
- Wu, Y.P.; Chou, H.; Ji, H.; Wu, Q.; Chen, S.; Jiang, W.; Hao, Y.; Kang, J.; Ren, Y.; Piner, R.D.; et al. Growth mechanism and controlled synthesis of AB-stacked bilayer graphene on Cu-Ni alloy foils. Acs Nano 2012, 6, 7731–7738. [Google Scholar]
- Liu, L.; Zhou, H.; Cheng, R.; Yu, W.J.; Liu, Y.; Chen, Y.; Shaw, J.; Zhong, X.; Huang, Y.; Duan, X. High-yield chemical vapor deposition growth of high-quality large-area AB-stacked bilayer graphene. Acs Nano 2012, 6, 8241–8249. [Google Scholar]
- Malard, L.M.; Pimenta, M.A.; Dresselhaus, G.; Dresselhaus, M.S. Raman spectroscopy in graphene. Phys. Rep. 2009, 473, 51–87. [Google Scholar]
- Latil, S.; Meunier, V.; Henrard, L. Massless fermions in multilayer graphitic systems with misoriented layers: Ab initio calculations and experimental fingerprints. Phys. Rev. B. 2007, 76, 201402(R). [Google Scholar]
- Trambly de Laissardière, G.; Mayou, D.; Magaud, L. Localization of dirac electrons in rotated graphene bilayers. Nano Lett 2010, 10, 804–808. [Google Scholar]
- Luican, A.; Li, G.; Reina, A.; Kong, J.; Nair, R.R.; Novoselov, K.S.; Geim, A.K.; Andrei, E.Y. Single-layer behavior and its breakdown in twisted graphene layers. Phys. Rev. Lett. 2011, 106, 126802. [Google Scholar]
- Hass, J.; Varchon, F.; Millan-Otoya, J.E.; Sprinkle, M.; Sharma, N.; de Heer, W.A.; Berger, C.; First, P.N.; Magaud, L.; Conrad, E.H. Why multilayer graphene on behaves like a single sheet of graphene. Phys. Rev. Lett. 2008, 100, 125504. [Google Scholar]
- Lopes dos Santos, J.M.B.; Peres, N.M.R.; Neto, A.H.C. Graphene bilayer with a twist: Electronic structure. Phys. Rev. Lett. 2007, 99, 256802. [Google Scholar]
- Varchon, F.; Mallet, P.; Magaud, L.; Veuillen, J.-Y. Rotational disorder in few-layer graphene films on 6H-SiC(000-1): A scanning tunneling microscopy study. Phys. Rev. B. 2008, 77, 165415. [Google Scholar]
- Shallcross, S.; Sharma, S.; Pankratov, O.A. Quantum interference at the twist boundary in graphene. Phys. Rev. Lett. 2008, 101, 056803. [Google Scholar]
- Moon, P.; Koshino, M. Energy spectrum and quantum hall effect in twisted bilayer graphene. Phys. Rev. B. 2012, 85, 195458. [Google Scholar]
- Morell, E.S.; Correa, J.D.; Vargas, P.; Pacheco, M.; Barticevic, Z. Flat bands in slightly twisted bilayer graphene: Tight-binding calculations. Phys. Rev. B. 2010, 82, 121407(R). [Google Scholar]
- Kim, K.; Coh, S.; Tan, L.Z.; Regan, W.; Yuk, J.M.; Chatterjee, E.; Crommie, M.F.; Cohen, M.L.; Louie, S.G.; Zettl, A. Raman spectroscopy study of rotated double-layer graphene: Misorientation-angle dependence of electronic structure. Phys. Rev. Lett. 2012, 108, 246103. [Google Scholar]
- Brihuega, I.; Mallet, P.; Gonzalez-Herrero, H.; de Laissardiere, G.T.; Ugeda, M.M.; Magaud, L.; Gomez-Rodriguez, J.M.; Yndurain, F.; Veuillen, J.-Y. Unraveling the intrinsic and robust nature of van Hove singularities in twisted bilayer graphene by scanning tunneling microscopy and theoretical analysis. Phys. Rev. Lett. 2012, 109, 196802. [Google Scholar]
- Yan, W.; Liu, M.; Dou, R.-F.; Meng, L.; Feng, L.; Chu, Z.-D.; Zhang, Y.; Liu, Z.; Nie, J.-C.; He, L. Angle-dependent van hove singularities in a slightly twisted graphene bilayer. Phys. Rev. Lett. 2012, 109, 126801. [Google Scholar]
- Sato, K.; Saito, R.; Cong, C.; Yu, T.; Dresselhaus, M.S. Zone folding effect in Raman G-band intensity of twisted bilayer graphene. Phys. Rev. B. 2012, 86, 125414. [Google Scholar]
- Carozo, V.; Almeida, C.M.; Ferreira, E.H.M.; Cancado, L.G.; Achete, C.A.; Jorio, A. Raman signature of graphene superlattices. Nano Lett. 2011, 11, 4527. [Google Scholar]
- He, R.; Chung, T.; Delaney, C.; Keiser, C.; Jauregui, L.A.; Shand, P.M.; Chancey, C.C.; Wang, Y.; Bao, J.; Chen, Y.P. Observation of low energy Raman modes in twisted bilayer graphene. Nano Lett. 2013, 13, 3594. [Google Scholar]
- Piscanec, S.; Lazzeri, M.; Mauri, F.; Ferrari, A.C.; Robertson, J. Kohn anomalies and electron-phonon interactions in graphite. Phys. Rev. Lett. 2004, 93, 185503. [Google Scholar]
- Araujo, P.T.; Mafra, D.L.; Sato, K.; Saito, R.; Kong, J.; Dresselhaus, M.S. Phonon self-energy corrections to nonzero wave-vector phonon modes in single-layer graphene. Phys. Rev. Lett. 2012, 109, 046801. [Google Scholar]
- Mafra, D.L.; Kong, J.; Sato, K.; Saito, R.; Dresselhaus, M.S.; Araujo, P.T. Using the G′ Raman cross-section to understand the phonon dynamics in bilayer graphene systems. Nano Lett. 2012, 12, 2883. [Google Scholar]
- Mafra, D.L.; Kong, J.; Sato, K.; Saito, R.; Dresselhaus, M.S.; Araujo, P.T. Using gate-modulated Raman scattering and electron-phonon interactions to probe single-layer graphene: A different approach to assign phonon combination modes. Phys. Rev. B. 2012, 86, 195434. [Google Scholar]
- Araujo, P.T.; Mafra, D.L.; Sato, K.; Saito, R.; Kong, J.; Dresselhaus, M.S. Unraveling the interlayer-related phonon self-energy renormalization in bilayer graphene. Nat. Sci. Rep. 2012, 2, 1017. [Google Scholar]
- Saito, R.; Sato, K.; Araujo, P.T.; Mafra, D.L.; Dresselhaus, M.S. Gate modulated Raman spectroscopy of graphene and carbon nanotubes. Solid State Commun 2013, 175–176, 18–34. [Google Scholar]
- Yan, J.; Zhang, Y.; Kim, P.; Pinczuk, A. Electric field effect tuning of electron-phonon coupling in graphene. Phys. Rev. Lett. 2007, 98, 166802. [Google Scholar]
- Yan, J.; Henriksen, E.A.; Kim, P.; Pinczuk, A. Observation of anomalous phonon softening in bilayer graphene. Phys. Rev. Lett. 2008, 101, 136804. [Google Scholar]
- Ohta, T.; Bostwick, A.; Seyller, T.; Horn, K.; Rotenberg, E. Controlling the electronic structure of bilayer graphene. Science 2006, 311, 951. [Google Scholar]
- Malard, L.M.; Guimaraes, M.H.D.; Mafra, D.L.; Mazzoni, M.S.C.; Jorio, A. Group-theory analysis of electrons and phonons in N-layer graphene systems. Phys. Rev. B. 2009, 79, 125426. [Google Scholar]
- Ando, T. Anomaly of optical phonon in bilayer graphene. J. Phys. Soc. Jpn. 2007, 76, 104711. [Google Scholar]
- Malard, L.M.; Elias, D.C.; Alves, E.S.; Pimenta, M.A. Observation of distinct electron-phonon couplings in gated bilayer graphene. Phys. Rev. Lett. 2008, 101, 257401. [Google Scholar]
- Ando, T.; Koshino, M. Field effects on optical phonons in bilayer graphene. J. Phys. Soc. Jpn. 2009, 78, 034709. [Google Scholar]
- Yan, J.; Villarson, T.; Henriksen, E.A.; Kim, P.; Pinczuk, A. Optical phonon mixing in bilayer graphene with a broken inversion symmetry. Phys. Rev. B. 2009, 80, 241417(R). [Google Scholar]
- Kalbac, M.; Farhat, H.; Kong, J.; Janda, P.; Kavan, L.; Dresselhaus, M.S. Raman spectroscopy and in situ Raman spectroelectrochemistry of bi-layer 12c/13c graphene. Nano Lett 2011, 11, 1957–1963. [Google Scholar]
- Kalbac, M.; Kong, J.; Dresselhaus, M.S. Raman spectroscopy as a tool to address individual graphene layers in few-layer graphene. J. Phys. Chem. C. 2012, 116, 19046–19050. [Google Scholar]
- Araujo, P.T.; Frank, O.; Mafra, D.L.; Fang, W.; Kong, J.; Dresselhaus, M.S.; Kalbac, M. Mass-related inversion symmetry breaking and phonon self-energy renormalization in isotopically labeled AB-stacked bilayer graphene. Nat. Sci. Rep. 2013, 3, 2061. [Google Scholar]
- Kalbac, M.; Reina, A.; Farhat, H.; Kong, J.; Kavan, L.; Dresselhaus, M.S. The influence of strong electron and hole doping on the Raman intensity of chemical vapor-deposition graphene. Acs Nano 2010, 4, 6055–6063. [Google Scholar]
- Das, A.; Pisana, S.; Chakraborty, B.; Piscanec, S.; Saha, S.K.; Waghmare, U.V.; Novoselov, K.S.; Krishnamurthy, H.R.; Geim, A.K.; Ferrari, A.C.; et al. Monitoring dopants by raman scattering in an electrochemically top-gated graphene transistor. Nat. Nanotechnol. 2008, 3, 210. [Google Scholar]
- Rodriguez-Nieva, J.F.; Saito, R.; Costa, S.D.; Dresselhaus, M.S. Effect of C-13 isotope doping on the optical phonon modes in graphene: Localization and Raman spectroscopy. Phys. Rev. B. 2012, 85, 245406. [Google Scholar]
- Mafra, D.L.; Gava, P.; Malard, L.M.; Borges, R.S.; Silva, G.G.; Leon, J.A.; Plentz, F.; Mauri, F.; Pimenta, M.A. Characterizing intrinsic charges in top gated bilayer graphene device by Raman spectroscopy. Carbon 2012, 50, 3435–3439. [Google Scholar]
- Das, A.; Chakraborty, B.; Piscanec, S.; Pisana, S.; Sood, A.K.; Ferrari, A.C. Phonon renormalization in doped bilayer graphene. Phys. Rev. B. 2009, 79, 155417. [Google Scholar]
- Bruna, M.; Borini, S. Observation of Raman G-band splitting in top-doped few-layer graphene. Phys. Rev. B. 2010, 81, 125421. [Google Scholar]
- Kalbac, M.; Frank, O.; Kavan, L. The control of graphene double-layer formation in copper-catalyzed chemical vapor deposition. Carbon 2012, 50, 3682–3687. [Google Scholar]
- Subramaniam, D.; Libisch, F.; Li, Y.; Pauly, C.; Geringer, V.; Reiter, R.; Mashoff, T.; Liebmann, M.; Burgdorfer, J.; Busse, C.; et al. Wave-function mapping of graphene quantum dots with soft confinement. Phys. Rev. Lett. 2012, 108, 046801. [Google Scholar]
- Castro, E.V.; Novoselov, K.S.; Morozov, S.V.; Peres, N.M.R.; Lopes dos Santos, J.M.B.; Nilsson, J.; Guinea, F.; Geim, A.K.; Neto, A.H.C. Biased bilayer graphene: Semiconductor with a gap tunable by the electric field effect. Phys. Rev. Lett. 2007, 99, 216802. [Google Scholar]
- Bandow, S.; Rao, A.M.; Sumanasekera, G.U.; Eklund, P.C.; Kokai, F.; Takahashi, K.; Yudasaka, M.; Iijima, S. Evidence for anomalously small charge transfer in doped single-wall carbon nanohorn aggregates with Li, K and Br. Appl. Phys. A. 2000, 71, 561–564. [Google Scholar]
- Li, Q.; Chou, H. Growth of adlayer graphene on Cu studied by carbon isotope labeling. Nano Lett 2013, 13, 486–490. [Google Scholar]
- Kalbac, M.; Green, A.A.; Hersam, M.C.; Kavan, L. Probing charge transfer between shells of double-walled carbon nanotubes sorted by outer-wall electronic type. Chem. Eur. J. 2011, 17, 9806–9815. [Google Scholar]
- Kalbac, M.; Farhat, H.; Kavan, L.; Kong, J.; Sasaki, K.-I.; Saito, R.; Dresselhaus, M.S. Electrochemical charging of individual single-walled carbon nanotubes. Acs Nano 2009, 3, 2320–2328. [Google Scholar]





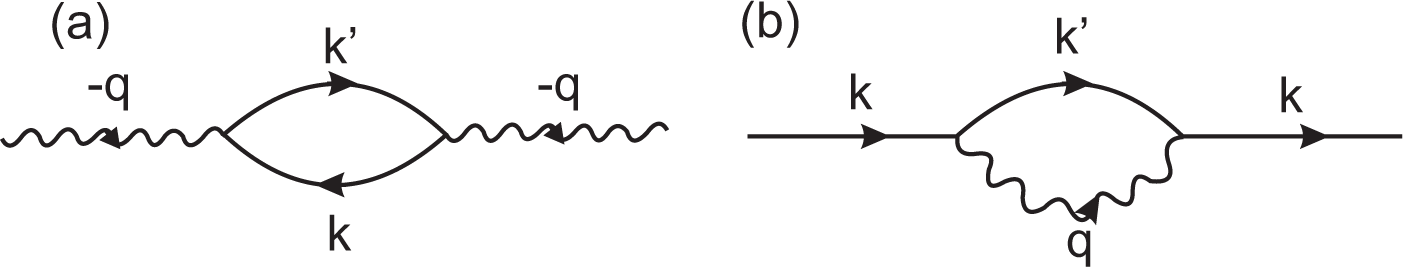








© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Mafra, D.L.; Araujo, P.T. Intra- and Interlayer Electron-Phonon Interactions in 12/12C and 12/13C BiLayer Graphene. Appl. Sci. 2014, 4, 207-239. https://doi.org/10.3390/app4020207
Mafra DL, Araujo PT. Intra- and Interlayer Electron-Phonon Interactions in 12/12C and 12/13C BiLayer Graphene. Applied Sciences. 2014; 4(2):207-239. https://doi.org/10.3390/app4020207
Chicago/Turabian StyleMafra, Daniela L., and Paulo T. Araujo. 2014. "Intra- and Interlayer Electron-Phonon Interactions in 12/12C and 12/13C BiLayer Graphene" Applied Sciences 4, no. 2: 207-239. https://doi.org/10.3390/app4020207




