Wing Geometry and Kinematic Parameters Optimization of Flapping Wing Hovering Flight
Abstract
:1. Introduction
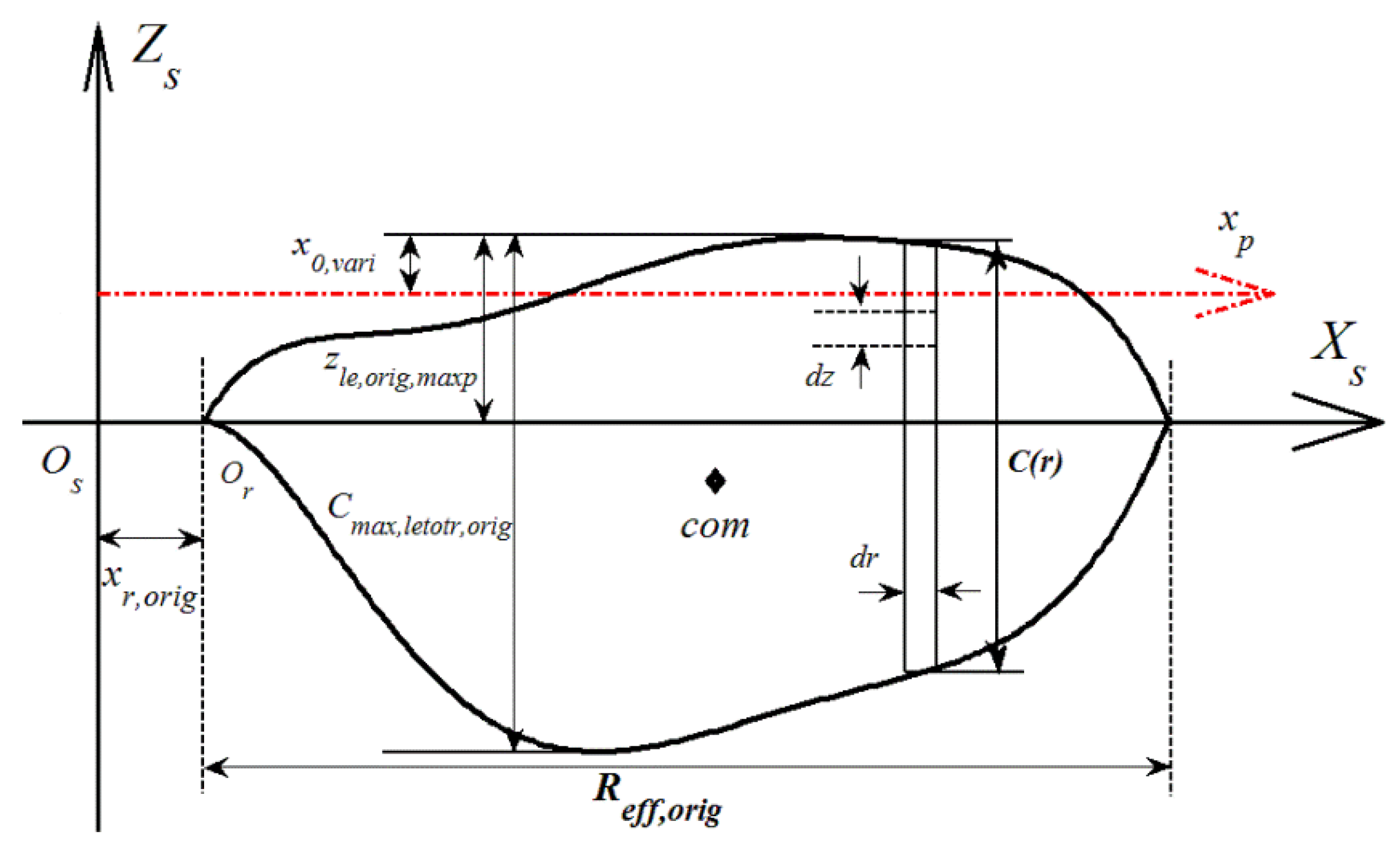
2. Wing Morphological Parametrization
2.1. Description of Wing Morphology
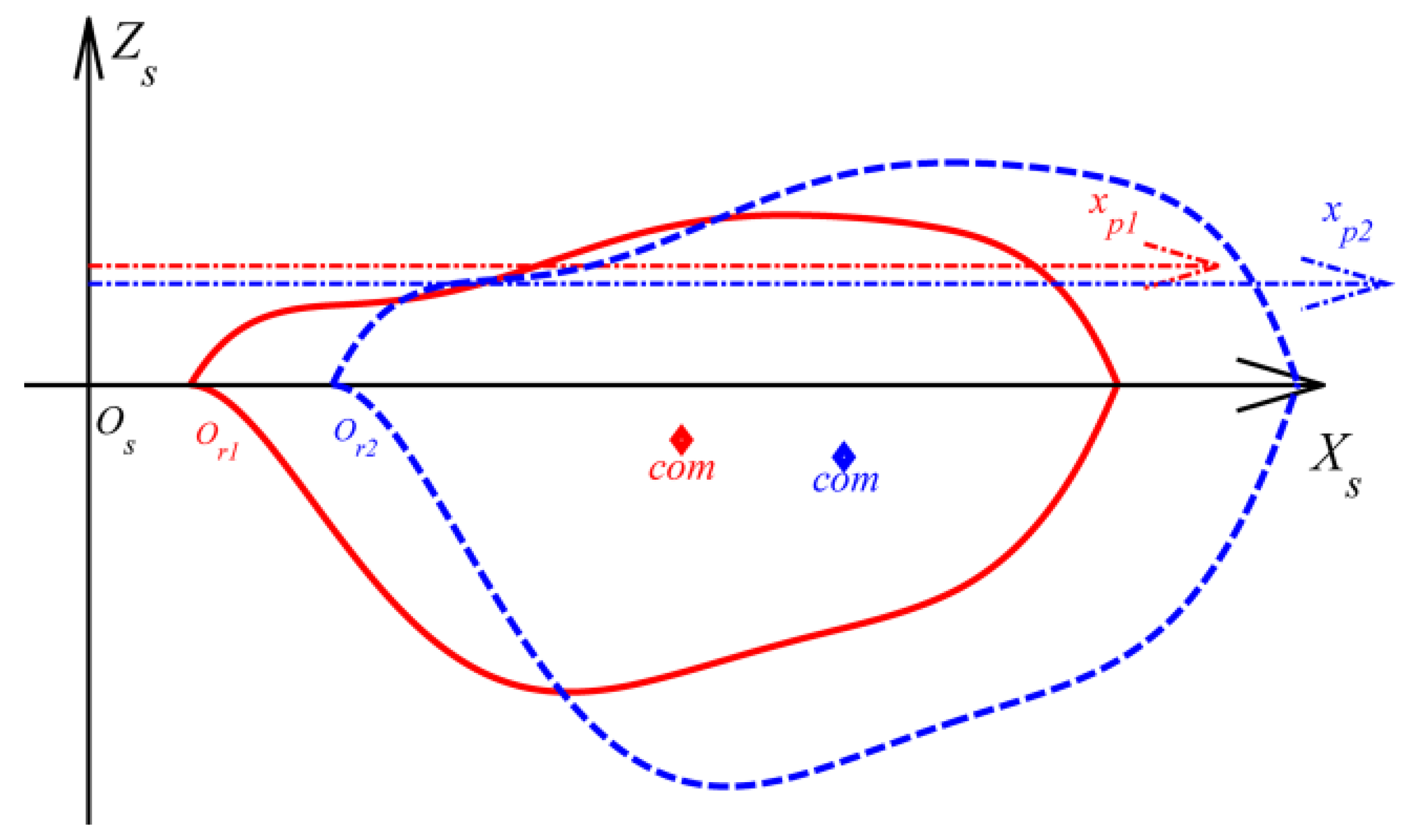
2.2. Non-Dimensional Parametrization of Wing Morphology
2.3. Characterization of Dynamically Scaled Wing
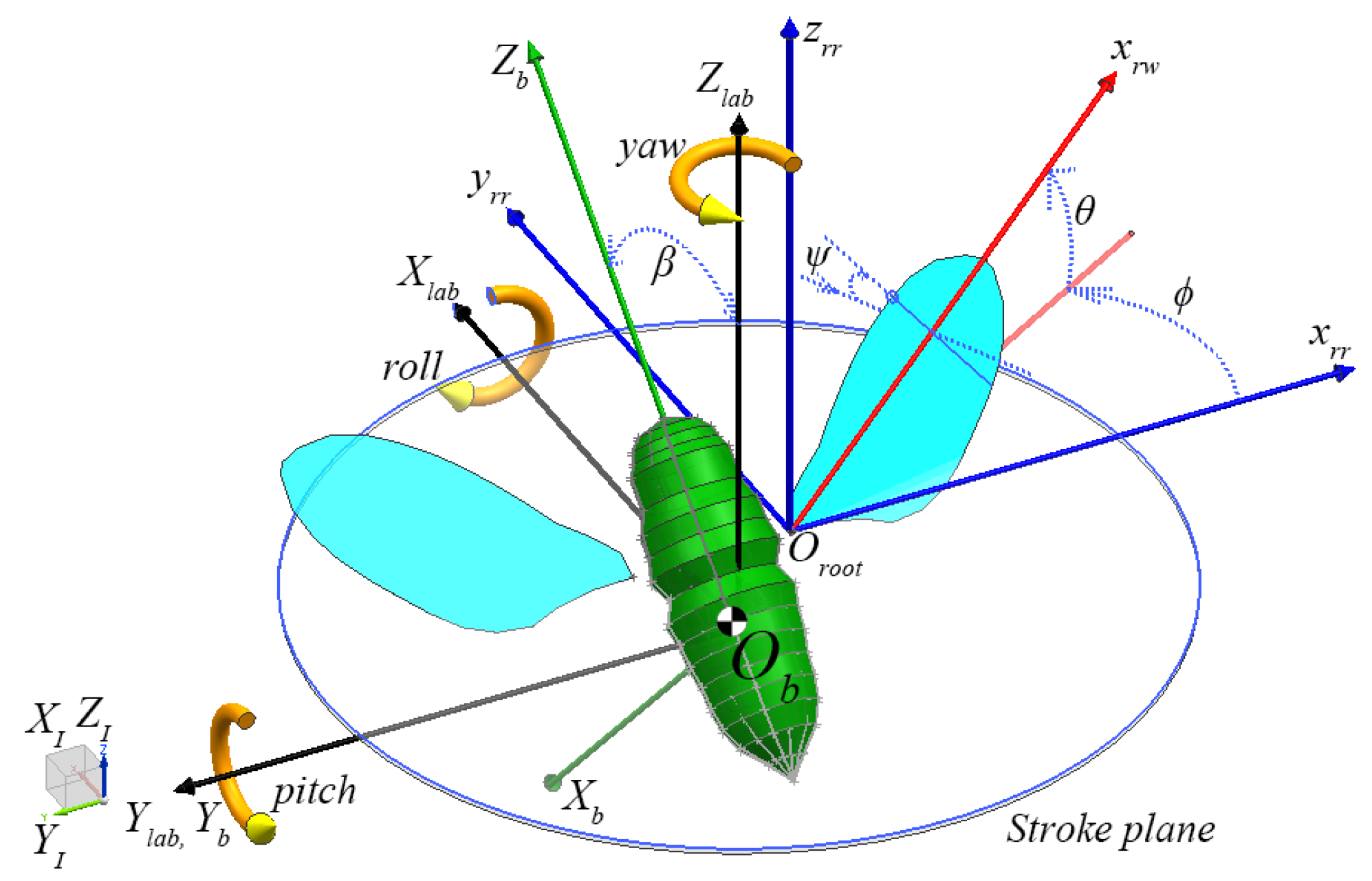
3. Wing Kinematics
4. Extended Quasi-Steady Aerodynamic Model
4.1. Aerodynamic Forces
4.2. Aerodynamic Moments
4.3. Horizontal and Vertical Force in Right Wing Root Frame of Reference
4.4. Aerodynamic Moments in Right Wing Root Frame of Reference
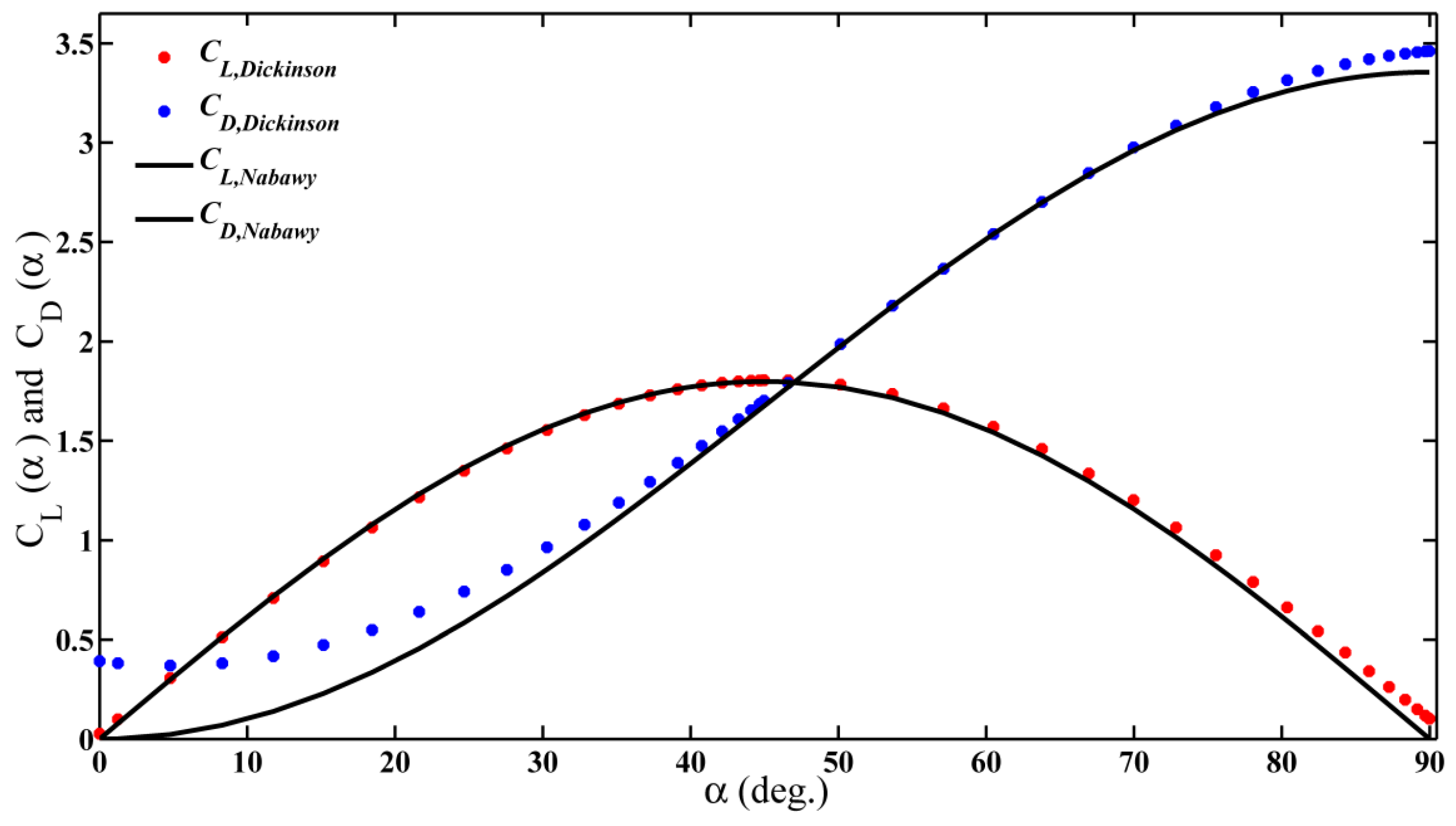
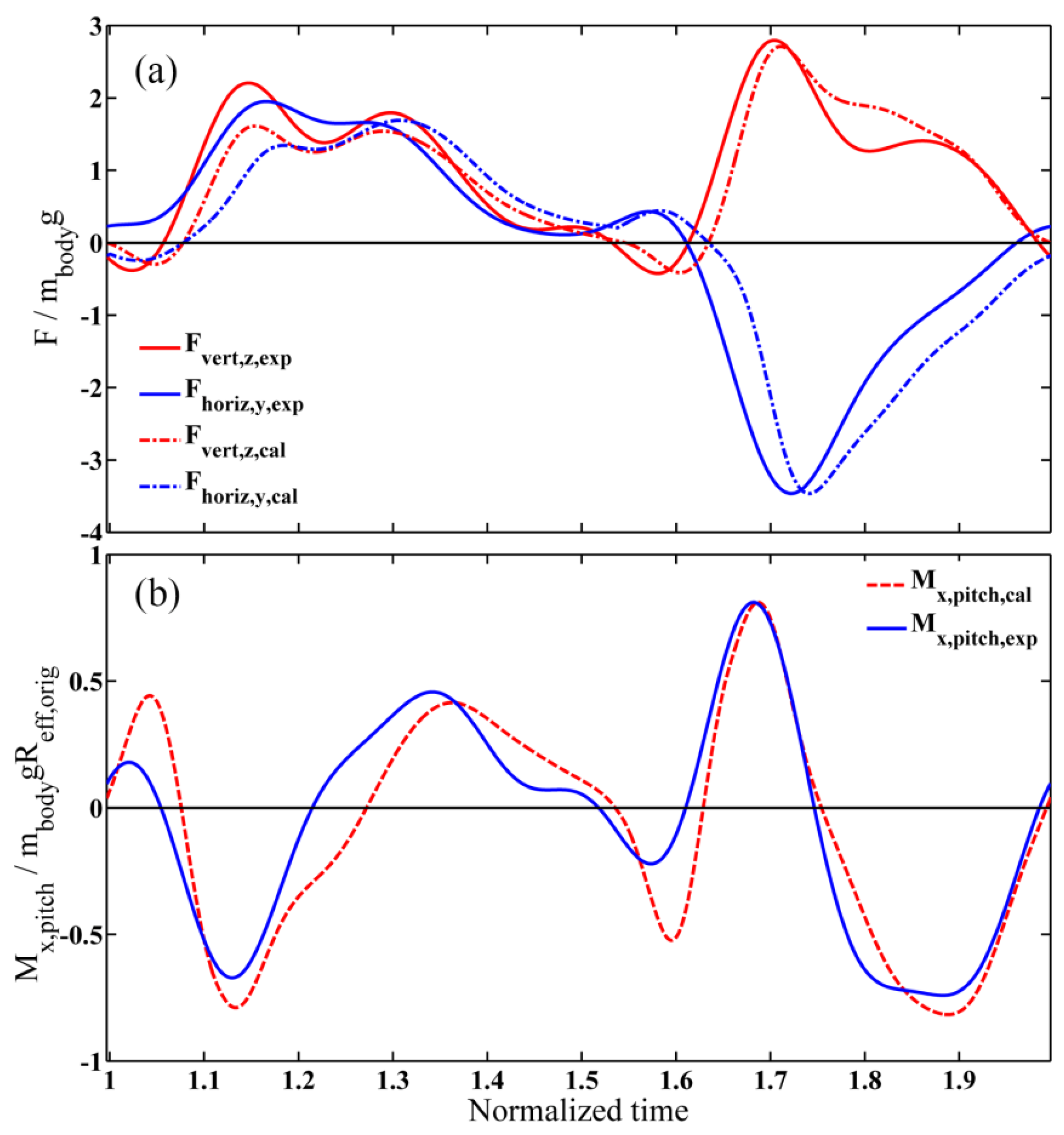
4.5. Verification and Validation
5. Optimization Problem’s Modeling and Formulation
5.1. Power Density Model
5.2. Formulation of the Optimization Problem
6. Optimization Results and Analysis
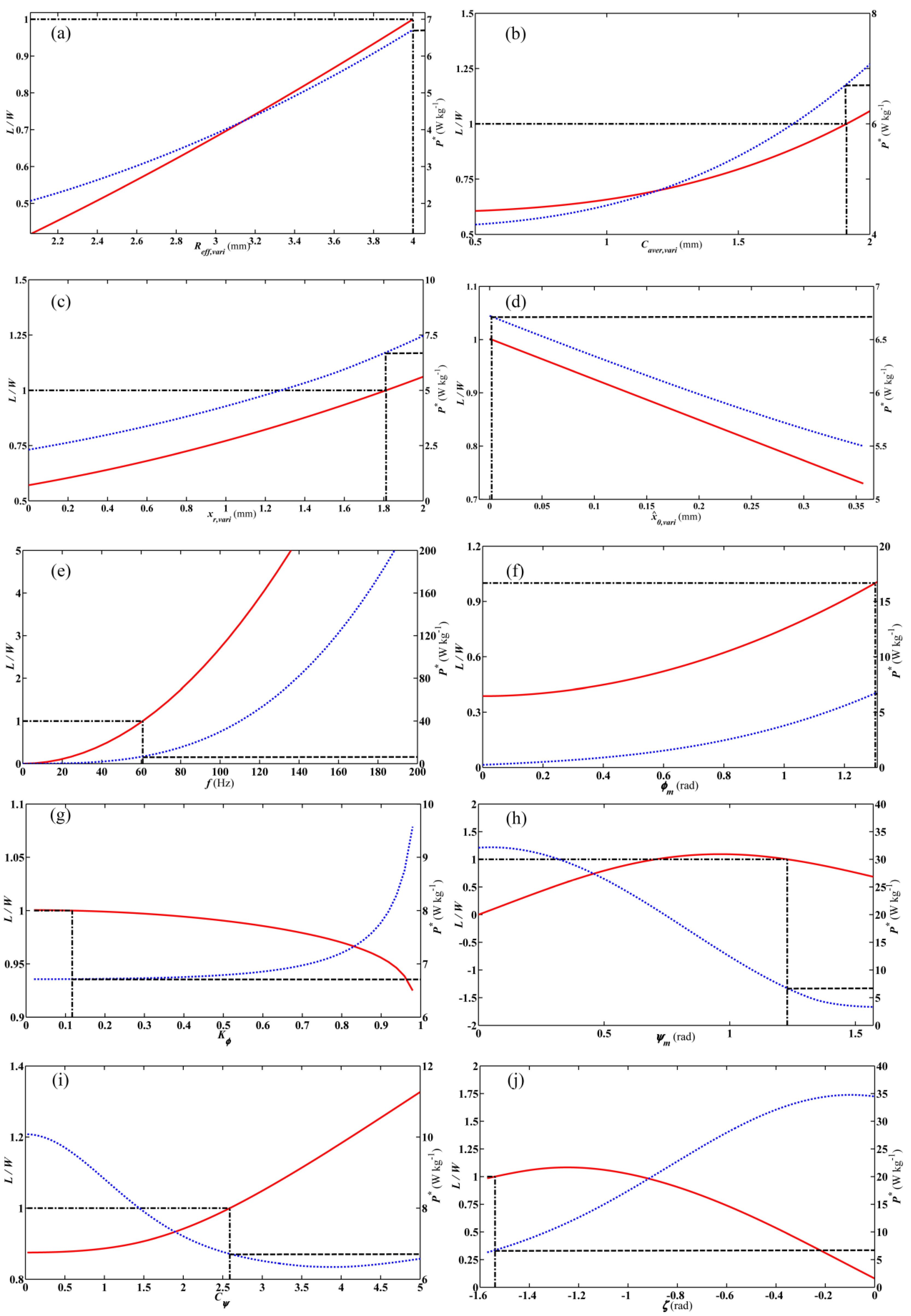
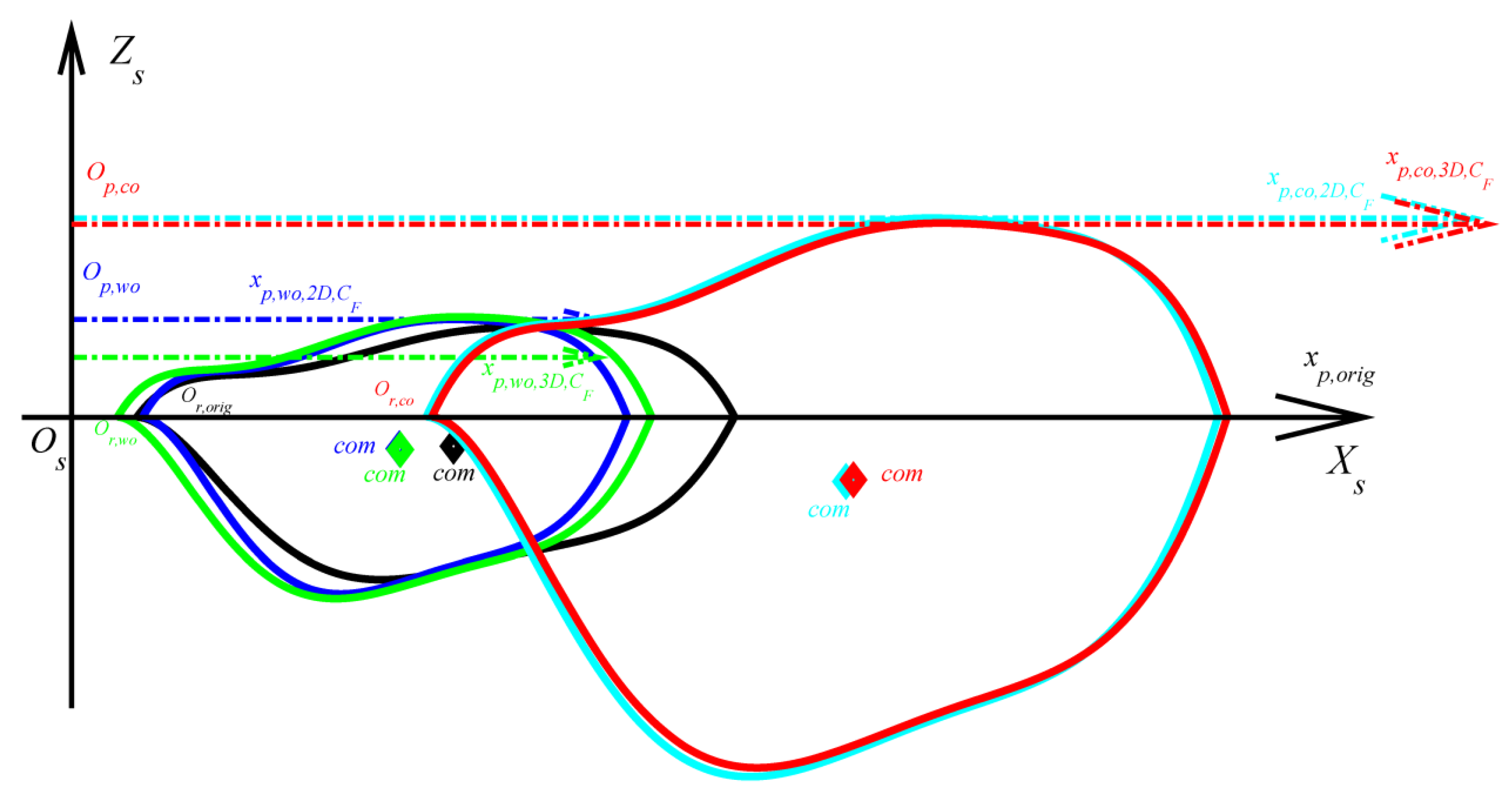
6.1. WGP Optimization Results
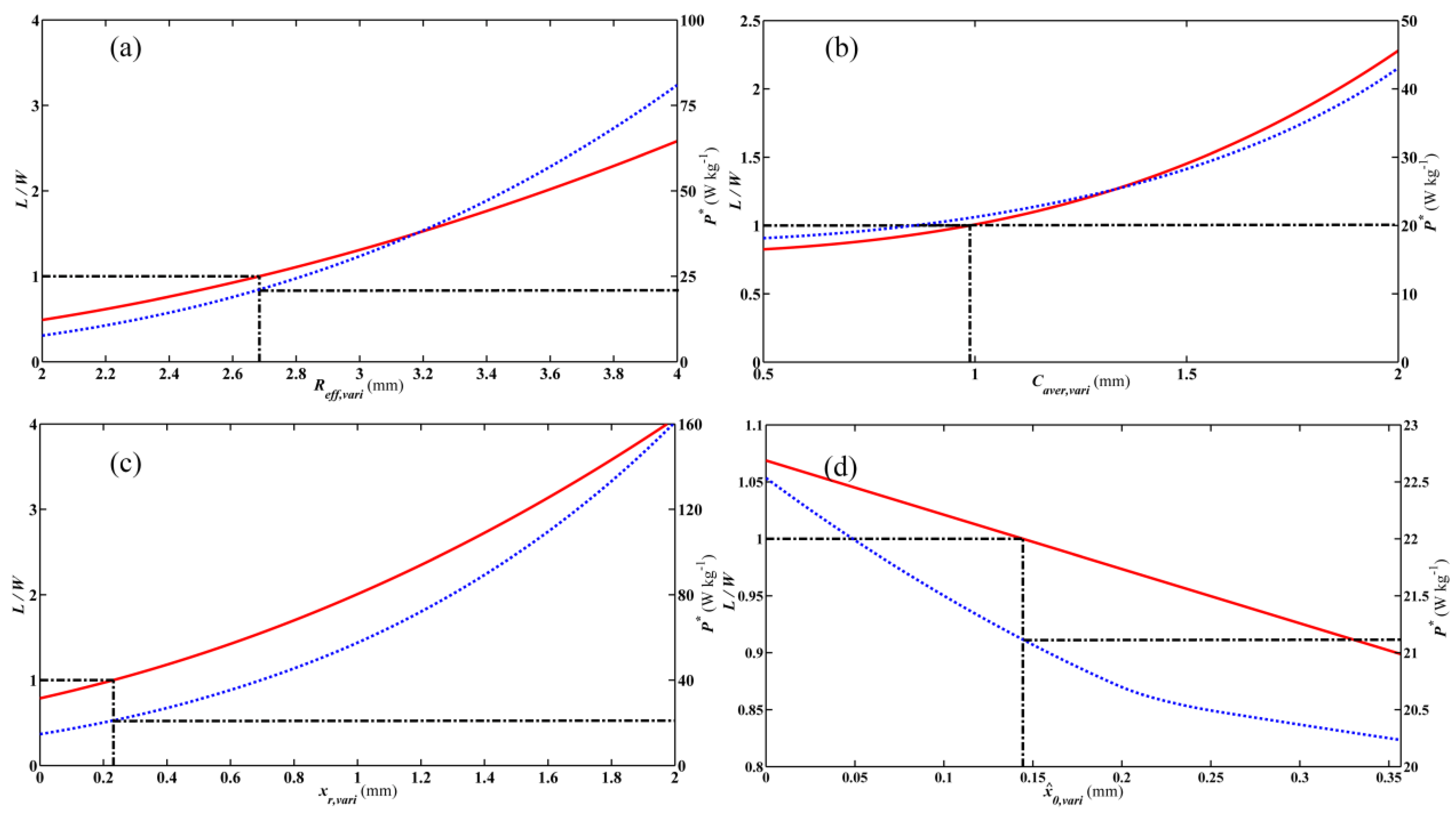
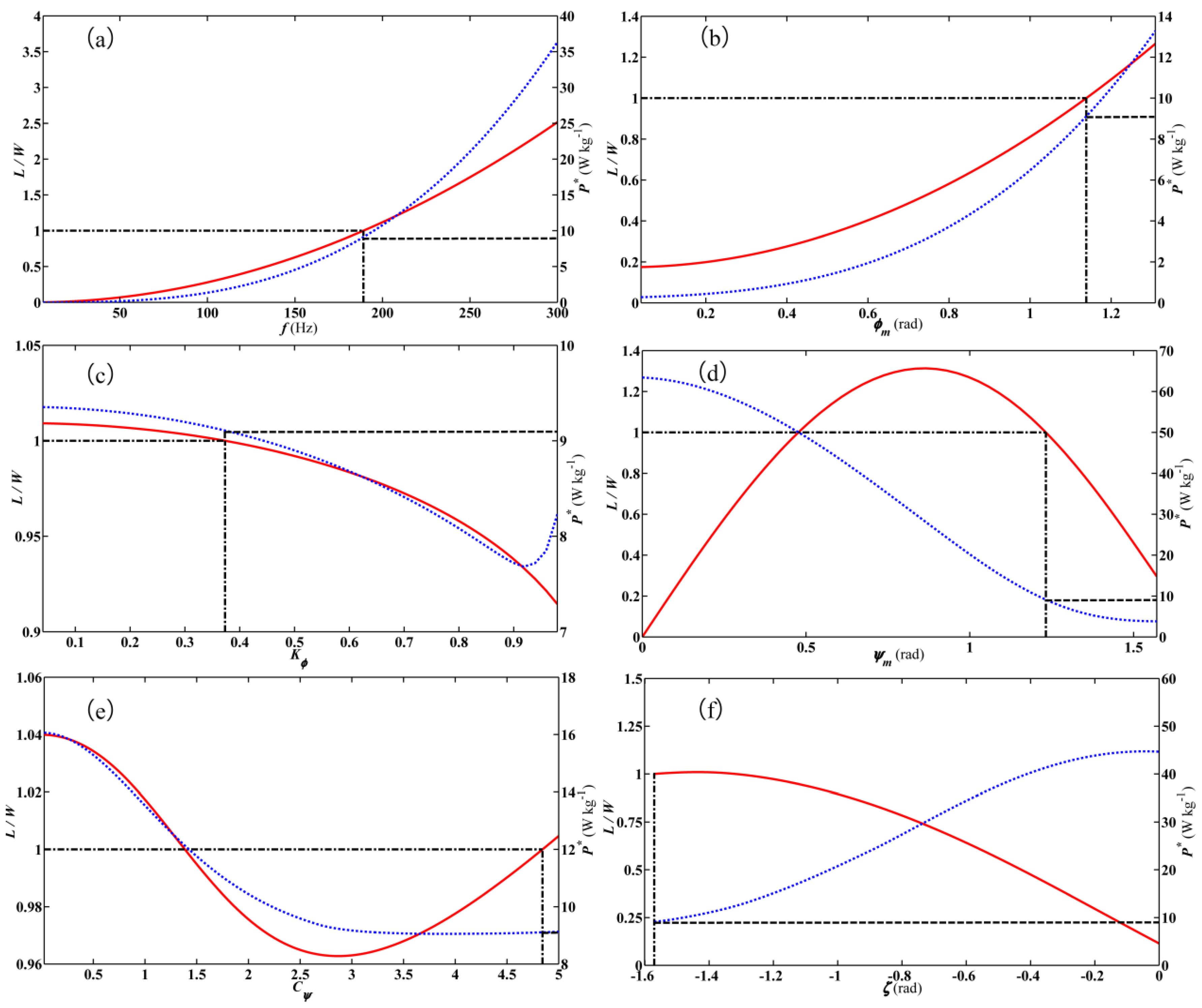
6.2. Sensitivity Analysis for Optimal WGP
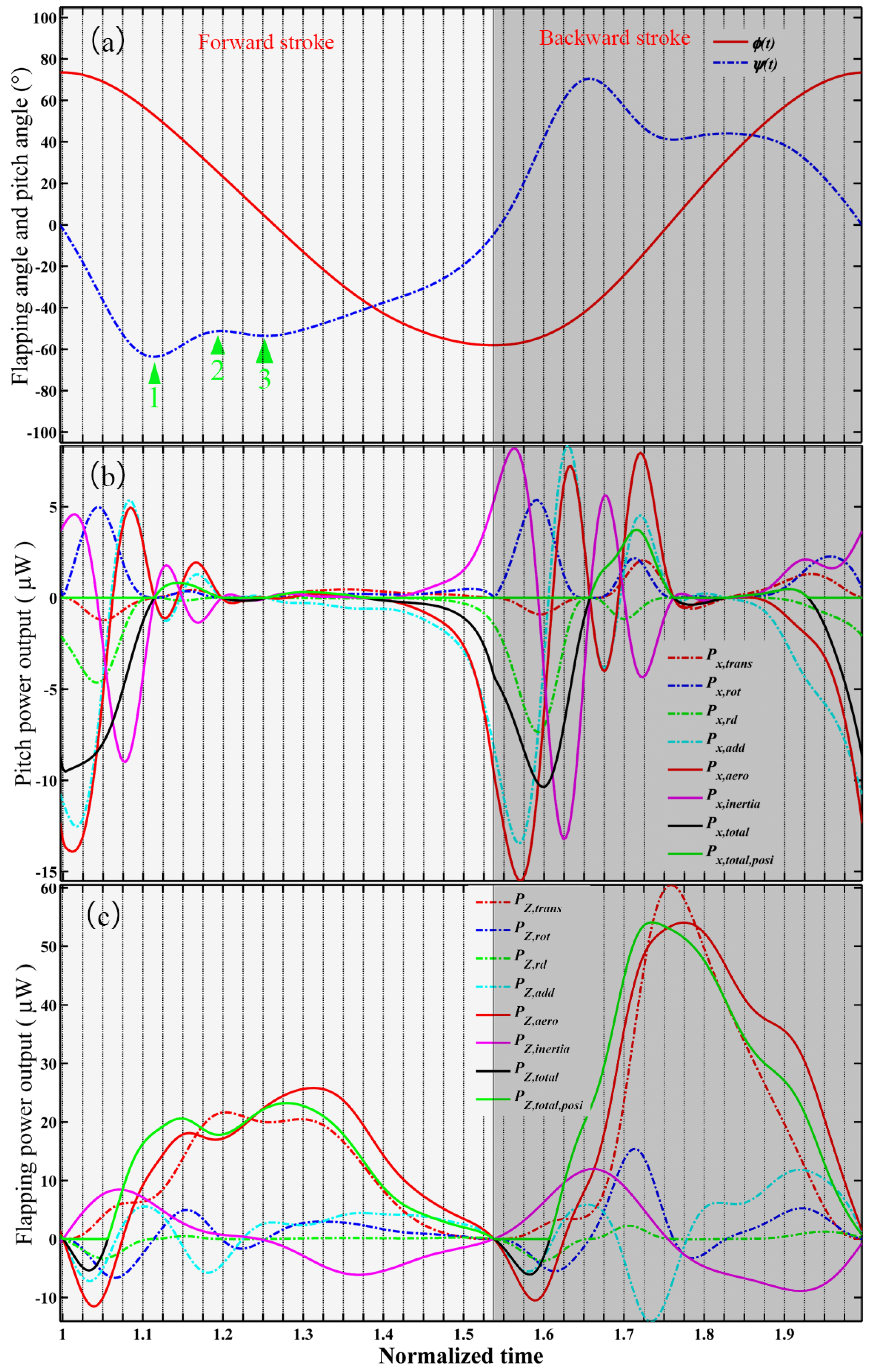
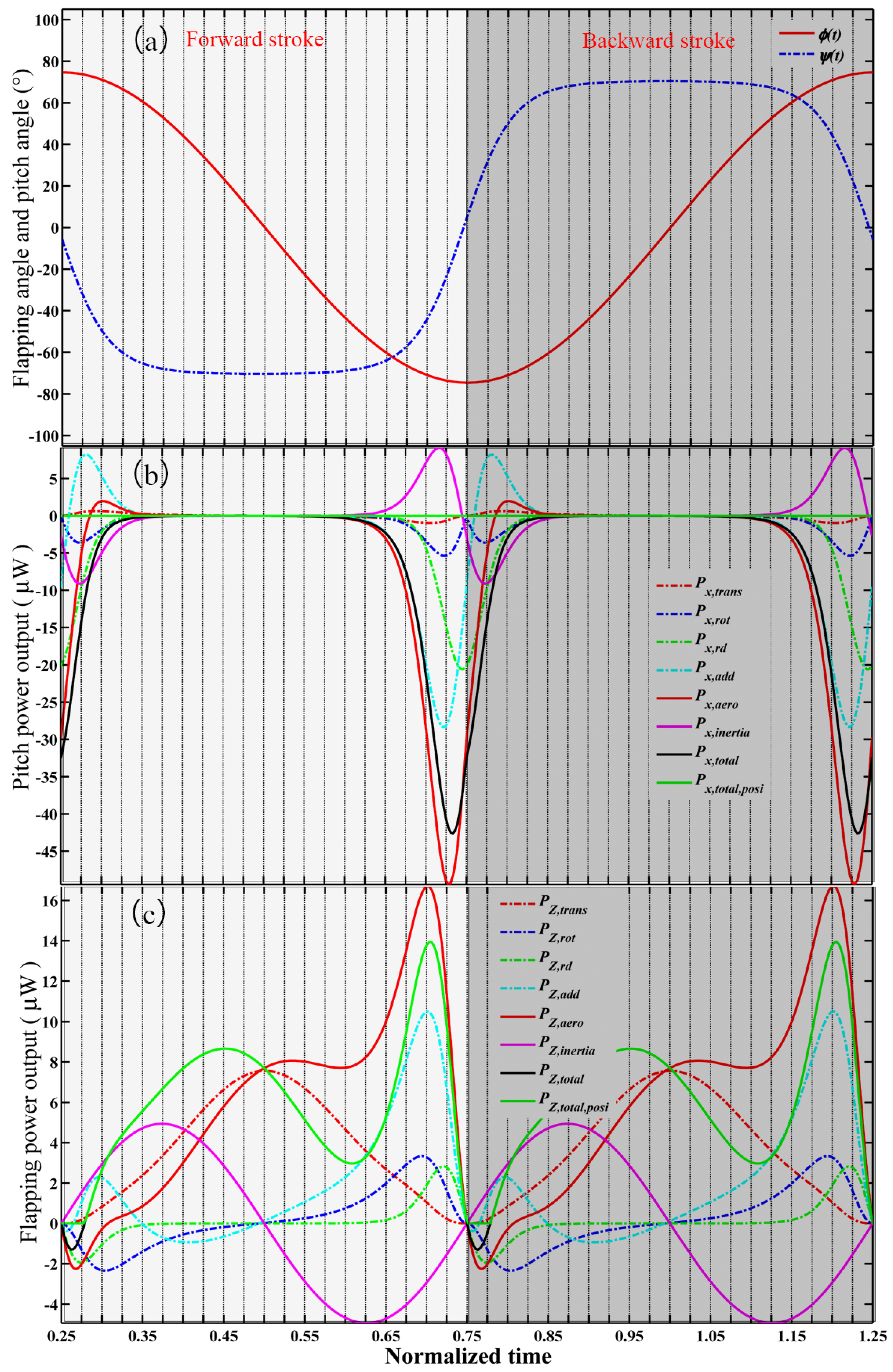
6.3. WKP optimization Results
6.4. Sensitivity Analysis for Optimal WKP
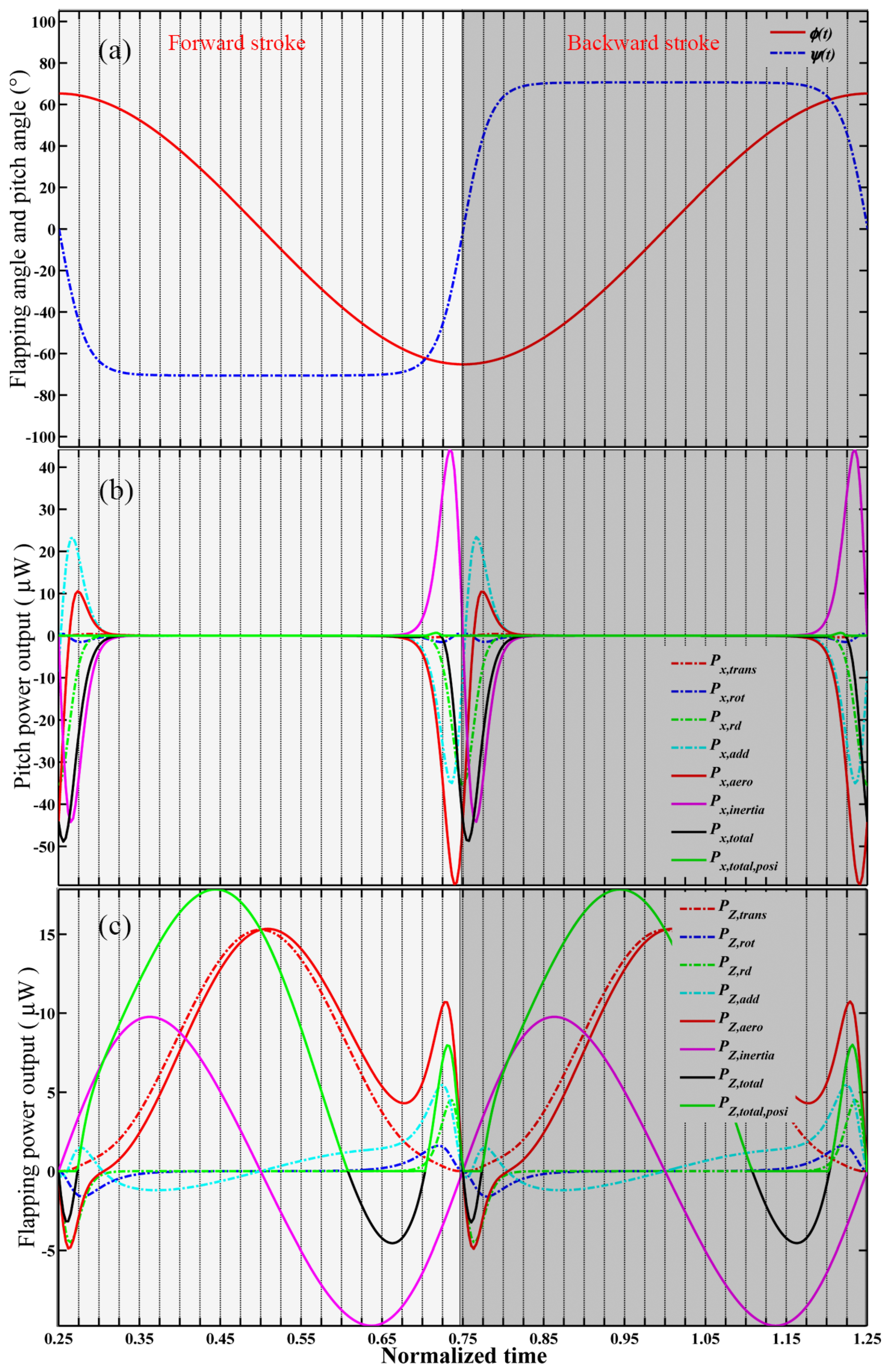
6.5. Combined Optimization Results for WGP and WKP
6.6. Sensitivity Analysis for Combined Optimal WGP and WKP
7. Discussion
8. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Abbreviations
| AR | Aspect ratio |
| Caver | Mean chord length |
| Re | Reynolds number |
| Variable mean chord length | |
| Variable wing effective length | |
| Non-dimensional chord distribution | |
| Variable non-dimensional wing root offset | |
| Variable non-dimensional pitch axis location | |
| Non-dimensional x-root offset | |
| , | Original leading-edge and trailing-edge profiles |
| , | Non-dimensional leading-edge and trailing-edge profiles |
| ϕ(t), ψ(t) | Flapping and pitch angle |
| ϕm, ψm | Flapping and pitch angle amplitude |
| Kϕ, Cψ | Regulating parameters of flapping and pitch angle profiles |
| ζ | Phase offset of pitch angle |
| P* | Power density |
| LtoW | Lift-to-weight ratio |
| , | Average flapping and pitch power |
| CN(α) | Normal translational aerodynamic force coefficient |
| CR | Theoretical rotational coefficient |
| Px,total, PZ,total | Flapping and pitch aerodynamic power |
| Px,trans, PZ,trans | Translational circulation power |
| Px,rot, PZ,rot | Rotational circulation power |
| Px,rd, PZ,rd | Rotational damping power |
| Px,add, PZ,add | Added-mass power |
| Px,inert, PZ,inert | Flapping and pitch inertial power |
| Px,total,posi, PZ,total,posi | Positive total flapping and pitch mechanical power |
References
- Wood, R.J.; Finio, B.; Karpelson, M.; Ma, K.; Pérez-arancibia, N.O.; Sreetharan, P.S.; Tanaka, H.; Whitney, J.P. Progress on ‘pico’ air vehicles. Int. J. Robot. Res. 2012, 31, 1292–1302. [Google Scholar] [CrossRef]
- Ma, K.Y.; Chirarattananon, P.; Fuller, S.B.; Wood, R.J. Controlled flight of a biologically inspired, insect-scale robot. Science 2013, 340, 603–607. [Google Scholar] [CrossRef] [PubMed]
- Chirarattananon, P.; Ma, K.Y.; Wood, R.J. Adaptive control of a millimeter-scale flapping-wing robot. Bioinspir. Biomim. 2014, 9, 025004. [Google Scholar] [CrossRef] [PubMed]
- Hines, L.; Campolo, D.; Sitti, M. Liftoff of a motor-driven, flapping-wing microaerial vehicle capable of resonance. IEEE Trans. Robot. 2014, 30, 220–232. [Google Scholar] [CrossRef]
- Roll, J.A.; Cheng, B.; Deng, X. An electromagnetic actuator for high-frequency flapping-wing microair vehicles. IEEE Trans. Robot. 2015, 31, 400–414. [Google Scholar] [CrossRef]
- Hedrick, T.L.; Daniel, T.L. Flight control in the hawkmoth manduca sexta: The inverse problem of hovering. J. Exp. Biol. 2006, 209, 3114–3130. [Google Scholar] [CrossRef] [PubMed]
- Rakotomamonjy, T.; Ouladsine, M.; Moing, T.L. Modelization and kinematics optimization for a flapping-wing microair vehicle. J. Aircr. 2007, 44, 217–231. [Google Scholar] [CrossRef]
- Berman, G.J.; Wang, Z.J. Energy-minimizing kinematics in hovering insect flight. J. Fluid Mech. 2007, 582, 153–168. [Google Scholar] [CrossRef]
- Wang, Z.J. Aerodynamic efficiency of flapping flight: Analysis of a two-stroke model. J. Exp. Biol. 2008, 211, 234–238. [Google Scholar] [CrossRef] [PubMed]
- Pesavento, U.; Wang, Z.J. Flapping wing flight can save aerodynamic power compared to steady flight. Phys. Rev. Lett. 2009, 103, 118102. [Google Scholar] [CrossRef] [PubMed]
- Kurdi, M.; Bret, S.; Philip, B. Kinematic optimization of insect flight for minimum mechanical power. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010; AIAA: Reston, VA, USA, 2010. [Google Scholar]
- Taha, H.E.; Hajj, M.R.; Nayfeh, A.H. Wing kinematics optimization for hovering micro air vehicles using calculus of variation. J. Aircr. 2013, 50, 610–614. [Google Scholar] [CrossRef]
- Nabawy, M.R.A.; Crowther, W.J. Aero-optimum hovering kinematics. Bioinspir. Biomim. 2015, 10, 44002. [Google Scholar] [CrossRef] [PubMed]
- Jones, M.; Yamaleev, N.K. Adjoint-based optimization of three-dimensional flapping-wing flows. AIAA J. 2015, 53, 934–947. [Google Scholar] [CrossRef]
- Lantman, M.P.V.S.; Fidkowski, K.J. Adjoint-based optimization of flapping kinematics in viscous flows. In Proceedings of the 21st AIAA Computational Fluid Dynamics Conference on Fluid Dynamics and Co-located Conferences, San Diego, CA, USA, 24–27 June 2013; AIAA: Reston, VA, USA, 2013. [Google Scholar]
- Nielsen, E.J.; Diskin, B. Discrete adjoint-based design for unsteady turbulent flows on dynamic overset unstructured grids. AIAA J. 2013, 51, 1355–1373. [Google Scholar] [CrossRef]
- Tuncer, I.H.; Kaya, M. Optimization of flapping airfoils for maximum thrust. AIAA J. 2005, 43, 2329–2336. [Google Scholar] [CrossRef]
- Stanford, B.K.; Beran, P.S. Analytical sensitivity analysis of an unsteady vortex-lattice method for flapping-wing optimization. J. Aircr. 2010, 47, 647–662. [Google Scholar] [CrossRef]
- Culbreth, M.; Allaneau, Y.; Jameson, A. High-fidelity optimization of flapping airfoils and wings. In Proceedings of the 29th AIAA Applied Aerodynamics Conference, Honolulu, HI, USA, 27–30 June 2011; AIAA: Reston, VA, USA, 2011. [Google Scholar]
- Soueid, H.; Guglielmini, L.; Airiau, C.; Bottaro, A. Optimization of the motion of a flapping airfoil using sensitivity functions. Comput. Fluids 2009, 38, 861–874. [Google Scholar] [CrossRef]
- Gogulapati, A.; Friedmann, P.P.; Martins, J.R.R.A. Optimization of flexible flapping-wing kinematics in hover. AIAA J. 2014, 52, 2342–2354. [Google Scholar] [CrossRef]
- Milano, M.; Gharib, M. Uncovering the physics of flapping flat plates with artificial evolution. J. Fluid Mech. 2005, 534, 403–409. [Google Scholar] [CrossRef]
- Khan, Z.A.; Agrawal, S.K. Design and optimization of a biologically inspired flapping mechanism for flapping wing micro air vehicles. In Proceedings of the IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; IEEE: New York, NY, USA, 2007; pp. 373–378. [Google Scholar]
- Khan, Z.A.; Agrawal, S.K. Optimal hovering kinematics of flapping wings for micro air vehicles. AIAA J. 2011, 49, 257–268. [Google Scholar] [CrossRef]
- Whitney, J.P.; Wood, R.J. Aeromechanics of passive rotation in flapping flight. J. Fluid Mech. 2010, 660, 197–220. [Google Scholar] [CrossRef]
- Wood, R.J.; Whitney, J.P.; Finio, B.M. Mechanics and actuation for flapping-wing robotic insects. In Encyclopedia of Aerospace Engineering; Blockley, R., Shyy, W., Eds.; John Wiley & Sons, Ltd.: Chichester, UK, 2010; pp. 1–14. [Google Scholar]
- Muijres, F.T.; Elzinga, M.J.; Melis, J.M.; Dickinson, M.H. Flies evade looming targets by executing rapid visually directed banked turns. Science 2014, 344, 172–177. [Google Scholar] [CrossRef] [PubMed]
- Whitney, J.P.; Wood, R.J. Conceptual design of flapping-wing micro air vehicles. Bioinspir. Biomim. 2012, 10, 036001. [Google Scholar] [CrossRef] [PubMed]
- Ansari, S.A.; Knowles, K.; Żbikowski, R. Insectlike flapping wings in the hover part 2: Effect of wing geometry. J. Aircr. 2008, 45, 1976–1990. [Google Scholar] [CrossRef]
- Nabawy, M.R.A.; Crowther, W.J. On the quasi-steady aerodynamics of normal hovering flight part II: Model implementation and evaluation. J. R. Soc. Interface 2014, 11, 20131197. [Google Scholar] [CrossRef] [PubMed]
- Ellington, C.P. The aerodynamics of hovering insect flight. II. Morphological parameters. Philos. Trans. R. Soc. Lond. B 1984, 305, 17–40. [Google Scholar] [CrossRef]
- Sane, S.P.; Dickinson, M.H. The aerodynamic effects of wing rotation and a revised quasi-steady model of flapping flight. J. Exp. Biol. 2002, 205, 1087–1096. [Google Scholar] [PubMed]
- Wood, R.J. The first takeoff of a biologically inspired at-scale robotic insect. IEEE Trans. Robot. 2008, 24, 341–347. [Google Scholar] [CrossRef]
- Dickinson, M.H.; Lehmann, F.-O.; Sane, S.P. Wing rotation and the aerodynamic basis of insect flight. Science 1999, 284, 1954–1960. [Google Scholar] [CrossRef] [PubMed]
- Sane, S.P.; Dickinson, M.H. The control of flight force by a flapping wing: Lift and drag production. J. Exp. Biol. 2001, 204, 2607–2626. [Google Scholar] [PubMed]
- Birch, J.M.; Dickson, W.B.; Dickinson, M.H. Force production and flow structure of the leading edge vortex on flapping wings at high and low reynolds numbers. J. Exp. Biol. 2004, 207, 1063–1072. [Google Scholar] [CrossRef] [PubMed]
- Sun, M. Insect flight dynamics: Stability and control. Rev. Mod. Phys. 2014, 86, 615–646. [Google Scholar] [CrossRef]
- Andersen, A.; Pesavento, U.; Wang, Z.J. Unsteady aerodynamics of fluttering and tumbling plates. J. Fluid Mech. 2005, 541, 65–90. [Google Scholar] [CrossRef]
- Andersen, A.; Pesavento, U.; Wang, Z.J. Analysis of transitions between fluttering, tumbling and steady descent of falling cards. J. Fluid Mech. 2005, 541, 91–104. [Google Scholar] [CrossRef]
- Bergou, A.J.; Sheng, X.; Wang, Z.J. Passive wing pitch reversal in insect flight. J. Fluid Mech. 2007, 591, 321–337. [Google Scholar] [CrossRef]
- Deng, X.; Schenato, L.; Wu, W.C.; Sastry, S.S. Flapping flight for biomimetic robotic insects: Part i system modeling. IEEE Trans. Robot. 2006, 22, 776–788. [Google Scholar] [CrossRef]
- Nabawy, M.R.A.; Crowther, W.J. Aero-optimum hovering kinematics. Bioinspir. Biomim. 2015, 10, 44002. [Google Scholar] [CrossRef] [PubMed]
- Birch, J.M.; Dickinson, M.H. Spanwise flow and the attachment of the leading-edge vortex on insect wings. Nature 2001, 412, 729–733. [Google Scholar] [CrossRef] [PubMed]
- Taha, H.E.; Hajj, M.R.; Beran, P.S. State-space representation of the unsteady aerodynamics of flapping flight. Aerosp. Sci. Technol. 2014, 34, 1–11. [Google Scholar] [CrossRef]
- Walker, J.A. Rotational lift: Something different or more of the same? J. Exp. Biol. 2002, 205, 3783–3792. [Google Scholar] [PubMed]
- Wang, W.B.; Hu, R.F.; Xu, S.J.; Wu, Z.N. Influence of aspect ratio on tumbling plates. J. Fluid Mech. 2013, 733, 650–679. [Google Scholar] [CrossRef]
- Dickson, W.B.; Straw, A.D.; Poelma, C.; Dickinson, M.H. An integrative model of insect flight control. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 Junary 2006; AIAA: Reston, VA, USA, 2006; Volume 34, pp. 1–19. [Google Scholar]
- Dickson, W.B.; Straw, A.D.; Dickinson, M.H. Integrative model of drosophila flight. AIAA J. 2008, 46, 2150–2164. [Google Scholar] [CrossRef]
- Fry, S.N.; Sayaman, R.; Dickinson, M.H. The aerodynamics of free-flight maneuvers in drosophila. Science 2003, 300, 495–498. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.J. Vortex shedding and frequency selection in flapping flight. J. Fluid Mech. 2000, 410, 323–341. [Google Scholar] [CrossRef]
- Nabawy, M.R.A.; Crowther, W.J. On the quasi-steady aerodynamics of normal hovering flight part I: The induced power factor. J. R. Soc. Interface 2014, 11, 20131196. [Google Scholar] [CrossRef] [PubMed]
- Dickson, W.B.; Polidoro, P.; Tanner, M.M.; Dickinson, M.H. A linear systems analysis of the yaw dynamics of a dynamically scaled insect model. J. Exp. Biol. 2010, 213, 3047–3061. [Google Scholar] [CrossRef] [PubMed]
- Elzinga, M.J.; Dickson, W.B.; Dickinson, M.H. The influence of sensory delay on the yaw dynamics of a flapping insect. J. R. Soc. Interface 2012, 9, 1685–1696. [Google Scholar] [CrossRef] [PubMed]
- Fry, S.N.; Sayaman, R.; Dickinson, M.H. The aerodynamics of hovering flight in drosophila. J. Exp. Biol. 2005, 208, 2303–2318. [Google Scholar] [CrossRef] [PubMed]
- Dickinson, M.H.; Lighton, J.R.B. Muscle efficiency and elastic storage in the flight motor of drosophila. Science 1995, 268, 87–90. [Google Scholar] [CrossRef] [PubMed]
- Lehmann, F.-O.; Dickinson, M.H. The changes in power requirements and muscle efficiency during elevated force production in the fruit fly drosophila melanogaster. J. Exp. Biol. 1997, 200, 1133–1143. [Google Scholar] [PubMed]
- Lehmann, F.-O.; Gorb, S.; Nasir, N.; Schützner, P. Elastic deformation and energy loss of flapping fly wings. J. Exp. Biol. 2011, 214, 2949–2961. [Google Scholar] [CrossRef] [PubMed]
- Zakaria, M.Y.; Taha, H.E.; Hajj, M.R. Shape and kinematic design optimization of the pterosaur replica. In Proceedings of the 14th AIAA Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 16–20 June 2014; AIAA: Reston, VA, USA, 2014; Volume 2869, pp. 1–14. [Google Scholar]
- Lentink, D.; Dickinson, M.H. Biofluiddynamic scaling of flapping, spinning and translating fins and wings. J. Exp. Biol. 2009, 212, 2691–2704. [Google Scholar] [CrossRef] [PubMed]
- Lentink, D.; Dickinson, M.H. Rotational accelerations stabilize leading edge vortices on revolving fly wings. J. Exp. Biol. 2009, 212, 2705–2719. [Google Scholar] [CrossRef] [PubMed]
- Kruyt, J.W.; Heijst, G.F.V.; Altshuler, D.L.; Lentink, D. Power reduction and the radial limit of stall delay in revolving wings of different aspect ratio. J. R. Soc. Interface 2015, 12, 20150051. [Google Scholar] [CrossRef] [PubMed]
- Sane, S.P. The aerodynamics of insect flight. J. Exp. Biol. 2003, 206, 4191–4208. [Google Scholar] [CrossRef] [PubMed]
- MATLAB. Software Package Ver. R2011b; Mathworks, Inc.: Natick, MA, USA, 2011. [Google Scholar]
- Ellington, C.P. The aerodynamics of hovering insect flight. IV. Aeorodynamic mechanisms. Philos. Trans. R. Soc. Lond. B 1984, 305, 79–113. [Google Scholar] [CrossRef]
- Beatus, T.; Cohen, I. Wing-pitch modulation in maneuvering fruit flies is explained by an interplay between aerodynamics and a torsional spring. Phys. Rev. E 2015, 92, 022712. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Gravish, N.; Desbiens, A.L.; Malka, R.; Wood, R.J. Experimental and computational studies of the aerodynamic performance of a flapping and passively rotating insect wing. J. Fluid Mech. 2016, 791, 1–33. [Google Scholar] [CrossRef]
- Ansari, S.; Zbikowski, R.; Knowles, K. Aerodynamic modelling of insect-like flapping flight for micro air vehicles. Prog. Aerosp. Sci. 2006, 42, 129–172. [Google Scholar] [CrossRef]
- Sun, M.D.G. Lift and power requirements of hovering insect flight. Acta Mech. Sin. 2003, 19, 458–469. [Google Scholar]

| Variables | Description | Min | Max |
|---|---|---|---|
| Reff,vari (mm) | wing effective length | 2 | 4 a |
| Caver,vari (mm) | mean chord length | 0.5 | 2 a |
| xr,vari (mm) | x-root offset | 0 | 2 a |
| rotational axis location | 0 | 0.36 | |
| f (Hz) | Frequency | 0 | ∞ |
| ϕm (rad) | Flapping amplitude | 0 | 1.309 |
| Kϕ | Regulating parameters of flapping angle profiles | 0 | 1 |
| ψm (rad) | Pitch amplitude | 0 | π/2 |
| ζ (rad) | Pitch phase offset | −π/2 | 0 |
| Cψ | Regulating parameters of pitch angle profiles | 0 | 5 |
| Aerodynamic Components | Abbreviation | Calculation Formulas |
|---|---|---|
| Translational components | ||
| Rotational components | ||
| Aerodynamic damping components | a | |
| Added-mass components | b | |
| b | ||
| b |
| Variables | Original WGP and WKP | Optimal WGP with 2D (Left) and 3D (Right) CF,trans (α) b | Optimal WKP | Combined Optimal WGP and WKP with 2D (Left) and 3D (Right) CF,trans (α) b | ||
|---|---|---|---|---|---|---|
| (mm) | 3.004 a | 2.4370 | 2.6843 | 3.004 a | 3.9813 | 4.000 |
| (mm) | 0.8854 a | 0.9626 | 0.9882 | 0.8854 a | 1.9600 | 1.9111 |
| (mm) | 0.3289 a | 0.3574 | 0.2315 | 0.3289 a | 1.7845 | 1.8118 |
| 0.36 a | 0 | 0.1443 | 0.36 a | 0.0001 | 0.0020 | |
| f (Hz) | 188.7 a | 188.7 a | 188.7 a | 189.1094 | 46.6104 | 60.7851 |
| ϕm | 1.1488 a | 1.1488 a | 1.1488 a | 1.1386 | 1.3076 | 1.3022 |
| null | null | null | 0.3733 | 0.1891 | 0.1170 | |
| ψm (rad) | 1.0157 a | 1.0157 a | 1.0157 a | 1.2324 | 1.2715 | 1.2287 |
| null | null | null | 4.8336 | 2.5103 | 2.5887 | |
| ζ (rad) | null | null | null | −1.5708 | -1.5169 | −1.5391 |
| For Original WGP and WKP | For Optimal WGP with 2D (Left) and 3D (Right) CF,trans (α) | For Optimal of WKP | For Combined Optimal WGP and WKP with 2D (Left) and 3D (Right) CF,trans (α) | |||
|---|---|---|---|---|---|---|
| AR | 3.7643 a | 2.9029 | 2.9506 | 3.7643 a | 2.9417 | 3.0411 |
| Re | 172.8926 a | 157.6046 | 168.8122 | 171.7340 | 186.1461 | 237.6147 |
| LtoW-1 | 0.2890 | 3.7 × 10−8 | 5.2 × 10−8 | 1.6 × 10−8 | 3.0 × 10−8 | 1.9 × 10−8 |
| 0.8834 | 0.8855 | 0.8960 | 1.1241 | 1.1089 | 1.0173 | |
| 8.4327 | 5.8237 | 5.7343 | 1.4711 | 3.7811 | 2.4905 | |
| P* (Wkg−1) | 33.0097 b | 20.4839 b | 21.1160 b | 9.1074 | 4.7867 | 6.7156 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ke, X.; Zhang, W. Wing Geometry and Kinematic Parameters Optimization of Flapping Wing Hovering Flight. Appl. Sci. 2016, 6, 390. https://doi.org/10.3390/app6120390
Ke X, Zhang W. Wing Geometry and Kinematic Parameters Optimization of Flapping Wing Hovering Flight. Applied Sciences. 2016; 6(12):390. https://doi.org/10.3390/app6120390
Chicago/Turabian StyleKe, Xijun, and Weiping Zhang. 2016. "Wing Geometry and Kinematic Parameters Optimization of Flapping Wing Hovering Flight" Applied Sciences 6, no. 12: 390. https://doi.org/10.3390/app6120390






