Passivity-Based Control for a Micro Air Vehicle Using Unit Quaternions

Abstract

In this paper the development and practical implementation of a Passivity-Based Control (PBC) algorithm to stabilize an Unmanned Aerial Vehicle (UAV) described with unit quaternions are presented. First, a mathematical model based on Euler-Lagrange formulation using a logarithmic mapping in the quaternion space is introduced. Then, a new methodology: a quaternion-passivity-based control is derived, which does not compute excessive and complex Partial Differential Equations (PDEs) for synthesizing the control law, making a significant advantage in comparison with other methodologies. Therefore, the control design to a system as the quad-rotor is easily solved by the proposed methodology. Another advantage is the possibility to stabilize quad-rotor full dynamics which may not be possible with classical PBC techniques. Experimental results and numerical simulations to validate our proposed scheme are presented.

1. Introduction

Many efforts have been made to model and control quad-rotor Unmanned Aerial Vehicles (UAVs). In recent years, a wide number of strategies have been developed to solve the stabilization problem for this type of system using different methodologies in terms of control techniques and modeling approaches, such as [1,2,3,4]. Several strategies based on Euler angles provide an intuitive and easy way to visualize the quad-rotor kinematic and dynamical properties, but some obstacles are found with this representation, for instance, certain orientations can not be defined due to mathematical singularities, also a problem known as “gimbal lock” exists, which consists on an infinite number of possible representations for a single rotation. A potential solution for this problem is the use of unit quaternions to represent the rigid body rotations.

In the last years, several researchers have explored unit quaternions as an alternative to avoid these kind of issues. For instance, a quaternion-based nonlinear $P^2$ controller, for solving the attitude problem of a quad-rotor is proposed in [5], the proposed control scheme performs very well with a very small overshoot and a very good reference tracking, however only numerical simulations are presented to prove the efficiency of the suggested scheme. In [6], a quaternion-based feedback is developed for the attitude stabilization of a quad-rotor. The control design takes into account a priori input bound and is based on nested saturations. The authors forced the closed-loop trajectories to enter in a fixed neighborhood around the origin in a finite time and remain thereafter. A quaternion-based nonlinear robust output feedback tracking controller is developed in [7] to address the attitude and altitude tracking problem of a quad-rotor, here, approximation components based on neural network are introduced to estimate the model uncertainties and robust feedback components are designed to compensate for external disturbances. Also, [8] investigates the attitude control design using backstepping technique for a quad-rotor represented by unit quaternions, external disturbance torques were taken into consideration, the attitude and the angular velocity of the quad-rotor were governed to be uniformly ultimately bounded by the proposed controller. Meanwhile, experimental results and implementation of a quaternion based attitude robust controller for quad-rotors are presented in [9]. Here, a state feedback controller which compensates nonlinearities and uncertainties is proposed, attenuating their effects in the closed-loop control system. A robust controller based on quaternion for the attitude control problem of quad-rotors with a nominal controller and a robust compensator is proposed in [10]. A quaternion based control scheme for the attitude control problem of a quad-rotor has been presented and experimentally evaluated in [11]. Recent works of quad-rotor’s control based on quaternions can be found in [12,13,14,15,16].

Few works based on PBC (Passivity-Based Control) strategies applied to UAVs can be found in the literature. For example in [17], the authors presented a nonlinear control technique based on passivity to solve the path tracking problem for the quad-rotor, but only one control loop was considered in their work. For this work Souza, et al. showed that the PBC formulation leads to a set of partial differential equations constraints due to the underactuation degree of the system. In [18] the authors proposed a controller based on an extension of Interconnection and Damping Assignment-Passivity Based Control (IDA-PBC) framework, for shaping the whole physical characteristics of a quad-rotor and for obtaining a desired interactive behavior between the vehicle and the environment. In [19] a passivity-based approach is designed for this vehicle. The authors reduced the problem to the longitudinal plane to avoid solving complicated PDEs (Partial Differential Equations). A passivity-based control for a quad-rotor transporting a cable-suspended payload is presented in [20]. Here, the problem is also reduced to the longitudinal plane to avoid complex PDEs. Finally, a passivity based controller for a PVTOL (Planar Vertical Take-Off and Landing) is introduced in [21].

On the one hand, observe in these works that it is not possible to use passivity-based strategies directly to control the vehicle’s full dynamics because certain passivity properties are not satisfied, i.e., when this methodology is used directly in the classical quad-rotors equations, then only the attitude can be stabilized. Nevertheless, controllers based on PBC can be used if the dynamics are modified, this requires the use of more complex algorithms and high computational cost implementations for just a partial stabilization. On the other hand, IDA-PBC strategy is designed for underactuated systems. However, it requires computing complex PDEs, many of which may have not solution. The design of an IDA-PBC for a quad-rotor has this problem. By avoiding the complex PDEs, we can only control the quad-rotor’s attitude.

Motivated by the aforementioned considerations, in this work we introduce a methodology to analyze the quad-rotor vehicle using a passivity-based control with unit quaternions. The PBC strategy is obtained from the mathematical model based on Euler-Lagrange formulation using a quaternion logarithmic mapping such that a fully actuated virtual system is proposed, then an attitude trajectory in the quaternion space is used to apply the mathematical restrictions inherent to the quad-rotor. The resulting control scheme does not compute excessive and complex PDEs and can be designed directly from the model and can control the full quad-rotor equations. The proposed approach has no issues with singularities and can be straightforwardly applied in real-time experiments.

The paper is organized as follows: A brief survey of the main concepts of unit quaternions and passivity is presented in Section 2. The representation of the quad-rotor dynamics in terms of unit quaternions is described with the logarithmic mapping in Section 3. The quaternion-passivity-based control is developed in Section 4. Numerical simulations are presented in Section 5. Real-time experimental results are shown in Section 6. Conclusions and perspectives are finally given in Section 7.

2. Preliminaries

2.1. Quaternion Background

A quaternion is basically a type of complex number that consists of four values, one of which is real, while the other three are imaginary [22,23,24,25]. The quaternion space is denoted by $\mathbb{H}$. Let $\mathit{q}$ be a quaternion expresses by:

$$\mathit{q}=q_0+\overline{q}=q_0+\left[\begin{array}{c}{q}_1\\ q_2\\ q_3\end{array}\right],q_0\in \mathbb{R},\overline{q}\in {\mathbb{R}}^3$$

where $\overline{q}$ represents the complex vectorial part of $\mathit{q}$, and $q_0$ denotes the scalar part of $\mathit{q}$. Note that if $q_0=0$, then $\mathit{q}=\overline{q}$, thus $\mathit{q}\in {\mathbb{R}}^3$, this implies that ${\mathbb{R}}^3$ is a subset of $\mathbb{H}$ in which $q_0=0$.

The quaternion basic operations are:

• Quaternion multiplication

  $$\begin{array}{c}\mathit{q}\otimes \mathit{r}=\left(q_0{r}_0-\overline{q}·\overline{r}\right)+\left(r_0\overline{q}+q_0\overline{r}+\overline{q}\times \overline{r}\right)\hfill \end{array}$$

  where $\mathit{r}$ is also a quaternion.
• Norm of a quaternion $\mathit{q}$

  $$\left|\right|\mathit{q}\left|\right|=\sqrt{\mathit{q}\otimes {\mathit{q}}^{*}}=\sqrt{q_0^2+q_1^2+q_2^2+q_3^2}$$

  In the case that $\left|\right|\mathit{q}\left|\right|=1$, $\mathit{q}$ represents an unit quaternion.
• Quaternion conjugate

  $${\mathit{q}}^{*}=q_0-\overline{q}$$
• Quaternion inverse

  $${\mathit{q}}^{-1}={\left|\right|\mathit{q}\left|\right|}^{-1}{\mathit{q}}^{*}$$

  If $\mathit{q}$ is unitary, then the inverse and the norm are equivalent.
• The derivative of a quaternion

  $$\begin{array}{c}\dot{\mathit{q}}={\displaystyle \frac{1}{2}}\mathit{q}\otimes \mathsf{\omega }\hfill \end{array}$$

  where $\mathsf{\omega }$ represents the angular velocity.

Any vector in a three-dimensional space can be rotated from one reference frame to another (for example a body frame), i.e.,

$$\begin{array}{c}{v}^{\prime }={\mathit{q}}^{*}\otimes v\otimes \mathit{q}\hfill \end{array}$$

(1)

where $v\in {\mathbb{R}}^3$ and $v^{\prime }\in {\mathbb{R}}^3$ are in the fixed and body frames respectively.

Any rotation can be expressed by its axis-angle representation, which is composed by a direction vector $\overline{e}\in {\mathbb{R}}^3,\left|\right|\overline{e}\left|\right|=1$ and its angle $\mathsf{\theta }\in \mathbb{R}$, as depicted in Figure 1. This yields to a single vector $\overline{\mathsf{\theta }}=\mathsf{\theta }\overline{e}$ with $\overline{\mathsf{\theta }}\in {\mathbb{R}}^3$.

The Euler-Rodrigues Formula then relates this rotation vector to a unit quaternion as

$$\mathit{q}=cos(\mathsf{\theta }/2)+\overline{e}sin(\mathsf{\theta }/2)$$

(2)

A logarithmic mapping can be used to change any unit quaternion to the axis-angle representation

$$\overline{\mathsf{\theta }}=2ln\mathit{q},\dot{\overline{\mathsf{\theta }}}=\mathsf{\omega },$$

where

$$\begin{array}{c}ln\mathit{q}=\left\{\begin{array}{cc}ln\left|\right|\mathit{q}\left|\right|+{\displaystyle \frac{\overline{q}}{\left|\right|\overline{q}\left|\right|}}arccos{\displaystyle \frac{q_0}{\left|\right|\mathit{q}\left|\right|}},\hfill & \hfill \left|\right|\overline{q}\left|\right|\ne 0\\ ln\left|\right|\mathit{q}\left|\right|,\hfill & \hfill \left|\right|\overline{q}\left|\right|=0\end{array}\right.\hfill \end{array}$$

Note that (2) implies that $\left|\right|\mathit{q}\left|\right|=1$ , thus the scalar part of the quaternion logarithm is zero, implying that $ln\mathit{q}\in {\mathbb{R}}^3\forall \mathit{q}\mid q_0=0$.

2.2. Passivity-Based Control Approach

Passivity is a fundamental property exhibited by many physical systems which involves energy dissipation and transformation. It is related to the notion of stability in an input-output sense, that is, a system is stable if bounded input energy supplied to the system produces bounded output energy. Passivity-based control methodology relies on synthesizing control law which render the closed loop system passive [26].

Let us consider a system described as follows

$$\left\{\begin{array}{c}\dot{x}\left(t\right)=f\left(x\right)+g\left(x\right)u\left(t\right)\hfill \\ \tilde{y}\left(t\right)=h\left(x\right)\hfill \end{array}\right.$$

(3)

where x∈${\mathbb{R}}^n$, u∈${\mathbb{R}}^m$ and $\tilde{y}$∈${\mathbb{R}}^m$, $f\left(x\right)$, $g\left(x\right)$ and $h\left(x\right)$ are smooth functions. There is a function $w\left[u,\tilde{y}\right]$ called supply rate, such that is locally integrable, i.e.,

$$\underset{t_0}{\overset{t_1}{\int }}w\left[u\left(t\right),\tilde{y}\left(t\right)\right]dt<\infty ,\forall t_0\le t_1$$

If there is a function $H\left(x\right)\ge 0$, $H\left(0\right)=0$, such that

$$H\left(x\left(t_1\right)\right)-H\left(x\left(t_0\right)\right)=\underset{t_0}{\overset{t_1}{\int }}w\left[u\left(t\right),\tilde{y}\left(t\right)\right]dt-d\left(t\right)$$

(4)

then, (3) is said to be a dissipative system. When $w\left[u\left(t\right),\tilde{y}\left(t\right)\right]={\tilde{y}}^T\left(t\right)u\left(t\right)$, (3) represents a passive system. Here, $H\left(x\right)$ represents the storage function and $d\left(t\right)$ is the dissipated energy function. For the system (3), passivity is equivalent to the existence of a scalar $H\left(x\right)$ such that,

$${\left({\nabla }_{x}H\right)}^{T}f\left(x\right)\le 0,h\left(x\right)=g^T\left(x\right){\nabla }_{x}H$$

2.3. Classical Algorithm Applied to a Quad-Rotor

The PBC strategy seen in the Section 2.2 can not be applied directly to a quad-rotor, since the vehicle is a under-actuated system. However, the approach IDA-PBC (for further details, the interested reader is referred to [27]) if can be applied. Hence the main difficulty is in the solution of complex PDEs, which often can not be computed. Also, it is only possible to stabilize the attitude of the quad-rotor.

We briefly review a classical procedure to design a IDA-PBC algorithm to stabilize a quad-rotor without using quaternions (for further details, the interested reader is referred to [18]).

From the Euler-Lagrange formulation the dynamic model of a quad-rotor can be expressed as

$$\mathcal{M}\left(\mathsf{\lambda }\right)\ddot{\mathsf{\lambda }}+D(\mathsf{\lambda },\dot{\mathsf{\lambda }})\dot{\mathsf{\lambda }}+G=B\left(\mathsf{\lambda }\right)u$$

(5)

where the state vector $\mathsf{\lambda }={\left[\begin{array}{cc}{p}^T& {\mathsf{\eta }}^T\end{array}\right]}^T$, $p={\left[\begin{array}{ccc}x& y& z\end{array}\right]}^T$ denotes the position of the UAV, $\mathsf{\eta }={\left[\begin{array}{ccc}\mathsf{\psi }& \mathsf{\theta }& \mathsf{\varphi }\end{array}\right]}^T$ are the Euler angles yaw, pitch and roll, respectively. The input vector $u={\left[\begin{array}{cc}{f}_{\mathrm{th}}& \mathsf{\tau }\end{array}\right]}^T$, $f_{\mathrm{th}}$ is the total thrust magnitude and $\mathsf{\tau }={\left[\begin{array}{ccc}{\mathsf{\tau }}_x& {\mathsf{\tau }}_y& {\mathsf{\tau }}_z\end{array}\right]}^T$. The matrix $B\left(\mathsf{\lambda }\right)$ is given as

$$B={\left[\begin{array}{cccccc}{s}_{\mathsf{\varphi }}{s}_{\mathsf{\psi }}+c_{\mathsf{\varphi }}{c}_{\mathsf{\psi }}{s}_{\mathsf{\theta }}& c_{\mathsf{\varphi }}{s}_{\mathsf{\theta }}{s}_{\mathsf{\psi }}-c_{\mathsf{\psi }}{s}_{\mathsf{\varphi }}& c_{\mathsf{\theta }}{c}_{\mathsf{\varphi }}& 0& 0& 0\\ 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 1\end{array}\right]}^T$$

Matrices $\mathcal{M}\left(\mathsf{\lambda }\right)$, $D(\mathsf{\lambda },\dot{\mathsf{\lambda }})$ and the vector G are defined in [28]. Notice that matrix $B\left(\mathsf{\lambda }\right)$ is not invertible. Then, if we applied the potential energy-shaping procedure of IDA-PBC, we can get the energy-shaping term as [27]

$$u_{\mathrm{es}}={\left(B^{T}B\right)}^{-1}{B}^T({\nabla }_{\mathsf{\lambda }}V-{\nabla }_{\mathsf{\lambda }}{V}_d)$$

(6)

where V denotes the potencial energy and $V_d$ the desired potencial energy.

The desired potential energy can be obtained from [27]

$$B^{\perp }\left\{{\nabla }_{\mathsf{\lambda }}V-{\nabla }_{\mathsf{\lambda }}{V}_d\right\}=0$$

(7)

A popular choice for the full rank left annihilator $B^{\perp }$ is [18]

$$B^{\perp }=\left[\begin{array}{cccccc}0& -1& \frac{c_{\mathsf{\varphi }}{s}_{\mathsf{\theta }}{s}_{\mathsf{\psi }}-c_{\mathsf{\psi }}{s}_{\mathsf{\varphi }}}{c_{\mathsf{\theta }}{c}_{\mathsf{\varphi }}}& 0& 0& 0\\ -1& 0& \frac{s_{\mathsf{\varphi }}{s}_{\mathsf{\psi }}+c_{\mathsf{\psi }}{c}_{\mathsf{\varphi }}{s}_{\mathsf{\theta }}}{c_{\mathsf{\theta }}{c}_{\mathsf{\varphi }}}& 0& 0& 0\end{array}\right]$$

Thus, substituting the above into (7), it follows that

$$\left\{\begin{array}{c}{\nabla }_y{V}_d-\frac{c_{\mathsf{\varphi }}{s}_{\mathsf{\theta }}{s}_{\mathsf{\psi }}-c_{\mathsf{\psi }}{s}_{\mathsf{\varphi }}}{c_{\mathsf{\theta }}{c}_{\mathsf{\varphi }}}\left({\nabla }_{z}V-{\nabla }_z{V}_d\right)=0\\ {\nabla }_x{V}_d-\frac{s_{\mathsf{\varphi }}{s}_{\mathsf{\psi }}+c_{\mathsf{\psi }}{c}_{\mathsf{\varphi }}{s}_{\mathsf{\theta }}}{c_{\mathsf{\theta }}{c}_{\mathsf{\varphi }}}\left({\nabla }_{z}V-{\nabla }_z{V}_d\right)=0\end{array}\right.$$

The previous implies the next simple solution

$$V_d\left(\mathsf{\lambda }\right)=-V+\mathsf{\varphi }(\mathsf{\varphi },\mathsf{\theta },\mathsf{\psi })$$

(8)

where $\mathsf{\varphi }(\mathsf{\varphi },\mathsf{\theta },\mathsf{\psi })$ is an arbitrary differentiable function that is selected to be a quadratic function.

Introducing (8) into (6) it can be observed that is only possible to control the attitude of the quad-rotor. Several solutions to stabilize the full dynamics can be found in the literature, for example [17], nevertheless they propose to rewrite the model in some special forms to apply their approach. Our contribution to solve this problem is to design a control strategy using a logarithmic mapping and an attitude trajectory in the quaternion space. This allows to stabilizes all the system states without any assumptions in the model.

3. Quad-Rotor Quaternion Dynamic Model

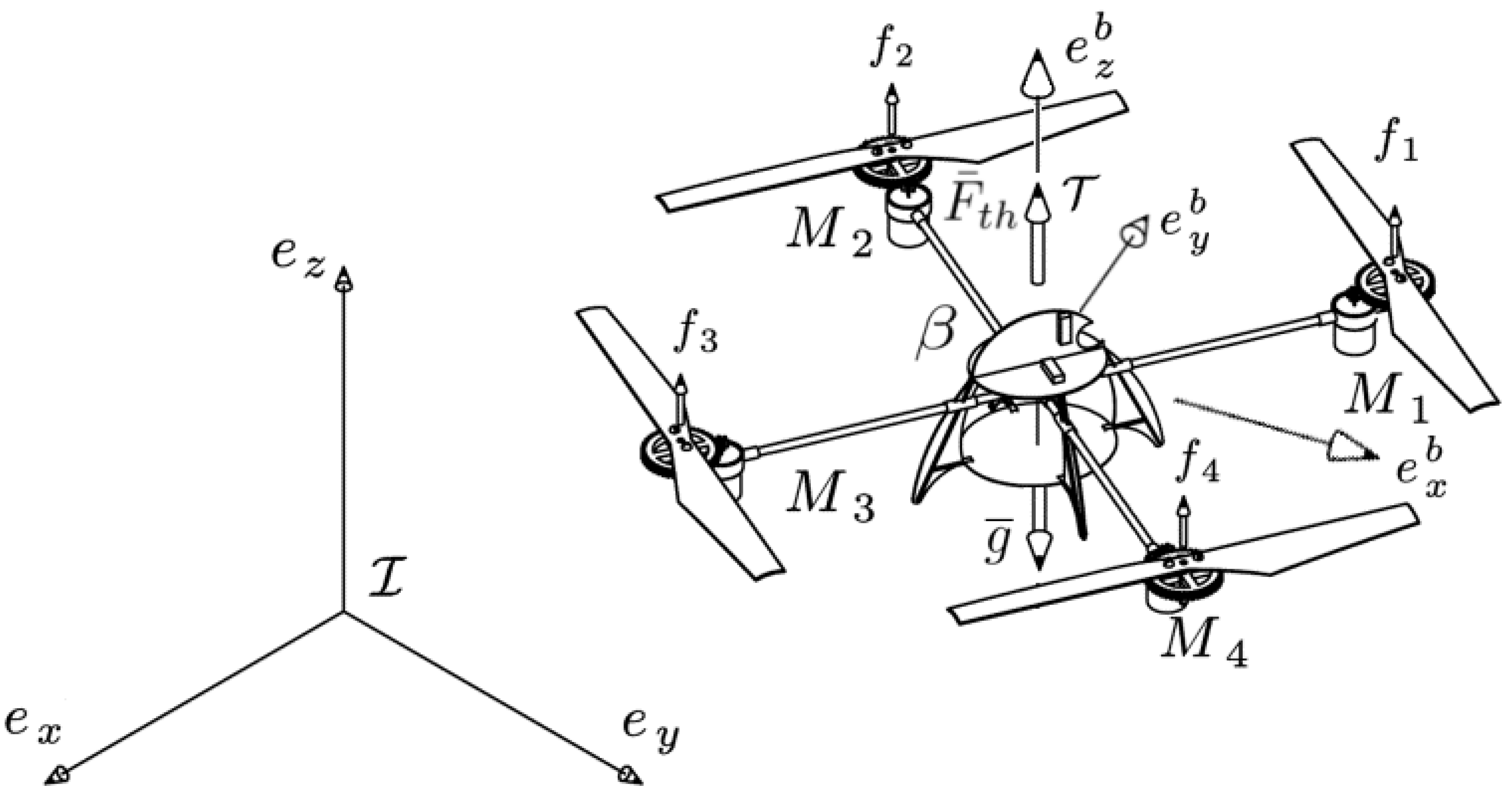
The body diagram of a quad-rotor can be drawn as in Figure 2.

Let us consider an inertial coordinate frame $I=\{e_x,e_y,e_z\}$ fixed to the ground, a body fixed coordinate frame $\mathsf{\beta }=\{e_x^b,e_y^b,e_z^b\}$. Then, the vector $\mathsf{\xi }={\left[\begin{array}{cc}p& \overline{\mathsf{\theta }}\end{array}\right]}^T$∈${\mathbb{R}}^6$ defines all the states variables of the quad-rotor, where $p={\left[\begin{array}{ccc}x& y& z\end{array}\right]}^T$ defines the position vector with respect to the inertial frame, $\overline{\mathsf{\theta }}=2ln\left(\mathit{q}\right)$ denotes the rotation quaternion expressed in its axis-angle notation. ${\overline{f}}_{\mathrm{th}}={\left[\begin{array}{ccc}0& 0& f_{\mathrm{th}}\end{array}\right]}^T$ defines the thrust vector generated by the four rotors, $\overline{g}={\left[\begin{array}{ccc}0& 0& -g\end{array}\right]}^T$ represents the gravity vector, $\mathsf{\tau }={\left[\begin{array}{ccc}{\mathsf{\tau }}_x& {\mathsf{\tau }}_y& {\mathsf{\tau }}_z\end{array}\right]}^T$ contains the torques applied to the body’s center of mass, expressed on the aerial vehicle in the body-fixed frame.

3.1. Euler-Lagrange Methodology

The Lagrangian equation is known to be the difference between the kinetic and potential energies

$$L=K-V,$$

(9)

We can obtain the motion equations applying the following expression

$$\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\mathsf{\xi }}}\right)-\frac{\partial L}{\partial \mathsf{\xi }}=u_u,$$

(10)

where $u_u={\left[\begin{array}{cc}{f}_u^T& {\mathsf{\tau }}_u^T\end{array}\right]}^T$ represents the input vector, $f_u$ expresses the input force with respect to the inertial frame and ${\mathsf{\tau }}_u$ denotes the input torque to be computed by the control law.

3.1.1. Kinetic Energy

The total kinetic energy is obtained by the sum of the translational and rotational kinetic energies, which are obtained using the translational and rotational velocities respectively,

$$K_{\mathrm{UAV}}=\frac{1}{2}m{\dot{p}}^T\dot{p}+\frac{1}{2}{\dot{\overline{\mathsf{\theta }}}}^{T}J\dot{\overline{\mathsf{\theta }}},$$

(11)

where m denotes the vehicle’s mass, and J represents the inertia matrix.

3.1.2. Potential Energy

The potential energy is described by the product of the mass, the gravity g, and the height z (the position in the vertical axis in the inertial frame)

$$V=mgz.$$

(12)

3.1.3. Lagrangian Expression

Substituting (11) and (12) into (9) the Lagrangian equation becomes

$$L=\frac{1}{2}m{\dot{p}}^T\dot{p}+\frac{1}{2}{\dot{\overline{\mathsf{\theta }}}}^{T}J\dot{\overline{\mathsf{\theta }}}-mgz,$$

(13)

Solving (13) with (10) the dynamic equations are obtained as

$$\left[\begin{array}{c}{f}_u\\ {\mathsf{\tau }}_u\end{array}\right]=\left[\begin{array}{c}m\ddot{p}-m\overline{g}\\ J\ddot{\overline{\mathsf{\theta }}}\end{array}\right].$$

(14)

Thus, the dynamic model can be expressed in matrix form as follows

$$M\ddot{\mathsf{\xi }}+G\left(\mathsf{\xi }\right)=u_u,$$

(15)

where the inertia matrix is given by

$$M=\left[\begin{array}{cc}m{I}_{3\times 3}& 0_{3\times 3}\\ 0_{3\times 3}& J\end{array}\right]$$

(16)

which is symmetric and positive definite. The gravitational vector is given by

$$G\left(\mathsf{\xi }\right)={\left[\begin{array}{cccccc}0& 0& mg& 0& 0& 0\end{array}\right]}^T,$$

(17)

3.2. Coupled Dynamics Strategy

Notice that the quad-rotor is an under-actuated system, then the force $f_u$ which is expressed in the inertial frame, is the force ${\overline{f}}_{\mathrm{th}}$ rotated using a quaternion double product

$$f_u=\mathit{q}\otimes {\overline{f}}_{\mathrm{th}}\otimes {\mathit{q}}^{*}$$

(18)

Since the angular acceleration is given by the external torques and the internal rotational dynamics, then by Newton’s equations of motion, it follows that

$$\ddot{\overline{\mathsf{\theta }}}=\dot{\mathsf{\omega }}=J^{-1}(\mathsf{\tau }-\mathsf{\omega }\times J\mathsf{\omega })$$

(19)

thus the relation between the computed control input ${\mathsf{\tau }}_u$ from (14) and the actual applied torque $\mathsf{\tau }$ from (19) becomes

$${\mathsf{\tau }}_u=\mathsf{\tau }-\mathsf{\omega }\times J\mathsf{\omega }.$$

(20)

It is known that the translational and rotational dynamics of the quad-rotor are coupled such that the direction of the total force $f_u$ depends only on the orientation of the UAV given by $\mathit{q}$, while its magnitude is equal to the total force given by the four rotors $\left|\right|{\overline{f}}_{\mathrm{th}}\left|\right|$, see Figure 2 and Equation (18). Then a rotation ${\overline{\mathsf{\theta }}}_d={\overline{e}}_d{\mathsf{\theta }}_d$ must exist such that ${\overline{f}}_{\mathrm{th}}$ is transformed into $f_u$ in the inertial frame.

If the scalar product between these two vectors is defined as

$${\overline{f}}_{\mathrm{th}}·f_u=\left|\right|f_u\left|\right|b·f_u=\left|\right|f_u{\left|\right|}^{2}cos\left({\mathsf{\theta }}_d\right)$$

(21)

where $b={\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}^T$ denotes the axis on which the thrust acts in the body frame. The cross product is expressed by

$${\overline{f}}_{\mathrm{th}}\times f_u=\left|\right|f_u\left|\right|b\times f_u=\left|\right|f_u{\left|\right|}^{2}sin\left({\mathsf{\theta }}_d\right){\overline{e}}_d$$

(22)

Using some trigonometric identities to introduce (21) and (22) into the Euler-Rodrigues Formula from (2), a quaternion attitude trajectory ${\mathit{q}}_d$ can be introduced as

$$\begin{array}{ccc}\hfill {\mathit{q}}_d& =& \frac{(b·f_u+\left|\right|f_u\left|\right|)+b\times f_u}{\left|\right|(b·f_u+\left|\right|f_u\left|\right|)+b\times f_u\left|\right|}\hfill \\ \hfill f_{\mathrm{th}}& =& \left|\right|f_u\left|\right|\hfill \end{array},$$

(23)

which is used to close the loop such that the orientation of ${\overline{f}}_{\mathrm{th}}$ coincides with $f_u$ thus the position is stabilized in the desired reference.

4. PBC Methodology for a Quad-Rotor Using Quaternions

The development of the mathematical model using quaternions simplifies the control law design. In the sense that the proposed control law is such that the quad-rotor system can be analyzed and controlled as a fully-actuated system. Also, the proposed control law avoids the issues with singularities.

The idea is to apply the PBC approach to (15). Thus, the total energy is

$$H(\mathsf{\xi },\dot{\mathsf{\xi }})=\frac{1}{2}{\dot{\mathsf{\xi }}}^{T}M\dot{\mathsf{\xi }}+V\left(\mathsf{\xi }\right)$$

(24)

In PBC methodology, the control input is naturally decomposed into two terms

$$u_u=u_{\mathrm{es}}\left(\mathsf{\xi }\right)+u_{\mathrm{di}}\left(\dot{\mathsf{\xi }}\right)$$

(25)

where the first term is designed to achieve the energy-shaping and the second one injects the damping.

From (4) notice that if we can find $u_{\mathrm{es}}$ such that

$$-{\int }_0^t{u}_{\mathrm{es}}^T\left[\mathsf{\xi }\left(t\right)\right]\tilde{y}\left(t\right)dt=H_a\left[\mathsf{\xi }\left(t\right)\right]+k$$

(26)

for some $H_a\left(\mathsf{\xi }\right)$ and some constant k, then the energy-shaping term $u_{\mathrm{es}}$ will ensure that the map $u_{\mathrm{es}}\to \tilde{y}$ is passive with the following form for the desired energy function

$$H_d(\mathsf{\xi },\dot{\mathsf{\xi }})=H(\mathsf{\xi },\dot{\mathsf{\xi }})+H_a\left(\mathsf{\xi }\right)$$

(27)

where $H_a\left(\mathsf{\xi }\right)$ represents the supplied energy by the controller. We will require that the function $H_d$ has an isolated minimum at ${\mathsf{\xi }}_{*}$, that is

$${\mathsf{\xi }}_{*}=argmin{H}_d(\mathsf{\xi },\dot{\mathsf{\xi }})$$

(28)

The passive outputs for this system are the generalized velocities, that is $\tilde{y}=\dot{\mathsf{\xi }}$. The easiest way to shape the energy is by [29]

$$u_{\mathrm{es}}={\nabla }_{\mathsf{\xi }}H(\mathsf{\xi },\dot{\mathsf{\xi }})-K_p(\mathsf{\xi }-{\mathsf{\xi }}_{*})$$

(29)

where $u_{\mathrm{es}}$ stabilizes ${\mathsf{\xi }}_{*}$ with Lyapunov function the difference between the stored and supplied energies.

Then, introducing (29) and $\tilde{y}=\dot{\mathsf{\xi }}$ into (26) we can obtain

$$H_a\left(\mathsf{\xi }\right)=-V\left(\mathsf{\xi }\right)+\frac{1}{2}\left(\mathsf{\xi }-{\mathsf{\xi }}_{*}\right)K_p\left(\mathsf{\xi }-{\mathsf{\xi }}_{*}\right)+k$$

(30)

where $K_p=K_p^T>0$ contains design parameters. Substituting (24) and (30) into (27), it follows that

$$H_d(\mathsf{\xi },\dot{\mathsf{\xi }})=\frac{1}{2}{\dot{\mathsf{\xi }}}^{T}M\dot{\mathsf{\xi }}+\frac{1}{2}\left(\mathsf{\xi }-{\mathsf{\xi }}_{*}\right)K_p\left(\mathsf{\xi }-{\mathsf{\xi }}_{*}\right)$$

(31)

The controller (29) can be rewritten as

$$u_{\mathrm{es}}\left(\mathsf{\xi }\right)={\nabla }_{\mathsf{\xi }}H(\mathsf{\xi },\dot{\mathsf{\xi }})-{\nabla }_{\mathsf{\xi }}{H}_d(\mathsf{\xi },\dot{\mathsf{\xi }})$$

(32)

From (32), we can ensure that the map $u_{\mathrm{es}}\to \tilde{y}$ is passive with (31) as the desired energy function.

The damping injection term is given by

$$u_{\mathrm{di}}\left(\dot{\mathsf{\xi }}\right)=-K_v\dot{\mathsf{\xi }}$$

(33)

where $K_v=K_v^T>0$ contains design parameters.

To compute the final control law, consider that $K_p=\left[\begin{array}{cc}{K}_{pt}& 0_{3\times 3}\\ 0_{3\times 3}& K_{pr}\end{array}\right]$ and $K_v=\left[\begin{array}{cc}{K}_{vt}& 0_{3\times 3}\\ 0_{3\times 3}& K_{vr}\end{array}\right]$. Now, we first determine the energy-shaping term $u_{\mathrm{es}}$ from (32), which, in this case, takes the form

$$u_{\mathrm{es}}=\left[\begin{array}{c}-m\overline{g}-K_{pt}\left(p-p_d\right)\\ -2K_{pr}ln\left({\mathit{q}}_e\right)\end{array}\right]$$

Note that the term ${\mathit{q}}_e=\mathit{q}\otimes {\mathit{q}}_d^{*}$ is the quaternion error between the actual orientation $\mathit{q}$ and the desired reference ${\mathit{q}}_d^{*}$. If the control law is such that $ln\left({\mathit{q}}_e\right)\to {\left[\begin{array}{ccc}0& 0& 0\end{array}\right]}^T$, then ${\mathit{q}}_e\to 1+{\left[\begin{array}{ccc}0& 0& 0\end{array}\right]}^T$, which implies that the orientation of the UAV converges to the desired reference $\mathit{q}\to {\mathit{q}}_d^{*}$. Here $p_d$ denotes the desired position.

Hence, we determine the damping injection term $u_{\mathrm{di}}$ from (33)

$$u_{\mathrm{di}}=\left[\begin{array}{c}-K_{vt}\left(\dot{p}-{\dot{p}}_d\right)\\ -K_{vr}\left(\dot{\overline{\mathsf{\theta }}}-{\dot{\overline{\mathsf{\theta }}}}_d\right)\end{array}\right]$$

where ${\overline{\mathsf{\theta }}}_d=2ln{\mathit{q}}_d$, and the matrices $K_i>0$, $i:pt,pr,vt,vr$ are composed by the tuning parameters. From (25) the control law is applied to the model (15) according to the following equivalence:

$$\left[\begin{array}{c}{F}_u\\ {\mathsf{\tau }}_u\end{array}\right]=\left[\begin{array}{c}-m\overline{g}-K_{pt}\left(p-p_d\right)-K_{vt}\left(\dot{p}-{\dot{p}}_d\right)\\ -2K_{pr}ln\left({\mathit{q}}_e\right)-K_{vr}\left(\dot{\overline{\mathsf{\theta }}}-{\dot{\overline{\mathsf{\theta }}}}_d\right)\end{array}\right],$$

(34)

The obtained control law in quaternion space guarantees the stabilization of all the system states without any change in the model or in the PBC strategy. From (8) can be observed that the PBC algorithm using Euler angles allows only to control the attitude.

Control Strategy Comparison

The comparison of various algorithms based on passivity applied to a quad-rotor are summarized on the

Table 1. Qualitative comparison of control algorithms based on passivity applied to a quad-rotor.

Characteristic	References
	[17]	[18]	[19]	[20]	[21]	Our work
The algorithm avoids complicated PDEs 1	×	×	×	×	√	√
Quad-rotor full dynamics control	√	√	×	√	√	√
There is not change in the UAV mechanical structure 2	×	×	√	√	√	√
Simple real-time experiments	×	×	×	√	×	√
Three-dimensional maneuvers	√	√	×	×	×	√
The algorithm has no issues with singularities	×	×	×	×	×	√

¹ The control algorithm allows to compute the control law without solving complex PDEs. PDEs: Partial Differential Equations; ² That is when the mechanical structure has not been modified in order to obtain coupling between longitudinal and lateral movements with roll and pitch motions. UAV: Unmanned Aerial Vehicle.

.

5. Numerical Validation

In order to validate the proposed mathematical scheme, the model and control law were simulated in a computer programming environment.

The control gains were selected beginning from identity matrices and adjusted empirically such that stable behavior of the system was well appreciated. $K_{pr}$ and $K_{pt}$ are adjusted to ensure the convergence to the desired references for the attitude and position respectively, while $K_{vr}$ and $K_{vt}$ act by reducing the setting time and the overshoot for the rotational and translational dynamics respectively. The values applied on the simulation are the following

$$\begin{array}{c}\hfill K_{pt}=k_{pt}{I}_{3\times 3},K_{pr}=k_{pr}{I}_{3\times 3}\\ \hfill K_{vt}=k_{vt}{I}_{3\times 3},K_{vr}=k_{vr}{I}_{3\times 3}\end{array}$$

with $k_{pt}=5$, $k_{pr}=50$, $k_{vt}=4$, and $k_{vr}=10$.

Our research team makes every effort to validate most of our algorithms in real experimental platforms. One of the drones we commonly use for tests is the Parrot AR Drone 2 which is cheap and easy to handle for attitude and position experiments, and was modified with a software framework that is compatible with other quad-rotors that our team has developed for more specific applications. For this reason, the mass and inertia matrix for the Parrot AR Drone 2 were needed, thus obtained from [30], and used in our simulations.

$$\begin{array}{ccc}\hfill J& =& \left[\begin{array}{ccc}2.04016& 0& 0\\ 0& 1.56771& 0\\ 0& 0& 3.51779\end{array}\right]\times {10}^4\left[gc{m}^3\right]\hfill \\ \hfill m& =& 430.6g\hfill \\ \hfill \end{array}$$

Simulation Results

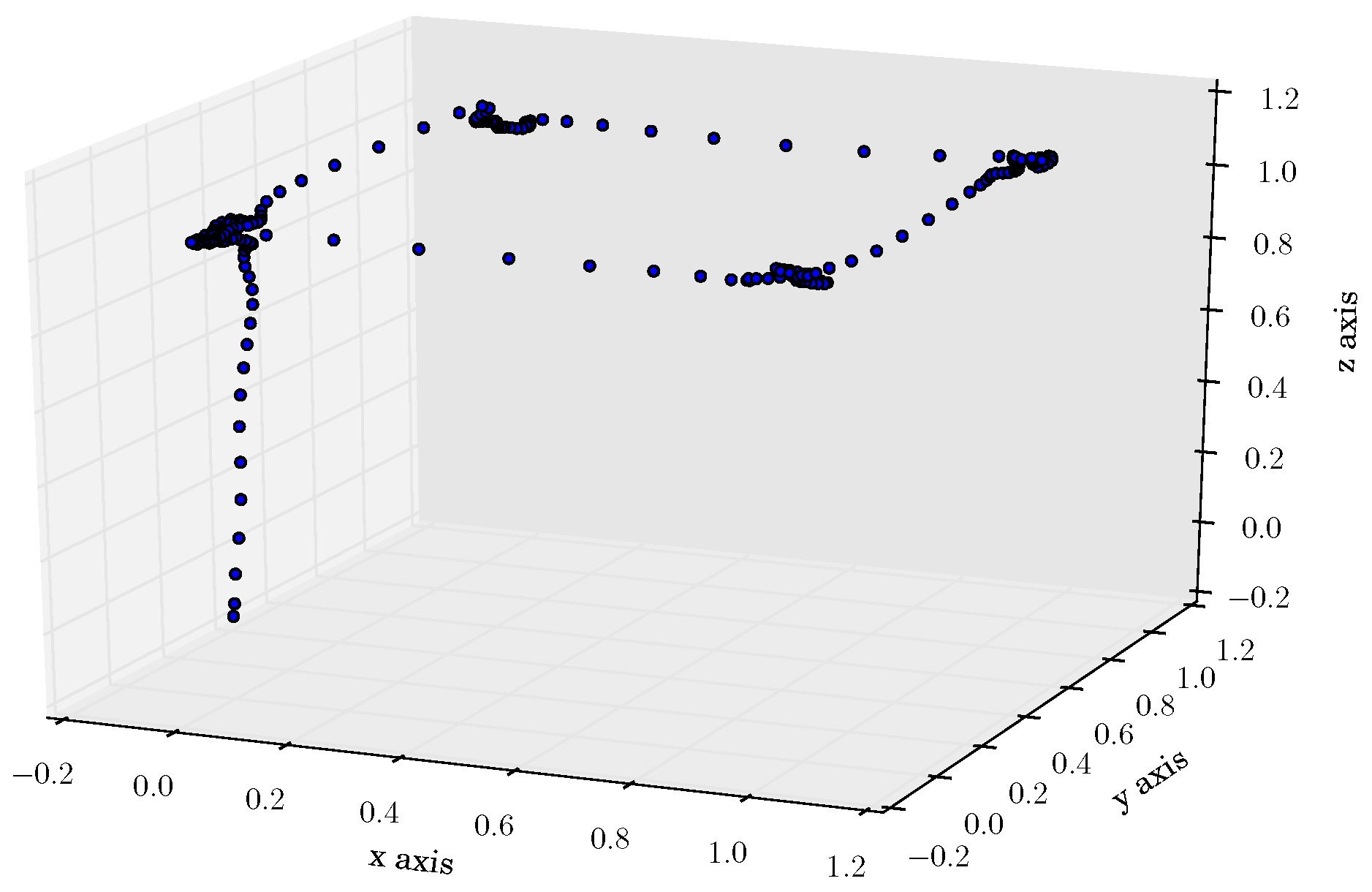
A simulated experiment was designed in which a position reference is given to the quad-rotor. A sequence of five set-points are defined in a time lapse of 25 seconds, thus following a 1 meter square at 1 meter height as illustrated in Figure 3.

$$p_d=\left\{\begin{array}{cccc}{\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}^T\hfill & ,& t& <5\hfill \\ {\left[\begin{array}{ccc}1& 0& 1\end{array}\right]}^T\hfill & ,& \hfill 5<=& t& <10\hfill \\ {\left[\begin{array}{ccc}1& 1& 1\end{array}\right]}^T\hfill & ,& \hfill 10<=& t& <15\hfill \\ {\left[\begin{array}{ccc}0& 1& 1\end{array}\right]}^T\hfill & ,& \hfill 15<=& t& <20\hfill \\ {\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}^T\hfill & ,& \hfill 20<=& t\end{array}\right.$$

(35)

In order to proof in simulation the robustness to unknown bounded perturbations, additive uniformly distributed noise was considered with bounds empirically chosen between $\pm 0.5\mathrm{m}$ for the position, and between $\pm 5\%$ for the orientation, and translational and rotational velocities.

The feedback translational signals plus the additive noise close the loop to calculate the required force (see Figure 4a) to move the vehicle in the 3D (3-dimensional) space. Note in this figure that the force in the z axis is stabilized around $mg=(0.4306)(9.81)=4.22\mathrm{N}$ in order to maintain the vehicle’s altitude. The control torques are calculated such that the vehicle’s orientation $\mathit{q}$ follows the trajectory ${\mathit{q}}_d$, see Figure 4b.

The force in the inertial frame is then used to compute the orientation trajectory which will point the thrust force to the required direction in the inertial frame. Figure 5 illustrates the trajectory tracking for the vehicle’s attitude, illustrated in axis-angle representation for a better understanding, here, $\overline{\mathsf{\theta }}=2ln\mathit{q}$, and ${\overline{\mathsf{\theta }}}_d=2ln{\mathit{q}}_d$.

Finally, Figure 6 represents the translational stabilization. In the first one, the position for each axis is stabilized according to the reference.

The quality indicator IAE (Integral of Absolute Error) is chosen to compare the behavior and efficiency of the proposed controller with other control techniques for a quad-rotor using a quaternion representation of the attitude. PD (Proportional Derivative), LQR (Linear Quadratic Regulator) and backstepping control strategies presented in [12] are selected to compare them with the PBC strategy. The results of IAE are shown in

Table 2. Comparison of control strategies applied to a quad-rotor.

Strategy	Quality Indicator IAE 1
	$I_{AEX}$	$I_{AEY}$	$I_{AEZ}$
PD 1	12.98	12.96	12.31
LQR 1	13.35	13.26	13.15
Backstepping	13.30	13.38	12.07
PBC 1	13.08	13.08	11.98

¹ IAE: Integral of Absolute Error; PD: Proportional Derivative; LQR: Linear Quadratic Regulator; PBC: Passivity-Based Control.

.

We can observe that the quality indicators IAE for the four strategies are similar, i.e., they exhibit a very similar behavior. The two controller with better performance are PD and PBC for the positions x and y, Backstepping and PBC for the position z.

6. Flight Tests

Our proposed strategy was validated with real time indoor experiments using one of our laboratory’s Parrot AR Drone 2 vehicles (Vedio S1). This UAV’s firmware was modified to work under a software framework which runs a Linux-based operating system, capable of implementing a wide range of conceived control schemes. An OptiTrack motion capture system was used to estimate the vehicle’s position and translational velocity, which was communicated to the drone using a Wi-Fi LAN, while its internal Inertial Measurement Unit (IMU) was used to measure its attitude quaternion and angular velocity, this configuration was chosen to maintain a minimal bandwidth usage in the wireless communications.

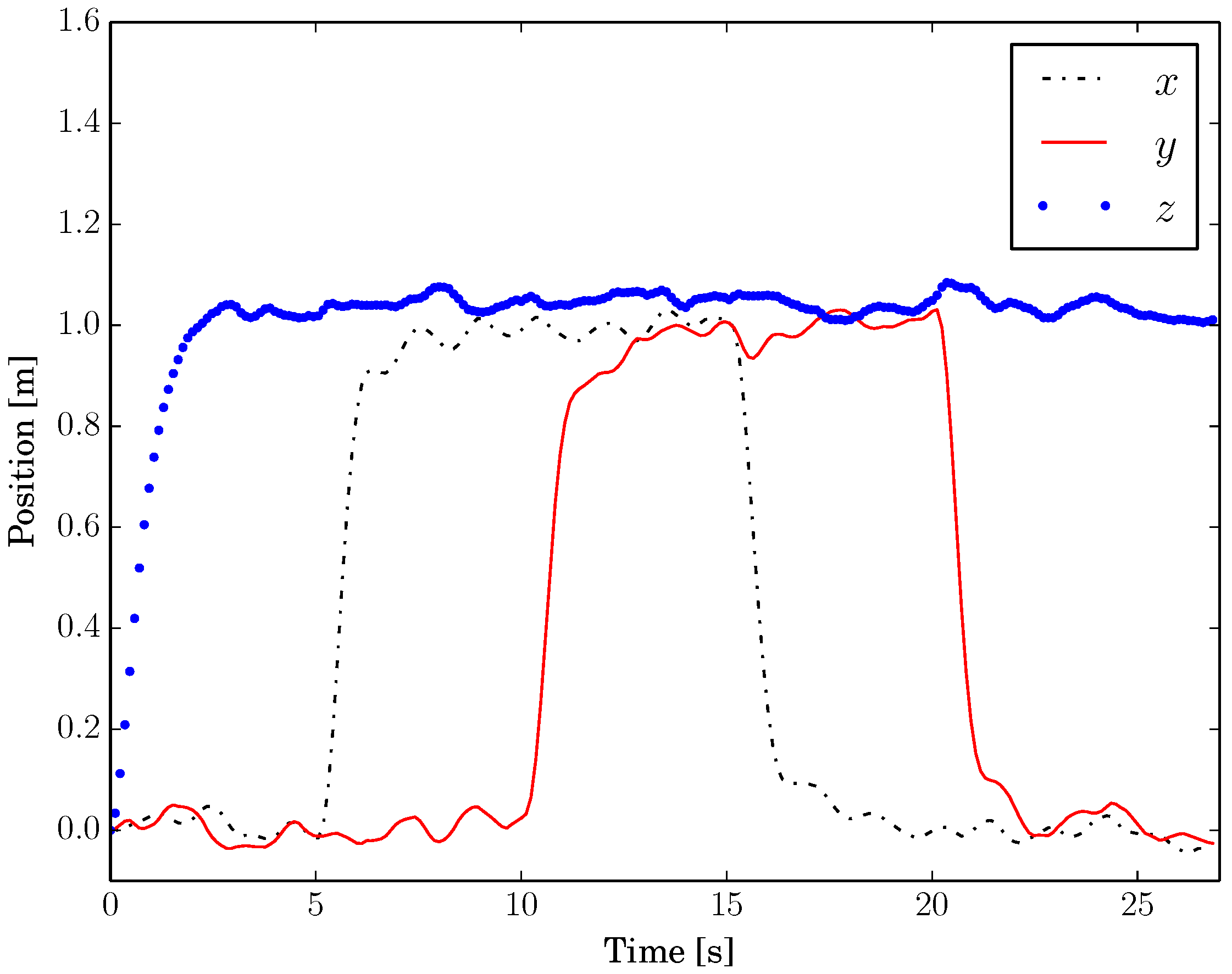
A Sony DualShock 3 controller was used to input a 3-dimensional position and velocity trajectory, which was controlled by one of our team members using joysticks. The generated trajectory was set as the desired position for the drone. Figure 7 illustrates the UAV’s real trajectory and its reference in a real time experiment.

The trajectory given by the joystick is considerably fast, making strong movements to prove robustness. Notice the delay between the quad-rotor’s position and its reference when it is moving, and the convergence to the desired position when the reference is held static.

A desired control force is then computed using the position error, which is represented in Figure 8. The z component maintains a negative offset due to a compensation of the gravitational effects.

Since our framework is compatible with three different UAV configurations and models, the thrust force was set to be dimensionless. This means a force with norm 1 makes the motors output a maximum thrust, while norm 0 translates in no thrust force.

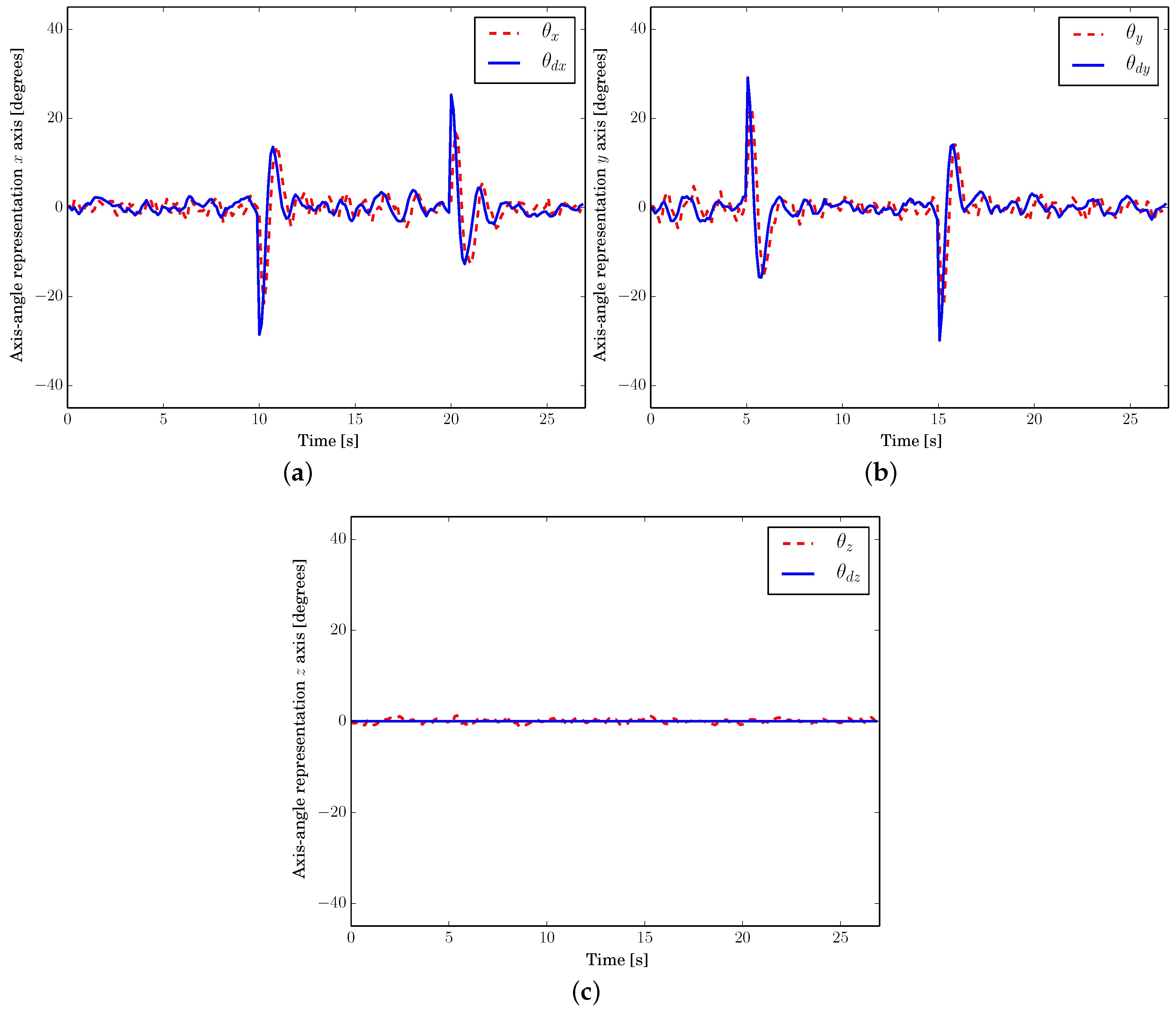
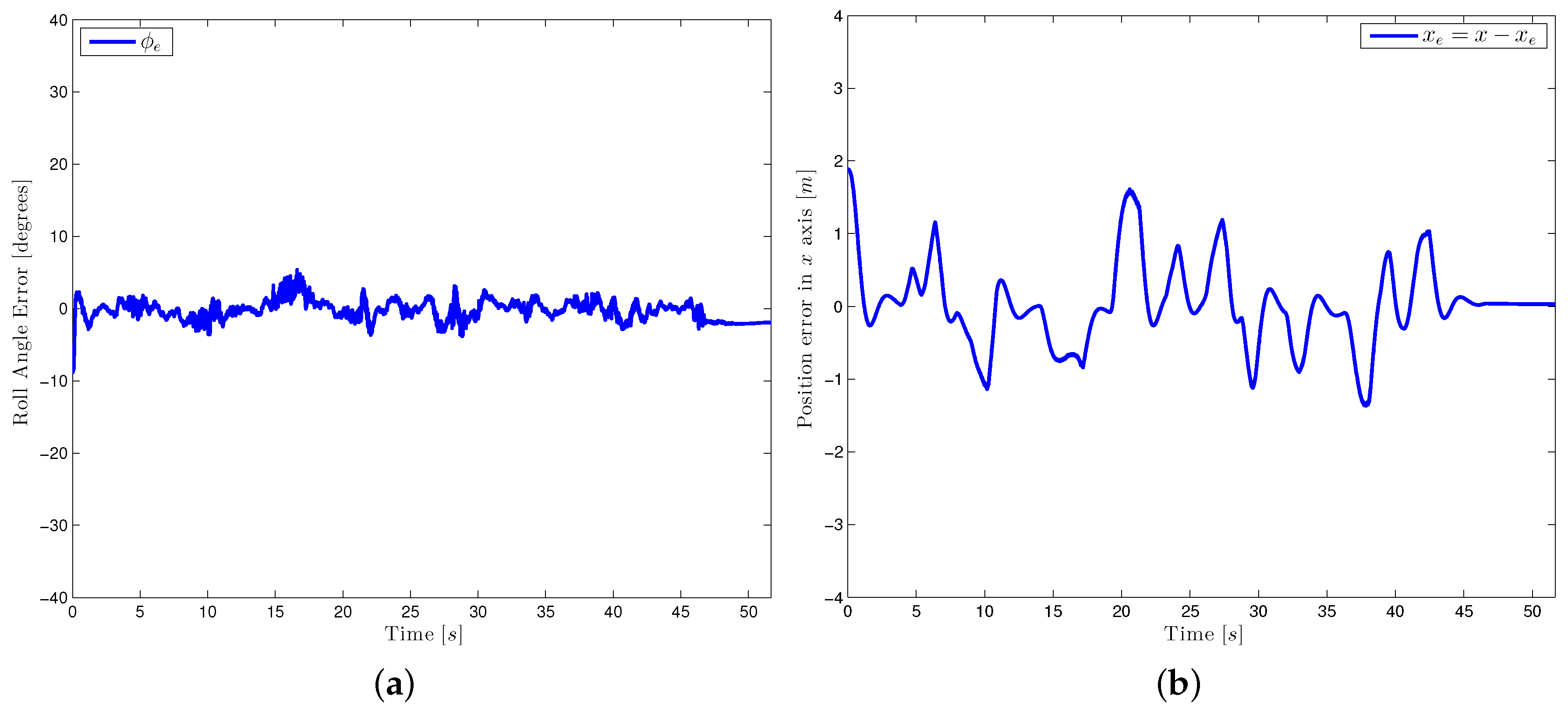
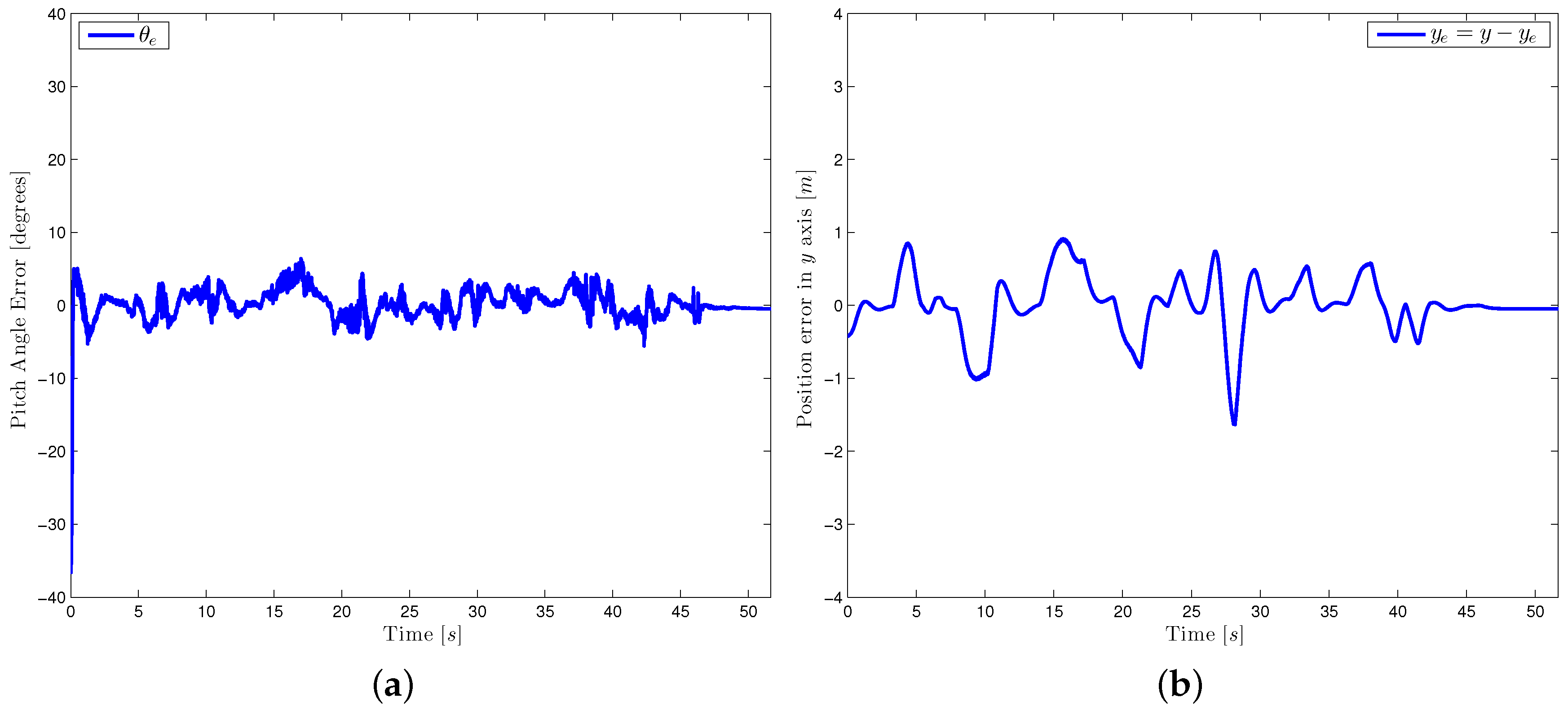
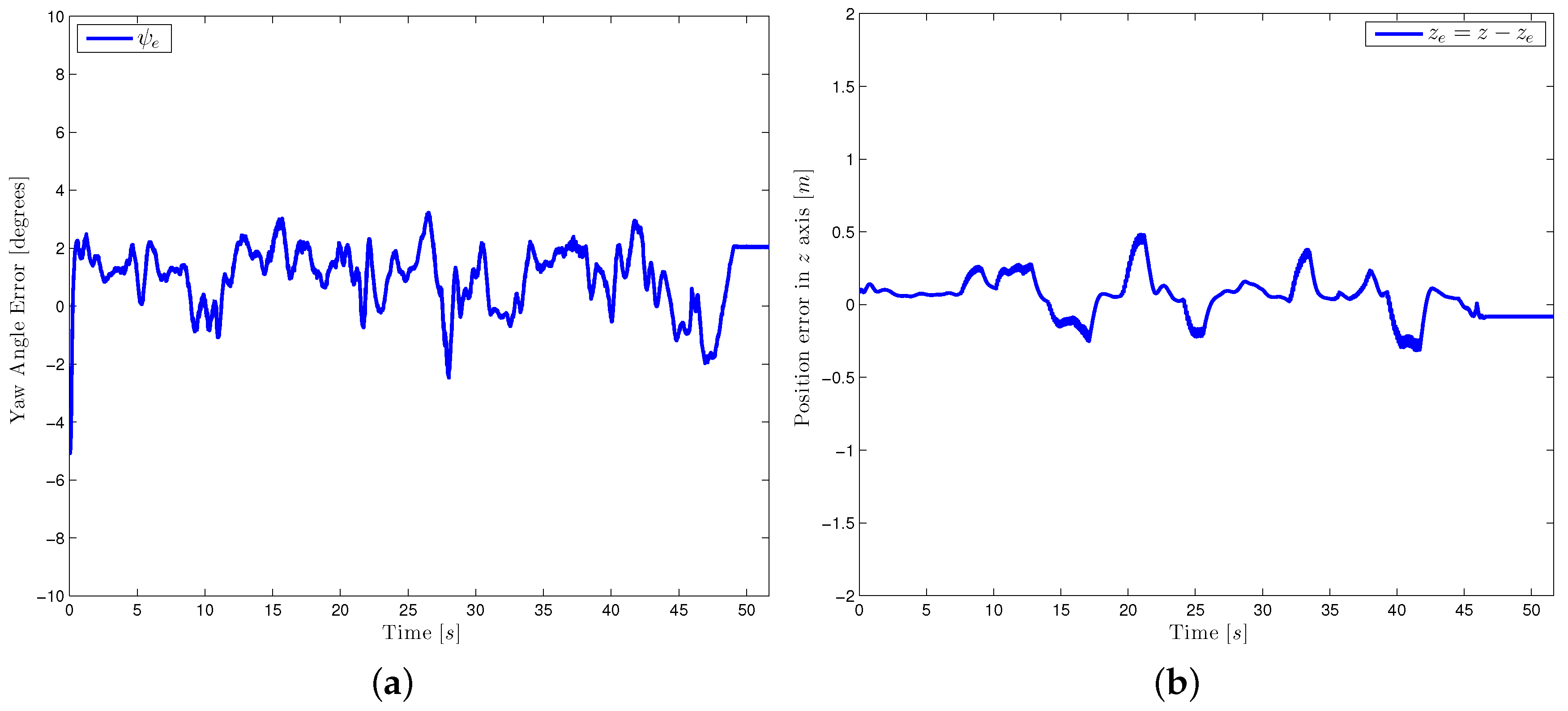
An attitude trajectory is now used to rotate the thrust force into the translational control law’s direction. The orientation controller then, assures the vehicle’s convergence to this reference. For a better visualization of the attitude dynamics, the equivalent Euler angles of the orientation error are illustrated in Figure 9a, Figure 10a, Figure 11a, note the stabilization of around zero.

Finally, Figure 9b, Figure 10b, Figure 11b represent the stabilization of the position error. Note the proposed control strategy well stabilizes the quad-rotor, even if the desired trajectories include strong displacements.

7. Conclusions

In this work, a mathematical model via the Euler-Lagrange formalism using the axis-angle attitude representation of a unit quaternion by its logarithmic mapping was presented. The mathematical model using quaternions was found to be a fully-actuated system and this simplifies the control law design.

A new methodology: quaternion-passivity-based control for a quad-rotor was presented. The proposed algorithm does not compute excessive and complex partial differential equations for obtaining the control law. The methodology can be designed directly from the model and can control the full quad-rotor dynamics.

The developed control scheme avoided the issues with singularities and was found to perform with good results for the control objective, as shown in the simulations and real-time results.

Future works include the use of this strategy for aerial manipulation tasks.