An Equivalent Layer-Wise Approach for the Free Vibration Analysis of Thick and Thin Laminated and Sandwich Shells
Abstract
:1. Introduction
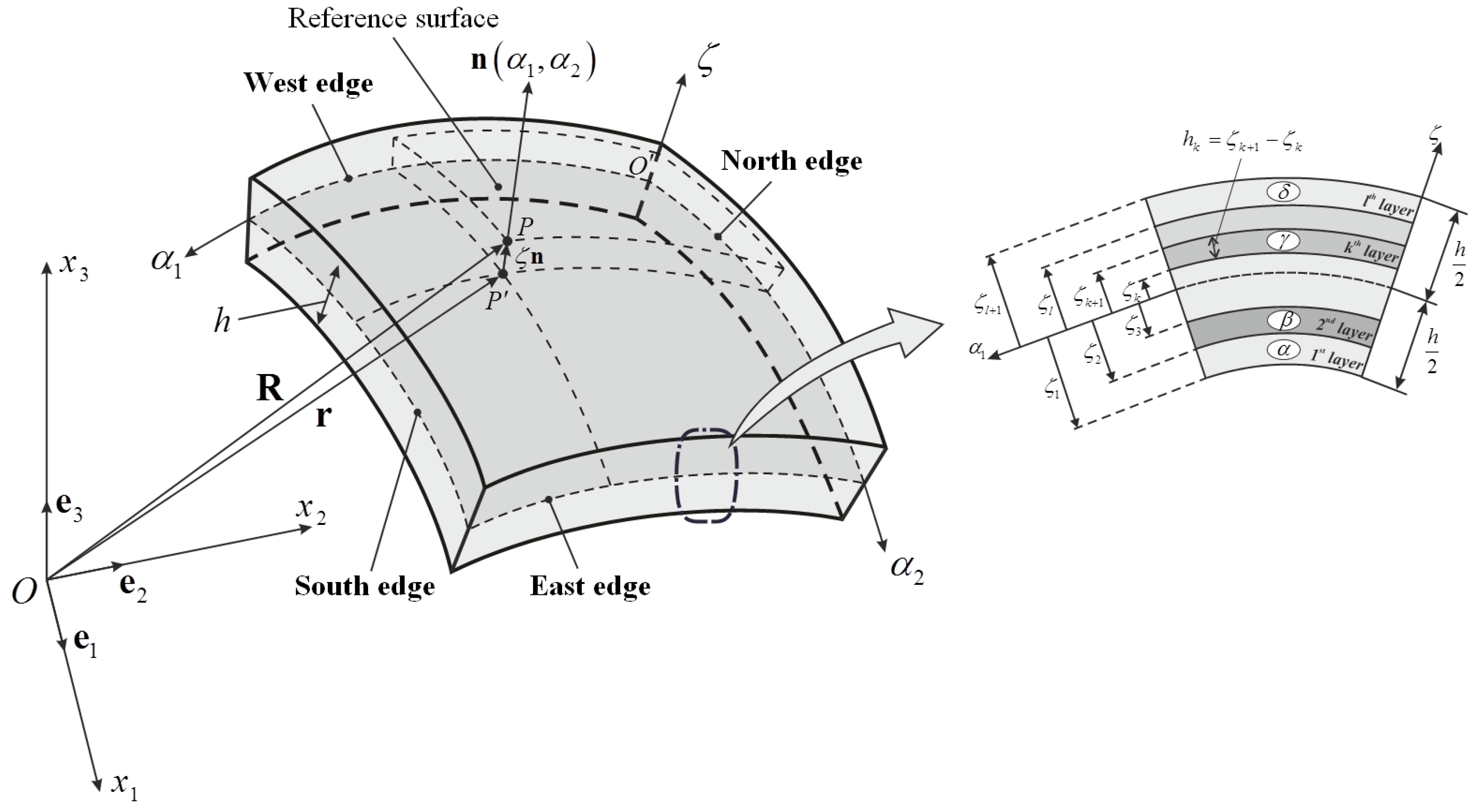
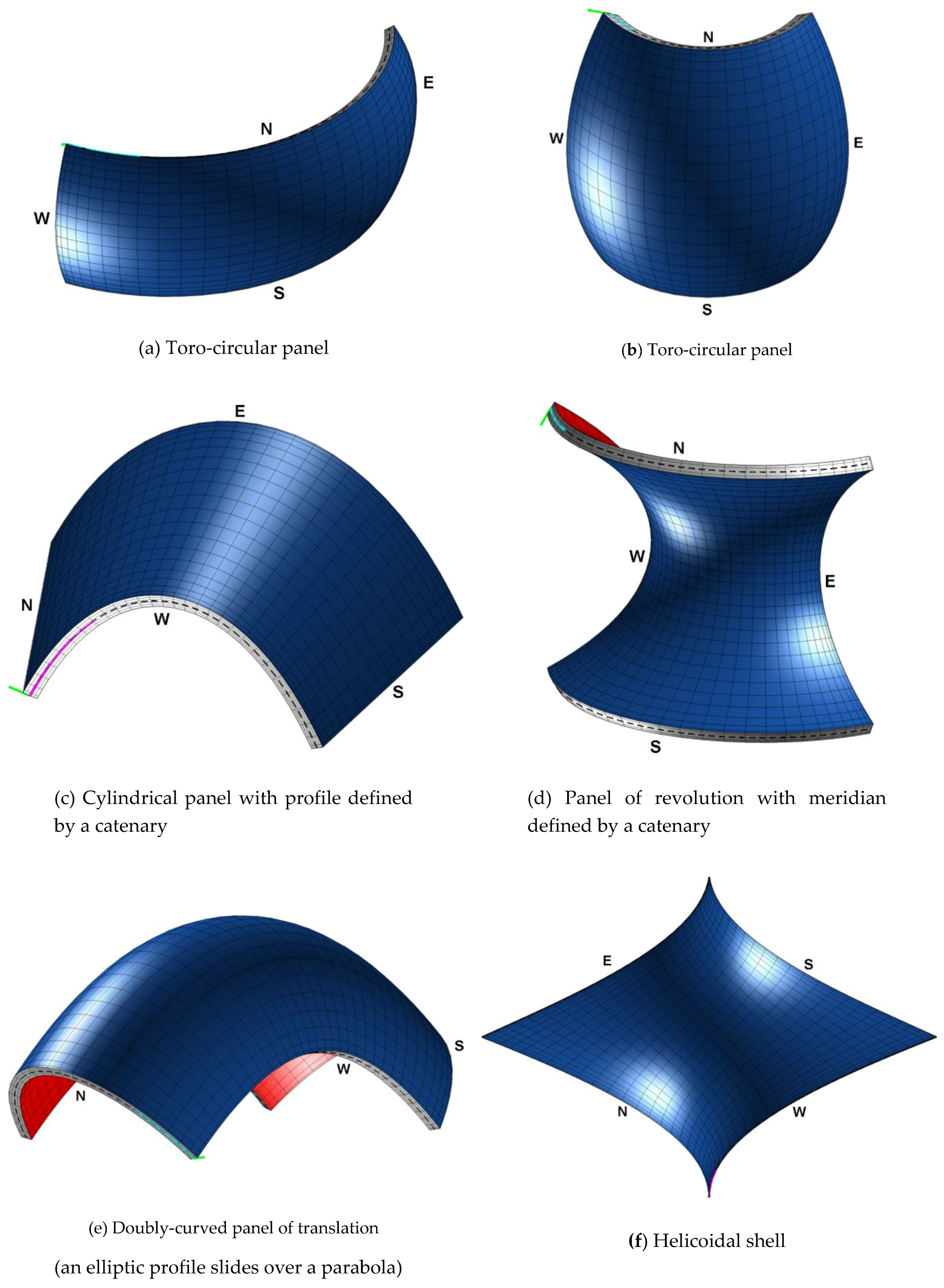
2. Definition of the Geometry
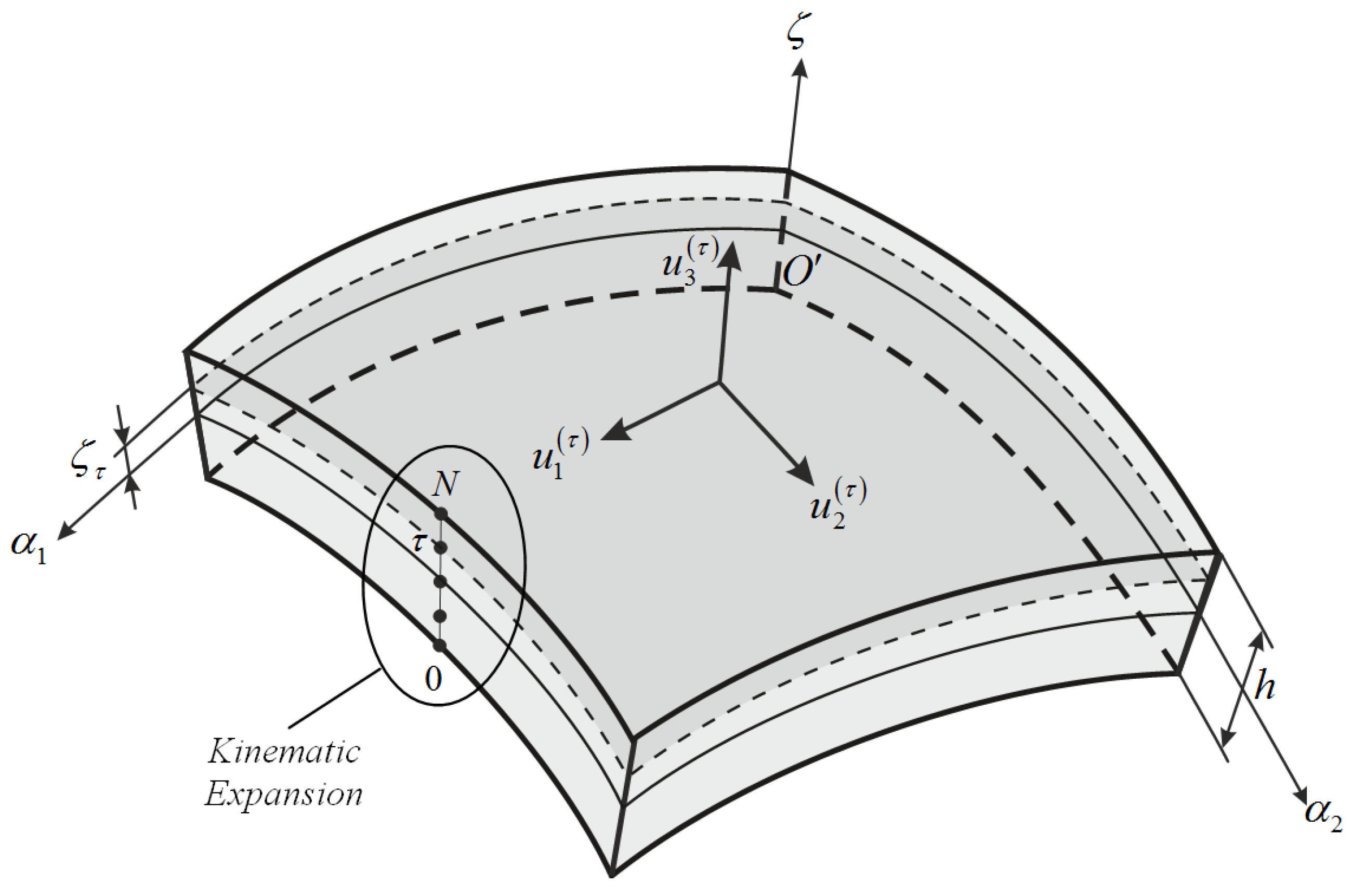
3. Higher-Order Equivalent Layer-Wise Approach
4. Generalized Differential Quadrature Method
5. Generalized Integral Quadrature Method
6. Free Vibration Analysis
7. Numerical Results
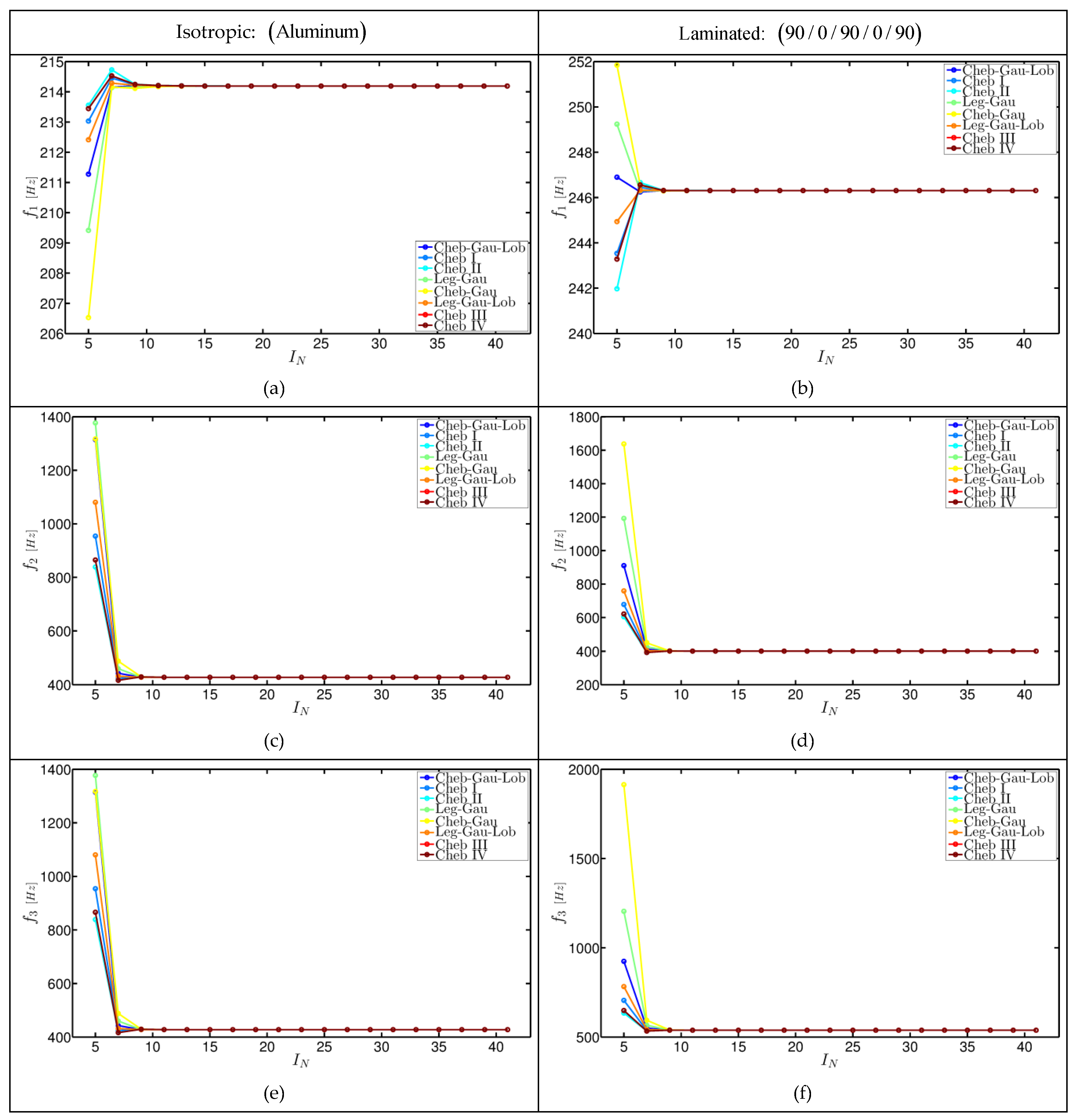
7.1. Convergence Analysis
7.2. Free vibrations of Laminated Composite Shells
7.3. Comparison with the LW and ESL Approaches
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Reddy, J.N. Mechanics of laminated composite plates and shells, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Laminated Composite Doubly-Curved Shell Structures. Differential Geometry Higher-order Structural Theories, 1st ed.; Societa Edirtrice Esculapio: Bologna, Italy, 2016. [Google Scholar]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Laminated Composite Doubly-Curved Shell Structures. Differential and Integral Quadrature. Strong Formulation Finite Element Method, 1st ed.; Societa Edirtrice Esculapio: Bologna, Italy, 2016. [Google Scholar]
- Fantuzzi, N.; Brischetto, S.; Tornabene, F.; Viola, E. 2D and 3D Shell Models for the Free Vibration Investigation of Functionally Graded Cylindrical and Spherical Panels. Compos. Struct. 2016, 154, 573–590. [Google Scholar] [CrossRef]
- Brischetto, S.; Tornabene, F.; Fantuzzi, N.; Viola, E. 3D Exact and 2D Generalized Differential Quadrature Models for Free Vibration Analysis of Functionally Graded Plates and Cylinders. Meccanica 2016, 51, 2059–2098. [Google Scholar] [CrossRef]
- Gutierrez Rivera, M.; Reddy, J.N.; Amabili, M. A new twelve-parameter spectral/hp shell finite element for large deformation analysis of composite shells. Compos. Struct. 2016, 151, 183–196. [Google Scholar] [CrossRef]
- Groh, R.M.J.; Weaver, P.M. A computationally efficient 2D model for inherently equilibrated 3D stress predictions in heterogeneous laminated plates. Part I: Model formulation. Compos. Struct. 2016, 156, 171–185. [Google Scholar]
- Groh, R.M.J.; Weaver, P.M. A computationally efficient 2D model for inherently equilibrated 3D stress predictions in heterogeneous laminated plates. Part II: Model validation. Compos. Struct. 2016, 156, 186–217. [Google Scholar]
- Amabili, M. A new third-order shear deformation theory with non-linearities in shear for static and dynamic analysis of laminated doubly curved shells. Compos. Struct. 2015, 128, 260–273. [Google Scholar] [CrossRef]
- Maturi, D.A.; Ferreira, A.J.M.; Zenkour, A.M.; Mashat, D.S. Analysis of Laminated Shells by Murakami’s Zig-Zag Theory and Radial Basis Functions Collocation. J. Appl. Math. 2013, 2013, 1–14. [Google Scholar] [CrossRef]
- Kulikov, G.M.; Mamontov, A.A.; Plotnikova, S.V.; Mamontov, S.A. Exact geometry solid-shell element based on a sampling surfaces technique for 3D stress analysis of doubly-curved composite shells. Curved Layer. Struct. 2016, 3, 1–16. [Google Scholar] [CrossRef]
- Neves, A.M.A.; Ferreira, A.J.M. Free vibrations and buckling analysis of laminated plates by oscillatory radial basis functions. Curved Layer. Struct. 2016, 3, 17–21. [Google Scholar] [CrossRef]
- Wang, Q.; She, D.; Pang, F.; Liang, Q. Vibrations of Composite Laminated Circular Panels and Shells of Revolution with General Elastic Boundary Conditions via Fourier-Ritz Method. Curved Layer. Struct. 2016, 3, 105–136. [Google Scholar] [CrossRef]
- Piskunov, V.G.; Verijenko, V.E.; Adali, S.; Summers, E.B. A Higher-order Theory for the Analysis of Laminated Plates and Shells with Shear and Normal Deformation. Int. J. Engng. Sci. 1993, 31, 967–988. [Google Scholar] [CrossRef]
- Wu, C.-P.; Hung, Y.-C. Asymptotic theory of laminated circular conical shells. Int. J. Engng. Sci. 1999, 37, 977–1005. [Google Scholar] [CrossRef]
- Brischetto, S. An exact 3d solution for free vibrations of multilayered cross-ply composite and sandwich plates and shells. Int. J. Appl. Mechanics 2014, 6, 1450076. [Google Scholar] [CrossRef]
- Brischetto, S.; Torre, R. Exact 3D solutions and finite element 2D models for free vibration analysis of plates and cylinders. Curved Layer. Struct. 2014, 1, 59–92. [Google Scholar] [CrossRef]
- Le, K.C.; Yi, J.-H. An asymptotically exact theory of smart sandwich shells. Int. J. Eng. Sci. 2016, 106, 179–198. [Google Scholar]
- Ye, T.; Jin, G.; Zhang, Y. Vibrations of composite laminated doubly-curved shells of revolution with elastic restraints including shear deformation, rotary inertia and initial curvature. Compos. Struct. 2015, 133, 202–225. [Google Scholar] [CrossRef]
- Kim, J.; Reddy, J.N. A general third-order theory of functionally graded plates with modified couple stress effect and the von Kármán nonlinearity: Theory and finite element analysis. Acta Mech. 2015, 226, 2973–2998. [Google Scholar] [CrossRef]
- Librescu, L.; Reddy, J.N. A few remarks concerning several refined theories of anisotropic composite laminated plates. Int. J. Eng. Sci. 1989, 27, 515–527. [Google Scholar] [CrossRef]
- Whitney, J.M.; Pagano, N.J. Shear Deformation in Heterogeneous Anisotropic Plates. J. Appl. Mech.-T. ASME 1970, 37, 1031–1036. [Google Scholar] [CrossRef]
- Whitney, J.M.; Sun, C.T. A Higher Order Theory for Extensional Motion of Laminated Composites. J. Sound Vib. 1973, 30, 85–97. [Google Scholar] [CrossRef]
- Reissner, E. On transverse bending of plates, including the effect of transverse shear deformation. Int. J. Solids Struct. 1975, 11, 569–573. [Google Scholar] [CrossRef]
- Murthy, M.V.V. An Improved Transverse Shear Deformation Theory for Laminated Anisotropic Plates; NASA Technical Paper; NASA: Hampton, VA, USA, 1981.
- Green, A.E.; Naghdi, P.M. A theory of composite laminated plates. IMA J. Appl. Math. 1982, 29, 1–23. [Google Scholar] [CrossRef]
- Bert, C.W. A Critical Evaluation of New Plate Theories Applied to Laminated Composites. Compos. Struct. 1984, 2, 329–347. [Google Scholar] [CrossRef]
- Reddy, J.N. A Simple Higher-Order Theory for Laminated Composite Plates. J. Appl. Mech.-T. ASME 1984, 51, 745–752. [Google Scholar] [CrossRef]
- Shirakawa, K. Bending of plates based on improved theory. Mech. Res. Commun. 1985, 10, 205–211. [Google Scholar] [CrossRef]
- Reddy, J.N.; Liu, C.F. A higher-order shear deformation theory for laminated elastic shells. Int. J. of Eng. Sci. 1985, 23, 319–330. [Google Scholar]
- Reddy, J.N. A Generalization of the Two-Dimensional Theories of Laminated Composite Plates. Commun. Appl. Numer. M. 1987, 3, 173–180. [Google Scholar] [CrossRef]
- Reddy, J.N. On Refined Theories of Composite Laminates. Meccanica 1990, 25, 230–238. [Google Scholar] [CrossRef]
- Robbins, D.H.; Reddy, J.N. Modeling of Thick Composites Using a Layer-Wise Laminate Theory. Int. J. Numer. Meth. Eng. 1993, 36, 655–677. [Google Scholar] [CrossRef]
- Alibeiglooa, A.; Shakeri, M.; Kari, M.R. Free vibration analysis of antisymmetric laminated rectangular plates with distributed patch mass using third-order shear deformation theory. Ocean Eng. 2008, 35, 183–190. [Google Scholar] [CrossRef]
- Xiang, S.; Wang, K.-M. Free vibration analysis of symmetric laminated composite plates by trigonometric shear deformation theory and inverse multiquadric RBF. Thin Wall. Struct. 2009, 47, 304–310. [Google Scholar] [CrossRef]
- Amabili, M.; Reddy, J.N. A new non-linear higher-order shear deformation theory for large-amplitude vibrations of laminated doubly curved shells. Int. J. Nonlinear Mech. 2010, 45, 409–418. [Google Scholar] [CrossRef]
- Thai, H.-T.; Kim, S.-E. Free vibration of laminated composite plates using two variable refined plate theory. Int. J. Mech. Sci. 2010, 52, 626–633. [Google Scholar] [CrossRef]
- Kumar, A.; Chakrabarti, A.; Bhargava, P. Vibration of laminated composites and sandwich shells based on higher order zigzag theory. Eng. Struct. 2013, 56, 880–888. [Google Scholar] [CrossRef]
- Viola, E.; Tornabene, F.; Fantuzzi, N. General Higher-Order Shear Deformation Theories for the Free Vibration Analysis of Completely Doubly-Curved Laminated Shells and Panels. Compos. Struct. 2013, 95, 639–666. [Google Scholar] [CrossRef]
- Viola, E.; Tornabene, F.; Fantuzzi, N. Static Analysis of Completely Doubly-Curved Laminated Shells and Panels Using General Higher-order Shear Deformation Theories. Compos. Struct. 2013, 101, 59–93. [Google Scholar] [CrossRef]
- Viola, E.; Rossetti, L.; Fantuzzi, N.; Tornabene, F. Static Analysis of Functionally Graded Conical Shells and Panels Using the Generalized Unconstrained Third Order Theory Coupled with the Stress Recovery. Compos. Struct. 2014, 112, 44–65. [Google Scholar] [CrossRef]
- Sahoo, R.; Singh, B.N. A new trigonometric zigzag theory for buckling and free vibration analysis of laminated composite and sandwich plates. Compos. Struct. 2014, 117, 316–332. [Google Scholar] [CrossRef]
- Vidal, P.; Polit, O.; D’Ottavio, M.; Valot, E. Assessment of the refined sinus plate finite element: Free edge effect and Meyer-Piening sandwich test. Finite Elem. Anal. Des. 2014, 92, 60–71. [Google Scholar] [CrossRef]
- Wang, X.; Shi, G. A refined laminated plate theory accounting for the third-order shear deformation and interlaminar transverse stress continuity. Appl. Math. Model. 2015, 39, 5659–5680. [Google Scholar] [CrossRef]
- Zuo, H.; Yang, Z.; Chen, X.; Xie, Y.; Miao, H. Analysis of laminated composite plates using wavelet finite element method and higher-order plate theory. Compos. Struct. 2015, 131, 248–258. [Google Scholar] [CrossRef]
- Viola, E.; Rossetti, L.; Fantuzzi, N.; Tornabene, F. Generalized Stress-Strain Recovery Formulation Applied to Functionally Graded Spherical Shells and Panels Under Static Loading. Compos. Struct. 2016, 156, 145–164. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Farid, M.; Zahedinejad, P. A three-dimensional layerwise-differential quadrature free vibration analysis of laminated cylindrical shells. Int. J. Pres. Ves. Pip. 2008, 85, 450–458. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Afsari, A.; Zahedinejad, P.; Bahadori, R. Three-dimensional layerwise-finite element free vibration analysis of thick laminated annular plates on elastic foundation. Appl. Math. Model. 2010, 34, 776–790. [Google Scholar] [CrossRef]
- Mantari, J.L.; Oktem, A.S.; Guedes Soares, C. A new trigonometric layerwise shear deformation theory for the finite element analysis of laminated composite and sandwich plates. Comput. Struct. 2012, 94–95, 45–53. [Google Scholar] [CrossRef]
- Thai, C.H.; Ferreira, A.J.M.; Carrera, E.; Nguyen-Xuan, H. Isogeometric analysis of laminated composite and sandwich plates using a layerwise deformation theory. Compos. Struct. 2013, 104, 196–214. [Google Scholar] [CrossRef]
- Mantari, J.L.; Guedes Soares, C. Generalized layerwise HSDT and finite element formulation for symmetric laminated and sandwich composite plates. Compos. Struct. 2013, 105, 319–331. [Google Scholar] [CrossRef]
- Guo, Y.; Nagy, A.P.; Gürdal, Z. A layerwise theory for laminated composites in the framework of isogeometric analysis. Compos. Struct. 2014, 107, 447–457. [Google Scholar] [CrossRef]
- Boscolo, M.; Banerjee, J.R. Layer-wise dynamic stiffness solution for free vibration analysis of laminated composite plates. J. Sound Vib. 2014, 333, 200–227. [Google Scholar] [CrossRef]
- Yazdani, S.; Ribeiro, P. A layerwise p-version finite element formulation for free vibration analysis of thick composite laminates with curvilinear fibres. Compos. Struct. 2015, 120, 531–542. [Google Scholar] [CrossRef]
- Band, U.N.; Desai, Y.M. Coupled higher order and mixed layerwise finite element based static and free vibration analyses of laminated plates. Compos. Struct. 2015, 128, 406–414. [Google Scholar] [CrossRef]
- Li, D.H. Extended layerwise method of laminated composite shells. Compos. Struct. 2016, 136, 313–344. [Google Scholar] [CrossRef]
- Carrera, E. Theories and Finite Elements for Multilayered, Anisotropic, Composite Plates and Shells. Arch. Comput. Meth. Eng. 2002, 9, 87–140. [Google Scholar] [CrossRef]
- Carrera, E. Historical review of zig-zag theories for multilayered plates and shells. Appl. Mech. Rev. 2003, 56, 287–308. [Google Scholar] [CrossRef]
- Carrera, E. On the use of the Murakami’s zig-zag function in the modeling of layered plates and shells. Comput. Struct. 2004, 82, 541–554. [Google Scholar] [CrossRef]
- Biscani, F.; Giunta, G.; Belouettar, S.; Hu, H.; Carrera, E. Mixed-dimensional modeling by means of solid and higher-order multi-layered plate finite elements. Mech. Adv. Mat. Struct. 2016, 23, 960–970. [Google Scholar] [CrossRef]
- Tornabene, F.; Viola, E.; Fantuzzi, N. General higher-order equivalent single layer theory for free vibrations of doubly-curved laminated composite shells and panels. Compos. Struct. 2013, 104, 94–117. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Viola, E.; Carrera, E. Static Analysis of Doubly-Curved Anisotropic Shells and Panels Using CUF Approach, Differential Geometry and Differential Quadrature Method. Compos. Struct. 2014, 107, 675–697. [Google Scholar] [CrossRef]
- Tornabene, F; Fantuzzi, N.; Viola, E.; Reddy, J.N. Winkler-Pasternak Foundation Effect on the Static and Dynamic Analyses of Laminated Doubly-Curved and Degenerate Shells and Panels. Compos. Part B-Eng. 2014, 57, 269–296. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. The Local GDQ Method Applied to General Higher-Order Theories of Doubly-Curved Laminated Composite Shells and Panels: The Free Vibration Analysis. Compos. Struct. 2014, 116, 637–660. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Free vibrations of free-form doubly-curved shells made of functionally graded materials using higher-order equivalent single layer theories. Compos. Part B Eng. 2014, 67, 490–509. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Viola, E.; Batra, R.C. Stress and strain recovery for functionally graded free-form and doubly-curved sandwich shells using higher-order equivalent single layer theory. Compos. Struct. 2015, 119, 67–89. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Higher-Order Theories for the Free Vibration of Doubly-Curved Laminated Panels with Curvilinear Reinforcing Fibers by Means of a Local Version of the GDQ Method. Compos. Part B-Eng. 2015, 81, 196–230. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Effect of Agglomeration on the Natural Frequencies of Functionally Graded Carbon Nanotube-Reinforced Laminated Composite Doubly-Curved Shells. Compos. Part B-Eng. 2016, 89, 187–218. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. The Local GDQ Method for the Natural Frequencies of Doubly-Curved Shells with Variable Thickness: A General Formulation. Compos. Part B-Eng. 2016, 92, 265–289. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Viola, E. Inter-Laminar Stress Recovery Procedure for Doubly-Curved, Singly-Curved, Revolution Shells with Variable Radii of Curvature and Plates Using Generalized Higher-Order Theories and the Local GDQ Method. Mech. Adv. Mat. Struct. 2016, 23, 1019–1045. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. The GDQ Method for the Free Vibration Analysis of Arbitrarily Shaped Laminated Composite Shells Using a NURBS-Based Isogeometric Approach. Compos. Struct. 2016, 154, 190–218. [Google Scholar] [CrossRef]
- Bacciocchi, M.; Eisenberger, M.; Fantuzzi, N.; Tornabene, F.; Viola, E. Vibration Analysis of Variable Thickness Plates and Shells by the Generalized Differential Quadrature Method. Compos. Struct. 2016, 156, 218–237. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Linear Static Response of Nanocomposite Plates and Shells Reinforced by Agglomerated Carbon Nanotubes. Compos. Part B-Eng. 2016, in press. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. On the Mechanics of Laminated Doubly-Curved Shells Subjected to Point and Line Loads. Int. J. Engng. Sci. 2016, 109, 115–164. [Google Scholar] [CrossRef]
- Dozio, L. A hierarchical formulation of the state-space Levy’s method for vibration analysis of thin and thick multilayered shells. Compos. Part B-Eng. 2016, 98, 97–107. [Google Scholar] [CrossRef]
- Dozio, L.; Alimonti, L. Variable kinematic finite element models of multilayered composite plates coupled with acoustic fluid. Mech. Adv. Mater. Struct. 2016, 23, 981–996. [Google Scholar] [CrossRef]
- Vescovini, R.; Dozio, L. A variable-kinematic model for variable stiffness plates: Vibration and buckling analysis. Compos. Struct. 2016, 142, 15–26. [Google Scholar] [CrossRef]
- Wenzel, C.; D’Ottavio, M.; Polit, O.; Vidal, P. Assessment of free-edge singularities in composite laminates using higher-order plate elements. Mech. Adv. Mat. Stuct. 2016, 23, 948–959. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Accurate Inter-Laminar Recovery for Plates and Doubly-Curved Shells with Variable Radii of Curvature Using Layer-Wise Theories. Compos. Struct. 2015, 124, 368–393. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Dimitri, R. Dynamic Analysis of Thick and Thin Elliptic Shell Structures Made of Laminated Composite Materials. Compos. Struct. 2015, 133, 278–299. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Dimitri, R. Free Vibrations of Composite Oval and Elliptic Cylinders by the Generalized Differential Quadrature Method. Thin-Wall. Struct. 2015, 97, 114–129. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Higher-Order Structural Theories for the Static Analysis of Doubly-Curved Laminated Composite Panels Reinforced by Curvilinear Fibers. Thin-Wall. Struct. 2016, 102, 222–245. [Google Scholar] [CrossRef]
- Tornabene, F. General Higher Order Layer-Wise Theory for Free Vibrations of Doubly-Curved Laminated Composite Shells and Panels. Mech. Adv. Mat. Struct. 2016, 23, 1046–1067. [Google Scholar] [CrossRef]
- Demasi, L. ∞3 Hierarchy plate theories for thick and thin composite plates: The generalized unified formulation. Compos. Struct. 2008, 84, 256–270. [Google Scholar] [CrossRef]
- D’Ottavio, M. A Sublaminate Generalized Unified Formulation for the analysis of composite structures. Compos. Struct. 2016, 142, 187–199. [Google Scholar] [CrossRef]
- Fazzolari, F.A. Reissner's Mixed Variational Theorem and variable kinematics in the modelling of laminated composite and FGM doubly-curved shells. Compos. Part B-Eng. 2016, 89, 408–423. [Google Scholar] [CrossRef]
- Fazzolari, F.A. Quasi-3D beam models for the computation of eigenfrequencies of functionally graded beams with arbitrary boundary conditions. Compos. Struct. 2016, 154, 239–255. [Google Scholar] [CrossRef]
- Fazzolari, F.A. Modal characteristics of P- and S-FGM plates with temperature-dependent materials in thermal environment. J. Therm. Stresses 2016, 39, 854–873. [Google Scholar] [CrossRef]
- Fazzolari, F.A.; Banerjee, J.R. Axiomatic/asymptotic PVD/RMVT-based shell theories for free vibrations of anisotropic shells using an advanced Ritz formulation and accurate curvature descriptions. Compos. Struct. 2014, 108, 91–110. [Google Scholar] [CrossRef]
- Shu, C. Differential quadrature and its application in engineering; Springer: Berlin, Germany, 2000. [Google Scholar]
- Tornabene, F.; Fantuzzi, N.; Ubertini, F.; Viola, E. Strong formulation finite element method based on differential quadrature: A survey. Appl. Mech. Rev. 2015, 67, 020801. [Google Scholar] [CrossRef]
- Tornabene, F.; Reddy, J.N. FGM and laminated doubly-curved and degenerate shells resting on nonlinear elastic foundations: A GDQ solution for static analysis with a posteriori stress and strain recovery. J. Indian Inst. Sci. 2013, 93, 635–688. [Google Scholar]
- Ferreira, A.J.M.; Carrera, E.; Cinefra, M.; Viola, E.; Tornabene, F.; Fantuzzi, N.; Zenkour, A.M. Analysis of Thick Isotropic and Cross-Ply Laminated Plates by Generalized Differential Quadrature Method and a Unified Formulation. Compos. Part B-Eng. 2014, 58, 544–552. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. The Strong Formulation Finite Element Method: Stability and Accuracy. Fract. Struct. Integr. 2014, 29, 251–265. [Google Scholar]
- Fantuzzi, N.; Bacciocchi, M.; Tornabene, F.; Viola, E.; Ferreira, A.J.M. Radial Basis Functions Based on Differential Quadrature Method for the Free Vibration of Laminated Composite Arbitrary Shaped Plates. Compos. Part B-Eng. 2015, 78, 65–78. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. A New Approach for Treating Concentrated Loads in Doubly-Curved Composite Deep Shells with Variable Radii of Curvature. Compos. Struct. 2015, 131, 433–452. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Tornabene, F. Strong Formulation Isogeometric Analysis (SFIGA) for Laminated Composite Arbitrarily Shaped Plates. Compos. Part B-Eng. 2016, 96, 173–203. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Neves, A.M.A.; Ferreira, A.J.M. MLSDQ Based on RBFs for the Free Vibrations of Laminated Composite Doubly-Curved Shells. Compos. Part B-Eng. 2016, 99, 30–47. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Dimitri, R.; Tornabene, F. A SFEM-Based Evaluation of Mode-I Stress Intensity Factor in Composite Structures. Compos. Struct. 2016, 145, 162–185. [Google Scholar] [CrossRef]
- Tornabene, F.; Dimitri, R.; Viola, E. Transient Dynamic Response of Generally-Shaped Arches Based on a GDQ-Time-Stepping Method. Int. J. Mech. Sci. 2016, 114, 277–314. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Tornabene, F.; Bacciocchi, M.; Dimitri, R. Free Vibration Analysis of Arbitrarily Shaped Functionally Graded Carbon Nanotube-Reinforced Plates. Compos. Part B-Eng. 2016, in press. [Google Scholar] [CrossRef]
- Dimitri, R.; Fantuzzi, N.; Tornabene, F.; Zavarise, G. Innovative Numerical Methods Based on SFEM and IGA for Computing Stress Concentrations in Isotropic Plates with Discontinuities. Int. J. Mech. Sci. 2016, 118, 166–187. [Google Scholar] [CrossRef]
- Kraus, H. Thin Elastic Shells; John Wiley & Sons: New York, NY, USA, 1967. [Google Scholar]
- Kulikov, G.M.; Carrera, E. Finite deformation higher-order shell models and rigid-body motions. Int. J. Solids Struct. 2008, 45, 3153–3172. [Google Scholar] [CrossRef]
- Kulikov, G.M.; Plotnikova, S.V. On the use of sampling surfaces method for solution of 3D elasticity problems for thick shells. Z. Angew.Math. Mech. 2012, 92, 910–920. [Google Scholar] [CrossRef]
- Viola, E.; Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. DiQuMASPAB Software. Bologna, Italy, 2013. Available online: http://software.dicam.unibo.it/diqumaspab-project.

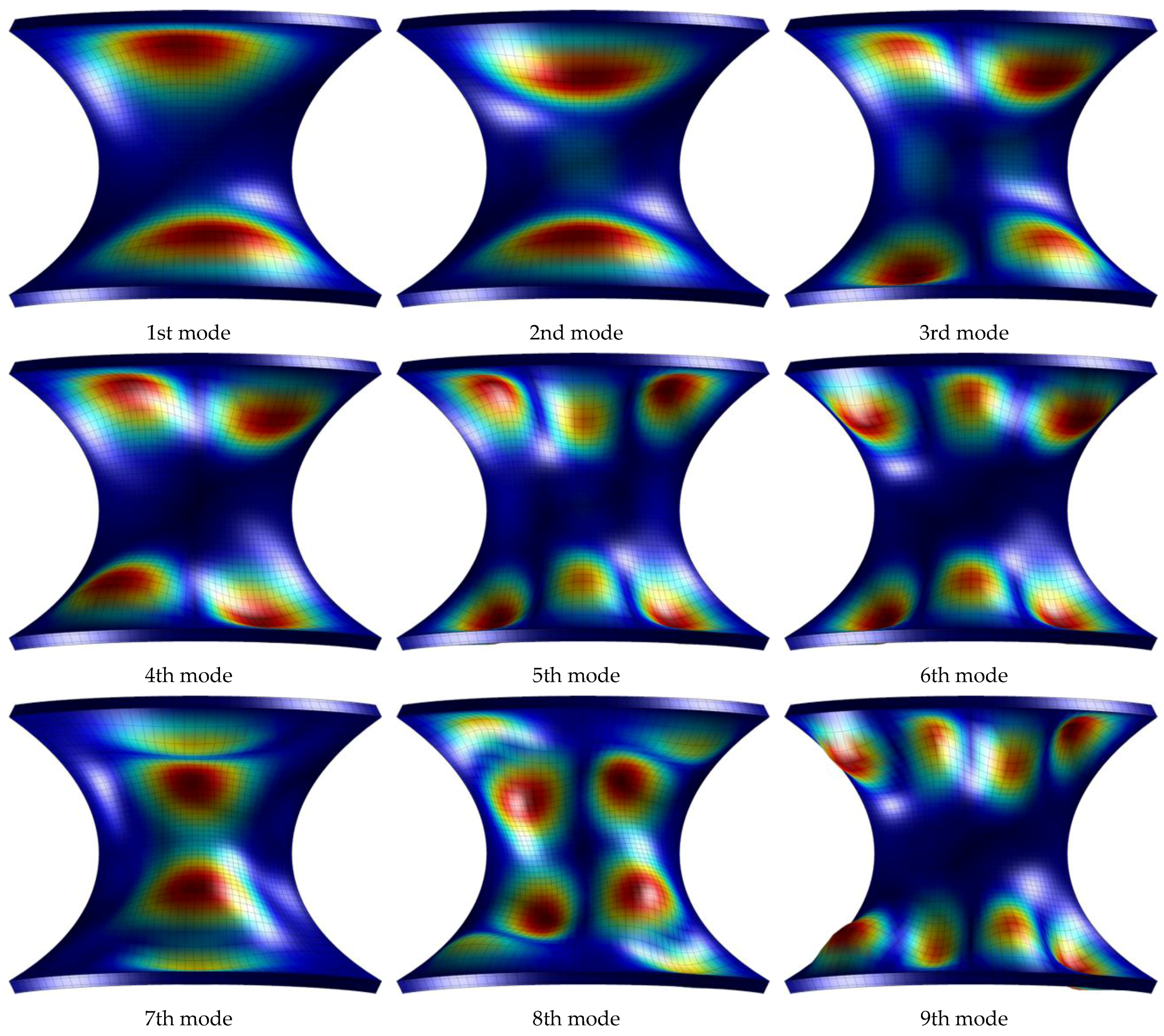
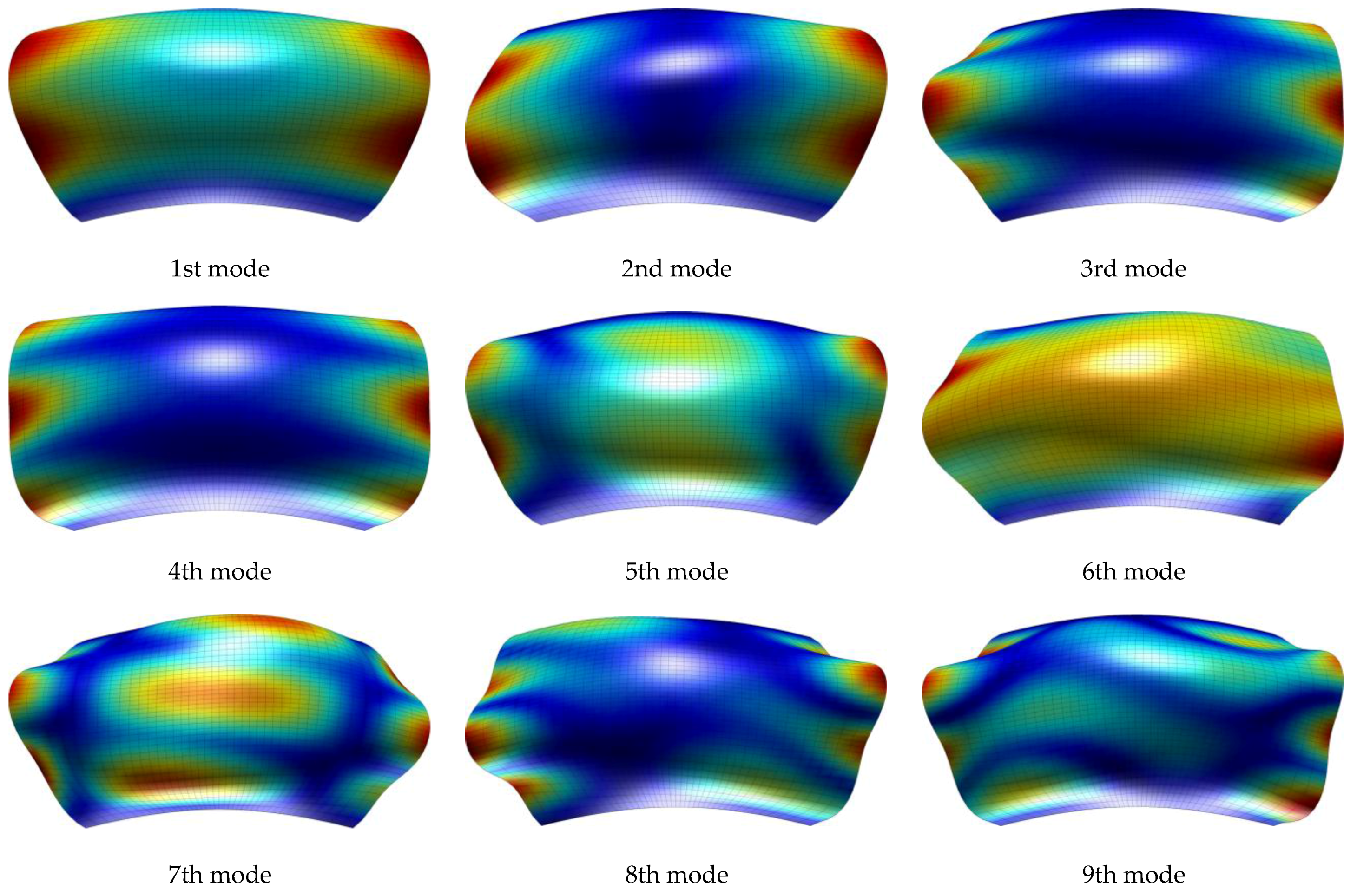
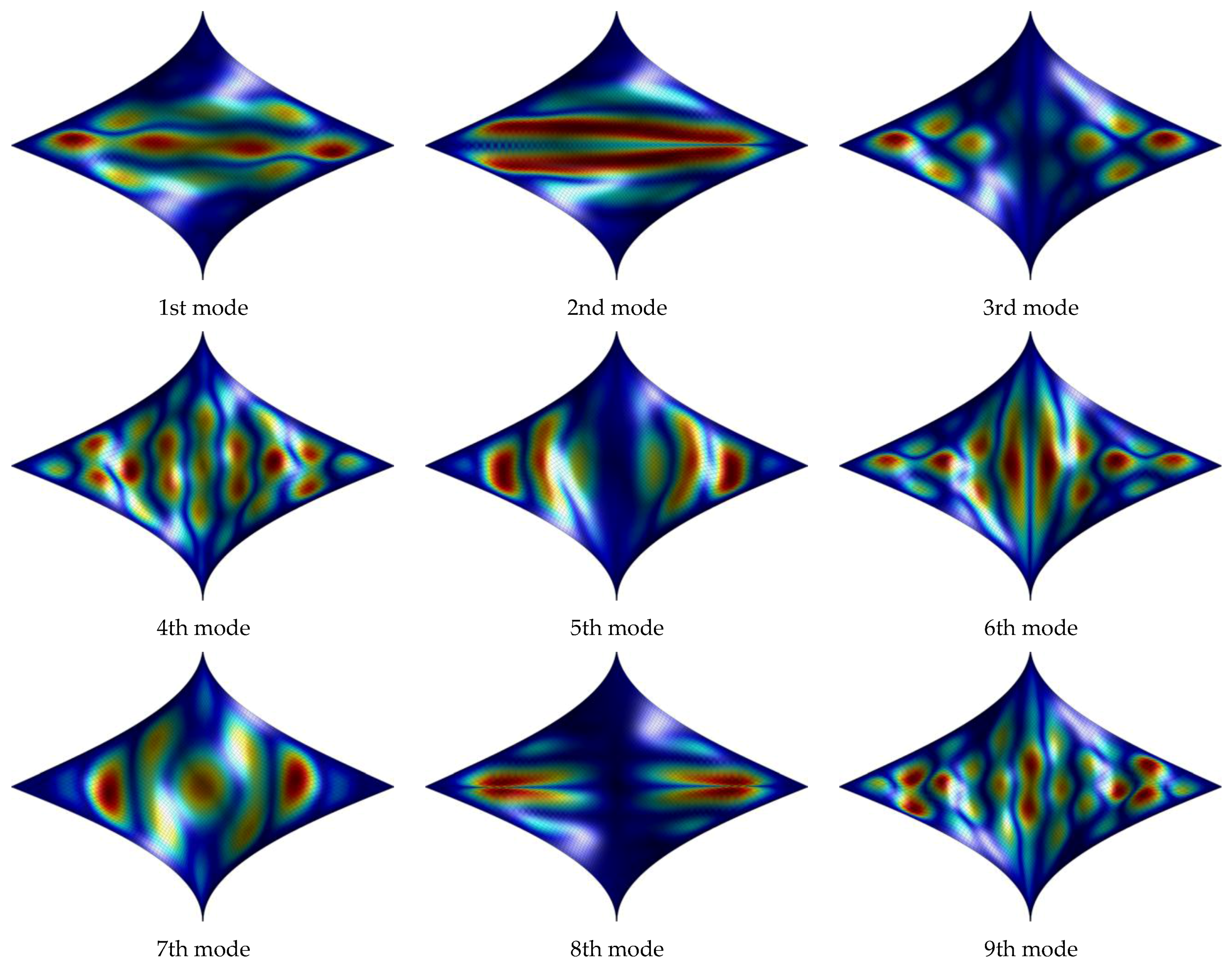
| Chebyshev I kind (Cheb I) | Chebyshev II kind (Cheb II) |
|---|---|
| Chebyshev III kind (Cheb III) | Chebyshev IV kind (Cheb IV) |
| Chebyshev-Gauss (Cheb-Gau) | Chebyshev-Gauss-Lobatto (Cheb-Gau-Lob) |
| Legendre-Gauss (Leg-Gau) | Legendre-Gauss-Lobatto (Leg-Gau-Lob) |
| Material | Mechanical properties |
|---|---|
| Ceramic Foam | , , |
| Aluminum | , , |
| Graphite-Epoxy | , , , , , , |
| [Hz] | |||||
|---|---|---|---|---|---|
| 1 | 214.190 | 214.683 | 214.920 | 214.876 | 215.192 |
| 2 | 427.796 | 428.731 | 429.542 | 429.441 | 430.078 |
| 3 | 427.796 | 428.731 | 429.542 | 429.441 | 430.078 |
| 4 | 619.213 | 620.487 | 622.090 | 621.925 | 622.811 |
| 5 | 745.318 | 746.861 | 749.071 | 748.859 | 749.996 |
| 6 | 750.039 | 751.614 | 753.784 | 753.573 | 754.725 |
| 7 | 920.267 | 922.063 | 925.309 | 925.028 | 926.343 |
| 8 | 920.267 | 922.063 | 925.309 | 925.028 | 926.343 |
| 9 | 1154.276 | 1156.519 | 1161.320 | 1160.926 | 1162.800 |
| 10 | 1154.276 | 1156.519 | 1161.320 | 1160.926 | 1162.800 |
| [Hz] | |||||
| 1 | 246.307 | 246.446 | 246.990 | 246.953 | 246.557 |
| 2 | 400.851 | 401.212 | 397.979 | 397.819 | 396.214 |
| 3 | 538.474 | 538.624 | 543.753 | 543.681 | 542.389 |
| 4 | 637.955 | 638.255 | 640.618 | 640.449 | 638.515 |
| 5 | 662.429 | 663.095 | 651.032 | 650.582 | 645.907 |
| 6 | 841.047 | 841.625 | 835.932 | 835.494 | 831.216 |
| 7 | 929.665 | 929.798 | 943.448 | 943.286 | 940.162 |
| 8 | 996.922 | 997.663 | 972.260 | 971.273 | 961.592 |
| 9 | 1001.255 | 1001.729 | 1012.078 | 1011.826 | 1008.405 |
| 10 | 1135.506 | 1136.416 | 1116.413 | 1115.444 | 1106.702 |
| [Hz] | |||||
| 1 | 245.325 | 245.508 | 246.829 | 246.7925 | 246.557 |
| 2 | 399.522 | 400.009 | 397.570 | 397.4074 | 396.214 |
| 3 | 534.090 | 534.394 | 543.140 | 543.0737 | 542.389 |
| 4 | 633.512 | 634.066 | 639.870 | 639.7048 | 638.515 |
| 5 | 659.868 | 660.852 | 650.005 | 649.5405 | 645.907 |
| 6 | 835.967 | 837.007 | 834.717 | 834.2726 | 831.216 |
| 7 | 919.201 | 919.694 | 941.974 | 941.8281 | 940.162 |
| 8 | 988.765 | 989.603 | 970.247 | 969.219 | 961.592 |
| 9 | 994.118 | 995.639 | 1010.533 | 1010.296 | 1008.405 |
| 10 | 1128.690 | 1130.407 | 1114.321 | 1113.323 | 1106.702 |
| Lamination scheme: | ||||||||||
| CCCC | FCFC | |||||||||
| Ref. [13] | Ref. [13] | |||||||||
| 1 | 2.2088 | 2.1984 | 2.1933 | 2.2096 | 2.2009 | 1.8129 | 1.8011 | 1.7928 | 1.8121 | 1.8019 |
| 2 | 2.2167 | 2.2051 | 2.2010 | 2.2171 | 2.2085 | 1.8129 | 1.8014 | 1.7930 | 1.8123 | 1.8021 |
| 3 | 2.3361 | 2.3356 | 2.3397 | 2.3431 | 2.3413 | 2.1349 | 2.1317 | 2.1315 | 2.1338 | 2.1326 |
| 4 | 2.3711 | 2.3602 | 2.3566 | 2.3727 | 2.3645 | 2.1883 | 2.1774 | 2.1727 | 2.1888 | 2.1800 |
| 5 | 2.3760 | 2.3619 | 2.3599 | 2.3754 | 2.3673 | 2.2132 | 2.2103 | 2.2119 | 2.2200 | 2.2162 |
| 6 | - | 2.3769 | 2.3804 | 2.3851 | 2.3828 | - | 2.2185 | 2.2135 | 2.2297 | 2.2211 |
| 7 | - | 2.4511 | 2.4524 | 2.4574 | 2.4550 | - | 2.2588 | 2.2607 | 2.2674 | 2.2641 |
| 8 | - | 2.5504 | 2.5444 | 2.5614 | 2.5533 | - | 2.2862 | 2.2842 | 2.2996 | 2.2913 |
| 9 | - | 2.5583 | 2.5581 | 2.5641 | 2.5613 | - | 2.3245 | 2.3287 | 2.3325 | 2.3305 |
| 10 | - | 2.7545 | 2.7495 | 2.7575 | 2.7536 | - | 2.3581 | 2.3622 | 2.3668 | 2.3645 |
| Lamination scheme: | ||||||||||
| CCCC | FCFC | |||||||||
| Ref. [13] | Ref. [13] | |||||||||
| 1 | 2.6711 | 2.6695 | 2.6709 | 2.6701 | 2.6698 | 2.1593 | 2.1562 | 2.1561 | 2.1562 | 2.1560 |
| 2 | 2.8511 | 2.8459 | 2.8509 | 2.8497 | 2.8494 | 2.5823 | 2.5791 | 2.5803 | 2.5798 | 2.5794 |
| 3 | 2.9112 | 2.9049 | 2.9105 | 2.9092 | 2.9088 | 2.6841 | 2.6804 | 2.6805 | 2.6823 | 2.6815 |
| 4 | 2.9297 | 2.9258 | 2.9272 | 2.9294 | 2.9286 | 2.6842 | 2.6806 | 2.6806 | 2.6826 | 2.6817 |
| 5 | 2.9315 | 2.9278 | 2.9290 | 2.9312 | 2.9304 | 2.7699 | 2.7644 | 2.7693 | 2.7684 | 2.7680 |
| 6 | - | 2.9717 | 2.9773 | 2.9758 | 2.9755 | - | 2.8093 | 2.8149 | 2.8139 | 2.8136 |
| 7 | - | 2.9899 | 2.9924 | 2.9947 | 2.9939 | - | 2.8519 | 2.8576 | 2.8564 | 2.8561 |
| 8 | - | 3.0306 | 3.0316 | 3.0335 | 3.0327 | - | 2.8937 | 2.8996 | 2.8983 | 2.8979 |
| 9 | - | 3.0690 | 3.0741 | 3.0722 | 3.0718 | - | 2.9204 | 2.9214 | 2.9235 | 2.9228 |
| 10 | - | 3.1432 | 3.1442 | 3.1457 | 3.1449 | - | 2.9285 | 2.9301 | 2.9324 | 2.9316 |
| Lamination scheme: | ||||||||||
| CCCC | FCFC | |||||||||
| Ref. [13] | Ref. [13] | |||||||||
| 1 | 2.4341 | 2.4330 | 2.4348 | 2.4341 | 2.4316 | 2.1490 | 2.1461 | 2.1460 | 2.1459 | 2.1455 |
| 2 | 2.5172 | 2.5155 | 2.5174 | 2.5164 | 2.5129 | 2.2328 | 2.2293 | 2.2002 | 2.1951 | 2.1740 |
| 3 | 2.5813 | 2.5769 | 2.5539 | 2.5488 | 2.5306 | 2.2331 | 2.2295 | 2.2004 | 2.1953 | 2.1742 |
| 4 | 2.5831 | 2.5793 | 2.5556 | 2.5503 | 2.5319 | 2.3303 | 2.3280 | 2.3286 | 2.3280 | 2.3243 |
| 5 | 2.6361 | 2.6347 | 2.6343 | 2.6326 | 2.6285 | 2.3939 | 2.3917 | 2.3928 | 2.3919 | 2.3876 |
| 6 | - | 2.7196 | 2.7000 | 2.6953 | 2.6776 | - | 2.4371 | 2.4391 | 2.4383 | 2.4348 |
| 7 | - | 2.7709 | 2.7472 | 2.7416 | 2.7234 | - | 2.4867 | 2.4892 | 2.4882 | 2.4849 |
| 8 | - | 2.7868 | 2.7858 | 2.7833 | 2.7780 | - | 2.5514 | 2.5275 | 2.5222 | 2.5037 |
| 9 | - | 3.0031 | 2.9781 | 2.9716 | 2.9527 | - | 2.5579 | 2.5599 | 2.5587 | 2.5445 |
| 10 | - | 3.0362 | 3.0440 | 3.0421 | 3.0366 | - | 2.5899 | 2.5675 | 2.5625 | 2.5552 |
| Lamination scheme: | ||||||||||
| CCCC | FCFC | |||||||||
| Ref. [13] | Ref. [13] | |||||||||
| 1 | 2.8072 | 2.7959 | 2.7873 | 2.7959 | 2.7913 | 1.7885 | 1.7822 | 1.7820 | 1.7824 | 1.7819 |
| 2 | 3.3888 | 3.3786 | 3.3647 | 3.3833 | 3.3747 | 1.9473 | 1.9363 | 1.9294 | 1.9462 | 1.9379 |
| 3 | 3.5562 | 3.5453 | 3.5193 | 3.5458 | 3.5337 | 1.9718 | 1.9606 | 1.9540 | 1.9710 | 1.9628 |
| 4 | 3.9024 | 3.8846 | 3.8603 | 3.8919 | 3.8791 | 2.1600 | 2.1405 | 2.1452 | 2.1489 | 2.1470 |
| 5 | 4.7013 | 4.6738 | 4.6458 | 4.6878 | 4.6687 | 2.2434 | 2.2266 | 2.2307 | 2.2351 | 2.2329 |
| 6 | - | 5.0277 | 4.9884 | 5.0442 | 5.0210 | - | 2.4506 | 2.4532 | 2.4556 | 2.4542 |
| 7 | - | 5.1616 | 5.0838 | 5.1565 | 5.1231 | - | 2.9766 | 2.9724 | 2.9835 | 2.9776 |
| 8 | - | 5.3075 | 5.2971 | 5.3167 | 5.3050 | - | 2.9978 | 2.9895 | 2.9968 | 2.9928 |
| 9 | - | 5.5571 | 5.5530 | 5.5797 | 5.5667 | - | 3.4699 | 3.4549 | 3.4732 | 3.4657 |
| 10 | - | 5.7521 | 5.6697 | 5.7570 | 5.7221 | - | 3.6648 | 3.6427 | 3.6825 | 3.6620 |
| Lamination scheme: | ||||||||||
| CCCC | FCFC | |||||||||
| Ref. [13] | Ref. [13] | |||||||||
| 1 | 3.0041 | 2.9988 | 3.0018 | 2.9987 | 2.9980 | 1.8115 | 1.8067 | 1.8065 | 1.8067 | 1.8062 |
| 2 | 3.5866 | 3.5814 | 3.5859 | 3.5780 | 3.5771 | 2.5355 | 2.5256 | 2.5293 | 2.5286 | 2.5278 |
| 3 | 3.7324 | 3.7309 | 3.7329 | 3.7334 | 3.7323 | 2.6693 | 2.6655 | 2.6643 | 2.6675 | 2.6659 |
| 4 | 4.0905 | 4.0886 | 4.0917 | 4.0890 | 4.0873 | 2.6769 | 2.6733 | 2.6722 | 2.6750 | 2.6735 |
| 5 | 4.6909 | 4.6891 | 4.6919 | 4.6681 | 4.6664 | 2.7271 | 2.7188 | 2.7239 | 2.7229 | 2.7223 |
| 6 | - | 5.0867 | 5.0964 | 5.0929 | 5.0895 | - | 2.9030 | 2.9078 | 2.9063 | 2.9058 |
| 7 | - | 5.1400 | 5.1635 | 5.1547 | 5.1530 | - | 3.2385 | 3.2426 | 3.2398 | 3.2392 |
| 8 | - | 5.4655 | 5.4688 | 5.4446 | 5.4420 | - | 3.5339 | 3.5357 | 3.5381 | 3.5370 |
| 9 | - | 5.5482 | 5.5507 | 5.5604 | 5.5581 | - | 3.8158 | 3.8176 | 3.8176 | 3.8166 |
| 10 | - | 5.7894 | 5.7931 | 5.7994 | 5.7969 | - | 3.9129 | 3.9159 | 3.9074 | 3.9069 |
| Lamination scheme: | ||||||||||
| CCCC | FCFC | |||||||||
| Ref. [13] | Ref. [13] | |||||||||
| 1 | 3.1249 | 3.1134 | 3.0945 | 3.0849 | 3.0749 | 1.7945 | 1.7891 | 1.7889 | 1.7889 | 1.7885 |
| 2 | 3.8595 | 3.8491 | 3.8144 | 3.8033 | 3.7836 | 2.2467 | 2.2327 | 2.2350 | 2.2350 | 2.2322 |
| 3 | 4.0712 | 4.0550 | 4.0193 | 4.0018 | 3.9832 | 2.3020 | 2.2942 | 2.2660 | 2.2651 | 2.2462 |
| 4 | 4.4237 | 4.4044 | 4.3688 | 4.3571 | 4.3358 | 2.3438 | 2.3360 | 2.3085 | 2.3077 | 2.2895 |
| 5 | 5.3687 | 5.3488 | 5.2850 | 5.2716 | 5.2334 | 2.3644 | 2.3517 | 2.3538 | 2.3535 | 2.3503 |
| 6 | - | 5.7751 | 5.7068 | 5.6908 | 5.6487 | - | 2.6369 | 2.6375 | 2.6357 | 2.6326 |
| 7 | - | 5.8228 | 5.7791 | 5.7581 | 5.7328 | - | 3.2942 | 3.2753 | 3.2709 | 3.2577 |
| 8 | - | 6.0390 | 5.9696 | 5.9195 | 5.8717 | - | 3.4992 | 3.4803 | 3.4693 | 3.4592 |
| 9 | - | 6.0813 | 6.0252 | 6.0053 | 5.9862 | - | 4.0633 | 4.0325 | 4.0220 | 4.0041 |
| 10 | - | 6.7394 | 6.6178 | 6.5692 | 6.5142 | - | 4.2428 | 4.1774 | 4.1735 | 4.1322 |
| [Hz] | |||||
| 1 | 56.890 | 58.220 | 58.166 | 58.113 | 57.997 |
| 2 | 74.436 | 75.752 | 75.622 | 75.536 | 75.229 |
| 3 | 116.262 | 118.091 | 117.910 | 117.753 | 117.083 |
| 4 | 150.388 | 152.559 | 152.155 | 152.044 | 151.589 |
| 5 | 151.874 | 154.839 | 154.584 | 154.518 | 153.710 |
| 6 | 162.006 | 164.176 | 164.010 | 163.810 | 162.855 |
| 7 | 176.095 | 178.608 | 178.291 | 178.160 | 177.017 |
| 8 | 187.827 | 188.950 | 188.336 | 188.123 | 187.234 |
| 9 | 216.823 | 220.875 | 220.638 | 220.328 | 218.822 |
| 10 | 222.697 | 226.597 | 226.457 | 226.199 | 224.561 |
| [Hz] | |||||
| 1 | 56.857 | 58.187 | 58.164 | 58.112 | 57.997 |
| 2 | 74.327 | 75.631 | 75.617 | 75.527 | 75.229 |
| 3 | 116.016 | 117.814 | 117.899 | 117.735 | 117.083 |
| 4 | 150.213 | 152.283 | 152.135 | 152.024 | 151.589 |
| 5 | 151.657 | 154.684 | 154.570 | 154.509 | 153.710 |
| 6 | 161.698 | 163.823 | 163.995 | 163.792 | 162.855 |
| 7 | 175.890 | 178.377 | 178.271 | 178.145 | 177.017 |
| 8 | 187.370 | 188.489 | 188.305 | 188.092 | 187.234 |
| 9 | 216.456 | 220.277 | 220.613 | 220.301 | 218.822 |
| 10 | 222.165 | 226.227 | 226.438 | 226.183 | 224.561 |
| [Hz] | |||||||
|---|---|---|---|---|---|---|---|
| 1 | 357.779 | 365.750 | 361.564 | 369.297 | 369.263 | 368.569 | 368.755 |
| 2 | 360.035 | 368.863 | 365.443 | 374.047 | 374.010 | 373.200 | 373.480 |
| 3 | 375.519 | 385.606 | 379.308 | 389.515 | 389.469 | 388.520 | 388.730 |
| 4 | 383.773 | 393.567 | 387.618 | 397.411 | 397.367 | 396.434 | 396.820 |
| 5 | 417.052 | 430.082 | 421.774 | 434.854 | 434.791 | 433.342 | 433.661 |
| 6 | 418.612 | 431.731 | 423.729 | 437.000 | 436.935 | 435.462 | 435.912 |
| 7 | 461.401 | 474.554 | 470.283 | 483.093 | 483.035 | 481.662 | 481.188 |
| 8 | 470.591 | 485.171 | 478.858 | 493.098 | 493.034 | 491.534 | 490.978 |
| 9 | 475.427 | 492.995 | 481.536 | 499.146 | 499.050 | 496.646 | 497.065 |
| 10 | 480.125 | 496.486 | 484.349 | 501.024 | 500.928 | 498.549 | 498.905 |
| Thickness functions: Legendre Polynomials | |||||||||
| [Hz] | |||||||||
| 1 | 122.947 | 122.185 | 125.737 | 125.687 | 125.918 | 125.808 | 125.779 | 125.835 | 125.713 |
| 2 | 155.668 | 155.006 | 159.086 | 159.037 | 159.181 | 159.051 | 159.072 | 159.150 | 158.697 |
| 3 | 231.539 | 229.731 | 238.266 | 238.112 | 238.944 | 238.618 | 238.482 | 238.630 | 238.079 |
| 4 | 240.059 | 238.120 | 246.659 | 246.500 | 247.382 | 247.107 | 246.952 | 247.061 | 246.443 |
| 5 | 327.335 | 326.622 | 333.781 | 333.697 | 334.027 | 333.964 | 333.892 | 333.893 | 332.061 |
| 6 | 384.994 | 384.495 | 389.841 | 389.760 | 390.008 | 389.934 | 389.831 | 389.834 | 388.658 |
| 7 | 388.042 | 386.488 | 393.963 | 393.830 | 394.506 | 394.373 | 394.185 | 394.207 | 392.639 |
| 8 | 417.904 | 415.005 | 426.528 | 426.222 | 428.037 | 427.658 | 427.306 | 427.408 | 425.921 |
| 9 | 422.965 | 420.254 | 433.492 | 433.235 | 434.847 | 434.558 | 434.193 | 434.256 | 433.063 |
| 10 | 451.770 | 449.739 | 458.130 | 457.903 | 458.815 | 458.635 | 458.367 | 458.367 | 456.530 |
| Thickness functions: Lagrange Polynomials | |||||||||
| [Hz] | |||||||||
| 1 | 122.947 | 122.185 | 125.737 | 125.687 | 125.918 | 125.808 | 125.779 | 125.835 | 125.713 |
| 2 | 155.668 | 155.006 | 159.086 | 159.037 | 159.181 | 159.051 | 159.072 | 159.150 | 158.697 |
| 3 | 231.539 | 229.731 | 238.266 | 238.112 | 238.944 | 238.618 | 238.482 | 238.630 | 238.079 |
| 4 | 240.059 | 238.120 | 246.659 | 246.500 | 247.382 | 247.107 | 246.952 | 247.061 | 246.443 |
| 5 | 327.335 | 326.622 | 333.781 | 333.697 | 334.027 | 333.964 | 333.892 | 333.893 | 332.061 |
| 6 | 384.994 | 384.495 | 389.841 | 389.760 | 390.008 | 389.934 | 389.831 | 389.834 | 388.658 |
| 7 | 388.042 | 386.488 | 393.963 | 393.830 | 394.506 | 394.373 | 394.185 | 394.207 | 392.639 |
| 8 | 417.904 | 415.005 | 426.528 | 426.222 | 428.037 | 427.658 | 427.306 | 427.408 | 425.921 |
| 9 | 422.965 | 420.254 | 433.492 | 433.235 | 434.847 | 434.558 | 434.193 | 434.256 | 433.063 |
| 10 | 451.770 | 449.739 | 458.130 | 457.903 | 458.815 | 458.635 | 458.367 | 458.367 | 456.530 |
| [Hz] | |||||
|---|---|---|---|---|---|
| 1 | 206.173 | 206.427 | 206.425 | 206.412 | 206.683 |
| 2 | 218.464 | 219.333 | 219.329 | 219.310 | 219.650 |
| 3 | 238.304 | 238.702 | 238.699 | 238.680 | 239.026 |
| 4 | 246.655 | 247.102 | 247.097 | 247.070 | 247.489 |
| 5 | 260.468 | 261.159 | 261.152 | 261.118 | 261.653 |
| 6 | 261.249 | 262.055 | 262.052 | 262.031 | 262.382 |
| 7 | 261.294 | 262.189 | 262.187 | 262.173 | 262.408 |
| 8 | 268.205 | 269.147 | 269.140 | 269.107 | 269.750 |
| 9 | 281.329 | 281.691 | 281.683 | 281.637 | 282.434 |
| 10 | 301.474 | 302.267 | 302.261 | 302.231 | 302.725 |
| [Hz] | Ref. [61] | Ref. [61] | Ref. [83] | Ref. [61] | ||
| 1 | 62.262 | 60.585 | 61.907 | 61.455 | 61.561 | 61.35 |
| 2 | 62.262 | 60.585 | 61.907 | 61.455 | 61.561 | 61.35 |
| 3 | 95.989 | 94.941 | 96.156 | 95.702 | 96.075 | 95.60 |
| 4 | 95.989 | 94.941 | 96.156 | 95.702 | 96.075 | 95.60 |
| 5 | 101.520 | 97.536 | 99.441 | 98.713 | 99.214 | 98.15 |
| 6 | 101.520 | 97.536 | 99.441 | 98.713 | 99.214 | 98.15 |
| 7 | 172.139 | 165.402 | 168.296 | 166.637 | 168.175 | 165.68 |
| 8 | 172.139 | 165.402 | 168.296 | 166.638 | 168.175 | 165.68 |
| 9 | 182.026 | 180.740 | 181.769 | 181.516 | 182.330 | 181.15 |
| 10 | 220.673 | 220.535 | 221.022 | 220.573 | 220.587 | 219.91 |
| [Hz] | Ref. [61] | Ref. [61] | Ref. [83] | Ref. [61] | ||
| 1 | 61.343 | 61.314 | 61.716 | 61.260 | 61.169 | 61.35 |
| 2 | 61.343 | 61.314 | 61.716 | 61.260 | 61.169 | 61.35 |
| 3 | 95.651 | 95.628 | 96.071 | 95.615 | 95.660 | 95.60 |
| 4 | 95.651 | 95.628 | 96.071 | 95.615 | 95.660 | 95.60 |
| 5 | 98.286 | 98.273 | 98.781 | 98.061 | 98.273 | 98.15 |
| 6 | 98.286 | 98.273 | 98.781 | 98.061 | 98.273 | 98.15 |
| 7 | 165.873 | 165.867 | 167.038 | 165.413 | 166.297 | 165.68 |
| 8 | 165.873 | 165.867 | 167.038 | 165.413 | 166.297 | 165.68 |
| 9 | 181.462 | 181.450 | 181.680 | 181.425 | 181.808 | 181.15 |
| 10 | 220.558 | 220.558 | 220.997 | 220.548 | 219.741 | 219.91 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Reddy, J.N. An Equivalent Layer-Wise Approach for the Free Vibration Analysis of Thick and Thin Laminated and Sandwich Shells. Appl. Sci. 2017, 7, 17. https://doi.org/10.3390/app7010017
Tornabene F, Fantuzzi N, Bacciocchi M, Reddy JN. An Equivalent Layer-Wise Approach for the Free Vibration Analysis of Thick and Thin Laminated and Sandwich Shells. Applied Sciences. 2017; 7(1):17. https://doi.org/10.3390/app7010017
Chicago/Turabian StyleTornabene, Francesco, Nicholas Fantuzzi, Michele Bacciocchi, and Junuthula N. Reddy. 2017. "An Equivalent Layer-Wise Approach for the Free Vibration Analysis of Thick and Thin Laminated and Sandwich Shells" Applied Sciences 7, no. 1: 17. https://doi.org/10.3390/app7010017








