Investigations on the Effects of Vortex-Induced Vibration with Different Distributions of Lorentz Forces
Abstract
:1. Introduction
2. Governing Equations
3. Hydrodynamic Forces
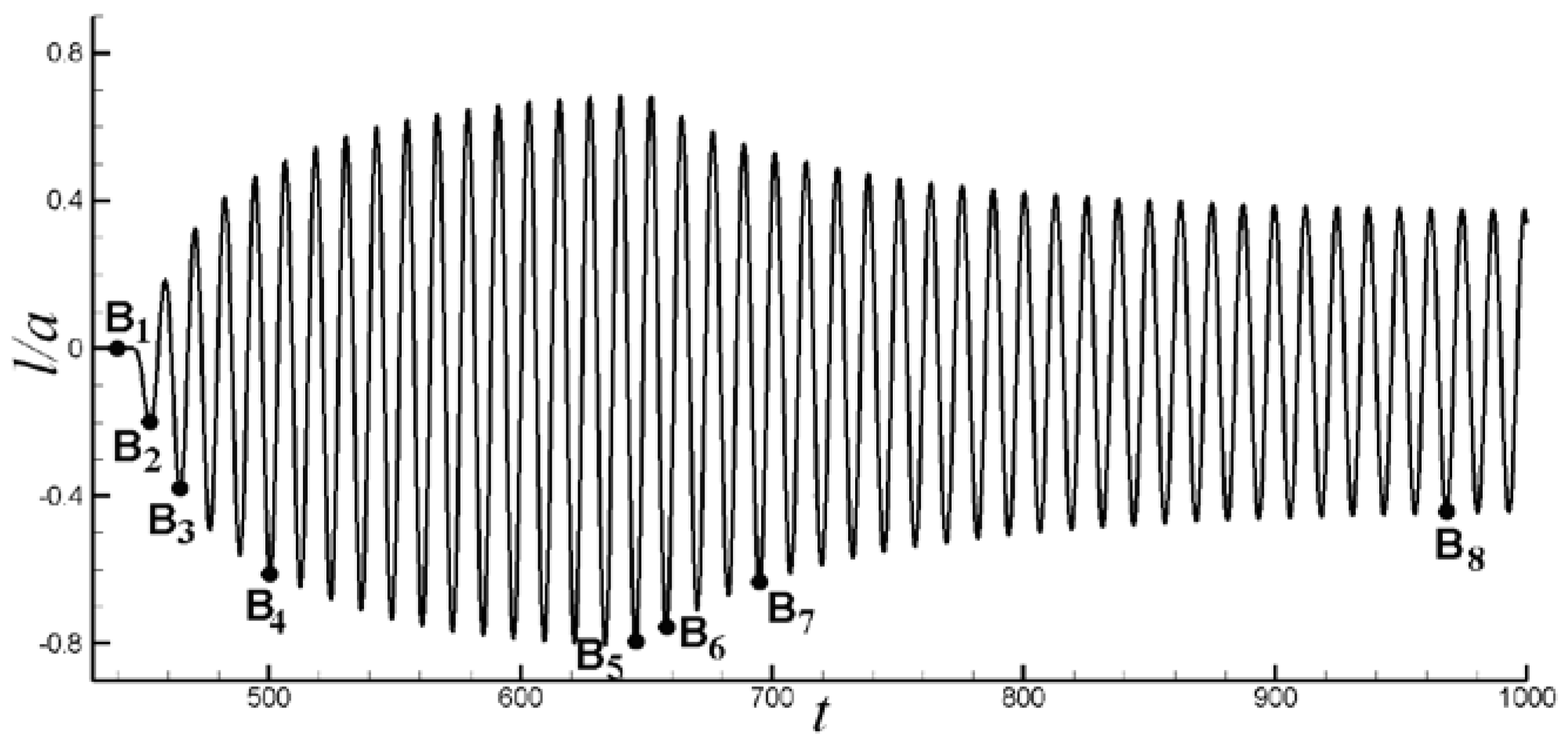
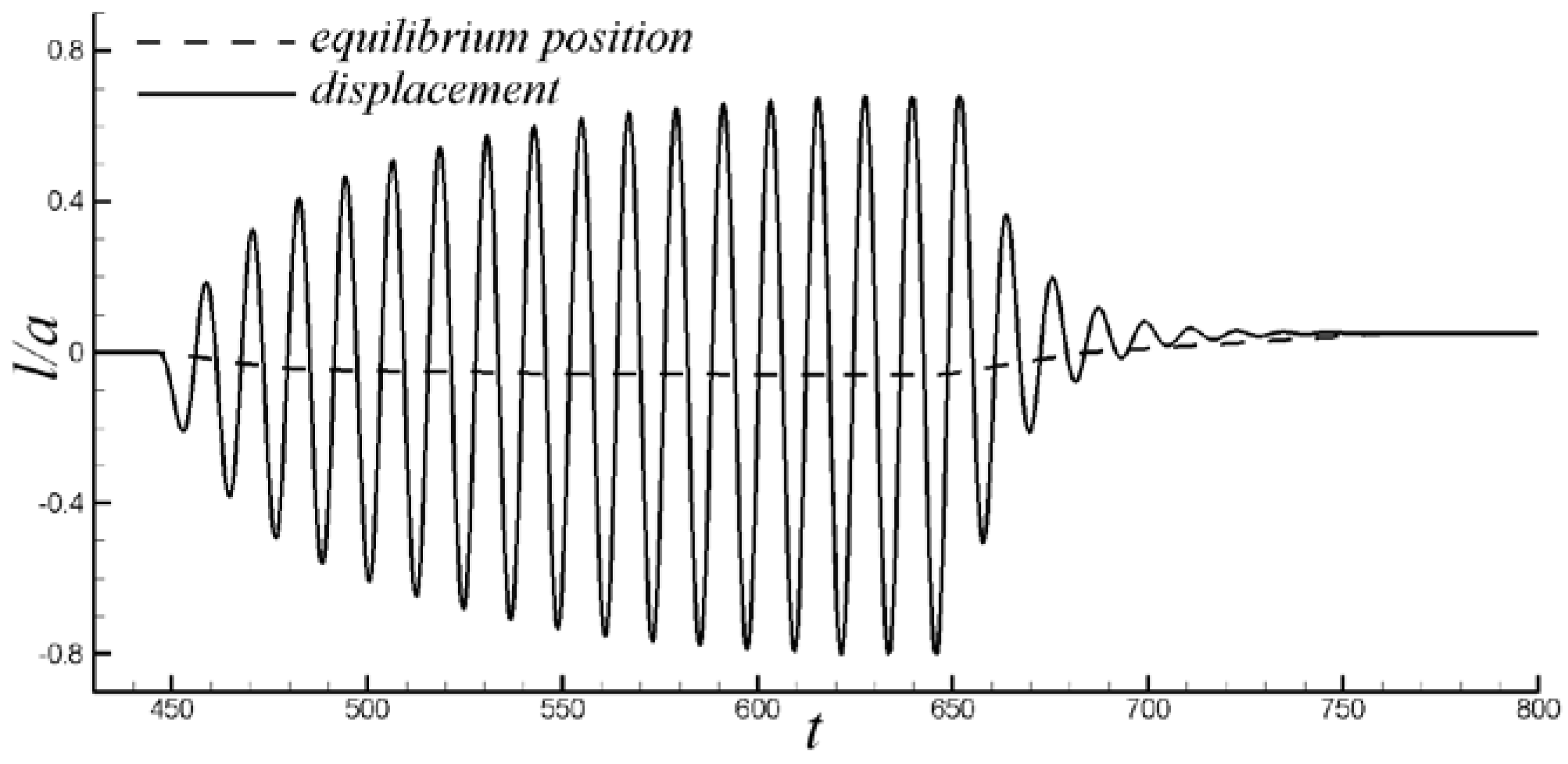
4. Cylinder Responses
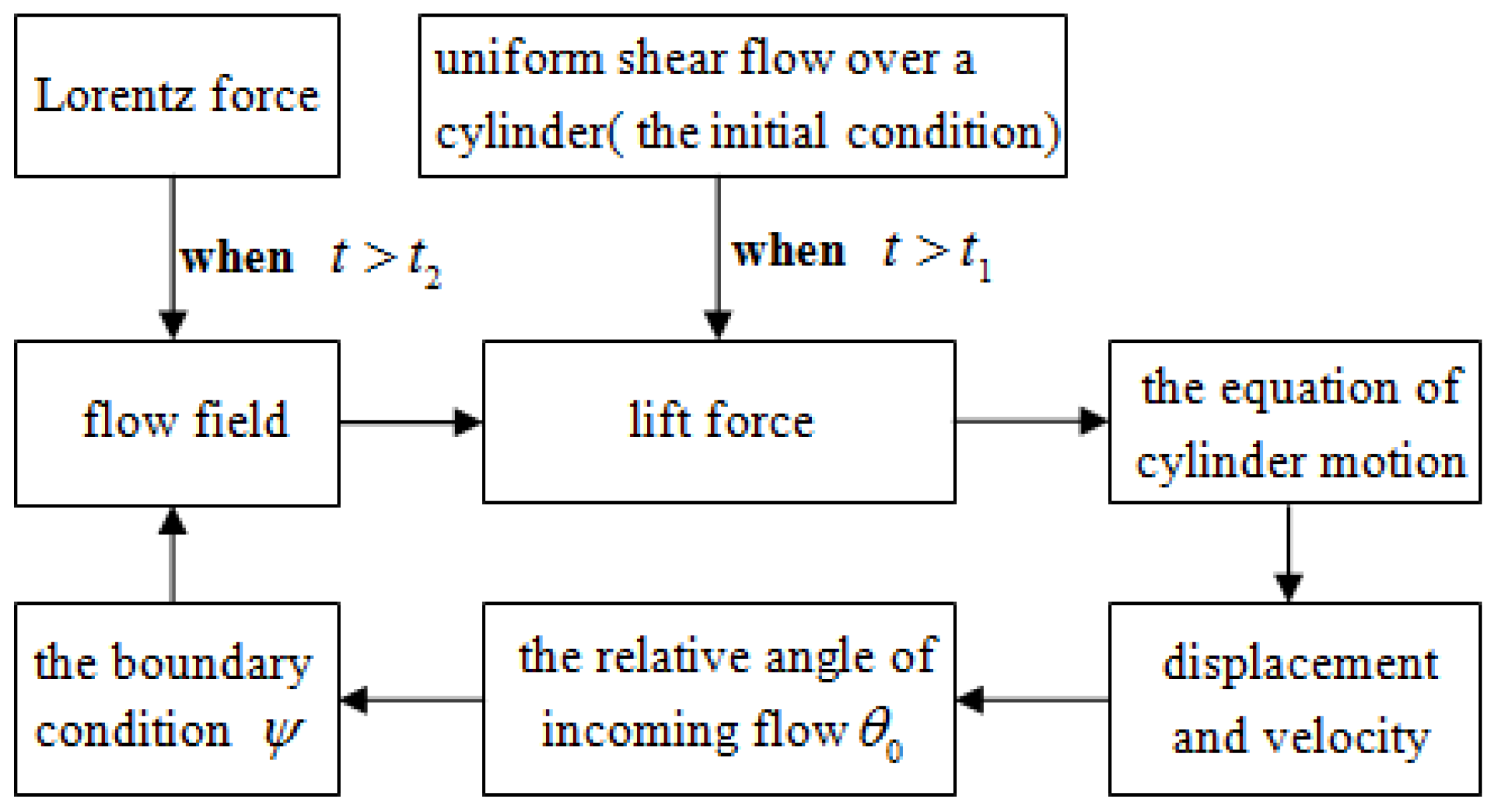
5. Numerical Approach and Procedure for Fluid-Structure Coupling
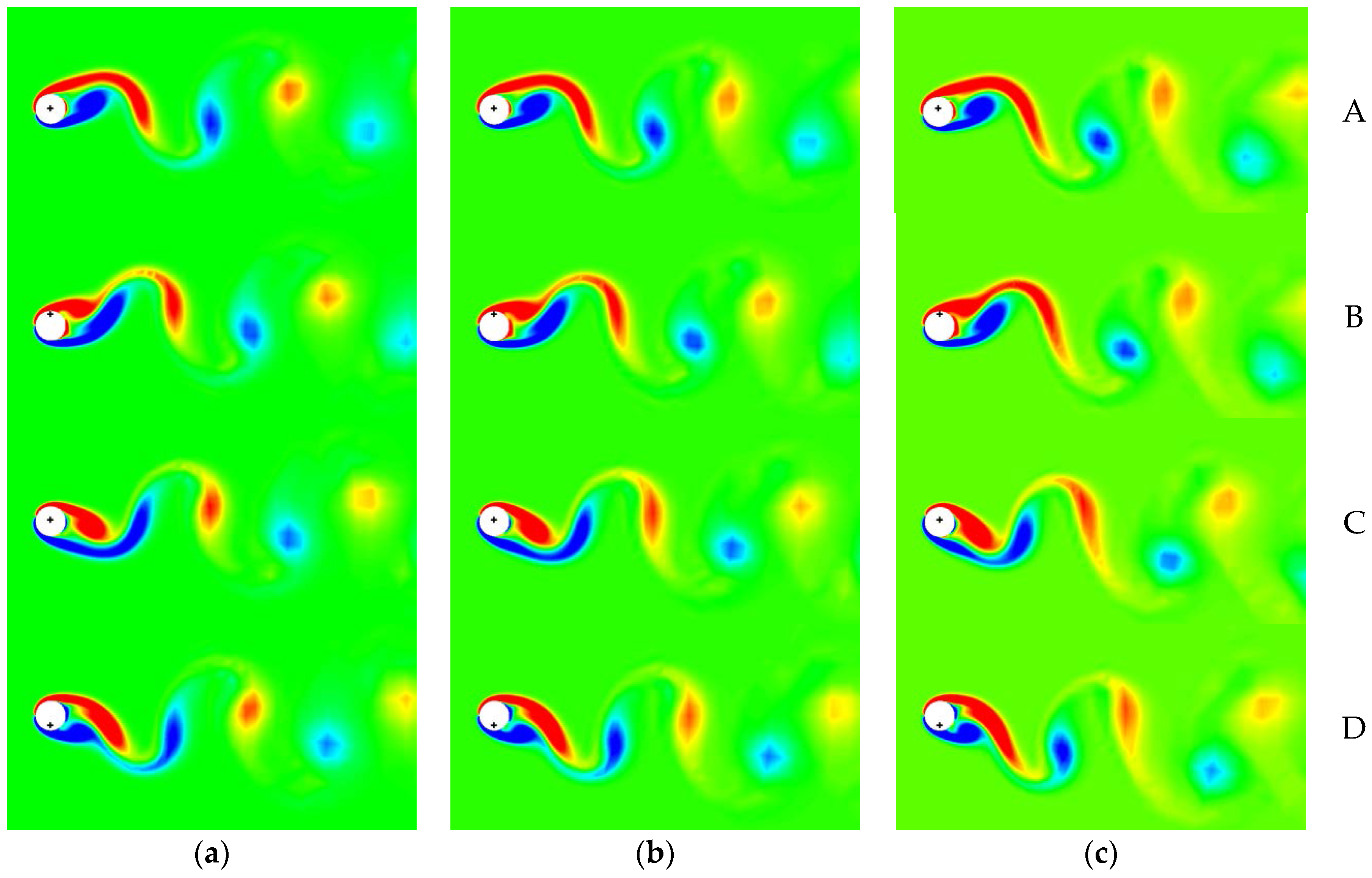
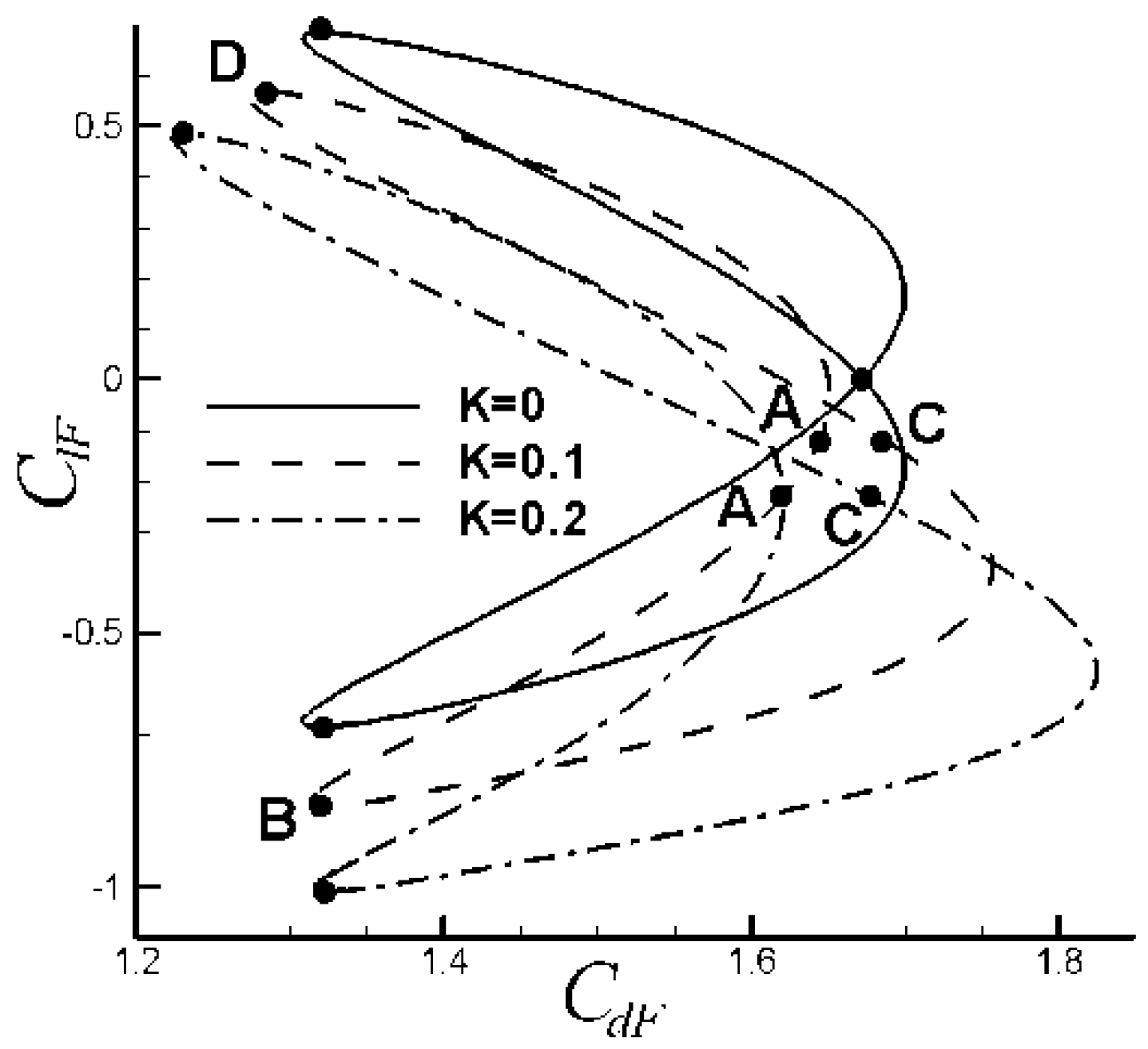
6. Results
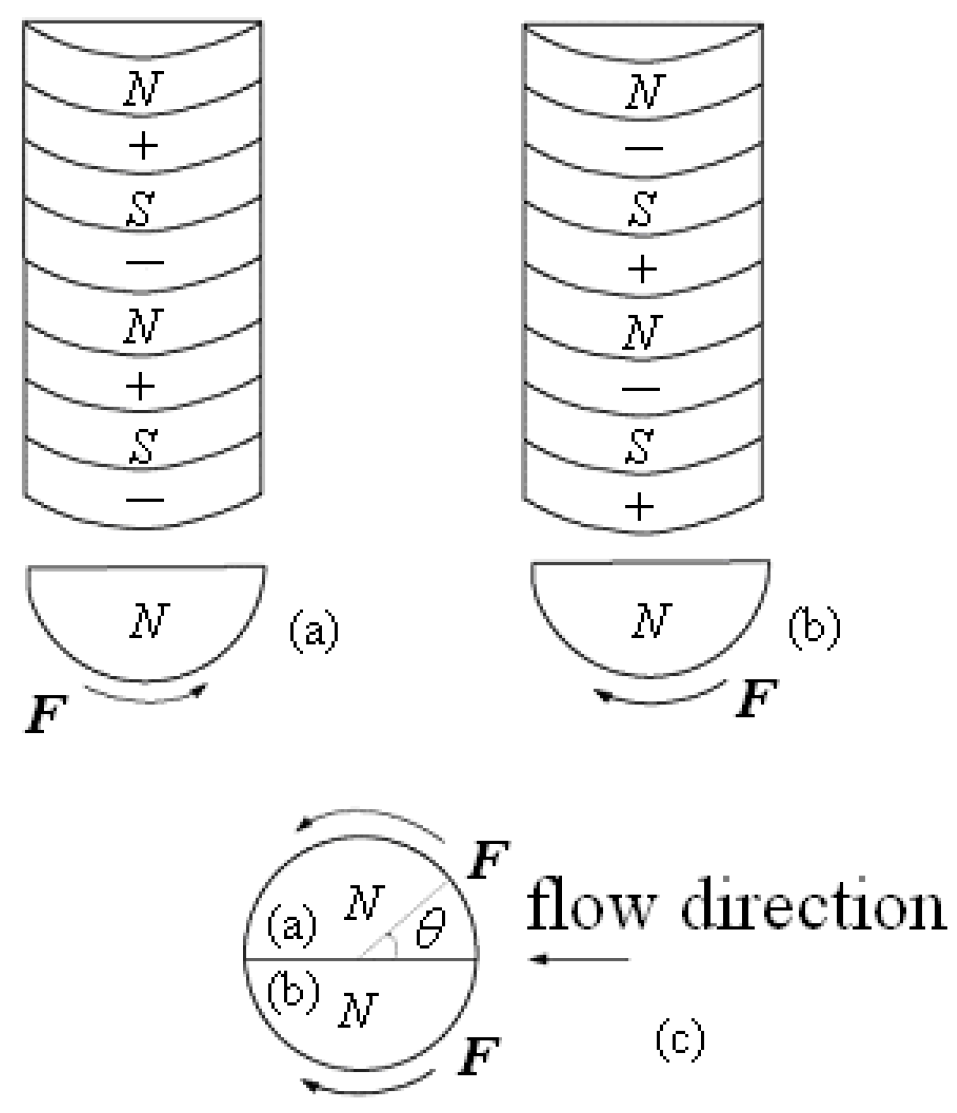
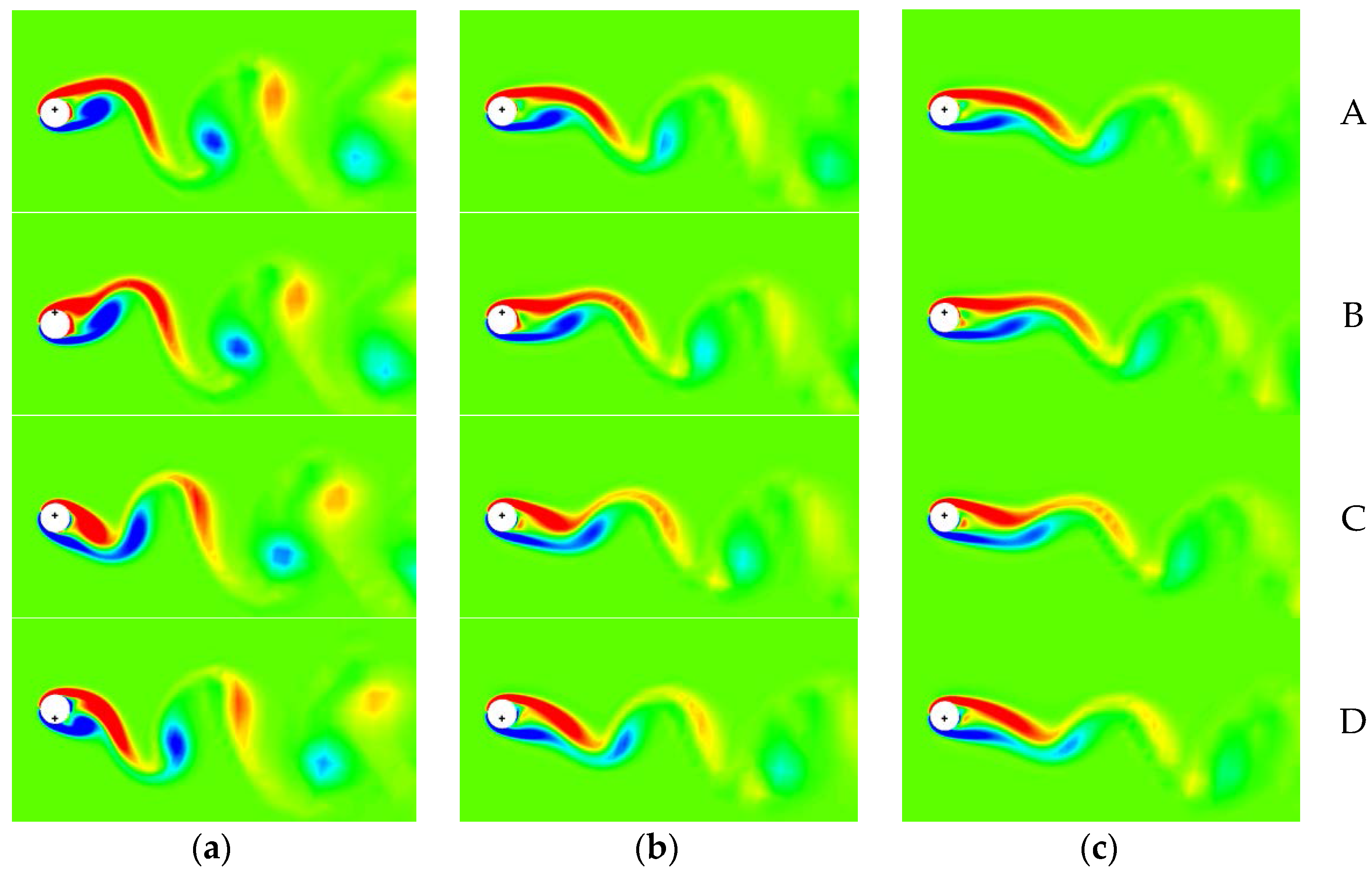
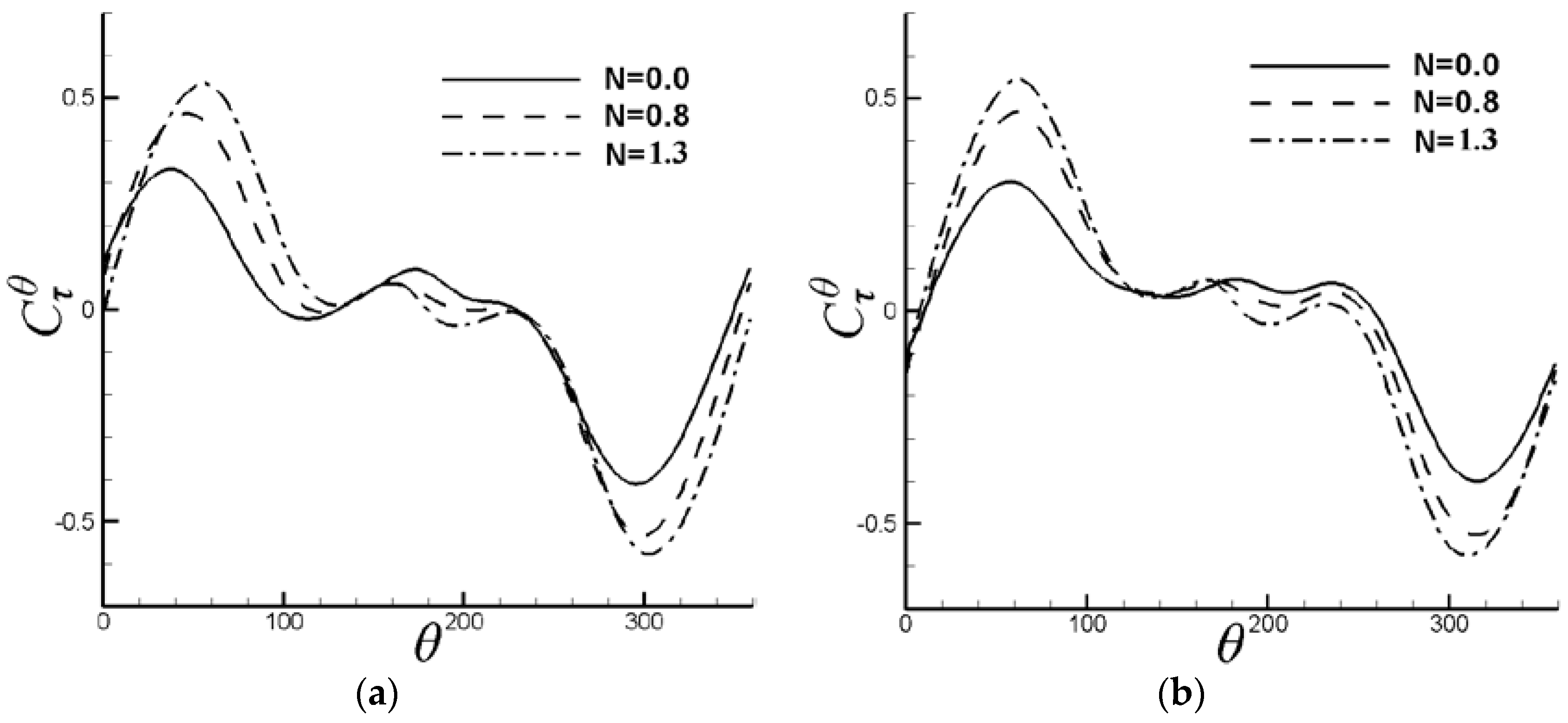
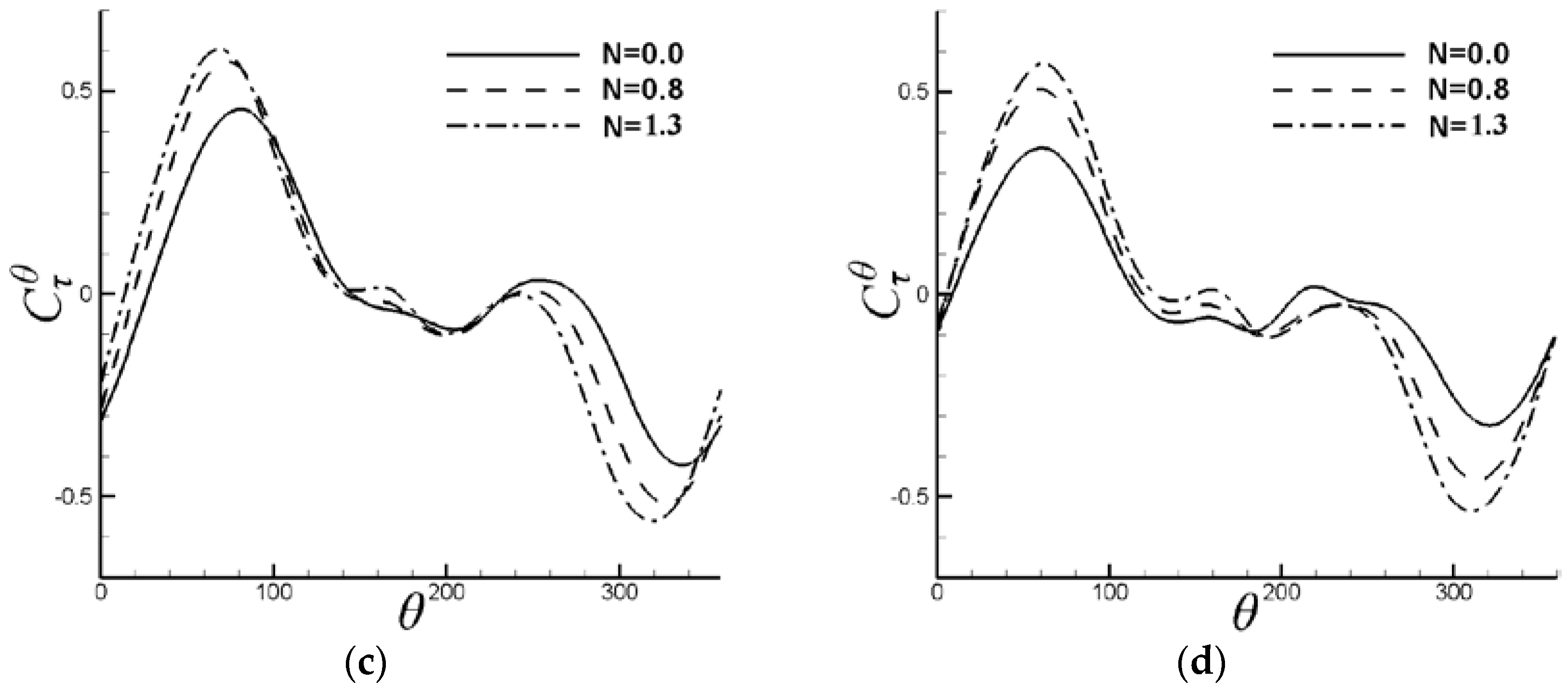
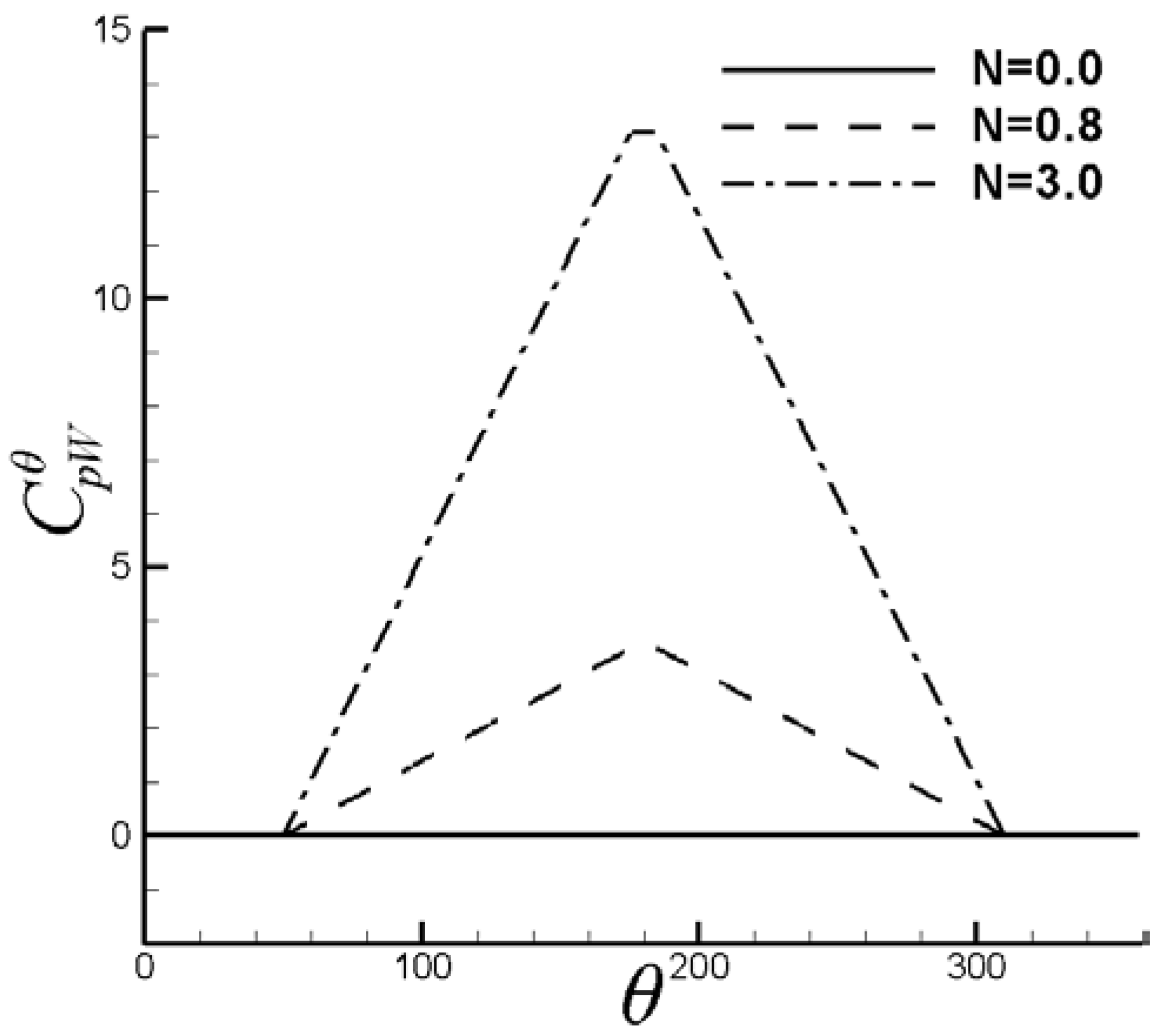
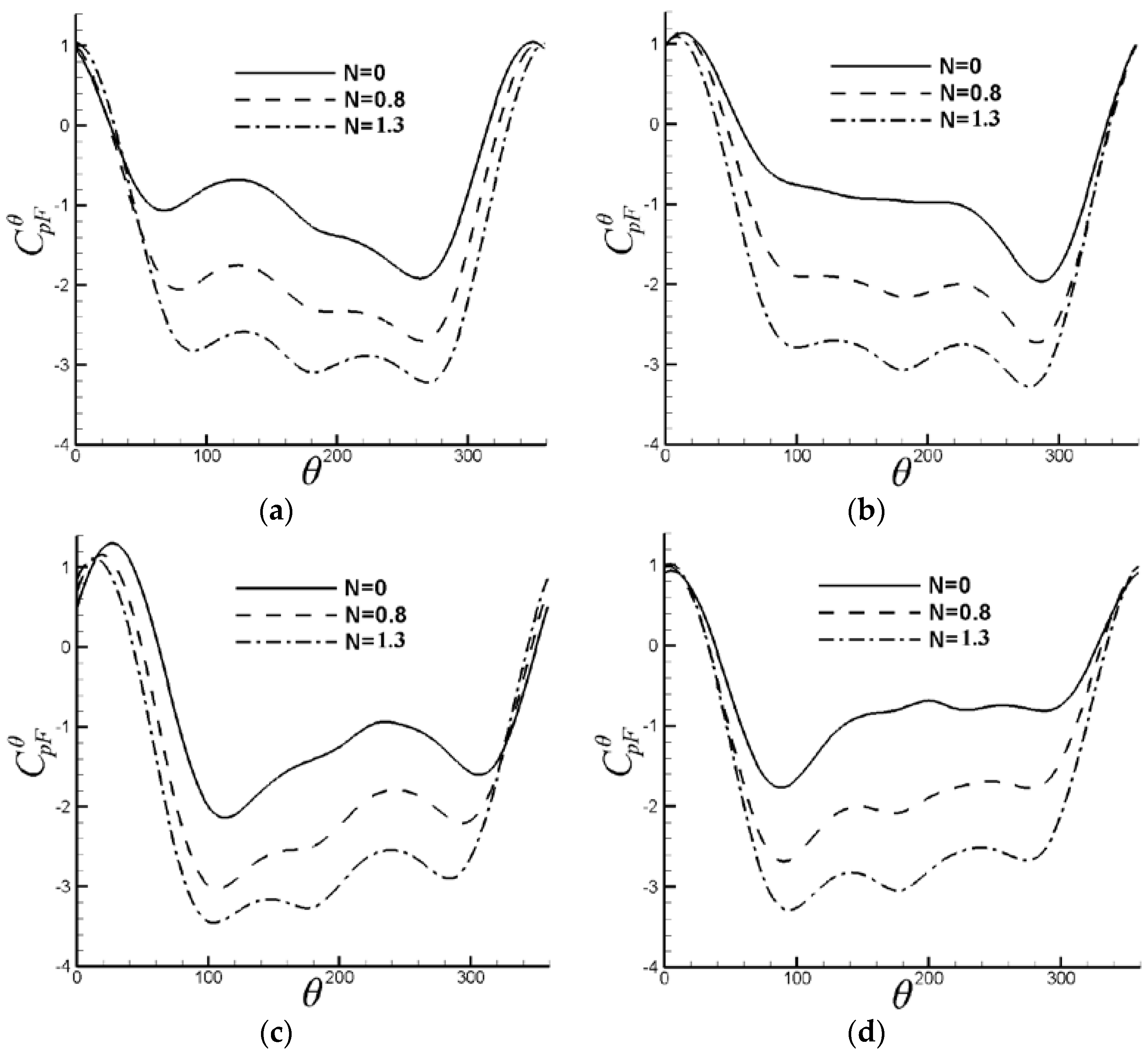
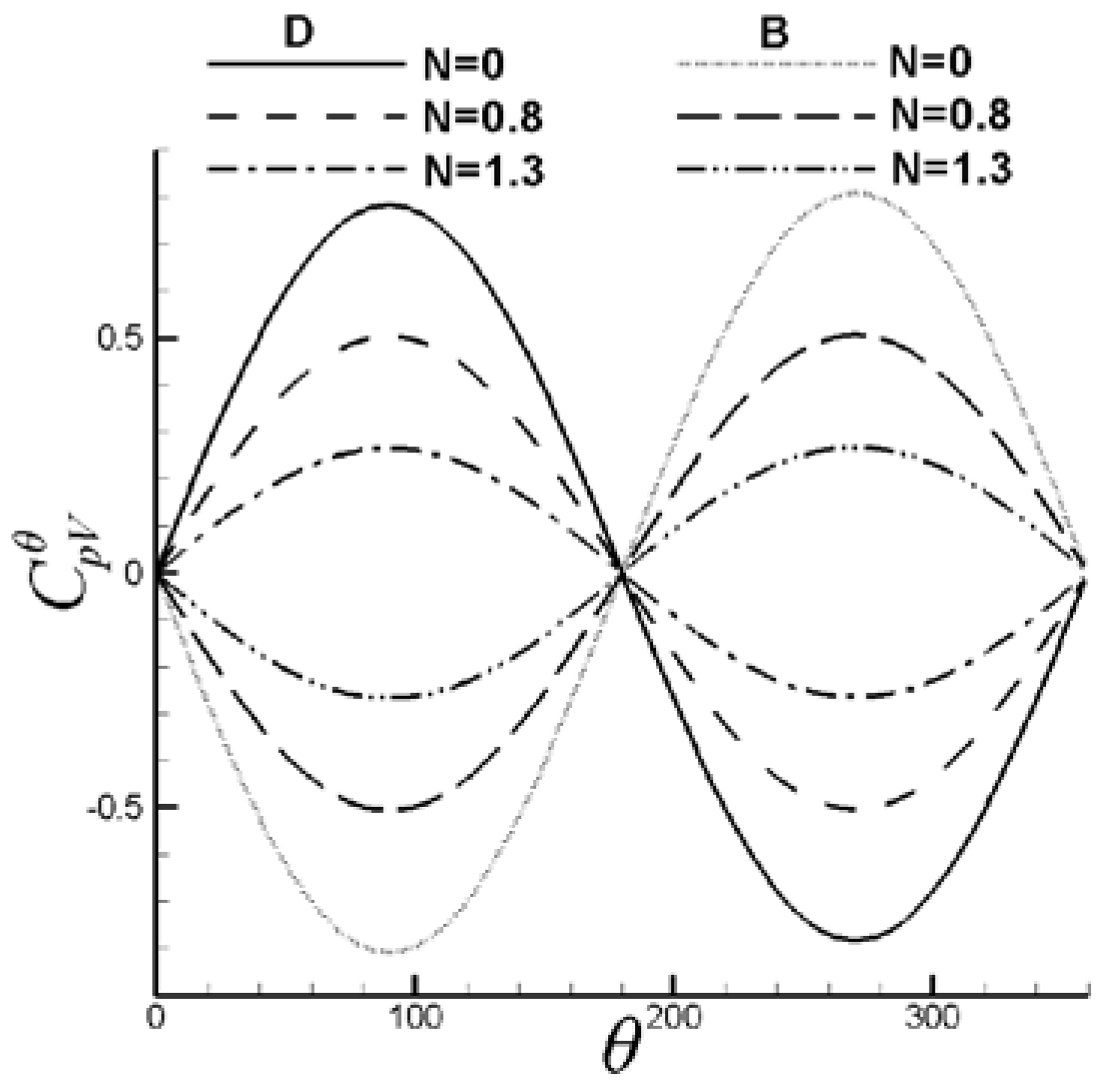
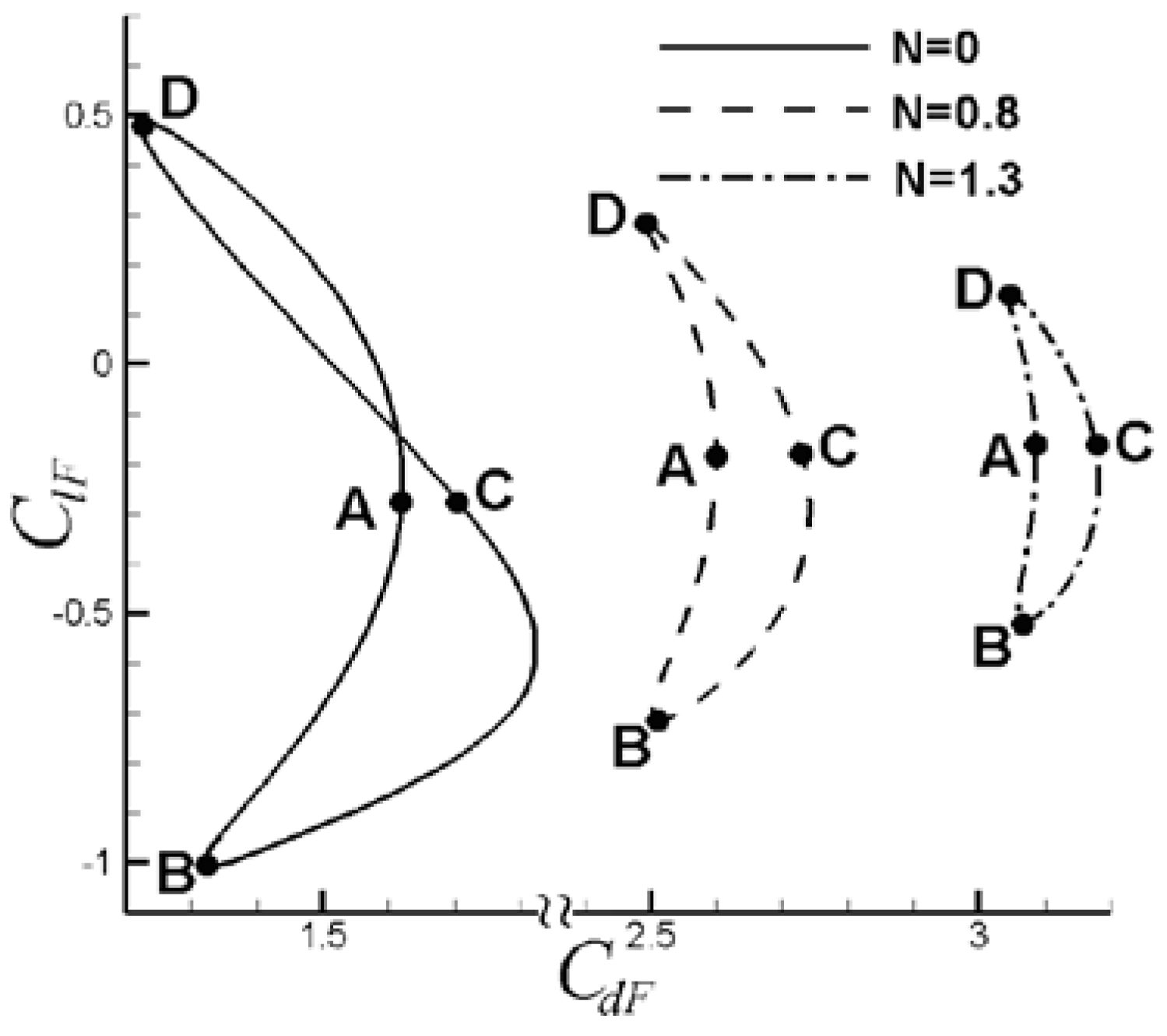
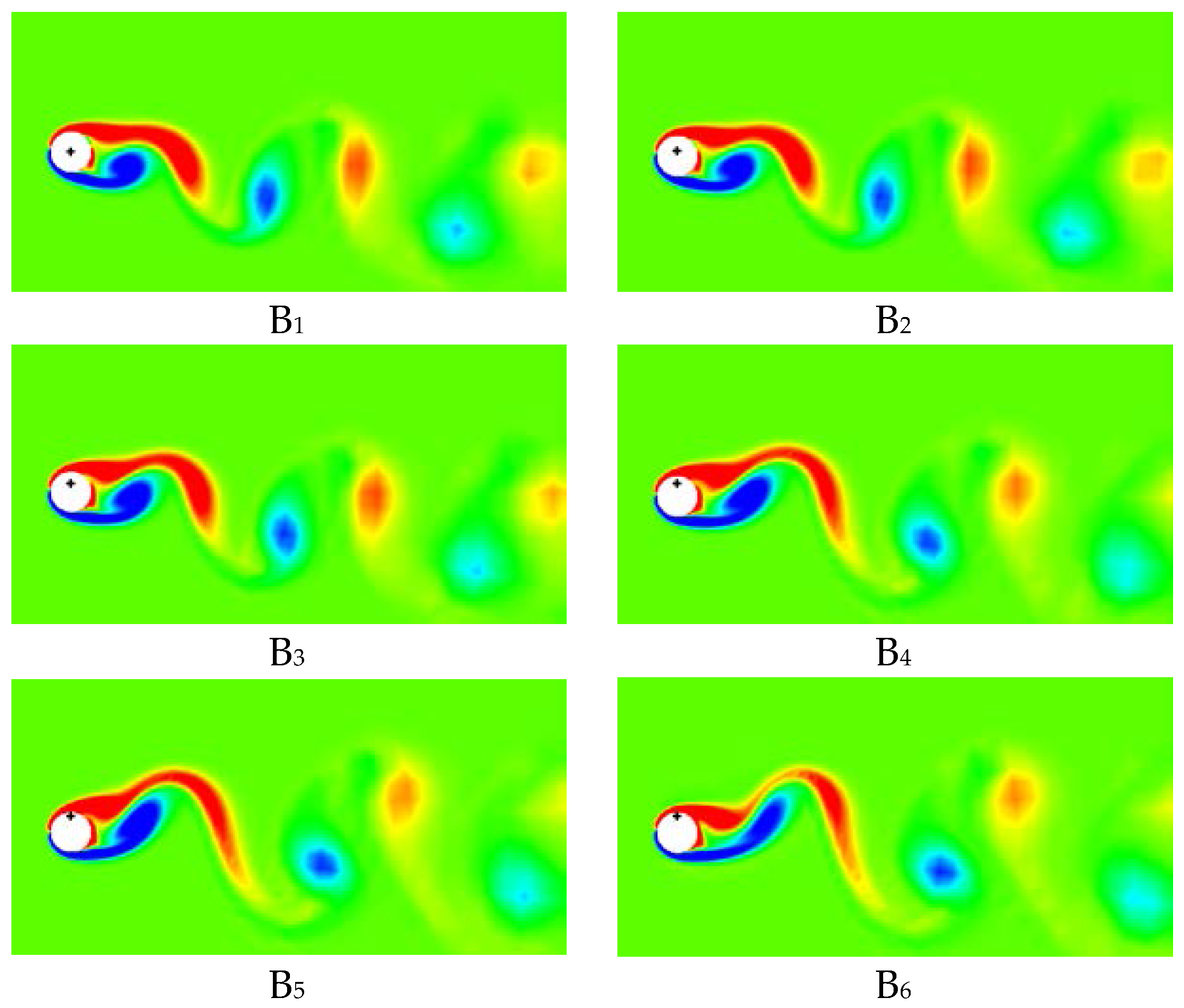
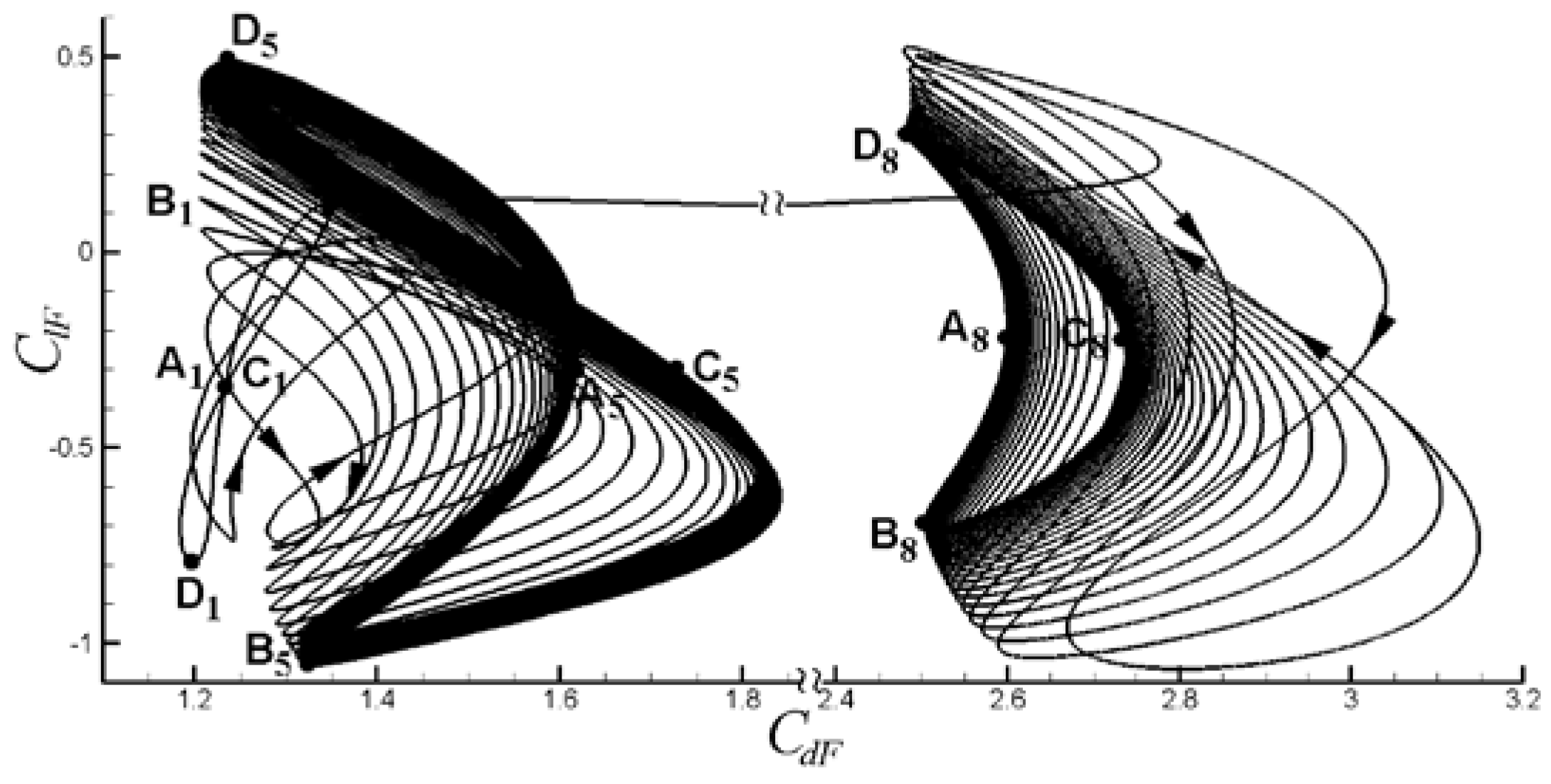
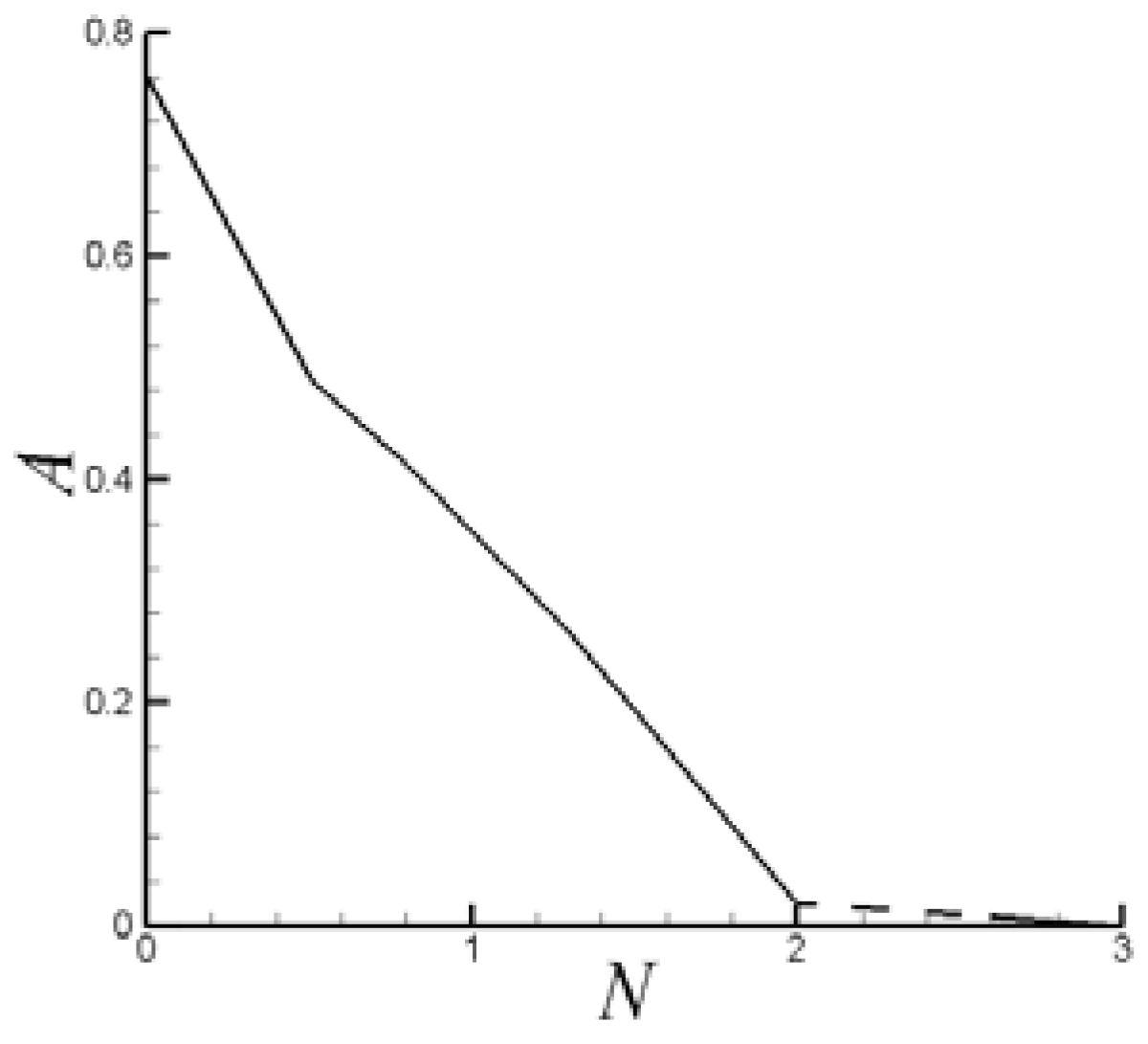
6.1. Control of VIV with Symmetrical Lorentz Force
6.2. Control of VIV with Asymmetrical Lorentz Force
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cachafeiro, H.; de Arevalo, L.F.; Vinuesa, R.; Lopez-Vizcaino, R.; Luna, M. Analysis of vacuum evolution inside Solar Receiver Tubes. Energy Procedia 2015, 69, 289–298. [Google Scholar] [CrossRef]
- Vinuesa, R.; de Arevalo, L.F.; Luna, M.; Cachafeiro, H. Simulations and experiments of heat loss from a parabolic trough absorber tube over a range of pressures and gas compositions in the vacuum chamber. J. Renew. Sustain. Energy 2016, 8, 023701. [Google Scholar] [CrossRef]
- Feng, C.C. The Measurement of Vortex-Induced Effects in Flow Past Stationary and Oscillating Circular and D-Section Cylinders; University of British Columbia: Vancouver, BC, Canada, 1968. [Google Scholar]
- Griffin, O.M.; Koopmann, G.H. The vortex-exited lift and reaction forces on resonantly vibrating cylinders. J. Sound Vib. 1977, 54, 435–448. [Google Scholar] [CrossRef]
- Griffin, O.M. Vortex-excited cross-flow vibrations of a single cylindrical tube. J. Press. Vessel Technol. 1980, 102, 158–166. [Google Scholar] [CrossRef]
- Griffin, O.M.; Ramberg, S.E. Some recent studies of vortex shedding with application to marine tubulars and risers. Eur. J. Mech. B Fluids 1993, 250, 481–508. [Google Scholar] [CrossRef]
- Brika, D.; Laneville, A. Vortex-induced vibration of a long flexible circular cylinder. ASME J. Energy Res. Technol. 1982, 104, 2–13. [Google Scholar] [CrossRef]
- Hover, F.S.; Miller, S.N.; Triantafyllou, M.S. Vortex-induced vibration of marine cables: Experiments using force feedback. J. Fluids Struct. 2011, 27, 354–366. [Google Scholar] [CrossRef]
- Gharib, M.R. Vortex-Induced Vibration, Absence of Lock-in and Fluid Force Deduction; California Institute of Technology: Pasadena, CA, USA, 1999. [Google Scholar]
- Khalak, A.; Williamson, C.H.K. Fluid forces and dynamics of a hydroelastic structure with very low mass and damping. J. Fluids Struct. 1997, 11, 973–982. [Google Scholar] [CrossRef]
- Slaouti, A.; Stansby, P.K. Forced Oscillation and Dynamics Response of a Cylinder in a Current Investigation by the Vortex Method. In Proceedings of the BOSS ’94 Conference, Cambridge, MA, USA, 12–15 July 1994; pp. 645–654.
- Zhou, C.Y.; So, R.M.C.; Lam, K. Vortex-induced vibrations of an elastic circular cylinder. J. Fluids Struct. 1999, 13, 165–189. [Google Scholar] [CrossRef]
- Shiels, D.; Leonard, A.; Roshko, A. Flow-induced vibration of a circular cylinder at limiting structural parameters. J. Fluid Mech. 2001, 15, 3–21. [Google Scholar] [CrossRef]
- Leonard, A.; Roshko, A. Aspect of flow-induced vibration. J. Fluids Struct. 2001, 15, 415–425. [Google Scholar] [CrossRef]
- Williamson, C.H.K.; Govardhan, R. Vortex-induced vibrations. Annu. Rev. Fluid Mech. 2004, 36, 413–455. [Google Scholar] [CrossRef]
- Morse, T.L.; Williamson, C.H.K. Prediction of vortex-induced vibration response by employing controlled motion. J. Fluid Mech. 2009, 634, 5–39. [Google Scholar] [CrossRef]
- Franzini, G.R.; Fujiarra, A.L.C.; Meneghini, J.R.; Korkischko, I.; Franciss, R. Experimental investigation of Vortex-Induced Vibration on rigid, smooth and inclined cylinders. J. Fluids Struct. 2009, 25, 742–750. [Google Scholar] [CrossRef]
- Lam, K.; Zou, L. Three-dimensional numerical simulation of cross-flow around four cylinders in an in-line square configuration. J. Fluids Struct. 2010, 26, 482–502. [Google Scholar] [CrossRef]
- Trim, A.D.; Braaten, H.; Lie, H.; Tognarelli, M.A. Experimental investigation of vortex-induced vibration of long marine risers. J. Fluids Struct. 2005, 21, 335–361. [Google Scholar] [CrossRef]
- Yeung, R.W. Fluid dynamics of finned bodies—From VIV to FPSO. In Proceedings of the 12th International Offshore and Polar Engineering Conference, Kitakyushu, Japan, 26–31 May 2002.
- Bearman, P.W.; Brankovic, M. Experimental studies of passive control of vortex-induced vibration. Eur. J. Mech. B Fluids 2004, 23, 9–15. [Google Scholar] [CrossRef]
- Allen, D.W.; Henning, D.L. Comparison of Various Fairing Geometries for Vortex Suppression at High Reynolds Numbers. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 5–8 May 2008.
- Assi, G.R.S.; Bearman, P.W.; Kitney, N. Low drag solutions for suppressing vortex-induced vibration of circular cylinders. J. Fluids Struct. 2009, 25, 666–675. [Google Scholar] [CrossRef]
- Galvao, R.; Lee, E.; Farrell, D.; Hover, F.; Triantafyllou, M.; Kitney, N.; Beynet, P. Flow control in flow–structure interaction. J. Fluids Struct. 2008, 24, 1216–1226. [Google Scholar] [CrossRef]
- Modi, V.J. Moving surface boundary-layer control: A review. J. Fluids Struct. 1997, 33, 229–242. [Google Scholar] [CrossRef]
- Munshi, S.R.; Modi, V.J.; Yokomizo, T. Aerodynamics and dynamics of rectangular prisms with momentum injection. J. Fluids Struct. 1997, 11, 873–892. [Google Scholar] [CrossRef]
- Korkischko, I.; Meneghini, J.R. Suppression of vortex-induced vibration using moving surface boundary-layer control. J. Fluids Struct. 2012, 34, 259–270. [Google Scholar] [CrossRef]
- Wu, C.J.; Wang, L.; Wu, J.Z. Suppression of the von Karman vortex street behind a circular cylinder by a traveling wave generated by a flexible surface. J. Fluid Mech. 2007, 574, 365–391. [Google Scholar] [CrossRef]
- Tchieu, A.A.; Leonard, A. Experimental investigation on the suppression of vortex-induced vibration of long flexible riser by multiple control rods. J. Fluids Struct. 2012, 30, 115–132. [Google Scholar]
- Gbadebo, S.A.; Cumpsty, N.A.; Hynes, T.P. Control of three-dimensional separations in axial compressors by tailored boundary layer suction. J. Turbomach. 2008, 130, 011004. [Google Scholar] [CrossRef]
- Chng, T.L.; Rachman, A.; Tsai, H.M.; Zha, G.C. Flow control of an airfoil via injection and suction. J. Aircr. 2009, 46, 291–300. [Google Scholar] [CrossRef]
- Arcas, D.; Redekopp, L. Aspects of wake vortex control through base blowing/suction. Phys. Fluids 2004, 16, 452–456. [Google Scholar] [CrossRef]
- Fransson, J.H.M.; Konieczny, P.; Alfredsson, P.H. Flow around a porous cylinder subject to continuous suction or blowing. J. Fluids Struct. 2004, 19, 1031–1048. [Google Scholar] [CrossRef]
- Patil, S.K.R.; Ng, T.T. Control of separation using span wise periodic porosity. AIAA J. 2010, 48, 174–187. [Google Scholar] [CrossRef]
- Crawford, C.H.; Karniadakis, G.E. Control of External Flows via Electro-Magnetic Fields. In Proceedings of the AIAA Fluid Dynamics Conference, San Diego, CA, USA, 19–22 June 1995.
- Weier, T.; Gerbeth, G.; Mutschke, G.; Platacis, E.; Lielausis, O. Experiments on cylinder wake stabilization in an electrolyte solution by means of electromagnetic forces localized on the cylinder surface. Exp. Therm. Fluid Sci. 1998, 16, 84–91. [Google Scholar] [CrossRef]
- Kim, S.; Lee, C.M. Control of flows around a circular cylinder: Suppression of oscillatory lift force. Fluid Dyn. Res. 2001, 29, 47–63. [Google Scholar] [CrossRef]
- Posdziech, O.; Grundmann, R. Electromagnetic control of seawater flow around circular cylinders. Eur. J. Mech. B Fluids 2001, 20, 255–274. [Google Scholar] [CrossRef]
- Zhang, H.; Fan, B.C.; Chen, Z.H. Computations of optimal cylinder flow control in weakly conductive fluids. Comput. Fluids 2010, 39, 1261–1266. [Google Scholar] [CrossRef]
- Zhang, H.; Fan, B.C.; Chen, Z.H. Optimal control of cylinder wake by electromagnetic force based on the adjoint flow field. Eur. J. Mech. B Fluids 2010, 29, 53–60. [Google Scholar] [CrossRef]
- Zhang, H.; Fan, B.C.; Chen, Z.H.; Li, Y.L. Effect of the Lorentz force on cylinder drag reduction and its optimal location. Fluid Dyn. Res. 2011, 43, 015506. [Google Scholar] [CrossRef]
- Zhang, H.; Fan, B.C.; Chen, Z.H.; Li, H.Z. An in-depth study on vortex-induced vibration of a circular cylinder with shear flow. Comput. Fluids 2014, 100, 30–44. [Google Scholar] [CrossRef]
- Lei, C.; Cheng, L.; Kavanagh, K. A finite difference solution of the shear flow over a circular cylinder. Ocean Eng. 2000, 27, 271–290. [Google Scholar] [CrossRef]
- Sarpkaya, T. A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 2004, 19, 389–447. [Google Scholar] [CrossRef]



© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Liu, M.-k.; Fan, B.-c.; Chen, Z.-h.; Li, J.; Gui, M.-y. Investigations on the Effects of Vortex-Induced Vibration with Different Distributions of Lorentz Forces. Appl. Sci. 2017, 7, 61. https://doi.org/10.3390/app7010061
Zhang H, Liu M-k, Fan B-c, Chen Z-h, Li J, Gui M-y. Investigations on the Effects of Vortex-Induced Vibration with Different Distributions of Lorentz Forces. Applied Sciences. 2017; 7(1):61. https://doi.org/10.3390/app7010061
Chicago/Turabian StyleZhang, Hui, Meng-ke Liu, Bao-chun Fan, Zhi-hua Chen, Jian Li, and Ming-yue Gui. 2017. "Investigations on the Effects of Vortex-Induced Vibration with Different Distributions of Lorentz Forces" Applied Sciences 7, no. 1: 61. https://doi.org/10.3390/app7010061




