Deterministic and Robust Optimization Approach for Single Artillery Unit Fire Scheduling Problem

Abstract

In this study, deterministic and robust optimization models for single artillery unit fire scheduling are developed to minimize the total enemy threat to friendly forces by considering the enemy target threat level, enemy target destruction time, and target firing preparation time simultaneously. Many factors in war environments are uncertain. In particular, it is difficult to evaluate the threat levels of enemy targets definitively. We consider the threat level of an enemy target to be an uncertain parameter and propose a robust optimization model that minimizes the total enemy threat to friendly forces. The robust optimization model represents a semi-infinite problem that has infinitely many constraints. Therefore, we reformulate the robust optimization model into a tractable robust counterpart formulation with a finite number of constraints. In the robust counterpart formulation with cardinality-constrained uncertainty, the conservativeness and robustness of the solution can be adjusted with an uncertainty degree, Γ. Further, numerical experiments are conducted to verify that the robust counterpart formulation with cardinality-constrained uncertainty can be made equivalent to the deterministic optimization model and the robust counterpart formulation with box uncertainty by setting Γ accordingly.

1. Introduction

The objective of this study is to determine the artillery firing sequence in military operations when a single artillery unit fires at multiple enemy targets, such that the enemy threat to friendly forces is minimized. The artillery firing problem can be separated into the problem of assigning targets to multiple artillery units and that of determining the firing sequence for the assigned targets. The problem of determining the firing sequence for the assigned targets can be further separated into the problem of determining the firing sequence of multiple artillery units and that of determining the firing sequence of a single artillery unit. Owing to the lower destructive power and performance of older artillery shells, multiple artillery units were required to fire simultaneously at a single enemy target to achieve surprise effects and sufficient destruction. Thus, the determination of the firing sequence of multiple artillery units was considered to minimize the firing operation completion time [1]. However, modern artillery shells have high destructive power, and the shell launch system is automated. Thus, a single artillery unit can operate independently. Therefore, the firing sequence of a single artillery unit is considered in this study.

The objective of an artillery unit is to support friendly forces by targeting remote enemy targets, including infantry, artillery, armored units, intelligence units, and command and communications facilities. Once a war commences, various enemy units may inflict severe damage on friendly forces unless they are destroyed by friendly artillery fire.

A single artillery unit cannot fire at multiple targets simultaneously; it must fire at them one at a time. Thus, a single artillery unit must determine the sequence of firing at enemy targets to minimize the total losses to friendly forces. In this study, the degree of threat of an enemy target is defined as the degree of the loss that it causes to friendly forces per unit time. We consider the enemy target threat level, destruction time, and firing preparation time simultaneously. Accordingly, we develop a deterministic model for determining the firing sequence to minimize the total threat of the enemy to friendly units until the end of the firing operation.

In general, military operational environments are uncertain, and decision-makers must base their decisions on uncertain battlefield information. In particular, it is impossible to assess the information related to the enemy definitively. Such information is highly uncertain because enemies often attempt to deceive their opponents and minimize their exposure. Thus, the enemy target threat is considered to be an uncertain parameter, and the model for determining the firing sequence is developed based on uncertain enemy information. Such a robust optimization (RO) model enables decision-makers to obtain robust solutions and to anticipate robustly the total threat of the enemy to friendly units.

The main contributions of this study are as follows.

-

A deterministic optimization model is developed to determine the firing sequence necessary to minimize the total enemy threat to friendly units by simultaneously considering the threat levels of the targets, destruction time, and firing preparation time.

-

Robust counterpart formulations are developed to determine the firing sequence required to minimize the total enemy threat to friendly units when the threat level of the enemy is uncertain.

-

Our experimental results verify that the robust counterpart formulation with cardinality-constrained uncertainty is equivalent to the deterministic optimization model for the firing sequence when the degree of uncertainty is minimum and that it is equivalent to the robust counterpart formulation with box uncertainty when the degree of uncertainty is at its maximum.

The remainder of this paper is organized as follows. Section 2 reviews previous studies related to the problems of artillery firing and RO. Section 3 describes the artillery fire scheduling problem and the development of the required models. Section 4 discusses the development of robust counterpart formulations that were reformulated into a linear problem to solve the RO problem described in Section 3. Section 5 presents the results of numerical experiments. Finally, Section 6 concludes the paper.

2. Literature Review

The artillery firing problem can be separated into the problem of assigning targets to multiple artillery units and that of determining the firing sequence for the assigned targets. The problem of assigning multiple enemy targets to multiple artillery units is a typical assignment problem, i.e., an NP-complete problem [2]. The problem of weapon-target assignment was first studied by Manne [3]. Since then, various methods have been investigated and developed by many researchers. Hosein and Athans [4] proposed a multi-stage version of the weapon-target assignment problem and developed a method to obtain the solution by transforming the problem into a deterministic one even when the number of targets is considerably large. Erdem and Ozdemirel [5] developed an evolutionary approach to the weapon-target assignment problem, whereas Lee and Lee [6] solved the problem using a hybrid algorithm that combines the ant colony optimization algorithm and the genetic algorithm. Ahuja et al. [7] proposed exact and heuristic algorithms to find optimal and approximate solutions by transforming the weapon–target assignment problem into integer and network flow problems, respectively.

In contrast to the weapon-target assignment problem, the problem of determining the firing sequence has not been studied extensively. The firing sequence problem was first studied by Kwon et al. [1], who proposed a greedy heuristic to minimize the firing completion time of multiple artillery units. In their work, multiple artillery units were restricted to fire at a single target simultaneously to achieve surprise effects and sufficient destruction.

Modern artillery shells can achieve sufficient surprise effects and destruction even if there is only a single firing unit. Hence, the restriction described above is not required. Instead, a method for determining the firing sequence of a single unit should be developed. Therefore, the firing sequence of a single artillery unit is considered in this study. Cha and Kim [8] assumed that the probability of target destruction by artillery fire decreases with time and developed a heuristic that minimizes the total threat of the surviving targets. In addition, Cha and Kim [8] assumed that the threat posed by an enemy target is independent of time. However, it is reasonable to assume that such a parameter is related to time, because while enemy targets exist, they can continue to cause damage to friendly units. We consider the threat level of an enemy target to increase with its survival time and develop a scheduling method to minimize the total threat of the enemy to friendly units until the end of the firing operation.

Most existing studies define the factors underlying the solution of the artillery firing problem as deterministic parameters. However, there are many uncertainties among these parameters that must be considered for operational decision-making. In particular, it is impossible to evaluate information related to the enemy definitively. Nevertheless, Erdem and Ozdemirel [5] and Ahuja et al. [7] solved the weapon-target assignment problem by considering the enemy target threats to be certain parameters. Similarly, Cha and Kim [8] solved the fire scheduling problem by considering the enemy target threat to be a certain parameter. However, in the present study, the enemy target threat is considered to be an uncertain parameter, and an RO formulation is proposed to determine the firing sequence. The RO approach was first studied by Soyster [9], and it was extended by Ben-Tal and Nemirovski [10] and Bertsimas and Sim [11]. RO has been applied to various problems, such as the vehicle routing problem (VRP) [12], supply chain management [13], location and allocation [14], and portfolio optimization [15]. However, to the best of our knowledge, no study has applied RO to the artillery fire scheduling problem thus far. In this study, we develop a robust firing sequence optimization model based on the work of Bertsimas and Sim [16], whereby the conservativeness and robustness of the solution can be adjusted with an uncertainty degree.

3. Fire Scheduling Problem

The objective of an artillery unit is to reduce the combat capabilities of the enemy and support friendly operations by firing at the targets that are assigned by higher units or that are requested by maneuvering units. In a war, artillery units are required to fire at numerous enemy targets of varying types and sizes. When the war commences, these enemy targets may cause severe damage to friendly forces. Because an artillery unit cannot fire at multiple enemy targets simultaneously, the firing sequence for the targets should be determined.

When a single artillery unit fires at enemy targets sequentially, enemy targets that are yet to be attacked by the artillery unit can continue performing missions that cause damage to friendly forces. The basic military strategy is to minimize the damage and achieve the mission objective. Therefore, artillery units must determine the firing sequence that will minimize the total threat of the enemy to friendly units until the end of the firing operation. When determining the firing sequence, artillery units must consider the threat levels of the enemy targets, destruction time, and preparation time to fire at the next target.

In this paper, we make the following assumptions:

(1)

The threat of enemy targets is determined by the type and size of the target.

(2)

While firing at one target, an artillery unit cannot fire at another target.

(3)

After firing at one target, it takes time for the artillery unit to fire at the next target.

(4)

An enemy target that is not attacked by an artillery unit causes damage to friendly units.

(5)

An enemy target that is attacked by an artillery unit does not cause damage to friendly units.

The following notations are used in the mathematical formulations.

Notations	Definitions
Decision variables
$x_j$	Firing start time for target j
$y_{jj\prime }$	If target j takes precedence over target j′, 1; otherwise, 0
Parameters
$j$	Target $j, j\in \mathrm{N}=\left\{1, \dots , n\right\}$
$f_j$	Nominal threat level of target j
${\overline{f}}_j$	Maximum threat level of target j
${\tilde{f}}_j$	Uncertain threat level of target j
${\widehat{f}}_j$	Difference between ${\tilde{f}}_j$ and $f_j$, ${\widehat{f}}_j={\tilde{f}}_j-f_j$
$s_{jj\prime }$	Preparation time to fire at target j′ after firing at target j
$p_j$	Amount of time required to destroy target j
$M$	Large positive value

3.1. Deterministic Model for Fire Scheduling Problem

It is assumed that there are n targets at which a single artillery unit should fire, and that the targets vary in type, size, and threat level. The threat level of a target is a certain parameter, and its value is known.

In this case, the problem of determining the firing sequence is a single machine scheduling problem [17,18,19]. If all of the parameters are deterministic, the deterministic fire scheduling (DFS) model for minimizing the total enemy threat to friendly forces until all of the targets are fired at is given by

$$minimize {\displaystyle \sum }_{j=1}^n{f}_j{x}_j\hspace{1em}\left(\mathrm{DFS}\right)$$

(1)

subject to

$$x_j+p_j+s_{j{j}^{\prime }}\le x_{j^{\prime }}+M\left(1-y_{j{j}^{\prime }}\right)\hspace{1em}j,j^{\prime }=1, 2,\dots , n; j^{\prime }>j$$

(2)

$$x_{j\prime }+p_{j\prime }+s_{j^{\prime }j}\le x_j+M{y}_{j{j}^{\prime }}\hspace{1em}j,j^{\prime }=1, 2, \dots , n; j^{\prime }>j$$

(3)

$$y_{j{j}^{\prime }}=0 or 1,\hspace{1em}j,j^{\prime }=1, 2, \dots , n$$

(4)

The objective function given by Equation (1) is intended to minimize the total threat of the enemy targets to friendly forces until a single artillery unit completes firing at n targets. Here, $f_j$ is the threat posed by target j to a friendly unit per unit time, and $x_j$ is the time at which a single artillery unit starts firing at target j. Thus, $f_j{x}_j$ is the threat of target j to friendly forces until the single artillery unit fires at target j. Further, once the single artillery unit has fired at target j, target j no longer causes damage to friendly forces. Equations (2) and (3) determine the sequence of firing at the targets, and the second target that is fired at between any two targets is constrained to consider the preceding target destruction time and current target preparation time. In Equation (4), $y_{j{j}^{\prime }}$ is a binary decision variable. If target j is fired at before target j′, $y_{j{j}^{\prime }}$ is 1; otherwise, it is 0.

3.2. Robust Optimization Model for Fire Scheduling Problem

It is important to note that in the DFS model described in the previous section, the enemy target threat level is an uncertain parameter. In a war, the enemy target threat level is evaluated through qualitative analysis by information gathering assets and analysts. However, because enemy targets minimize their exposure and attempt to deceive their opponents, it is impossible to assess the threat level of the enemy definitively. Therefore, the threat level of the enemy target should be considered to be an uncertain threat level (${\tilde{f}}_j$), and in this paper, it is assumed that the threat level of the enemy target belongs to an uncertainty set $U_j$.

The RO model for minimizing the total enemy threat to friendly forces when the enemy target threat level is uncertain is given by

$$\mathrm{minimize} y\hspace{1em}\left(\mathrm{RFS}\right)$$

(5)

subject to

$${\displaystyle \sum }_{j=1}^n{\tilde{f}}_j{x}_j\le y\hspace{1em}{\tilde{f}}_j\in U_j, j=1,2, \dots , n$$

(6)

(2), (3), and (4).

The objective function in Equation (5) yields the best worst-case objective value for the uncertain threat level of all of the enemy targets. Equation (6) guarantees a feasible solution for all cases in which the uncertain threat level of the enemy target belongs to the uncertainty set $U_j$. The uncertain threat level ${\tilde{f}}_j$ belongs to the uncertainty set $U_j$, and its value is unknown. The robust fire scheduling (RFS) model represents a semi-infinite problem; it has infinitely many constraints. Therefore, it cannot be solved directly; instead, a tractable robust counterpart formulation with a finite number of constraints is required.

4. Robust Counterpart Formulation

The objective of the robust counterpart formulation is to find a solution that can best respond to various occurrences of uncertain data in an RO model [20]. The RFS model with uncertain data can be transformed into a robust counterpart optimization problem for which solutions can be found even if there is no probability distribution or scenario of uncertain data. It is assumed that the values of the uncertain parameters are unknown but bounded.

4.1. Robust Counterpart Formulation with Box Uncertainty

To transform the RFS model proposed in Section 3.2 into a robust counterpart formulation with box uncertainty, we assume that the uncertain enemy target threat level ${\tilde{f}}_j$ belongs to the box set $\left[f_j, f_j+{\widehat{f}}_j\right]$. With respect to the uncertain data ${\tilde{f}}_j$, the random variable, ${\eta }_j=\left({\tilde{f}}_j-f_j\right)/{\widehat{f}}_j$ can be defined. This variable is unknown but lies within the interval [0,1].

Proposition 1.

Equation (6) can be transformed into the following equation when the uncertain enemy target threat level ${\tilde{f}}_j$ lies within the predefined interval$\left[f_j, f_j+{\widehat{f}}_j\right]$:

$${\displaystyle \sum }_{j=1}^n{\overline{f}}_j{x}_j\le y\hspace{1em}j=1,2, \dots , n$$

(7)

where ${\overline{f}}_j$ is the maximum threat level of target j.

Proof. 

On the left-hand side of Equation (6), both the uncertain enemy target threat level ${\tilde{f}}_j$ and the starting time $x_j$ for firing at target $j$ are nonnegative. Therefore, we have the following relationship:

$${\displaystyle \sum }_{j=1}^n{\tilde{f}}_j{x}_j= {\displaystyle \sum }_{j=1}^n{f}_j{x}_j+{\displaystyle \sum }_{j=1}^n{\widehat{f}}_j{\eta }_j{x}_j\le {\displaystyle \sum }_{j=1}^n{f}_j{x}_j+{\displaystyle \sum }_{j=1}^n{\widehat{f}}_j{x}_j={\displaystyle \sum }_{j=1}^n{\overline{f}}_j{x}_j \le \mathrm{y}$$

(8)

RFS can be transformed into robust counterpart formulation with box uncertainty (RCFB) by Equation (8). Thus, RCFB becomes a tractable problem:

$$\mathrm{minimize} y\hspace{1em}\left(\mathrm{RCFB}\right)$$

subject to

$${\displaystyle \sum }_{j=1}^n{\overline{f}}_j{x}_j\le y\hspace{1em}j=1,2, \dots , n$$

(2), (3), and (4).

The solution of the discrete optimization model RCFB is feasible for all uncertain target threat levels, but it is too conservative [9]. To overcome the drawback of the excessively conservative solution of the robust counterpart formulation with box uncertainty, Ben-Tal [10] proposed an efficient algorithm for solving convex optimization problems with data uncertainty by considering the uncertainty set of the data to be an ellipsoid. However, because the formulations proposed by Ben-Tal involve conic quadratic problems, his method cannot be applied directly to discrete optimization. Bertsimas and Sim proposed a method to control the level of conservatism in the solution [11,16]. The advantage of their method is that it can be transformed into a linear discrete optimization problem and applied directly. In the next section, we propose a single artillery unit fire scheduling model by applying the methodology of Bertsimas and Sim [11,16].

4.2. Robust Counterpart Formulation with Cardinality-Constrained Uncertainty

In this section, a robust counterpart formulation with cardinality-constrained uncertainty is proposed. This formulation overcomes the drawback of the excessively conservative solution of the robust counterpart formulation with box uncertainty (RCFB). The RCFB model assumes that all of the target threat levels are maximized in the interval $\left[f_j, f_j+{\widehat{f}}_j\right]$; however, the actual probability of such a scenario is quite low. Therefore, by considering the possibility that there may be targets with zero deviation of the uncertain enemy target threat level, a parameter, Γ, is included in Equation (9). Γ represents the uncertainty degree and it controls the conservative level of the solution. The value of Γ lies in the interval [0, n − 1] and is not necessarily an integer. The maximum value of Γ is n – 1 because the enemy target that the artillery unit first fires at does not cause damage to friendly forces; only the remaining n − 1 enemy targets do so. Γ in Equation (9) allows up to $\lfloor \Gamma \rfloor$ of n uncertain enemy target threat levels to attain their worst-case values simultaneously and allows one uncertain enemy target threat level to change by $\left(\Gamma -\lfloor \Gamma \rfloor \right){\widehat{f}}_t$. Therefore, the decision-maker adjusts the robustness of the solution by changing the value of Γ in the range [0, n − 1].

The robust counterpart formulation with cardinality-constrained uncertainty (RCFC 1) is given by

$$\mathrm{minimize} y\hspace{1em}\left(\mathrm{RCFC} 1\right)$$

subject to

$$y\ge {\displaystyle \sum }_j^n{f}_j{x}_j+\beta \left(x^{*},\Gamma \right)$$

(9)

where

$$\beta \left(x^{*},\Gamma \right)=\underset{\left\{S{{\displaystyle \cup }}^{}\left\{t\right\}\right|S\subseteq J,\left|S\right|=\Gamma ,t\in J\backslash S\}}{\mathit{max}}\left\{{\displaystyle \sum }_{j\in S}{\widehat{f}}_j{x}_j^{*}+(\Gamma -\lfloor \Gamma \rfloor {\widehat{f}}_t{x}_j^{*}\right\}$$

(2), (3), and (4).

If $\Gamma$ is 0 in RCFC 1, then RCFC 1 is equivalent to DFS, in which the threat level of all enemy targets is certain. Furthermore, if $\Gamma$ is n − 1 in RCFC 1, then RCFC 1 is equivalent to RCFB with the maximum threat level for all of the targets. RCFC 1 can adjust the conservativeness and robustness of the solution with the uncertainty degree, Γ, when the enemy target threat levels are uncertain, but it is a nonlinear optimization problem that is intractable. Therefore, RCFC 1 can be transformed into a linear discrete optimization problem that is tractable by following the method of Bertsimas and Sim [16].

Proposition 2.

Equation (9) can be reformulated as a linear optimization problem when the uncertain enemy target threat level ${\tilde{f}}_j$ lies within the predefined interval $\left[f_j, f_j+{\widehat{f}}_j\right]$.

Proof. 

The objective value of the robustness cost function $\beta \left(x^{*},\Gamma \right)$ (RCF) is equivalent to the objective value of the following linear optimization problem (LP).

$$\beta \left(x^{*},\Gamma \right)=\mathrm{maximize} {\displaystyle \sum }_{j\in J}^{}{\widehat{f}}_j{x}^{*}{z}_j\hspace{1em}\mathrm{RCF}$$

subject to

$${\displaystyle \sum }_{j\in J}^{}{z}_j\le \Gamma$$

(10)

$$0\le z_j\le 1 \forall j\in J$$

(11)

The dual problem of RCF is given by

$$\mathrm{minimize} \Gamma u+{\displaystyle \sum }_j^n{\pi }_j\hspace{1em}\mathrm{LP}$$

subject to

$$u+{\pi }_j\ge {\widehat{f}}_j x_j\hspace{1em}j=1,2, \dots , n$$

$u\ge 0$, and

$${\pi }_j\ge 0\hspace{1em}j=1,2, \dots , n$$

where $u$ is the dual variable corresponding to the inequality given by Equation (10) and ${\pi }_j$ is the dual variable corresponding to the inequality given by Equation (11). RCF is feasible and it is bounded for $\Gamma \in \left[0, n-1\right]$. In addition, LP is feasible and bounded for $\Gamma \in \left[0, n-1\right]$ by the strong duality theorem, and the optimal objective values of RCF and LP are the same. Thus, RCFC 1 can be reformulated as follows:

$$\mathrm{minimize} y\hspace{1em}\left(\mathrm{RCFC} 2\right)$$

subject to

$$y\ge {\displaystyle \sum }_j^n{f}_j{x}_j+\Gamma u+{\displaystyle \sum }_j^n{\pi }_j$$

$$x_j+p_j+s_{j{j}^{\prime }}\le x_{j^{\prime }}+M\left(1-y_{j{j}^{\prime }}\right)\hspace{1em}j,j^{\prime }=1, 2,\dots , n; j^{\prime }>j,$$

$$x_{j\prime }+p_{j\prime }+s_{j^{\prime }j}\le x_j+M{y}_{j{j}^{\prime }}\hspace{1em}j,j^{\prime }=1, 2, \dots , n; j^{\prime }>j,$$

$$y_{j{j}^{\prime }}=0 or 1\hspace{1em}j,j^{\prime }=1, 2, \dots , n$$

$$u+{\pi }_j\ge {\widehat{f}}_j x_j\hspace{1em}j=1,2, \dots , n$$

$u\ge 0$, and

$${\pi }_j\ge 0\hspace{1em}=1,2, \dots , n$$

RCFC 1 is equivalent to RCFC 2 (robust counterpart formulation with cardinality-constrained uncertainty). RCFC 2 is a linear discrete optimization problem that is tractable. Moreover, if $\Gamma$ is 0 in RCFC 2, then RCFC 2 is equivalent to DFS, in which the threat level of all of the enemy targets is certain. Furthermore, if $\Gamma$ is n − 1 in RCFC 2, then RCFC 2 is equivalent to RCFB with the maximum threat level for all targets.

5. Experimental Results and Discussion

We generated and tested a set of problems using the proposed models. First, we verified that the robust counterpart formulation with cardinality-constrained uncertainty (RCFC 2) is equivalent to the deterministic optimization model (DFS) for fire scheduling when the uncertainty degree is zero and that it is equivalent to the robust counterpart formulation with box uncertainty when the uncertainty degree is n − 1. Next, we observed the objective values according to the changes in Γ and ε in the robust counterpart formulation with cardinality-constrained uncertainty, where Γ is the uncertainty degree and ε is the uncertainty level. The number of targets was set to 5, 10, 15, and 20. Threat levels, $f_j$, were randomly generated in [25,100] as specified by Ahuja et al. [7]. $p_j$ and $s_{jj\prime }$ were generated based on field artillery tactics [21]. When the single artillery unit fires at one target, $p_j$ is the amount of time required to destroy target j and is determined based on the type and size of the enemy target. This value can range from 1 min to 3 min. $s_{jj\prime }$ is the preparation time required to fire at target j′ after firing at target j and is determined based on the location of target j and the type of shell. This value can range from 0 min to 2 min. Accordingly, $p_j$ and $s_{jj\prime }$ are randomly generated in [1,3] and [0,2], respectively. The numerical experiments were implemented using the IBM ILOG CPLEX 12.6.1 (IBM software, New York, NY, USA). The computer environment was an Intel Core i5-6600 CPU (3.3 GHz) with 8 GB RAM (random-access memory).

First, we solved the test problems using the proposed models and verified the robust counterpart formulation with cardinality-constrained uncertainty (RCFC 2). In these experiments, the uncertain threat level, ${\tilde{f}}_j$, belonged to the uncertainty set $U_j=\left\{{\tilde{f}}_j:f_j\le {\tilde{f}}_j\le f_j+{\widehat{f}}_j\right\}$, where ${\widehat{f}}_j=\epsilon f_j$ and ε was selected from the set {0.2, 0.4, 0.6, 0.8, 1.0}. The numerical experiments were repeated 100 times for each case.

Table 1. Comparison of objective values and CPU times of DFS (deterministic fire scheduling), RCFB (robust counterpart formulation with box uncertainty), and RCFC 2 (robust counterpart formulation with cardinality-constrained uncertainty) with various Γ.

	Objective Values					CPU Time (s)
n	ε	DFS	RCFB	RCFC 2		DFS	RCFB	RCFC 2 (Γ = 0)
				Γ = 0	Γ = n − 1
6	0.2	1603.7	1924.4	1603.7	1924.4	0.07	0.09	0.08
	0.4		2245.1	1603.7	2245.1		0.10	0.09
	0.6		2565.8	1603.7	2565.8		0.09	0.08
	0.8		2886.6	1603.7	2886.6		0.09	0.08
	1.0		3207.3	1603.7	3207.3		0.10	0.08
9	0.2	3556.6	4267.9	3556.6	4267.9	0.45	0.61	0.50
	0.4		4979.2	3556.6	4979.2		0.59	0.51
	0.6		5690.5	3556.6	5690.5		0.62	0.49
	0.8		6401.8	3556.6	6401.8		0.60	0.50
	1.0		7113.1	3556.6	7113.1		0.64	0.49
12	0.2	6602.9	7923.5	6602.9	7923.5	15.2	39.58	29.99
	0.4		9244.1	6602.9	9244.1		40.20	28.35
	0.6		10,564.7	6602.9	10,564.7		40.45	27.69
	0.8		11,885.3	6602.9	11,885.3		41.78	28.18
	1.0		13,205.9	6602.9	13,205.9		41.80	28.17
15	0.2	9441.5	11,329.8	9441.5	11,329.8	1870.8	3495.32	2622.35
	0.4		13,218.1	9441.5	13,218.1		3756.60	2628.80
	0.6		15,106.4	9441.5	15,106.4		3703.69	2633.03
	0.8		16,994.7	9441.5	16,994.7		3813.11	2637.34
	1.0		18,883.0	9441.5	18,883.0		3885.60	2661.50

lists the objective values and CPU times of DFS, RCFB, and RCFC 2 with various Γ. The objective value of RCFC 2 is the same as that of DFS when the uncertainty degree is zero, regardless of the number of enemy targets. Moreover, the objective value of RCFC 2 is the same as that of RCFB when the uncertainty degree is maximized, regardless of the number of enemy targets. Therefore, RCFC 2 with Γ = 0 is equivalent to DFS and RCFC 2, with Γ = n − 1 is equivalent to RCFB, so the DFS and RCFB problems can be solved by changing only Γ in the RCFC 2 model. No significant differences were observed among the CPU times of the proposed models. However, as the number of targets increased, the CPU time increased exponentially. The computational complexity of a large-scale fire scheduling problem is extremely high. Therefore, heuristics are required to solve such large-scale problems.

Next, when number of targets was set to 12, we observed the objective values according to the changes in ε and Γ in RCFC 2. In these experiments, the uncertain threat level, ${\tilde{f}}_j$, belonged to the uncertainty set $U_j=\left\{{\tilde{f}}_j:f_j\le {\tilde{f}}_j\le f_j+{\widehat{f}}_j\right\}$, where ${\widehat{f}}_j=\epsilon f_j$ and ε was selected from the set {0.2, 0.4, 0.6, 0.8, 1.0}.

Table 2. Objective values for different $\epsilon$ and Γ (n = 12).

Γ		0	1	2	3	4	5	6	7	8	9	10	11
$\epsilon$	0.2	6602.9	6835.0	7033.6	7204.3	7359.2	7499.8	7628.1	7733.5	7813.2	7869.2	7905.4	7923.5
	0.4	6602.9	7062.7	7451.7	7793.8	8104.8	8389.4	8646.1	8855.7	9017.1	9132.5	9206.9	9244.1
	0.6	6602.9	7286.1	7859.6	8374.8	8840.1	9269.5	9657.7	9977.0	10,219.8	10,394.3	10,507.9	10,564.7
	0.8	6602.9	7505.0	8263.6	8946.5	9568.7	10,143.3	10,661.8	11,095.1	11,422.5	11,656.0	11,808.5	11,885.3
	1.0	6602.9	7719.1	8665.0	9516.9	10,295.0	11,014.5	11,659.8	12,207.0	12,624.7	12,917.7	13,109.0	13,205.9

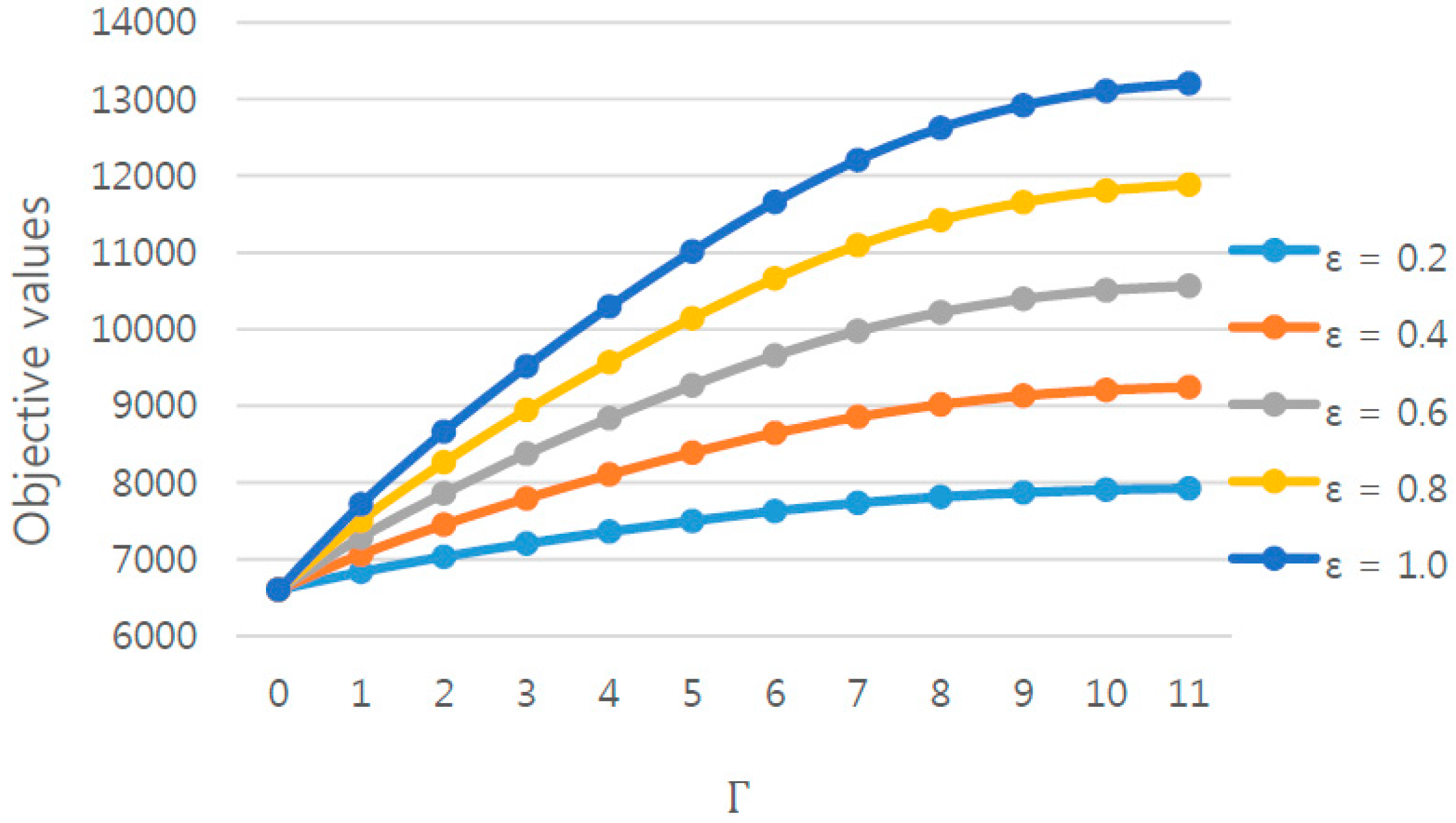
lists the objective values of RCFC 2 for different $\epsilon$ and $\Gamma$. It can be seen that as $\Gamma$ increases, the rate of increase of the objective values decreases, as shown in Figure 1, regardless of $\epsilon$. RCFC 2 provides a solution that does not increase the total threat to friendly forces significantly, even if the decision-makers do not know the uncertainty degree or if the uncertainty degree increases.

Regarding the effect of $\epsilon$ on the objective value, as $\Gamma$ increases, the difference of the objective value with respect to $\epsilon$ also increases, as shown in Figure 2. For example, the objective value in the case of $\epsilon$ = 0.2 lies between 6602.9 and 7923.5, while that in the case of $\epsilon$ = 1.0 lies between 6602.9 and 13,205.9. The greater the accuracy of the information about the enemy threat level, the greater is the accuracy with which the total threat of the enemy to friendly forces can be predicted. Therefore, efforts should be devoted toward making information about enemy target threats more accurate.

6. Conclusions

To the best of our knowledge, no study thus far has involved determining the firing sequence for enemy targets to minimize the total threat of the enemy to friendly forces until the end of the firing operation. In this paper, we proposed a single artillery unit fire scheduling model that minimizes the total enemy threat to friendly forces by simultaneously considering the threats of the enemy targets, enemy target destruction time, and firing preparation time.

Most of the factors in a battlefield environment are uncertain, and it is especially difficult to assess the information related to the enemy. We considered the threat level of the enemy target to be an uncertain parameter and proposed an RO model for fire scheduling. However, the proposed RO model represents a semi-infinite problem that has infinitely many constraints. Therefore, we developed robust counterpart formulations for the proposed model. In the robust counterpart formulation with cardinality-constrained uncertainty, the conservativeness of the solution can be controlled by adjusting Γ. Using this model, decision-makers in the battlefield can determine robust firing sequences and associated objective values by considering the uncertainty. Thus, various battlefield operations can be planned.

Our experimental results verified that the robust counterpart formulation with cardinality-constrained uncertainty is equivalent to the deterministic optimization model for the firing sequence when the uncertainty degree is zero and that it is equivalent to the robust counterpart formulation with box uncertainty when the uncertainty degree is at its maximum. Therefore, the robust counterpart formulation with cardinality-constrained uncertainty can be used to obtain solutions for deterministic optimization modeling and worst-case modeling by changing the value of Γ.

If the number of targets is large, then the solution of the model presented in this paper cannot be found in a short time. Because the available time for operation preparation in a war scenario is always limited, prompt operation preparation is critical. In the future, we will develop heuristics to find the optimal solution in a short time for a large number of targets. In addition, uncertain factors besides the threat level of the enemy targets exist in war scenarios. Therefore, to obtain more realistic solutions, we will consider a more general uncertainty set for the uncertain factors, such as the central limit theorem uncertainty set [22].