Input–Output Finite Time Stabilization of Time-Varying Impulsive Positive Hybrid Systems under MDADT

Abstract

Time-varying impulsive positive hybrid systems based on finite state machines (FSMs) are considered in this paper, and the concept of input–output finite time stability (IO-FTS) is extended for this type of hybrid system. The IO-FTS analysis of the single linear time-varying system is given first. Then, the sufficient conditions of IO-FTS for hybrid systems are proposed via the mode-dependent average dwell time (MDADT) technique. Moreover, the output feedback controller which can stabilize the non-autonomous hybrid systems is derived, and the obtained results are presented in a linear programming form. Finally, a numerical example is provided to show the theoretical results.

1. Introduction

Hybrid systems play an important role in practical applications, such as intelligent transportation systems and manufacturing systems. In fact, hybrid systems are formed by the discrete event dynamical subsystem and the continuous variable dynamical subsystem that interact and intermix with each other [1,2]. Generally, the former can be modeled as a Petri net [3,4], or a finite state machine (FSM) [5,6]. Some basic research results on FSMs have been obtained [6,7,8], concerning its structure, stability, observability, and liveliness.

If hybrid systems consist of a family of dynamical subsystems and a switching signal which determines the switching manner between the subsystems, they are called switched systems [9,10,11]. A system is positive if for any nonnegative initial condition its state variables and outputs naturally take non-negative values for all nonnegative times. Generally, positive systems have many special and interesting properties [12,13,14,15]. Moreover, positive switched systems switch between several positive subsystems [16]. The importance of positive switched systems has received much attention due to their broad applications in communication systems [17], formation flying [18], systems theory [19], and so on. Actually, the study of positive switched systems is more challenging than that of general switched systems because the features of positive systems and the features of switched systems have to be combined to obtain elegant results [20]. It should be pointed out that many previous results on positive switched systems focus mainly on stability analysis and controller synthesis [21,22,23,24,25,26,27,28,29], such as exponential stability [21,22,23,24,25], asymptotic stability [26], finite time stability (FTS) [27,28], and input–output finite time stability (IO-FTS) [30].

If the state of a system does not exceed a prescribed threshold during a fixed finite-time interval, then the system is said to have FTS [31]. This is different from Lyapunov asymptotic stability. Obviously, a finite-time stable system may not have Lyapunov stability, and a Lyapunov stable system may not be finite-time stable. The study of FTS is useful for dealing with the behavior of a system within a finite time interval. Much work on FTS has been done [27,28,31,32,33]. Furthermore, input-to-state FTS [34], robust-FTS [35] and IO-FTS [29,30,36,37,38] have also been investigated. In particular, in [27,28], the FTS is investigated with respect to positive switched linear systems by designing average dwell time (ADT) as the switching strategy.

The ADT approach is proposed and used to investigate the stability and stabilization problems for time-dependent hybrid systems [39,40]. Recently, a new switching strategy called the mode-dependent average dwell time (MDADT) technique was proposed [41]. It allows each mode in the underlying systems to have its own ADT, therefore, it is more applicable in practice than the ADT technique. Based on the MDADT technique, the periodic switching law was designed for periodic switching systems in order to achieve optimal switching control [42]. This technique is also used to deal with the stability and stabilization problems of positive switched systems [23].

The concept of IO-FTS was proposed for a linear time-varying system in [37]. Roughly speaking, a system is said to have IO-FTS if, given a class of norm bounded input signals over a specified time interval $[t_0,T]$, the outputs of the system do not exceed an assigned threshold during $[t_0,T]$. The author of [37] points out that IO-FTS is dependent on IO stability, because it involves signals defined over a finite-time interval, does not require the inputs and outputs to belong to the same class, and quantitative bounds on both inputs and outputs must be specified. Based on [37], some research results were derived. In [38], the IO-FTS was studied for a class of impulsive dynamical linear systems, and both static output and state feedback controllers were designed to stabilize the impulsive systems. In [43], using coupled differential linear matrix inequality, a pair of necessary and sufficient conditions for the IO-FTS of impulsive linear systems were proposed. By applying the MDADT technique, the IO-FTS was considered for a class of discrete-time positive switched systems with delays [30] and a class of continuous-time positive switched systems with delays [29] respectively, and the sufficient conditions were presented to guarantee the systems had IO-FTS. However, the IO-FTS of positive hybrid systems based on FSM was not mentioned.

Compared with some positive hybrid systems, time-varying impulsive positive hybrid systems are more general, and the existence of impulse makes it more practical. In addition, the concept of IO-FTS is defined with the finite-time interval, and the transient performance of the system can be obtained with this interval. In practical systems, the system performance is usually only concerned with the finite-time, for example, multiple guided missiles transmission, and so on. Therefore, the research on the IO-FTS of the time-varying impulsive positive hybrid systems has certain practical value and theoretical significance.

Motivated by the above backgrounds, we consider a class of hybrid systems whose discrete event subsystem is modeled as an FSM, and the continuous variable subsystem consists of several continuous time-varying impulsive positive systems. Such systems are called hybrid systems based on FSM. In fact, they are event-driven systems. The main contributions of this paper are given as follows: firstly, the concept of IO-FTS is extended for such hybrid systems. Secondly, under two different classes of exogenous input signals, the sufficient conditions of IO-FTS of a single linear system are deduced by co-positive Lyapunov function. Furthermore, by combining the multiple co-positive Lyapunov functions and MDADT technique, the sufficient conditions of IO-FTS of hybrid systems are derived, and they have good flexibility and weak conservatism. Next, the output feedback controller for stabilization problem is also deduced, and the obtained results are presented under linear programming form. Finally, a numerical example is given to ensure the accuracy of the results.

Our work is organized as follows: in Section 2, some definitions and FSM are introduced, and the problems which will be dealt with are stated. In Section 3, four theorems of IO-FTS for time-varying positive linear systems are derived and the corresponding proofs are given. In Section 4, four theorems of IO-FTS for time-varying positive hybrid systems are derived and the corresponding proofs are given. In Section 5, an example is given to show the effectiveness of the theorem. Some conclusions are given in Section 6.

Notation: Throughout our paper, ${\mathbb{R}}^{+}$ denotes the set of nonnegative real numbers, ${\mathbb{R}}^n$ represents the vector of n-tuples of real numbers, ${\mathbb{R}}^{n\times m}$ is the space of matrices with real entries, and $I_n$ denotes an identity matrix. For a given matrix $A\in {\mathbb{R}}^{n\times m}$, $a_{ij}$ stands for the element in ith row and jth column of A, and $A\prec 0$ ($⪯0$) means all elements of A are positive (nonnegative), i.e., $a_{ij}<0$ ($\le 0$). $A\succ 0$ ($⪰0$) means all elements of A are negative (non-positive), i.e., $a_{ij}>0$ ($\ge 0$). A matrix A is called a Metzler matrix if its off-diagonal elements are all nonnegative real numbers. The symbol ${\mathcal{L}}_p$ denotes the space of vector-valued signals whose p-th power is absolutely integrable over $[0,\infty ]$. The restriction of ${\mathcal{L}}_p$ to $\mathsf{\Omega }\subset [0,\infty ]$ is denoted by ${\mathcal{L}}_{p,\mathsf{\Omega }}$. Given a set $\mathsf{\Omega }\subseteq \mathbb{R}$, a vector-valued function $\xi (·)\succ 0$ and a vector-valued signal $\upsilon (·)\succ 0$, the weighted norm ${\int }_{\mathsf{\Omega }}{\xi }^{\mathrm{T}}\left(\tau \right)\upsilon \left(\tau \right)d\tau$ is denoted by ${\left|\upsilon \right|}_{\mathsf{\Omega },\xi (·)}$.

2. Problem Formulation and Preliminaries

2.1. FSM

In this section, the FSM and the related definitions will be introduced.

Consider the FSM $G=(\mathsf{\Xi },\Sigma ,\mathsf{\zeta })$ described by

$$\begin{array}{c}\hfill \left\{\begin{array}{c}q\left(t_{k+1}\right)\in \phi (q\left(t_k\right),\sigma \left(t_{k+1}\right))\hfill \\ \sigma \left(t_{k+1}\right)\in \varphi (q\left(t_k\right),x\left(t_{k+1}\right))\hfill \\ \psi \left(t_{k+1}\right)=\zeta (q\left(t_k\right),\sigma \left(t_{k+1}\right))\hfill \end{array}\right.\end{array}$$

(1)

where $q\left(t_k\right)\in \mathsf{\Xi }$, $\sigma \left(t_k\right)\in \Sigma$, and $\psi \left(t_k\right)\in \mathsf{\Psi }$ are, respectively, the discrete state, the input event and the output of FSM at time $t_k$, and $t_k$ is the $k-th$ jumping instant. $\mathsf{\Xi }=\{q_1,\dots ,q_m\}$, $\Sigma =\{{\sigma }_1,\dots ,{\sigma }_{\overline{m}}\}$ and $\mathsf{\Psi }\subseteq \mathsf{\Xi }$ are the finite sets of states, input events and outputs, respectively. $\phi :\mathsf{\Xi }\times \Sigma \to 2^{\mathsf{\Xi }}$ is the FSM transition function, $\varphi :\mathsf{\Xi }\times X\to 2^{\Sigma }$ is the function specifying the possible events, and $\zeta :\mathsf{\Xi }\times \Sigma \to \mathsf{\Psi }$ is the output function. $x(·)\in X$ is the continuous system state, $X\in {\mathbb{R}}^n$, and $q\left(t\right)$ is the current node of FSM.

Remark 1.

Note that the state transitions of the hybrid systems depend on the current node evolution of FSM, and the current node $q\left(t\right)\in \mathsf{\Xi }$ specifies the corresponding subsystem of continuous dynamics being active. $q\left(t\right)=q\left(t^{+}\right)$ means there is no jumping, and $q\left(t\right)\ne q\left(t^{+}\right)$ means the object will jump from the current node to another.

Remark 2.

From (1), it can be seen that the state transition may be not unique when a deterministic input event occurs. This type of FSM is the non-deterministic FSM, which can be described by a state transition graph. For example, Figure 1 shows an FSM with five nodes, where the set of node is $\mathsf{\Xi }=\{q_1,q_2,q_3,q_4,q_5\}$, and the set of the input event is $\Sigma =\{{\sigma }_1,{\sigma }_2,{\sigma }_3,{\sigma }_4\}$. The jumping rule of FSM is that the current node jumps from one node to another when a particular input event occurs. However, there may be more than one node that the current node could jump to, thus, except the jump which is needed, all other jumps should be limited via controlling. After the jump, the limitation should be released to maintain the liveliness of FSM. For the FSM shown in Figure 1, the current node is $q_5$, and when the input event ${\sigma }_4$ occurs, the current node jumps from node $q_5$ to $q_4$, then the current node is $q_4$. At this time, if the input event ${\sigma }_1$ occurs, the current node can jump from $q_4$ to $q_3$ or to $q_2$. The jump from $q_4$ to $q_3$ can be limited, and then the current node jumps from $q_4$ to $q_2$. After that, the limitation will be released.

Definition 1.

Given FSM (1) and any $q_i,q_j\in \mathsf{\Xi }$, if there is an input event sequence $\{{\sigma }^1,\cdots ,{\sigma }^{\ell }\}\in \Sigma$ resulting in the current node jumping along the node sequence $\{q^0,q^1,\cdots ,q^{\ell }\}$, where $\ell \in \mathbb{N}$, $q^0=q_i$ and $q^{\ell }=q_j$, then the node sequence $\{q^0,\cdots ,q^{\ell }\}$ is called the path from $q_i$ to $q_j$. The jumping number ℓ is the length of the path from $q_i$ to $q_j$. Let $\hslash (q_i,q_j)$ denote the set of all paths from node $q_i$ to $q_j$. If the path $\{q^0,q^1,\cdots ,q^{\ell }\}\in \hslash (q_i,q_j)$ has the least number of nodes, then it is called the shortest path from $q_i$ to $q_j$. Furthermore, the length of the shortest path from $q_i$ to $q_j$ is called the distance from $q_i$ to $q_j$, and it can be denoted by $d(q_i,q_j)=\ell$. In the case that there is no path from $q_i$ to $q_j$, the distance is denoted by $d(q_i,q_j)=\infty$, $i,j,\ell \in \mathbb{N}$.

Remark 3.

Since the directionality property of FSM is considered in the distance from $q_i$ to $q_j$, generally, $d(q_i,q_j)\ne d(q_j,q_i)$.

Next, let us introduce the distance from one node to a subset $E=\{q_{p_1},\cdots ,q_{p_s}\}$ which denotes a specified subset of $\mathsf{\Xi }$. We call subset E the desired set of FSM.

Definition 2.

Given FSM (1) and a desired set E, the value $d(q_i,E)\stackrel{\Delta }{=}\underset{q_{p_j}\in E}{min}d(q_i,q_{p_j})$ is called the distance from $q_i$ to E, and the corresponding path is called the shortest path from $q_i$ to E, $q_i\in \mathsf{\Xi }$. If $q_i\in E$, then $d(q_i,E)=0$. If there is no path from $q_i$ to E, then $d(q_i,E)=\infty$.

Definition 3.

Given FSM (1), a desired set E, and node $q_i\in \mathsf{\Xi }$, if

(1) 

there is a shortest path from $q_i$ to E, and the current node jumps along this path; and

(2) 

there is a positive integer $\mathcal{K}$, for any $k\ge \mathcal{K}$, $q\left(t_k\right)\in E$;

then the FSM is stable with regard to (w.r.t.) $(q_i,E,\mathcal{K})$.

2.2. IO-FTS

Consider the following impulsive hybrid systems:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\dot{x}\left(t\right)=A_{q\left(t\right)}\left(t\right)x\left(t\right)+H_{q\left(t\right)}\left(t\right)\upsilon \left(t\right),\hfill & q\left(t\right)=q\left(t^{+}\right)\hfill \\ x\left(t^{+}\right)=D_{q\left(t\right)}\left(t\right)x\left(t\right),\hfill & q\left(t\right)\ne q\left(t^{+}\right)\hfill \\ y\left(t\right)=C_{q\left(t\right)}\left(t\right)x\left(t\right),\hfill \\ G=(\mathsf{\Xi },\Sigma ,\zeta ),\hfill \end{array}\right.\end{array}$$

(2)

where $x\left(t\right)\in {\mathbb{R}}^n$ is the system state, $\upsilon \left(t\right)\in {\mathbb{R}}^r$ is the particular exogenous input, and $y\left(t\right)\in {\mathbb{R}}^h$ is the system output. $A_{q\left(t\right)}(·):{\mathbb{R}}^{+}\to {\mathbb{R}}^{n\times n}$, $H_{q\left(t\right)}(·):{\mathbb{R}}^{+}\to {\mathbb{R}}^{n\times r}$, $D_{q\left(t\right)}(·):{\mathbb{R}}^{+}\to {\mathbb{R}}^{n\times n}$, and $C_{q\left(t\right)}(·):{\mathbb{R}}^{+}\to {\mathbb{R}}^{h\times n}$ are continuous matrix-valued functions. $G=(\mathsf{\Xi },\Sigma ,\zeta )$ is an FSM which is introduced in Section 2.1, and $q\left(t\right)\in \mathsf{\Xi }$ is the current node.

Definition 4

([12]). The hybrid systems (2) are said to be positive if, for any initial state $x\left(t_0\right)⪰0$, all $\upsilon \left(t\right)⪰0$ and any jumping signal $q\left(t\right)\in \mathsf{\Xi }$, the corresponding trajectory $x\left(t\right)⪰0$ and $y\left(t\right)⪰0$ hold for all $t\ge 0$.

Lemma 1

([12]). The hybrid systems (2) are positive if and only if $A_{q\left(t\right)}\left(t\right)$ is a Metzler matrix, $H_{q\left(t\right)}\left(t\right)⪰0$, $D_{q\left(t\right)}\left(t\right)⪰0$, and $C_{q\left(t\right)}\left(t\right)⪰0$ for each $q\left(t\right)\in \mathsf{\Xi }$.

Lemma 2

([23]). A matrix $A\in {\mathbb{R}}^{n\times n}$ is a Metzler matrix if and only if there exists a positive constant δ such that $A+\delta I_n⪰0$.

Let us extend the definition of IO-FTS given in [37] to the impulsive hybrid systems previously introduced.

Definition 5.

Given a positive scalar T, a positive integer $\mathcal{K}$, the initial node $q\left(t_0\right)\in \mathsf{\Xi }$, the desired set E, and a vector-valued function $\eta (·)\succ 0$, the positive hybrid systems (2) are said to be IO-FTS w.r.t. $(E,\omega ,\eta (·),T)$ if

(1) 

the FSM is stable w.r.t. $(q\left(t_0\right),E,\mathcal{K})$, $t_{\mathcal{K}}\le T$, and

(2) 

$\upsilon (·)\in \omega \Rightarrow {\eta }^{\mathrm{T}}\left(t\right)y\left(t\right)<1$,

where ω are a class of particular exogenous input signals defined over $[t_0,T]$, and $t\in [t_0,T]$.

In this paper, two different classes of exogenous input signals are considered (as has been done in [37]), and the vector-valued function $\xi (·)$ always satisfies $\xi \left(t\right)⪰0$ for $t\in [t_0,T]$.

(1)

The set $\omega$ coincides with the set of norm-bounded integrable signals over $[t_0,T]$, defined as follows:

${\omega }_1(t_0,T,\xi (·)):=\{\upsilon (·)\in {\mathcal{L}}_{1,[t_0,T]}{:\left|\upsilon \right|}_{[t_0,T],\xi (·)}\le 1\}$.

(2)

The set $\omega$ coincides with the set of uniformly bounded signals over $[t_0,T]$, defined as follows:

${\omega }_{\infty }(t_0,T,\xi (·)):=\{\upsilon (·)\in {\mathcal{L}}_{\infty ,[t_0,T]}:{\xi }^{\mathrm{T}}\left(t\right)\upsilon \left(t\right)\le 1,t\in [t_0,T]\}$.

The definitions of ${\omega }_1(t_0,T,\xi (·))$ and ${\omega }_{\infty }(t_0,T,\xi (·))$ depend on the choice of $t_0$, T, and $\xi (·)$, but these arguments will be omitted for brevity in the rest of the paper.

Consider a class of impulsive hybrid systems:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\dot{x}\left(t\right)=A_{q\left(t\right)}\left(t\right)x\left(t\right)+B_{q\left(t\right)}\left(t\right)u\left(t\right)+H_{q\left(t\right)}\left(t\right)\upsilon \left(t\right),\hfill & q\left(t\right)=q\left(t^{+}\right)\hfill \\ x\left(t^{+}\right)=D_{q\left(t\right)}\left(t\right)x\left(t\right),\hfill & q\left(t\right)\ne q\left(t^{+}\right)\hfill \\ y\left(t\right)=C_{q\left(t\right)}\left(t\right)x\left(t\right)\hfill \\ G=(\mathsf{\Xi },\Sigma ,\zeta ),\hfill \end{array}\right.\end{array}$$

(3)

where $u(·)\in {\mathbb{R}}^{\kappa }$ is the control input, and $B_{q(·)}(·):{\mathbb{R}}^{+}\to {\mathbb{R}}^{n\times \kappa }$ is continuous matrix-valued function.

Given a positive scalar T and a class of particular exogenous input signals $\omega$ defined over $[t_0,T]$, the objective of the paper is to find a output feedback control law $u\left(t\right)=K_{q\left(t\right)}\left(t\right)y\left(t\right)$, where $K_{q\left(t\right)}\left(t\right):{\mathbb{R}}^{+}\to {\mathbb{R}}^{\kappa \times h}$ is the control gain, such that the closed-loop system

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\dot{x}\left(t\right)={\tilde{A}}_{q\left(t\right)}\left(t\right)x\left(t\right)+H_{q\left(t\right)}\left(t\right)\upsilon \left(t\right)\hfill & q\left(t\right)=q\left(t^{+}\right)\hfill \\ x\left(t^{+}\right)=D_{q\left(t\right)}\left(t\right)x\left(t\right),\hfill & q\left(t\right)\ne q\left(t^{+}\right)\hfill \\ y\left(t\right)=C_{q\left(t\right)}\left(t\right)x\left(t\right)\hfill \\ G=(\mathsf{\Xi },\Sigma ,\zeta ),\hfill \end{array}\right.\end{array}$$

(4)

is positive and there is IO-FTS w.r.t. $(E,\omega ,\eta (·),T)$, where ${\tilde{A}}_{q\left(t\right)}\left(t\right)=A_{q\left(t\right)}\left(t\right)+B_{q\left(t\right)}\left(t\right)K_{q\left(t\right)}\left(t\right)C_{q\left(t\right)}\left(t\right)$, E is a desired set of FSM (1), $q\left(t\right)\in \mathsf{\Xi }$, and $t\in [t_0,T]$.

Definition 6

([44]). For an FSM and any $t_2\ge t_1\ge 0$, let $N_{q_i}(t_1,t_2)$ denote the number of node $q_i$ in the switched sequence over the interval $[t_1,t_2]$, and let $T_{q_i}(t_1,t_2)$ denote the total activated time of node $q_i$ over the interval $[t_1,t_2]$, $q\left(t\right)\in \mathsf{\Xi }$. We say that FSM has an MDADT ${\tau }_{q_i}$, if there exist positive numbers $N_{q_i}^0$ (we call $N_{q_i}^0$ is the mode-dependent chatter bounds) and ${\tau }_{q_i}$ such that

$$\begin{array}{c}\hfill N_{q_i}(t_1,t_2)\le N_{q_i}^0+\frac{T_{q_i}(t_1,t_2)}{{\tau }_{q_i}},t_2\ge t_1\ge 0\end{array}$$

(5)

3. Single Linear System

Before dealing with the IO-FTS of hybrid systems, let us first consider a single linear time-varying system which is described as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\dot{x}\left(t\right)=A\left(t\right)x\left(t\right)+B\left(t\right)u\left(t\right)+H\left(t\right)\upsilon \left(t\right)\hfill \\ y\left(t\right)=C\left(t\right)x\left(t\right)\hfill \end{array}\right.\end{array}$$

(6)

where $x\left(t\right)\in {\mathbb{R}}^n$ is the system state, $\upsilon \left(t\right)\in {\mathbb{R}}^r$ is the particular exogenous input, $u(·)\in {\mathbb{R}}^{\kappa }$ is the control input, and $y\left(t\right)\in {\mathbb{R}}^h$ is the output. $A(·):{\mathbb{R}}^{+}\to {\mathbb{R}}^{n\times n}$, $B(·):{\mathbb{R}}^{+}\to {\mathbb{R}}^{n\times \kappa }$, $H(·):{\mathbb{R}}^{+}\to {\mathbb{R}}^{n\times r}$, and $C(·):{\mathbb{R}}^{+}\to {\mathbb{R}}^{h\times n}$ are continuous matrix-valued functions.

The problem which will be solved is the design a state feedback control law $u\left(t\right)=K\left(t\right)x\left(t\right)$ for system (6), such that the closed-loop system

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\dot{x}\left(t\right)=\tilde{A}\left(t\right)x\left(t\right)+H\left(t\right)\upsilon \left(t\right)\hfill \\ y\left(t\right)=C\left(t\right)x\left(t\right)\hfill \end{array}\right.\end{array}$$

(7)

is positive and there is IO-FTS w.r.t. $(\omega ,\eta (·),T)$, where $\tilde{A}\left(t\right)=A\left(t\right)+B\left(t\right)K\left(t\right)$, $K\left(t\right):{\mathbb{R}}^{+}\to {\mathbb{R}}^{\kappa \times n}$ is the control gain, and T is a positive scalar.

3.1. Stability of Autonomous System

When $B(·)$ is a zero matrix, and the system (6) is autonomous, $\tilde{A}\left(t\right)=A\left(t\right)$, then the following theorems are obtained.

Theorem 1.

The constants are $T,\rho ,\lambda ,\alpha >0$ with $\rho \alpha <1$, and vector-value function $\eta \left(t\right)\succ 0$. If there exist vector-valued functions $v\left(t\right),\vartheta \left(t\right),\pi \left(t\right):{\mathbb{R}}^{+}\to {\mathbb{R}}_{+}^n$ and $\theta \left(t\right):{\mathbb{R}}^{+}\to {\mathbb{R}}^n$ such that

(1) 

${\dot{v}}^{\mathrm{T}}\left(t\right)+v^{\mathrm{T}}\left(t\right)A\left(t\right)+{\pi }^{\mathrm{T}}\left(t\right)+{\theta }^{\mathrm{T}}\left(t\right)\prec 0$,

(2) 

$v^{\mathrm{T}}\left(t\right)H\left(t\right)+{\vartheta }^{\mathrm{T}}\left(t\right)-\rho {\xi }^{\mathrm{T}}\left(t\right)⪯0$,

(3) 

$\lambda {\pi }^{\mathrm{T}}\left(t\right)+{\dot{\theta }}^{\mathrm{T}}\left(t\right)+{\theta }^{\mathrm{T}}\left(t\right)A\left(t\right)+\lambda {\theta }^{\mathrm{T}}\left(t\right)⪰0$,

(4) 

$\lambda {\vartheta }^{\mathrm{T}}\left(t\right)+{\theta }^{\mathrm{T}}\left(t\right)H\left(t\right)⪰0$, and

(5) 

${\eta }^{\mathrm{T}}\left(t\right)C\left(t\right)-\alpha v^{\mathrm{T}}\left(t\right)⪯0$,

hold, then the system (6) is positive and there is IO-FTS w.r.t. $({\omega }_1,\eta (·),T)$, where $A\left(t\right)$ is a Metzler matrix-valued function, $H\left(t\right)⪰0$, $C\left(t\right)⪰0$, $x\left(t_0\right)=0$, $\upsilon (·)\in {\omega }_1$, and $t\in [t_0,T]$.

Proof. 

When $A\left(t\right)$ is a Metzler matrix-valued function, $H\left(t\right)⪰0$ and $C\left(t\right)⪰0$, system (6) is positive by Lemma 1. Choosing co-positive Lyapunov function

$$V(t,x\left(t\right))=v^{\mathrm{T}}\left(t\right)x\left(t\right)+{\int }_{t_0}^t{e}^{-\lambda (t-s)}{\pi }^{\mathrm{T}}\left(s\right)x\left(s\right)ds+{\int }_{t_0}^t{e}^{-\lambda (t-s)}{\vartheta }^{\mathrm{T}}\left(s\right)\upsilon \left(s\right)ds,$$

according to conditions (1) and (2) of Theorem 1, we get

$$\begin{array}{ccc}\dot{V}(t,x\left(t\right))\hfill & =\hfill & ({\dot{v}}^{\mathrm{T}}(t)+v^{\mathrm{T}}\left(t\right)A\left(t\right))x\left(t\right)+v^{\mathrm{T}}\left(t\right)H\left(t\right)\upsilon \left(t\right)+{\pi }^{\mathrm{T}}\left(t\right)x\left(t\right)-\hfill \\ & & \lambda {\int }_{t_0}^t{e}^{-\lambda (t-s)}{\pi }^{\mathrm{T}}\left(s\right)x\left(s\right)ds+{\vartheta }^{\mathrm{T}}\left(t\right)\upsilon \left(t\right)-\lambda {\int }_{t_0}^t{e}^{-\lambda (t-s)}{\vartheta }^{\mathrm{T}}\left(s\right)\upsilon \left(s\right)ds\hfill \\ & =& ({\dot{v}}^{\mathrm{T}}\left(t\right)+v^{\mathrm{T}}\left(t\right)A\left(t\right)+{\pi }^{\mathrm{T}}\left(t\right))x\left(t\right)+(v^{\mathrm{T}}\left(t\right)H\left(t\right)+{\vartheta }^{\mathrm{T}}\left(t\right)-\rho {\xi }^{\mathrm{T}}\left(t\right))\upsilon \left(t\right)+\rho {\xi }^{\mathrm{T}}\left(t\right)\upsilon \left(t\right)-\\ & & \lambda {\int }_{t_0}^t{e}^{-\lambda (t-s)}{\pi }^{\mathrm{T}}\left(s\right)x\left(s\right)ds-\lambda {\int }_{t_0}^t{e}^{-\lambda (t-s)}{\vartheta }^{\mathrm{T}}\left(s\right)\upsilon \left(s\right)ds.\hfill \end{array}$$

(8)

Due to ${\int }_{t_0}^t{e}^{-\lambda (t-s)}d\left({\theta }^{\mathrm{T}}\left(s\right)x\left(s\right)\right)={\theta }^{\mathrm{T}}\left(t\right)x\left(t\right)-\lambda {\int }_{t_0}^t{e}^{-\lambda (t-s)}{\theta }^{\mathrm{T}}\left(s\right)x\left(s\right)ds$, $\dot{x}\left(t\right)=A\left(t\right)x\left(t\right)+H\left(t\right)\upsilon \left(t\right)$,

$$\begin{array}{ccc}{\int }_{t_0}^t{e}^{-\lambda (t-s)}d\left({\theta }^{\mathrm{T}}\left(s\right)x\left(s\right)\right)\hfill & =\hfill & {\int }_{t_0}^t{e}^{-\lambda (t-s)}({\dot{\theta }}^{\mathrm{T}}\left(s\right)x\left(s\right)+{\theta }^{\mathrm{T}}\left(s\right)\dot{x}\left(s\right))ds\hfill \\ \hfill & =\hfill & {\int }_{t_0}^t{e}^{-\lambda (t-s)}({\dot{\theta }}^{\mathrm{T}}\left(s\right)x\left(s\right)+{\theta }^{\mathrm{T}}\left(s\right)A\left(s\right)x\left(s\right)+{\theta }^{\mathrm{T}}\left(s\right)H\left(s\right)\upsilon \left(s\right))ds,\hfill \end{array}$$

(9)

therefore,

$$\begin{array}{c}\hfill {\theta }^{\mathrm{T}}\left(t\right)x\left(t\right)-{\int }_{t_0}^t{e}^{-\lambda (t-s)}({\dot{\theta }}^{\mathrm{T}}\left(s\right)+{\theta }^{\mathrm{T}}\left(s\right)A\left(s\right)+\lambda {\theta }^{\mathrm{T}}\left(s\right))x\left(s\right)ds-{\int }_{t_0}^t{e}^{-\lambda (t-s)}{\theta }^{\mathrm{T}}\left(s\right)H\left(s\right)\upsilon \left(s\right)ds=0.\end{array}$$

(10)

Taking (10) into (8), we can obtain

$$\begin{array}{ccc}\dot{V}(t,x\left(t\right))\hfill & =\hfill & ({\dot{v}}^{\mathrm{T}}\left(t\right)+v^{\mathrm{T}}\left(t\right)A\left(t\right)+{\pi }^{\mathrm{T}}\left(t\right)+{\theta }^{\mathrm{T}}\left(t\right))x\left(t\right)+(v^{\mathrm{T}}\left(t\right)H\left(t\right)+{\vartheta }^{\mathrm{T}}\left(t\right)-\rho {\xi }^{\mathrm{T}}\left(t\right))\upsilon \left(t\right)+\hfill \\ & & \rho {\xi }^{\mathrm{T}}\left(t\right)\upsilon \left(t\right)-{\int }_{t_0}^t{e}^{-\lambda (t-s)}(\lambda {\pi }^{\mathrm{T}}\left(s\right)+{\dot{\theta }}^{\mathrm{T}}\left(s\right)+{\theta }^{\mathrm{T}}\left(s\right)A\left(s\right)+\lambda {\theta }^{\mathrm{T}}\left(s\right))x\left(s\right)ds-\hfill \\ & & {\int }_{t_0}^t{e}^{-\lambda (t-s)}(\lambda {\vartheta }^{\mathrm{T}}\left(s\right)+{\theta }^{\mathrm{T}}\left(s\right)H\left(s\right))\upsilon \left(s\right)ds,\hfill \end{array}$$

(11)

According to conditions (1)–(4) of Theorem 1, we find

$$\begin{array}{c}\hfill \dot{V}(t,x\left(t\right)<\rho {\xi }^{\mathrm{T}}\left(t\right)\upsilon \left(t\right).\end{array}$$

(12)

Integrating (12) between $t_0$ and t, and taking into account that $\upsilon (·)\in {\omega }_1$ and $x\left(t_0\right)=0$, we obtain

$$V(t,x\left(t\right))<\rho {\int }_{t_0}^t{\xi }^{\mathrm{T}}\left(\tau \right)\upsilon \left(\tau \right)dt\le \rho .$$

From condition (5) of Theorem 1,

$${\eta }^{\mathrm{T}}\left(t\right)y\left(t\right)={\eta }^{\mathrm{T}}\left(t\right)C\left(t\right)x\left(t\right)\le \alpha v^{\mathrm{T}}x\le \alpha V(t,x\left(t\right))<1.$$

Then the system (6) is positive and there is IO-FTS w.r.t. $({\omega }_1,\eta (·),T)$ in the sense of Definition 4 and Definition 5. ☐

Remark 4.

Compared with Lemma 2 in [42], there are more adjustable parameters in the conditions of Theorem 1, and therefore, the conditions of Theorem 1 are more flexible.

When the parameter in Theorem 1 $\vartheta \left(t\right)=\pi \left(t\right)=\theta \left(t\right)=0$, the following corollary can be easily obtained.

Corollary 1.

The constants are $T,\rho$, $\alpha >0$ with $\rho \alpha <1$, and vector-value function $\eta \left(t\right)\succ 0$. If there exists a vector-valued function $v\left(t\right)\succ 0$ such that

(1) 

${\dot{v}}^{\mathrm{T}}\left(t\right)+v^{\mathrm{T}}\left(t\right)A\left(t\right)\prec 0$,

(2) 

$v^{\mathrm{T}}\left(t\right)H\left(t\right)-\rho {\xi }^{\mathrm{T}}\left(t\right)⪯0$, and

(3) 

${\eta }^{\mathrm{T}}\left(t\right)C\left(t\right)-\alpha v^{\mathrm{T}}\left(t\right)⪯0$,

hold, then system (6) is positive and there is IO-FTS w.r.t. $({\omega }_1,\eta (·),T)$, where $A\left(t\right)$ is a Metzler matrix-valued function, $H\left(t\right)⪰0$, $C\left(t\right)⪰0$, $x\left(t_0\right)=0$, $\upsilon (·)\in {\omega }_1$, and $t\in [t_0,T]$.

Theorem 2.

The constants are $T,\rho ,\lambda ,\alpha >0$ with $\rho \alpha <1$, and vector-value function $\eta \left(t\right)\succ 0$. If there exist vector-valued functions $v\left(t\right),\vartheta \left(t\right),\pi \left(t\right):{\mathbb{R}}_{+}\to {\mathbb{R}}_{+}^n$ and $\theta \left(t\right):{\mathbb{R}}_{+}\to {\mathbb{R}}^n$, such that

(1) 

${\dot{v}}^{\mathrm{T}}\left(t\right)+v^{\mathrm{T}}\left(t\right)A\left(t\right)+{\pi }^{\mathrm{T}}\left(t\right)+{\theta }^{\mathrm{T}}\left(t\right)\prec 0$,

(2) 

$v^{\mathrm{T}}\left(t\right)H\left(t\right)+{\vartheta }^{\mathrm{T}}\left(t\right)-\rho {\xi }^{\mathrm{T}}\left(t\right)⪯0$,

(3) 

$\lambda {\pi }^{\mathrm{T}}\left(t\right)+{\dot{\theta }}^{\mathrm{T}}\left(t\right)+{\theta }^{\mathrm{T}}\left(t\right)A\left(t\right)+\lambda {\theta }^{\mathrm{T}}\left(t\right)⪰0$,

(4) 

$\lambda {\vartheta }^{\mathrm{T}}\left(t\right)+{\theta }^{\mathrm{T}}\left(t\right)H\left(t\right)⪰0$, and

(5) 

${\tilde{\eta }}^{\mathrm{T}}\left(t\right)C\left(t\right)-\alpha v^{\mathrm{T}}\left(t\right)⪯0$,

hold, then system (6) is positive and there is IO-FTS w.r.t. $({\omega }_{\infty },\eta (·),T)$, where $A\left(t\right)$ is a Metzler matrix-valued function, $H\left(t\right)⪰0$, $C\left(t\right)⪰0$, $\tilde{\eta }\left(t\right)=(t-t_0)\eta \left(t\right)$, $x\left(t_0\right)=0$, $\upsilon (·)\in {\omega }_{\infty }$, and $t\in [t_0,T]$.

Proof. 

When $A\left(t\right)$ is a Metzler matrix-valued function and $H\left(t\right)\succ 0$, system (6) is positive by Lemma 1. Choose

$$V(t,x\left(t\right))=v^{\mathrm{T}}\left(t\right)x\left(t\right)+{\int }_{t_0}^t{e}^{-\lambda (t-s)}{\pi }^{\mathrm{T}}\left(s\right)x\left(s\right)ds+{\int }_{t_0}^t{e}^{-\lambda (t-s)}{\vartheta }^{\mathrm{T}}\left(s\right)\upsilon \left(s\right)ds.$$

According to the proof process of Theorem 1, for any $t\in [t_0,T]$, $x\left(t_0\right)=0$, and $\upsilon (·)\in {\omega }_{\infty }$, we can obtain

$$V(t,x\left(t\right))\le {\int }_{t_0}^t{\xi }^{\mathrm{T}}\left(\tau \right)\upsilon \left(\tau \right)dt<\rho (t-t_0).$$

From condition (5) of Theorem 2,

$${\tilde{\eta }}^{\mathrm{T}}y\left(t\right)={\tilde{\eta }}^{\mathrm{T}}C\left(t\right)x\left(t\right)\le \alpha v^{\mathrm{T}}x\le \alpha V(t,x\left(t\right))<t-t_0,$$

then

$${\eta }^{\mathrm{T}}\left(t\right)y\left(t\right)=\frac{1}{t-t_0}{\tilde{\eta }}^{\mathrm{T}}y\left(t\right)<1.$$

Thus system (6) is positive and there is IO-FTS w.r.t. $({\omega }_{\infty },\eta (·),T)$ in the sense of Definitions 4 and 5. ☐

3.2. Stabilization of Non-Autonomous Systems

When $B(·)$ is a non-zero matrix, and system (6) is non-autonomous, the following theorems are obtained.

Theorem 3.

The constants are $T,\rho ,\lambda$, $\alpha >0$ with $\rho \alpha <1$, and vector-value function $\eta \left(t\right)\succ 0$. If there exist vector-valued functions $v\left(t\right),\vartheta \left(t\right),\pi \left(t\right):{\mathbb{R}}_{+}\to {\mathbb{R}}_{+}^n$ and $\theta \left(t\right):{\mathbb{R}}_{+}\to {\mathbb{R}}^n$ such that

(1) 

$\tilde{A}\left(t\right)+\delta I_n⪰0$,

(2) 

${\dot{v}}^{\mathrm{T}}\left(t\right)+v^{\mathrm{T}}\left(t\right)\tilde{A}\left(t\right)+{\pi }^{\mathrm{T}}\left(t\right)+{\theta }^{\mathrm{T}}\left(t\right)\prec 0$,

(3) 

$v^{\mathrm{T}}\left(t\right)H\left(t\right)+{\vartheta }^{\mathrm{T}}\left(t\right)-\rho {\xi }^{\mathrm{T}}\left(t\right)⪯0$,

(4) 

$\lambda {\pi }^{\mathrm{T}}\left(t\right)+{\dot{\theta }}^{\mathrm{T}}\left(t\right)+{\theta }^{\mathrm{T}}\left(t\right)\tilde{A}\left(t\right)+\lambda {\theta }^{\mathrm{T}}\left(t\right)⪰0$,

(5) 

$\lambda {\vartheta }^{\mathrm{T}}\left(t\right)+{\theta }^{\mathrm{T}}\left(t\right)H\left(t\right)⪰0$, and

(6) 

${\eta }^{\mathrm{T}}\left(t\right)C\left(t\right)-\alpha v^{\mathrm{T}}\left(t\right)⪯0$,

hold, then under control law $u\left(t\right)=K\left(t\right)x\left(t\right)$, the closed-loop system (7) is positive and there is IO-FTS w.r.t. $({\omega }_1,\eta (·),T)$. Therefore, the system (6) is positive and stabilizable, where $\tilde{A}\left(t\right)=A\left(t\right)+B\left(t\right)K\left(t\right)$, $H\left(t\right)⪰0$, $C\left(t\right)⪰0$, $\delta >0$, $x\left(t_0\right)=0$, $\upsilon (·)\in {\omega }_1$, and $t\in [t_0,T]$.

Proof. 

From Lemma 2 and condition (1) of Theorem 3, we know $\tilde{A}\left(t\right)$ is a Metzler matrix, $H\left(t\right)⪰0$, $C\left(t\right)⪰0$, and $\upsilon \left(t\right)⪰0$, which means system (7) is positive. Then, under the control law $u\left(t\right)=K\left(t\right)x\left(t\right)$, replacing $A\left(t\right)$ in Theorem 1 with $\tilde{A}\left(t\right)$, we can get condition (2) of Theorem 3. Therefore, system (7) is positive, there is IO-FTS w.r.t. $({\omega }_1,\eta (·),T)$, and system (6) is positive and stabilizable. ☐

Theorem 4.

The constants are $T,\rho ,\lambda ,\alpha >0$ with $\rho \alpha <1$, and the vector-value function $\eta \left(t\right)\succ 0$. If there exist vector-valued functions $v\left(t\right),\vartheta \left(t\right),\pi \left(t\right):{\mathbb{R}}_{+}\to {\mathbb{R}}_{+}^n$ and $\theta \left(t\right):{\mathbb{R}}_{+}\to {\mathbb{R}}^n$ such that

(1) 

$\tilde{A}\left(t\right)+\delta I_n⪰0$,

(2) 

${\dot{v}}^{\mathrm{T}}\left(t\right)+v^{\mathrm{T}}\left(t\right)\tilde{A}\left(t\right)+{\pi }^{\mathrm{T}}\left(t\right)+{\theta }^{\mathrm{T}}\left(t\right)\prec 0$,

(3) 

$v^{\mathrm{T}}\left(t\right)H\left(t\right)+{\vartheta }^{\mathrm{T}}\left(t\right)-\rho {\xi }^{\mathrm{T}}\left(t\right)⪯0$,

(4) 

$\lambda {\pi }^{\mathrm{T}}\left(t\right)+{\dot{\theta }}^{\mathrm{T}}\left(t\right)+{\theta }^{\mathrm{T}}\left(t\right)\tilde{A}\left(t\right)+\lambda {\theta }^{\mathrm{T}}\left(t\right)⪰0$,

(5) 

$\lambda {\vartheta }^{\mathrm{T}}\left(t\right)+{\theta }^{\mathrm{T}}\left(t\right)H\left(t\right)⪰0$, and

(6) 

${\tilde{\eta }}^{\mathrm{T}}\left(t\right)C\left(t\right)-\alpha v^{\mathrm{T}}\left(t\right)⪯0$,

hold, then under the control law $u\left(t\right)=K\left(t\right)x\left(t\right)$, the closed-loop system (7) is positive and there is IO-FTS w.r.t. $({\omega }_{\infty },\eta (·),T)$. Therefore, system (6) is positive and stabilizable, where $\tilde{A}\left(t\right)=A\left(t\right)+B\left(t\right)K\left(t\right)$, $H\left(t\right)⪰0$, $C\left(t\right)⪰0$, $\tilde{\eta }\left(t\right)=(t-t_0)\eta \left(t\right)$, $\delta >0$, $x\left(t_0\right)=0$, $\upsilon (·)\in {\omega }_{\infty }$, and $t\in [t_0,T]$.

By similar analysis of Theorem 3, we can obtain the desired results.

4. Hybrid Systems

The results of IO-FTS for single linear system are obtained in Section 3. However, if the system is not a single linear system, but is an impulsive positive hybrid system based on FSM, the research on IO-FTS of such systems is as follows in this section.

Assume that the following assumption is always satisfied in the subsequent discussion.

Assumption 1.

Given an FSM and the desired set E, for initial node $q\left(t_0\right)\in \mathsf{\Xi }$, the path from $q\left(t_0\right)$ to E always exists, i.e., $d(q\left(t_0\right),E)\ne \infty$.

For an FSM, define $x_d^{\mathrm{T}}\left(t_k\right)=\left(d(q\left(t_k\right),E)\frac{1}{1+{\mathrm{E}}_0^k\left[q\left(t_i\right)\right]}\right)$, $x_{d,1}\left(t_k\right)=d(q\left(t_k\right),E)$, and $x_{d,2}\left(t_k\right)=\frac{1}{1+{\mathrm{E}}_0^k\left[q\left(t_i\right)\right]}$, where ${\mathrm{E}}_0^k$ is the number of the node jumping in desired set E over $[t_0,t_k]$. For example, desired set $E=\{2,3\}$, if the node jumping sequence is $\{q\left(t_0\right),q\left(t_1\right),q\left(t_2\right),q\left(t_3\right),q\left(t_4\right)\}=\{1,2,4,3,2\}$, then ${\mathrm{E}}_k^0\left[q\left(t_i\right)\right]=3$.

4.1. Stability of Autonomous Hybrid Systems

Firstly, consider the case where the impulsive positive hybrid systems (2) based on FSM are autonomous.

Theorem 5.

The constants are $\mu \ge 1$, $T,\alpha ,\lambda >0$ with $\lambda \alpha <1$, and suppose E is the desired set. If there exists a vector-valued function $v_{q\left(t\right)}\left(t\right)\succ 0$ such that

(1) 

$\parallel x_d\left(t_k\right){\parallel }_1$ is strictly monotonically decreasing w.r.t. k,

(2) 

${\dot{v}}_{q\left(t\right)}^{\mathrm{T}}\left(t\right)+v_{q\left(t\right)}^{\mathrm{T}}\left(t\right)A_{q\left(t\right)}\left(t\right)\prec 0$, $q\left(t^{-}\right)=q\left(t\right)$

(3) 

$v_{q\left(t\right)}^{\mathrm{T}}\left(t\right)H_{q\left(t\right)}\left(t\right)-\lambda {\xi }^{\mathrm{T}}\left(t\right)⪯0$, $q\left(t^{-}\right)=q\left(t\right)$

(4) 

$v_{q\left(t\right)}^{\mathrm{T}}\left(t\right)D_{q\left(t^{-}\right)}\left(t\right)⪯{\mu }_{q\left(t\right)}{v}_{q\left(t^{-}\right)}^{\mathrm{T}}\left(t\right)$, $q\left(t^{-}\right)\ne q\left(t\right)$ and

(5) 

${\eta }^{\mathrm{T}}\left(t\right)C_{q\left(t\right)}\left(t\right)⪯\alpha v_{q\left(t\right)}^{\mathrm{T}}\left(t\right)$,

hold, then system (2) is positive and there is IO-FTS w.r.t. $(E,{\omega }_1,\eta (·),T)$ under MDADT

$$\begin{array}{c}\hfill {\tau }_{q_i}\ge {\tau }_{q_i}^{*}=\frac{(T-t_0)ln{\mu }_{q_i}}{-ln\lambda \alpha },\end{array}$$

(13)

where $A_{q\left(t\right)}\left(t\right)$ is a Metzler matrix-valued function, $H_{q\left(t\right)}\left(t\right)⪰0$, $D_{q\left(t\right)}\left(t\right)⪰0$, $C_{q\left(t\right)}\left(t\right)⪰0$, $x\left(t_0\right)=0$, $\upsilon (·)\in {\omega }_1$, $q\left(t\right)\in \mathsf{\Xi }$, and $t\in [t_0,T]$.

Proof. 

Firstly, we shall prove the stability of FSM. From Assumption 1, we know that the shortest path from $q\left(t_0\right)$ to E exists. Meanwhile, $q\left(t_0\right)\in E$, $x_{d,1}\left(t_0\right)=0$ and $x_{d,2}\left(t_0\right)<1$. According to condition (1) of Theorem 5, $x_{d,2}\left(t_k\right)$ is strictly monotonically decreasing w.r.t. k, i.e., ${\mathrm{E}}_0^k\left[q\left(t_i\right)\right]$ is strictly monotonically increasing w.r.t. k. Therefore, the condition (2) of Definition 3 is satisfied. Meanwhile, $q\left(t_0\right)\in \mathsf{\Xi }/E$, $x_{d,1}\left(t_0\right)\ge 1$ and $x_{d,2}\left(t_0\right)=1$. Because $x_{d,1}\left(t_k\right)$ is an integer, the integer $\mathcal{K}>0$ must exist, and $x_{d,1}\left(t_{\mathcal{K}}\right)=0$. When the $k<\mathcal{K}$, condition (1) of Theorem 5 implies that $x_{d,1}\left(t_k\right)$ is strictly monotonically decreasing w.r.t. k, so condition (1) of Definition 3 is satisfied. When $k\ge \mathcal{K}$, the condition (1) of Theorem 5 implies that $x_{d,2}\left(t_k\right)$ is strictly monotonically decreasing w.r.t. k, i.e., ${\mathrm{E}}_0^k\left[q\left(t_i\right)\right]$ is strictly monotonically increasing w.r.t. k, so the condition (2) of Definition 3 is satisfied. Thus, the FSM is stable w.r.t. $(q\left(t_0\right),E,\mathcal{K})$, and condition (1) of Definition 5 is satisfied.

Now, we shall prove the stability of continuous dynamics. Since $A_{q\left(t\right)}\left(t\right)$ is a Metzler matrix-valued function, $H_{q\left(t\right)}\left(t\right)⪰0$, $D_{q\left(t\right)}\left(t\right)⪰0$, and $C_{q\left(t\right)}\left(t\right)⪰0$. System (2) is positive by Lemma 1. Choose a co-positive type Lyapunov function $V_{q\left(t_k\right)}(t,x\left(t\right))=v_{q\left(t_k\right)}^{\mathrm{T}}\left(t\right)x\left(t\right)$. According to conditions (2) and (3) of Theorem 5, for any $t\in [t_k,t_{k+1})$, we have $q\left(t\right)=q\left(t_k\right)=q\left(t_{k+1}^{-}\right)$, and

$$\begin{array}{cc}\hfill {\dot{V}}_{q\left(t_k\right)}(t,x\left(t\right))& =\left(v_{q\left(t\right)}^{\mathrm{T}}\left(t\right)A_{q\left(t\right)}\left(t\right)+{\dot{v}}_{q\left(t\right)}^{\mathrm{T}}\left(t\right)\right)x+\left(v_{q\left(t\right)}^{\mathrm{T}}\left(t\right)H_{q\left(t\right)}\left(t\right)-\lambda {\xi }^{\mathrm{T}}\left(t\right)\right)\upsilon \left(t\right)\hfill \\ & +\lambda {\xi }^{\mathrm{T}}\left(t\right)\upsilon \left(t\right)<\lambda {\xi }^{\mathrm{T}}\left(t\right)\upsilon \left(t\right)\hfill \end{array}$$

(14)

Noticing that condition (4) of Theorem 5 and integrating (14) between $t_k$ and t, we obtain

$$\begin{array}{ccc}{V}_{q\left(t_k\right)}(t,x\left(t\right))\hfill & <\hfill & \lambda {\int }_{t_k}^t{\xi }^{\mathrm{T}}\left(\tau \right)\upsilon \left(\tau \right)d\tau +v_{q\left(t_k\right)}^{\mathrm{T}}\left(t_k\right)x\left(t_k\right)=\lambda {\int }_{t_k}^t{\xi }^{\mathrm{T}}\left(\tau \right)\upsilon \left(\tau \right)d\tau +v_{q\left(t_k\right)}^{\mathrm{T}}\left(t_k\right)D_{q\left(t_k^{-}\right)}\left(t_k\right)x\left(t_k^{-}\right)\hfill \\ & \le \hfill & \lambda {\int }_{t_k}^t{\xi }^{\mathrm{T}}\left(\tau \right)\upsilon \left(\tau \right)d\tau +{\mu }_{q\left(t_k\right)}{v}_{q\left(t_k^{-}\right)}^{\mathrm{T}}\left(t_k^{-}\right)x\left(t_k^{-}\right)=\lambda {\int }_{t_k}^t{\xi }^{\mathrm{T}}\left(\tau \right)\upsilon \left(\tau \right)d\tau +{\mu }_{q\left(t_k\right)}{V}_{q\left(t_{k-1}\right)}(t_k^{-},x\left(t_k^{-}\right))\hfill \\ & \le \hfill & \lambda {\int }_{t_k}^t{\xi }^{\mathrm{T}}\left(\tau \right)\upsilon \left(\tau \right)d\tau +{\mu }_{q\left(t_k\right)}\lambda {\int }_{t_{k-1}}^{t_k}{\xi }^{\mathrm{T}}\left(\tau \right)\upsilon \left(\tau \right)d\tau +{\mu }_{q\left(t_k\right)}{V}_{q\left(t_{k-1}\right)}(t_{k-1},x\left(t_{k-1}\right))\hfill \\ & \le \hfill & \lambda {\mu }_{q\left(t_k\right)}{\int }_{t_{k-1}}^t{\xi }^{\mathrm{T}}\left(\tau \right)\upsilon \left(\tau \right)d\tau +{\mu }_{q\left(t_k\right)}{V}_{q\left(t_{k-1}\right)}(t_{k-1},x\left(t_{k-1}\right))\hfill \\ & \le \hfill & \cdots \le \lambda {\prod }_{i=1}^k{\mu }_{q\left(t_i\right)}{\int }_{t_0}^t{\xi }^{\mathrm{T}}\left(\tau \right)\upsilon \left(\tau \right)d\tau +{\prod }_{i=1}^k{\mu }_{q\left(t_i\right)}{V}_{q\left(t_0\right)}(t_0,x\left(t_0\right))\hfill \\ & =\hfill & \lambda {\prod }_{i=1}^k{\mu }_{q\left(t_i\right)}{\int }_{t_0}^t{\xi }^{\mathrm{T}}\left(\tau \right)\upsilon \left(\tau \right)d\tau .\hfill \end{array}$$

(15)

According to the MDADT (13), Definition 6, and $\upsilon (·)\in {\omega }_1$,

$$\begin{array}{ccc}{V}_{q\left(t_k\right)}(t,x\left(t\right))\hfill & <\hfill & \lambda {\prod }_{i=1}^k{\mu }_{q\left(t_i\right)}=\lambda {\prod }_{i=1}^m{\mu }_{q_i}^{N_i(t_0,t)}=\lambda e^{{\displaystyle \sum _{i=1}^m}\frac{T_{q_i}(t_0,t)}{{\tau }_{q_i}}ln{\mu }_{q_i}}\hfill \\ & \le \hfill & \lambda e^{{\displaystyle \sum _{i=1}^m}\frac{T_{q_i}(t_0,t)ln\lambda \alpha }{-(T-t_0)ln{\mu }_{q_i}}ln{\mu }_{q_i}}\hfill \\ & \le \hfill & \lambda e^{{\displaystyle \sum _{i=1}^m}\frac{T_{q_i}(t_0,t)ln\lambda \alpha }{-(T-t_0)ln{\mu }_{q_i}}ln{\mu }_{q_i}}=\lambda e^{\frac{(t-t_0)ln\lambda \alpha }{-(T-t_0)}}\le \frac{1}{\alpha }\hfill \end{array}$$

(16)

From condition (5) of Theorem 5, we know

$${\eta }^{\mathrm{T}}\left(t\right)y\left(t\right)={\eta }^{\mathrm{T}}\left(t\right)C_{q\left(t\right)}\left(t\right)x\left(t\right)\le \alpha v_{q\left(t\right)}^{\mathrm{T}}\left(t\right)x\left(t\right)<1,$$

and then the condition (2) of Definition 5 is satisfied.

Thus, the system (2) is positive and there is IO-FTS $(E,{\omega }_1,\eta (·),T)$ in the sense of Definitions 4 and 5. ☐

Remark 5.

We note that the MDADT (13) depends on the parameter ${\mu }_{q_i}$. When ${\mu }_{q_i}>1$, obviously, ${\tau }_{q_i}>0$. This can prevent the hybrid systems from exhibiting Zeno behavior ([41]). If ${\mu }_{q_i}=1$, then ${\tau }_{q_i}^{*}=0$, that is to say, the jump can be arbitrary.

Theorem 6.

The constants are $\mu \ge 1$, $T,\alpha ,\lambda >0$ with $\lambda \alpha (T-t_0)<1$, and suppose E is the desired set. If there exists a vector-valued function $v_{q\left(t\right)}\left(t\right)\succ 0$ such that

(1) 

$\parallel x_d\left(t_k\right){\parallel }_1$ is strictly monotonically decreasing w.r.t. k,

(2) 

${\dot{v}}_{q\left(t\right)}^{\mathrm{T}}\left(t\right)+v_{q\left(t\right)}^{\mathrm{T}}\left(t\right)A_{q\left(t\right)}\left(t\right)\prec 0$, $q\left(t^{-}\right)=q\left(t\right)$

(3) 

$v_{q\left(t\right)}^{\mathrm{T}}\left(t\right)H_{q\left(t\right)}\left(t\right)-\lambda {\xi }^{\mathrm{T}}\left(t\right)⪯0$, $q\left(t^{-}\right)=q\left(t\right)$

(4) 

$v_{q\left(t\right)}^{\mathrm{T}}\left(t\right)D_{q\left(t^{-}\right)}\left(t\right)⪯{\mu }_{q\left(t\right)}{v}_{q\left(t^{-}\right)}^{\mathrm{T}}\left(t\right)$, $q\left(t^{-}\right)\ne q\left(t\right)$ and

(5) 

${\eta }^{\mathrm{T}}\left(t\right)C_{q\left(t\right)}\left(t\right)⪯\alpha v_{q\left(t\right)}^{\mathrm{T}}\left(t\right)$,

hold, then system (2) is positive and there is IO-FTS w.r.t. $(E,{\omega }_{\infty },\eta (·),T)$ under MDADT

$$\begin{array}{c}\hfill {\tau }_{q_i}\ge {\tau }_{q_i}^{*}=\frac{(T-t_0)ln{\mu }_{q_i}}{-ln\left(\lambda \alpha (T-t_0)\right)},\end{array}$$

(17)

where $A_{q\left(t\right)}\left(t\right)$ is a Metzler matrix-valued function, $H_{q\left(t\right)}\left(t\right)⪰0$, $D_{q\left(t\right)}\left(t\right)⪰0$, $C_{q\left(t\right)}\left(t\right)⪰0$, $x\left(t_0\right)=0$, $\upsilon (·)\in {\omega }_{\infty }$, $q\left(t\right)\in \mathsf{\Xi }$, and $t\in [t_0,T]$.

Proof. 

The proof of the stability for FSM is the same as that of Theorem 5, thus, condition (1) of the Definition 5 is satisfied.

Now, let us discuss the stability of the continuous dynamics. From the proof process of Theorem 5, we know the system (2) is positive, and

$$\begin{array}{c}\hfill V_{q\left(t_k\right)}(t,x\left(t\right))<\lambda {\prod }_{i=1}^k{\mu }_{q\left(t_i\right)}{\int }_{t_0}^t{\xi }^{\mathrm{T}}\left(\tau \right)\upsilon \left(\tau \right)d\tau .\end{array}$$

(18)

Because of $\upsilon (·)\in {\omega }_{\infty }$ and MDADT (17), we can get

$$\begin{array}{ccc}{V}_{q\left(t_k\right)}(t,x\left(t\right))\hfill & <\hfill & \lambda {\prod }_{i=1}^k{\mu }_{q\left(t_i\right)}(t-t_0)=\lambda {\prod }_{i=1}^m{\mu }_{q_i}^{N_i(t_0,t)}(t-t_0)=\lambda (t-t_0)e^{{\displaystyle \sum _{i=1}^m}\frac{T_{q_i}(t_0,t)}{{\tau }_{q_i}}ln{\mu }_{q_i}}\hfill \\ & \le \hfill & \lambda (t-t_0)e^{{\displaystyle \sum _{i=1}^m}\frac{T_{q_i}(t_0,t)ln\left(\lambda \alpha (T-t_0)\right)}{-(T-t_0)ln{\mu }_{q_i}}ln{\mu }_{q_i}}\hfill \\ & \le \hfill & \lambda (t-t_0)e^{{\displaystyle \sum _{i=1}^m}\frac{T_{q_i}(t_0,t)ln\left(\lambda \alpha (T-t_0)\right)}{-(T-t_0)ln{\mu }_{q_i}}ln{\mu }_{q_i}}=\lambda (t-t_0)e^{\frac{(t-t_0)ln\left(\lambda \alpha (T-t_0)\right)}{-(T-t_0)}}\le \frac{1}{\alpha }.\hfill \end{array}$$

(19)

From condition (5) of Theorem 6, we know

$${\eta }^{\mathrm{T}}\left(t\right)y\left(t\right)={\eta }^{\mathrm{T}}\left(t\right)C_{q\left(t\right)}\left(t\right)x\left(t\right)\le \alpha v_{q\left(t\right)}^{\mathrm{T}}\left(t\right)x\left(t\right)<1,$$

and then the condition (2) of Definition 5 is satisfied.

Thus, the system (2) is positive and there is IO-FTS $(E,{\omega }_{\infty },\eta (·),T)$ in the sense of the Definitions 4 and 5. ☐

4.2. Stabilization of Non-Autonomous Hybrid Systems

Next, consider the case where impulsive positive hybrid systems (3) based on FSM are non-autonomous. Designing the output feedback controller $u\left(t\right)=K_{q\left(t\right)}\left(t\right)y\left(t\right)$ and taking it into systems (3), then the closed-loop systems (4) can be obtained.

Theorem 7.

The constants are $\mu \ge 1$, $T,\alpha ,\lambda >0$ with $\lambda \alpha <1$, and suppose E is the desired set. If there exists a vector-valued function $v_{q\left(t\right)}\left(t\right)\succ 0$ such that

(1) 

$\parallel x_d\left(t_k\right){\parallel }_1$ is strictly monotonically decreasing w.r.t. k,

(2) 

${\tilde{A}}_{q\left(t\right)}\left(t\right)+\delta I_n⪰0$,

(3) 

${\dot{v}}_{q\left(t\right)}^{\mathrm{T}}\left(t\right)+v_{q\left(t\right)}^{\mathrm{T}}\left(t\right){\tilde{A}}_{q\left(t\right)}\left(t\right)\prec 0$, $q\left(t^{-}\right)=q\left(t\right)$

(4) 

$v_{q\left(t\right)}^{\mathrm{T}}\left(t\right)H_{q\left(t\right)}\left(t\right)-\lambda {\xi }^{\mathrm{T}}\left(t\right)⪯0$, $q\left(t^{-}\right)=q\left(t\right)$

(5) 

$v_{q\left(t\right)}^{\mathrm{T}}\left(t\right)D_{q\left(t^{-}\right)}\left(t\right)⪯{\mu }_{q\left(t\right)}{v}_{q\left(t^{-}\right)}^{\mathrm{T}}\left(t\right)$, $q\left(t^{-}\right)\ne q\left(t\right)$ and

(6) 

${\eta }^{\mathrm{T}}\left(t\right)C_{q\left(t\right)}\left(t\right)⪯\alpha v_{q\left(t\right)}^{\mathrm{T}}\left(t\right)$,

hold, then system (4) is positive and there is IO-FTS w.r.t. $(E,{\omega }_1,\eta (·),T)$ under MDADT (13); that is to say, system (3) is positive and stabilizable, where ${\tilde{A}}_{q\left(t\right)}\left(t\right)=A_{q\left(t\right)}\left(t\right)+B_{q\left(t\right)}\left(t\right)K_{q\left(t\right)}\left(t\right)C_{q\left(t\right)}\left(t\right)$, $H_{q\left(t\right)}\left(t\right)⪰0$, $D_{q\left(t\right)}\left(t\right)⪰0$, $C_{q\left(t\right)}\left(t\right)⪰0$, $\delta >0$, $x\left(t_0\right)=0$, $\upsilon (·)\in {\omega }_1$, $q\left(t\right)\in \mathsf{\Xi }$, and $t\in [t_0,T]$.

Proof. 

From Lemma 2 and condition (2) of Theorem 7, we know ${\tilde{A}}_{q\left(t\right)}\left(t\right)$ is a Metzler matrix, $H_{q\left(t\right)}\left(t\right)⪰0$, $D_{q\left(t\right)}\left(t\right)⪰0$, $C_{q\left(t\right)}\left(t\right)⪰0$, and ${\upsilon }_{q\left(t\right)}\left(t\right)⪰0$ for each $q\left(t\right)\in \mathsf{\Xi }$. According to Lemma 1, system (4) is positive. Then, under the output feedback controller $u\left(t\right)=K_{q\left(t\right)}\left(t\right)y\left(t\right)$, replacing $A_{q\left(t\right)}\left(t\right)$ in Theorem 5 with ${\tilde{A}}_{q\left(t\right)}\left(t\right)$, condition (3) of Theorem 7 can be obtained. By Theorem 5, we can easily find that system (4) is positive and there is IO-FTS w.r.t. $(E,{\omega }_1,\eta (·),T)$ under MDADT (13). Therefore, system (3) is positive and stabilizable. ☐

Theorem 8.

The constants are $\mu \ge 1$, $T,\alpha ,\lambda >0$ with $\lambda \alpha (T-t_0)<1$, and suppose E is the desired set. If there exists a vector-valued function $v_{q\left(t\right)}\left(t\right)\succ 0$ such that

(1) 

$\parallel x_d\left(t_k\right){\parallel }_1$ is strictly monotonically decreasing w.r.t. k,

(2) 

${\tilde{A}}_{q\left(t\right)}\left(t\right)+\delta I_n⪰0$,

(3) 

${\dot{v}}_{q\left(t\right)}^{\mathrm{T}}\left(t\right)+v_{q\left(t\right)}^{\mathrm{T}}\left(t\right){\tilde{A}}_{q\left(t\right)}\left(t\right)\prec 0$, $q\left(t^{-}\right)=q\left(t\right)$

(4) 

$v_{q\left(t\right)}^{\mathrm{T}}\left(t\right)H_{q\left(t\right)}\left(t\right)-\lambda {\xi }^{\mathrm{T}}\left(t\right)⪯0$, $q\left(t^{-}\right)=q\left(t\right)$

(5) 

$v_{q\left(t\right)}^{\mathrm{T}}\left(t\right)D_{q\left(t^{-}\right)}\left(t\right)⪯{\mu }_{q\left(t\right)}{v}_{q\left(t^{-}\right)}^{\mathrm{T}}\left(t\right)$, $q\left(t^{-}\right)\ne q\left(t\right)$ and

(6) 

${\eta }^{\mathrm{T}}\left(t\right)C_{q\left(t\right)}\left(t\right)⪯\alpha v_{q\left(t\right)}^{\mathrm{T}}\left(t\right)$,

hold, then system (4) is positive and there is IO-FTS w.r.t. $(E,{\omega }_{\infty },\eta (·),T)$ under MDADT (17). That is to say, system (3) is positive and stabilizable, where ${\tilde{A}}_{q\left(t\right)}\left(t\right)=A_{q\left(t\right)}\left(t\right)+B_{q\left(t\right)}\left(t\right)K_{q\left(t\right)}\left(t\right)C_{q\left(t\right)}\left(t\right)$, $H_{q\left(t\right)}\left(t\right)⪰0$, $D_{q\left(t\right)}\left(t\right)⪰0$, $C_{q\left(t\right)}\left(t\right)⪰0$, $\delta >0$, $x\left(t_0\right)=0$, $\upsilon (·)\in {\omega }_{\infty }$, $q\left(t\right)\in \mathsf{\Xi }$, and $t\in [t_0,T]$.

By similar analysis of Theorem 7, Theorem 8 can be easily proved.

Remark 6.

Compared with the literature [28], the MDADT technique is used for Theorems 5–8 in this paper. It allows every node of FSM to have its own ADT, therefore, the sufficient conditions of IO-FTS have good flexibility and weak conservatism.

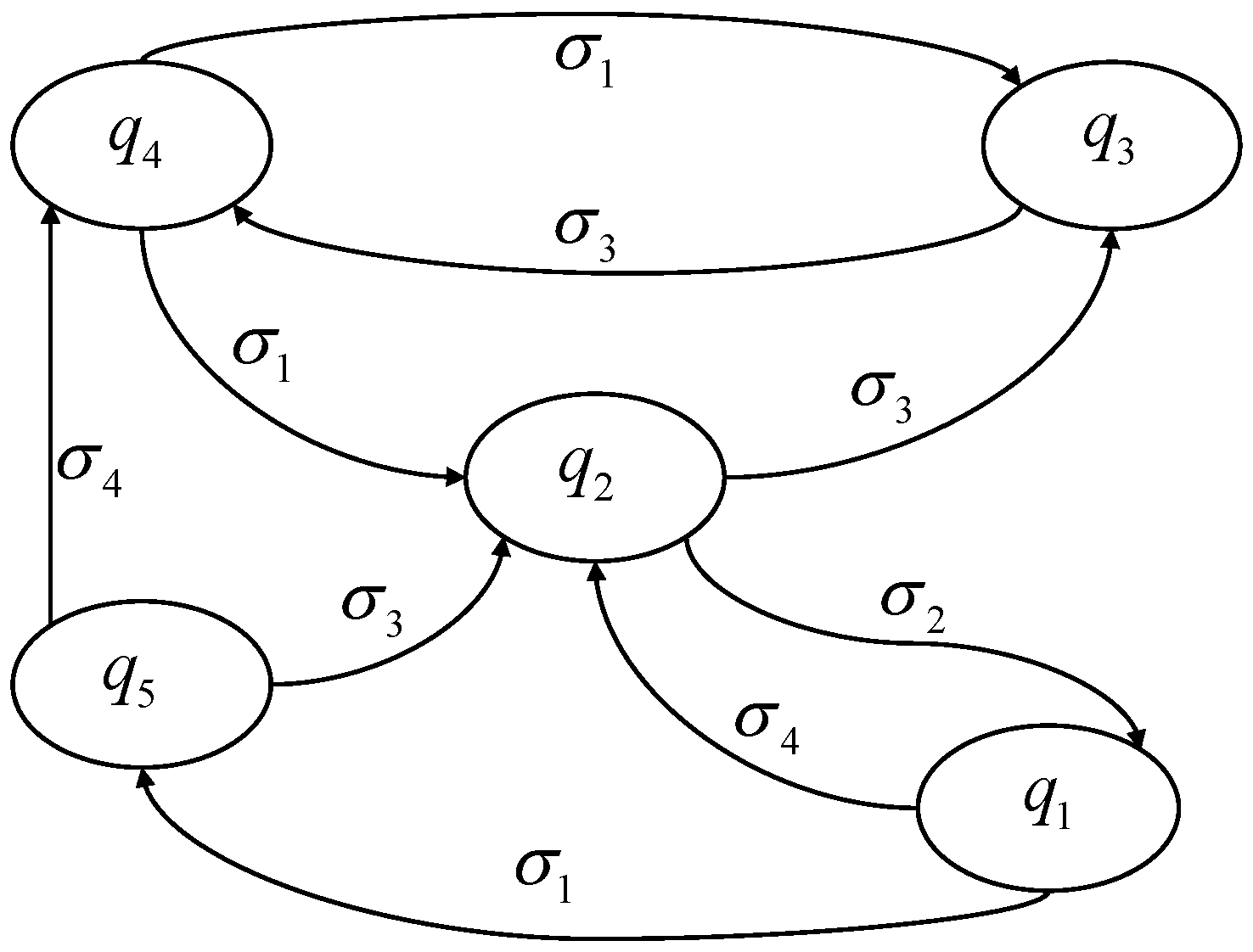
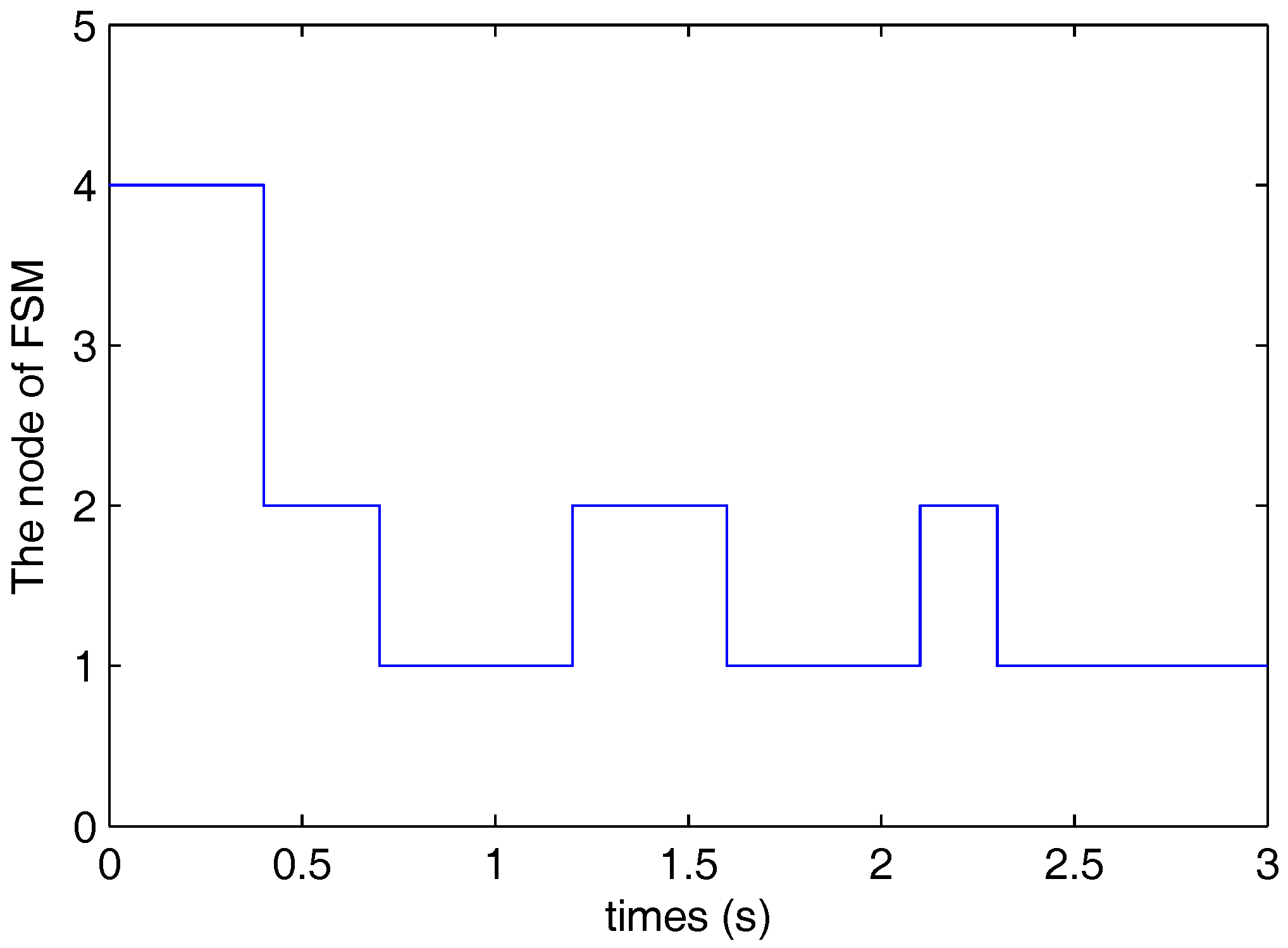
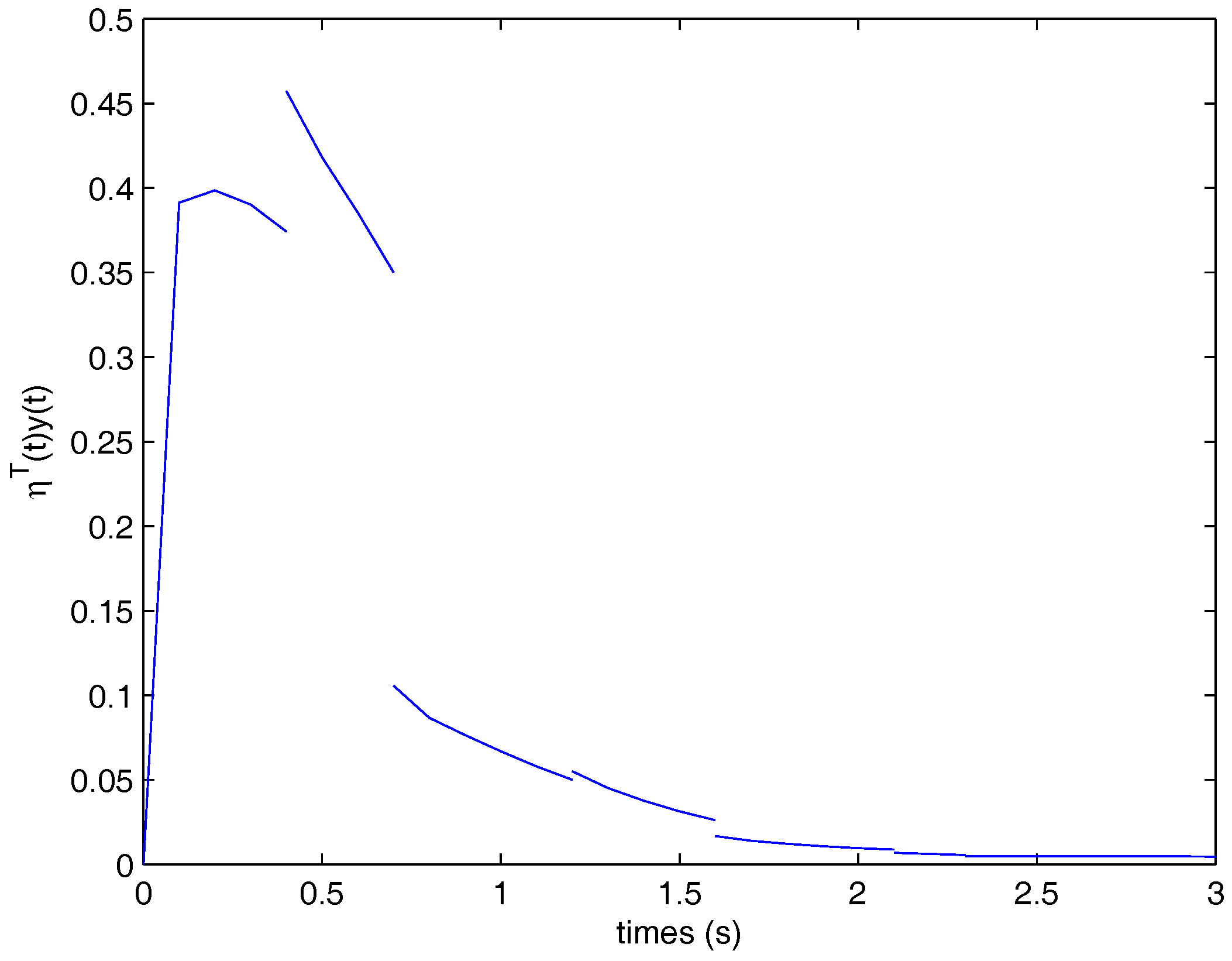
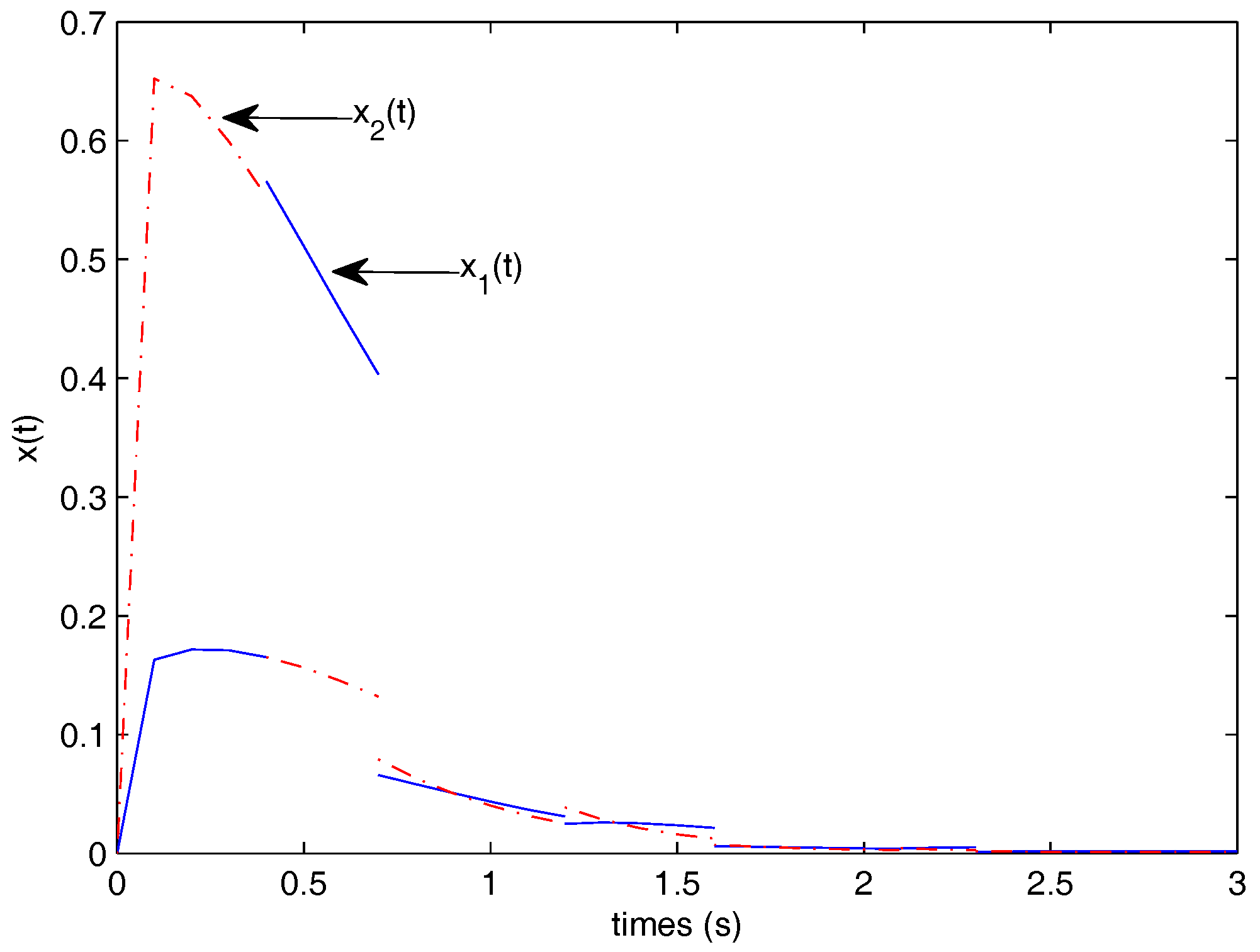
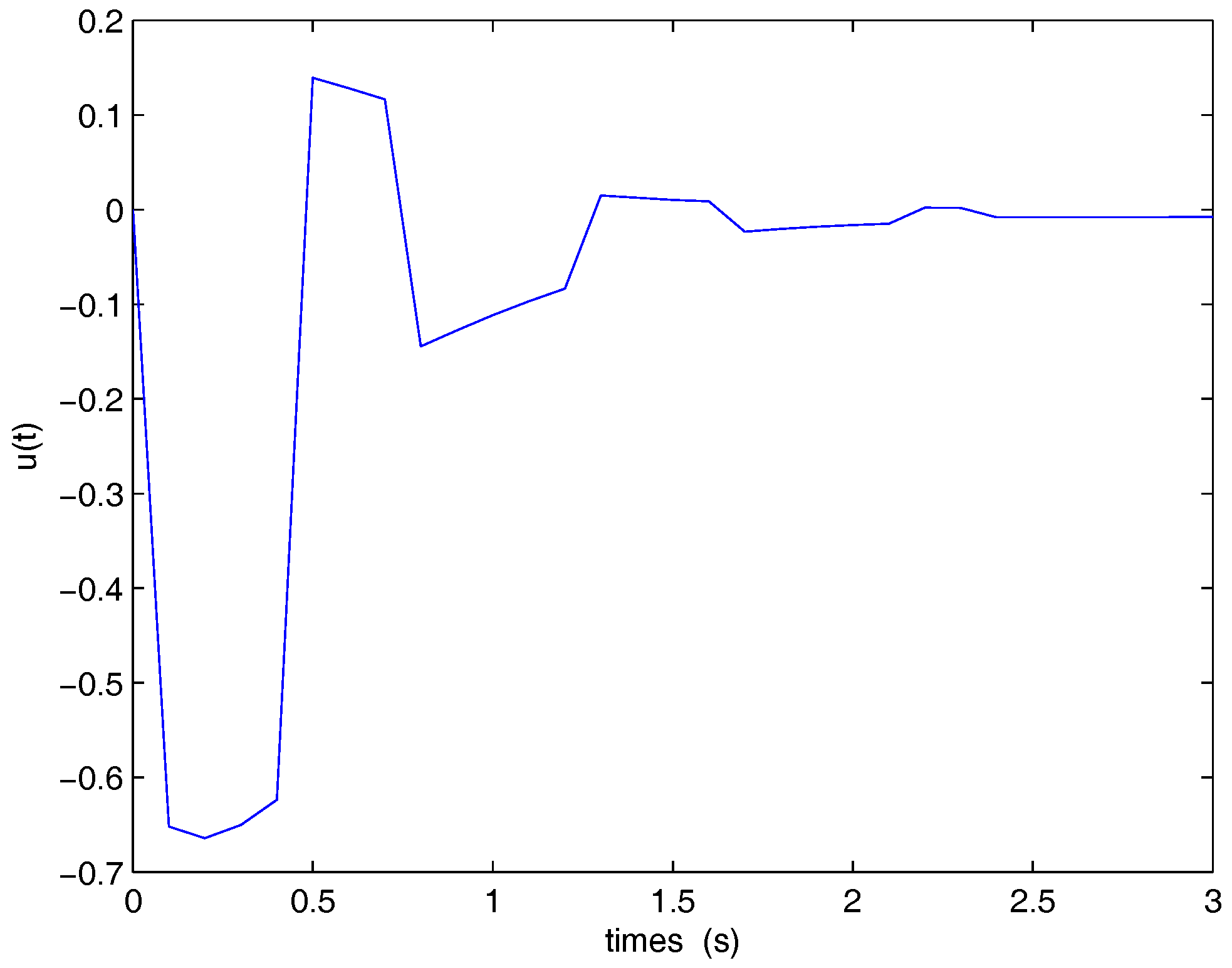
5. Numerical Example

In this section, a numerical example is presented via MATLAB to verify the effectiveness of the theoretical results in Section 4.

Consider the time-varying impulsive positive hybrid systems based on FSM in form (3), where FSM $G=(\mathsf{\Xi },\Sigma ,\zeta )$ is reported in Figure 1, $\mathsf{\Xi }=\{q_1,q_2,q_3,q_4,q_5\}$, and $\Sigma =\{{\sigma }_1,{\sigma }_2,{\sigma }_3,{\sigma }_4\}$. The system matrices are $A_{q_1}=\left(\begin{array}{cc}-1& 1.8+t\\ 0.5& -1.9-t\end{array}\right)$, $A_{q_2}=\left(\begin{array}{cc}-1.2-t& 0.8-0.2t\\ 0.3& -2.2-1.2t\end{array}\right)$, $A_{q_4}=\left(\begin{array}{cc}-1& 1.5\\ 2+t& -t\end{array}\right)$, $B_{q_1}=\left(\begin{array}{c}1\\ 0\end{array}\right)$, $B_{q_2}=B_{q_4}=\left(\begin{array}{c}1\\ 1\end{array}\right)$, $H_{q_1}=\left(\begin{array}{c}0.1\\ 0.1\end{array}\right)$, $H_{q_2}=\left(\begin{array}{c}0.3\\ 0.1\end{array}\right)$, $H_{q_4}=\left(\begin{array}{c}0.1\\ 0.4\end{array}\right)$, $D_{q_1}=\left(\begin{array}{cc}0.4t& 0.4\\ 0.6& 0.8\end{array}\right)$, $D_{q_2}=\left(\begin{array}{cc}0& 0.5\\ 0& 0.6\end{array}\right)$, $D_{q_4}=\left(\begin{array}{cc}0.2t& 1\\ 1& 0\end{array}\right)$, $C_{q_1}=\left(\begin{array}{cc}0.9t& 1+t\end{array}\right)$, $C_{q_2}=\left(\begin{array}{cc}1& 0.8+sin\left(t\right)\end{array}\right)$, $C_{q_4}=\left(\begin{array}{cc}0.8+t& 0.8\end{array}\right)$.

The desired set is $E=\{q_1,q_2\}$ and particular exogenous input $\upsilon \left(t\right)=\frac{16.3}{1+150t}\in {\omega }_1$. Let $T=3$, $\xi \left(t\right)=1.5$, $\eta \left(t\right)=0.6$, $\alpha =\lambda =0.6$, ${\mu }_1=1.1$, ${\mu }_2=1.2$, ${\mu }_4=1.14$, $x\left(0\right)=\left(\begin{array}{c}0\\ 0\end{array}\right)$, and $q\left(0\right)=q_4$. From condition (1) of Theorem 7, the evolution path of current node of FSM can be obtained as $q_4\stackrel{{\sigma }_1}{\to }{q}_2\stackrel{{\sigma }_2}{\to }{q}_1\stackrel{{\sigma }_4}{\to }{q}_2\stackrel{{\sigma }_2}{\to }\cdots$. According to the conditions of Theorem 7 and MDADT (13), applying the linear matrix inequality (LMI) Control Toolbox and the linear programming toolbox in MATLAB, the following results can be obtained: ${\tau }_1=0.2799$, ${\tau }_2=0.5435$, ${\tau }_4=0.3848$, $K_1=K_4=-1$, $K_2=0.2$, $v_{q_1}=\left(\begin{array}{c}1+t\\ 1+t\end{array}\right)$, $v_{q_2}=\left(\begin{array}{c}1\\ 1+t\end{array}\right)$, and $v_{q_4}=\left(\begin{array}{c}1+t\\ 1\end{array}\right)$.

The node $q_3$ and node $q_5$ are not in the evolution path. That is to say, the continuous subsystems at node $q_3$ and node $q_5$ are not activated, so they are not mentioned.

The simulation results are obtained by MATLAB. The current node evolution of FSM is shown in Figure 2, where $1,2,3,4,5$ of the y-axis represent the nodes $q_1,q_2,q_3,q_4,q_5$, respectively. Obviously, the average dwell time of every node is different and satisfies MDADT (13), and the FSM is stable w.r.t. $(q_4,\{q_1,q_2\},2)$. The trajectory of output ${\eta }^{\mathrm{T}}\left(t\right)y\left(t\right)$ and the trajectory of the system state $x\left(t\right)$ are shown in Figure 3 and Figure 4. Because the systems are impulsive positive hybrid systems, these trajectories are positive and have impulses. Moreover, the trajectory of output ${\eta }^{\mathrm{T}}\left(t\right)y\left(t\right)<1$ and $\upsilon \left(t\right)=\frac{16.3}{1+150t}\in {\omega }_1$, therefore, the given hybrid systems are positive and there is IO-FTS w.r.t. ($\{q_1,q_2\},{\omega }_1,0.6,3$) in the sense of Definition 5. In Figure 5, the evolution of the control input is shown, and it is not always positive. Thus, the Theorem 7 is effective.

6. Conclusions

In this paper, the stability and stabilization of time-varying impulsive positive hybrid systems based on FSM have been studied. First we consider the case where there is only one time-varying positive linear system, and the stability and the state feedback controller are easily obtained. Then, we extend it to the case with time-varying impulsive positive hybrid systems based on FSM, and the stability is also obtained and proved. Furthermore, the output feedback controller is derived to stabilize the systems. The simulation results show the feasibility and effectiveness of the proposed results.

As Cyber-Social-Physical Spaces (CSPS) [45] is essentially a hybrid system, the proposed method in the paper may be applied in the CSPS or the Cyber Physical System (CPS). This will be an interesting direction in the future.