A Time Finite Element Method Based on the Differential Quadrature Rule and Hamilton’s Variational Principle
Abstract
:1. Introduction
- (1)
- The general form of Hamilton’s variational principle, the DQ rule, and the Gauss–Lobatto quadrature rule are used to formulate a TFEM for structural dynamic analysis.
- (2)
- The Gauss–Lobatto quadrature points are used as time sampling points or nodes of the time element, which results in more accurate results with the same number of nodes.
- (3)
- The nodal velocities are only involved at two end nodes of the time element, implying that the number of Degrees of Freedom (DOFs) is less than that of the existing TFEMs based on the variational principle and Hermite interpolations.
- (4)
- Lagrange interpolations are employed instead of Hermite interpolations in the construction of the C1 time element, and the stability and accuracy of DQTFEM are studied in detail.
2. Basic Formulations
- (1)
- Usually for conservative systems, the actual path will be the one for which the integral of Lagrangian function (T − V) is an extremum, and for the non-conservative system considered here, the general form of Hamilton’s variational principle is used and the integral still exists; however, there exists no functional that must be an extremum [49].
- (2)
- The method of imposing initial conditions in the present method is standard and similar to the one used in the FEM; see Equation (25).
- (3)
- DQTFEM is a new TFEM, since Gauss–Lobatto quadrature and DQ rules are used for the first time in the construction of a TFEM. The high accuracy and efficiency due to the employment of Gauss–Lobatto quadrature and DQ rules are validated in the following numerical comparisons; see Section 4.
3. Stability Analysis
- (1)
- ρ(J) ≥ 1 for any N, and when N becomes larger, the first stable interval also becomes larger. Although there are several stable intervals with ρ(J) = 1 except for N = 3, the first stable interval is significant and practical; therefore, only the first intervals are listed in Table 1 whose elements are obtained by using the criterion (ρ − 1) < 10−6.
- (2)
- ρ(J) < 1 in the TFEM by Hulbert [35], but ρ(J) = 1 in DQTFEM for all stable intervals, hence DQTFEM is more accurate than that of Hulbert [35] since DQTFEM is a high-order method that has a smaller phase error than lower order methods. Note that the stability of CDM is ωh ≤ 2, and for four-order explicit RKM, and the stability of the present method is .
- (3)
- DQTFEM is highly symplectic. If the Jacobi matrix J of a method satisfies Equation (35) as followsthen the method is symplectic. For the present single DOF system, all variables in Equation (35) are numbers and Table 2 shows that the precision of Equation (35) (especially J3~J6) is satisfactory, which indicates that DQTFEM is a symplectic method. In fact, we have numerically verified that DQTFEM is symplectic even if it is not stable. For a stable symplectic method, the magnitudes of all eigenvalues of J are equal to 1, therefore all eigenvalues of J of the present method are equal to 1 when it is stable.
4. Numerical Results and Discussion
4.1. Free Vibration of a Two-DOF System
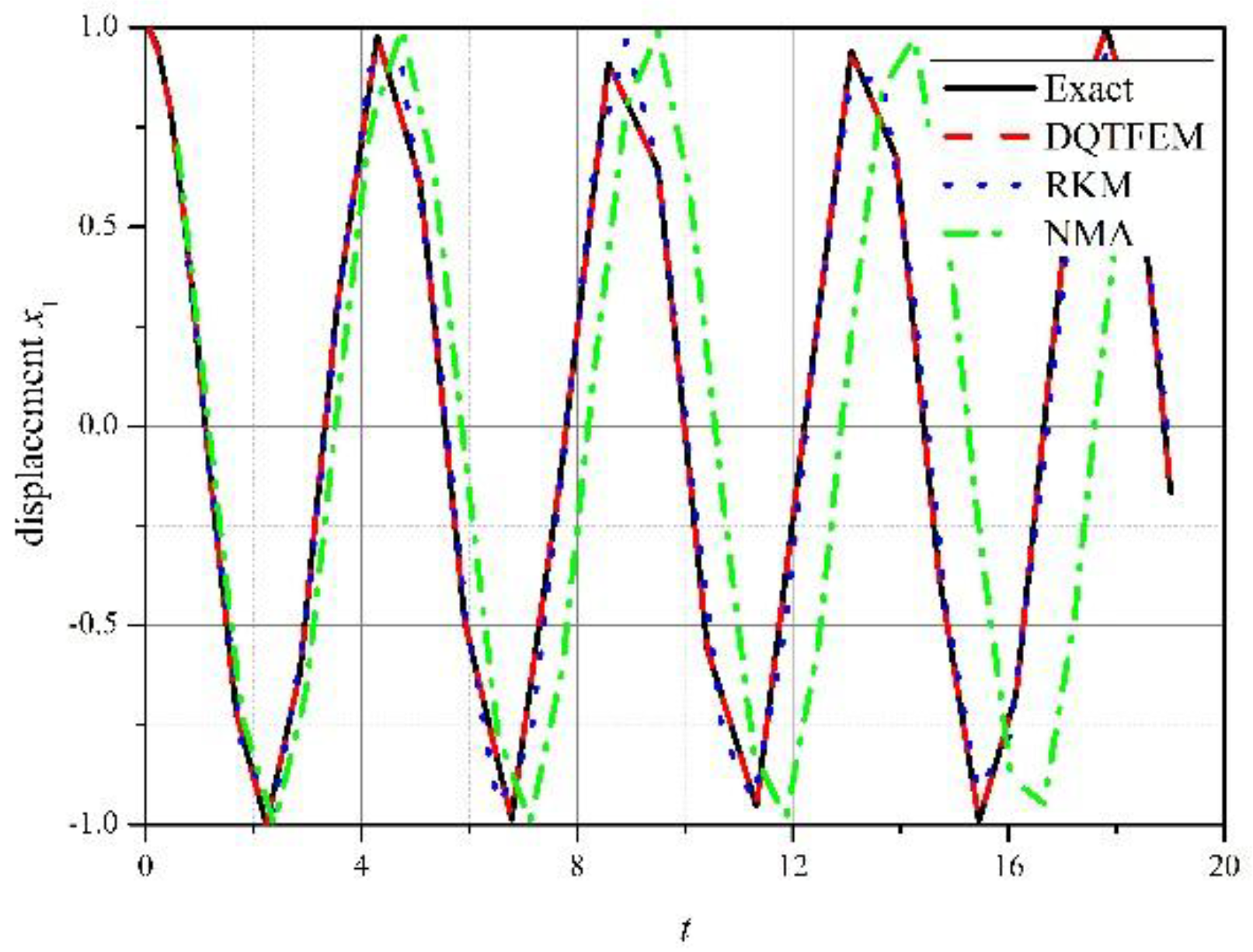
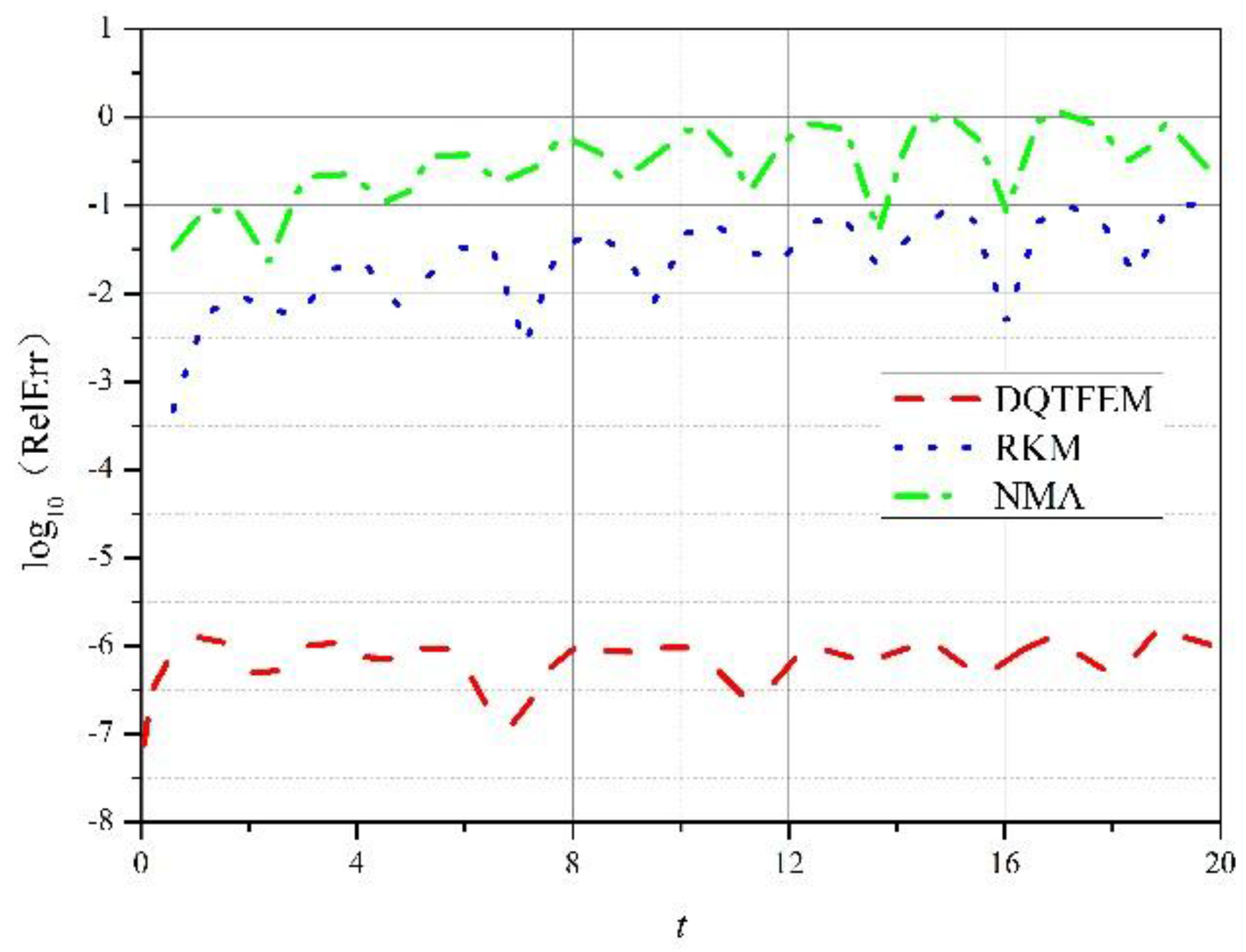
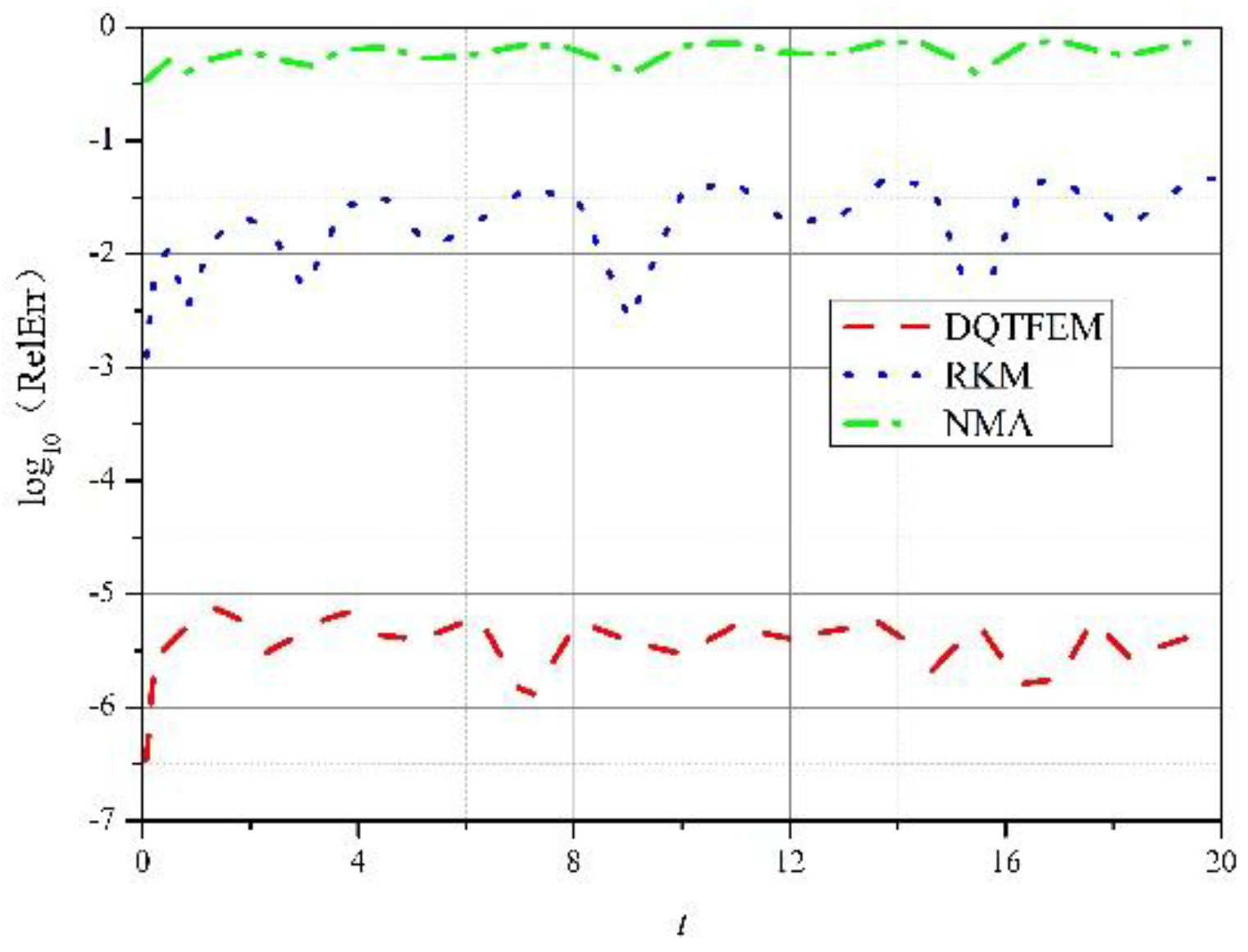
4.1.1. Accuracy Comparison
4.1.2. Efficiency Comparison
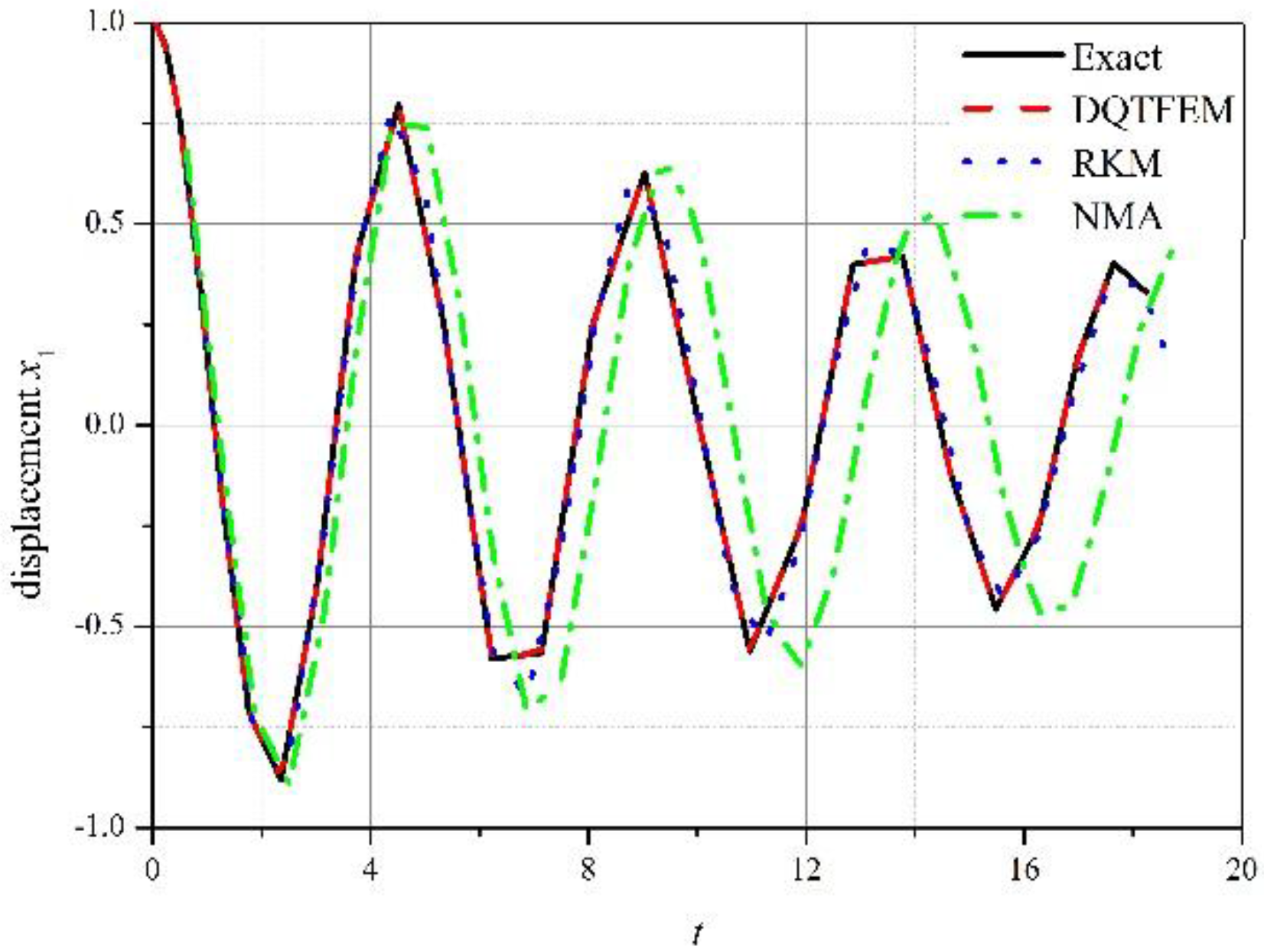
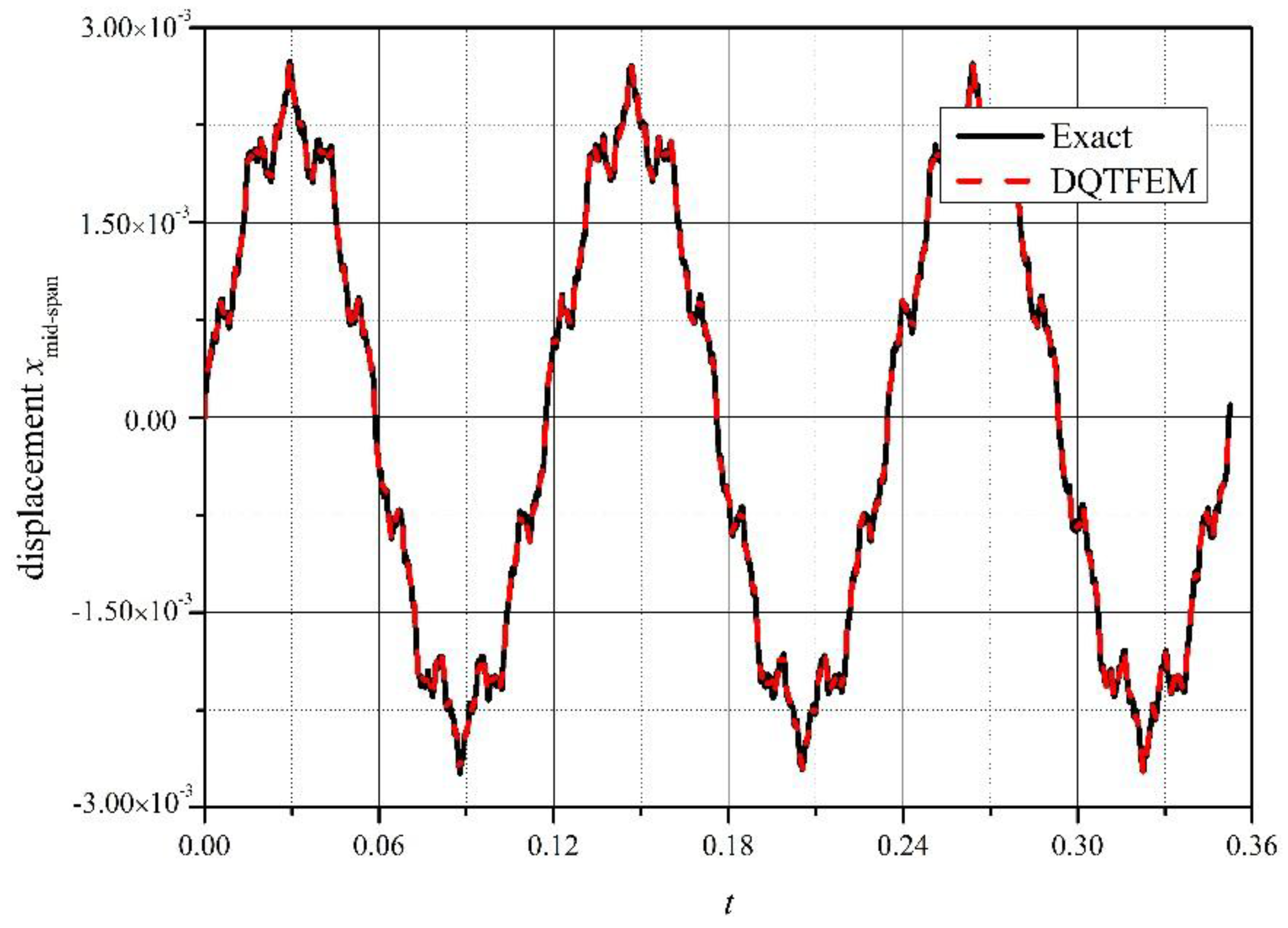
4.1.3. Damping Vibration
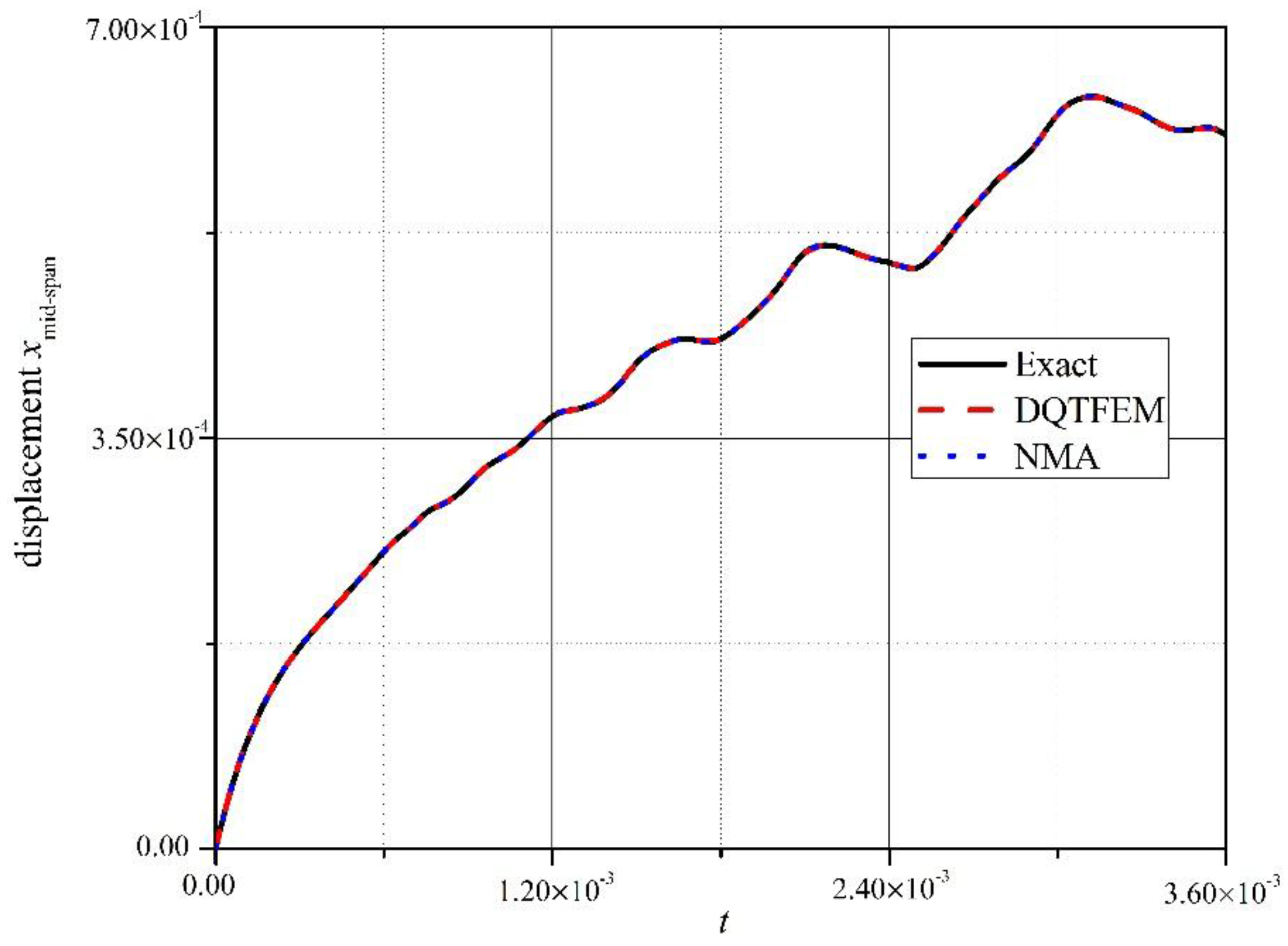
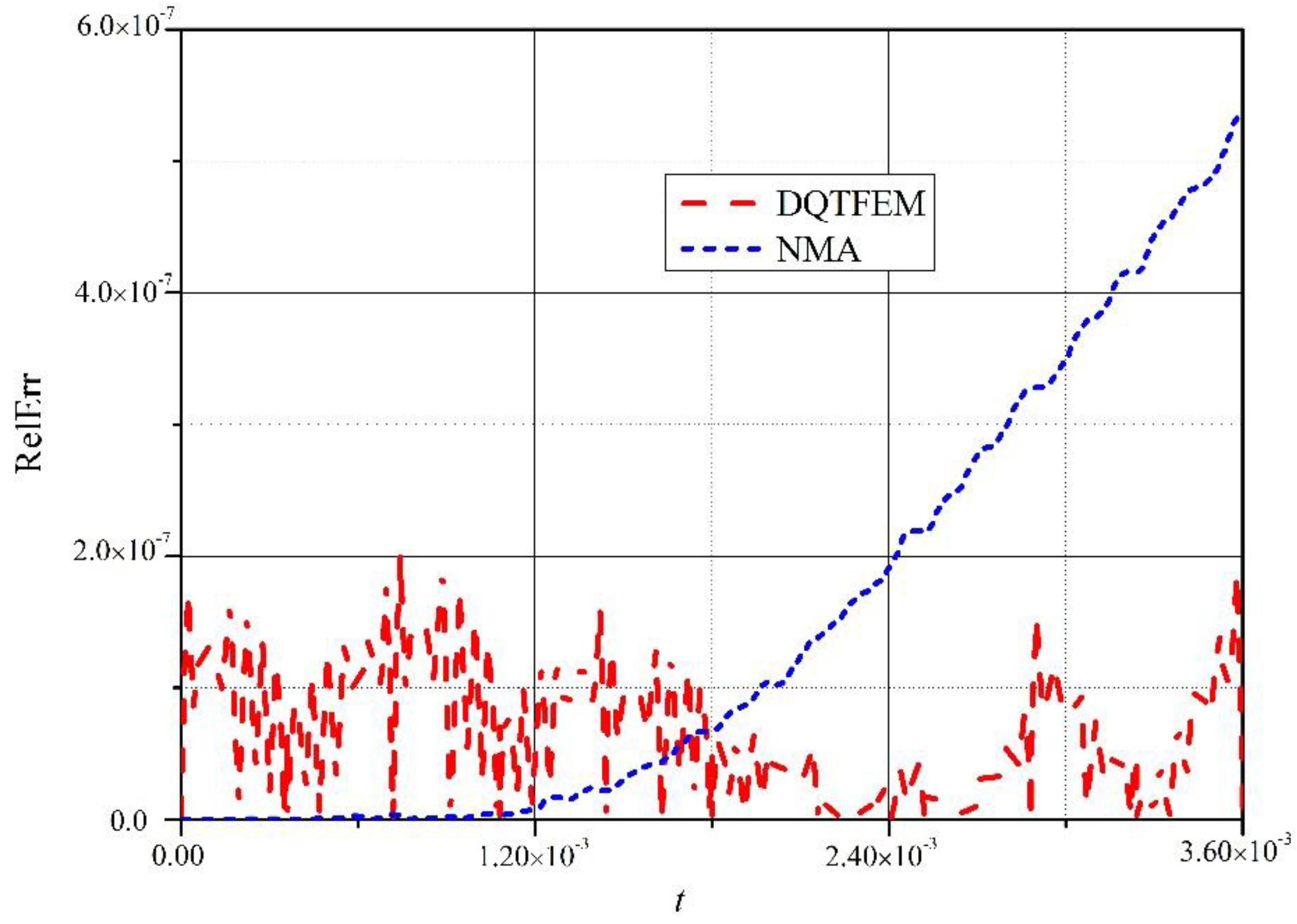
4.2. Free Vibration of a Simply Supported Euler Beam
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Feng, K. Difference schemes for hamiltonian formalism and symplectic geometry. J. Comput. Math. 1986, 4, 279–289. [Google Scholar]
- Zienkiewicz, O.C. A new look at the newmark, houbolt and other time stepping formulas. A weighted residual approach. Earthq. Eng. Struct. Dyn. 1977, 5, 413–419. [Google Scholar] [CrossRef]
- Argyris, J.H.; Scharpf, D.W. Finite elements in time and space. Nucl. Eng. Des. 1969, 10, 456–464. [Google Scholar] [CrossRef]
- Fried, I. Finite element analysis of time dependent phenomena. AIAA J. 1969, 7, 1170–1173. [Google Scholar] [CrossRef]
- Tang, W.S.; Sun, Y.J. Time finite element methods: A unified framework for numerical discretizations of odes. Appl. Math. Comput. 2012, 219, 2158–2180. [Google Scholar] [CrossRef]
- Simkins, T.E. Finite elements for initial value problems in dynamics. AIAA J. 1981, 19, 1357–1362. [Google Scholar] [CrossRef]
- Brugnano, L.; Iavernaro, F.; Trigiante, D. A simple framework for the derivation and analysis of effective one-step methods for odes. Appl. Math. Comput. 2012, 218, 8475–8486. [Google Scholar] [CrossRef]
- Wilson, E.L.; Nickell, R.E. Application of the finite element method to heat conduction analysis. Nucl. Eng. Des. 1966, 4, 276–287. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Wood, W.L.; Hine, N.W.; Taylor, R.L. A unified set of single step algorithms. Part 1: General formulation and applications. Int. J. Numer. Methods Eng. 1984, 20, 1529–1553. [Google Scholar] [CrossRef]
- Richter, T.; Wick, T. Variational localizations of the dual weighted residual estimator. J. Comput. Appl. Math. 2015, 279, 192–209. [Google Scholar] [CrossRef]
- Ma, L.M.; He, Y.A. A single-step time element method for dynamic response by gurtin variational principle. Eng. Mech. 1995, 12, 24–29. [Google Scholar]
- Zhong, W.; Yao, Z. Time domain fem and symplectic conservation. J. Mech. Strength 2005, 27, 178–183. [Google Scholar]
- Ding, X.C.; Chen, Q.W. Subinterval method for direct calculation of response of dynamic system by using hamilton’s principle. Earthq. Eng. Eng. Vib. 1987, 7, 9–19. [Google Scholar]
- Tung, M.M.; Defez, E.; Sastre, J. Numerical solutions of second-order matrix models using cubic-matrix splines. Comput. Math. Appl. 2008, 56, 2561–2571. [Google Scholar] [CrossRef]
- Bellour, A.; Sbibih, D.; Zidna, A. Two cubic spline methods for solving fredholm integral equations. Appl. Math. Comput. 2016, 276, 1–12. [Google Scholar] [CrossRef]
- Givoli, D.; Hagstrom, T.; Patlashenko, I. Finite element formulation with high-order absorbing boundary conditions for time-dependent waves. Comput. Methods Appl. Mech. Eng. 2006, 195, 3666–3691. [Google Scholar] [CrossRef]
- Jiang, Y.J.; Ma, J.T. High-order finite element methods for time-fractional partial differential equations. J. Comput. Appl. Math. 2011, 235, 3285–3291. [Google Scholar] [CrossRef]
- Krishna, M.S.; Manjeet, S.K. Three and four step least square finite element schemes in the time domain. Commun. Numer. Methods Eng. 1996, 12, 425–432. [Google Scholar]
- Jiwari, R. Lagrange interpolation and modified cubic b-spline differential quadrature methods for solving hyperbolic partial differential equations with dirichlet and neumann boundary conditions. Comput. Phys. Commun. 2015, 193, 55–66. [Google Scholar] [CrossRef]
- Kawahara, M.; Hasegawa, K. Periodic galerkin finite element method of tidal flow. Int. J. Numer. Methods Eng. 1978, 12, 115–128. [Google Scholar] [CrossRef]
- Jia, Z.; Cheng, X.; Zhao, M. A new method for roots of monic quaternionic quadratic polynomial. Comput. Math. Appl. 2009, 9, 1852–1859. [Google Scholar] [CrossRef]
- Hoff, C.; Hughes, T.J.R.; Hulbert, G.; Pahl, P.J. Extended comparison of the hilber-hughes-taylor α-method and the θ1-method. Comput. Methods Appl. Mech. Eng. 1989, 76, 87–94. [Google Scholar] [CrossRef]
- Chang, J.C. Combining genetic algorithm and taylor series expansion approach for doa estimation in space-time cdma systems. Appl. Soft Comput. J. 2015, 28, 208–217. [Google Scholar] [CrossRef]
- Khan, I.R.; Ohba, R.; Hozumi, N. Mathematical proof of closed form expressions for finite difference approximations based on taylor series. J. Comput. Appl. Math. 2003, 150, 303–310. [Google Scholar] [CrossRef]
- Hoff, C.; Pahl, P.J. Practical performance of the θ1-method and comparison with other dissipative algorithms in structural dynamics. Comput. Methods Appl. Mech. Eng. 1988, 67, 87–111. [Google Scholar] [CrossRef]
- Reed, W.H.; Hill, T.R. Triangular Mesh Methods for the Neutron Transport Equation; Los Alamos Scientific Laboratory: Los Alamos, NM, USA, 1973. [Google Scholar]
- Lasaint, P.; Raviart, P.A. On a finite element method for solving the neutron transport equation. In Mathematical Aspects of Finite Elements in Partial Differential Equations, Proceedings of a Symposium Conducted by the Mathematics Research Center, the University of Wisconsin-Madison, Madison, WI, USA, 1–3 April, 1974; Elsevier: Amsterdam, The Netherlands, 1974; Volume 56, pp. 89–124. [Google Scholar]
- Gudla, P.K.; Ganguli, R. Discontinuous galerkin finite element in time for solving periodic differential equations. Comput. Methods Appl. Mech. Eng. 2006, 196, 682–697. [Google Scholar] [CrossRef]
- Gao, Y.L.; Mei, L.Q.; Li, R. A time-splitting galerkin finite element method for the davey-stewartson equations. Comput. Phys. Commun. 2015, 197, 35–43. [Google Scholar] [CrossRef]
- Delfour, M.; Hager, W.; Trochu, F. Discontinuous galerkin methods for ordinary differential equations. Math. Comput. 1981, 36, 455–474. [Google Scholar] [CrossRef]
- Hughes, T.J.R.; Hulbert, G.M. Space-time finite element methods for elastodynamics: Formulations and error estimates. Comput. Methods Appl. Mech. Eng. 1988, 66, 339–364. [Google Scholar] [CrossRef]
- Hulbert, G.M.; Hughes, T.J.R. Space-time finite element methods for second-order hyperbolic equations. Comput. Methods Appl. Mech. Eng. 1990, 84, 327–349. [Google Scholar] [CrossRef]
- Chessa, J.; Belytschko, T. A local space–time discontinuous finite element method. Comput. Methods Appl. Mech. Eng. 2006, 195, 1325–1344. [Google Scholar] [CrossRef]
- Dyniewicz, B. Space-time finite element approach to general description of a moving inertial load. Finite Elem. Anal. Des. 2012, 62, 8–18. [Google Scholar] [CrossRef]
- Hulbert, G.M. Time finite element methods for structural dynamics. Int. J. Numer. Methods Eng. 1992, 33, 307–331. [Google Scholar] [CrossRef]
- Nam, J.; Behr, M.; Pasquali, M. Space-time least-squares finite element method for convection-reaction system with transformed variables. Comput. Methods Appl. Mech. Eng. 2011, 200, 2562–2577. [Google Scholar] [CrossRef] [PubMed]
- Chien, C.C.; Wu, T.Y. An improved predictor/multi-corrector algorithm for a time-discontinuous galerkin finite element method in structural dynamics. Comput. Mech. 2000, 25, 430–438. [Google Scholar] [CrossRef]
- Aubry, D.; Lucas, D.; Tie, B. Adaptive strategy for transient/coupled problems applications to thermoelasticity and elastodynamics. Comput. Methods Appl. Mech. Eng. 1999, 1, 41–51. [Google Scholar] [CrossRef]
- Larsson, F.; Hansbo, P.; Runesson, K. Space-time finite elements and an adaptive strategy for the coupled thermoelasticity problem. Int. J. Numer. Methods Eng. 2003, 56, 261–294. [Google Scholar] [CrossRef]
- Bellman, R.; Casti, J. Differential quadrature and long-term integration. J. Math. Anal. Appl. 1971, 34, 235–239. [Google Scholar] [CrossRef]
- Shu, C. Differential Quadrature and Its Application in Engineering; Springer: London, UK, 2000. [Google Scholar]
- Eftekhari, S.A.; Khani, M. A coupled finite element-differential quadrature element method and its accuracy for moving load problem. Appl. Math. Model. 2010, 34, 228–238. [Google Scholar] [CrossRef]
- Eftekhari, S.A.; Jafari, A.A. Mixed finite element and differential quadrature method for free and forced vibration and buckling analysis of rectangular plates. Appl. Math. Mech. 2012, 33, 81–98. [Google Scholar] [CrossRef]
- Wang, X.; Yuan, Z. Harmonic differential quadrature analysis of soft-core sandwich panels under locally distributed loads. Appl. Sci. 2016, 6, 361. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Ubertini, F.; Viola, E. Strong formulation finite element method based on differential quadrature: A survey. Appl. Mech. Rev. 2015, 1, 145–175. [Google Scholar] [CrossRef]
- Bert, C.W.; Malik, M. Differential quadrature method in computational mechanics: A review. Appl. Mech. Rev. 1996, 49, 1–29. [Google Scholar] [CrossRef]
- Xing, Y.; Liu, B. High-accuracy differential quadrature finite element method and its application to free vibrations of thin plate with curvilinear domain. Int. J. Numer. Methods Eng. 2009, 80, 1718–1743. [Google Scholar] [CrossRef]
- Xing, Y.F.; Liu, B.; Liu, G. A differential quadrature finite element method. Int. J. Appl. Mech. 2012, 2, 207–227. [Google Scholar] [CrossRef]
- Reddy, J.N. Energy and Variational Methods in Applied Mechanics; John Wiley & Sons: New York, NY, USA, 1984. [Google Scholar]
- Fung, T.C. Solving initial value problems by differential quadrature method-part 1: First-order equations. Int. J. Numer. Methods Eng. 2001, 50, 1411–1428. [Google Scholar] [CrossRef]
- Bartels, R.H.; Stewart, G.W. Solution of the matrix equation ax + xb = c. Commun. ACM 1972, 15, 820–826. [Google Scholar] [CrossRef]
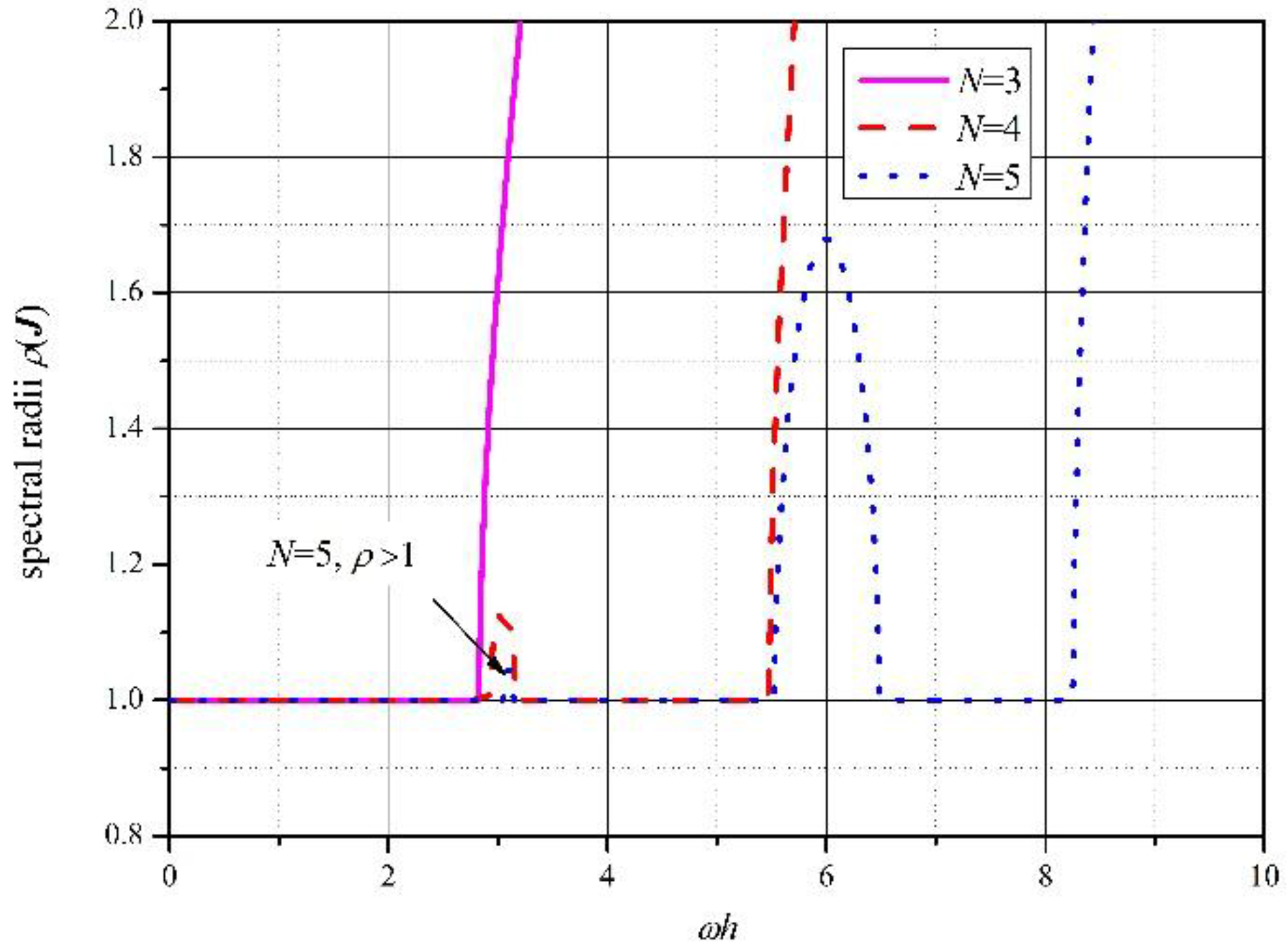
| N | 3 | 4 | 5 | 10 | 15 | 20 | 25 | 30 | 36 |
|---|---|---|---|---|---|---|---|---|---|
| 0 < ωh ≤ | 2.828 | 2.927 | 3.055 | 9.404 | 15.71 | 25.11 | 34.55 | 37.69 | 50.25 |
| (N, max(ωh)) | abs(J1 − 1) | abs(J2 − 1) | Ji, i = 3, 4, 5, 6 | abs(|J| − 1) | abs(ρ(J) − 1) |
|---|---|---|---|---|---|
| (3, 2.828) | 2.459 × 10−7 | 2.459 × 10−7 | 0 | 2.812 × 10−7 | 1.486 × 10−9 |
| (4, 2.927) | 6.758× 10−8 | 6.758 × 10−8 | 0 | 7.002 × 10−8 | 4.289 × 10−9 |
| (5, 3.055) | 2.817 × 10−8 | 2.817 × 10−8 | 0 | 3.018 × 10−8 | 1.087 × 10−9 |
| (10, 9.404) | 3.648 × 10−10 | 3.648 × 10−10 | 0 | 3.821 × 10−10 | 1.821 × 10−12 |
| (15, 15.70) | 1.085 × 10−10 | 1.085 × 10−10 | 0 | 1.663 × 10−10 | 7.223 × 10−12 |
| (20, 25.11) | 3.345 × 10−10 | 3.345 × 10−10 | 0 | 3.598 × 10−10 | 4.538 × 10−11 |
| (25, 34.55) | 1.784 × 10−8 | 1.784 × 10−8 | 0 | 1.999 × 10−8 | 6.046 × 10−10 |
| (30, 37.69) | 4.586 × 10−6 | 4.586 × 10−6 | 0 | 4.939 × 10−6 | 7.919 × 10−8 |
| (35, 50.25) | 3.882 × 10−6 | 3.882 × 10−6 | 0 | 4.051 × 10−6 | 6.124 × 10−8 |
| Method | RelErr = 10−6 | RelErr = 10−2 | ||||
|---|---|---|---|---|---|---|
| h | Time Steps | CPU (s) | h | Time Steps | CPU (s) | |
| DQTFEM | 1.26 | 1588 | 0.4932 | |||
| RKM | 5 × 10−2 | 4 × 105 | 4.743 | 0.32 | 6.25 × 103 | 0.7843 |
| NMA | 1 × 10−3 | 2 × 106 | 249.4 | 4.5 × 10−2 | 4.445 × 104 | 1.184 |
| Method | h (s) | Time Steps | CPU (s) |
|---|---|---|---|
| DQTFEM | 3.6 × 10−4 | 10 | 0.9376 |
| NMA | 1.706 × 10−8 | 2.110 × 105 | 294.8 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, Y.; Qin, M.; Guo, J. A Time Finite Element Method Based on the Differential Quadrature Rule and Hamilton’s Variational Principle. Appl. Sci. 2017, 7, 138. https://doi.org/10.3390/app7020138
Xing Y, Qin M, Guo J. A Time Finite Element Method Based on the Differential Quadrature Rule and Hamilton’s Variational Principle. Applied Sciences. 2017; 7(2):138. https://doi.org/10.3390/app7020138
Chicago/Turabian StyleXing, Yufeng, Mingbo Qin, and Jing Guo. 2017. "A Time Finite Element Method Based on the Differential Quadrature Rule and Hamilton’s Variational Principle" Applied Sciences 7, no. 2: 138. https://doi.org/10.3390/app7020138






