Heat Transfer Investigation of the Unsteady Thin Film Flow of Williamson Fluid Past an Inclined and Oscillating Moving Plate
Abstract
:1. Introduction
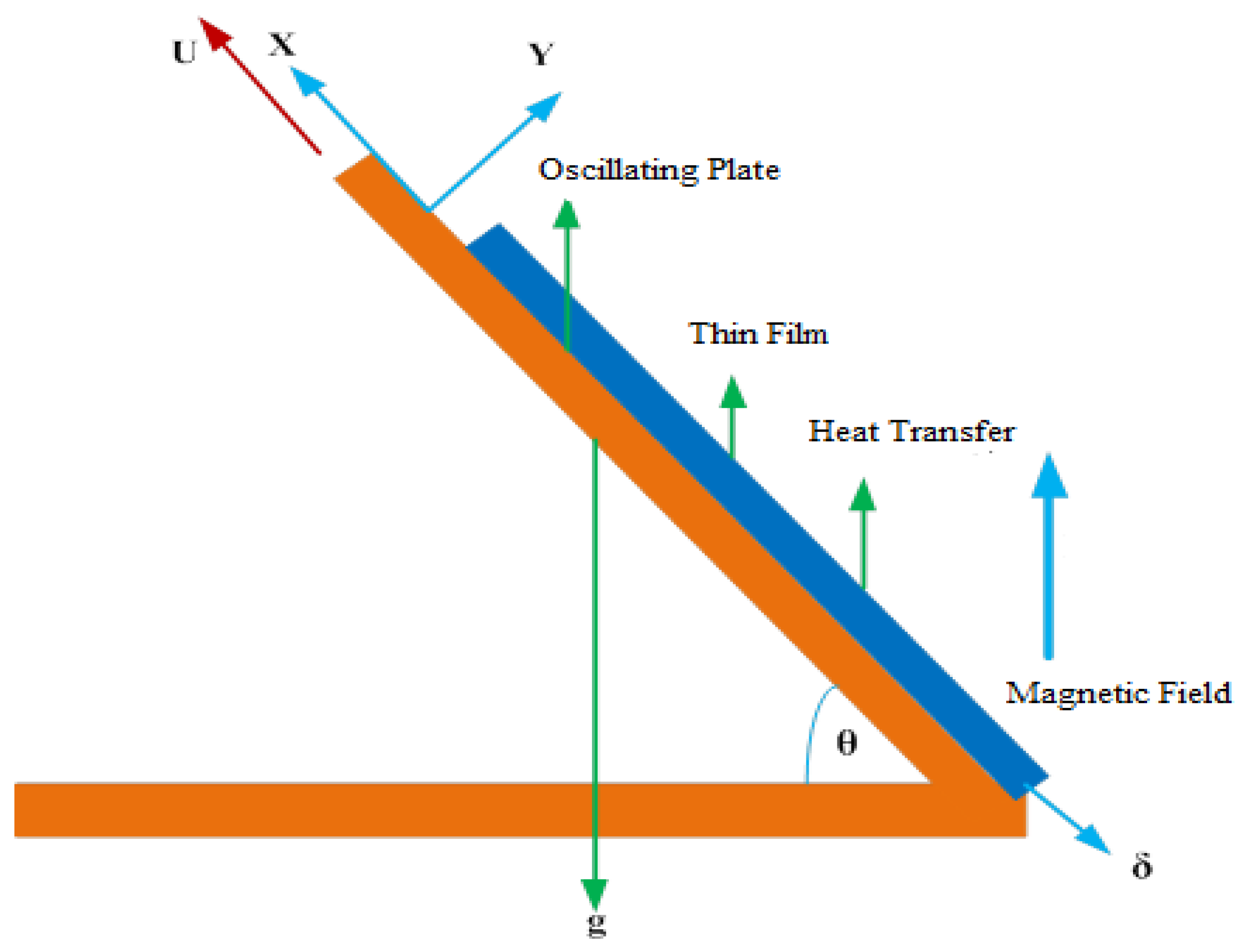
2. Materials and Methods
Solution by OHAM
3. Basic Idea of Adomian Decomposition Method (ADM)
The ADM Solution of the Problem
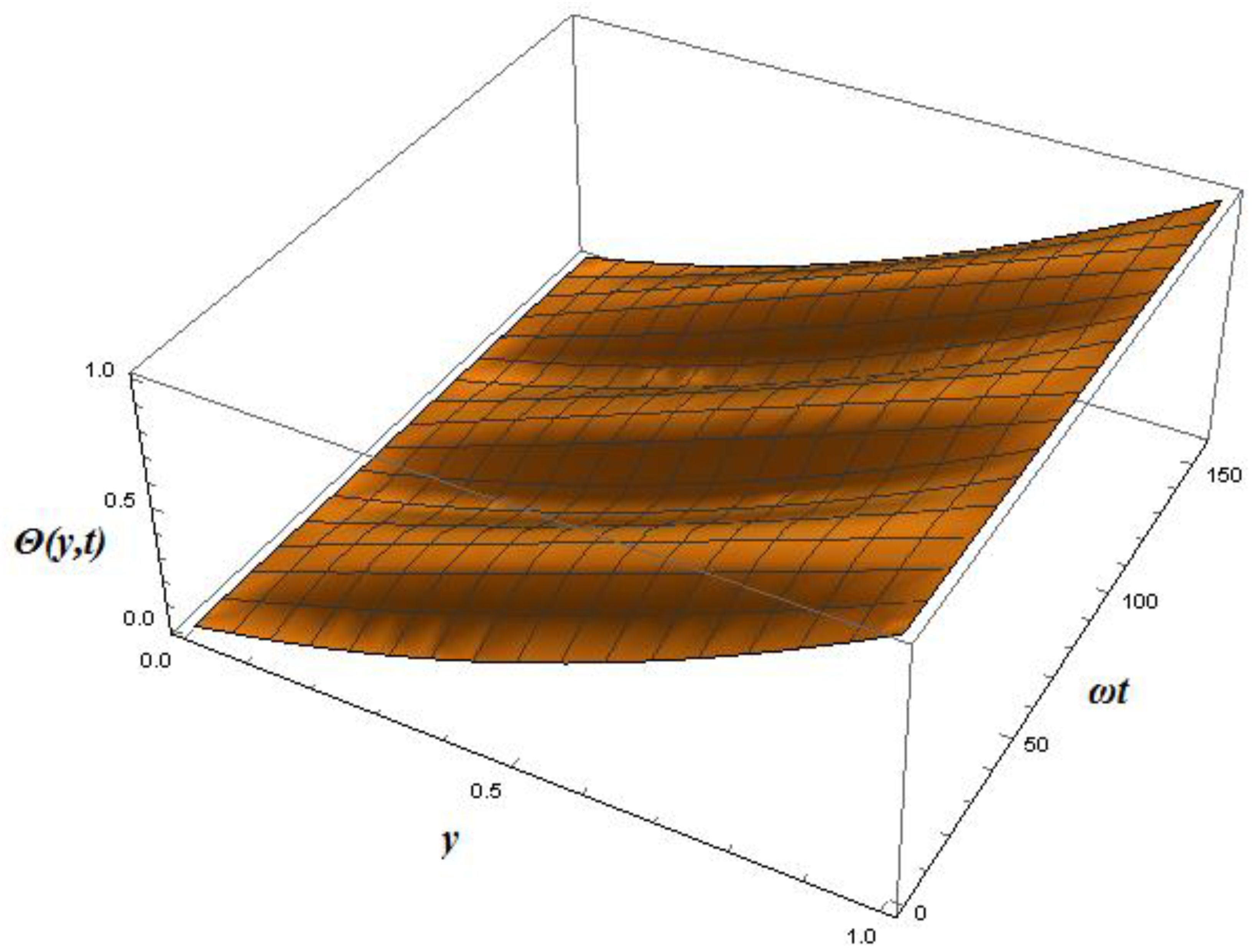
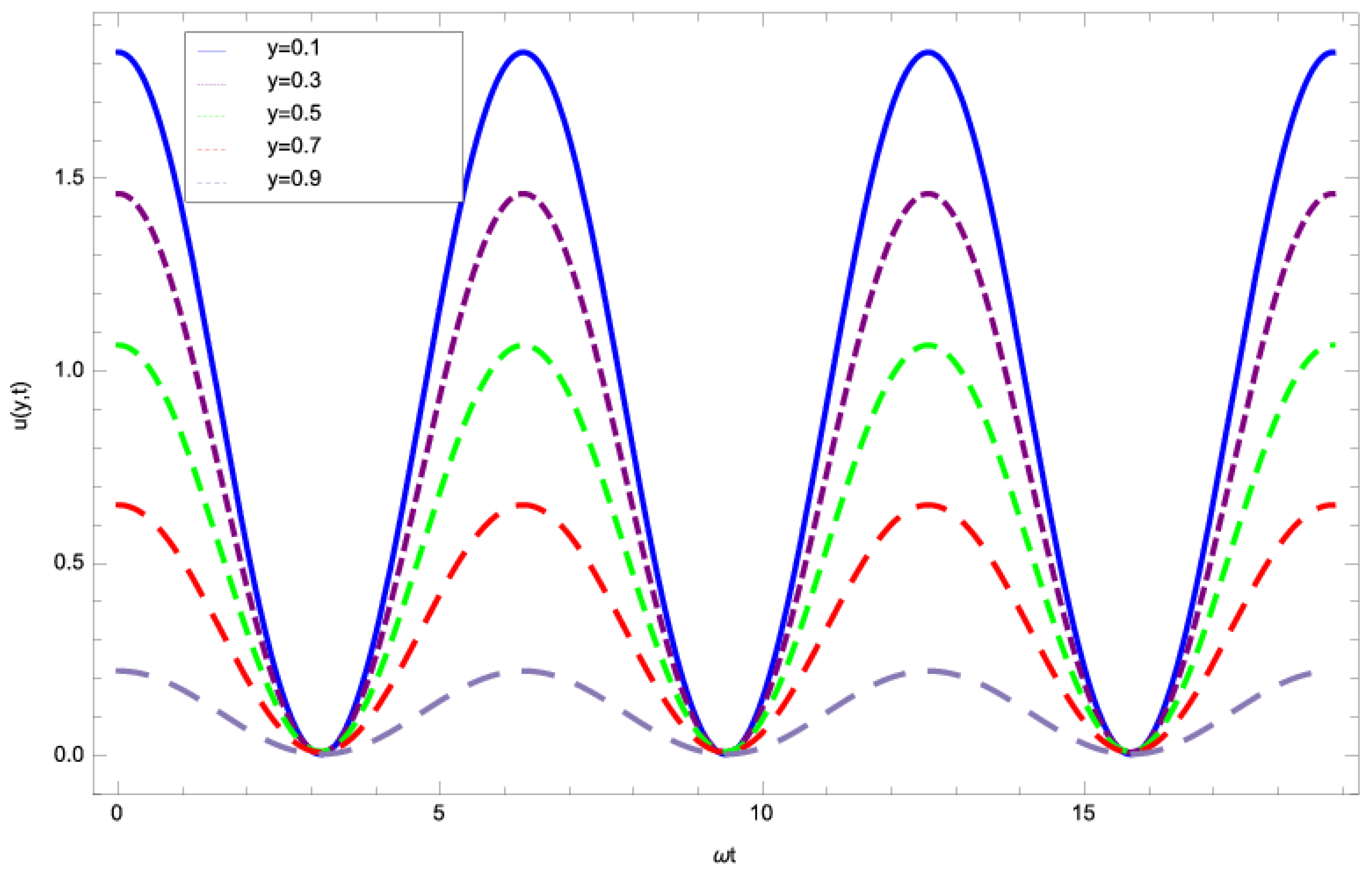
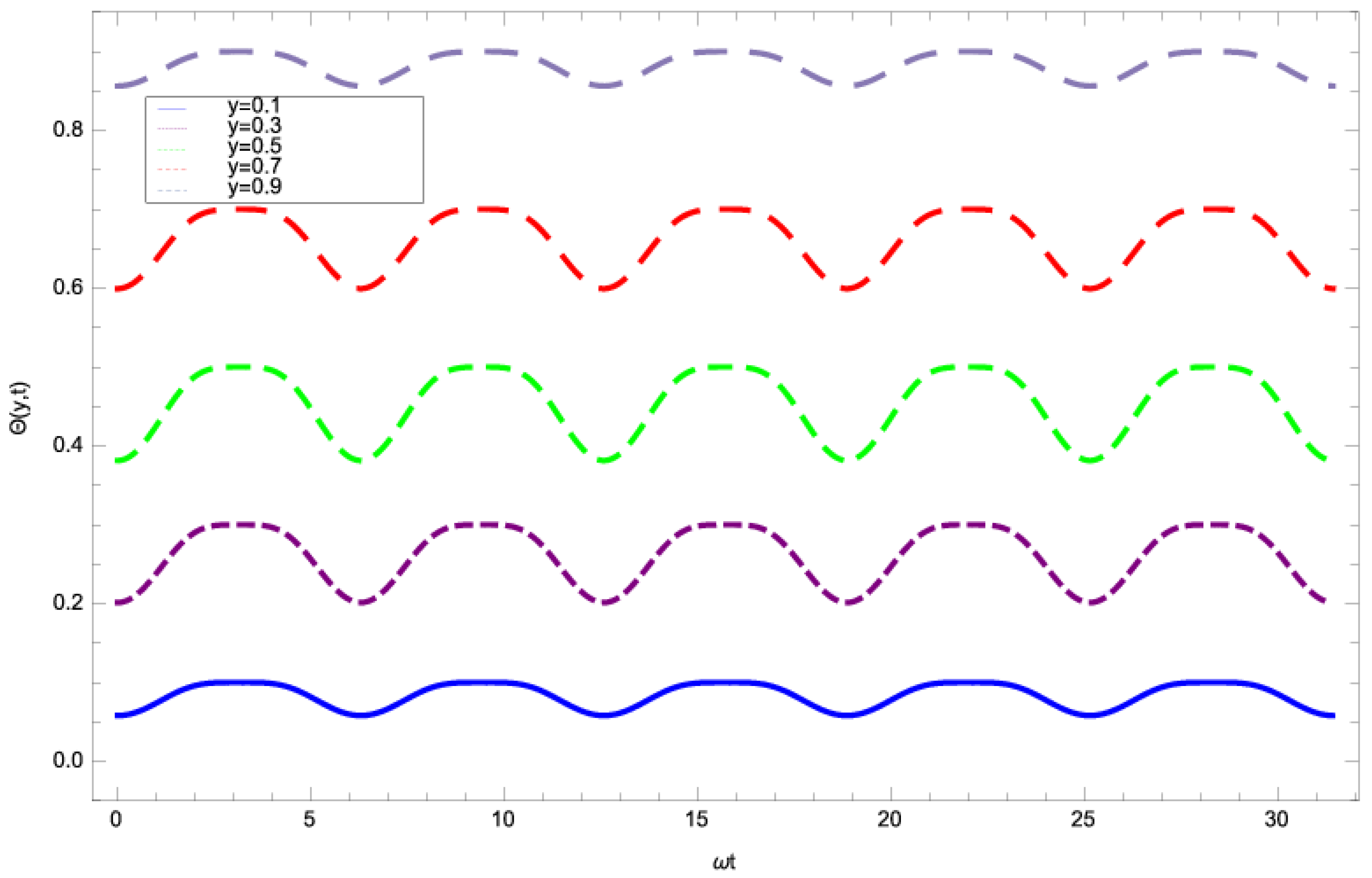
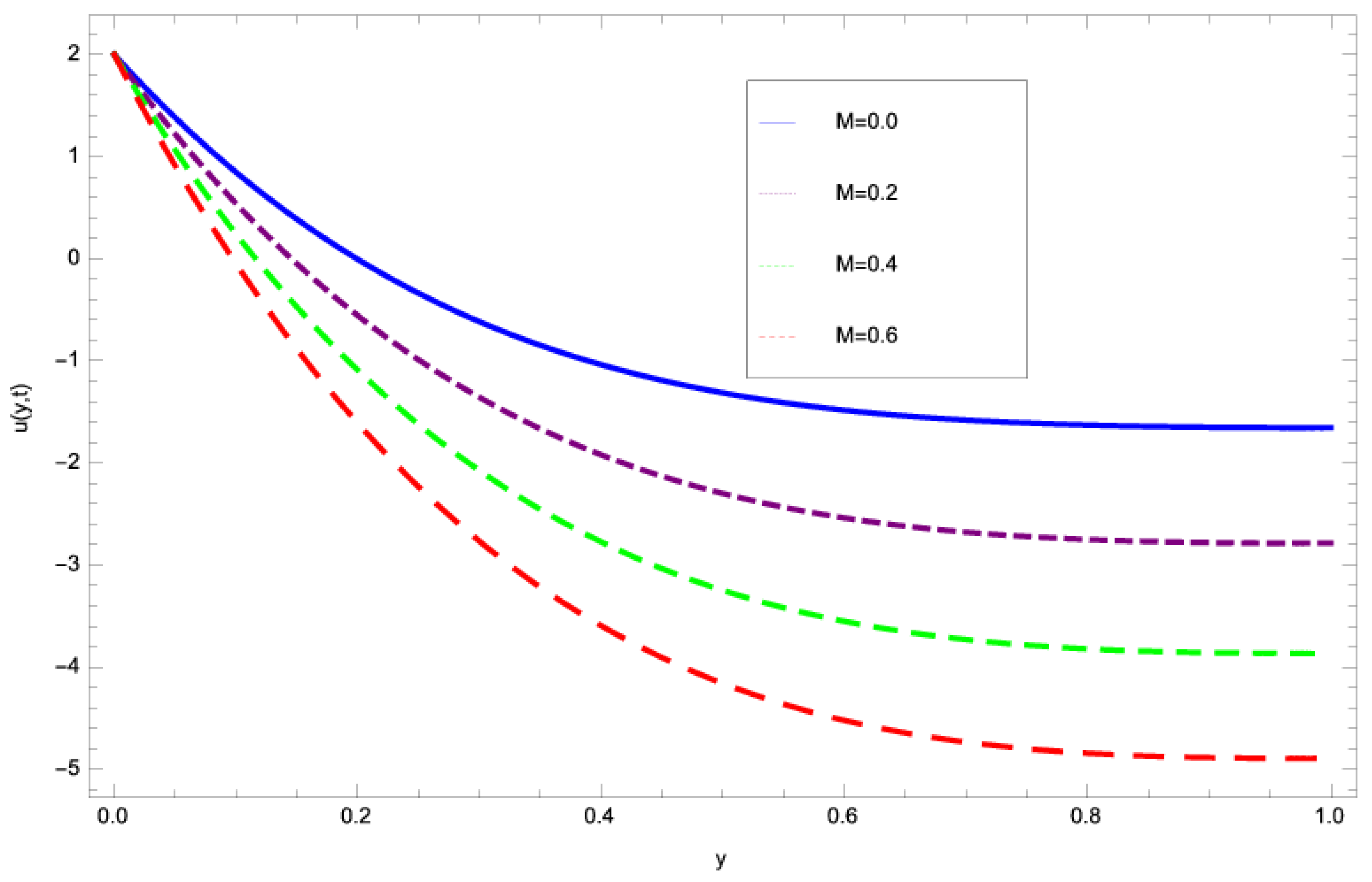
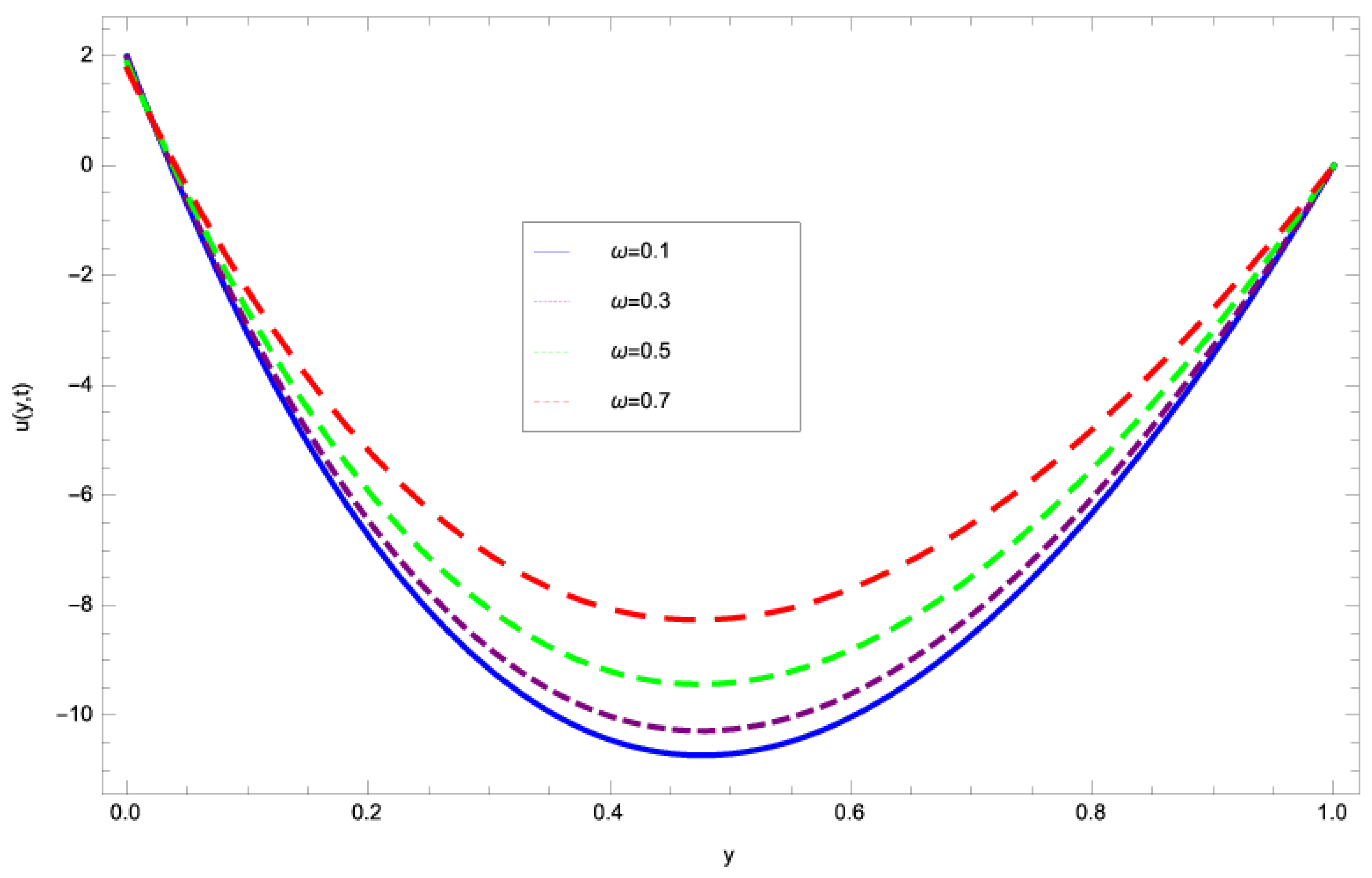
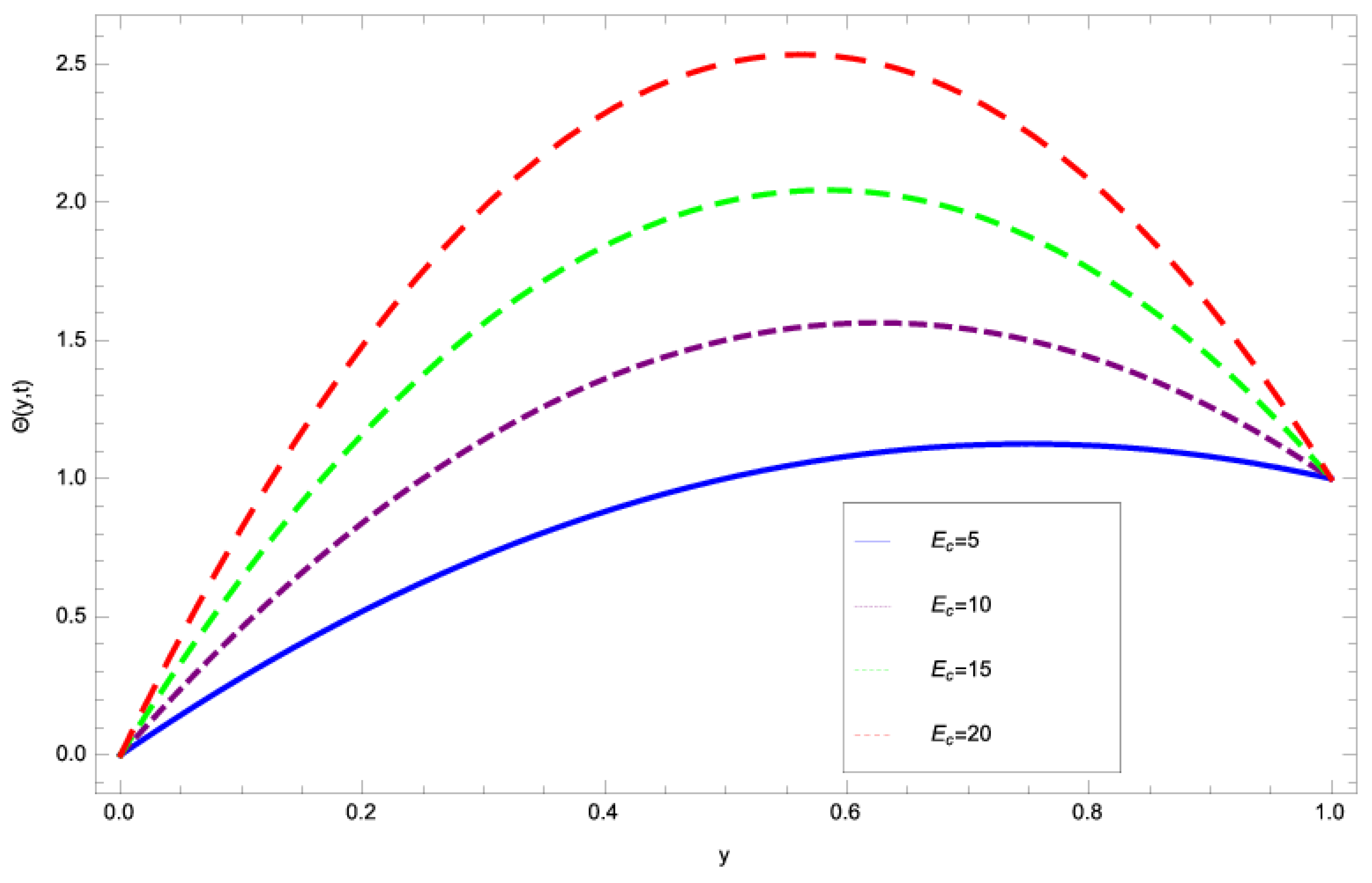
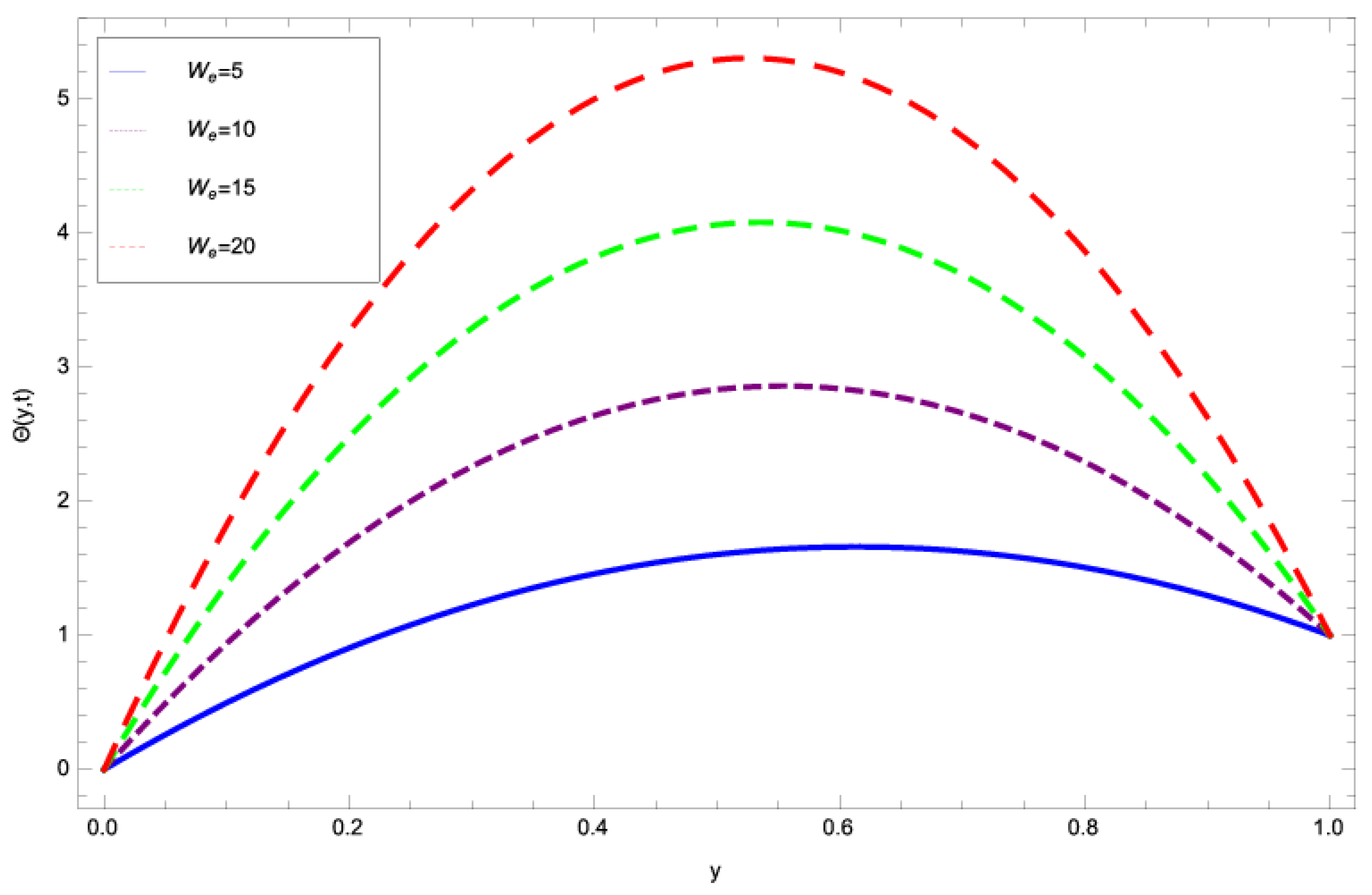
4. Discussion
5. Conclusions
- Initially, the liquid film oscillates jointly with the plate for a selected domain and this oscillation rises slowly towards the free surface.
- The gravitational effect near the belt is smaller due to the friction force, and this effect is more clear and rapid at the free surface.
- The magnetic effect on the flow field has been observed, which opposes the fluid motion.
- The thermal boundary layer thickness increases with larger values of Eckert number and the inter molecular forces among the fluid particles decrease and, as a result, the velocity of fluid film increases.
- The fast convergence of OHAM has been observed by comparing its results with ADM.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Velocity field | |
| Constant velocity | |
| Gravitational parameter | |
| Magnetic parameter | |
| Frequency parameter | |
| Amplitude | |
| Infinite viscosity | |
| Second invariant strain tensor | |
| Williamson parameter | |
| Eckert number | |
| Temperature field | |
| Dimensionless temperature field | |
| Thickness of the liquid film | |
| Prandtl number | |
| Lorentz force | |
| Electrical conductivity of the fluid | |
| Gravitational force | |
| Extra stress tensor | |
| Time constant | |
| Zero viscosity |
Appendix A
References
- Ancey, C. Plasticity and geophysical flows: A review. J. Non-Newton. Fluid Mech. 2007, 142, 4–35. [Google Scholar] [CrossRef]
- Griffiths, R.W. The dynamics of lava flows. Annu. Rev. Fluid Mech. 2000, 32, 477–518. [Google Scholar] [CrossRef]
- Williamson, R.V. The flow of pseudoplastic materials. Ind. Eng. Chem. Res. 1929, 21, 1108–1111. [Google Scholar] [CrossRef]
- Dapra, I.; Scarpi, G. Perturbation solution for pulsatile flow of a non-Newtonian Williamson fluid in a rock fracture. Int. J. Rock Mech. Min. Sci. 2006, 44, 1–8. [Google Scholar] [CrossRef]
- Gamal, M.; Abdel, R. Unsteady magnetohydrodynamic flow of non-Newtonian fluids obeying power law model. J. Interdiscip. Math. 2007, 10, 363–368. [Google Scholar]
- Khan, N.A.; Khan, S.; Riaz, F. Boundary Layer Flow of Williamson Fluid with Chemically Reactive Species. Math. Sci. Lett. 2014, 3, 199–205. [Google Scholar] [CrossRef]
- Hayat, T.; Shafiq, A.; Alsaedi, A. Hydromagnetic boundary layer flow of Williamson fluid in the presence of thermal radiation and Ohmic dissipation. Alex. Eng. J. 2016, 55, 2229–2240. [Google Scholar] [CrossRef]
- Nadeem, S.; Hussain, S.T.; Lee, C. Flow of Williamson Fluid over a Stretching Sheet. Braz. J. Chem. Eng. 2013, 30, 619–625. [Google Scholar] [CrossRef]
- Waris, K.; Gul, T.; Idrees, M.; Islam, S.; Khan, I.; Dennis, L. Thin Film Williamson Nanofluid Flow with Varying Viscosity and Thermal Conductivity on a Time-Dependent Stretching Sheet. Appl. Sci. 2016, 6, 334. [Google Scholar]
- Abdollahzadeh Jamalabadi, M.Y.; Hooshmand, P.; Bagheri, N.; KhakRah, H.; Dousti, M. Numerical simulation of Williamson combined natural and forced convective fluid flow between parallel vertical walls with slip effects and radiative heat transfer in a porous medium. Entropy 2016, 18, 147. [Google Scholar] [CrossRef]
- Noor, K.; Gul, T.; Islam, S.; Khan, I.; Aisha, M.A.; Ali, S.A. Magnetohydrodynamic nanoliquid thin film sprayed on a stretching cylinder with heat transfer. Appl. Sci. 2017, 7, 271. [Google Scholar]
- Gul, T.; Saeed, I.; Shah, R.A.; Khan, I.; Shafie, S. Thin film flow in MHD third grade fluid on a vertical belt with temperature dependent viscosity. PLoS ONE 2014, 9, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Miladinova, S.; Lebon, G.; Toshev, E. Thin Film Flow of a Power Law Liquid Falling Down an Inclined Plate. J. Non-Newton. Fluid Mech. 2014, 122, 69–70. [Google Scholar] [CrossRef]
- Siddiqui, A.M.; Mahmood, R.; Ghori, Q.K. Homotopy perturbation method for thin film flow of a fourth grade fluid down a vertical cylinder. Phys. Lett. A 2006, 352, 404–410. [Google Scholar] [CrossRef]
- Fetecau, C. Starting solutions for some unsteady unidirectional flows of a second grade fluid. Int. J. Eng. Sci. 2005, 43, 781–789. [Google Scholar] [CrossRef]
- Majeed, A.; Zeeshan, A.; Ellahi, R. Unsteady Ferromagnetic Liquid Flow and Heat Transfer Analysis over a Stretching Sheet with the Effect of Dipole and Prescribed Heat Flux. J. Mol. Liquid 2016, 223, 528–533. [Google Scholar] [CrossRef]
- Keslerova, R.; Karel, K. Numerical study of steady and unsteady flow for power-law type generalized Newtonian fluids. Computing 2013, 95, 409–424. [Google Scholar] [CrossRef]
- Andrew, D.; Rees, S.; Andrew, P.B. Unsteady thermal boundary layer flows of a Bingham fluid in a porous medium. Int. J. Heat Mass Transf. 2015, 82, 460–467. [Google Scholar]
- Morteza, B.N.; Maziar, C. Reduced-order modeling of three-dimensional unsteady partial cavity flows. J. Fluids Struct. 2015, 52, 1–15. [Google Scholar]
- Fatimah, A.Z.M.S.; Jaworski, A.J. Friction factor correlation for regenerator working in a travelling-wave thermo acoustic system. Appl. Sci. 2017, 7, 253. [Google Scholar]
- Huang, J.; Liu, M.; Jin, T. A Comprehensive Empirical Correlation for Finned Heat Exchangers with Parallel PlatesWorking in Oscillating Flow. Appl. Sci. 2017, 7, 117. [Google Scholar] [CrossRef]
- Gul, T.; Islam, S.; Rehan, A.S.; Khan, I.; Sharidan, S. Analysis of thin film flow over a vertical oscillating belt with a second grade fluid. Eng. Sci. Technol. Int. J. 2015, 18, 207–217. [Google Scholar] [CrossRef]
- Shah, A.R.; Islam, S.; Siddiqui, A.M.; Haroon, T. OHAM solution of unsteady second grade fluid in wire coating analysis. J. KSIAM 2011, 15, 201–222. [Google Scholar]
- Yongqi, W.; Wei, W. Unsteady flow of a fourth-grade due to an oscillating plate. Non-Linear Mech. 2007, 42, 432–441. [Google Scholar]
- Gul, T.; Islam, S.; Shah, R.A.; Khan, I.; Khalid, A.; Safie, S. Heat Transfer Analysis of MHD Thin Film Flow of an Unsteady Second Grade Fluid Past a Vertical Oscillating Belt. PLoS ONE 2014, 9, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Gul, T.; Islam, S.; Shah, R.A.; Khalid, A.; Khan, I.; Shafie, S. Unsteady MHD Thin Film Flow of an Oldroyd B Fluid over an Oscillating Inclined Belt. PLoS ONE 2015, 10, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Gul, T.; Fazle, G.; Islam, S.; Shah, R.A.; Khan, I.; Nasir, S.; Sharidan, S. Unsteady thin film flow of a fourth grade fluid over a vertical moving and oscillating belt. Propuls. Power Res. 2016, 5, 223–235. [Google Scholar] [CrossRef]
- Ellahi, R.; Tariq, M.H.; Hassan, M.; Vafai, K. On boundary layer magnetic flow of nano-Ferroliquid under the influence of low oscillating over stretchable rotating disk. J. Mol. Liquids 2017, 229, 339–345. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ellahi, R. Electrohydrodynamic nanofluid hydrothermal treatment in an enclosure with sinusoidal upper wall. Appl. Sci. 2015, 5, 294–306. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Zaigham Zia, Q.M.; Ellahi, R. Influence of induced magnetic field on free convection of nanofluid considering Koo-Kleinstreuer (KKL) correlation. Appl. Sci. 2016, 6, 324. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A. Shape effects of nanosize particles in Cu-H2O nanofluid on entropy generation. Int. J. Heat Mass Transf. 2015, 81, 449–456. [Google Scholar] [CrossRef]
- Wang, L.; Chen, X. Approximate Analytical Solutions of Time Fractional Whitham-Broer-Kaup Equations by a Residual Power Series Method. Entropy 2015, 17, 6519–6533. [Google Scholar] [CrossRef]
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1994. [Google Scholar]
- Adomian, G. A Review of the Decomposition Method and Some Recent Results for Non-Linear Equations. Math. Comput. Model. 1992, 13, 287–299. [Google Scholar]
- Wazwaz, A.; Adomian, M. Decomposition Method for a Reliable Treatment of the Bratu-Type Equations. Appl. Math. Comput. 2005, 166, 652–663. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Adomian Decomposition Method for a Reliable Treatment of the Emden-Fowler Equation. Appl. Math. Comput. 2005, 161, 543–560. [Google Scholar] [CrossRef]
- Marinca, V.; Herisanu, N.; Bota, C.; Marinca, B. An optimal homotopy asymptotic method applied to the steady flow of fourth grade fluid pasta porous plate. Appl. Math. Lett. 2009, 22, 245–251. [Google Scholar] [CrossRef]
- Marinca, V.; Herisanu, N. Application of optimal homotopy asymptotic method for solving non-linear equations arising in heat transfer. Int. Commun. Heat Mass Transf. 2008, 35, 710–715. [Google Scholar] [CrossRef]
- Marinca, V.; Herisanu, N.; Nemes, I. Optimal homotopy asymptotic method with application to thin film flow. Cent. Eur. J. Phys. 2008, 6, 648–653. [Google Scholar] [CrossRef]
- Mabood, F.; Khan, W.A.; Ismail, A. Optimal homotopy asymptotic method for flow and heat transfer of a viscoelastic fluid in an axisymmetric channel with a porous wall. PLoS ONE 2013, 8, 1–8. [Google Scholar] [CrossRef] [PubMed]



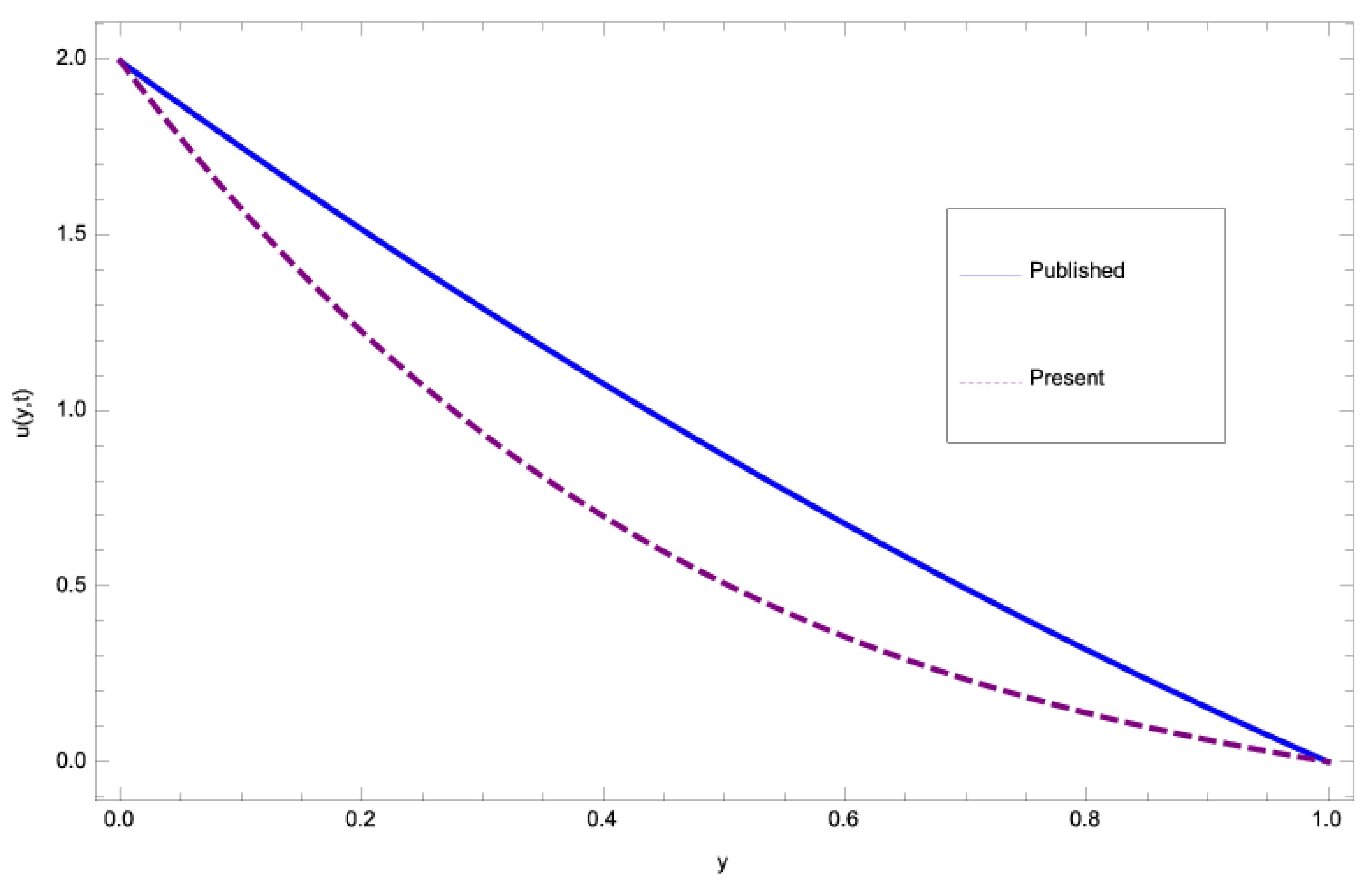
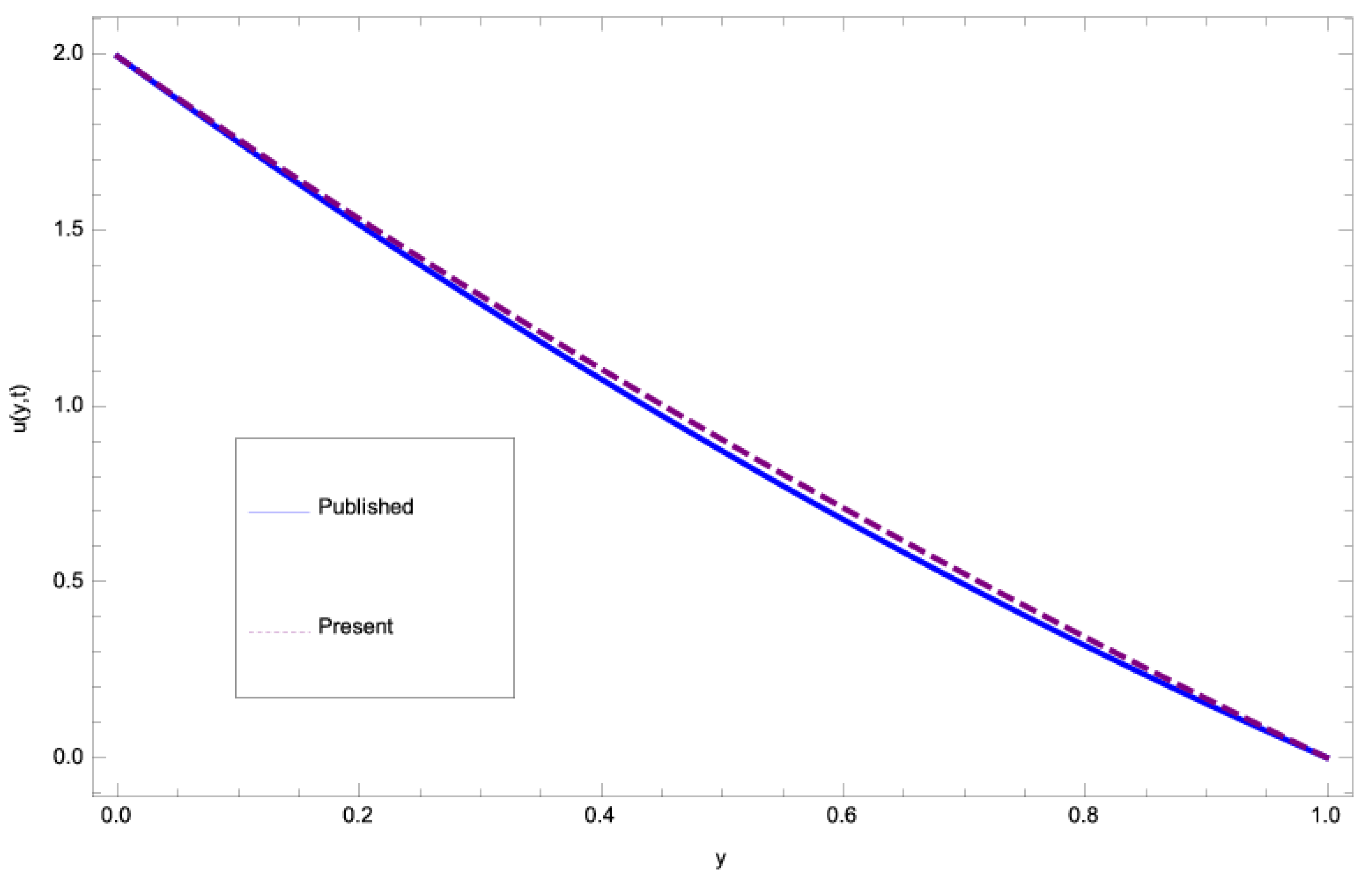
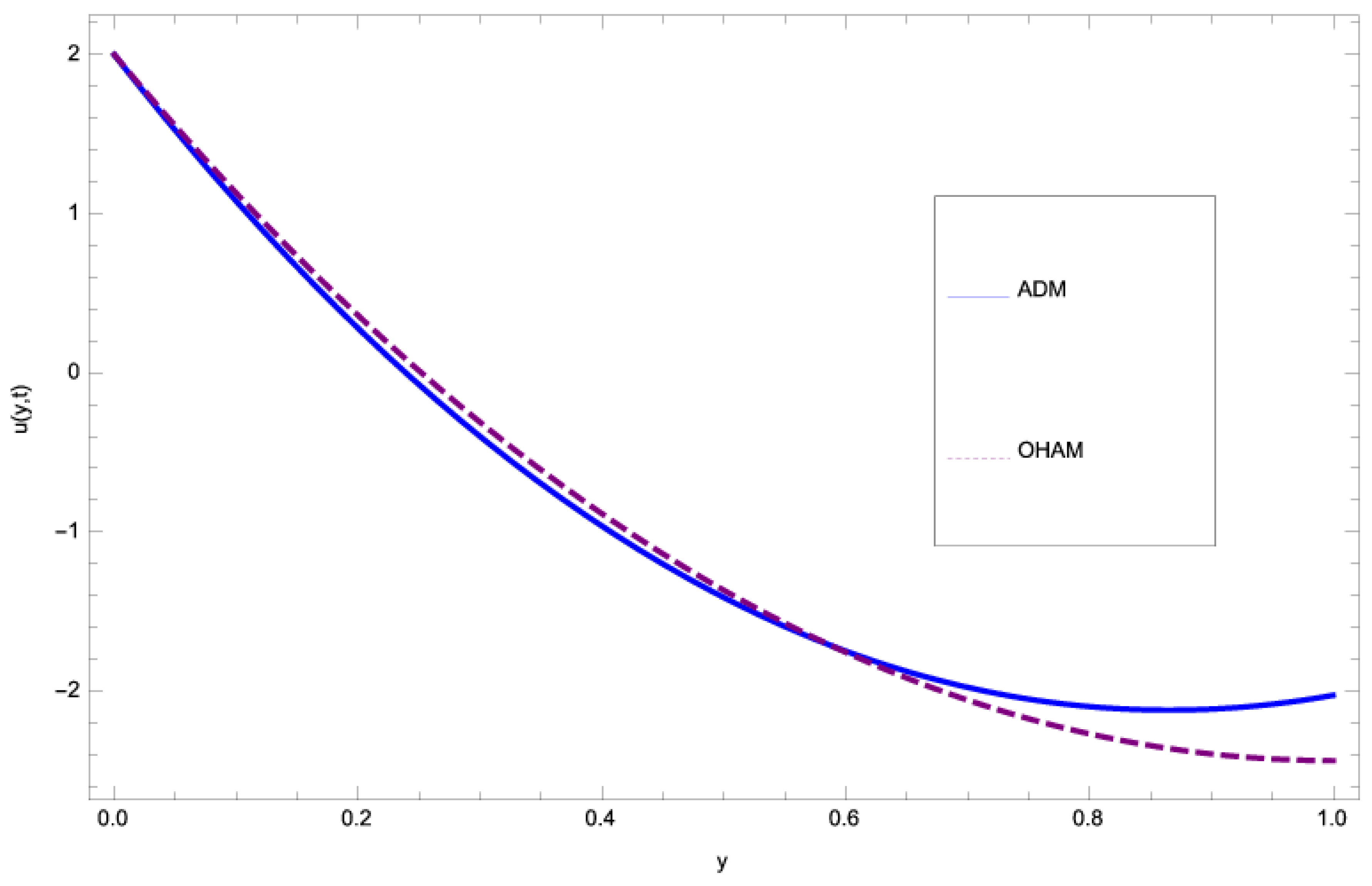
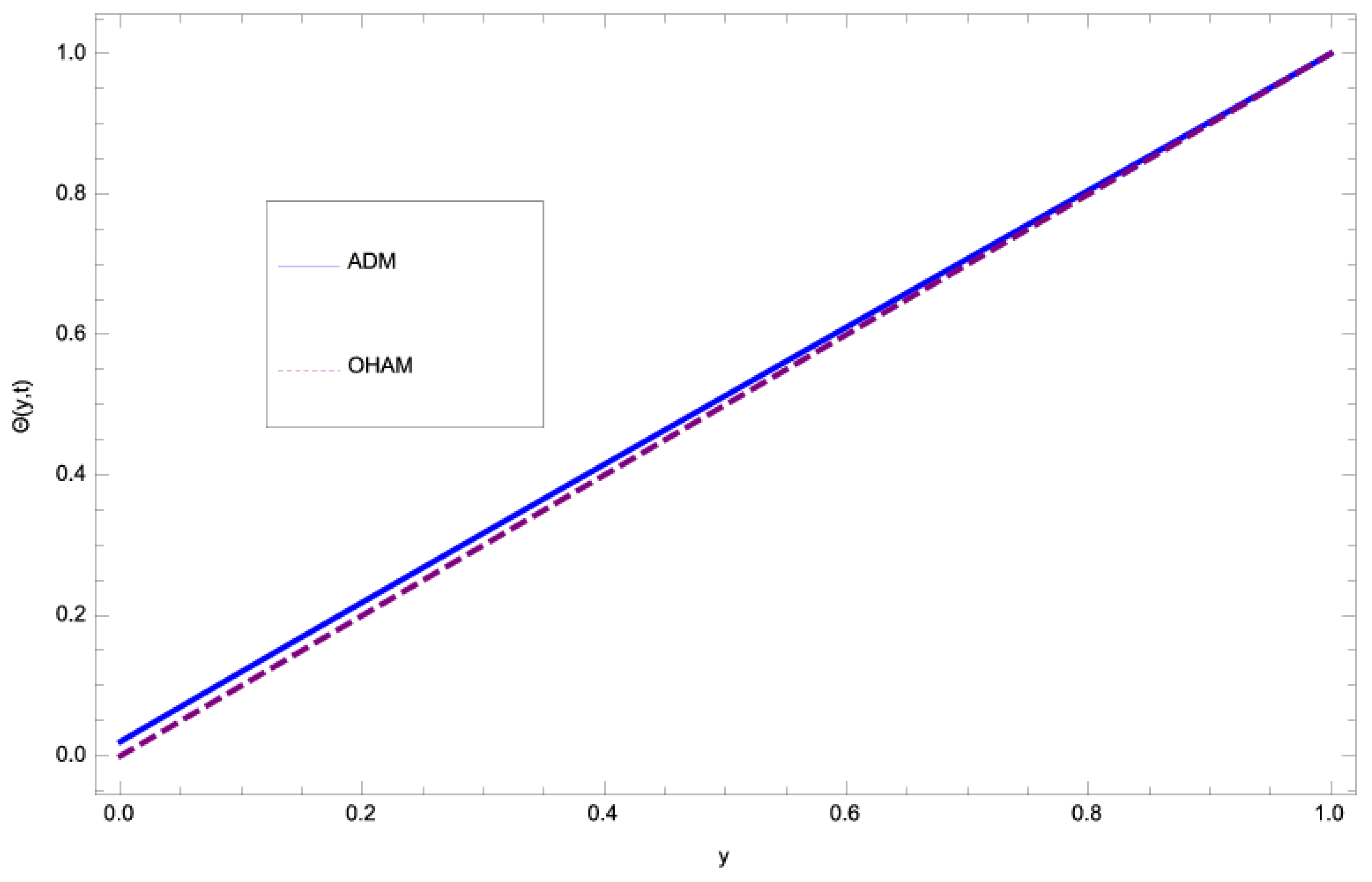
| Y | Published Work | Present Work | Absolute Error |
|---|---|---|---|
| 0 | 1.99281 | 1.99281 | 0. |
| 0.2 | 1.51428 | 1.22328 | 0.290999 |
| 0.4 | 1.07569 | 0.6983 | 0.377391 |
| 0.6 | 0.677106 | 0.355481 | 0.321626 |
| 0.8 | 0.318544 | 0.139077 | 0.179467 |
| 1 | 0. |
| Y | Published Work | Present Work | Absolute Error |
|---|---|---|---|
| 0 | 1.99281 | 1.99281 | 0. |
| 0.2 | 1.51428 | 1.53087 | 0.016596 |
| 0.4 | 1.07569 | 1.10485 | 0.0291587 |
| 0.6 | 0.677106 | 0.710142 | 0.033036 |
| 0.8 | 0.318544 | 0.342897 | 0.0243532 |
| 1 |
| Y | ADM | OHAM | Absolute Error |
|---|---|---|---|
| 0 | 1.91632177045 | 1.91632177045 | 0 |
| 0.2 | 0.24289103594 | 0.3191514078391 | 0.076260371897 |
| 0.4 | −0.96869527228 | −0.8959030788252 | 0.072792193456 |
| 0.6 | −1.73745720196 | −1.7459175340616 | 0.008460332096 |
| 0.8 | −2.08139220298 | −2.2461895367629 | 0.164797333778 |
| 1 | −2.01747533731 | −2.4102387658252 | 0.392763428507 |
| Y | ADM | OHAM | Absolute Error |
|---|---|---|---|
| 0 | 0.0199375363 | −0.0004475377 | 0.020385074 |
| 0.2 | 0.21851290935 | 1.53087 | 0.016596 |
| 0.4 | 0.415049659642 | 1.10485 | 0.0291587 |
| 0.6 | 0.610432176595 | 0.710142 | 0.033036 |
| 0.8 | 0.8052896112883 | 0.342897 | 0.0243532 |
| 1 | 1.000000000000 | 1 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gul, T.; Khan, A.S.; Islam, S.; Alqahtani, A.M.; Khan, I.; Alshomrani, A.S.; Alzahrani, A.K.; Muradullah. Heat Transfer Investigation of the Unsteady Thin Film Flow of Williamson Fluid Past an Inclined and Oscillating Moving Plate. Appl. Sci. 2017, 7, 369. https://doi.org/10.3390/app7040369
Gul T, Khan AS, Islam S, Alqahtani AM, Khan I, Alshomrani AS, Alzahrani AK, Muradullah. Heat Transfer Investigation of the Unsteady Thin Film Flow of Williamson Fluid Past an Inclined and Oscillating Moving Plate. Applied Sciences. 2017; 7(4):369. https://doi.org/10.3390/app7040369
Chicago/Turabian StyleGul, Taza, Abdul Samad Khan, Saeed Islam, Aisha M. Alqahtani, Ilyas Khan, Ali Saleh Alshomrani, Abdullah K. Alzahrani, and Muradullah. 2017. "Heat Transfer Investigation of the Unsteady Thin Film Flow of Williamson Fluid Past an Inclined and Oscillating Moving Plate" Applied Sciences 7, no. 4: 369. https://doi.org/10.3390/app7040369





