A Study of the Transient Response of Duct Junctions: Measurements and Gas-Dynamic Modeling with a Staggered Mesh Finite Volume Approach
Abstract
:1. Introduction
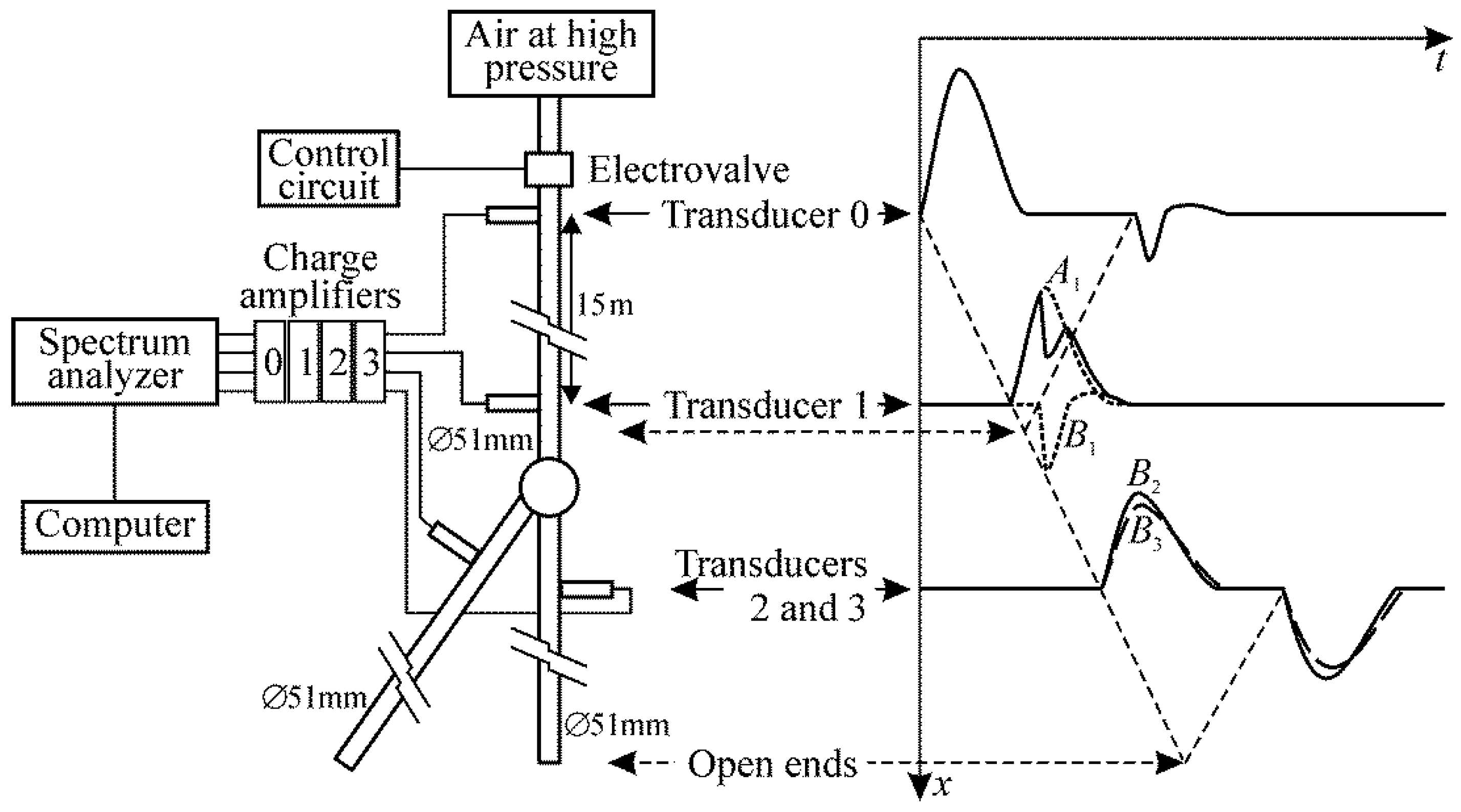
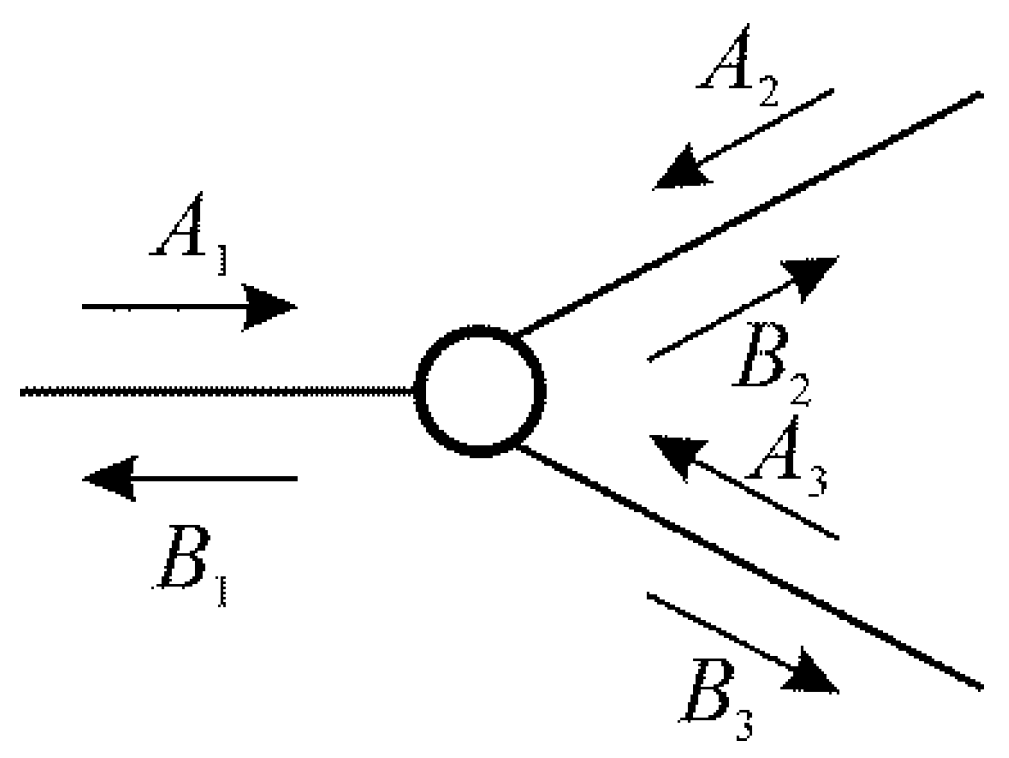
2. Materials and Methods
3. Results and Discussion
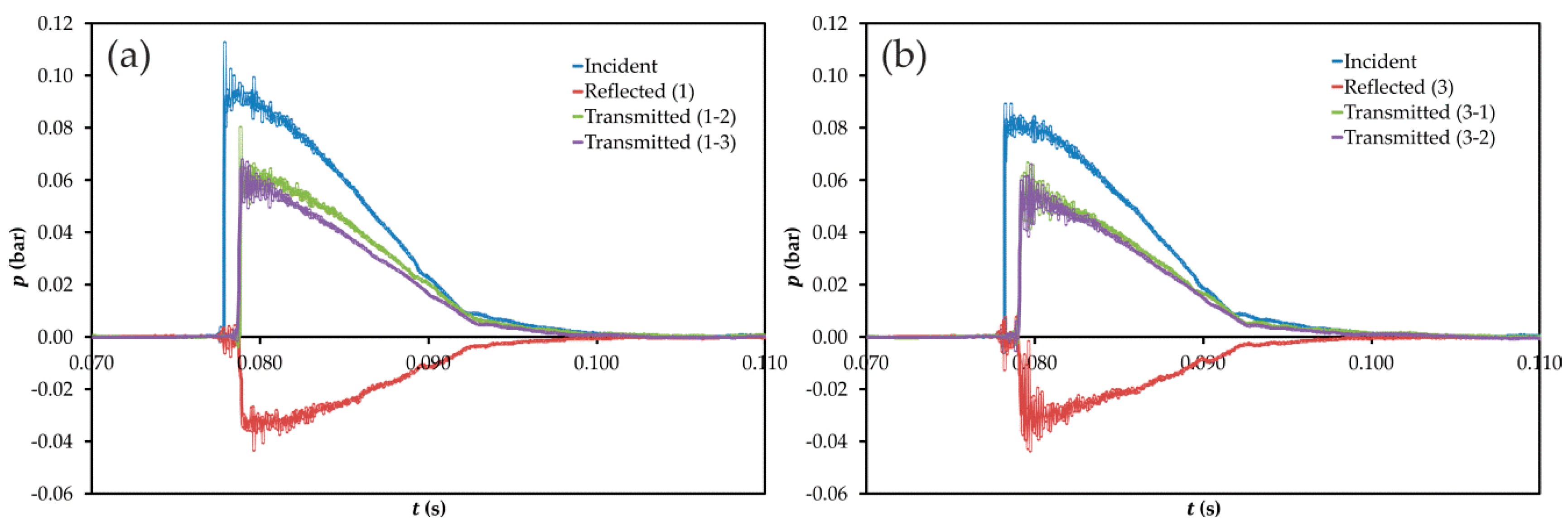
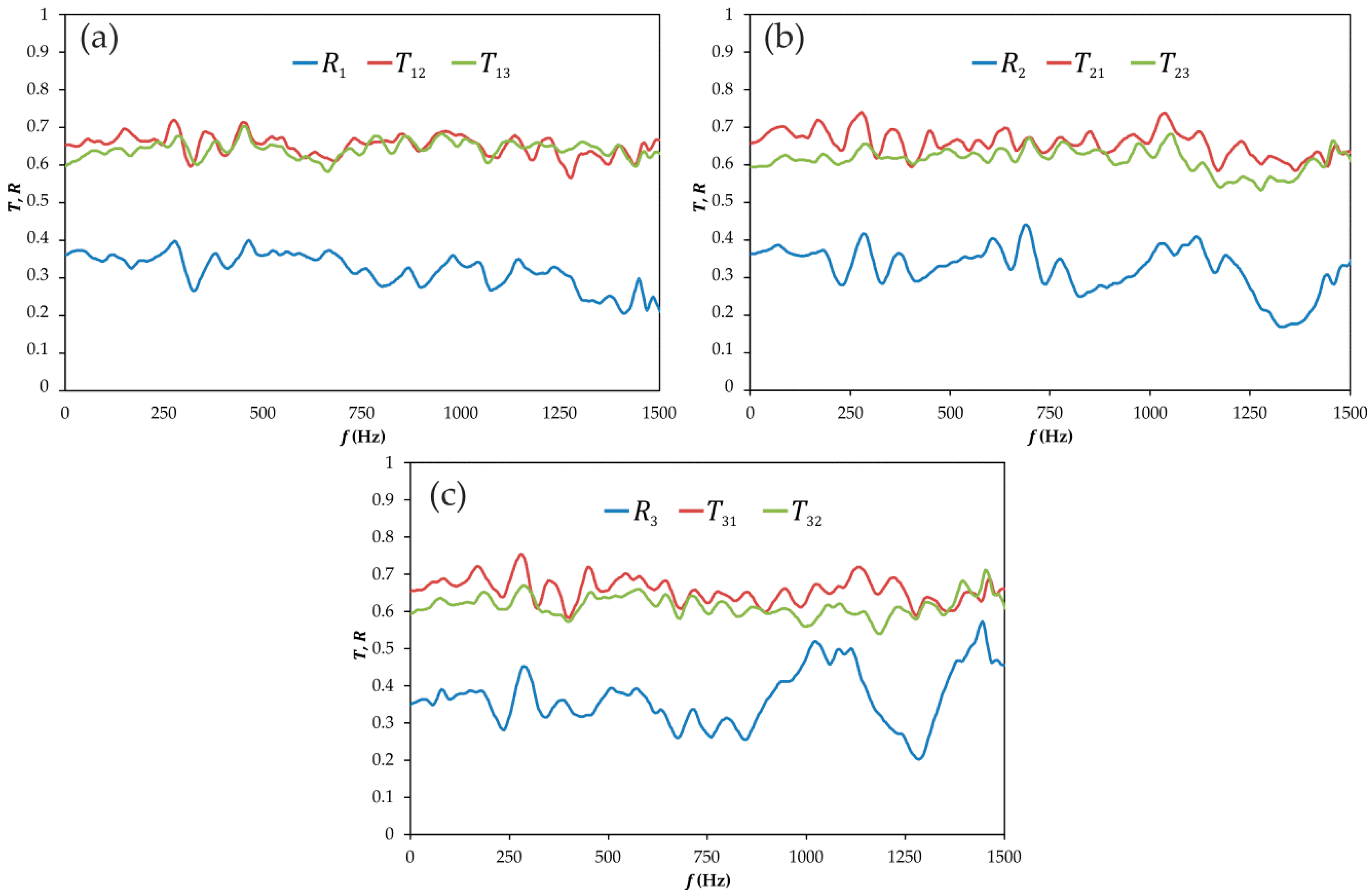
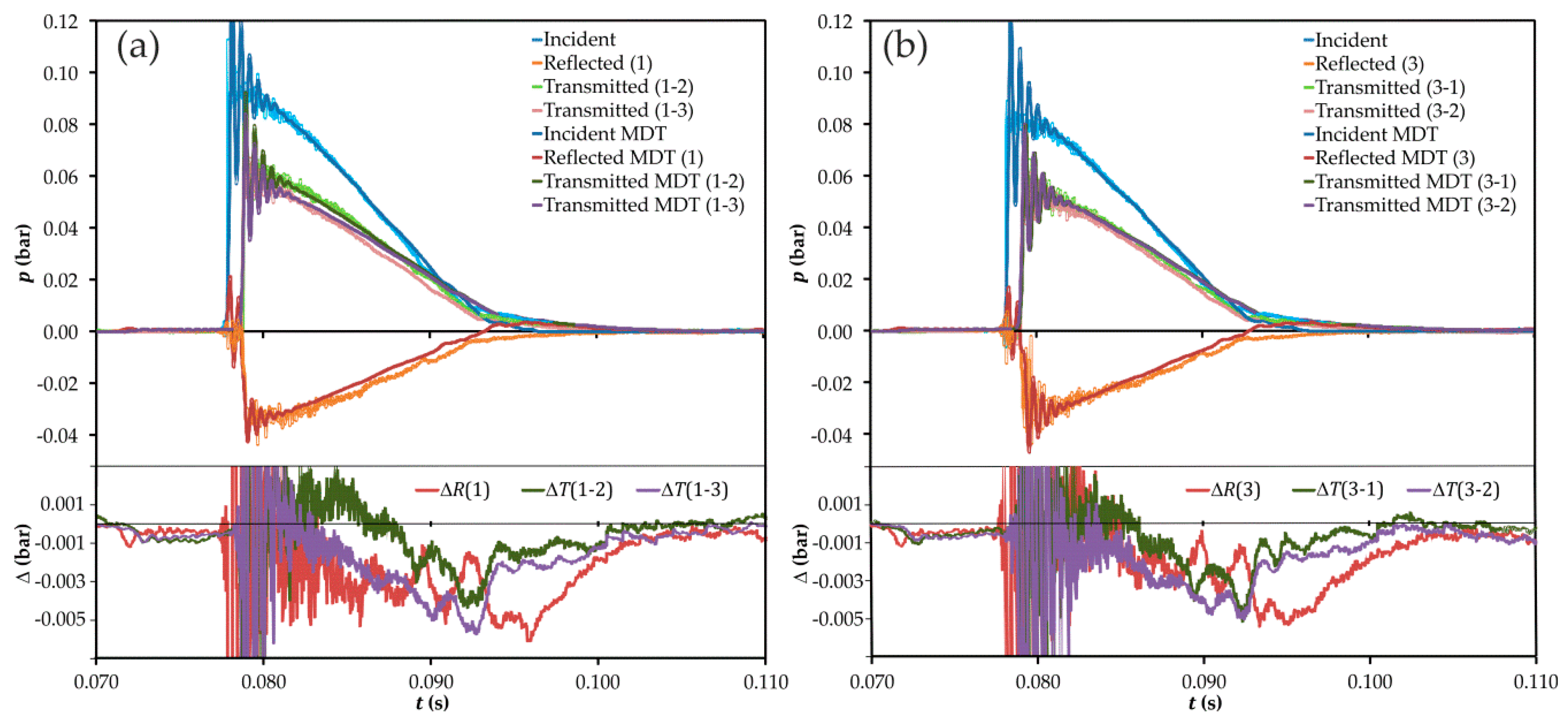
3.1. Experimental Results
3.1.1. Time Domain Analysis
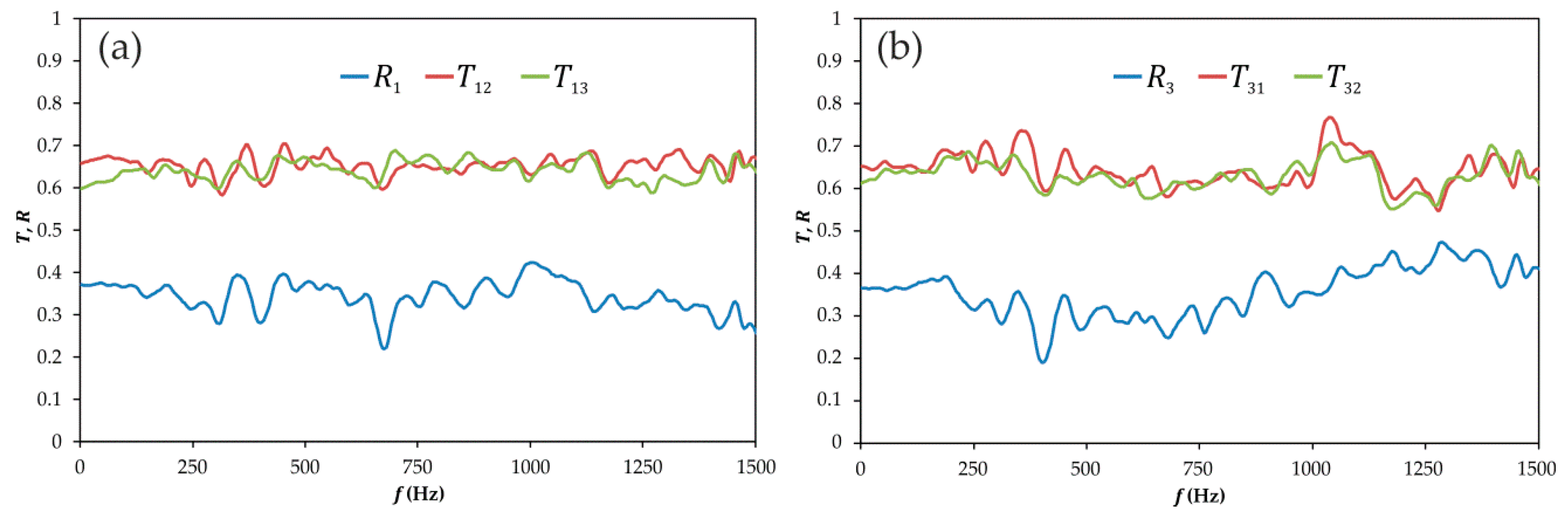
3.1.2. Frequency Domain Analysis
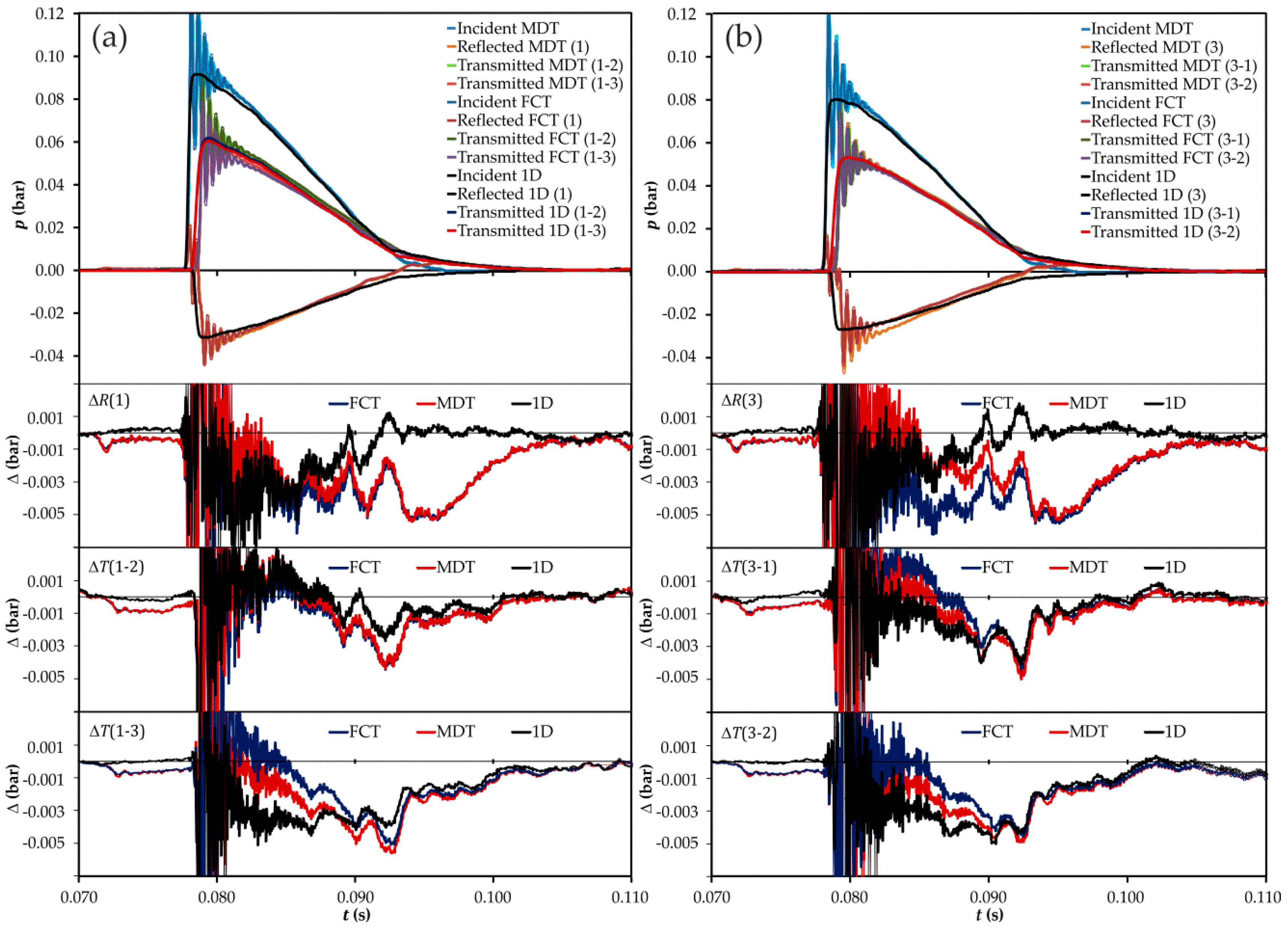
3.2. Assessment of Modelling Approaches Considering a 0D Description of the Junction
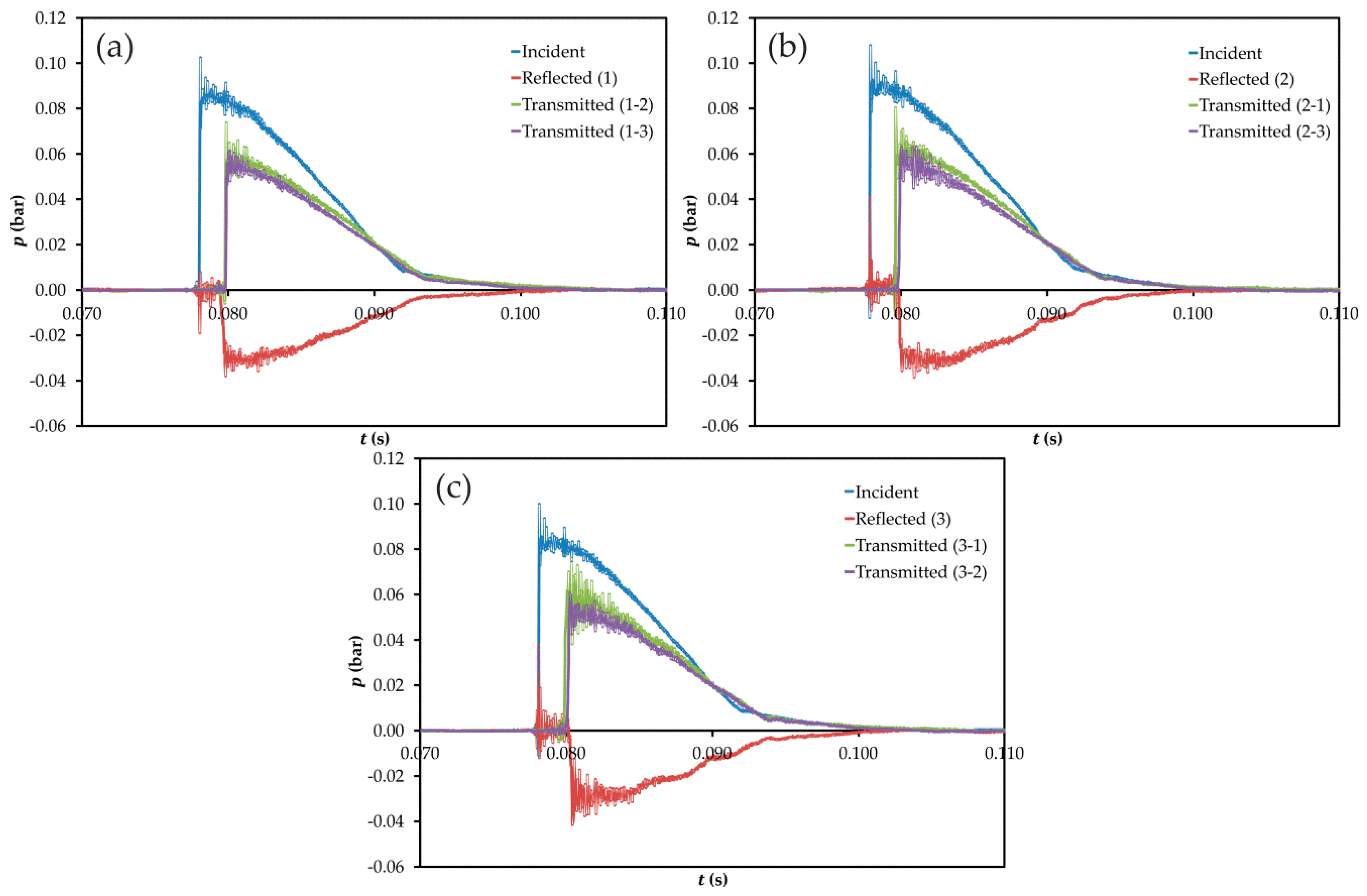
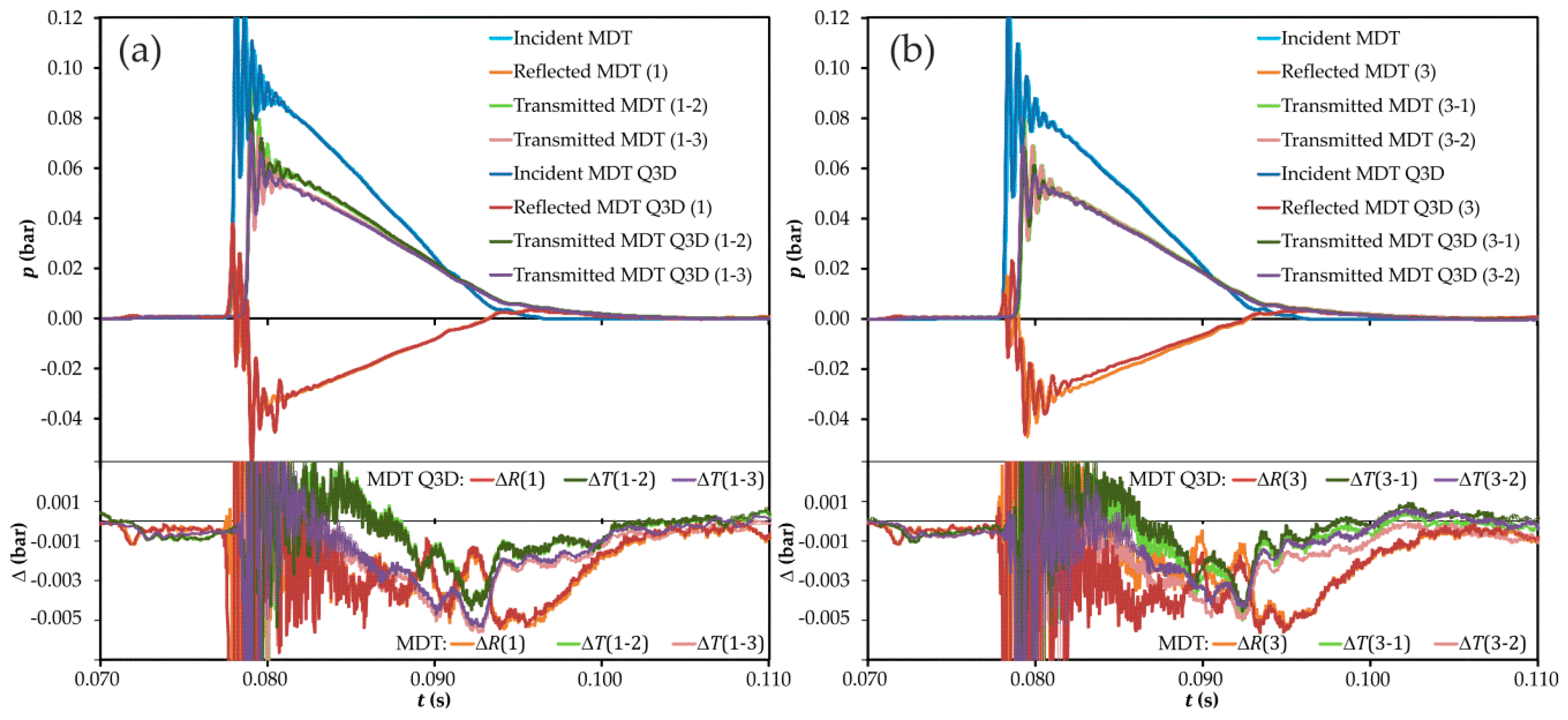
3.2.1. Time Domain Assessment
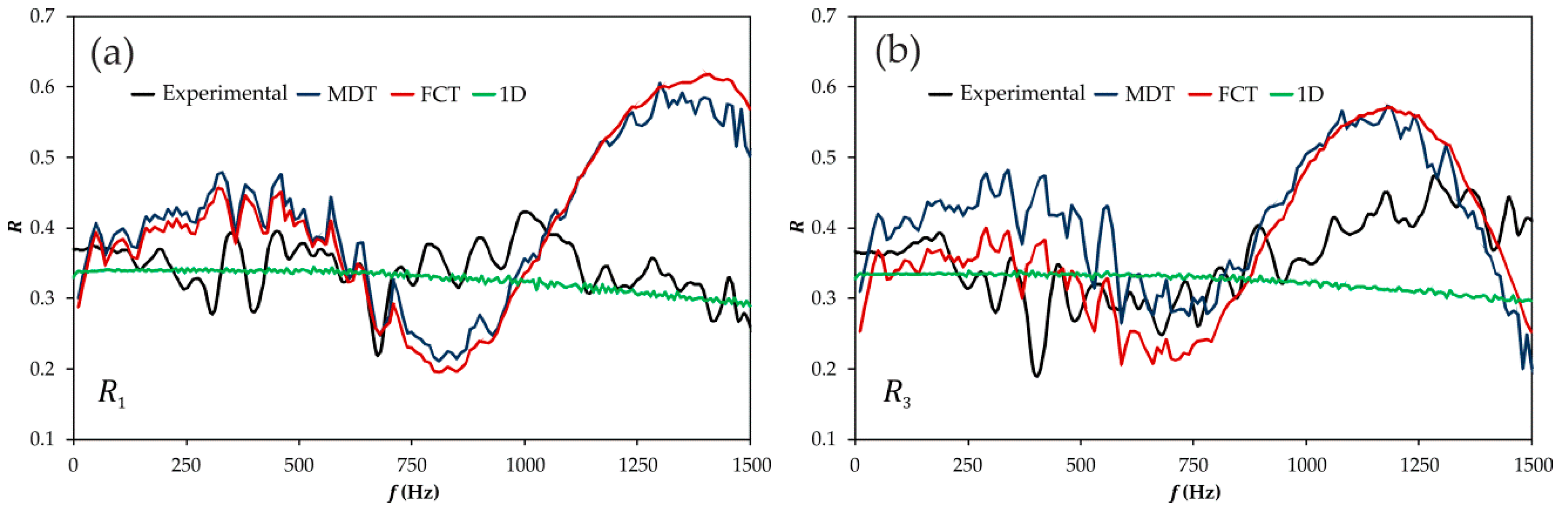
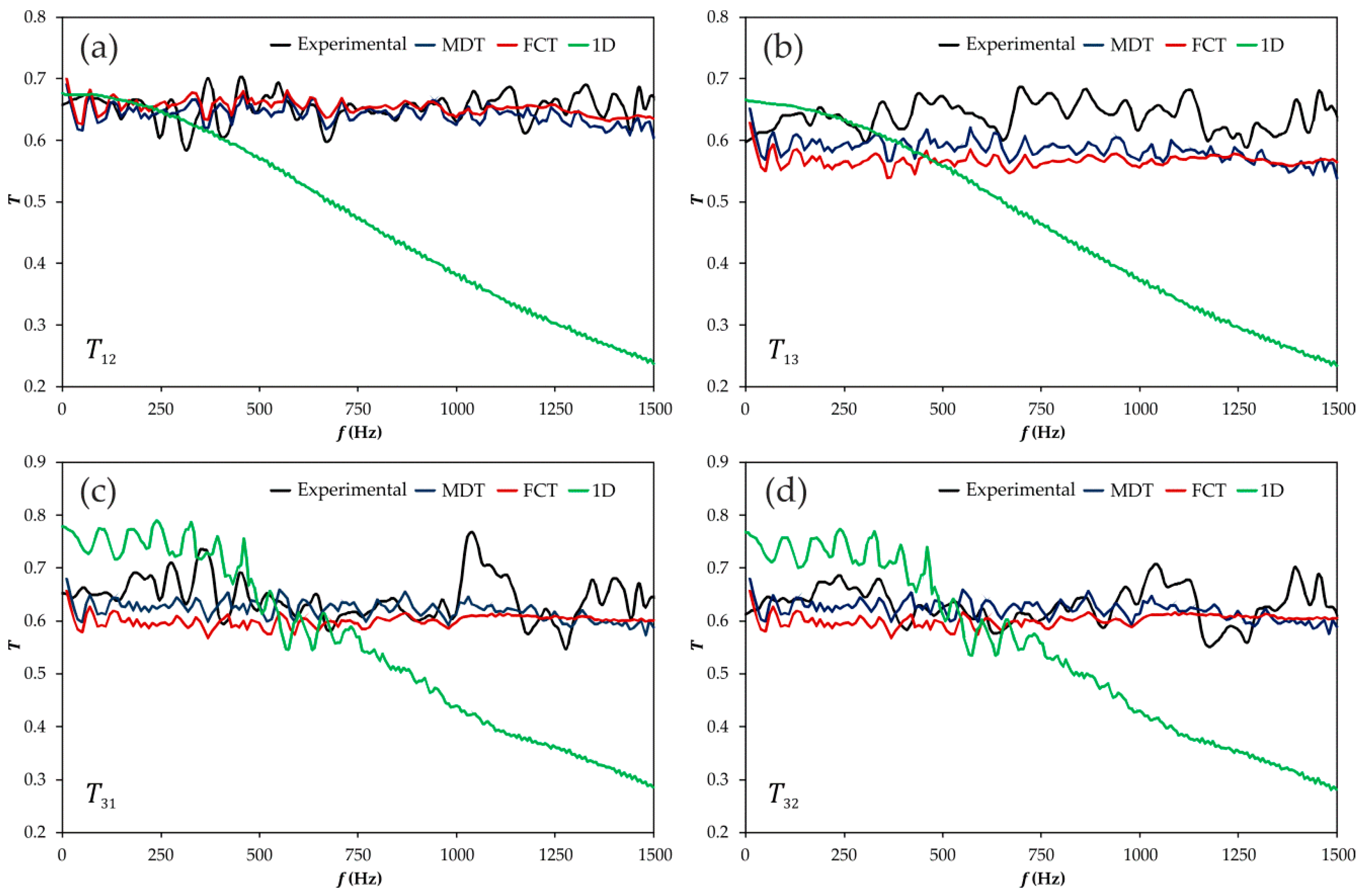
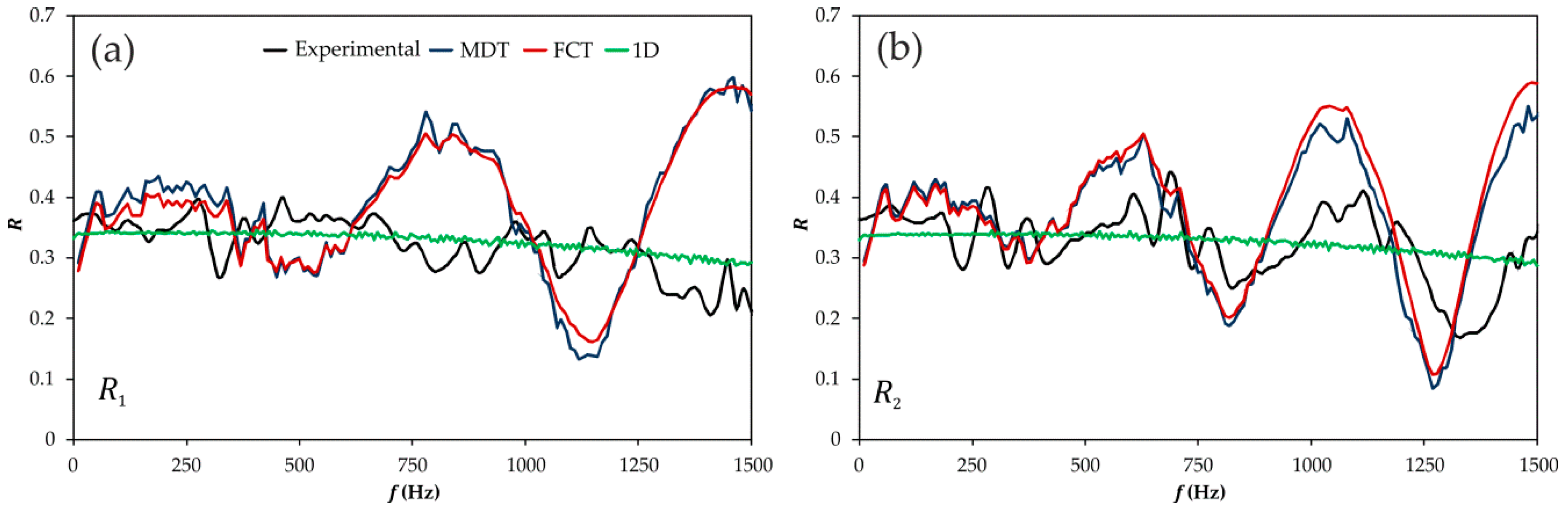
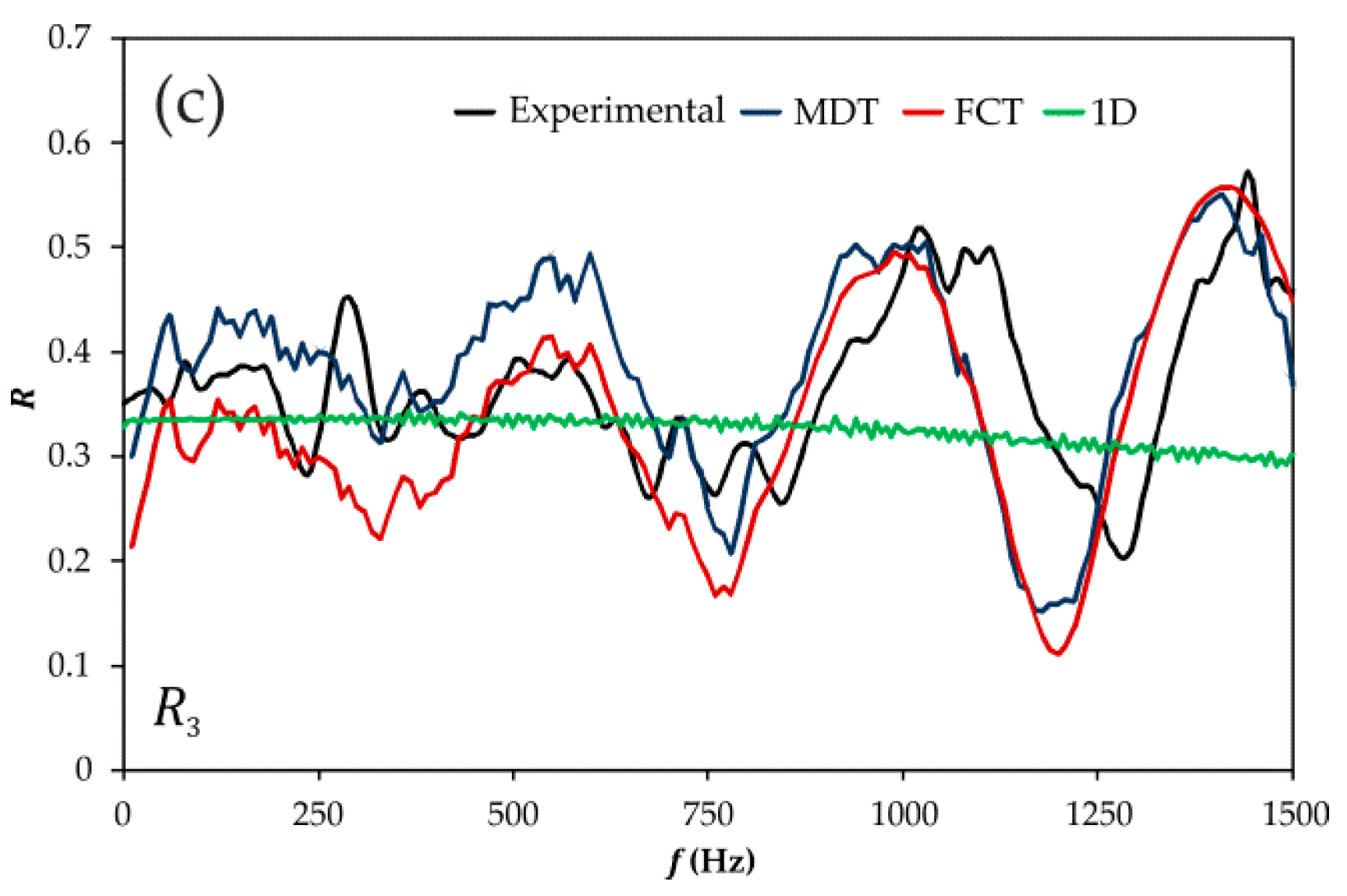
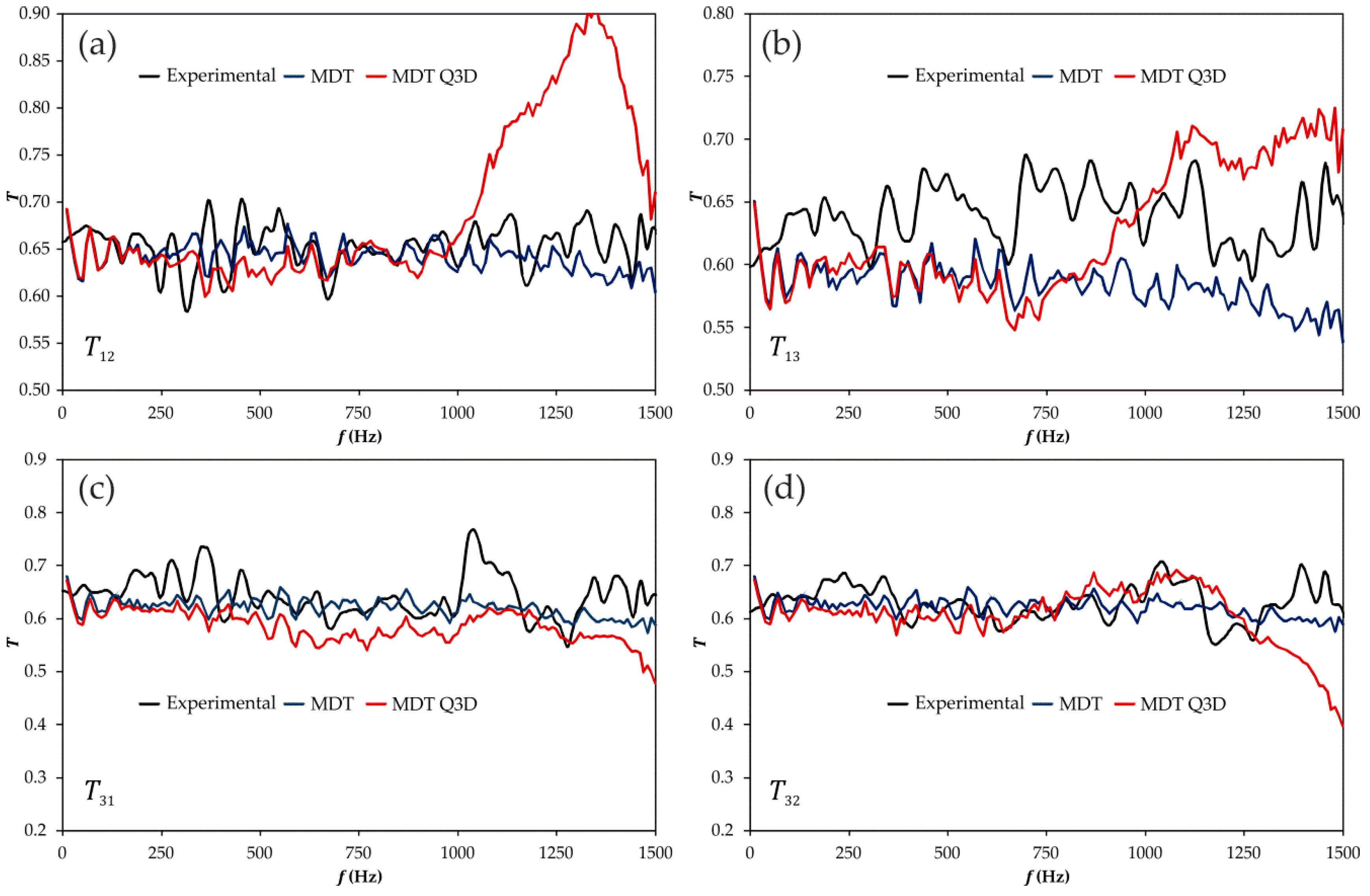
3.2.2. Frequency Domain Assessment
3.3. Assessment of a Modelling Approach with a Quasi-3D Description of the Junction
3.3.1. Time Domain Assessment
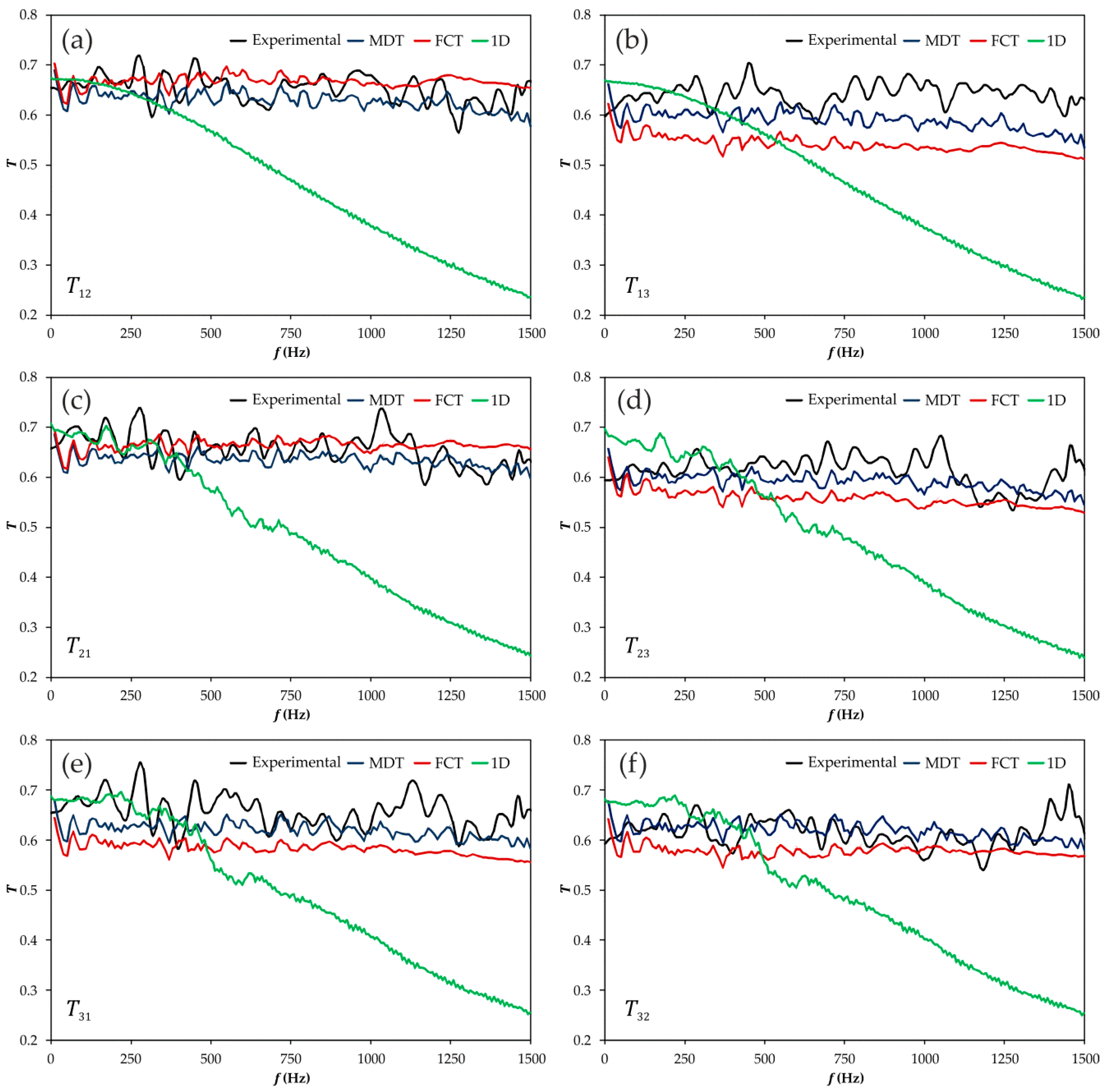
3.3.2. Frequency Domain Assessment
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Experimental Procedure
- Excitation in duct 1, with anechoic terminations in ducts 2 and 3, so that and , and thus,
- Excitation in duct 2, with anechoic terminations in ducts 1 and 3, so that and ; then,
- Excitation in duct 3, with anechoic terminations in ducts 1 and 2, so that and , so that,
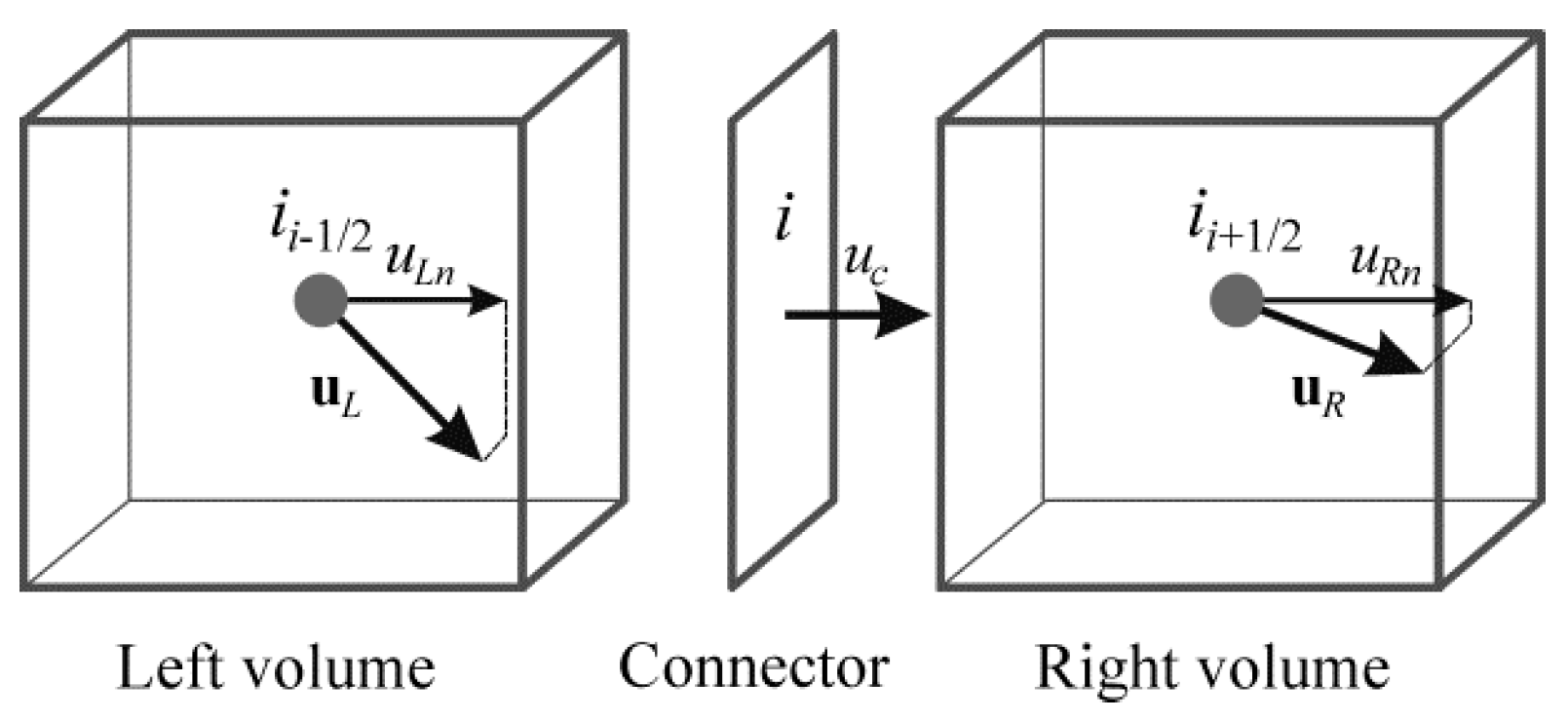
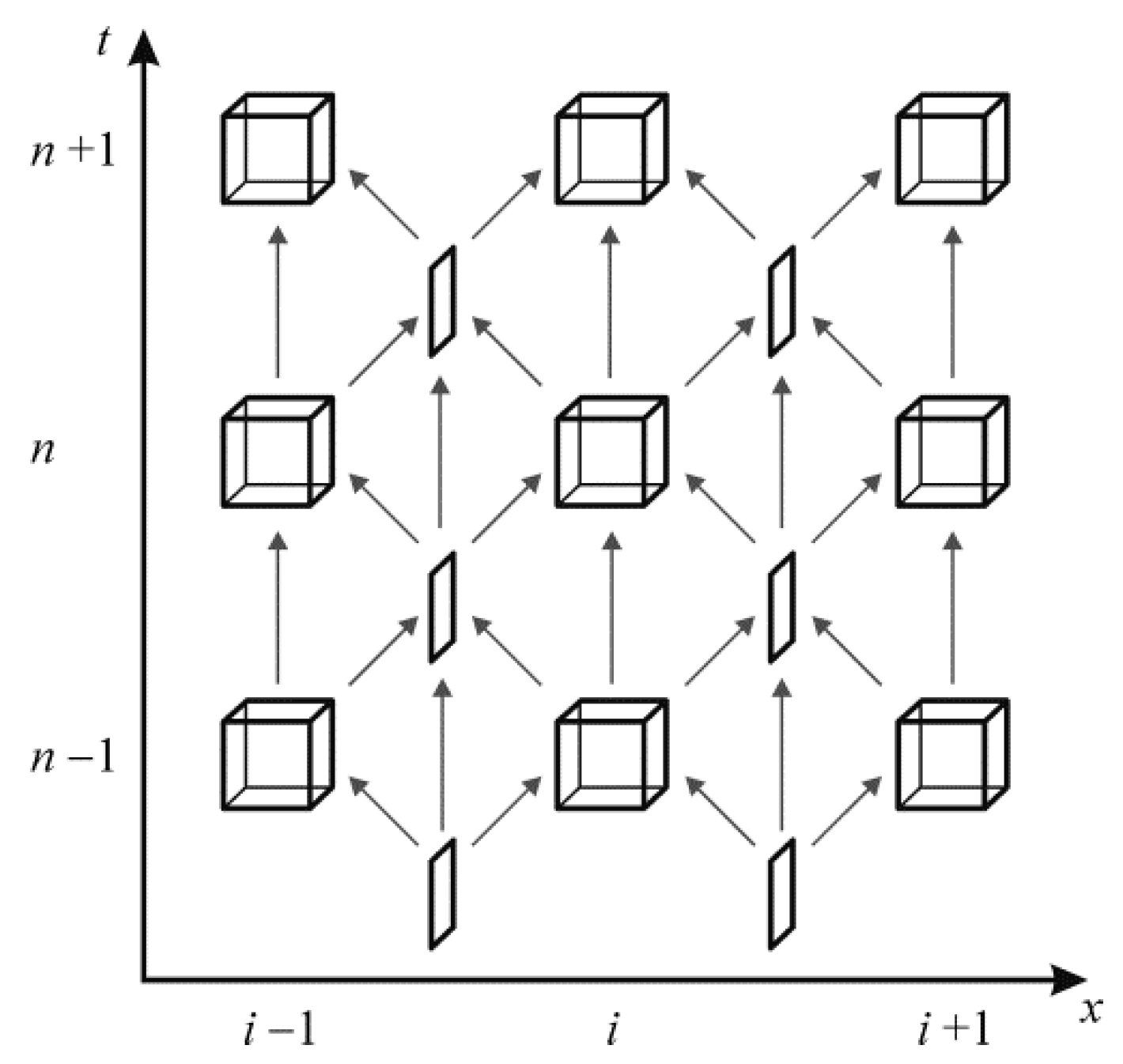
Appendix B. Staggered-Grid Finite-Volume Approach
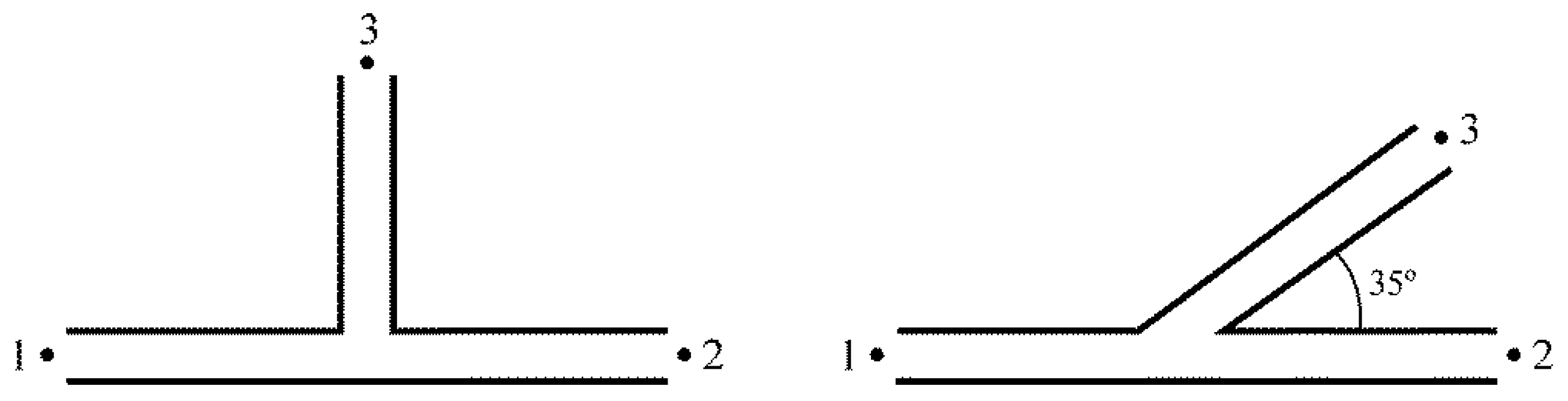
Appendix C. 1D Method with Pressure Loss-Based Junction Model
References
- Winterbone, D.E.; Pearson, R.J. Design Techniques for Engine Manifolds, 3rd ed.; Professional Engineering Pub. Ltd.: London, UK, 1999. [Google Scholar]
- Payri, F.; Reyes, E.; Galindo, J. Analysis and modelling of the fluid-dynamic effects in branched exhaust junctions of I.C.E. J. Eng. Gas Turbines Power 2001, 123, 197–203. [Google Scholar] [CrossRef]
- Tang, S.K. Sound transmission characteristics of Tee-junctions and the associated length corrections. J. Acoust. Soc. Am. 2004, 115, 218–227. [Google Scholar] [CrossRef] [PubMed]
- Harrison, M.F.; De Soto, I.; Rubio-Unzueta, P.L. A linear acoustic model for multi-cylinder IC engine intake manifolds including the effects of the intake throttle. J. Sound Vib. 2004, 278, 975–1011. [Google Scholar] [CrossRef]
- Karlsson, M.; Abom, M. Quasi-steady model of the acoustic scattering properties of a T-junction. J. Sound Vib. 2011, 330, 5131–5137. [Google Scholar] [CrossRef]
- Karlsson, M.; Abom, M. Aeroacoustics of T-junctions—An experimental investigation. J. Sound Vib. 2010, 329, 1793–1808. [Google Scholar] [CrossRef]
- Desantes, J.M.; Torregrosa, A.J.; Broatch, A. Experiments on flow noise generation in simple exhaust geometries. Acta Acust. United Acust. 2001, 87, 46–55. [Google Scholar]
- Benson, R.S. The Thermodynamics and Gas Dynamics of Internal-Combustion Engines; Clarendon Press: Oxford, UK, 1982; Volume 1. [Google Scholar]
- Corberán, J.M. A new constant pressure model for N-branch junctions. Proc. Inst. Mech. Eng. D 1992, 206, 117–123. [Google Scholar] [CrossRef]
- Schmandt, B.; Herwig, H. The head change coefficient for branched flows: Why ‘‘losses’’ due to junctions can be negative. Int. J. Heat Fluid Flow 2015, 54, 268–275. [Google Scholar] [CrossRef]
- Shaw, C.T.; Lee, D.J.; Richardson, S.H.; Pierson, S. Modelling the effect of plenum-runner interface geometry on the flow through an inlet system. SAE Tech. Pap. Ser. 2000. [Google Scholar] [CrossRef]
- Pérez-García, J.; Sanmiguel-Rojas, E.; Hernández-Grau, J.; Viedma, A. Numerical and experimental investigations on internal compressible flow at T-type junctions. Exp. Therm. Fluid Sci. 2006, 31, 61–74. [Google Scholar] [CrossRef]
- Naeimi, H.; Domiry Ganji, D.; Gorji, M.; Javadirad, G.; Keshavarz, M. A parametric design of compact exhaust manifold junction in heavy duty diesel engine using computational fluid dynamics codes. Therm. Sci. 2011, 15, 1023–1033. [Google Scholar] [CrossRef]
- Sakowitz, A.; Mihaescu, M.; Fuchs, L. Turbulent flow mechanisms in mixing T-junctions by Large Eddy Simulations. Int. J. Heat Fluid Flow 2014, 45, 135–146. [Google Scholar] [CrossRef]
- Bassett, M.D.; Winterbone, D.E.; Pearson, R.J. Calculation of steady flow pressure loss coefficients for pipe junctions. Proc. Inst. Mech. Eng. C 2001, 215, 861–881. [Google Scholar] [CrossRef]
- Hager, W.H. An approximate treatment of flow in branches and bends. Proc. Inst. Mech. Eng. C 1984, 198, 63–69. [Google Scholar] [CrossRef]
- Paul, J.; Selamet, A.; Miazgowicz, K.D.; Tallio, K.V. Combining flow losses at circular T-junctions representative of intake plenum and primary runner interface. SAE Tech. Pap. Ser. 2007. [Google Scholar] [CrossRef]
- Pérez-García, J.; Sanmiguel-Rojas, E.; Viedma, A. New coefficient to characterize energy losses in compressible flow at T-junctions. Appl. Math Model. 2010, 34, 4289–4305. [Google Scholar] [CrossRef]
- Wang, W.; Lu, Z.; Deng, K.; Qu, S. An experimental study of compressible combining flow at 45° T-junctions. Proc. Inst. Mech. Eng. C 2015, 229, 1600–1610. [Google Scholar] [CrossRef]
- Peters, B.; Gosman, A.D. Numerical simulation of unsteady flow in engine intake manifolds. SAE Tech. Pap. Ser. 1993. [Google Scholar] [CrossRef]
- Bingham, J.F.; Blair, G.P. An improved branched pipe model for multi-cylinder automotive engine calculations. Proc. Inst. Mech. Eng. Part D 1985, 199, 65–77. [Google Scholar] [CrossRef]
- William-Louis, M.J.P.; Ould-El-Hadrami, A.; Tournier, C. On the calculation of the unsteady compressible flow through an N-branch junction. Proc. Inst. Mech. Eng. C 1998, 212, 49–56. [Google Scholar] [CrossRef]
- Bassett, M.D.; Pearson, R.J.; Fleming, N.P.; Winterbone, D.E. A multi-pipe junction model for one-dimensional gas-dynamic simulations. SAE Tech. Pap. Ser. 2003. [Google Scholar] [CrossRef]
- Pearson, R.J.; Bassett, M.D.; Batten, P.; Winterbone, D.E.; Weaver, N.W.E. Multi-dimensional wave propagation in pipe junctions. SAE Tech. Pap. Ser. 1999. [Google Scholar] [CrossRef]
- Bassett, M.D.; Winterbone, D.E.; Pearson, R.J. Modelling engines with pulse converted exhaust manifolds using one-dimensional techniques. SAE Tech. Pap. Ser. 2000. [Google Scholar] [CrossRef]
- Montenegro, G.; Onorati, A.; Piscaglia, F.; D’Errico, G. Integrated 1D-multiD fluid dynamic models for the simulation of I.C.E. intake and exhaust systems. SAE Tech. Pap. Ser. 2007. [Google Scholar] [CrossRef]
- Onorati, A.; Montenegro, G.; D’Errico, G.; Piscaglia, F. Integrated 1D-3D fluid dynamic simulation of a turbocharged Diesel engine with complete intake and exhaust systems. SAE Tech. Pap. Ser. 2010. [Google Scholar] [CrossRef]
- Montenegro, G.; Onorati, A.; Della Torre, A. The prediction of silencer acoustical performances by 1D, 1D-3D and quasi-3D non-linear approaches. Comput. Fluids 2013, 71, 208–223. [Google Scholar] [CrossRef]
- Morel, T.; Silvestri, J.; Goerg, K.; Jebasinski, R. Modeling of engine exhaust acoustics. SAE Tech. Pap. Ser. 1999. [Google Scholar] [CrossRef]
- Sapsford, S.M.; Richards, V.C.M.; Amlee, D.R.; Morel, T.; Chappell, M.T. Exhaust system evaluation and design by non-linear modeling. SAE Tech. Pap. Ser. 1992. [Google Scholar] [CrossRef]
- Montenegro, G.; Della Torre, A.; Onorati, A.; Fairbrother, R.; Dolinar, A. Development and application of 3D generic cells to the acoustic modelling of exhaust systems. SAE Tech. Pap. Ser. 2011. [Google Scholar] [CrossRef]
- Payri, F.; Desantes, J.M.; Broatch, A. Modified impulse method for the measurement of the frequency response of acoustic filters to weakly nonlinear transient excitations. J. Acoust. Soc. Am. 2000, 107, 731–738. [Google Scholar] [CrossRef] [PubMed]
- Torregrosa, A.J.; Broatch, A.; Fernández, T.; Denia, F.D. Description and measurement of the acoustic characteristics of two-tailpipe mufflers. J. Acoust. Soc. Am. 2006, 119, 723–728. [Google Scholar] [CrossRef]
- Torregrosa, A.J.; Broatch, A.; Arnau, F.J.; Hernández, M. A non-linear quasi-3D model with Flux- Corrected-Transport for engine gas-exchange modelling. J. Comput. Appl. Math. 2016, 291, 103–111. [Google Scholar] [CrossRef]
- Montenegro, G.; Della Torre, A.; Onorati, A.; Fairbrother, R. Nonlinear quasi-3D approach for the modeling of mufflers with perforated elements and sound-absorbing material. Adv. Acoust. Vib. 2013, 2013, 546120. [Google Scholar] [CrossRef]
- OpenWAM. CMT—Motores Térmicos, Universitat Politècnica de València. Available online: http://www.openwam.org/ (accessed on 20 March 2017).
- Ikeda, T.; Nakagawa, T. On the SHASTA FCT algorithm for the equation ∂ρ/∂t+(∂/∂x)(v(ρ)ρ)=0. Math. Comput. 1979, 33, 1157–1169. [Google Scholar] [CrossRef]
- Toro, E.F.; Spruce, M.; Speares, W. Restoration of the contact surface in the HLL-Riemann solver. Shock Waves 1994, 4, 25–34. [Google Scholar] [CrossRef]
- Van Leer, B. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]

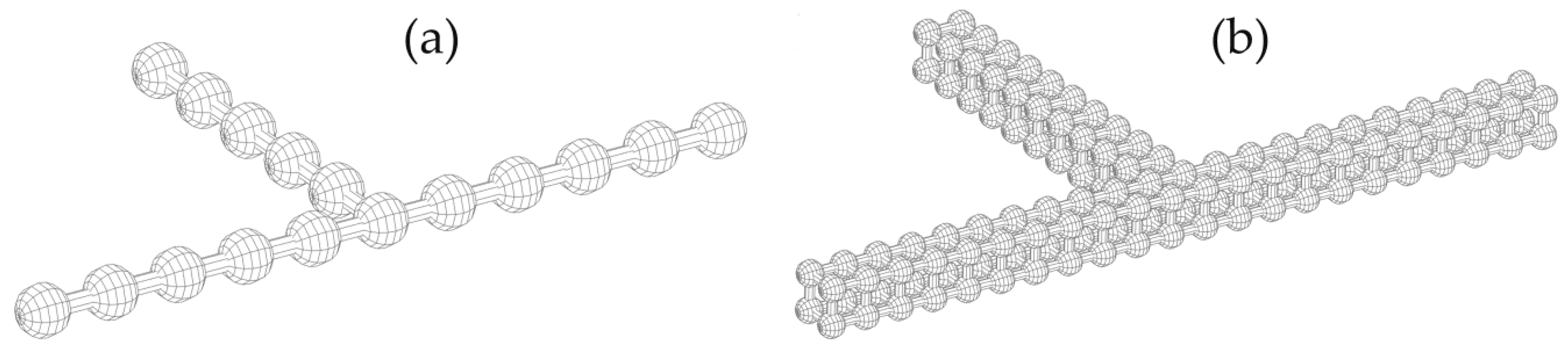


| Path | MDT | FCT | 1D |
|---|---|---|---|
| R(1) | 1.514 × 10−4 | 1.842 × 10−4 | 1.448 × 10−4 |
| R(3) | 1.102 × 10−4 | 2.046 × 10−4 | 1.019 × 10−4 |
| T(1–2) | 1.005 × 10−4 | 9.932 × 10−5 | 6.926 × 10−5 |
| T(1–3) | 1.609 × 10−4 | 1.298 × 10−4 | 1.774 × 10−4 |
| T(3–1) | 1.121 × 10−4 | 1.094 × 10−4 | 1.114 × 10−4 |
| T(3–2) | 1.554 × 10−4 | 1.245 × 10−4 | 1.833 × 10−4 |
| Path | MDT | FCT | 1D |
|---|---|---|---|
| R(1) | 1.575 × 10−4 | 1.915 × 10−4 | 1.273 × 10−4 |
| R(2) | 1.992 × 10−4 | 2.172 × 10−4 | 1.681 × 10−4 |
| R(3) | 1.648 × 10−4 | 2.945 × 10−4 | 1.394 × 10−4 |
| T(1–2) | 1.171 × 10−4 | 1.369 × 10−4 | 9.186 × 10−5 |
| T(1–3) | 1.514 × 10−4 | 1.322 × 10−4 | 1.742 × 10−4 |
| T(2–1) | 1.992 × 10−4 | 2.172 × 10−4 | 1.681 × 10−4 |
| T(2–3) | 1.336 × 10−4 | 1.296 × 10−4 | 1.141 × 10−4 |
| T(3–1) | 1.669 × 10−4 | 1.949 × 10−4 | 1.355 × 10−4 |
| T(3–2) | 2.117 × 10−4 | 1.516 × 10−4 | 1.751 × 10−4 |
| Path | MDT | MDT Q3D |
|---|---|---|
| R(1) | 1.514 × 10−4 | 1.513 × 10−4 |
| R(3) | 1.102 × 10−4 | 1.809 × 10−4 |
| T(1–2) | 1.005 × 10−4 | 1.018 × 10−4 |
| T(1–3) | 1.609 × 10−4 | 1.469 × 10−4 |
| T(3–1) | 1.121 × 10−4 | 1.044 × 10−4 |
| T(3–2) | 1.554 × 10−4 | 1.249 × 10−4 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torregrosa, A.J.; Broatch, A.; García-Cuevas, L.M.; Hernández, M. A Study of the Transient Response of Duct Junctions: Measurements and Gas-Dynamic Modeling with a Staggered Mesh Finite Volume Approach. Appl. Sci. 2017, 7, 480. https://doi.org/10.3390/app7050480
Torregrosa AJ, Broatch A, García-Cuevas LM, Hernández M. A Study of the Transient Response of Duct Junctions: Measurements and Gas-Dynamic Modeling with a Staggered Mesh Finite Volume Approach. Applied Sciences. 2017; 7(5):480. https://doi.org/10.3390/app7050480
Chicago/Turabian StyleTorregrosa, Antonio J., Alberto Broatch, Luis M. García-Cuevas, and Manuel Hernández. 2017. "A Study of the Transient Response of Duct Junctions: Measurements and Gas-Dynamic Modeling with a Staggered Mesh Finite Volume Approach" Applied Sciences 7, no. 5: 480. https://doi.org/10.3390/app7050480







