Rogue Wave Modes for the Coupled Nonlinear Schrödinger System with Three Components: A Computational Study
Abstract
:1. Introduction
2. Formulation of the Rogue Wave Modes
3. The Effect of Coupling
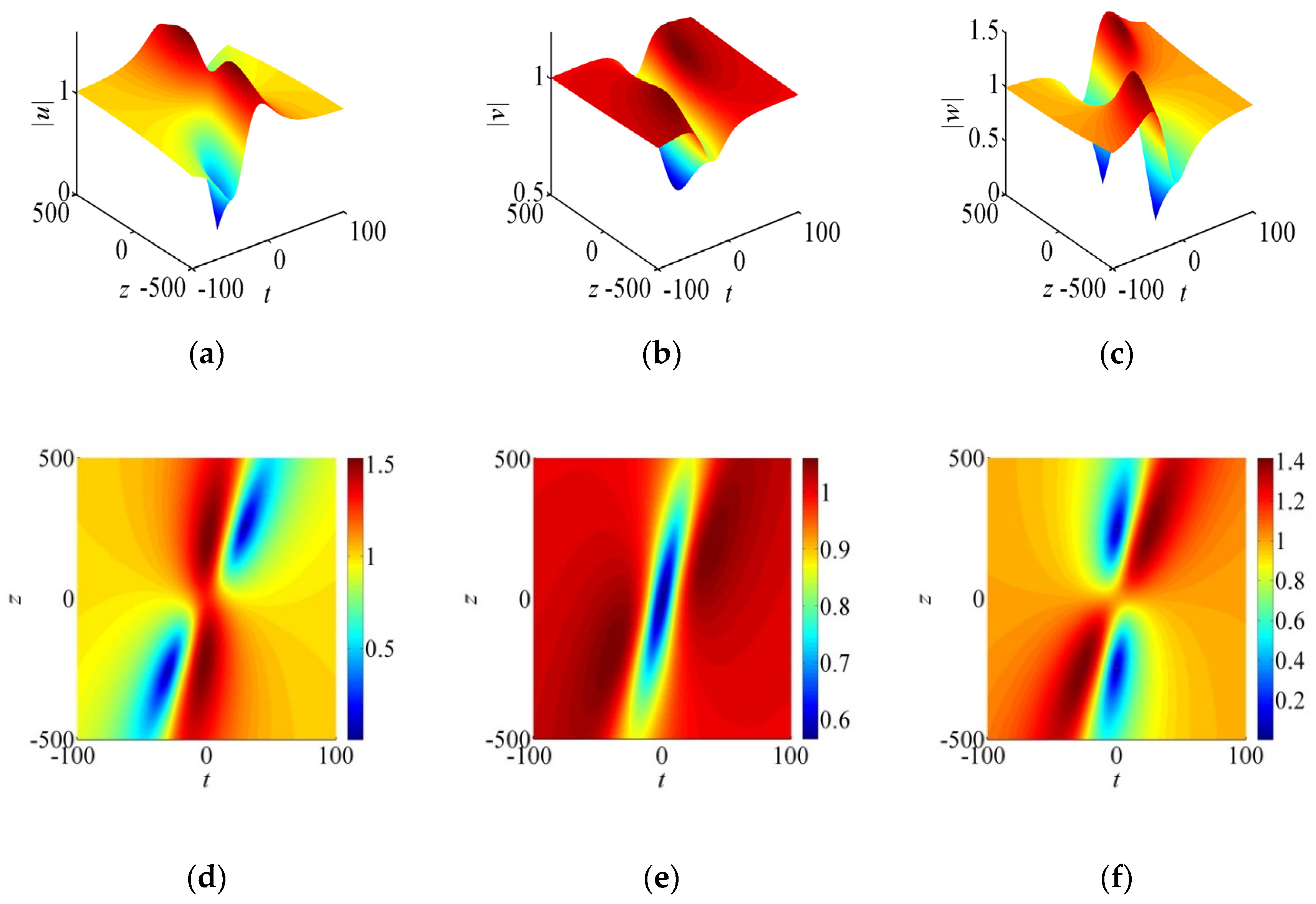
3.1. Extension of Existence Regime
3.2. Enhancement of Amplitude
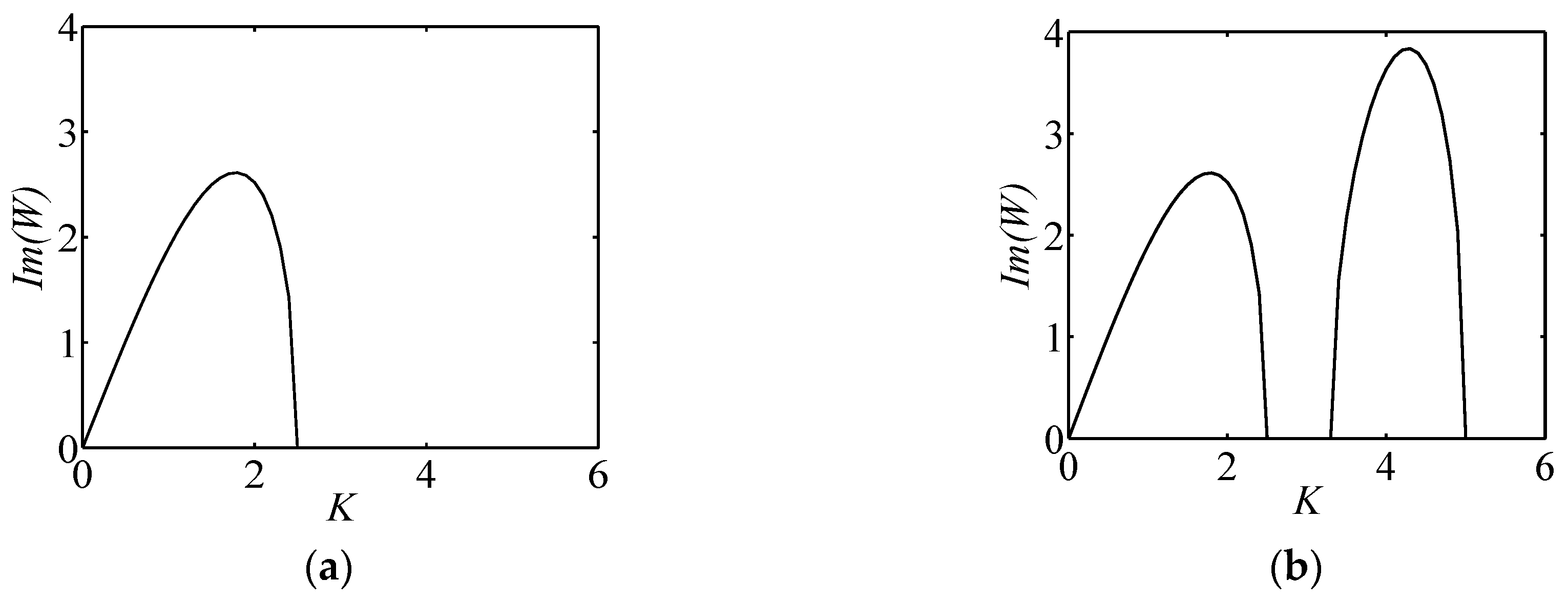
4. Baseband Modulation Instability
4.1. Analytical Approach
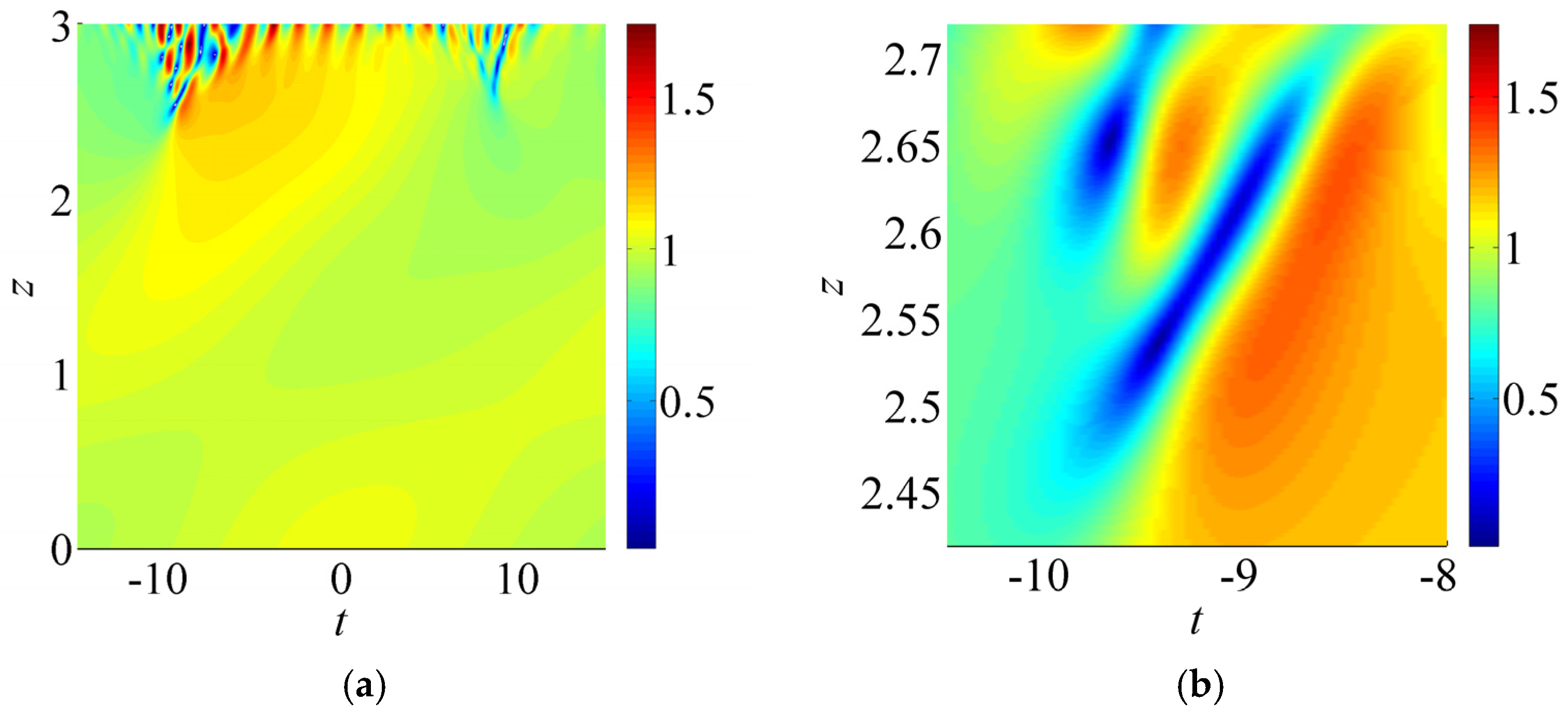
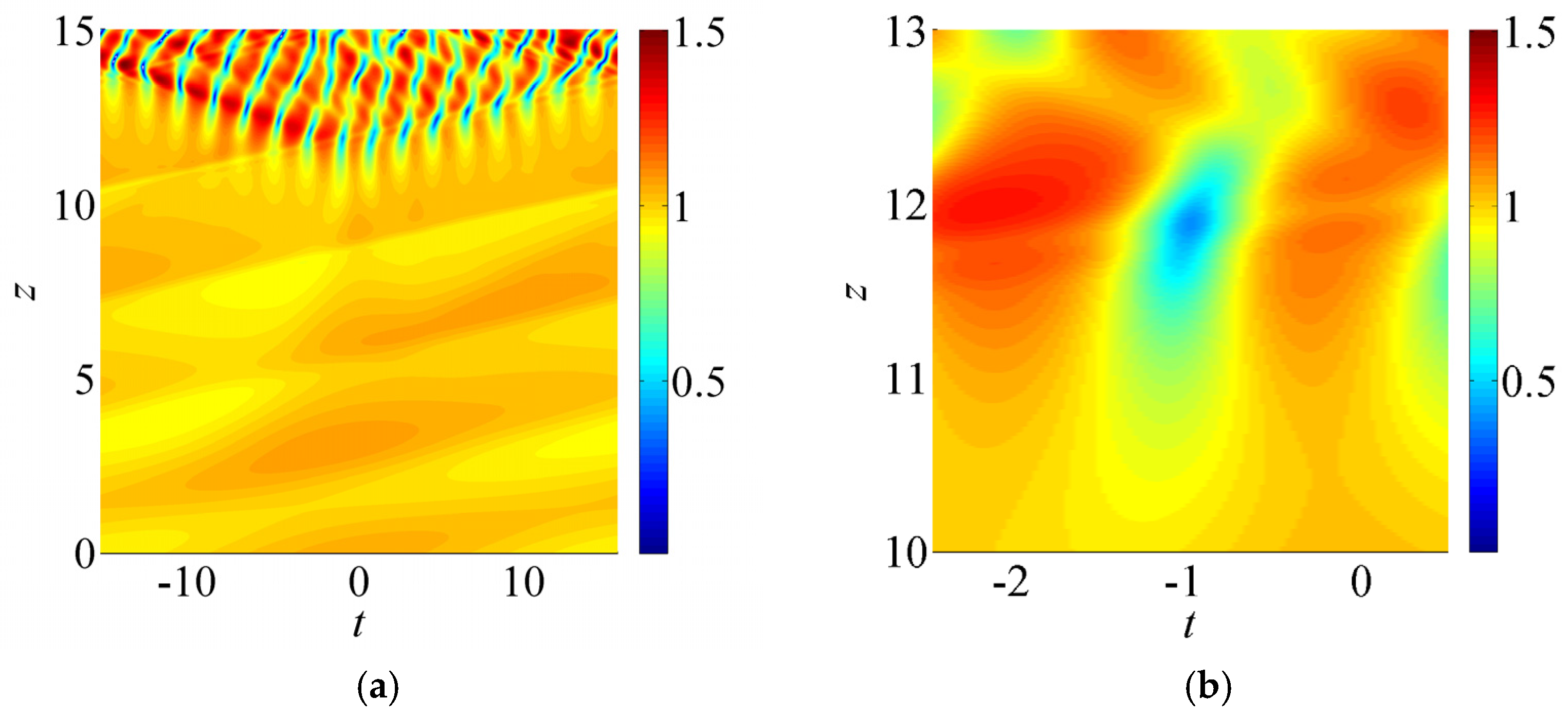
4.2. Computational Approach
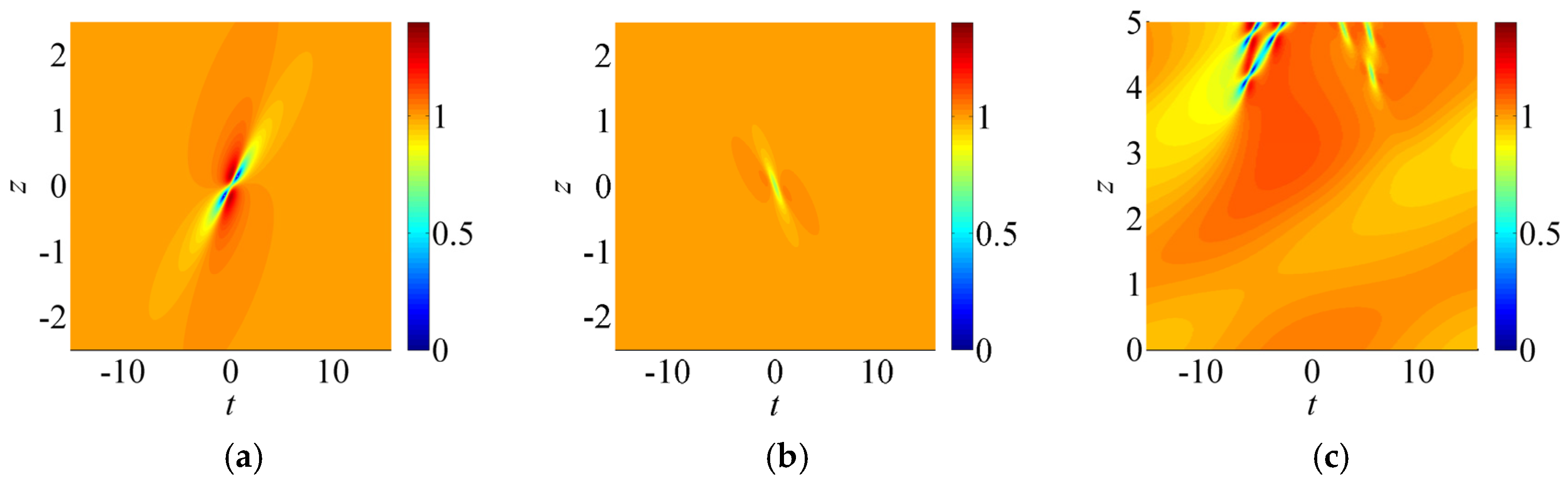
5. Asymmetric Breathers
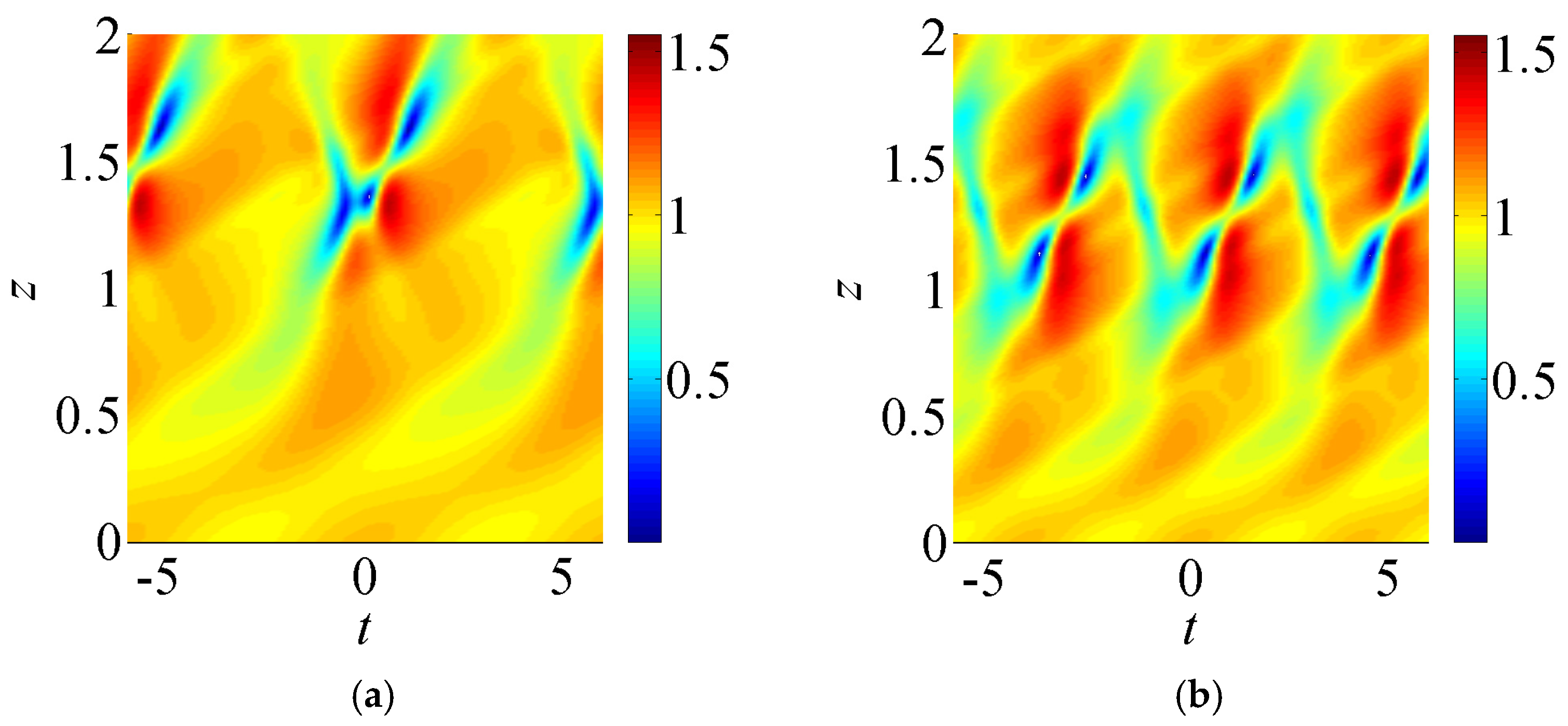
6. Rogue Wave in Non-integrable Systems
7. Discussions and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Kharif, C.; Pelinovsky, E.; Slunyaev, A. Rogue Waves in the Ocean, 1st ed.; Springer: Berlin, Germany, 2009. [Google Scholar]
- Dysthe, K.B.; Krogstad, H.E.; Müller, P. Oceanic rogue waves. Ann. Rev. Fluid Mech. 2008, 40, 287–310. [Google Scholar] [CrossRef]
- Adcock, T.A.A.; Taylor, P.H. The physics of anomalous (‘rogue’) ocean waves. Rep. Prog. Phys. 2014, 77, 105901. [Google Scholar] [CrossRef] [PubMed]
- Cousins, W.; Sapsis, T.P. Quantification and prediction of extreme events in a one-dimensional nonlinear dispersive wave model. Physica D 2014, 280–281, 48–58. [Google Scholar] [CrossRef]
- Onorato, M.; Residori, S.; Bortolozzo, U.; Montina, A.; Arecchi, F.T. Rogue waves and their generating mechanisms in different physical contexts. Phys. Rep. 2013, 528, 47–89. [Google Scholar] [CrossRef]
- Shemer, L.; Alperovich, L. Peregrine breather revisited. Phys. Fluids 2013, 25, 051701. [Google Scholar] [CrossRef]
- Grimshaw, R.H.J.; Tovbis, A. Rogue waves: analytical predictions. Proc. R. Soc. A 2013, 469, 20130094. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Horikis, T.P. Interacting nonlinear wave envelopes and rogue wave formation in deep water. Phys. Fluids 2012, 27, 012107. [Google Scholar] [CrossRef]
- Onorato, M.; Residori, S.; Baronio, F. Rogue and Shock Waves in Nonlinear Dispersive Media, 1st ed.; Springer: Basel, Switzerland, 2016. [Google Scholar]
- Solli, D.R.; Ropers, C.; Koonath, P.; Jalali, B. Optical rogue waves. Nature 2007, 450, 1054–1058. [Google Scholar] [CrossRef] [PubMed]
- Dudley, J.M.; Dias, F.; Erkintalo, M.; Genty, G. Instabilities, breathers and rogue waves in optics. Nat. Photonics 2014, 8, 755–764. [Google Scholar] [CrossRef]
- Akhmediev, N.; Kibler, B.; Baronio, F.; Belić, M.; Zhong, W.-P.; Zhang, Y.; Chang, W.; Soto-Crespo, J.M.; Vouzas, P.; Grelu, P.; et al. Roadmap on optical rogue waves and extreme events. J. Opt. 2016, 18, 063001. [Google Scholar] [CrossRef]
- Zhong, W.-P.; Belić, M.; Malomed, B.A. Rogue waves in a two-component Manakov system with variable coefficients and an external potential. Phys. Rev. E 2015, 92, 053201. [Google Scholar] [CrossRef] [PubMed]
- Akhmediev, N.; Ankiewicz, A.; Soto-Crespo, J.M. Rogue waves and rational solutions of the nonlinear Schrödinger equation. Phys. Rev. E 2009, 80, 026601. [Google Scholar] [CrossRef] [PubMed]
- Shrira, V.I.; Geogjaev, V.V. What makes the Peregrine soliton so special as a prototype of freak waves? J. Eng. Math. 2010, 67, 11–22. [Google Scholar] [CrossRef]
- Chan, H.N.; Chow, K.W.; Kedziora, D.J.; Grimshaw, R.H.J.; Ding, E. Rogue wave modes for a derivative nonlinear Schrödinger model. Phys. Rev. E 2014, 89, 032914. [Google Scholar] [CrossRef] [PubMed]
- Dhar, A.K.; Das, K.P. Fourth-order nonlinear evolution equation for two Stokes wave trains in deep water. Phys. Fluids 1991, 3, 3021–3026. [Google Scholar] [CrossRef]
- Gramstad, O.; Trulsen, K. Fourth-order coupled nonlinear Schrödinger equations for gravity waves on deep water. Phys. Fluids 2011, 23, 062102. [Google Scholar] [CrossRef]
- Chen, Z.; Segev, M.; Coskun, T.H.; Christodoulides, D.N.; Kivshar, Y.S. Coupled photorefractive spatial-soliton pairs. J. Opt. Soc. Am. B 1997, 14, 3066–3077. [Google Scholar] [CrossRef]
- Agrawal, G.P. Nonlinear Fiber Optics, 4th ed.; Academic Press: New York, NY, USA, 2006. [Google Scholar]
- Mecozzi, A.; Antonelli, C.; Shtaif, M. Nonlinear propagation in multi-mode fibers in the string coupling regime. Opt. Express 2012, 20, 11673–11678. [Google Scholar] [CrossRef] [PubMed]
- Mumtaz, S.; Essiambre, R.; Agrawal, G.P. Nonlinear propagation in multimode and multicore fibers: generalization of the Manakov equations. J. Lightwave Technol. 2013, 31, 398–406. [Google Scholar] [CrossRef]
- Guasoni, M. Generalized modulational instability in multimode fibers: wideband multimode parametric amplification. Phys. Rev. A 2015, 92, 033849. [Google Scholar] [CrossRef]
- Wang, D.S.; Shi, Y.R.; Chow, K.W.; Yu, Z.X.; Li, X.G. Matter-wave solitons in a spin-1 Bose-Einstein condensate with time-modulated external potential and scattering lengths. Eur. Phys. J. D 2013, 67, 242. [Google Scholar] [CrossRef]
- Baronio, F.; Degasperis, A.; Conforti, M.; Wabnitz, S. Solutions of the vector nonlinear Schrödinger equations: evidence for deterministic rogue waves. Phys. Rev. Lett. 2012, 109, 044102. [Google Scholar] [CrossRef] [PubMed]
- Ling, L.; Guo, B.; Zhao, L.C. High-order rogue waves in vector nonlinear Schrödinger equations. Phys. Rev. E 2014, 89, 041201(R). [Google Scholar] [CrossRef] [PubMed]
- He, J.; Guo, L.; Zhang, Y.; Chabchoub, A. Theoretical and experimental evidence of non-symmetric doubly localized rogue waves. Proc. R. Soc. A 2014, 470, 20140318. [Google Scholar] [CrossRef] [PubMed]
- Degasperis, A.; Lombardo, S. Rational solitons of wave resonant-interaction models. Phys. Rev. E 2013, 88, 052914. [Google Scholar] [CrossRef] [PubMed]
- Baronio, F.; Conforti, M.; Degasperis, A.; Lombardo, S.; Onorato, M.; Wabnitz, S. Vector rogue waves and baseband modulation instability in the defocusing regime. Phys. Rev. Lett. 2014, 113, 034101. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Soto-Crespo, J.M.; Grelu, P. Dark three-sister rogue waves in normally dispersive optical fibers with random birefringence. Opt. Express 2014, 22, 27632–27642. [Google Scholar] [CrossRef] [PubMed]
- Li, J.H.; Chan, H.N.; Chiang, K.S.; Chow, K.W. Breathers and ‘black’ rogue waves of coupled nonlinear Schrödinger equations with dispersion and nonlinearity of opposite signs. Commun. Nonlinear Sci. Numer. Simulat. 2015, 28, 28–38. [Google Scholar] [CrossRef]
- Frisquet, B.; Kibler, B.; Fatome, J.; Morin, P.; Baronio, F.; Conforti, M.; Millot, G.; Wabnitz, S. Polarization modulation instability in a Manakov fiber system. Phys. Rev. A 2015, 92, 053854. [Google Scholar] [CrossRef]
- Frisquet, B.; Kibler, B.; Morin, P.; Baronio, F.; Conforti, M.; Millot, G.; Wabnitz, S. Optical dark rogue wave. Sci. Rep. 2016, 6, 20785. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.C.; Liu, J. Rogue-wave solutions of a three-component coupled nonlinear Schrödinger equation. Phys. Rev. E 2013, 87, 013201. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Yang, Z.-Y.; Zhao, L.-C.; Yang, W.-L. Vector breathers and the inelastic interaction in a three-mode nonlinear optical fiber. Phys. Rev. A 2014, 89, 055803. [Google Scholar] [CrossRef]
- Xu, T.; Chen, Y. Localized waves in three-component coupled nonlinear Schrödinger equation. Chin. Phys. B 2016, 25, 090201. [Google Scholar] [CrossRef]
- Hirota, R. The Direct Method in Soliton Theory, 1st ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Chan, H.N.; Malomed, B.A.; Chow, K.W.; Ding, E. Rogue waves for a system of coupled derivative nonlinear Schrödinger equations. Phys. Rev. E 2016, 93, 012217. [Google Scholar] [CrossRef] [PubMed]
- Chan, H.N.; Chow, K.W. Rogue waves for an alternative system of coupled Hirota equations: structural robustness and modulation instabilities. Stud. Appl. Math. 2017. [Google Scholar] [CrossRef]
- Chen, S.; Soto-Crespo, J.M.; Grelu, P. Coexisting rogue waves within the (2+1)-component long-wave-short-wave resonance. Phys. Rev. E 2014, 90, 033203. [Google Scholar] [CrossRef] [PubMed]
- Chan, H.N.; Ding, E.; Kedziora, D.J.; Grimshaw, R.H.J.; Chow, K.W. Rogue waves for a long wave-short wave resonance model with multiple short waves. Nonlinear Dyn. 2016, 85, 2827–2841. [Google Scholar] [CrossRef]
- Baronio, F.; Chen, S.; Grelu, P.; Wabnitz, S.; Conforti, M. Baseband modulation instability as the origin of rogue waves. Phys. Rev. A 2015, 91, 033804. [Google Scholar] [CrossRef]
- Yang, J. Nonlinear Waves in Integrable and Nonintegrable Systems, 1st ed.; SIAM: Philadelphia, PA, USA, 2010. [Google Scholar]
- Wang, L.; Zhang, L.-L.; Zhu, Y.-J.; Qi, F.-H.; Wang, P.; Guo, R.; Li, M. Modulational instability, nonautonomous characteristics and semirational solutions for the coupled nonlinear Schrödinger equations in inhomogeneous fibers. Commun. Nonlinear Sci. Numer. Simul. 2016, 40, 216–237. [Google Scholar] [CrossRef]
- Tiofack, C.G.L.; Coulibaly, S.; Taki, M.; De Bièvre, S.; Dujardin, G. Comb generation using multiple compression points of Peregrine rogue waves in periodically modulated nonlinear Schrödinger equations. Phys. Rev. A 2015, 92, 043837. [Google Scholar] [CrossRef]
- Baronio, F. Akhmediev breathers and Peregrine solitary waves in a quadratic medium. Opt. Lett. 2017, 42, 1756–1759. [Google Scholar] [CrossRef] [PubMed]
- Manikandan, K.; Senthilvelan, M.; Kraenkel, R.A. On the characterization of vector rogue waves in two-dimensional two coupled nonlinear Schrödinger equations with distributed coefficients. Eur. Phys. J. B 2016, 89, 218. [Google Scholar] [CrossRef]
- Tan, Z.; Tian, B.; Jiang, Y.; Wang, P.; Li, M. Dynamics of the Manakov solitons in biased guest-host photorefractive polymer. Commun. Theor. Phys. 2013, 60, 150–158. [Google Scholar] [CrossRef]
- Tsitsas, N.L.; Lakhtakia, A.; Frantzeskakis, D.J. Vector solitons in nonlinear isotropic chiral metamaterials. J. Phys. A Math. Theor. 2011, 44, 435203. [Google Scholar] [CrossRef]
- Boscolo, S.; Peng, J.; Finot, C. Design and applications of in-cavity pulse shaping by spectral sculpturing in mode-locked fibre lasers. Appl. Sci. 2015, 5, 1379–1398. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Musslimani, Z.H. Integrable nonlocal nonlinear Schrödinger equation. Phys. Rev. Lett. 2013, 110, 064105. [Google Scholar] [CrossRef] [PubMed]
- Gupta, S.K.; Sarma, A.K. Peregrine rogue wave dynamics in the continuous nonlinear Schrödinger system with parity-time symmetric Kerr nonlinearity. Commun. Nonlinear Sci. Numer. Simulat. 2016, 36, 141–147. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chan, H.N.; Chow, K.W. Rogue Wave Modes for the Coupled Nonlinear Schrödinger System with Three Components: A Computational Study. Appl. Sci. 2017, 7, 559. https://doi.org/10.3390/app7060559
Chan HN, Chow KW. Rogue Wave Modes for the Coupled Nonlinear Schrödinger System with Three Components: A Computational Study. Applied Sciences. 2017; 7(6):559. https://doi.org/10.3390/app7060559
Chicago/Turabian StyleChan, Hiu Ning, and Kwok Wing Chow. 2017. "Rogue Wave Modes for the Coupled Nonlinear Schrödinger System with Three Components: A Computational Study" Applied Sciences 7, no. 6: 559. https://doi.org/10.3390/app7060559



