Soliton Content of Fiber-Optic Light Pulses
Abstract
:1. Introduction
2. The Nonlinear Schrödinger Equation and Some of Its Solutions
2.1. Soliton Solutions
2.1.1. The Fundamental Soliton
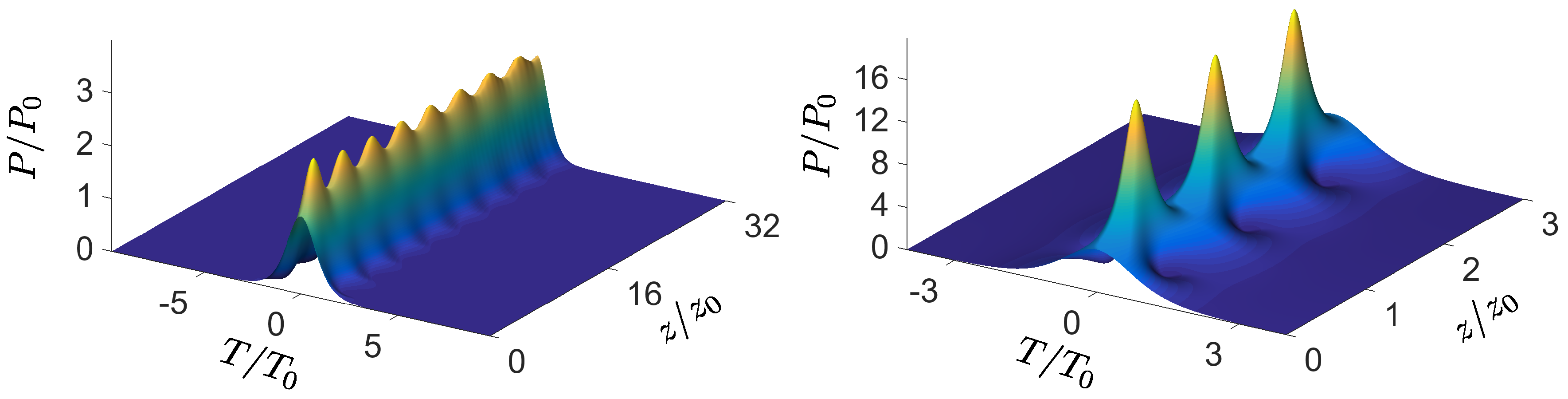
2.1.2. Radiation and Higher-Order Solitons
2.1.3. Soliton Interaction
2.2. Breather Solutions
3. Extensions to the Nonlinear Schrödinger Equation
3.1. Generalized Nonlinear Schrödinger Equation
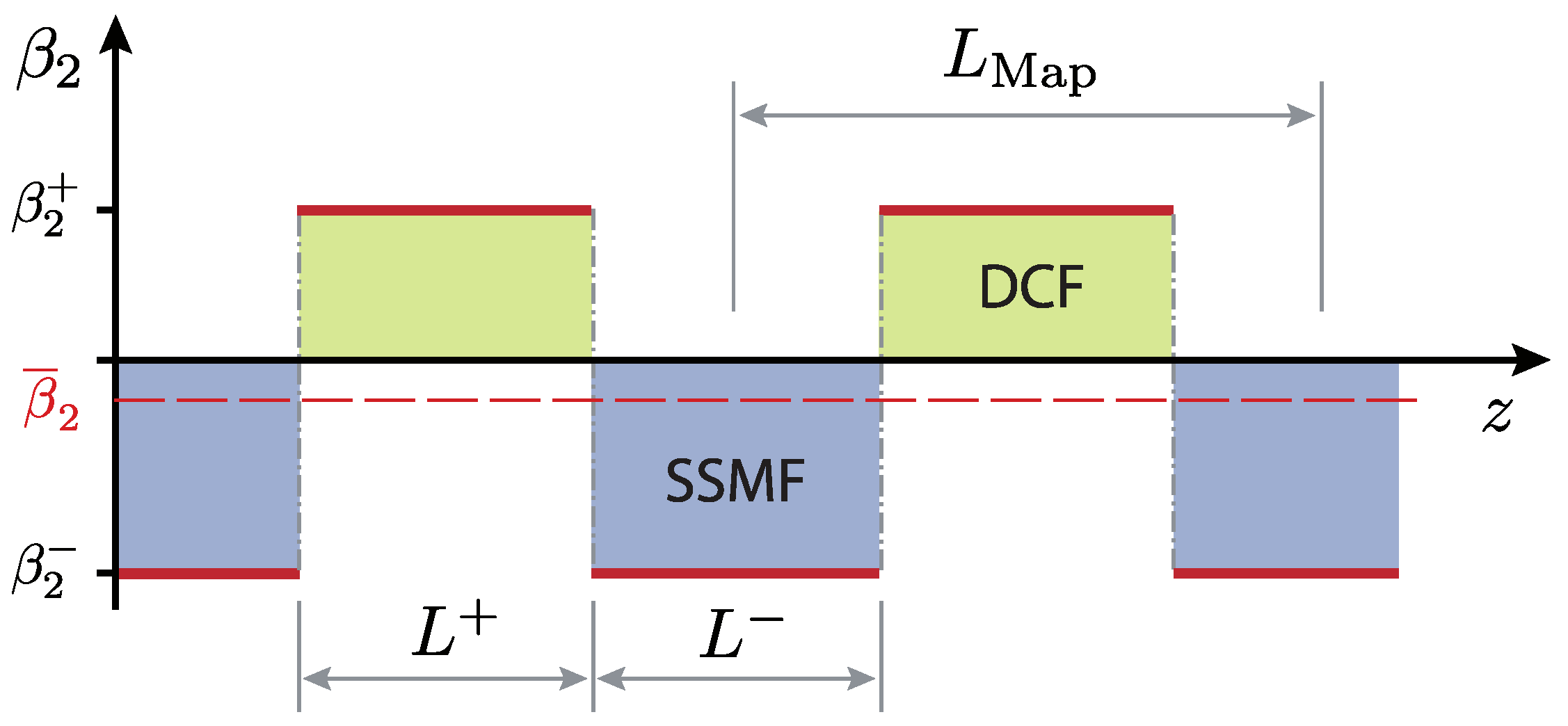
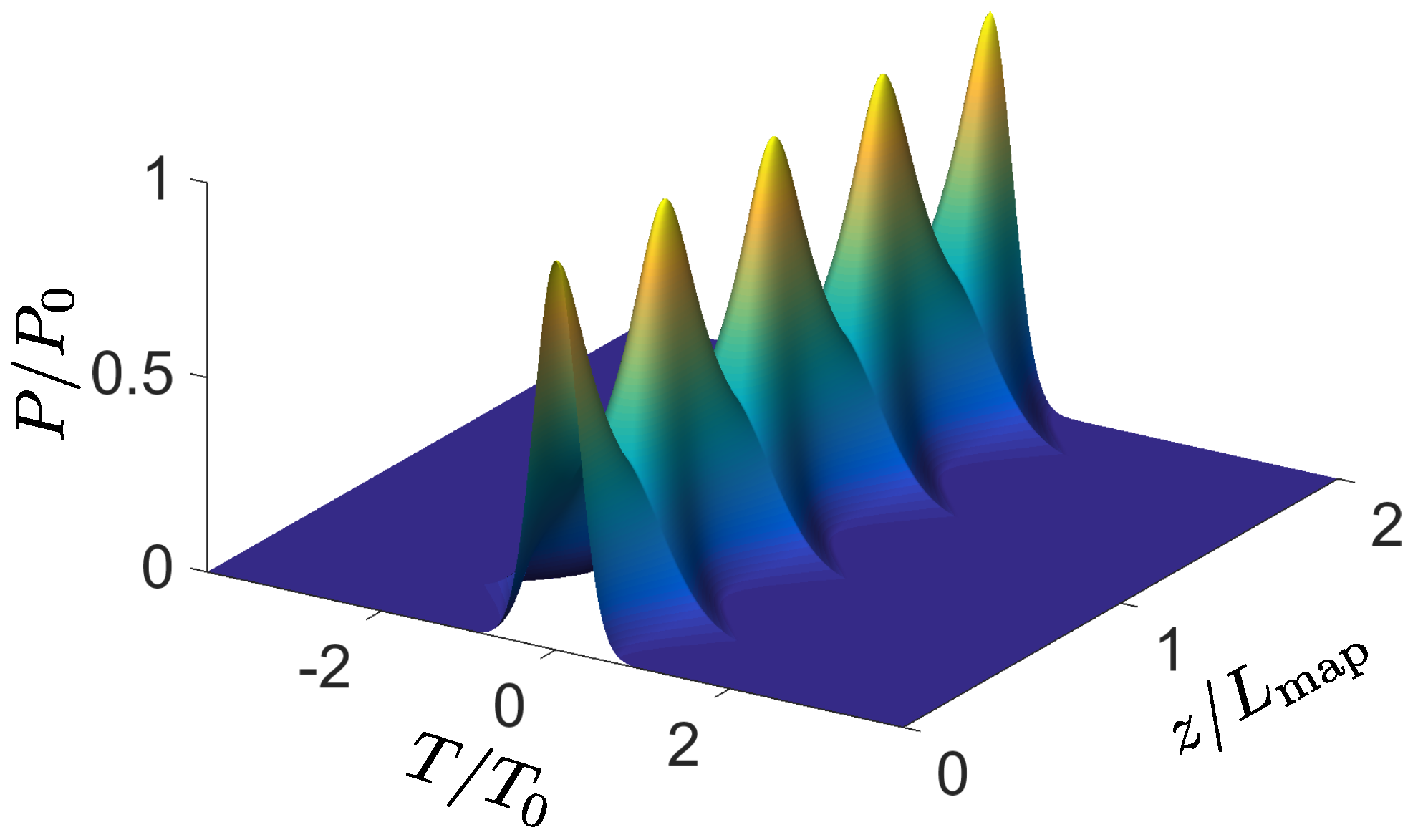
3.2. Dispersion-Managed Fibers
3.3. Cases Involving Several Solitons
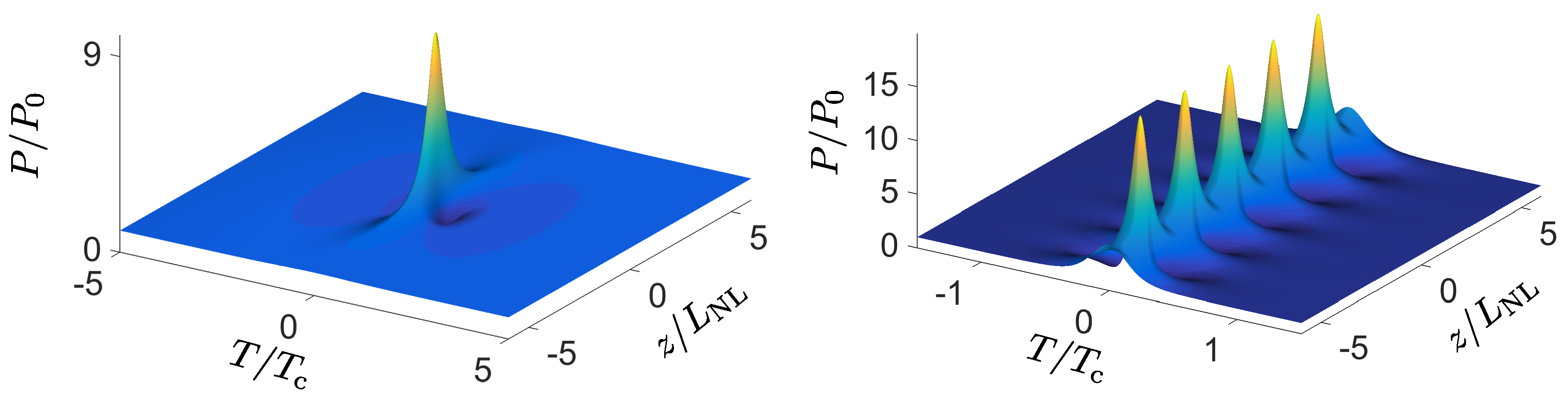
3.3.1. Soliton Molecules
3.3.2. Soliton Gas and Crystal
3.3.3. Supercontinuum Generation
4. Methods to Verify Soliton Content
4.1. The Inverse and Direct Scattering Transform
4.1.1. The Method
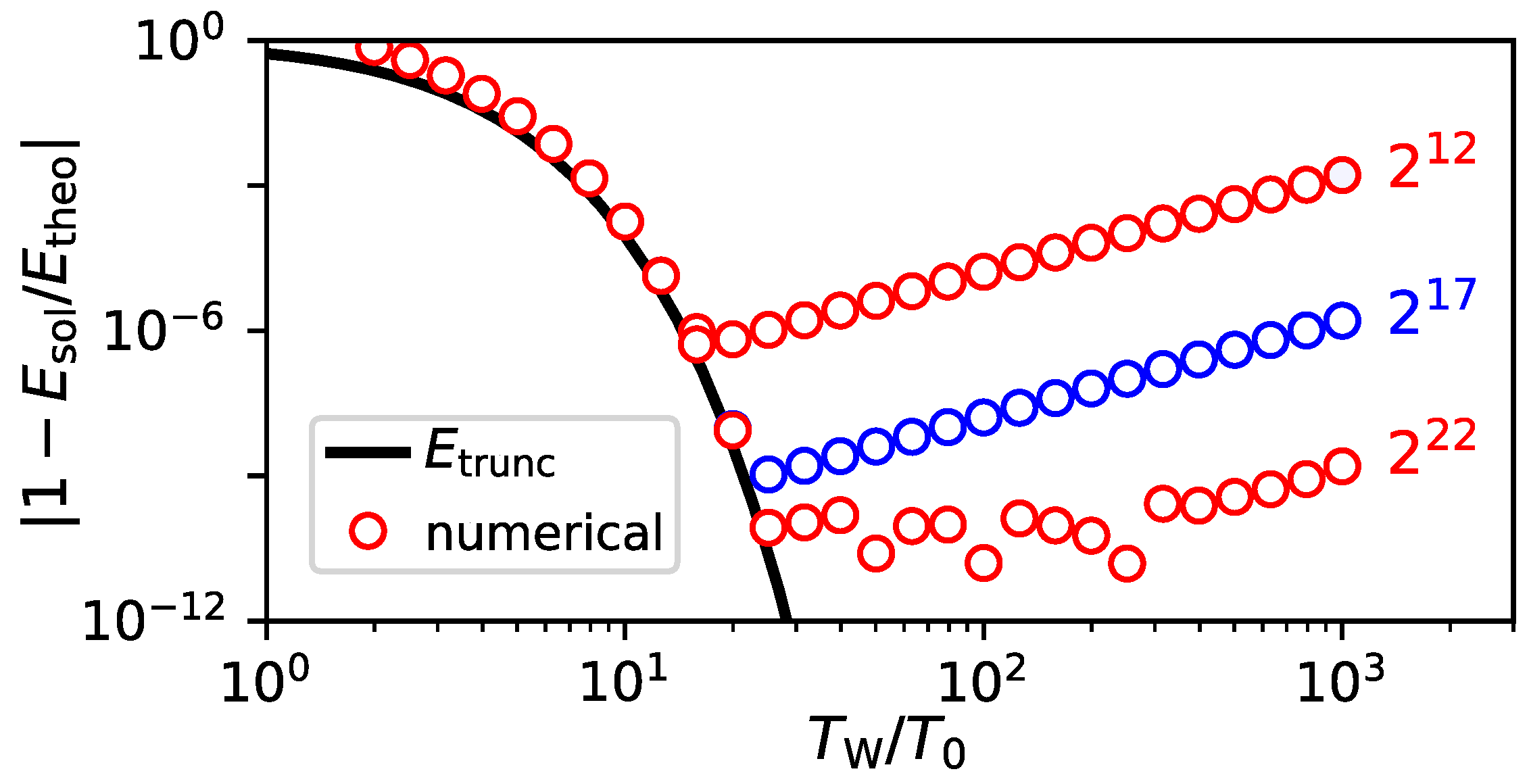
4.1.2. Numerical Restrictions
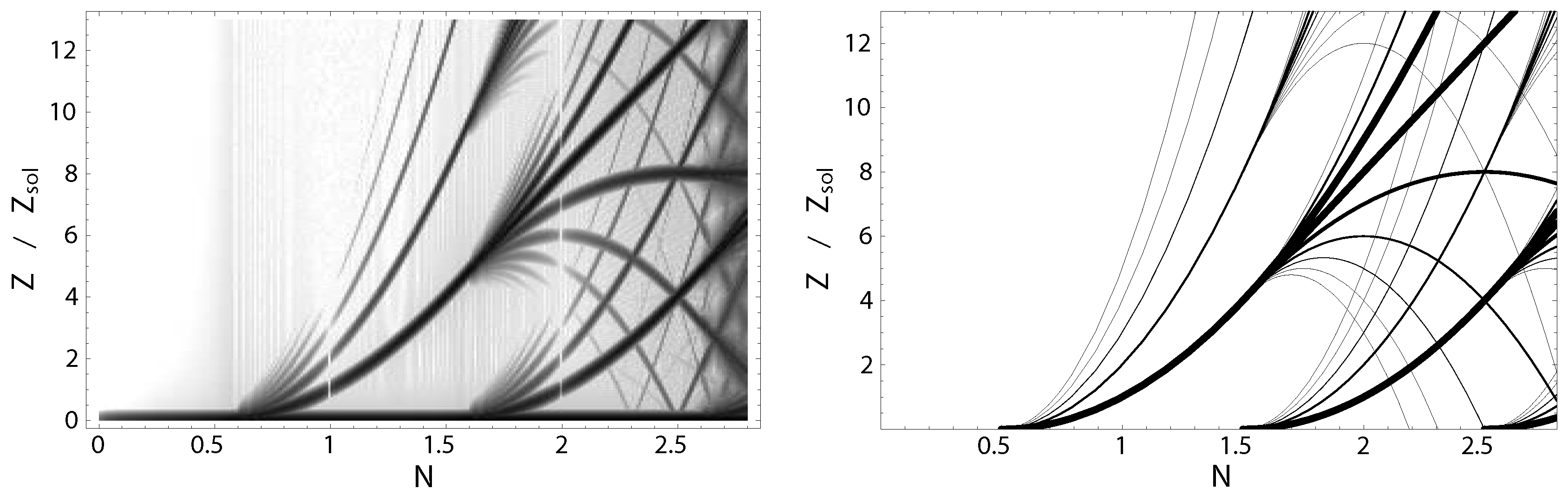
4.1.3. Applications and Limitations of DST
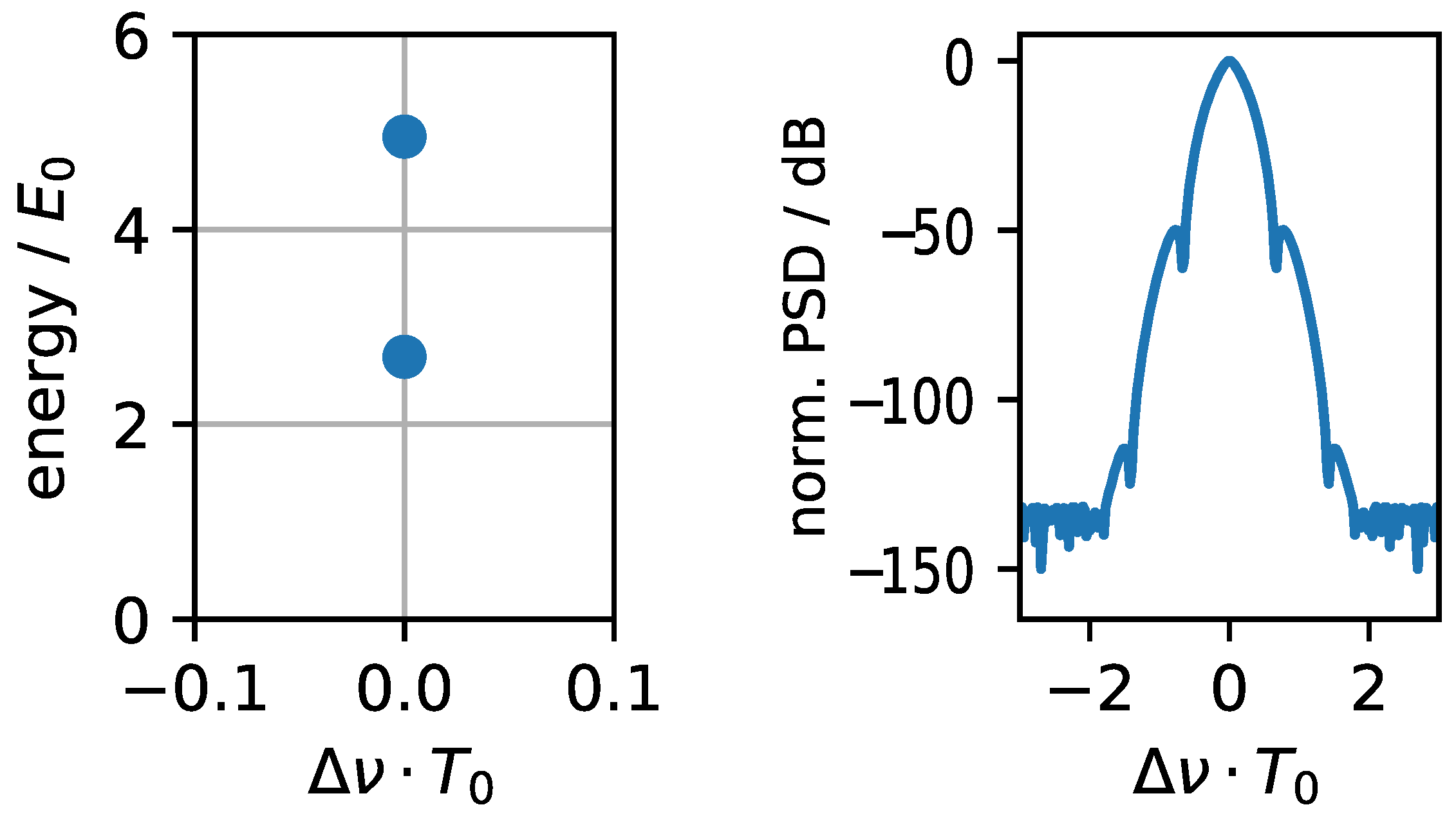
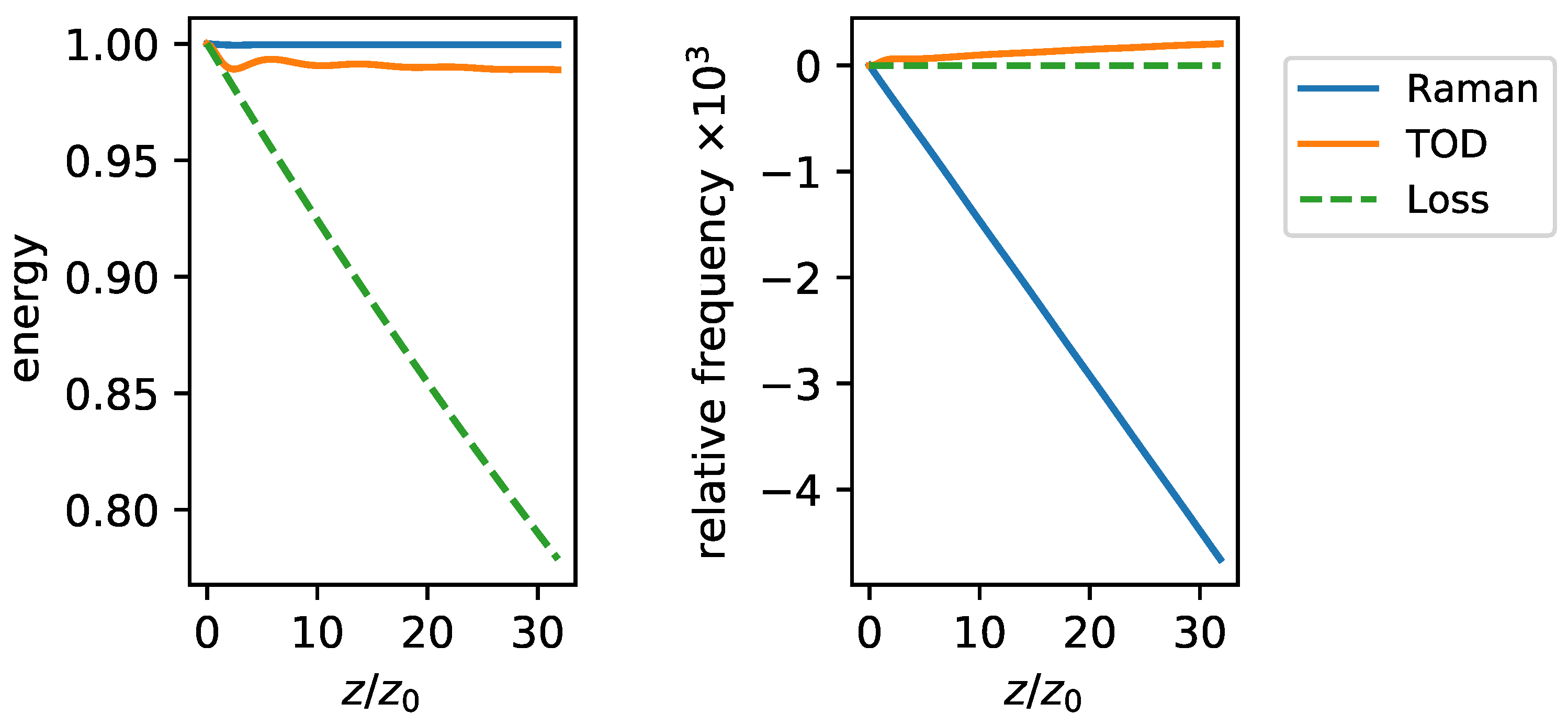
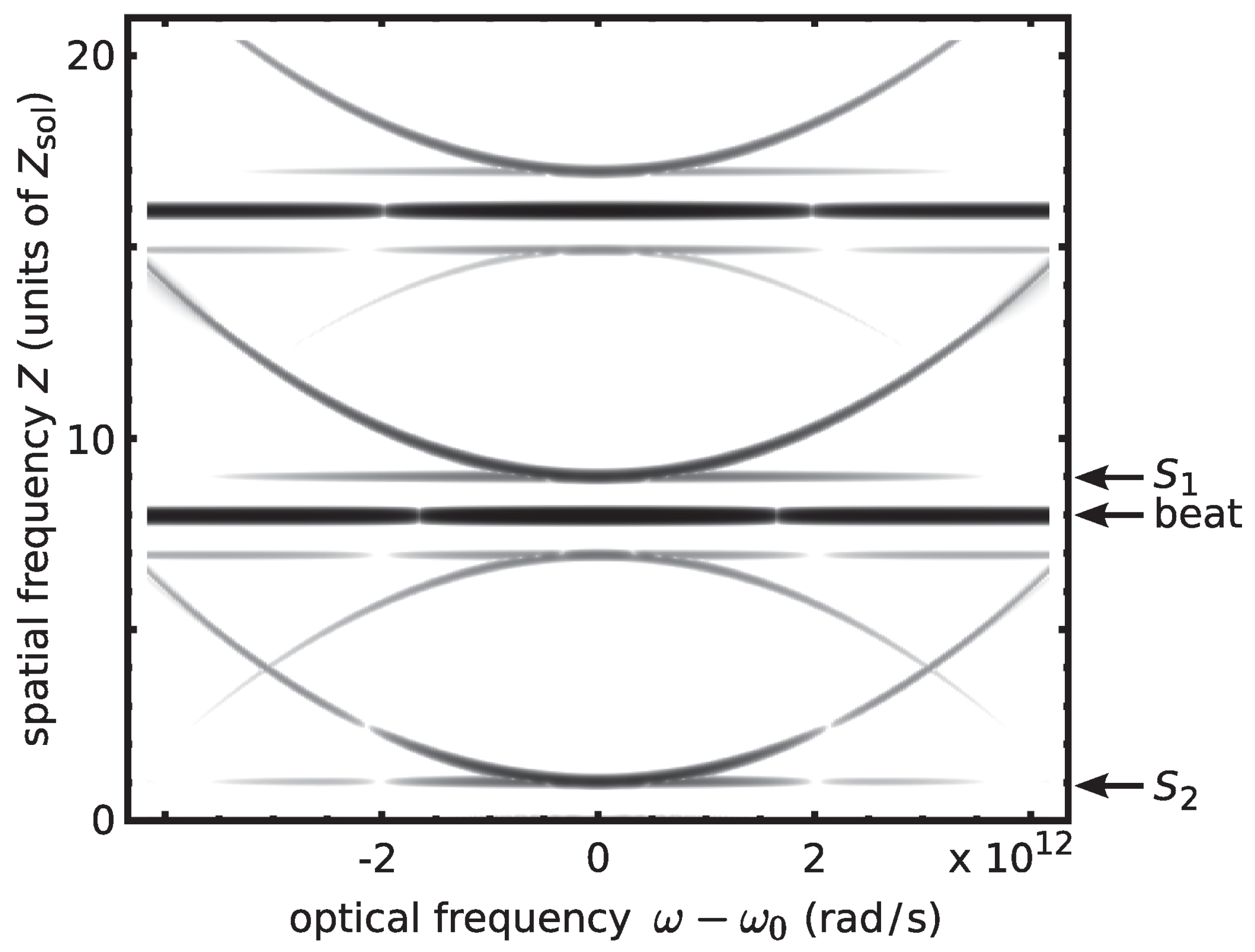
4.2. Soliton Radiation Beat Analysis
5. Conclusions
Author Contributions
Conflicts of Interest
Abbreviations
| cw | continuous wave |
| DM | dispersion-management |
| DST | direct scattering transform |
| IST | inverse scattering transform |
| NLSE | nonlinear Schrödinger equation |
| SRBA | soliton radiation beat analysis |
References
- Agrawal, G.P. Nonlinear Fiber Optics, 5th ed.; Academic Press: Oxford, UK, 2013. [Google Scholar]
- Mitschke, F. Fiber Optics. Physics and Technology, 2nd ed.; Springer: Heidelberg, Germany, 2016. [Google Scholar]
- Stolen, R.H.; Lin, C. Self-phase-modulation in silica optical fibers. Phys. Rev. A 1978, 17, 1448–1453. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Shabat, A.B. Exact Theory of Two-Dimensional Self-Focusing and One-Dimensional Self-Modulation of Waves in Nonlinear Media. Sov. Phys. JETP 1972, 34, 62–69. [Google Scholar]
- Gardner, C.S.; Greene, J.M.; Kruskal, M.D.; Miura, R.M. Method for Solving the Korteweg-de Vries Equation. Phys. Rev. Lett. 1967, 19, 1095–1097. [Google Scholar] [CrossRef]
- Satsuma, J.; Yajima, N. Initial Value Problem of One-Dimensional Self-Modulation of Nonlinear Waves in Dispersive Media. Prog. Theor. Phys. Suppl. 1974, 55, 284–306. [Google Scholar] [CrossRef]
- Hasegawa, A.; Tappert, F. Transmission of stationary nonlinear optical pulses in dispersive dielectric fibers. I. Anomalous dispersion. Appl. Phys. Lett. 1973, 23, 142–144. [Google Scholar] [CrossRef]
- Mollenauer, L.F.; Stolen, R.H.; Gordon, J.P. Experimental Observation of Picosecond Pulse Narrowing and Solitons in Optical Fibers. Phys. Rev. Lett. 1980, 45, 1095–1098. [Google Scholar] [CrossRef]
- Yang, J. Nonlinear Waves in Integrable and Nonintegrable Systems; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 2010. [Google Scholar]
- Kivshar, Y.S.; Agrawal, G.P. Optical Solitons. From Fibers to Photonic Crystals; Academic Press: London, UK, 2003. [Google Scholar]
- Schrader, D. Explicit calculation of N-Soliton Solutions of the nonlinear Schrödinger equation. IEEE J. Quantum Electron. 1995, 31, 2221–2225. [Google Scholar] [CrossRef]
- Gordon, J.P. Interaction forces among solitons in optical fibers. Opt. Lett. 1983, 8, 596–598. [Google Scholar] [CrossRef] [PubMed]
- Mitschke, F.; Mollenauer, L.F. Experimental observation of interaction forces between solitons in optical fibers. Opt. Lett. 1987, 12, 355–357. [Google Scholar] [CrossRef] [PubMed]
- Desem, C.; Chu, P.L. Reducing soliton interaction in single-mode optical fibres. IEEE Proc. 1987, 134, 145–151. [Google Scholar] [CrossRef]
- Akhmediev, N.N.; Korneev, V.I. Modulation instability and periodic solutions of the nonlinear Schrödinger equation. Theor. Math. Phys. 1986, 69, 1089–1093. [Google Scholar] [CrossRef]
- Mahnke, C.; Mitschke, F. Ultrashort Light Pulses Generated from Modulation Instability: Background Removal and Soliton Content. Appl. Phys. B 2013, 116, 15–20. [Google Scholar] [CrossRef]
- Dudley, J.M.; Genty, G.; Dias, F.; Kibler, B.; Akhmediev, N. Modulation instability, Akhmediev Breathers and continuous wave supercontinuum generation. Opt. Express 2009, 17, 21497–21508. [Google Scholar] [CrossRef] [PubMed]
- Hammani, K.; Wetzel, B.; Kibler, B.; Fatome, J.; Finot, C.; Millot, G.; Akhmediev, N.; Dudley, J.M. Spectral dynamics of modulation instability described using Akhmediev breather theory. Opt. Lett. 2011, 36, 2140–2142. [Google Scholar] [CrossRef] [PubMed]
- Hasegawa, A. Generation of a train of soliton pulses by induced modulational instability in optical fibers. Opt. Lett. 1984, 9, 288–290. [Google Scholar] [CrossRef] [PubMed]
- Peregrine, D.H. Water waves, nonlinear Schrödinger equations and their solutions. J. Aust. Math. Soc. B 1983, 25, 16–43. [Google Scholar] [CrossRef]
- Kibler, B.; Fatome, J.; Finot, C.; Dias, F.; Genty, G.; Akhmediev, N.; Dudley, J.M. The Peregrine soliton in nonlinear fiber optics. Nat. Phys. 2010, 6, 790–795. [Google Scholar] [CrossRef]
- Kibler, B.; Fatome, J.; Finot, C.; Millot, G.; Genty, G.; Wetzel, B.; Akhmediev, N.; Dias, F.; Dudley, J.M. Observation of the Kuznetsov-Ma soliton dynamics in optical fibre. Sci. Rep. 2012, 2, 463. [Google Scholar] [CrossRef] [PubMed]
- Anderson, D.; Lisak, M. Nonlinear asymmetric self-phase modulation and self-steepening of pulses in long optical waveguides. Phys. Rev. A 1983, 27, 1393–1398. [Google Scholar] [CrossRef]
- Stolen, R.H.; Lee, C.; Jain, R.K. Development of the stimulated Raman spectrum in single-mode silica fibers. J. Opt. Soc. Am. B 1984, 1, 652–657. [Google Scholar] [CrossRef]
- Gordon, J.P. Theory of the soliton self frequency shift. Opt. Lett. 1986, 11, 662–664. [Google Scholar] [CrossRef] [PubMed]
- Stolen, R.H.; Gordon, J.P.; Tomlinson, W.J.; Haus, H.A. Raman response function of silica-core fibers. J. Opt. Soc. Am. B 1989, 6, 1159–1166. [Google Scholar] [CrossRef]
- Mamyshev, P.V.; Chernikov, S.V. Ultrashort-pulse propagation in optical fibers. Opt. Lett. 1990, 15, 1076–1078. [Google Scholar] [CrossRef] [PubMed]
- Lin, Q.; Agrawal, G.P. Raman response function for silica fibers. Opt. Lett. 2006, 31, 3086–3088. [Google Scholar] [CrossRef] [PubMed]
- Kaup, D.J. A perturbation expansion for the Zakharov–Shabat inverse scattering transform. SIAM J. Appl. Math. 1976, 31, 121–133. [Google Scholar] [CrossRef]
- Hasegawa, A.; Kodama, Y. Amplification and reshaping of optical solitons in a glass fiber—I. Opt. Lett. 1982, 7, 285–287. [Google Scholar] [CrossRef] [PubMed]
- Turitsyn, S.K.; Bale, B.G.; Fedoruk, M.P. Dispersion-managed solitons in fibre systems and lasers. Phys. Rep. 2012, 521, 135–203. [Google Scholar] [CrossRef]
- Smith, N.J.; Knox, F.M.; Doran, N.J.; Blow, K.J.; Bennion, I. Enhanced power solitons in optical fibres with periodic dispersion management. Electron. Lett. 1996, 32, 54–55. [Google Scholar] [CrossRef]
- Nijhof, J.H.B.; Doran, N.J.; Forysiak, W.; Knox, F.M. Stable soliton-like propagation in dispersion managed systems with net anomalous, zero and normal dispersion. Electron. Lett. 1997, 33, 1726–1727. [Google Scholar] [CrossRef]
- Chen, Y.; Haus, H.A. Dispersion-managed solitons with net positive dispersion. Opt. Lett. 1998, 23, 1013–1015. [Google Scholar] [CrossRef] [PubMed]
- Turytsin, S.K.; Shapiro, E.G. Dispersion-managed solitons in optical amplifier transmission systems with zero average dispersion. Opt. Lett. 1998, 23, 682–684. [Google Scholar] [CrossRef]
- Kutz, J.N.; Evangelides, S.G. Dispersion-managed breathers with average normal dispersion. Opt. Lett. 1998, 23, 685–687. [Google Scholar] [CrossRef] [PubMed]
- Grigoryan, V.S.; Menyuk, C.R. Dispersion-managed solitons at normal average dispersion. Opt. Lett. 1998, 23, 609–611. [Google Scholar] [CrossRef] [PubMed]
- Turitsyn, S.; Shapiro, E.; Medvedev, S.; Fedoruk, M.P.; Mezentsev, V. Physics and mathematics of dispersion managed optical solitons. C. R. Phys. 2003, 4, 145–161. [Google Scholar] [CrossRef]
- Lushnikov, P.M. Oscillating tails of a dispersion-managed soliton. J. Opt. Soc. Am. B 2004, 21, 1913–1918. [Google Scholar] [CrossRef]
- Nijhof, J.H.B.; Forysiak, W.; Doran, N.J. The averaging method for finding exactly periodic dispersion-managed solitons. IEEE J. Sel. Top. Quantum Electron. 2000, 5, 330–336. [Google Scholar] [CrossRef]
- Stratmann, M.; Pagel, T.; Mitschke, F. Experimental Observation of Temporal Soliton Molecules. Phys. Rev. Lett. 2005, 95, 143902. [Google Scholar] [CrossRef] [PubMed]
- Hause, A.; Hartwig, H.; Seifert, B.; Stolz, H.; Böhm, M.; Mitschke, F. Phase structure of soliton molecules. Phys. Rev. A 2007, 75, 063836. [Google Scholar] [CrossRef]
- Hause, A.; Hartwig, H.; Böhm, M.; Mitschke, F. Binding mechanism of temporal soliton molecules. Phys. Rev. A 2008, 78, 063817. [Google Scholar] [CrossRef]
- Rohrmann, P.; Hause, A.; Mitschke, F. Solitons Beyond Binary: Possibility of Fibre-Optic Transmission of Two Bits per Clock Period. Sci. Rep. 2012, 2, 866. [Google Scholar] [CrossRef] [PubMed]
- Rohrmann, P.; Hause, A.; Mitschke, F. Two-soliton and three-soliton molecules in optical fibers. Phys. Rev. A 2013, 87, 043834. [Google Scholar] [CrossRef]
- Hause, A.; Mitschke, F. Higher-order equilibria of temporal soliton molecules in dispersion-managed fibers. Phys. Rev. A 2013, 88, 063843. [Google Scholar] [CrossRef]
- Steinmeyer, G.; Buchholz, A.; Hänsel, M.; Heuer, M.; Schwache, A.; Mitschke, F. Dynamical pulse shaping in a nonlinear resonator. Phys. Rev. A 1995, 52, 830–838. [Google Scholar] [CrossRef] [PubMed]
- Schwache, A.; Mitschke, F. Properties of an optical soliton gas. Phys. Rev. E 1997, 55, 7720–7725. [Google Scholar] [CrossRef]
- Malomed, B.A.; Schwache, A.; Mitschke, F. Soliton lattice and gas in passive fiber-ring resonators. Fiber Integr. Opt. 1998, 17, 267–277. [Google Scholar]
- Amrani, F.; Haboucha, A.; Salhi, M.; Leblond, H.; Komarov, A.; Sanchez, F. Dissipative solitons compounds in a fiber laser. Analogy with the states of the matter. Appl. Phys. B 2010, 99, 107–114. [Google Scholar] [CrossRef]
- Grelu, P.; Soto-Crespo, J.M. Temporal soliton “molecules” in mode-locked lasers: Collisions, pulsations, and vibrations. In Dissipative Solitons: From Optics to Biology and Medicine; Lecture Notes in Physics; Akhmediev, N., Ankiewicz, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 751, pp. 137–173. [Google Scholar]
- Chouli, S.; Grelu, P. Soliton rains in a fiber laser: An experimental study. Phys. Rev. A 2010, 81, 063829. [Google Scholar] [CrossRef]
- Soto-Crespo, J.M.; Akhmediev, N.N.; Afanasjev, V.V. Stability of the pulselike solutions of the quintic complex Ginzburg–Landau equation. J. Opt. Soc. Am. B 1996, 13, 1439–1449. [Google Scholar] [CrossRef]
- Grelu, P.; Akhmediev, N.N. Dissipative solitons for mode-locked lasers. Nat. Photonics 2012, 6, 84–92. [Google Scholar] [CrossRef]
- Akhmediev, N.; Ankiewicz, A. (Eds.) Dissipative Solitons: From Optics to Biology and Medicine; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2008; Volume 751. [Google Scholar]
- Husakou, A.V.; Herrmann, J. Supercontinuum generation of higher-order solitons by fission in photonic crystal fibers. Phys. Rev. Lett. 2001, 87, 203901. [Google Scholar] [CrossRef] [PubMed]
- Roy, S.; Bhadra, S.K.; Agrawal, G.P. Perturbation of higher-order solitons by fourth-order dispersion in optical fibers. Opt. Commun. 2009, 282, 3798–3803. [Google Scholar] [CrossRef]
- Dudley, J.M.; Genty, G.; Coen, S. Supercontinuum generation in photonic crystal fiber. Rev. Mod. Phys. 2006, 78, 1135–1184. [Google Scholar] [CrossRef]
- Solli, D.R.; Ropers, C.; Koonath, P.; Jalali, B. Optical Rogue Waves. Nature 2007, 450, 1054–1057. [Google Scholar] [CrossRef] [PubMed]
- Akhmediev, N.; Kibler, B.; Baronio, F.; Belić, M.; Zhong, W.P.; Zhang, Y.; Chang, W.; Soto-Crespo, J.M.; Vouzas, P.; Grelu, P.; et al. Roadmap on optical rogue waves and extreme events. J. Opt. 2016, 18, 063001. [Google Scholar] [CrossRef]
- Lax, P.D. Integrals of nonlinear equations of evolution and solitary waves. Commun. Pure Appl. Math. 1968, 21, 467–490. [Google Scholar] [CrossRef]
- Hasegawa, A.; Nyu, T. Eigenvalue communication. J. Lightwave Technol. 1993, 11, 395–399. [Google Scholar] [CrossRef]
- Turitsyn, S.K.; Prilepsky, J.E.; Le, S.T.; Wahls, S.; Frumin, L.L.; Kamalian, M.; Derevyanko, S.A. Nonlinear Fourier transform for optical data processing and transmission: Advances and perspectives. Optica 2017, 4, 307–322. [Google Scholar] [CrossRef]
- Manakov, S.V. Nonlinear Fraunhofer diffraction. Zh. Eksp. Teor. Fiz. 1973, 65, 1392–1398. [Google Scholar]
- Boffetta, G.; Osborne, A. Computation of the Direct Scattering Transform for the Nonlinear Schroedinger Equation. J. Comput. Phys. 1992, 102, 252–264. [Google Scholar] [CrossRef]
- Kamalian, M.; Prilepsky, J.E.; Le, S.T.; Turitsyn, S.K. Periodic nonlinear Fourier transform for fiber-optic communications, Part I: Theory and numerical methods. Opt. Express 2016, 24, 18353–18369. [Google Scholar] [CrossRef] [PubMed]
- Kamalian, M.; Prilepsky, J.E.; Le, S.T.; Turitsyn, S.K. Periodic nonlinear Fourier transform for fiber-optic communications, Part II: Eigenvalue communication. Opt. Express 2016, 24, 18370–18381. [Google Scholar] [CrossRef] [PubMed]
- Yousefi, M.I.; Kschischang, F.R. Information transmission using the nonlinear Fourier transform, Part II: Numerical methods. IEEE Trans. Inf. Theory 2014, 60, 4329–4345. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Kaup, D.J.; Newell, A.C.; Segur, H. Nonlinear-Evolution Equations of Physical Significance. Phys. Rev. Lett. 1973, 31, 125–127. [Google Scholar] [CrossRef]
- Prilepsky, J.E.; Derevyanko, S.A. Breakup of a multisoliton state of the linearly damped nonlinear Schrödinger equation. Phys. Rev. E 2007, 75, 036616. [Google Scholar] [CrossRef] [PubMed]
- Kodama, Y.; Hasegawa, A. Nonlinear pulse propagation in a monomode dielectric guide. IEEE J. Quantum Electron. 1987, 23, 510–524. [Google Scholar] [CrossRef]
- Tai, K.; Bekki, N.; Hasegawa, A. Fission of optical solitons induced by stimulated Raman effect. Opt. Lett. 1988, 13, 392–394. [Google Scholar] [CrossRef] [PubMed]
- Gölles, M.; Uzunov, I.M.; Lederer, F. Break up of N-soliton bound states due to intrapulse Raman scattering and third-order dispersion—An eigenvalue analysis. Phys. Lett. A 1997, 231, 195–200. [Google Scholar] [CrossRef]
- Mahnke, C.; Mitschke, F. Possibility of an Akhmediev breather decaying into solitons. Phys. Rev. A 2012, 82, 033808. [Google Scholar] [CrossRef]
- Its, A.R.; Matveev, V.B. Schrödinger operators with finite-gap spectrum and N-soliton solutions of the Korteweg—de Vries equation. Theor. Math. Phys. 1975, 23, 51–68. [Google Scholar] [CrossRef]
- Kawata, T.; Inoue, H. Inverse scattering method for the nonlinear evolution equations under nonvanishing conditions. J. Phys. Soc. Jpn. 1978, 44, 1722–1729. [Google Scholar] [CrossRef]
- Ma, Y.C.; Ablowitz, M.J. The periodic cubic Schrodinger equation. Stud. Appl. Math. 1981, 65, 113–158. [Google Scholar] [CrossRef]
- Ma, Y.C. The Perturbed Plane Wave Solutions of the Cubic Schrödinger Equation. Stud. Appl. Math. 1979, 60, 43–58. [Google Scholar] [CrossRef]
- Tracy, E.R.; Chen, H.H. Nonlinear self-modulation: An exactly solvable model. Phys. Rev. A 1988, 37, 815–839. [Google Scholar] [CrossRef]
- Osborne, A. Nonlinear Ocean Waves and the Inverse Scattering Transform; International Geophysics Series; Academic Press: Burlington, MA, USA, 2010; Volume 97. [Google Scholar]
- Olivier, C.P.; Herbst, B.M.; Molchan, M.A. A numerical study of the large-period limit of a Zakharov–Shabat eigenvalue problem with periodic potentials. J. Phys. A Math. Theor. 2012, 45, 255205–255211. [Google Scholar] [CrossRef]
- Wahls, S.; Poor, H.V. Introducing the fast nonlinear Fourier transform. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013. [Google Scholar]
- Wahls, S.; Poor, H.V. Fast numerical nonlinear Fourier transforms. IEEE Trans. Inf. Theory 2015, 61, 6957–6974. [Google Scholar] [CrossRef]
- Randoux, S.; Suret, P.; El, G. Inverse scattering transform analysis of rogue waves using local periodization procedure. Sci. Rep. 2016, 6, 29238. [Google Scholar] [CrossRef] [PubMed]
- Weerasekara, G.; Tokunaga, A.; Terauchi, H.; Eberhard, M.; Maruta, A. Soliton’s eigenvalue based analysis on the generation mechanism of rogue wave phenomenon in optical fibers exhibiting weak third order dispersion. Opt. Express 2015, 23, 143–153. [Google Scholar] [CrossRef] [PubMed]
- Weerasekara, G.; Maruta, A. Characterization of optical rogue wave based on solitons’ eigenvalues of the integrable higher-order nonlinear Schrödinger equation. Opt. Commun. 2017, 382, 639–645. [Google Scholar] [CrossRef]
- Akhmediev, N.; Soto-Crespo, J.M.; Devine, N. Breather turbulence versus soliton turbulence: Rogue waves, probability density functions, and spectral features. Phys. Rev. E 2016, 94, 022212. [Google Scholar] [CrossRef] [PubMed]
- Böhm, M.; Mitschke, F. Soliton radiation beat analysis. Phys. Rev. E 2006, 73, 066615. [Google Scholar] [CrossRef] [PubMed]
- Böhm, M.; Mitschke, F. Soliton content of arbitrarily shaped light pulses in fibers analysed using a soliton-radiation beat pattern. Appl. Phys. B 2007, 86, 407–411. [Google Scholar] [CrossRef]
- Böhm, M.; Mitschke, F. Solitons in lossy fibers. Phys. Rev. A 2007, 76, 063822. [Google Scholar] [CrossRef]
- Zajnulina, M.; Böhm, M.; Blow, K.; Rieznik, A.A.; Giannone, D.; Haynes, R.; Roth, M.M. Soliton radiation beat analysis of optical pulses generated from two continuous-wave lasers. Chaos 2015, 25, 103104. [Google Scholar] [CrossRef] [PubMed]
- Zajnulina, M.; Böhm, M.; Bodenmüller, D.; Blow, K.; Chavez Boggio, J.M.; Rieznik, A.A.; Roth, M.M. Characteristics and stability of soliton crystals in optical fibres for the purpose of optical frequency comb generation. Opt. Commun. 2017, 393, 95–102. [Google Scholar] [CrossRef]
- Hartwig, H.; Böhm, M.; Hause, A.; Mitschke, F. Slow oscillations of dispersion-managed solitons. Phys. Rev. A 2010, 81, 033810. [Google Scholar] [CrossRef]
- Mitschke, F.; Halama, I.; Schwache, A. Soliton Gas. Chaos Solitons Fractals 1999, 10, 913–920. [Google Scholar]
- Kruskal, M.D.; Zabusky, N.J. Interaction of “solitons” in a collisionless plasma and the recurrence of initial states. Phys. Rev. Lett. 1965, 15, 240–243. [Google Scholar]




© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mitschke, F.; Mahnke, C.; Hause, A. Soliton Content of Fiber-Optic Light Pulses. Appl. Sci. 2017, 7, 635. https://doi.org/10.3390/app7060635
Mitschke F, Mahnke C, Hause A. Soliton Content of Fiber-Optic Light Pulses. Applied Sciences. 2017; 7(6):635. https://doi.org/10.3390/app7060635
Chicago/Turabian StyleMitschke, Fedor, Christoph Mahnke, and Alexander Hause. 2017. "Soliton Content of Fiber-Optic Light Pulses" Applied Sciences 7, no. 6: 635. https://doi.org/10.3390/app7060635




