Remaining Useful Life Prediction of Hybrid Ceramic Bearings Using an Integrated Deep Learning and Particle Filter Approach
Abstract
:1. Introduction
2. Methodology
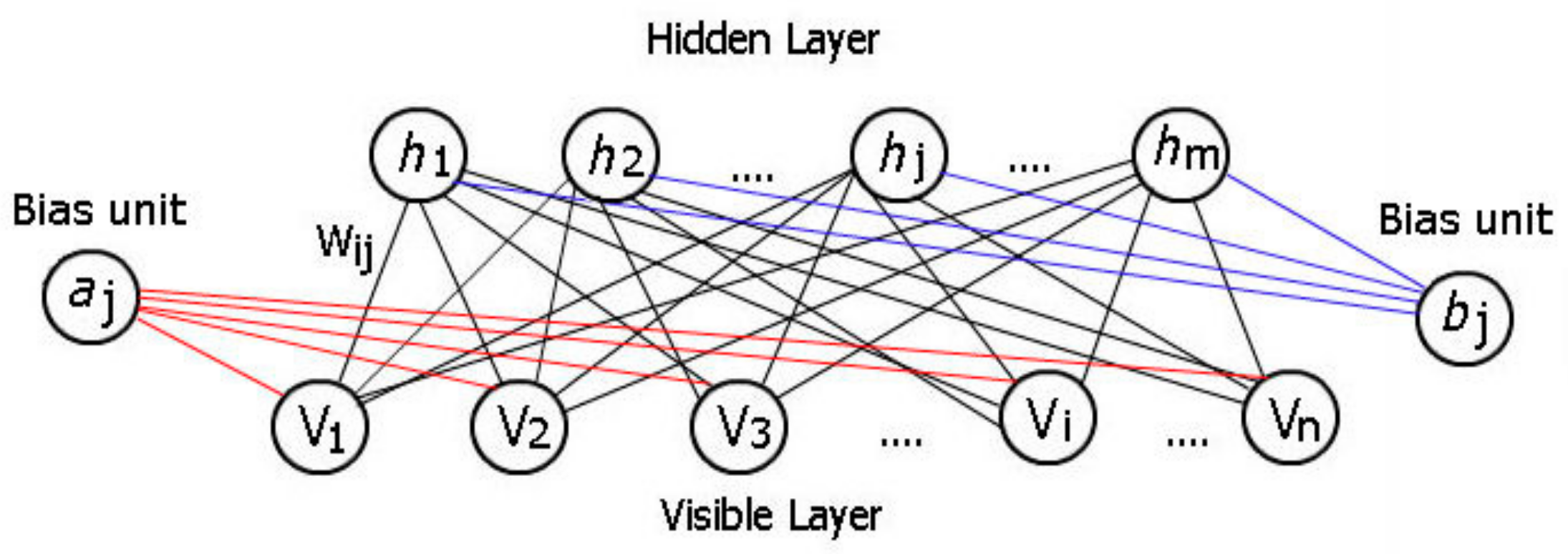
2.1. The Restricted Boltzmann Machine
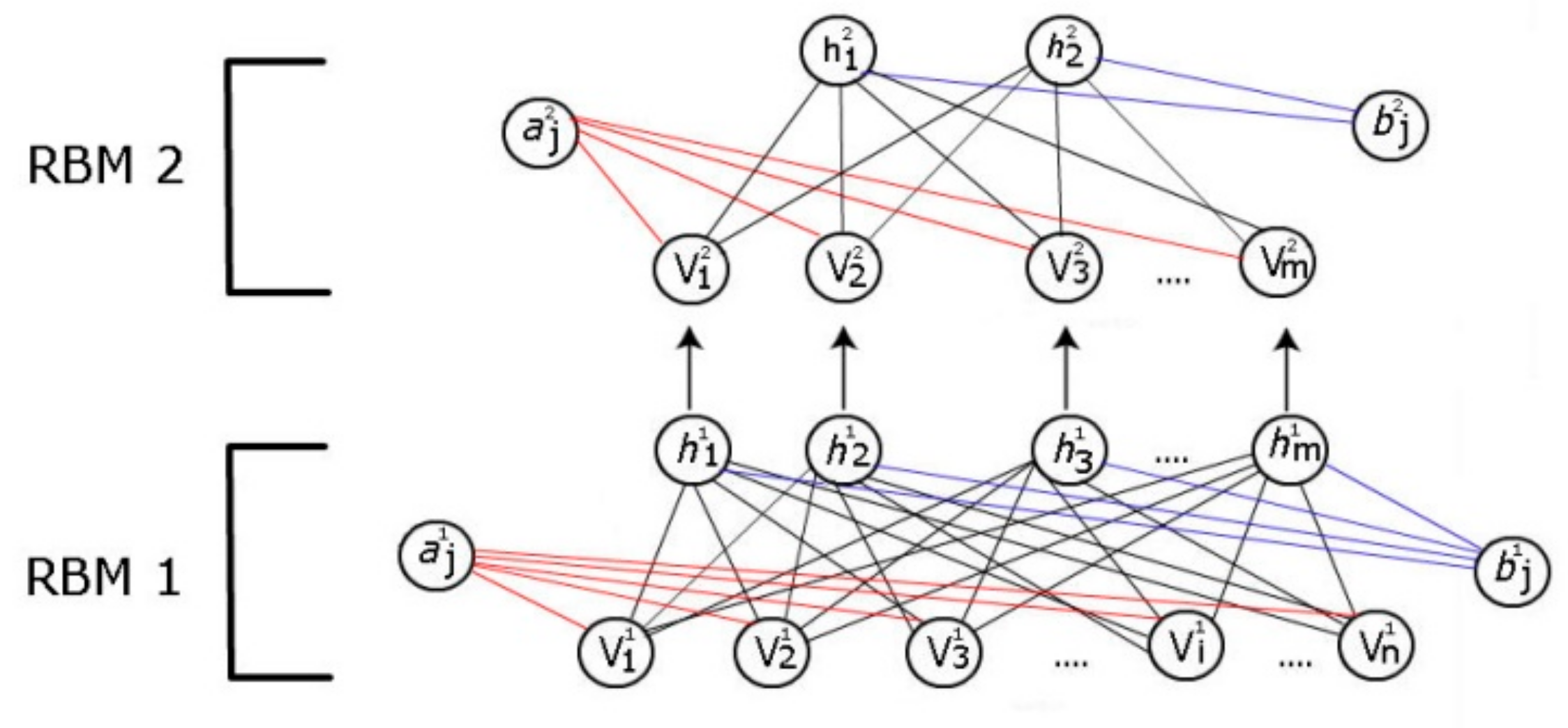
2.2. The Deep Belief Network
2.3. Particle Filter
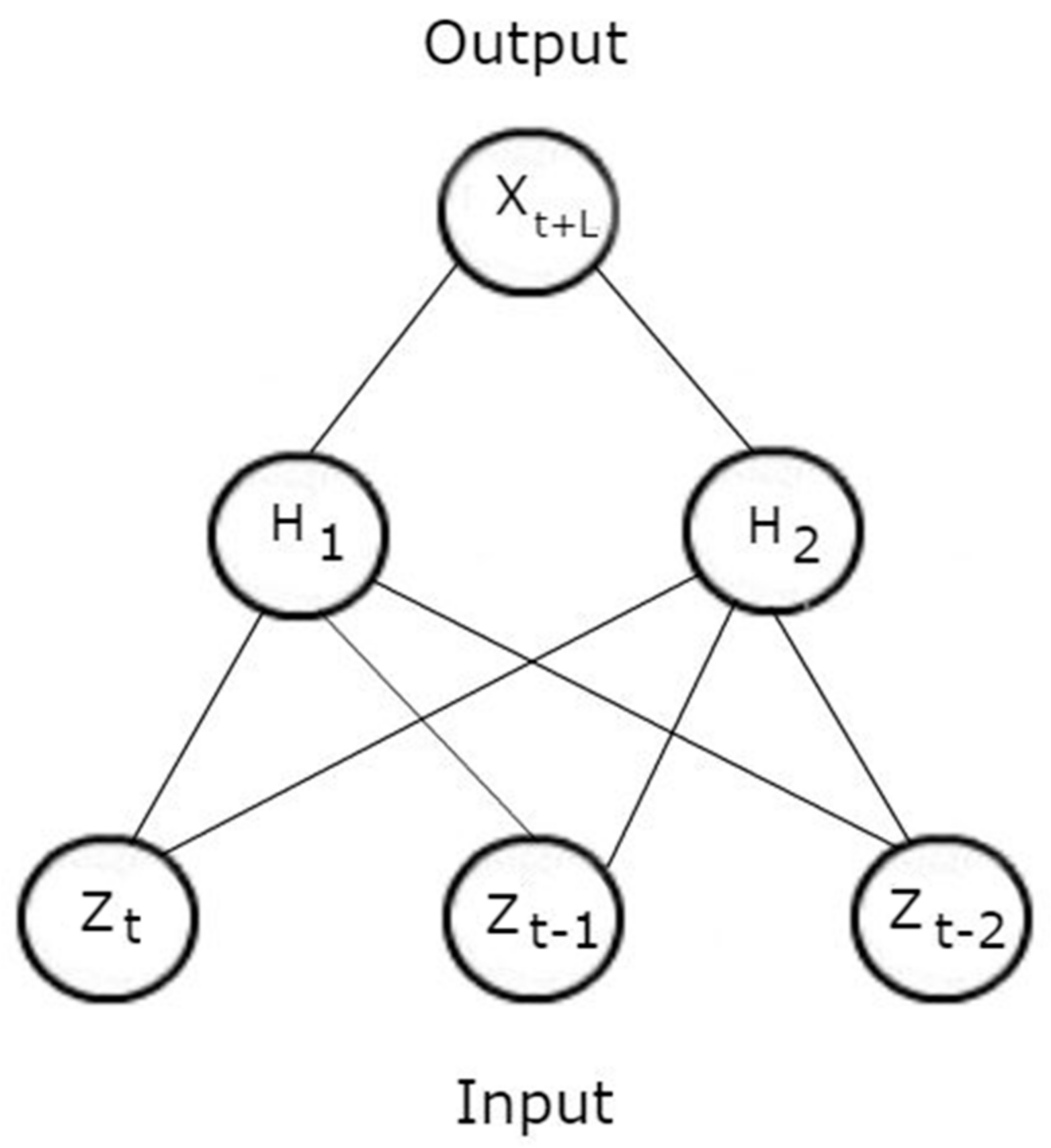
2.4. Combined DBN and Particle Filter-Based Approaches for RUL Prediction
| Step 1 | Let the last 100 rows be equal to the testing set, and set the rest of the data to the training set. | |
| Step 2 | Approximate the state transition model. | |
| a | Reconstruct the time series of the signal features into a matrix with an embedding dimension of . This will serve as the input, and the output will be the mapped state , where . | |
| b | Create bootstrapped data sets using the data created in Step 1. | |
| c | Initialize the weights and biases of the FNN by training the DBN on the input data with all the data except for the last 100 rows. The rest of the data is the testing set. | |
| d | Train the FNN. Fine tune the weights in a supervised fashion by minimizing the loss function on the training set and by using the back-propagation algorithm. | |
| e | Predict the . This is accomplished by subtracting the network’s output by L, i.e., = . | |
| f | Let , and update the training vector with input features . | |
| g | Repeat Steps 2e–2f, until all 100 points have been predicted. | |
| Step 3 | Estimate the measurement distribution. Create a new dataset of the form Generate B bootstraps from this training dataset and apply Equations (22)–(28) to obtain the measurement distribution. The DBN can be used for estimates in Equations (22) and (27). | |
| Step 4 | Estimate the state. The predicted state can be obtained by sampling with probability [from Equation (15)]. | |
3. Validation
3.1. Hybrid Ceramic Bearing Run-to-Failure Test Setup
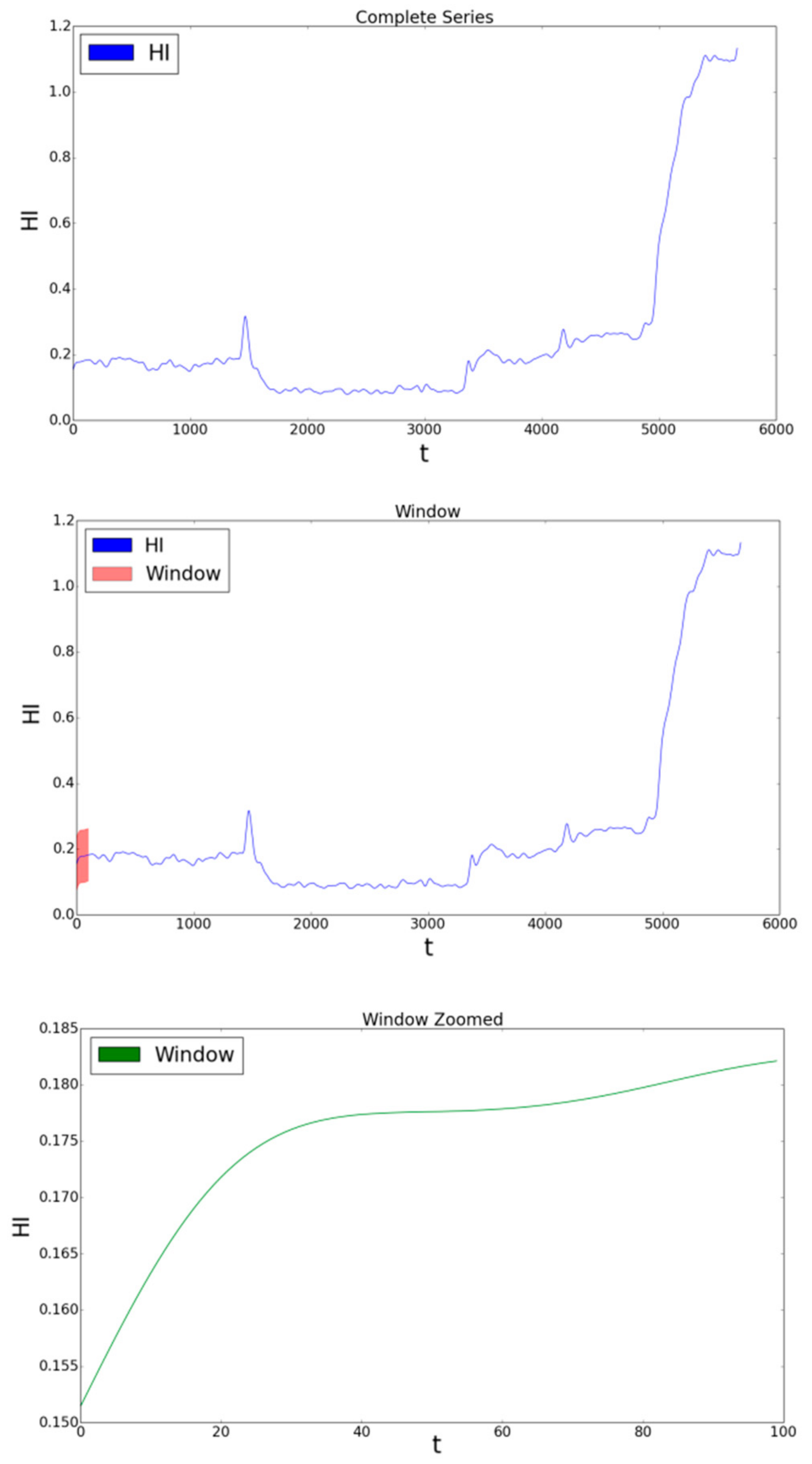
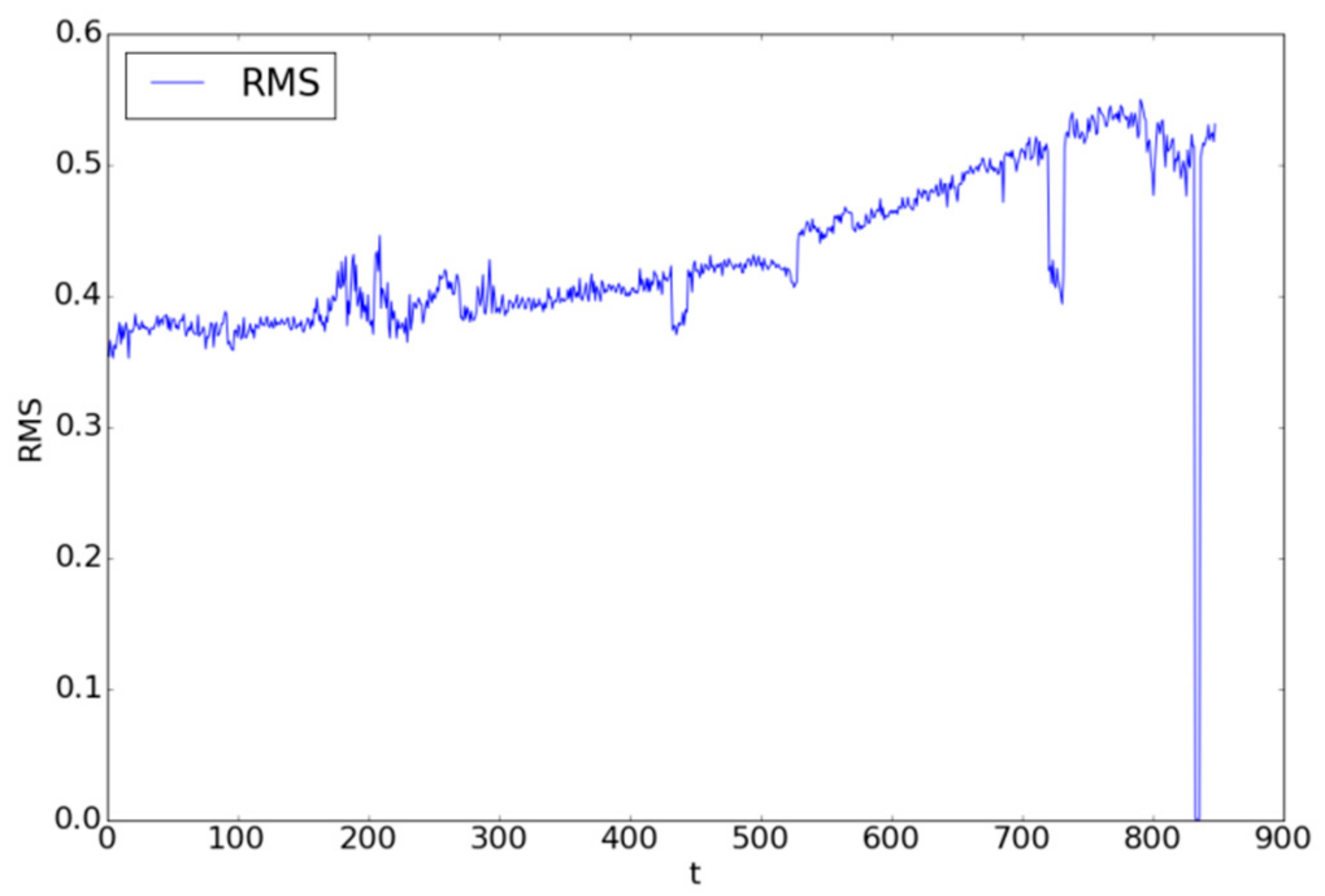
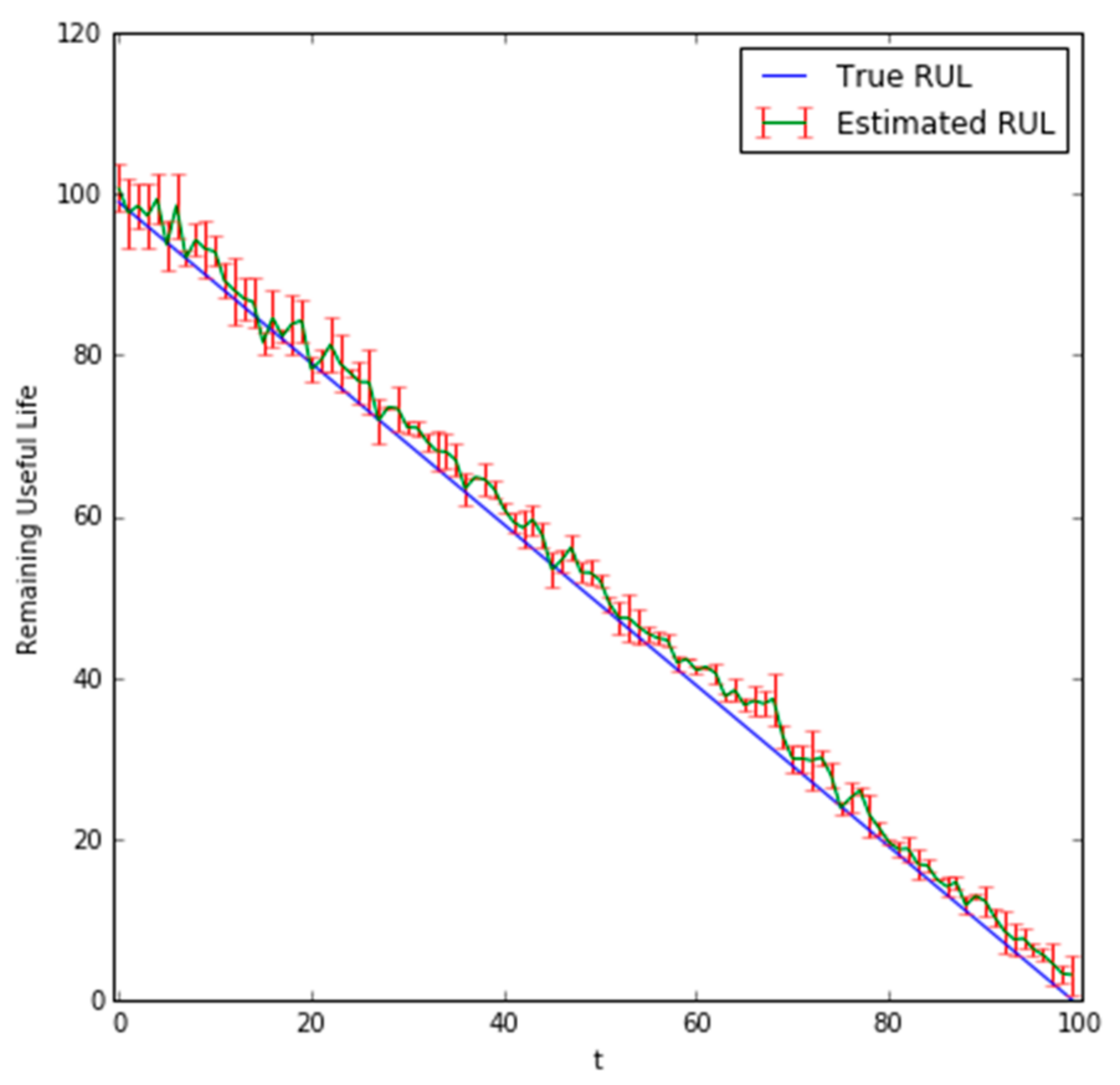
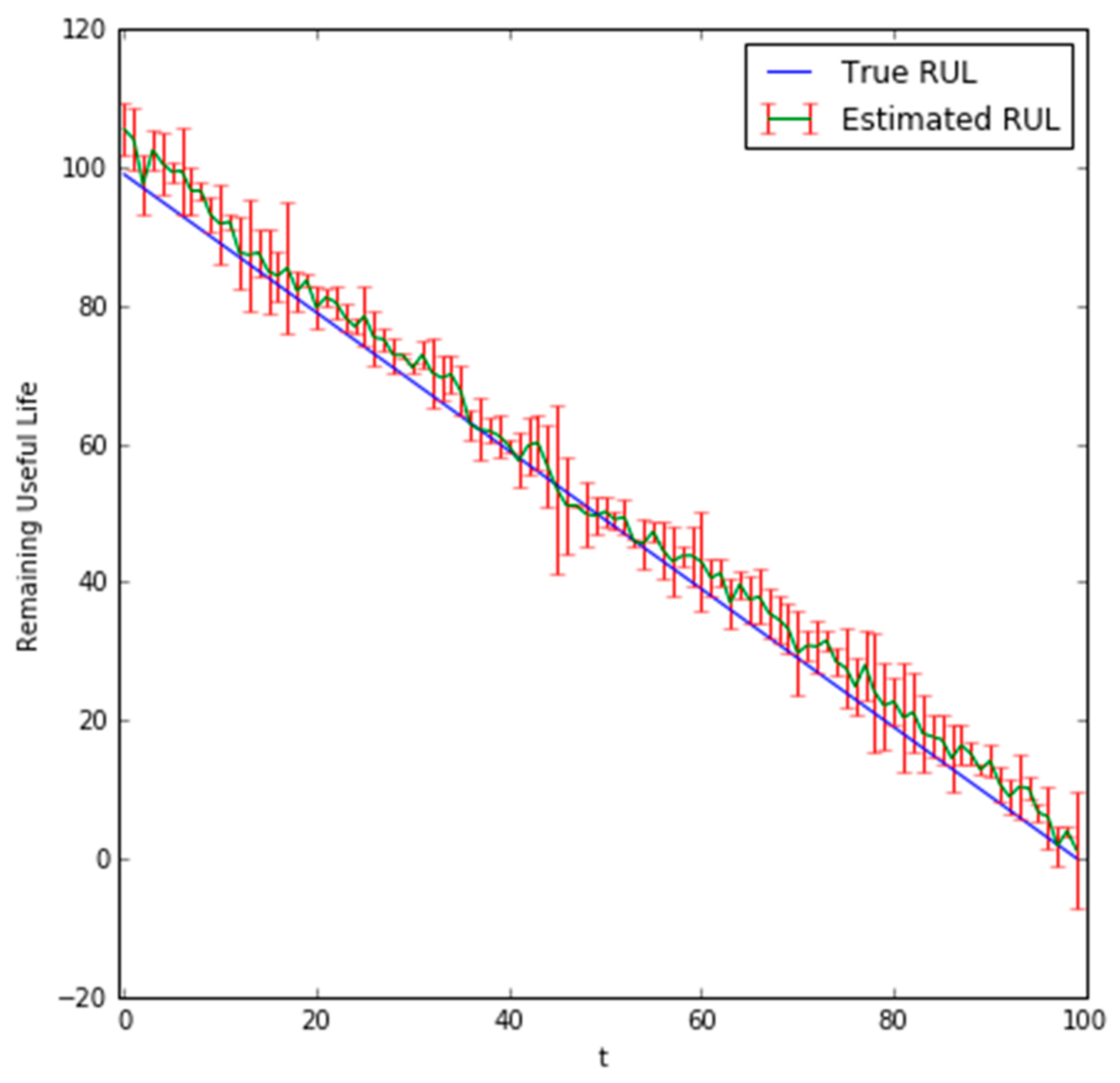
3.2. Hybrid Ceramic Bearing RUL Prediction Results
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Huynh, K.T.; Castro, I.T.; Barros, A.; Bérenguer, C. On the use of mean residual life as a condition index for condition-based maintenance decision-making. IEEE Trans. Syst. Man Cybern. Syst. 2014, 44, 877–893. [Google Scholar] [CrossRef]
- Vachtsevanos, G.; Lewis, F.L.; Roemer, M.; Hess, A.; Wu, B. Intelligent Fault Diagnosis and Prognosis for Engineering System; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Malhi, A.; Yan, R.; Gao, R.X. Prognosis of defect propagation based on recurrent neural networks. IEEE Trans. Instrum. Meas. 2011, 60, 703–711. [Google Scholar] [CrossRef]
- Heimes, F. Recurrent neural networks for remaining useful life estimation. In Proceedings of the 2008 IEEE International Conference of Prognostics and Health Management, Denver, CO, USA, 6–9 October 2008; pp. 1–6. [Google Scholar]
- Lim, P.; Goh, C.K.; Tan, K.C.; Dutta, P. Estimation of remaining useful life based on switching Kalman filter neural network ensemble. In Proceedings of the 2014 Annual Conference of the Prognostics and Health Management Society, Fort Worth, TX, USA, 29 September–2 October 2014; pp. 2–9. [Google Scholar]
- Baraldi, P.; Mangili, F.; Zio, E. A Kalman filter-based ensemble approach with application to turbine creep prognostics. IEEE Trans. Reliab. 2012, 61, 966–977. [Google Scholar] [CrossRef]
- Bechhoefer, E.; Clark, S.; He, D. A state space model for vibration based prognostics. In Proceedings of the 2010 Annual Conference of the Prognostics and Health Management Society, Portland, OR, USA, 10–16 October 2010. [Google Scholar]
- Codetta-Raiteri, D.; Portinale, L. Dynamic Bayesian networks for fault detection, identification, and recovery in autonomous spacecraft. IEEE Trans. Syst. Man Cybern. Syst. 2015, 45, 13–24. [Google Scholar] [CrossRef]
- Yin, X.; Li, Z. Reliable decentralized fault prognosis of discrete-event systems. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 1598–1603. [Google Scholar] [CrossRef]
- Daigle, M.J.; Goebel, K. Model-based prognostics with concurrent damage progression processes. IEEE Trans. Syst. Man Cybern. Syst. 2013, 43, 535–546. [Google Scholar] [CrossRef]
- Baraldi, P.; Compare, M.; Sauco, S.; Zio, E. Ensemble neural network-based particle filtering for prognostics. Mech. Syst. Signal Process. 2013, 41, 288–300. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, B.; Vachtsevanos, G.; Orchard, M. Machine condition prediction based on adaptive neuro–fuzzy and high-order particle filtering. IEEE Trans. Ind. Electron. 2011, 58, 4353–4364. [Google Scholar] [CrossRef]
- He, D.; Bechhoefer, E.; Ma, J.; Li, R. Particle filtering based gear prognostics using one-dimensional health index. In Proceedings of the 2011 Annual Conference of the Prognostics and Health Management Society, Montreal, QC, Canada, 25–29 September 2011. [Google Scholar]
- Daroogheh, N.; Baniamerian, A.; Meskin, N.; Khorasani, K. Prognosis and health monitoring of nonlinear systems using a hybrid scheme through integration of PFs and neural networks. IEEE Trans. Syst. Man Cybern. Syst. 2016, PP, 1–15. [Google Scholar] [CrossRef]
- Bououden, S.; Chadli, M.; Allouani, F.; Filali, S. A new approach for fuzzy predictive adaptive controller design using particle swarm optimization algorithm. Int. J. Innov. Comput. Inf. Control 2013, 9, 3741–3758. [Google Scholar]
- Arulampalam, M.S.; Makell, S.; Gordon, N.; Clapp, T. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Trans. Signal Process. 2002, 50, 174–188. [Google Scholar] [CrossRef]
- Yoon, J.; He, D. Development of an efficient prognostic estimator. J. Fail. Anal. Prev. 2015, 15, 129–138. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.-W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Zeng, X.; Li, W.; Liao, G. Machine fault classification using deep belief network. In Proceedings of the 2016 IEEE International Instrumentation and Measurement Technology Conference, Taipei, Taiwan, 23–26 May 2016; pp. 1–6. [Google Scholar]
- Shao, H.; Jiang, H.; Zhang, X.; Niu, M. Rolling bearing fault diagnosis using an optimization deep belief network. Meas. Sci. Technol. 2015, 26, 115002. [Google Scholar] [CrossRef]
- Lv, Y.; Duan, Y.; Kang, W.; Li, Z.; Wang, F.-Y. Traffic flow prediction with big data: A deep learning approach. IEEE Trans. Intell. Transp. Syst. 2015, 16, 865–873. [Google Scholar] [CrossRef]
- Hossain, M.; Rekabdar, B.; Louis, S.J.; Dascalu, S. Forecasting the weather of Nevada: A deep learning approach. In Proceedings of the 2015 International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 12–17 July 2015; pp. 1–6. [Google Scholar]
- Tao, Y.; Chen, H.; Qiu, C. Wind power prediction and pattern feature based on deep learning method. In Proceedings of the 2014 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Hong Kong, China, 7–10 December 2014; pp. 1–4. [Google Scholar]
- Oliveira, T.P.; Barbar, J.S.; Soares, A.S. Multilayer perceptron and stacked autoencoder for Internet traffic prediction. In Proceedings of the 11th IFIP International Conference on Network and Parallel Computing (NPC), Ilan, Taiwan, 18–20 September 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 61–71. [Google Scholar]
- Deutsch, J.; He, D. Using deep learning based approach to predict remaining useful life of rotating components. IEEE Trans. Syst. Man Cybern. Syst. 2017, PP, 1–10. [Google Scholar] [CrossRef]
- Smolensky, P. Information Processing in Dynamical Systems: Foundations of Harmony Theory. In Parallel Distributed Processing: Explorations in the Microstructure of Cognition, Volume 1: Foundations; MIT Press: Cambridge, MA, USA, 1986; Chapter 6; pp. 194–281. [Google Scholar]
- Hinton, G.E. Training products of experts by minimizing contrastive divergence. Neural Comput. 2002, 14, 1711–1800. [Google Scholar] [CrossRef] [PubMed]
- Bengio, Y.; Lamblin, P.; Popovici, D.; Larochelle, H. Greedy layer-wise training of deep networks. In Proceedings of the 19th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 4–7 December 2006; MIT Press: Cambridge, MA, USA, 2006; Volume 19, pp. 153–160. [Google Scholar]
- Erhan, D.; Bengio, Y.; Courville, A.; Manzagol, P.; Vincent, P.; Bengio, S. Why does unsupervised pre-training help deep learning? J. Mach. Learn. Res. 2010, 11, 625–660. [Google Scholar]
- Gordon, N.; Salmond, D.; Smith, A. Novel approach to nonlinear/non-Gaussian Bayesian state estimation. IEE Proc. F Radar Signal Process. 1993, 140, 107–113. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Frank, R.J.; Davey, N.; Hunt, S.P. Time series prediction and neural networks. J. Intell. Robot. Syst. 2001, 31, 91–103. [Google Scholar] [CrossRef]
- Khosravi, A.; Nahavandi, S.; Creighton, D.; Atiya, A.F. Comprehensive review of neural network-based prediction intervals and new advances. IEEE Trans. Neural Netw. 2011, 22, 1341–1356. [Google Scholar] [CrossRef] [PubMed]
- Al-Dahidi, S.; Di Maio, F.; Baraldi, P.; Zio, E. Remaining useful life estimation in heterogeneous fleets working under variable operating conditions. Reliab. Eng. Syst. Saf. 2016, 156, 109–124. [Google Scholar] [CrossRef]
- Saxena, A.; Celaya, J.; Saha, B.; Saha, S.; Goebel, K. Metrics for offline evaluation of prognostic performance. Int. J. Progn. Health Manag. 2010, 1, 4–23. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2002, 13, 281–305. [Google Scholar]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep sparse rectifier neural networks. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics (AISTATS), Ft. Lauderdale, FL, USA, 11–13 April 2011; pp. 315–323. [Google Scholar]
- Maio, F.; Zio, E. Failure prognostics by a data-driven similarity-based approach. Int. J. Reliab. Qual. Saf. Eng. 2013, 20, 1–17. [Google Scholar]

| Test Bearing Name | Type of Bearing | Load (psi) | Input Shaft Speed (hz) |
|---|---|---|---|
| B2 | Hybrid ceramic bearing | 600 | 30 |
| Parameter | Specification |
|---|---|
| Bearing material | Stainless steel 440c |
| Ball material | Ceramic SI3N4 |
| Inner diameter (d) | 25 mm |
| Outer diameter (D) | 52 mm |
| Width | 15 mm |
| Enclosure | Two shields |
| Enclosure material | Stainless steel |
| Enclosure type | Removable (S) |
| Retainer material | Stainless steel |
| ABEC/ISO rating | ABEC #3/ISOP6 |
| Radial play | C3 |
| Lube | Klubber L55 grease |
| RPM grease (×1000 rpm) | 19 |
| RPM oil (×1000): | 22 |
| Dynamic load (kgf) | 1429 |
| Basic load (kgf) | 804 |
| Working temperature (°C) | 121 |
| Weight (g) | 110.32 |
| Combined DBN and Particle Filter-Based Approach | |||
|---|---|---|---|
| RMSE | MAPE | Accuracy (α = 10%) | |
| 1 | 2.04 | 7.33% | 0.80 |
| 10 | 3.52 | 8.68% | 0.61 |
| Particle Filter-Based Approach | |||
| RMSE | MAPE | Accuracy (α = 10%) | |
| 1 | 2.53 | 7.47% | 0.71 |
| 10 | 3.65 | 8.73% | 0.53 |
| DBN Learning Rate | DBN Epochs | Hidden Layer Structure | FNN Learning Rate | FNN Epochs | |
|---|---|---|---|---|---|
| 1 | 0.002 | 74 | [146, 53] | 0.0017 | 176 |
| 10 | 0.0023 | 82 | [120, 54] | 0.0014 | 92 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deutsch, J.; He, M.; He, D. Remaining Useful Life Prediction of Hybrid Ceramic Bearings Using an Integrated Deep Learning and Particle Filter Approach. Appl. Sci. 2017, 7, 649. https://doi.org/10.3390/app7070649
Deutsch J, He M, He D. Remaining Useful Life Prediction of Hybrid Ceramic Bearings Using an Integrated Deep Learning and Particle Filter Approach. Applied Sciences. 2017; 7(7):649. https://doi.org/10.3390/app7070649
Chicago/Turabian StyleDeutsch, Jason, Miao He, and David He. 2017. "Remaining Useful Life Prediction of Hybrid Ceramic Bearings Using an Integrated Deep Learning and Particle Filter Approach" Applied Sciences 7, no. 7: 649. https://doi.org/10.3390/app7070649






