The New Concept of Nano-Device Spectroscopy Based on Rabi–Bloch Oscillations for THz-Frequency Range
Abstract
:1. Introduction
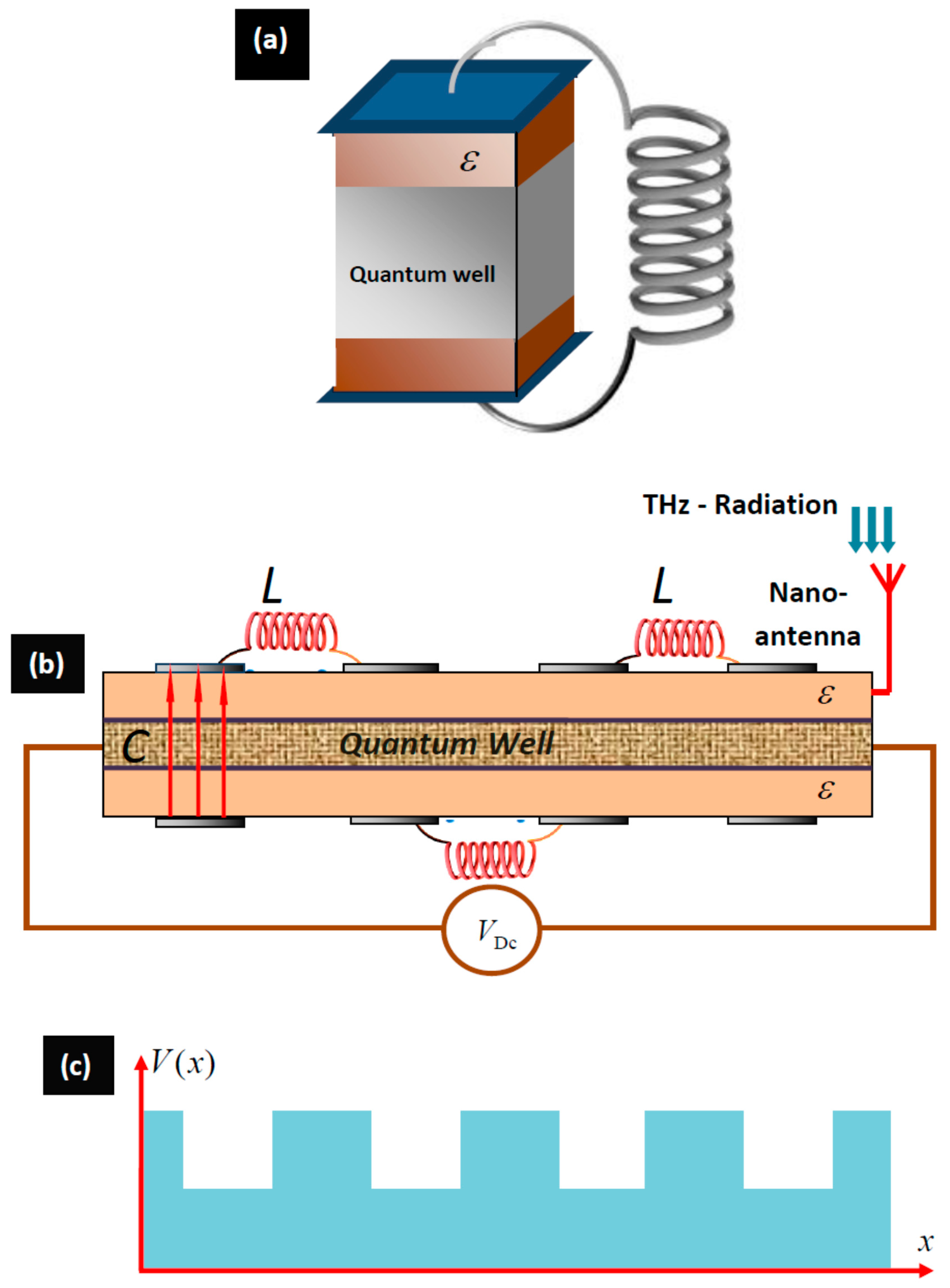
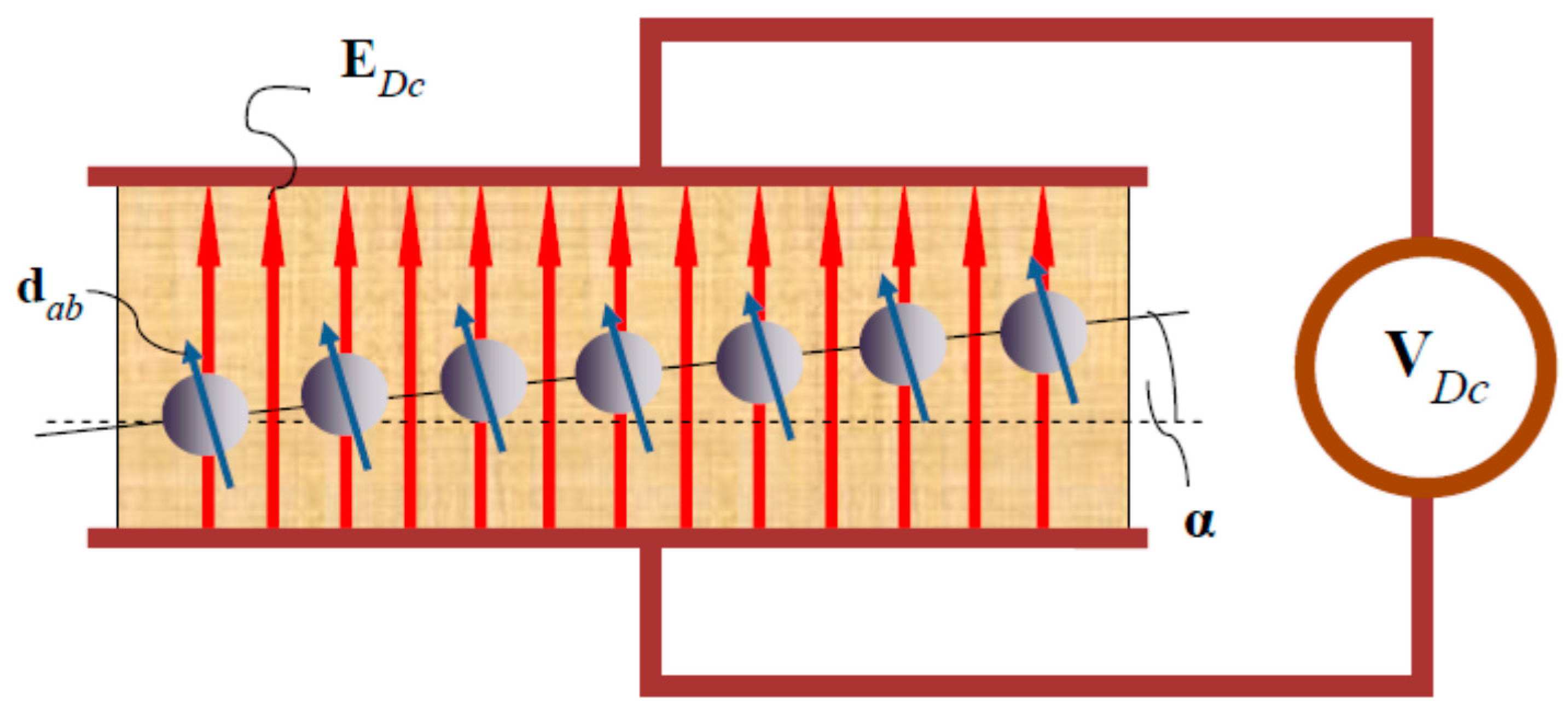
2. Structures and Models
3. Strong Coupling Regime: Analytical Approximation
3.1. Travelling Rabi-Waves
3.2. Tunneling Current
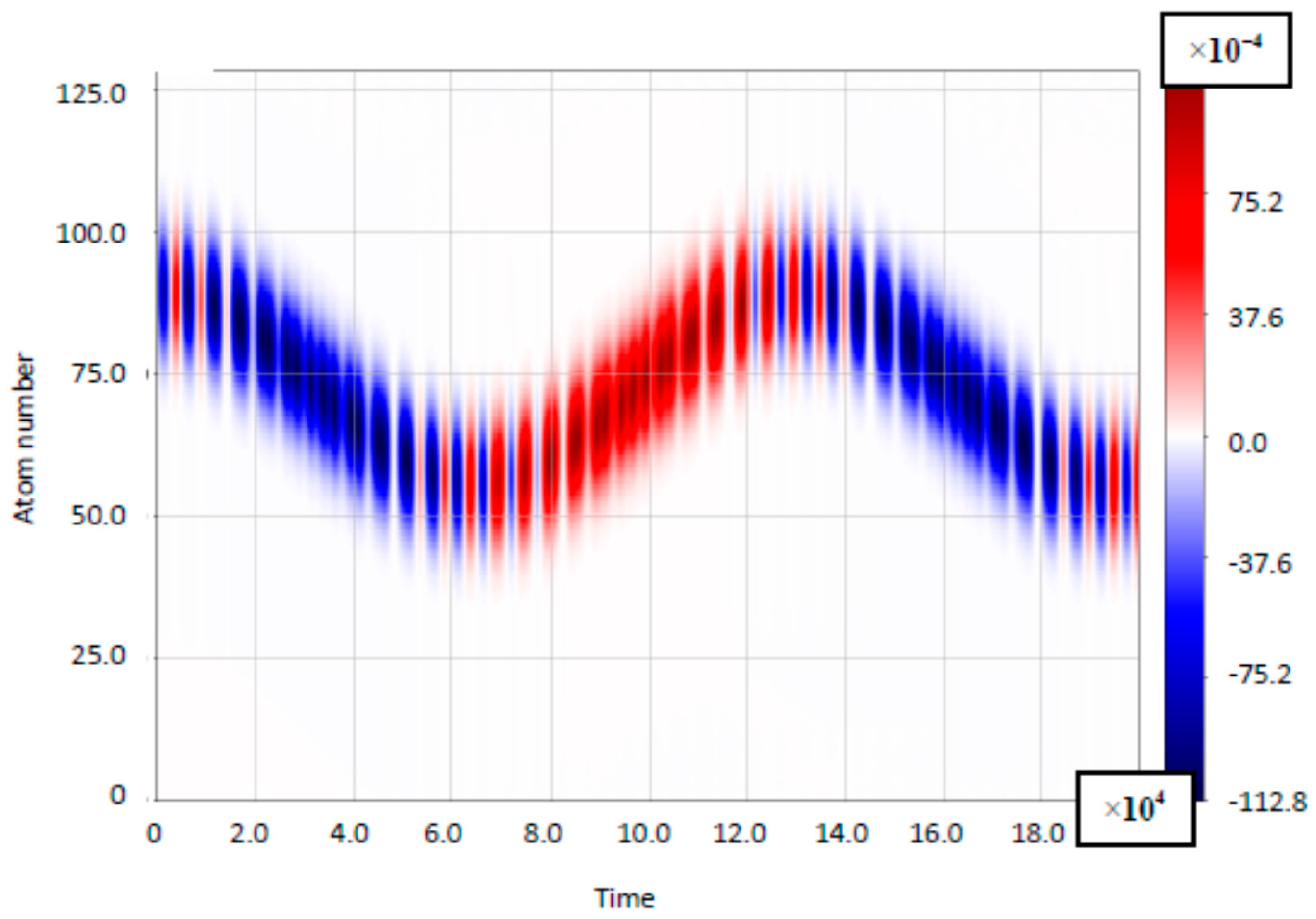
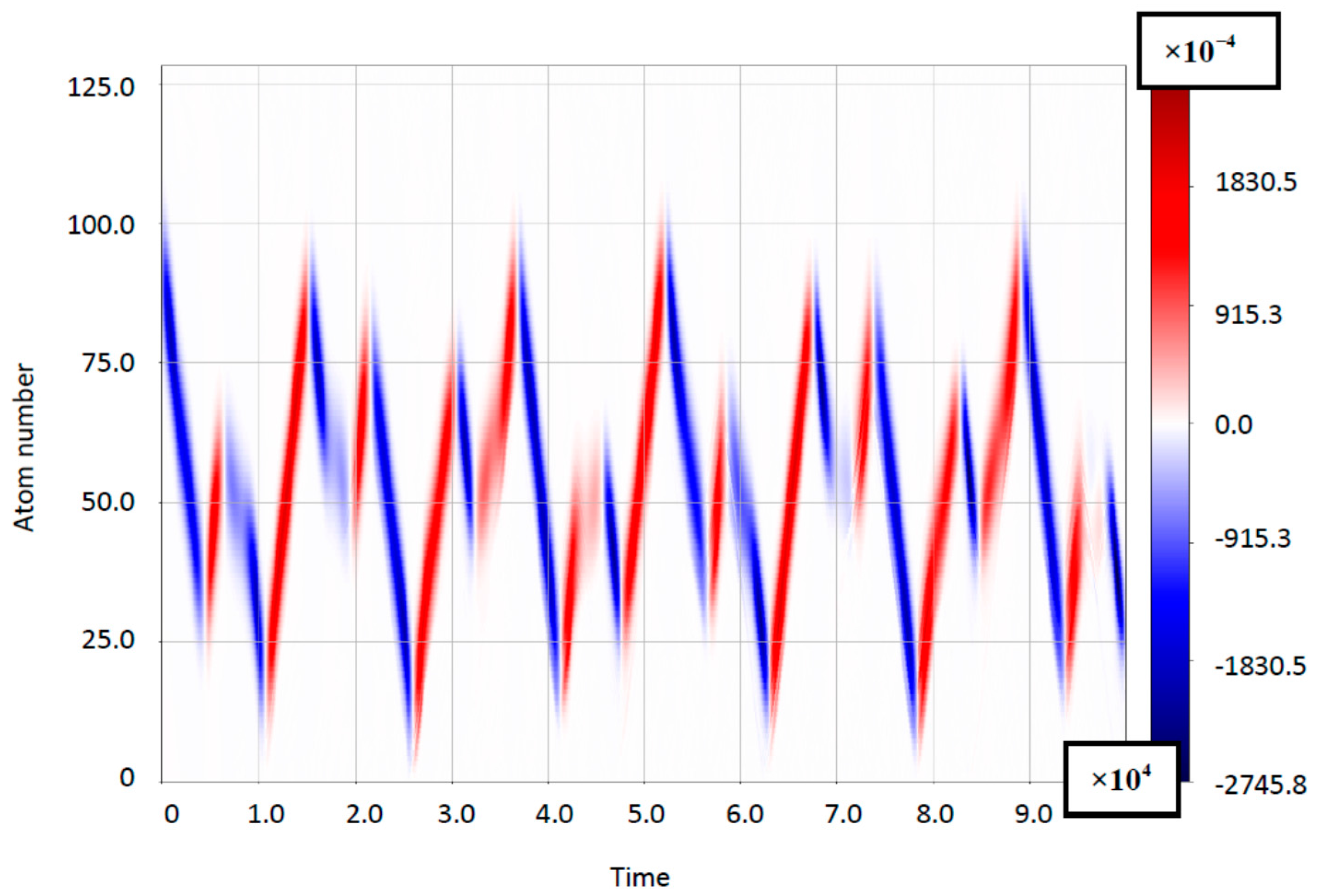
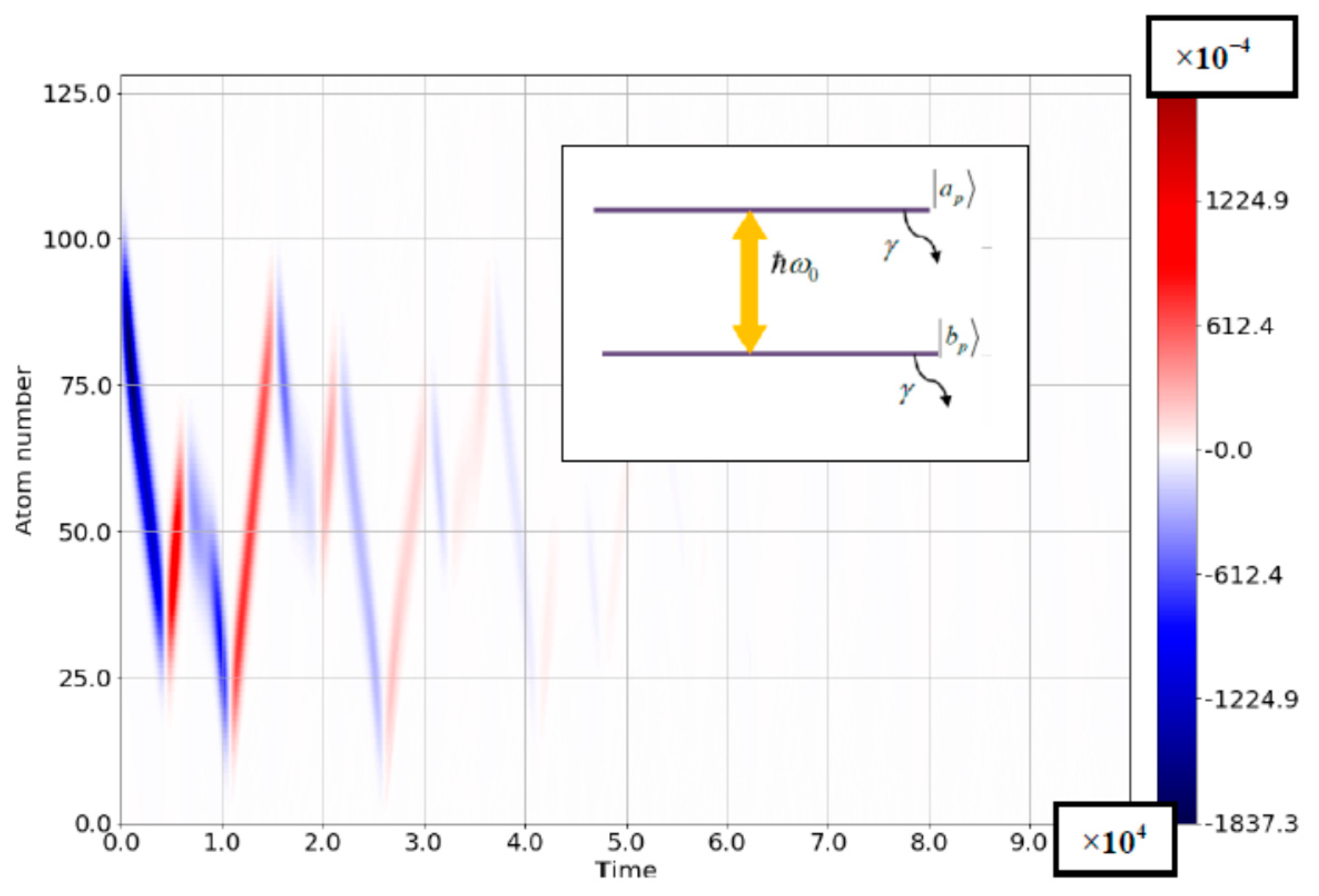
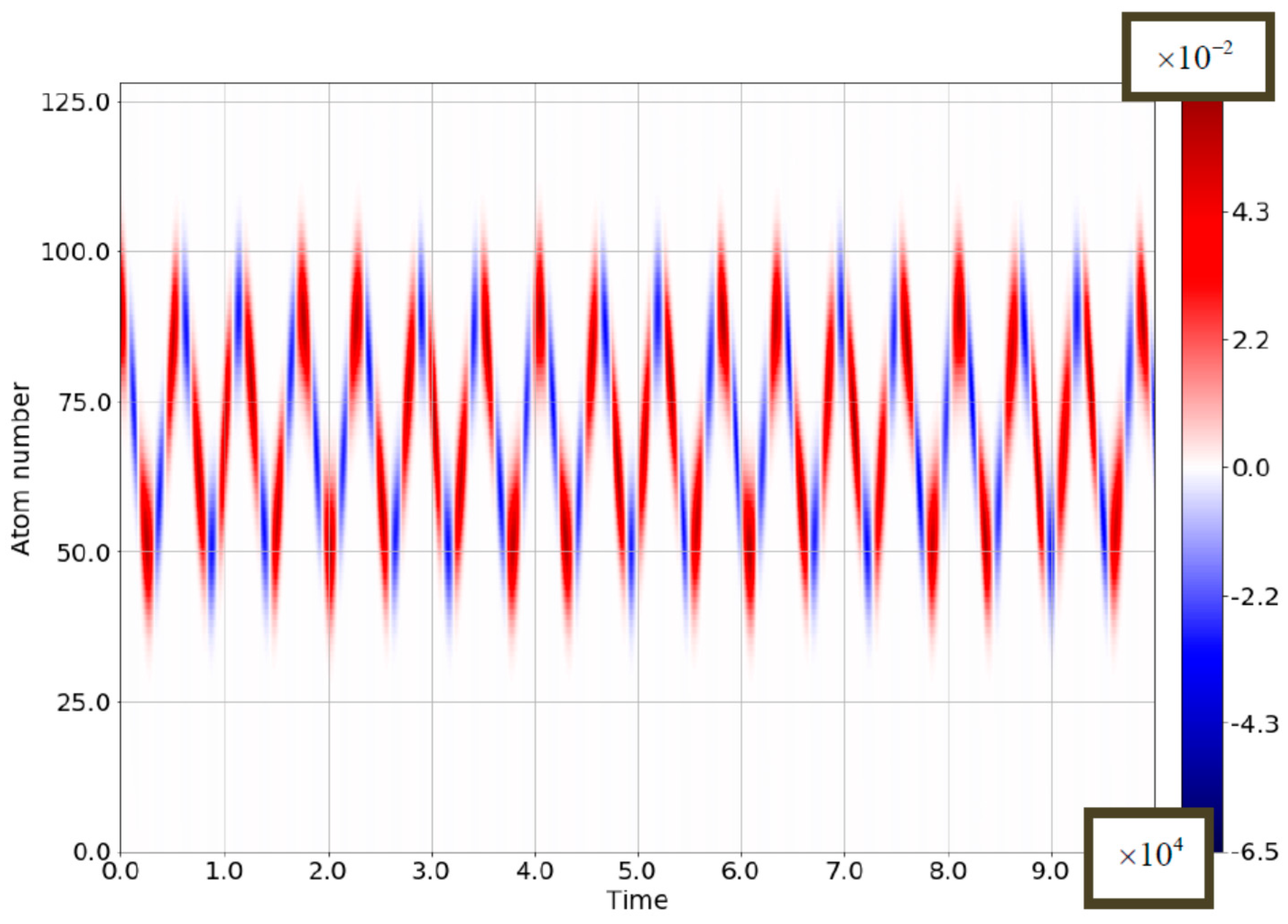
3.3. Rabi–Bloch Oscillations: Quasiclassical Model
4. Ultrastrong Coupling: Results and Discussion
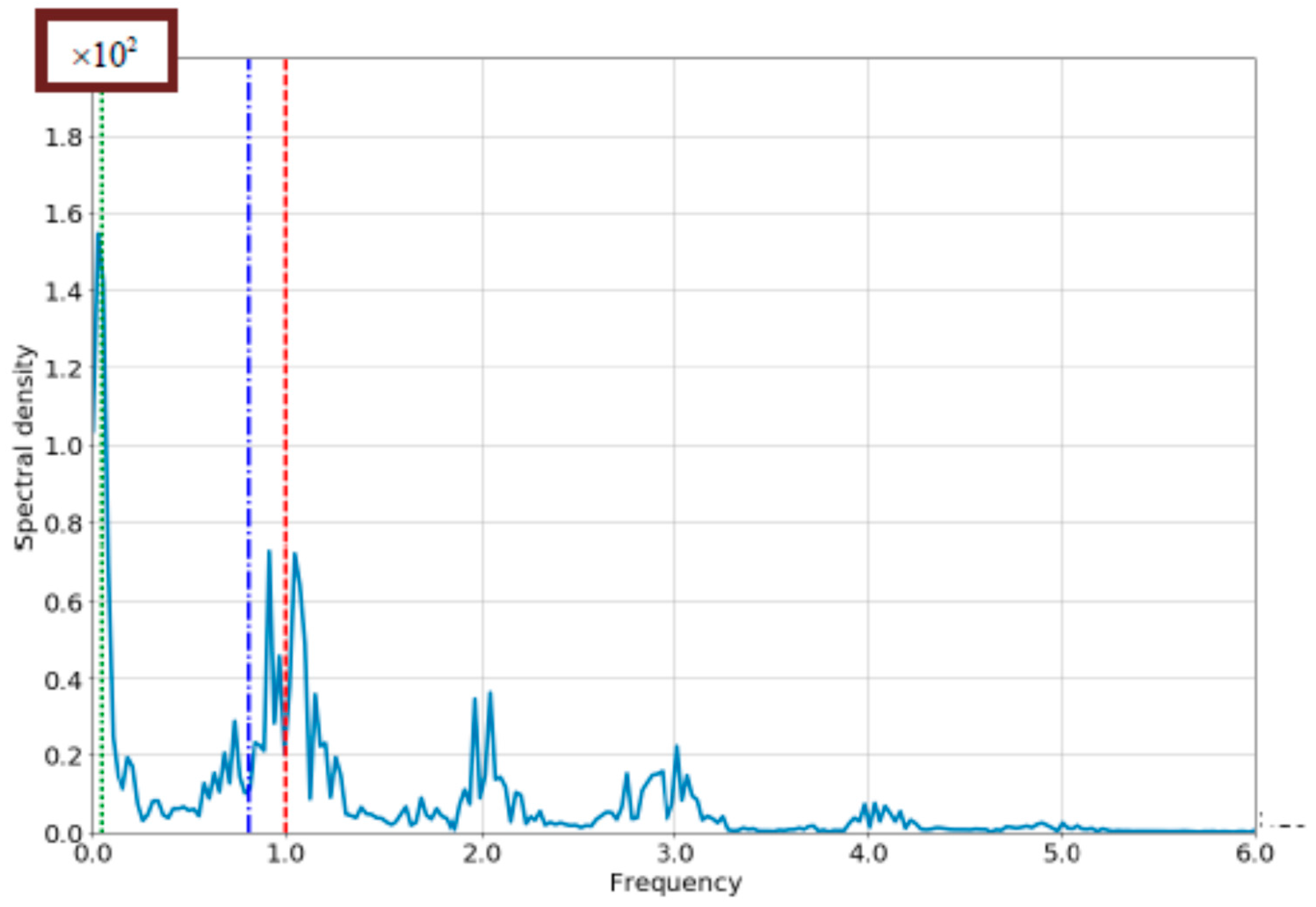
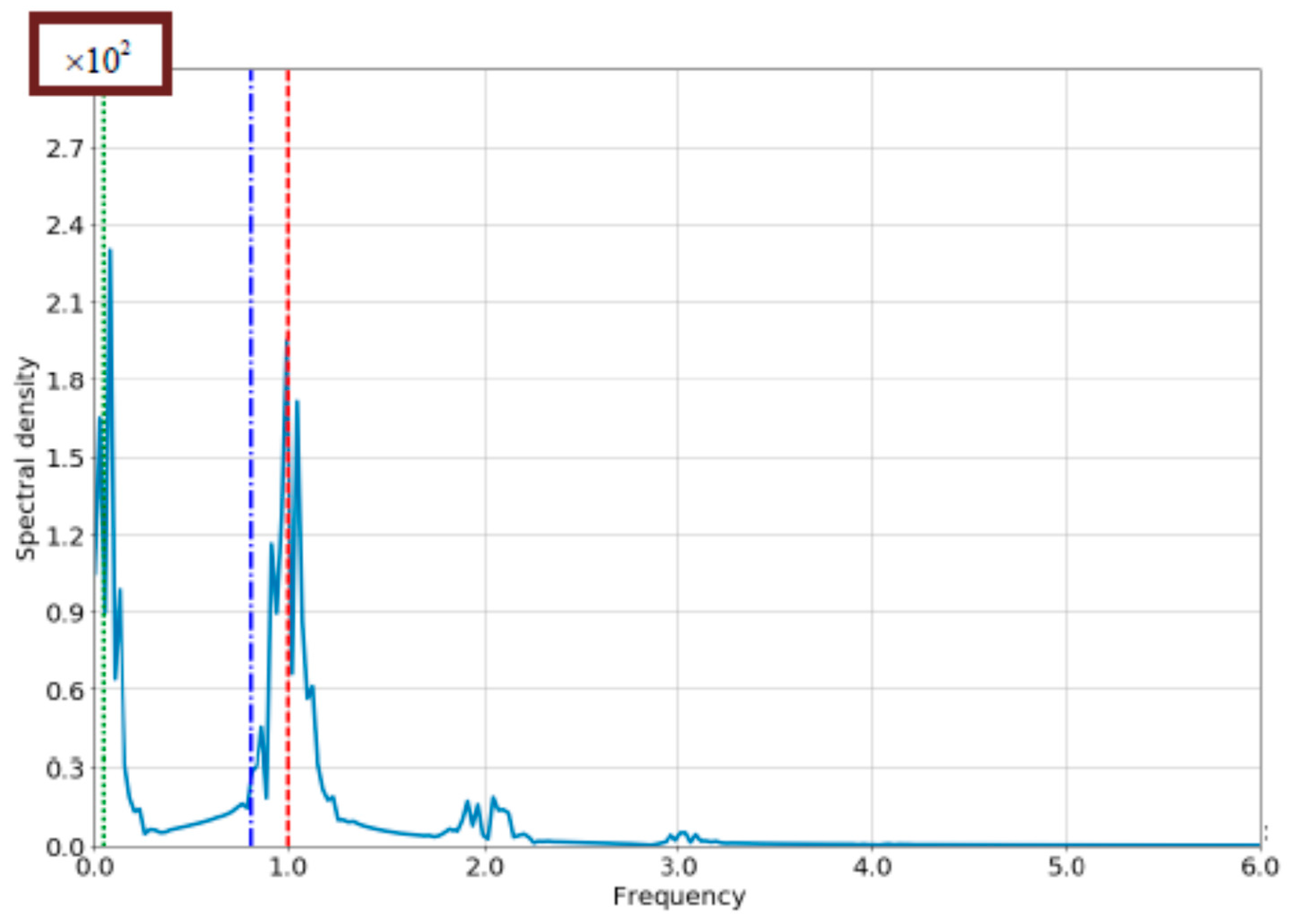
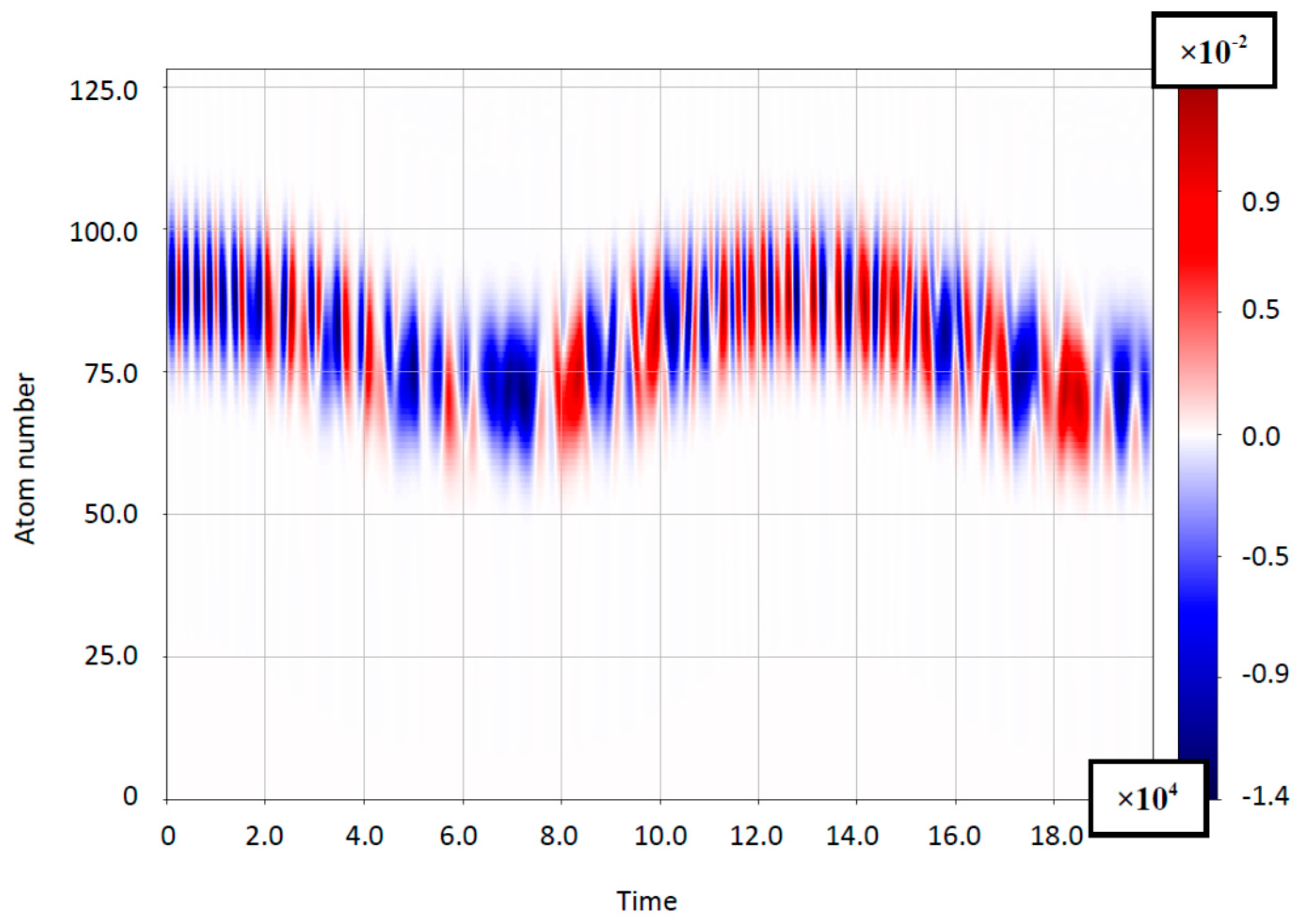
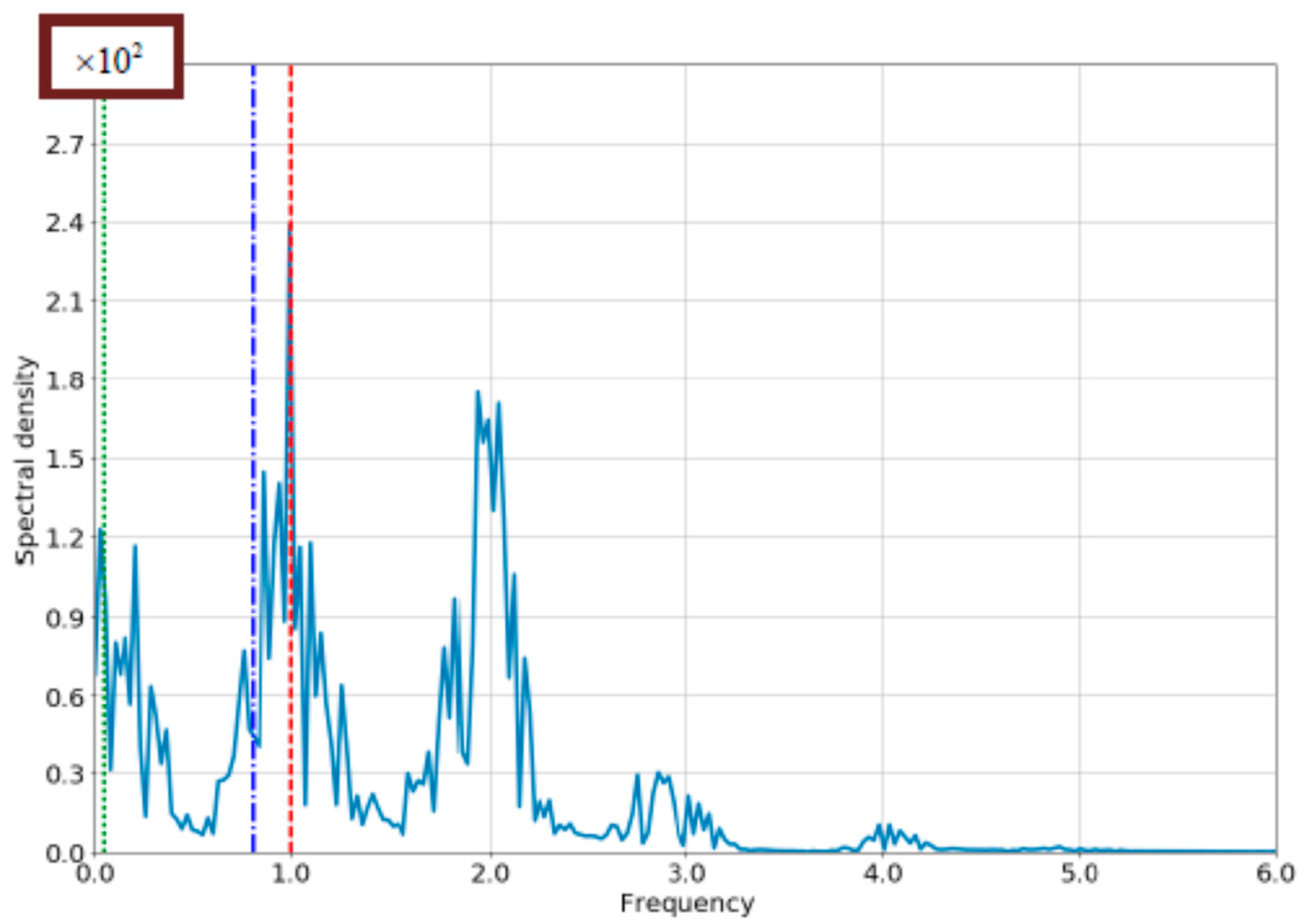
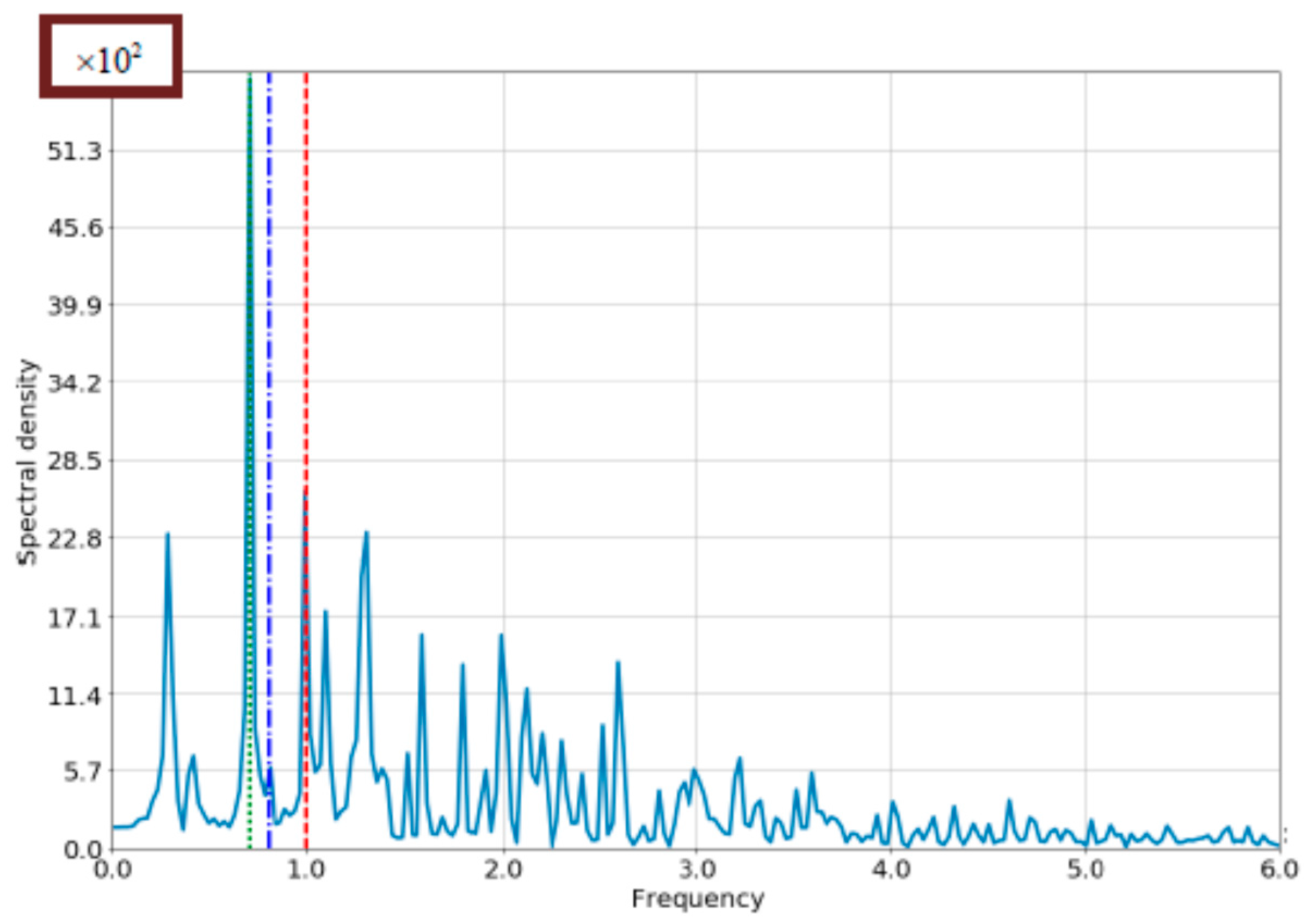
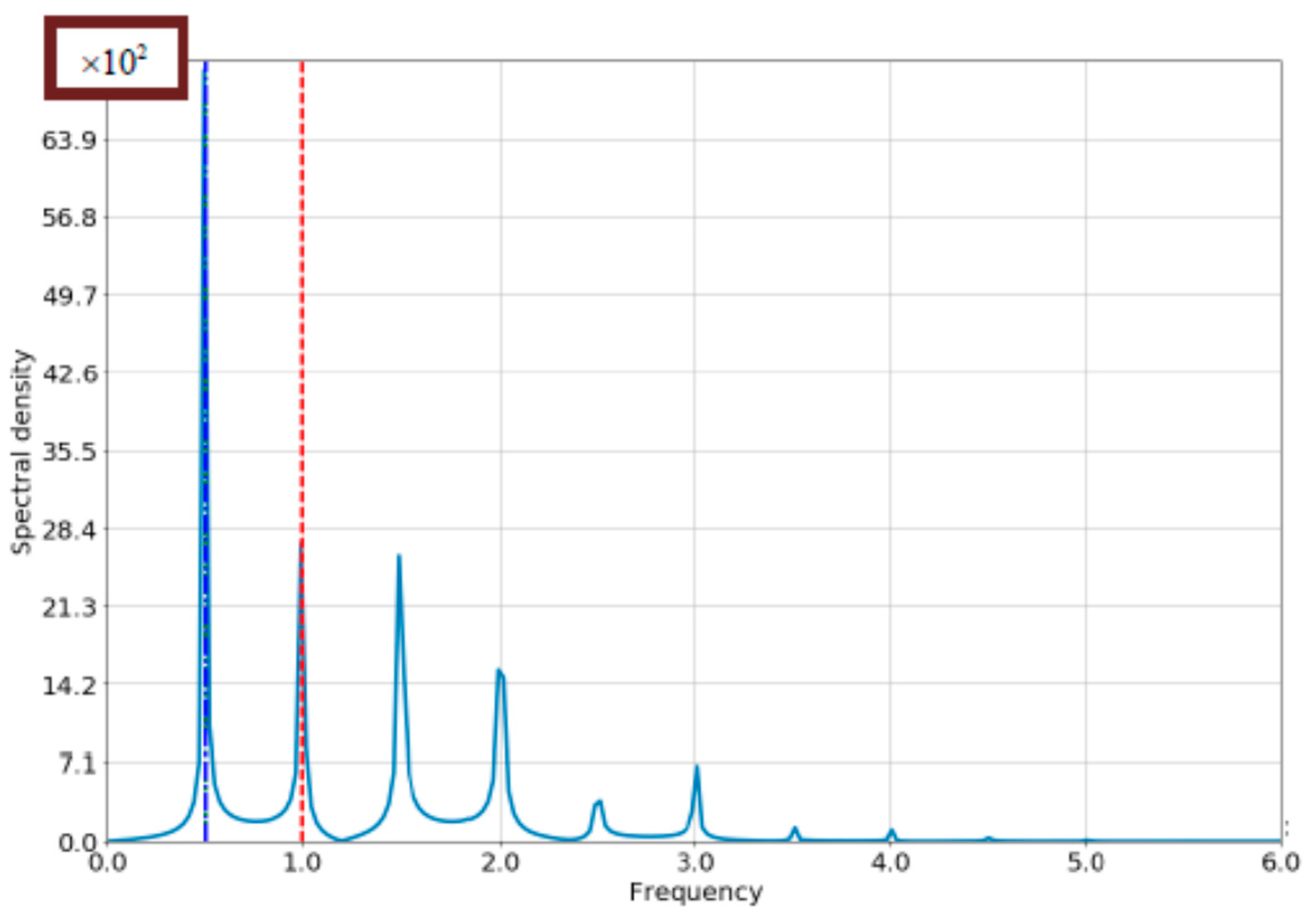
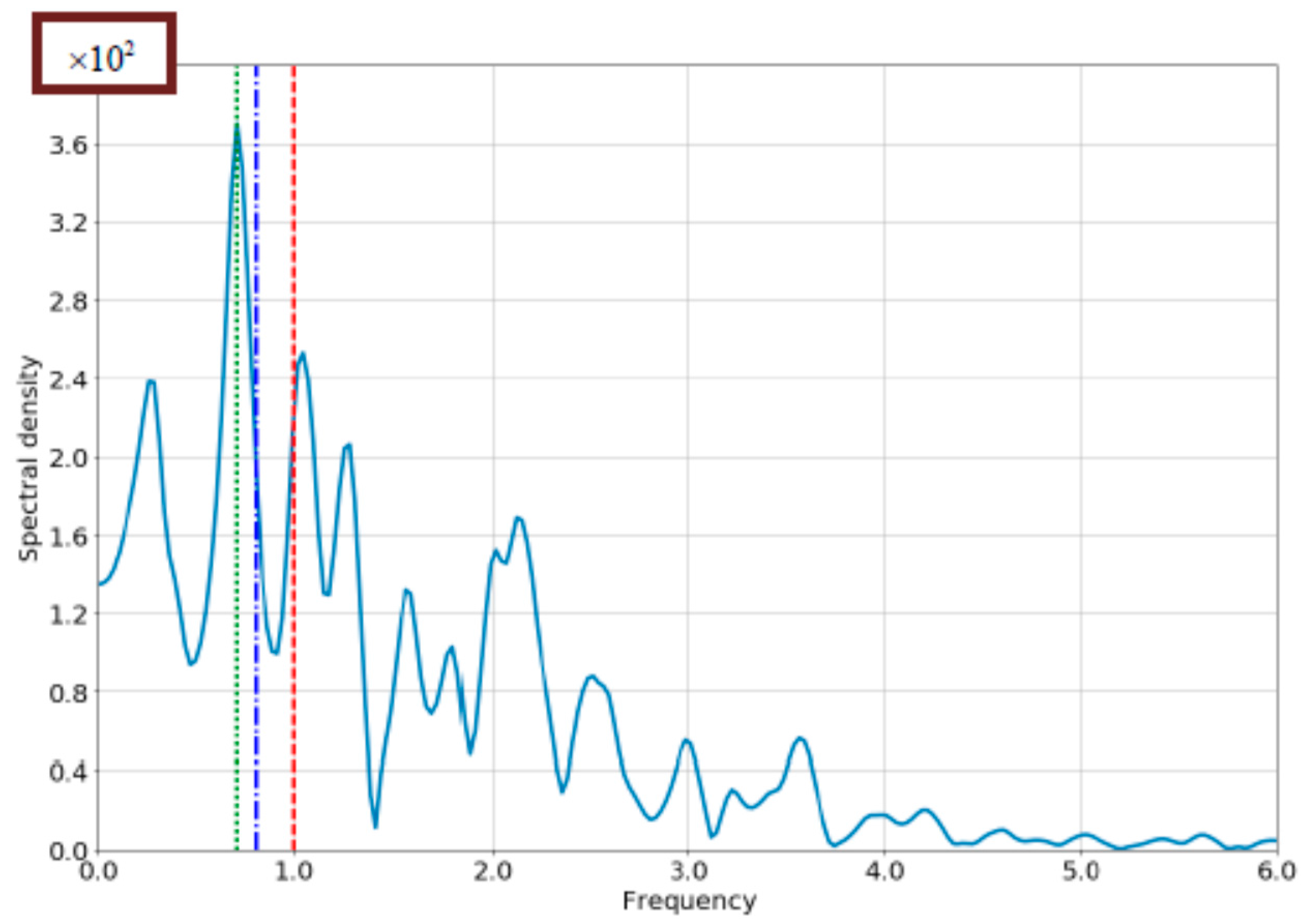
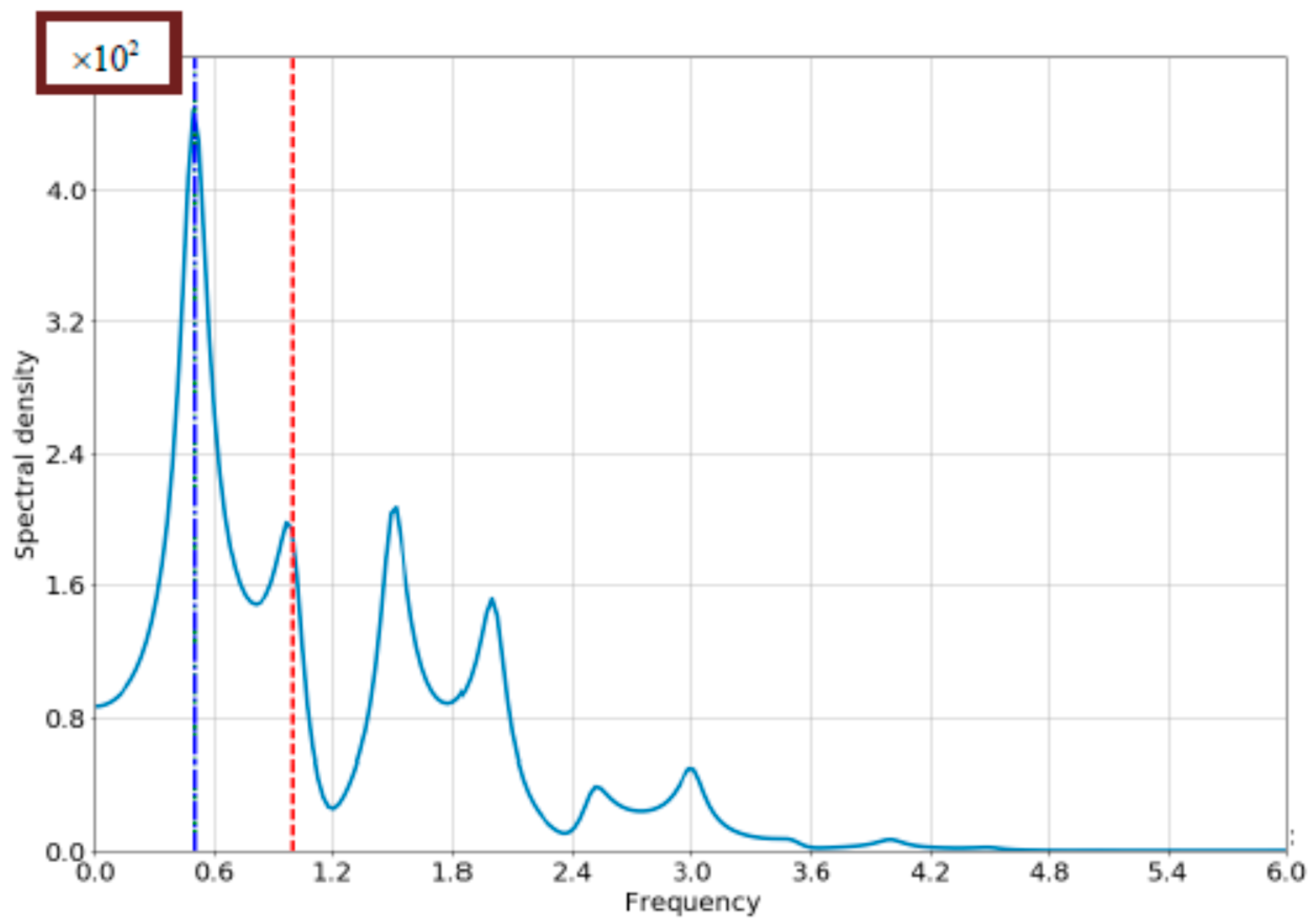
4.1. The Case of Small Bloch-Frequency
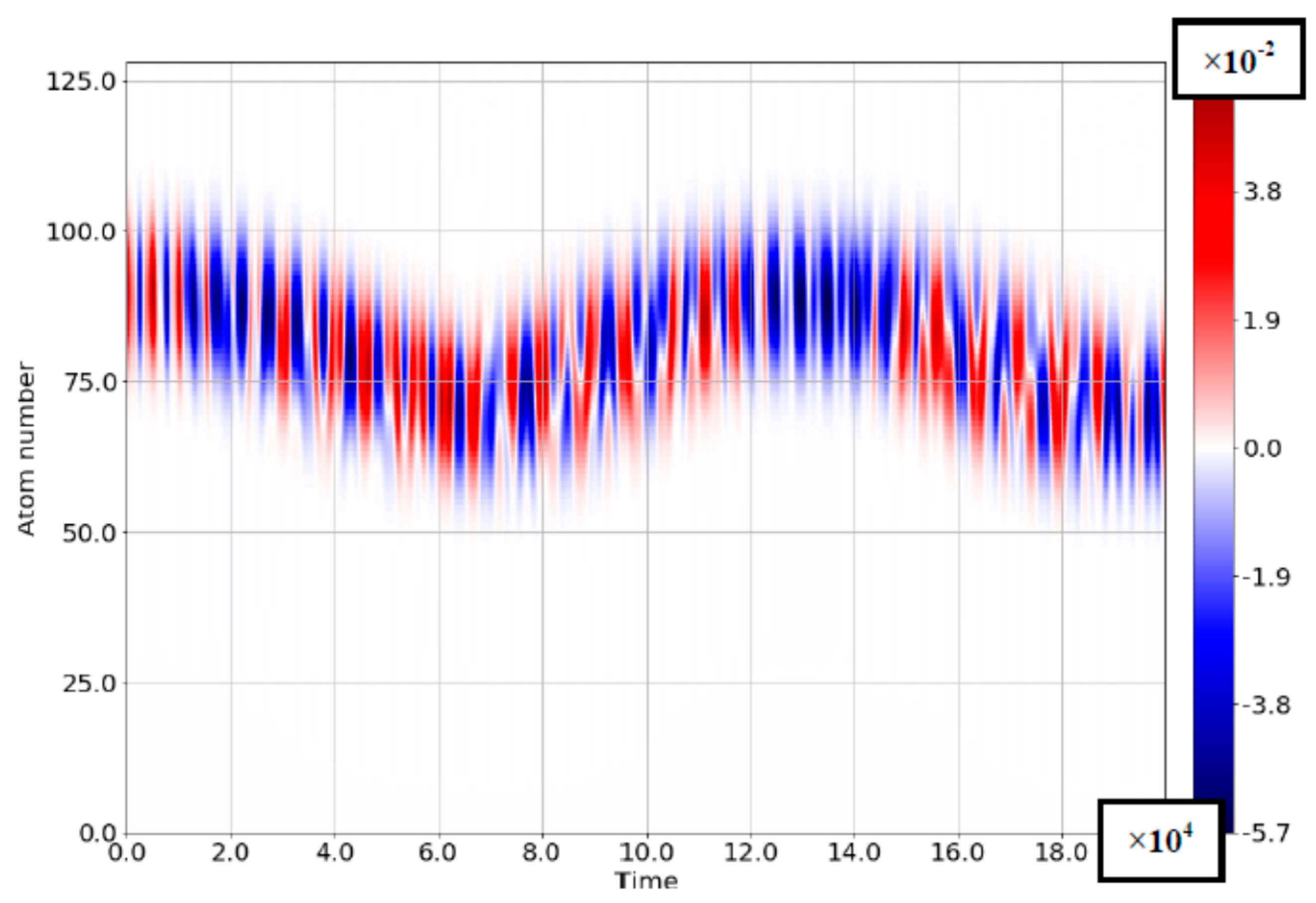
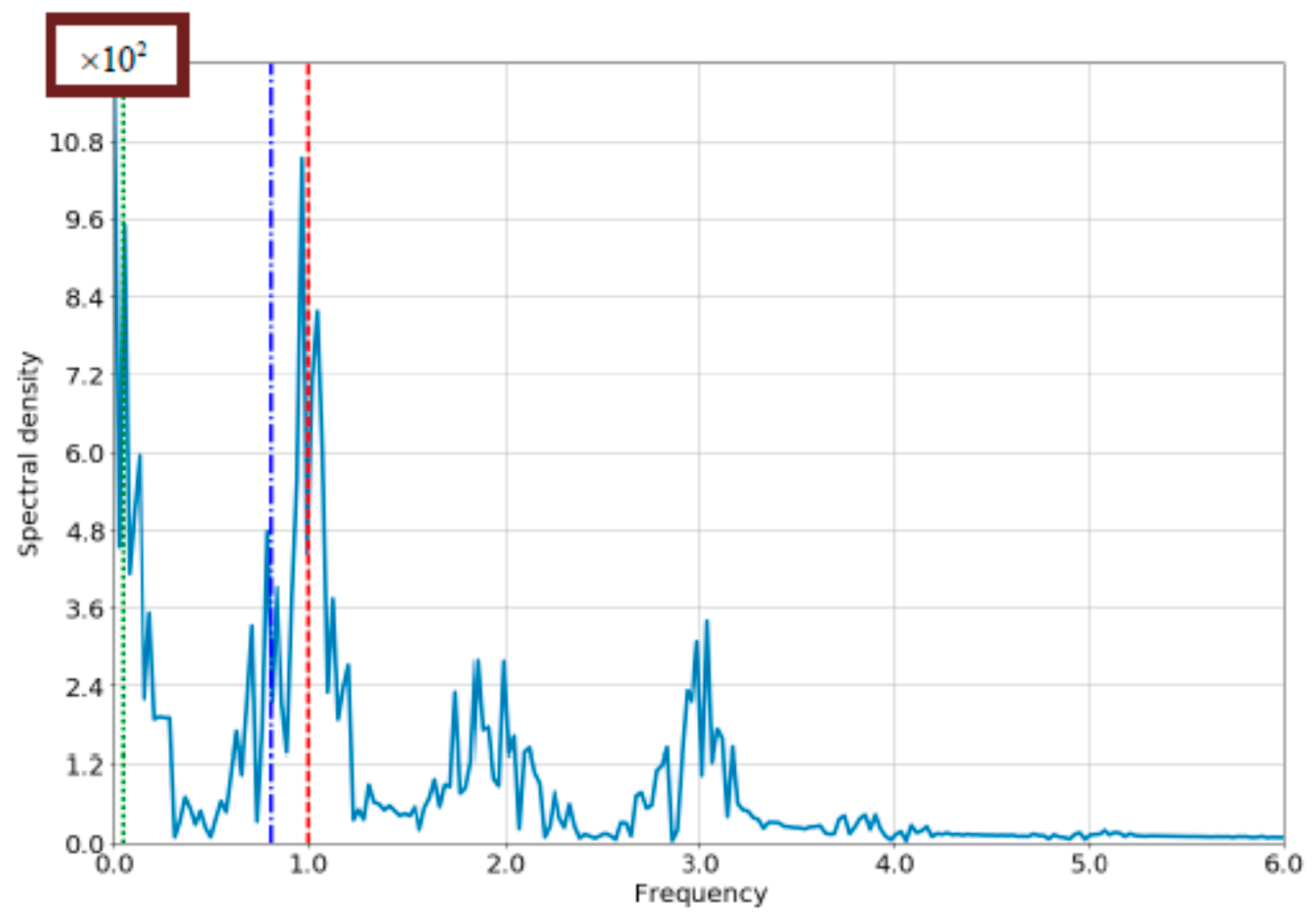
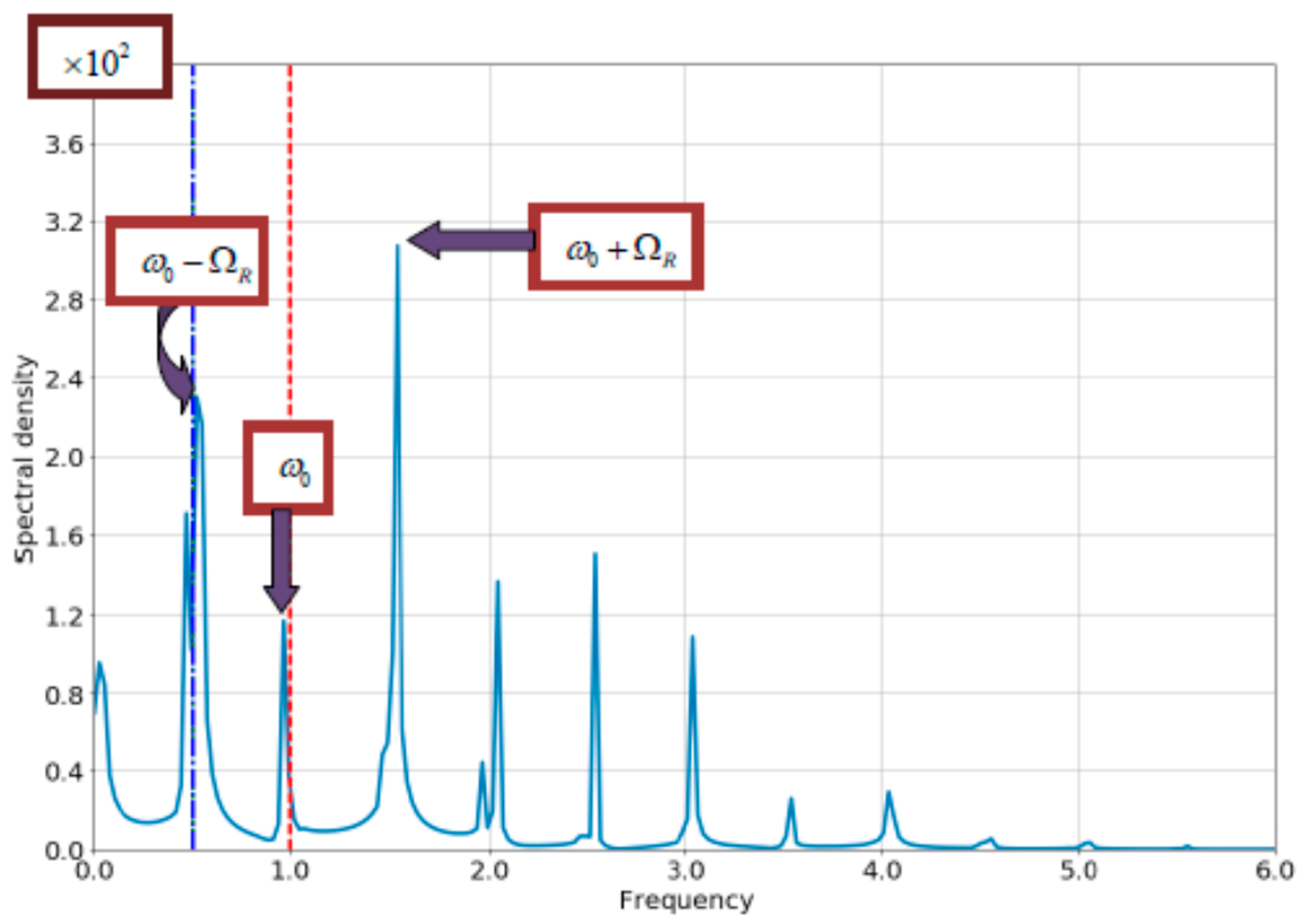
4.2. The Case of Comparable Rabi- and Bloch Frequencies
4.3. The Role of the Losses
4.4. Stark Effect in One-Dimensional Atomic Chains
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Scully, M.O.; Zubairy, M.S. Quantum Optics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Rabi, I.I. Space Quantization in a Gyrating Magnetic Field. Phys. Rev. 1937, 51. [Google Scholar] [CrossRef]
- Hocker, G.B.; Tang, C.L. Observation of the Optical Transient Nutation Effect. Phys. Rev. Lett. 1968, 21. [Google Scholar] [CrossRef]
- Kamada, H.; Gotoh, U.; Temmyo, J.; Takagahara, T.; Ando, H. Exciton Rabi Oscillation in a Single Quantum Dot. Phys. Rev. Lett. 2001, 87. [Google Scholar] [CrossRef] [PubMed]
- Blais, A.; Huang, R.S.; Wallraff, A.; Girvin, S.M.; Schoelkopf, R.J. Cavity quantum electrodynamics for superconducting electrical circuits: An architecture for quantum computation. Phys. Rev. A 2004, 69. [Google Scholar] [CrossRef]
- Gambetta, J.; Blais, A.; Schuster, D.I.; Wallraff, A.; Frunzio, L.; Majer, J.; Devoret, M.H.; Girvin, S.M.; Schoelkopf, R.J. Qubit-photon interactions in a cavity: Measurement-induced dephasing and number splitting. Phys. Rev. A 2006, 74. [Google Scholar] [CrossRef]
- Blais, A.; Gambetta, J.; Wallraff, A.; Schuster, D.I.; Girvin, S.M.; Devoret, M.H.; Schoelkopf, R.J. Quantum-information processing with circuit quantum electrodynamics. Phys. Rev. A 2007, 75. [Google Scholar] [CrossRef]
- Burkard, G.; Imamoglu, A. Ultra-long-distance interaction between spin qubits. Phys. Rev. B 2006, 74. [Google Scholar] [CrossRef]
- Barrett, S.D.; Milburn, G.J. Measuring the decoherence rate in a semiconductor charge qubit. Phys. Rev. B 2003, 68, 155307. [Google Scholar] [CrossRef]
- Kibis, O.V.; Slepyan, G.Y.; Maksimenko, S.A.; Hoffmann, A. Matter Coupling to Strong Electromagnetic Fields in Two-Level Quantum Systems with Broken Inversion Symmetry. Phys. Rev. Lett. 2009, 102, 023601. [Google Scholar] [CrossRef] [PubMed]
- Slepyan, G.Y.; Yerchak, Y.D.; Maksimenko, S.A.; Hoffmann, A. Wave propagation of Rabi oscillations in one-dimensional quantum dot chain. Phys. Lett. A 2009, 373, 1374–1378. [Google Scholar] [CrossRef]
- Slepyan, G.Y.; Yerchak, Y.D.; Maksimenko, S.A.; Hoffmann, A.; Bass, F.G. Mixed states in Rabi waves and quantum nanoantennas. Phys. Rev. B 2012, 85. [Google Scholar] [CrossRef]
- Yerchak, Y.; Slepyan, G.Y.; Maksimenko, S.A.; Hoffmann, A.; Bass, F. Array of tunneling-coupled quantum dots as a terahertz range quantum nanoantenna. J. Nanophotonics 2013, 7. [Google Scholar] [CrossRef]
- Slepyan, G.Y.; Yerchak, Y.D.; Hoffmann, A.; Bass, F.G. Strong electron-photon coupling in a one-dimensional quantum dot chain: Rabi waves and Rabi wave packets. Phys. Rev. B 2010, 81. [Google Scholar] [CrossRef]
- Gligorić, G.; Maluckov, A.; Hadžievski, L.; Slepyan, G.Y.; Malomed, B.A. Discrete solitons in an array of quantum dots. Phys. Rev. B 2013, 88. [Google Scholar] [CrossRef]
- Gligorić, G.; Maluckov, A.; Hadžievski, L.; Slepyan, G.Y.; Malomed, B.A. Soliton nanoantennas in two-dimensional arrays of quantum dots. J. Phys. 2015, 27. [Google Scholar] [CrossRef] [PubMed]
- Bloch, F. UЁ ber die Quantenmechanik der Elektronen in Kristallgittern. Z. Phys. 1929, 52, 555–600. [Google Scholar] [CrossRef]
- Zener, C.A. Theory of electrical breakdown of solid dielectrics. Proc. R. Soc. Lond. A 1934, 145, 523–529. [Google Scholar] [CrossRef]
- Wannier, G.H. Wave functions and effective Hamiltonian for Bloch electrons in an electric field. Phys. Rev. 1960, 117. [Google Scholar] [CrossRef]
- Wannier, G.H. Stark ladder in solids? A reply. Phys. Rev. 1969, 181. [Google Scholar] [CrossRef]
- Duan, F.; Guojin, J. Introduction to Condensed Matter Physics; World Scientific: Hackensack, NJ, USA, 2007. [Google Scholar]
- Waschke, C.; Roskos, H.; Schwedler, R.; Leo, K.; Kurz, H.; Köhler, K. Coherent submillimeter-wave emission from Bloch oscillations in a semiconductor superlattice. Phys. Rev. Lett. 1993, 70, 3319–3322. [Google Scholar] [CrossRef] [PubMed]
- Preiss, P.M.; Ma, R.; Tai, M.E.; Lukin, A.; Rispoli, M.; Zupanic, P.; Lahini, Y.; Islam, R.; Greiner, M. Strongly correlated quantum walks in optical lattices. Science 2015, 347, 1229–1233. [Google Scholar] [CrossRef] [PubMed]
- Gluck, M.; Kolovsky, A.R.; Korsch, H.J. Wannier–Stark resonances in optical and semiconductor superlattices. Phys. Rep. 2002, 366, 103–182. [Google Scholar] [CrossRef]
- Dahan, M.B.; Peik, E.; Reichel, J.; Castin, Y.; Salomon, C. Bloch Oscillations of Atoms in an Optical Potential. Phys. Rev. Lett. 1996, 76, 4508–4511. [Google Scholar] [CrossRef] [PubMed]
- Madison, K.W.; Fischer, M.C.; Diener, R.B.; Niu, Q.; Raizen, M.G. Dynamical Bloch Band Suppression in an Optical Lattice. Phys. Rev. Lett. 1998, 81, 5093–5096. [Google Scholar] [CrossRef]
- Morsch, O.; Muller, J.H.; Cristiani, M.; Ciampini, D.; Arimondo, E. Bloch Oscillations and Mean-Field Effects of Bose-Einstein Condensates in 1D Optical Lattices. Phys. Rev. Lett. 2001, 87, 140402–140410. [Google Scholar] [CrossRef] [PubMed]
- Bongs, K.; Sengstock, K. Physics with Coherent Matter Waves. Rep. Prog. Phys. 2004, 67, 907–963. [Google Scholar] [CrossRef]
- Ferrari, G.; Poli, N.; Sorrentino, F.; Tino, G.M. Long-Lived Bloch Oscillations with Bosonic Sr Atoms and Application to Gravity Measurement at the Micrometer Scale. Phys. Rev. Lett. 2006, 97. [Google Scholar] [CrossRef] [PubMed]
- Battesti, R.; Cladé, P.; Guellati-Khélifa, S.; Schwob, C.; Grémaud, B.; Nez, F.; Julien, L.; Biraben, F. Bloch Oscillations of Ultracold Atoms: A Tool for a Metrological Determination of h/mRb. Phys. Rev. Lett. 2004, 92, 253001–253005. [Google Scholar] [CrossRef] [PubMed]
- Morandotti, R.; Peschel, U.; Aitchison, J.S.; Eisenberg, H.S.; Silberberg, Y. Experimental Observation of Linear and Nonlinear Optical Bloch Oscillations. Phys. Rev. Lett. 1999, 83, 4756–4759. [Google Scholar] [CrossRef]
- Pertsch, T.; Dannberg, P.; Elflein, W.; Bräuer, A.; Lederer, F. Optical Bloch Oscillations in Temperature Tuned Waveguide Arrays. Phys. Rev. Lett. 1999, 83, 4752–4755. [Google Scholar] [CrossRef]
- Peschel, U.; Pertsch, T.; Lederer, F. Optical Bloch oscillations in waveguide arrays. Opt. Lett. 1998, 23, 1701–1703. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, G.S. Quantum Optics; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Bromberg, Y.; Lahini, Y.; Silberberg, Y. Bloch Oscillations of Path-Entangled Photons. Phys. Rev. Lett. (E) 2011, 105. [Google Scholar] [CrossRef] [PubMed]
- Afek, I.; Natan, A.; Ambar, O.; Silberberg, Y. Quantum state measurements using multipixel photon detectors. Phys. Rev. A 2009, 79. [Google Scholar] [CrossRef]
- Afek, I.; Ambar, O.; Silberberg, Y. High-NOON States by Mixing Quantum and Classical Light. Science 2010, 328, 879–881. [Google Scholar] [CrossRef] [PubMed]
- Sanchis-Alepuz, H.; Kosevich, Y.A.; Sanchez-Dehesa, J. Acoustic Analogue of Electronic Bloch Oscillations and Resonant Zener Tunneling in Ultrasonic Superlattices. Phys. Rev. Lett. 2007, 98, 134301. [Google Scholar] [CrossRef] [PubMed]
- Anderson, B.P.; Kasevich, M.A. Macroscopic quantum interference from atomic tunnel arrays. Science 1998, 282, 1686–1689. [Google Scholar] [CrossRef] [PubMed]
- Kudo, K.; Monteiro, T.S. Theoretical analysis of super–Bloch oscillations. Phys. Rev. A 2011, 83, 053627. [Google Scholar] [CrossRef]
- Hartmann, T.; Keck, F.; Korsch, H.J.; Mossmann, S. Dynamics of Bloch oscillations. New J. Phys. 2004, 6. [Google Scholar] [CrossRef]
- Ciuti, C.; Bastard, G.; Carusotto, I. Quantum Vacuum Properties of the Intersubband Cavity Polariton Field. Phys. Rev. B 2005, 72. [Google Scholar] [CrossRef]
- Todorov, Y.; Sirtori, C. Few-Electron Ultrastrong Light-Matter Coupling in a Quantum LC Circuit. Phys. Rev. X 2014, 4. [Google Scholar] [CrossRef]
- Hagenmüller, D.; De Liberato, S.; Ciuti, C. Ultrastrong Coupling between a Cavity Resonator and the Cyclotron Transition of a Two-Dimensional Electron Gas in the Case of an Integer Filling Factor. Phys. Rev. B 2010, 81. [Google Scholar] [CrossRef]
- Peropadre, B.; Forn-Díaz, P.; Solano, E.; Grcía-Ripoll, J.J. Switchable Ultrastrong Coupling in Circuit QED. Phys. Rev. Lett. 2010, 105. [Google Scholar] [CrossRef] [PubMed]
- Anappara, A.A.; De Liberato, S.; Tredicucci, A.; Ciuti, C.; Biasiol, G.; Sorba, L.; Beltram, F. Signatures of the Ultrastrong Light-Matter Coupling Regime. Phys. Rev. B 2009, 79. [Google Scholar] [CrossRef]
- Todorov, Y.; Andrews, A.M.; Colombelli, R.; De Liberato, S.; Ciuti, C.; Klang, P.; Strasser, G.; Sirtori, C. Ultrastrong Light-Matter Coupling Regime with Polariton Dots. Phys. Rev. Lett. 2010, 105. [Google Scholar] [CrossRef] [PubMed]
- Geiser, M.; Castellano, F.; Scalari, G.; Beck, M.; Nevou, L.; Faist, J. Ultrastrong Coupling Regime and Plasmon Polaritons in Parabolic Semiconductor Quantum Wells. Phys. Rev. Lett. 2012, 108. [Google Scholar] [CrossRef] [PubMed]
- Delteil, A.; Vasanelli, A.; Todorov, Y.; Feuillet Palma, C.; Renaudat St-Jean, M.; Beaudoin, G.; Sagnes, I.; Sirtori, C. Charge-Induced Coherence between Intersubband Plasmons in a Quantum Structure. Phys. Rev. Lett. 2012, 109. [Google Scholar] [CrossRef] [PubMed]
- Scalari, G.; Maissen, C.; Turcinková, D.; Hagenmüller, D.; De Liberato, S.; Ciuti, C.; Reichl, C.; Schuh, D.; Wegscheider, W.; Beck, M.; et al. Ultrastrong Coupling of the Cyclotron Transition of a 2D Electron Gas to a THz Metamaterial. Science 2012, 335, 1323–1326. [Google Scholar] [CrossRef] [PubMed]
- Niemczyk, T.; Deppe, F.; Huebl, H.; Menzel, E.P.; Hocke, F.; Schwarz, M.J.; Garcia-Ripoll, J.J.; Zueco, D.; Hümmer, T.; Solano, E.; et al. Circuit Quantum Electrodynamics in the Ultrastrong-Coupling Regime. Nat. Phys. 2010, 6, 772–776. [Google Scholar] [CrossRef]
- Schwartz, T.; Hutchison, J.A.; Genet, C.; Ebbesen, T.W. Reversible Switching of Ultrastrong Light-Molecule Coupling. Phys. Rev. Lett. 2011, 106. [Google Scholar] [CrossRef] [PubMed]
- Levie, I.; Kastner, R.; Slepyan, G. Rabi-Bloch Oscillations in Spatially Distributed Systems: Temporal Dynamics and Frequency Spectra. In Quantum Physics (quant-ph); Cornell University Library: Ithaca, NY, USA, 2017. [Google Scholar]
- Biagioni1, P.; Huang, J.S.; Hecht, B. Nanoantennas for visible and infrared radiation. Rep. Prog. Phys. 2012, 75. [Google Scholar] [CrossRef] [PubMed]
- Bharadwaj, P.; Deutsch, B.; Novotny, L. Optical Antennas. Adv. Opt. Photonics 2009, 1, 438–483. [Google Scholar] [CrossRef]
- Novotny, L.; Van Hulst, N. Antennas for light. Nat. Photonics 2011, 5, 83–90. [Google Scholar] [CrossRef]
- Burke, P.J.; Li, S.; Yu, Z. Quantitative theory of nanowire and nanotube antenna performance. IEEE Trans. Nanotechnol. 2006, 5, 314–334. [Google Scholar] [CrossRef]
- Hao, J.; Hanson, G.W. Infrared and optical properties of carbon nanotube dipole antennas. IEEE Trans. Nanotechnol. 2006, 5, 766–775. [Google Scholar] [CrossRef]
- Alu, A.; Engheta, N. Input impedance, nanocircuit loading, and radiation tuning of optical nanoantennas. Phys. Rev. Lett. 2008, 101. [Google Scholar] [CrossRef] [PubMed]
- Alu, A.; Engheta, N. Hertzian plasmonic nanodimer as an efficient optical nanoantenna. Phys. Rev. B 2008, 78. [Google Scholar] [CrossRef]
- Greffet, J.-J.; Laroche, J.-J.; Marquir, F. Impedance of a Nanoantenna and a Single Quantum Emitter. Phys. Rev. Lett. 2010, 105. [Google Scholar] [CrossRef] [PubMed]
- Slepyan, G.Y.; Boag, A. Quantum Nonreciprocity of Nanoscale Antenna Arrays in Timed Dicke States. Phys. Rev. Lett. 2013, 111. [Google Scholar] [CrossRef] [PubMed]
- Mokhlespour, S.; Haverkort, J.E.M.; Slepyan, G.; Maksimenko, S.; Hoffmann, A. Collective spontaneous emission in coupled quantum dots: Physical mechanism of quantum nanoantenna. Phys. Rev. B 2012, 86. [Google Scholar] [CrossRef]
- Soriano, A.; Navarro, E.A.; Porti, J.A.; Such, V. Analysis of the finite difference time domain technique to solve the Schrodinger equation for quantum devices. J. Appl. Phys. 2004, 95, 8011–8018. [Google Scholar] [CrossRef]
- Peskin, U.; Galperin, M. Coherently controlled molecular junctions. J. Chem. Phys. 2012, 136. [Google Scholar] [CrossRef] [PubMed]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics, Course of Theoretical Physics; Section 132; Pergamon Press: Oxford, UK, 1965. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Mechanics, Course of Theoretical Physics; Pergamon Press: Oxford, UK, 1960. [Google Scholar]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Clarendon Press: Oxford, UK, 2002. [Google Scholar]
- Bamba, M.; Imoto, N. Maxwell boundary conditions imply non-Lindblad master equation. Phys. Rev. A 2016, 94. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics, Course of Theoretical Physics; Section 76; Pergamon Press: Oxford, UK, 1965. [Google Scholar]
- Wang, L.; May, L. Theory of multiexciton dynamics in molecular chains. Phys. Rev. B 2016, 94. [Google Scholar] [CrossRef]




© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Levie, I.; Slepyan, G. The New Concept of Nano-Device Spectroscopy Based on Rabi–Bloch Oscillations for THz-Frequency Range. Appl. Sci. 2017, 7, 721. https://doi.org/10.3390/app7070721
Levie I, Slepyan G. The New Concept of Nano-Device Spectroscopy Based on Rabi–Bloch Oscillations for THz-Frequency Range. Applied Sciences. 2017; 7(7):721. https://doi.org/10.3390/app7070721
Chicago/Turabian StyleLevie, Ilay, and Gregory Slepyan. 2017. "The New Concept of Nano-Device Spectroscopy Based on Rabi–Bloch Oscillations for THz-Frequency Range" Applied Sciences 7, no. 7: 721. https://doi.org/10.3390/app7070721




