The Synchrosqueezing Algorithm Based on Generalized S-transform for High-Precision Time-Frequency Analysis

Abstract

In this paper, a new time-frequency analysis method—Synchrosqueezing Generalized S-transform (SSGST)—is proposed to meet the needs of high-resolution seismic signal processing and interpretation. The basic wavelet of the generalized S-transform (GST) in the paper is a modulated harmonic wave with four undetermined parameters that can be constructed by adjusting the four parameters to make the GST more suitable for seismic signals processing. The SSGST method squeezes and reconstructs the complex coefficient spectra of GST results along the frequency direction so that the energy distributions on the time-frequency spectra are concentrated around the real instantaneous frequency of the signal; thus, the time-frequency resolution can be improved. Based on mathematical theory, the basic principle of the new transformation method is given, and the mathematical expressions of the positive transformation and lossless inverse transformation of the method are strictly deduced. The experimental results of numerical signals illustrate that the proposed method can correctly decompose signals with different spectral characteristics into a high time-frequency resolution spectrum and can recovery the original signal from the time-frequency spectrum with satisfying reconstructing accuracy. Application on field seismic data shows the superiority of the new method in seismic time-frequency analysis for hydrocarbon detection.

1. Introduction

Time-frequency analysis, a powerful tool for seismic data analysis, plays a significant role in oil and gas exploration and development. It maps a 1D signal in the time domain into a 2D time-frequency spectrum, which can effectively reveal important details of seismic data and provide valuable information for reservoir characterization.

The commonly used methods for seismic time-frequency analysis include short-time Fourier transform (STFT), wavelet transform (WT), and S-transform (ST). STFT suffers from a fixed time-frequency resolution caused by a preselecting window length. To overcome this disadvantage, wavelet-based methods have been adopting and show obvious superiority in spectral resolution (e.g., [1]). Although WT leads to a more flexible trade-off between frequency and time resolution due to the variable length of the mother wavelet, it still displays spectral smearing due to the finite size of the operator. The S-transform (ST) proposed by Stockwell et al. [2] can be interpreted as a special case of the Continuous Wavelet Transform (CWT) based on Morlet wavelet, but with minor phase and amplitude adjustments.. It eliminates the limitation of fixed window length in STFT and also has the multi-resolution ability of WT. In other words, ST can effectively avoid the existing deficiencies of the above two methods [3]. Nevertheless, the fixed changing trend of the basic wavelet in ST limits its practical application. Therefore, many researchers have proposed a variety of forms of generalized S transform (GST) on the basis of ST by introducing variable window parameters to improve the flexibility and adaptability of the wavelet window [4,5,6,7,8,9]. The method based on Empirical Mode Decomposition (EMD) [10] or its extended algorithms (e.g., ensemble empirical mode decomposition (EEMD), complete ensemble empirical mode decomposition (CEEMD)) are other time-frequency transforms, which have also been applied in seismic data and have achieved excellent time-frequency resolution (e.g., [11,12,13,14]). Although EMD-based methods are useful for many applications, there is still a lack of mathematical foundation and a high computational cost.

Synchrosqueezing transform (SST) is a relatively new technique based on the combination of time-frequency methods followed by a reassignment step [15,16] that can be also regarded as an alternative to the EMD method considering their similar time-frequency resolution. SST can improve the energy concentration of time-frequency representation by applying a post-processing reallocation to the original representation. At each time or space location, the SST reassigns values of the initial representation based on their local oscillation. However, differing from EMD, the transformation process of SST is generated by strict mathematical derivation, which is beneficial to the understanding of the method and can be improved according to the specific application. At present, the synchrosqueezing algorithm has been extended to time-frequency representations based on the STFT [17,18,19], the wave packet transform [20], the curvelet transform [21], the ST [22], or the CWT [23,24], which is used in the synthetic examples of this paper. SST was originally applied to the audio signal analysis. Subsequently, many efforts have been made to use this method for seismic data processing and interpretation. In 2014, Herrera et al. [25] identified channels from seismic data using SST successfully and highlighted the advantages of this method over EMD and EEMD. In 2015, they also used SST to separate the P and S waves of microseismic data [26]. Later, Mousavi et al. (2016) [27] used it for microseismic detection. Mousavi and Langston (2017) [28] showed that SST can be used to improve the denoising of seismic data. Tary et al. (2017) [15,29] used it for attenuation estimation.

The generalized S-transform (GST) introduced by Gao et al. [6] overcomes the dilemma of the fixed wavelet in ST by introducing four undetermined parameters (amplitude, energy decay rate, energy delay time, and video rate) to construct the basic wavelet adaptive to the non-stationary signal characteristics in practical application. Due to having no restriction of the time window length, GST can obtain real time-frequency spectra with excellent time-frequency resolution, which provides more possibility and higher accuracy for the detailed information extraction of complicated non-stationary signals than ST. Since seismic signals are non-stationary and non-linear and show the characteristics of broadband and multi-frequency, using the GST instead of ST for seismic time-frequency analysis has been proven to be advisable.

In this paper, inspired by the theory of SST and the advantages of the GST over ST, we propose a novel time-frequency analysis method that we have named synchrosqueezing generalized S-transform (SSGST). The rest of this paper is organized as follows: Section 2 gives a brief review of GST and SST and then deduces the mathematical formulas of the newly proposed method in detail. In Section 3, three synthetic examples are employed to explore the performance of the SSGST method. Section 4 illustrates the effectiveness of the proposed method in the field seismic data analysis for hydrocarbon detections. Conclusions are drawn in Section 5.

2. Principles

2.1. Generalized S-transform (GST) with Four Parameters

Standard S-transform (ST) is proposed by Stockwell et al. [2]. This transform is defined as,

$$S{T}_x(\tau ,f)={\displaystyle {\int }_{-\infty }^{+\infty }x(t)\frac{\left|f\right|}{\sqrt{2\pi }}\exp \left\{-{\left(t-\tau \right)}^2{f}^2/2-i2\pi ft\right\}}dt$$

(1)

The basic wavelet function in standard ST is,

$$w_f\left(t\right)=\frac{\left|f\right|}{\sqrt{2\pi }}\exp \left(-t^2{f}^2/2-i2\pi ft\right),$$

(2)

where $x(t)$ represents a signal, $S{T}_x$ denotes the ST of $x(t)$. $f$ is frequency, $t$ is time and $\tau$ denotes the time shift.

The inverse transform of the standard ST is obtained by,

$$x(t)={\displaystyle {\int }_{-\infty }^{+\infty }\left\{{\displaystyle {\int }_{-\infty }^{+\infty }S{T}_x(\tau ,f)d\tau }\right\}\exp \left(i2\pi ft\right)}df$$

(3)

Although ST inherits the advantages of STFT and WT, its application is limited because of its fixed basic wavelet function. Gao et al. use a modulated harmonic wave with four undetermined parameters to replace the basic wavelet in ST to overcome the disadvantage caused by the fixed basic wavelet function. The modulated harmonic wave is written as,

$$w_f\left(t\right)=A\left|f\right|\exp \left[-\alpha {\left(ft-\beta \right)}^2-i2\pi f_{0}ft\right],$$

(4)

where $A$ is amplitude of the basic wavelet, $\alpha$ is energy attenuation ratio $\left(\alpha >0\right)$, $\beta$ is energy delay time and $f_0$ is video frequency of the basic wavelet.

So the generalized S-transform (GST) with four parameters of a signal $x(t)$ is,

$$GS{T}_x\left(\tau ,f\right)=A\left|f\right|{\displaystyle {\int }_{-\infty }^{\infty }x\left(t\right)}\exp \left\{-\alpha {\left[f\left(t-\tau \right)-\beta \right]}^2\right\}\exp \left(-i2\pi f_{0}ft\right)dt,$$

(5)

where $GS{T}_x$ denotes the result of the GST with four parameters. Its inverse transform is,

$$x\left(\frac{t}{f_0}\right)=f_{0}IFT\left[\frac{1}{A}\sqrt{\frac{\alpha }{\pi }}{\displaystyle {\int }_{-\infty }^{\infty }\hspace{0.17em}}GS{T}_x\left(\tau ,f\right)d\tau \right]\left(t\right),$$

(6)

where $IFT$ represents the inverse transform of Fourier transform.

It is obvious that the four-parameter GST is degenerated into a standard ST when $A=1$, $\alpha =\frac{1}{2}$, $\beta =0$ and $f_0=1$.

2.2. Synchrosqueezing Transform (SST)

SST is a new reassignment technique and a powerful tool for precisely decomposing and analyzing a signal. It can provide a sharpened time-frequency representation by applying a post-processing reallocation to the original representation. Thus, the SST algorithm can be divided into two step: (1) computing the instantaneous frequency using the original time-frequency coefficients and (2) squeezing and reassigning step. So far, many researchers have developed SST algorithms combining a reassignment step and different time-frequency decomposing methods such as continuous wavelet transform, short-time Fourier transform, curvelet tranform, S-transform, and wavelet packet transform.

Among these algorithms, synchrosqueezing continuous wavelet transform (SSCWT) is used for comparison with the new method proposed in this paper. It was proposed by Daubechies et al. [24] and can obtain higher resolution time-frequency spectra by squeezing and reconstructing the values of continuous wavelet transform (CWT) in the frequency direction. Thus, taking this method as an example, we briefly introduce the principle of SST.

First, we calculate the CWT of a signal $x(t)$ as,

$$W{T}_x\left(a,b\right)=\frac{1}{\sqrt{a}}{\displaystyle {\int }_{-\infty }^{\infty }x\left(t\right)}\overline{\psi \left(\frac{t-b}{a}\right)}dt,$$

(7)

where $W{T}_x$ denotes the continuous wavelet transform of a signal $x(t)$. $a$ is the scale factor, and $b$ is the time translation factor. $\psi \left(t\right)$ is a mother wavelet and $\overline{\psi }$ is the complex conjugate of $\psi \left(t\right)$.

Then, the instantaneous frequency at any time-scale location $\left(a,b\right)$ is,

$$\omega \left(a,b\right)=\{\begin{array}{c}{\left[iW{T}_x\left(a,b\right)\right]}^{-1}\frac{\partial W{T}_x\left(a,b\right)}{\partial b}\begin{array}{cc}& W{T}_x\left(a,b\right)\ne 0\end{array}\\ \begin{array}{cc}\begin{array}{ccc}& & \begin{array}{ccc}\begin{array}{ccc}\begin{array}{cc}& \infty \end{array}& & \end{array}& & \end{array}\end{array}& \hspace{1em}W{T}_x\left(a,b\right)=0\end{array}\end{array}$$

(8)

Secondly, we reassign values of the time-frequency representation based on its local oscillation. The result of SST is,

$$SS{T}_x\left({\omega }_l,b\right)=\frac{1}{\Delta \omega }{\displaystyle \sum _{a_i:\left|\omega \left(a_i,b\right)-{\omega }_l\right|\le \frac{\Delta \omega }{2}}W{T}_x\left(a_i,b\right)a_i^{-\frac{3}{2}}\Delta a_i},$$

(9)

where $a_i$ is the $i-th$ scale value and $\Delta a_i=a_i-a_{i-1}$. ${\omega }_l$ denotes the $l-th$ frequency point. The Equation (9) means that the CWT spectra values between $\left[{\omega }_l-\frac{1}{2}\Delta \omega ,{\omega }_l+\frac{1}{2}\Delta \omega \right]$ are squeezed to the ${\omega }_l$ frequency point along the frequency direction. Thus, the time-frequency resolution becomes better.

The inverse transform of SST is written as

$$x\left(b\right)=\mathrm{Re}\left[C_{\psi }^{-1}{\displaystyle \sum _{l}SS{T}_x\left({\omega }_l,b\right)\Delta \omega }\right]$$

(10)

In Equation (10), $C_{\psi }=\frac{1}{2}{\displaystyle {\int }_0^{\infty }\hspace{0.17em}}\overline{\widehat{\psi }\left(\xi \right)} {\xi }^{-1}d\xi$, $\overline{\widehat{\psi }\left(\xi \right)}$ is the complex conjugate of the Fourier transform of the mother wavelet $\psi \left(t\right)$.

2.3. Synchrosqueezing Generalized S-transform (SSGST)

In this part, we give the basic principle of SSGST and derive the mathematical expressions of the positive transformation and lossless inverse transformation based on the mathematical theory.

First, the Equation (5) can be reformulated as,

$$\begin{array}{cc}\hfill GS{T}_x\left(f,b\right)& =A\left|f\right|\exp \left(-i2\pi f_{0}fb\right)\hfill \\ & \times {\displaystyle {\int }_{-\infty }^{\infty }x\left(t\right)\hspace{0.17em}}\exp \left\{-\alpha {\left[f\left(t-b\right)-\beta \right]}^2\right\}\exp \left[-i2\pi f_{0}f\left(t-b\right)\right]dt\hfill \end{array}$$

(11)

Let $\psi \left(t\right)=A\exp \left[-\alpha \left(t-\beta \right)\right]\exp \left(i2\pi f_{0}t\right)$, then Equation (11) is expressed as,

$$GS{T}_x\left(f,b\right)=\left|f\right|\exp \left(-i2\pi f_{0}fb\right){\displaystyle {\int }_{-\infty }^{\infty }x\left(t\right)}\overline{\psi \left[f\left(t-b\right)\right]}dt,$$

(12)

where, $\overline{\psi \left(t\right)}$ represents the complex conjugate of $\psi \left(t\right)$.

According to the Parseval theorem and transformation properties of scale and translation in Fourier Transform, the Equation (13) can be derived as follows:

$$GS{T}_x\left(f,b\right)=\frac{1}{2\pi }\exp \left(-i2\pi f_{0}fb\right){\displaystyle {\int }_{-\infty }^{\infty }\widehat{x}\left(\omega \right)\hspace{0.17em}}\overline{\widehat{\psi }\left(f^{-1}\omega \right)} e^{ib \omega }d\omega ,$$

(13)

where, $\widehat{x}\left(\omega \right)$ denotes the Fourier Transform result of the signal $x\left(t\right)$. $\overline{\widehat{\psi }\left(\omega \right)}$ is the complex conjugate of the Fourier Transform result of $\psi \left(t\right)$. Especially, if $\omega <0$, $\widehat{\psi }\left(\omega \right)=0$.

Then, we can calculate the instantaneous frequency of the signal $x\left(t\right)$ by using Equation (14):

$$f_x(f,b)=f_{0}f+{[i2\pi GS{T}_x\left(f,b\right)]}^{-1}\frac{\partial GS{T}_x\left(f,b\right)}{\partial b}$$

(14)

Now, we testify the feasibility and rationality of Equation (14) using an example of a harmonic wave $x\left(t\right)=A_1\cos 2\pi f_1 t$. The Fourier transform result $\widehat{x}\left(\omega \right)$ of the signal $x\left(t\right)$ is given as,

$$\widehat{x}\left(\omega \right)=A_1\pi \left[\delta (\omega -2\pi f_1)+\delta (\omega +2\pi f_1)\right],$$

(15)

where $A_1$ and $f_1$ denote, respectively, the amplitude and frequency of the harmonic wave $x\left(t\right)$.

The GST of the harmonic wave $x\left(t\right)$ can be calculated by substituting Equation (15) into Equation (13) and is given as,

$$GS{T}_x\left(f,b\right)=\frac{A_1}{2}\exp \left[-i2\pi \left(f_{0}f-f_1\right)b\right]\overline{\widehat{\psi }\left(2\pi f^{-1}{f}_1\right)}$$

(16)

According to Equation (14), the instantaneous frequency of the harmonic signal $x\left(t\right)$ is,

$$\begin{array}{ll}{f}_x(f,b)& =f_{0}f+{[i2\pi GS{T}_x\left(f,b\right)]}^{-1}\frac{\partial GS{T}_x\left(f,b\right)}{\partial b}\\ & =f_{0}f+\frac{i{A}_1\pi \left(f_1-f_{0}f\right)\times \exp \left[-i2\pi \left(f_{0}f-f_1\right)b\right]\times \overline{\widehat{\psi }\left(2\pi f^{-1}{f}_1\right)}}{i 2\pi \times \frac{A_1}{2}\times \exp \left[-i2\pi \left(f_{0}f-f_1\right) b\right]\times \overline{\widehat{\psi }\left(2\pi f^{-1}{f}_1\right)}}=f_1\end{array}$$

(17)

Therefore, the instantaneous frequency can be estimated by Equation (14). SSGST is defined as the Equation (18) according to the theories of synchrosqueezing.

$$SSGS{T}_x\left(f_l,b\right)=L_f^{-1}{\displaystyle \sum _{f_k:\left|f_x\left(f_k,b\right)-f_l\right|\le \Delta f/2}GS{T}_x\left(f_k,b\right)\exp \left(i2\pi f_0{f}_{k}b\right)f_{{}_k}^{-1}\Delta f_k},$$

(18)

where, $f_l$ is the frequency of the SSGST result. $L_f$ is the half length of frequency range $[f_l-L_f,f_l+L_f]$ centered on the frequency point $f_l$. $f_k$ denotes the discrete frequency points in frequency ranges of the GST, and $\Delta f_k=f_k-f_{k-1}$.

The Equation (18) represents that the time-frequency spectra values among the frequency range $[f_l-L_f,f_l+L_f]$ are superimposed on the frequency point $f_l$, so that the SSGST has higher accuracy of time-frequency decomposition ability.

Next, the inverse transform of SSGST is derived as follows:

We integrate over frequency $f$ on both sides of Equation (13), and obtain the Equation (19) by replacing $f^{-1}\omega$ with $\xi$.

$${\displaystyle {\int }_0^{\infty }GS{T}_x\left(f,b\right)}\exp \left(i2\pi f_{0}fb\right)f^{-1}df=\frac{1}{2}{\displaystyle {\int }_0^{\infty }\hspace{0.17em}}\overline{\widehat{\psi }\left(\xi \right)} {\xi }^{-1} d\xi \cdot \frac{1}{\pi }{\displaystyle {\int }_0^{\infty }\widehat{x}\left(\omega \right)\exp \left(ib \omega \right)d\omega }$$

(19)

Let $C_{\psi }=\frac{1}{2}{\displaystyle {\int }_0^{\infty }\hspace{0.17em}}\overline{\widehat{\psi }\left(\xi \right)} {\xi }^{-1} d\xi$, (19) can be rewritten as,

$$\frac{1}{\pi }{\displaystyle {\int }_0^{\infty }\widehat{x}\left(\omega \right)\exp \left(ib \omega \right)d\omega }=C_{\psi }^{-1}{\displaystyle {\int }_0^{\infty }GS{T}_x\left(f,b\right)}\exp \left(i2\pi f_{0}fb\right)f^{-1}df$$

(20)

Because the signal $x\left(t\right)$ is the real signal, we extract the real component $x\left(b\right)$ from the Equation (20) as the following reconstructed signal:

$$x\left(b\right)=\frac{1}{\pi }\mathrm{Re}\left[{\displaystyle {\int }_0^{\infty }\widehat{x}\left(\omega \right)\exp \left(ib\omega \right)d\omega }\right]=\mathrm{Re}\left[C_{\psi }^{-1}{\displaystyle {\int }_0^{\infty }GS{T}_x\left(f,b\right)}\exp \left(i2\pi f_{0}fb\right)f^{-1}df\right]$$

(21)

Through discretizing the equation on the right-hand side of Equation (21) and combining Equation (18), the inverse transform of SSGST is given as,

$$x\left(b\right)=\mathrm{Re}\left[C_{\psi }^{-1}{\displaystyle \sum _{l}SSGS{T}_x\left(f_l,b\right)L_f}\right]$$

(22)

Therefore, we can recover the original signal from the SSGST spectrum by using the Equation (22).

3. Synthetic Examples

In this section, to clarify the superiority of the proposed SSGST method, two signals that are commonly used for testing the performance of time-frequency distribution have been adopt. We also designed a synthetic signal to further illustrate the effectiveness of the proposed method for separating different frequency components from complicated signals and signal reconstruction. In processing numerical signals, comparisons are made between SSGST and the other time-frequency methods, such as CWT, GST, and SSCWT.

3.1. The Double Linear Chirped Signal

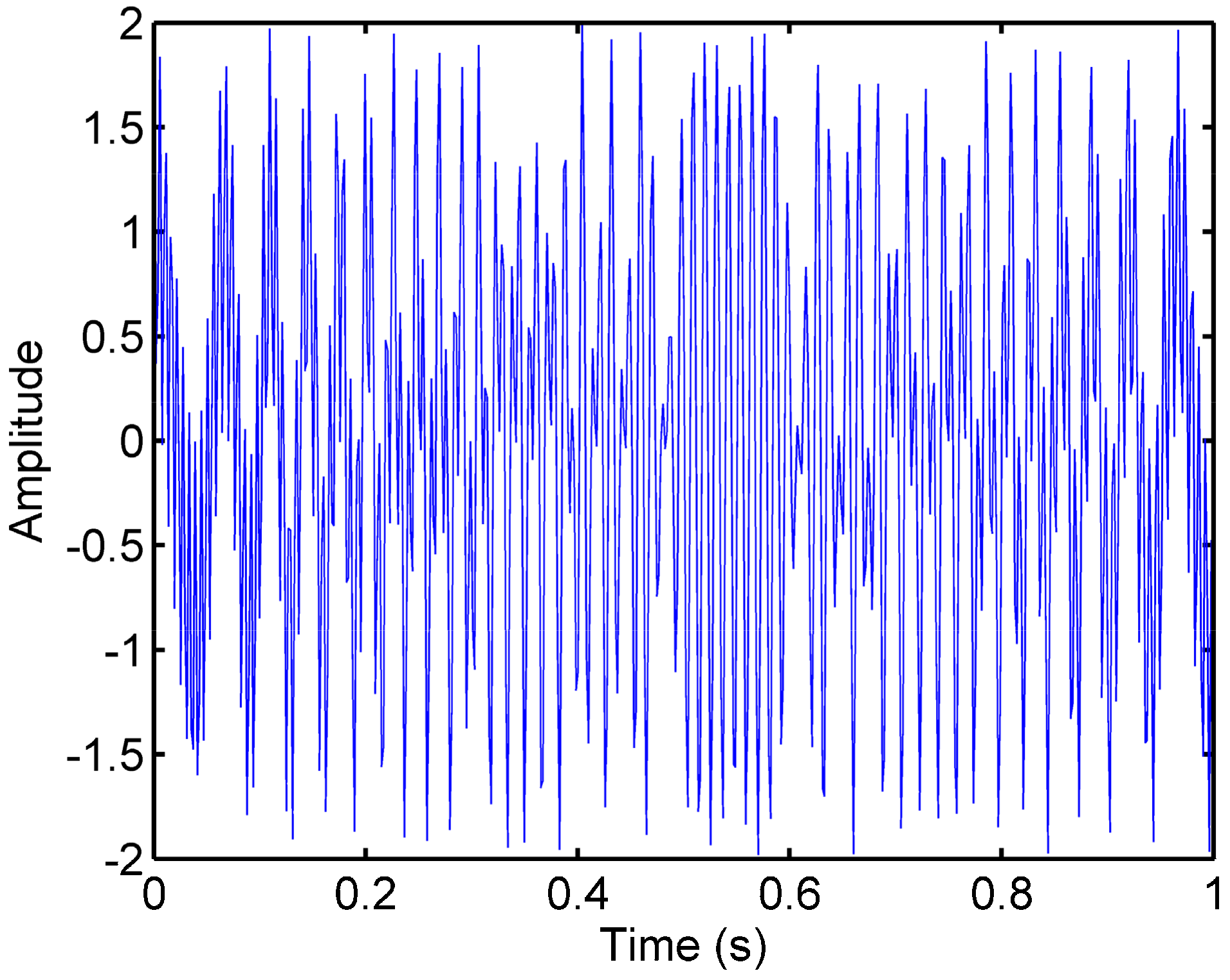
Linear frequency-modulated (FM) signal is a generally accepted model that is used to test the performance of time-frequency distribution. The double linear chirped signal shown in Figure 1 is composed of two crossing linear chirps whose main frequencies are linearly increasing and decreasing with time, respectively.

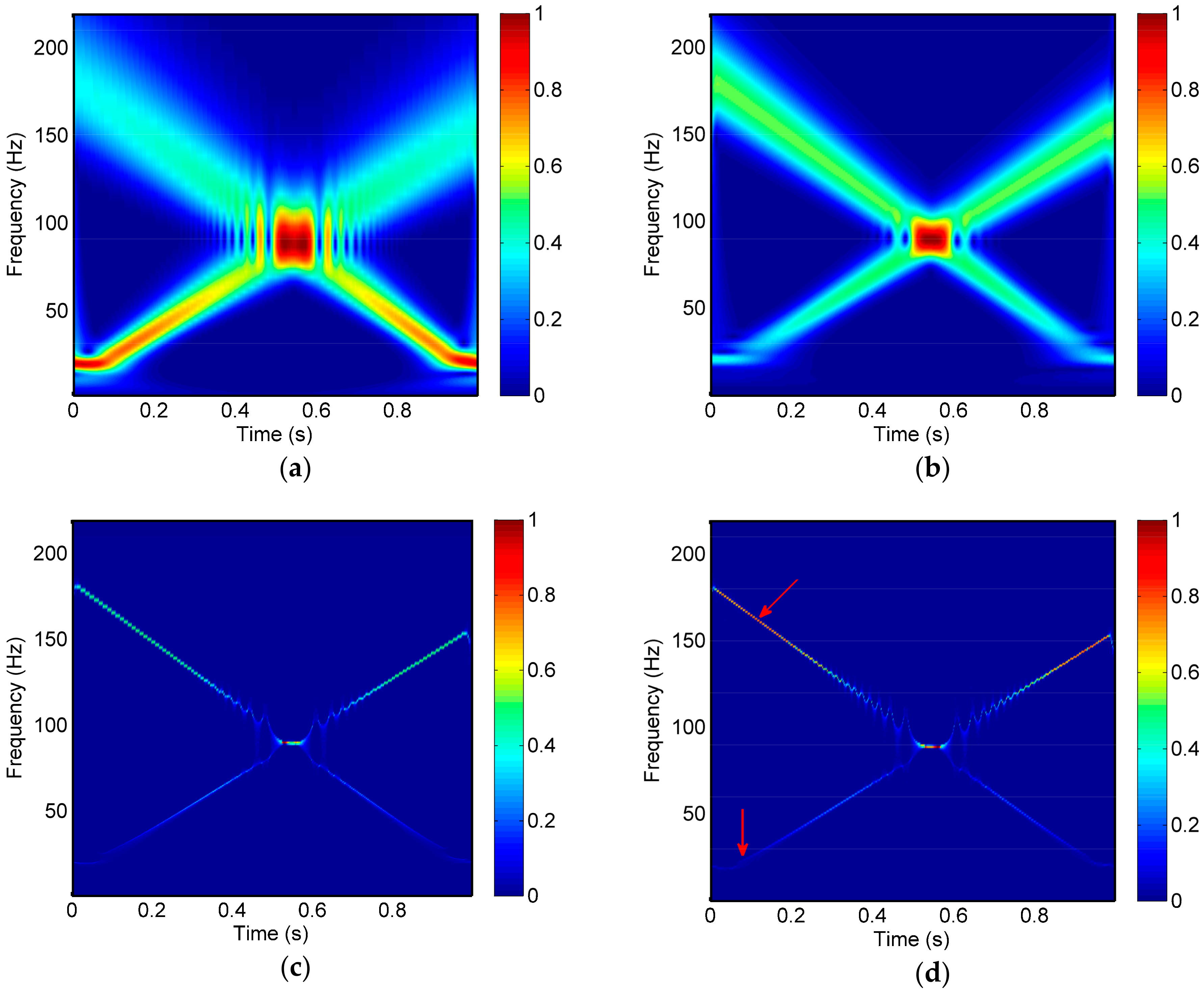
The CWT, GST, SSCWT, and SSGST methods are applied to this signal, and the relative results analysis are shown in Figure 2. As can be seen, although all energy centers around the true instantaneous frequencies of the signal, the energy of the CWT and GST results smears heavily (Figure 2a,b). In contrast, due to the effect of the “squeezing,” SSCWT and SSGST squeeze all time-frequency coefficients into the time-frequency trajectory, which makes the spectra more energy-concentrated, as displayed in Figure 2c,d. In other words, SSCWT and SSGST show higher time-frequency resolution than CWT and GST. Furthermore, compared with the result of SSCWT, SSGST shows that the signal energy is much more concentrated around the ridge and that the time-frequency resolution performs better. The arrows show that there is no distinct “steps” in the SSGST result compared with the result of SSCWT.

3.2. The Double Hyperbolic Chirped Signal

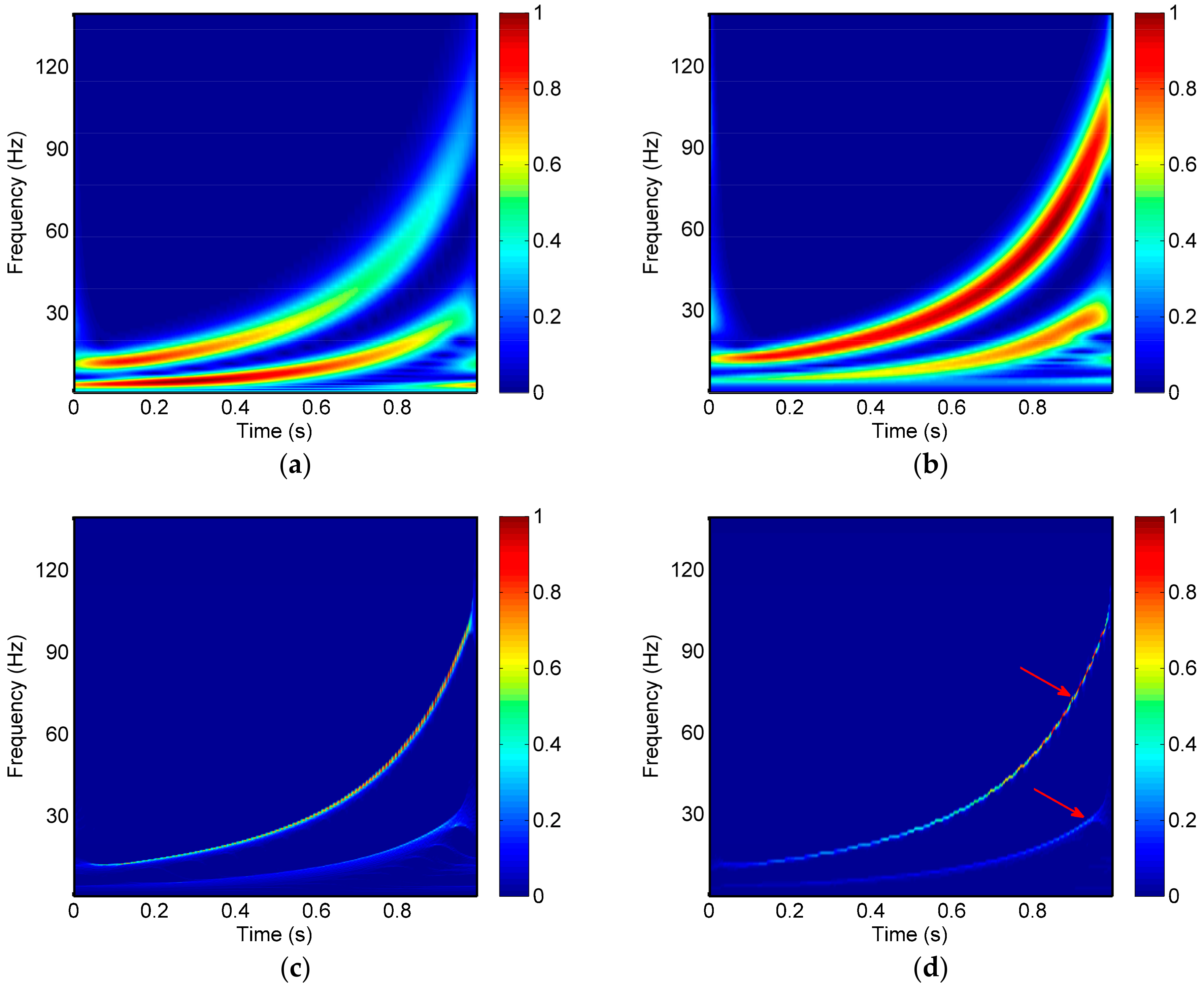
In order to futher verify the effectiveness of the SSGST method in dealing with non-stationary signal whose time-frequency characteristics is more complicated, we apply it to the double hyperbolic chirped signal (Figure 3), whose main frequency hyperbolic increases.

The results generated by the CWT, GST, SSCWT, and SSGST methods are shown in Figure 4. The time-frequency represents in Figure 4a,b resulted from the CWT and GST show poor energy concentration. However, as can be seen from Figure 4c,d, both SSCWT and SSGST provide higher resolution time-frequency result than CWT and GST, and they are good approximations of the signal’s instantaneous frequency. Compared with the SSCWT result, the SSGST representation shows an obviously higher energy concentration (see Figure 4c,d).

According to the comparison of the SSGST method with the CWT, GST, and SSCWT methods, we find that the SSGST method has better performance in improving time-frequency resolution and accuracy of time-frequency resolution. Moreover, there is no spurious frequency in the time-frequency spectrum of SSGST; thus, high-resolution time-frequency analysis results can be obtained accurately by the SSGST method.

3.3. A Synthetic Seismic Signal

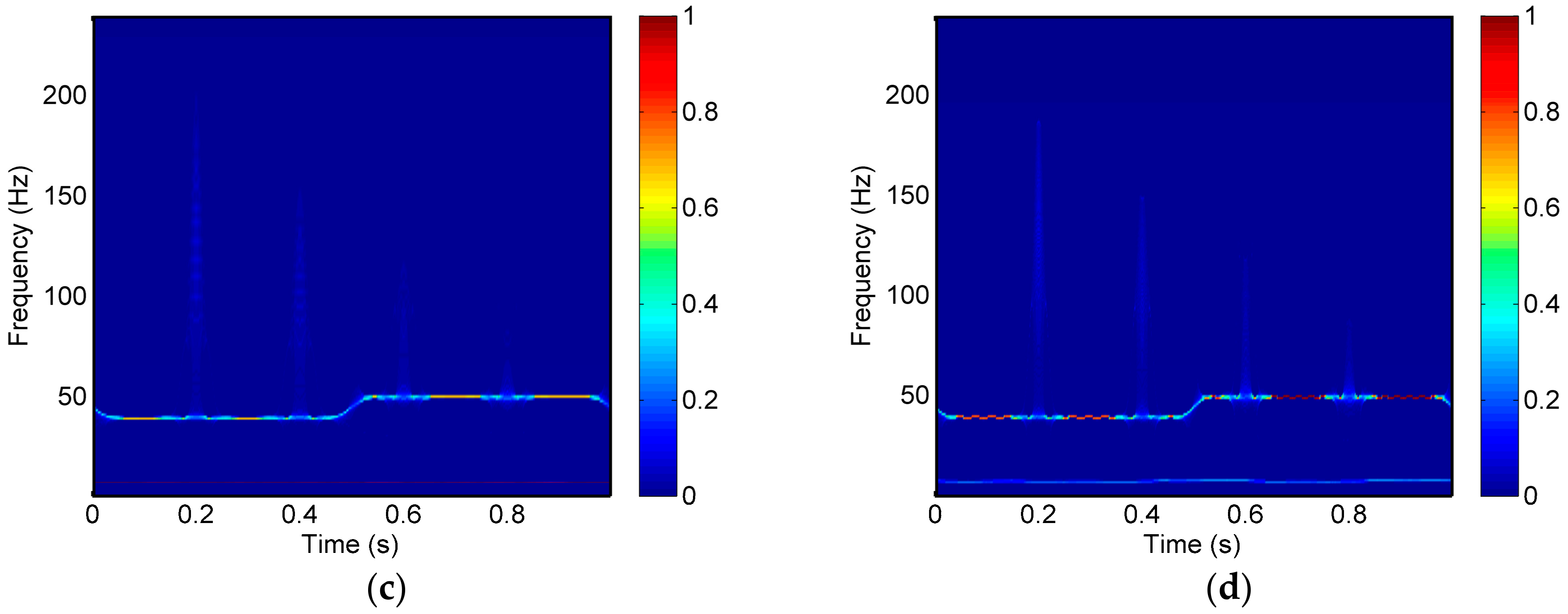
Next, we apply CWT GST, SSCWT, and SSGST to a synthetic seismic signal for illustrating the effectiveness of separating the different frequency components of seismic signals. The synthetic signal is comprised of a cosinusoid signal $si{g}_1$, two intermittent signal $si{g}_2$ and $si{g}_3$, and a simulated attenuate seismic signal $si{g}_4$, which is composed of four different frequency Ricker wavelets at 0.2 s, 0.4 s, 0.6 s, and 0.8 s of 100 Hz, 80 Hz, 65 Hz, and 55 Hz, respectively (Figure 5).

$$si{g}_1=1.5\cos (16\pi t)$$

(23)

$$si{g}_2=\{\begin{array}{ll}\cos (80\pi t),& t\in [0,0.5]\\ 0,& \mathrm{otherwise}\end{array}$$

(24)

$$si{g}_3=\{\begin{array}{ll}0,& \mathrm{otherwise}\\ \cos (100\pi t),& t\in (0.5\begin{array}{c},\end{array}\begin{array}{c}1\end{array}]\end{array}$$

(25)

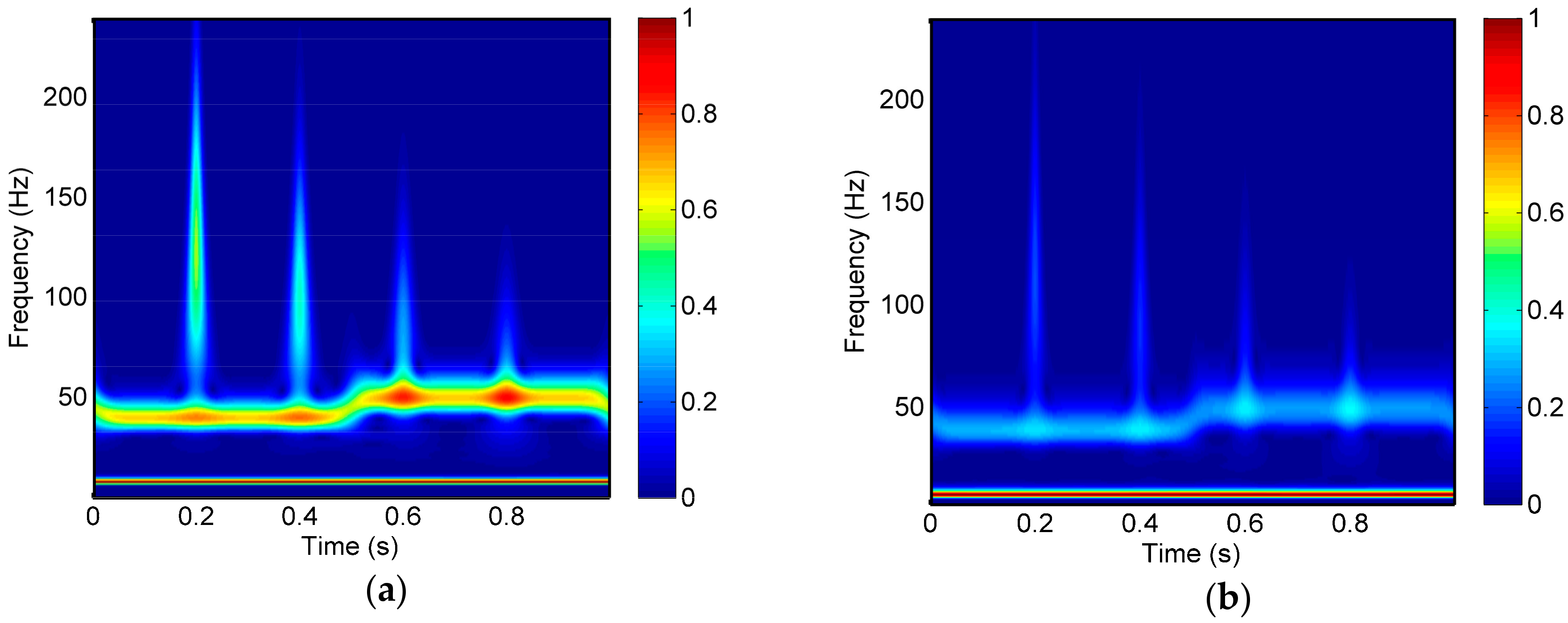
The results of the synthetic signal obtained by CWT, GST, SSCWT, and SSGST are presented in Figure 6. As can be seen in Figure 6, all methods can separate the frequency components well, and the time-frequency representation generated by the SSCWT and SSGST methods provide clearer time-frequency resolution than the CWT and GST methods. Comparing Figure 6b with Figure 6d, SSGST and SSCWT show similar frequency resolution. However, SSGST can depict the 8Hz cosine signal with higher resolution than SSCWT.

3.4. Comparative Quantification and Reconstruction Analysis

To quantify the performance of the SSGST and the other algorithms for generating TF representations of synthetic examples, we choose Rényi Entroy [30] as a quantitative performance index. The Rényi entropy is an objective indicator to evaluate the energy concentration of a time-frequency result; a lower Rényi entropy value denotes a more energy-concentrated time-frequency representation. The corresponding Rényi entropies are listed in

Table 1. The Rényi Entropies of three synthetic examples based on the Continuous Wavelet Transform (CWT), Generalized S-transform (GST), Synchrosqueezing continuous wavelet transform (SSCWT), and Synchrosqueezing Generalized S-transform (SSGST) methods. Signal₁ is the double hyperbolic chirped signal. Signal₂ is the double hyperbolic chirped signal. Signal₃ is the synthesized signal.

Rényi Entropy	CWT	GST	SSCWT	SSGST
Signal1	5.1846	6.0156	2.3329	1.1779
Signal2	6.6262	4.9479	1.6304	0.8297
Signal3	7.0540	5.0889	1.2518	1.4250

. As can be seen in Table 1, in terms of the first and second synthetic examples, the SSGST result has the lowest Rényi entropy compared with the other time-frequency transforms. In the synthetic seismic signal processing, the Rényi entropy of the SSGST result ranks behind only the SSCWT. Therefore, in summary, compared with the other methods mentioned above, the SSGST method is more likely to obtain an energy-concentrated time-frequency result.

We adopted the mean square error (MSE) to validate the reconstruction ability of the SSGST method. The corresponding MSE of the SSGST and the other algorithms are listed in

Table 2. The mean square error (MSE) values of synthetic examples based on the Synchrosqueezing Generalized S-transform (SSGST) and the other algorithms.

MSE	CWT	GST	SSCWT	SSGST
Signal1	0.0121	3.6979 × 10−27	2.3060 × 10−5	1.8626 × 10−5
Signal2	0.0181	3.2963 × 10−27	0.0214	0.0083
Signal3	0.0221	5.0622 × 10−26	7.5347 × 10−8	1.0925 × 10−4

. As shown in Table 2, the MSE values of SSGST are in the range of acceptable reconstruction error while taking the MSE values of other time frequency transforms as references.

Therefore, the SSGST method improves the resolution of time-frequency and also has a good reflection of strong or weak amplitude and high or low frequency. The newly proposed method can also reconstruct the original signal well with a lower reconstruction error.

4. Field Data Examples

When seismic waves propagate through hydrocarbon reservoirs, waves induced by fluid flow can lead to abnormal attenuation of energy and frequency (e.g., [31,32]). The phenomenon of abnormal attenuation mainly shows the loss of high-frequency energy and the conservation of strong low-frequency energy (e.g., [33,34,35,36,37]). Spectral decomposition technology can be utilized to identify hydrocarbon reservoirs by analyzing the different frequency response characteristics among different scale geological bodies (e.g., [38]). Here, we apply the SSGST method to seismic field data from the ZhongJiang Gas Field located in the western Sichuan Basin, China, in order to identify hydrocarbon reservoirs by analyzing the abnormal instantaneous frequency and energy.

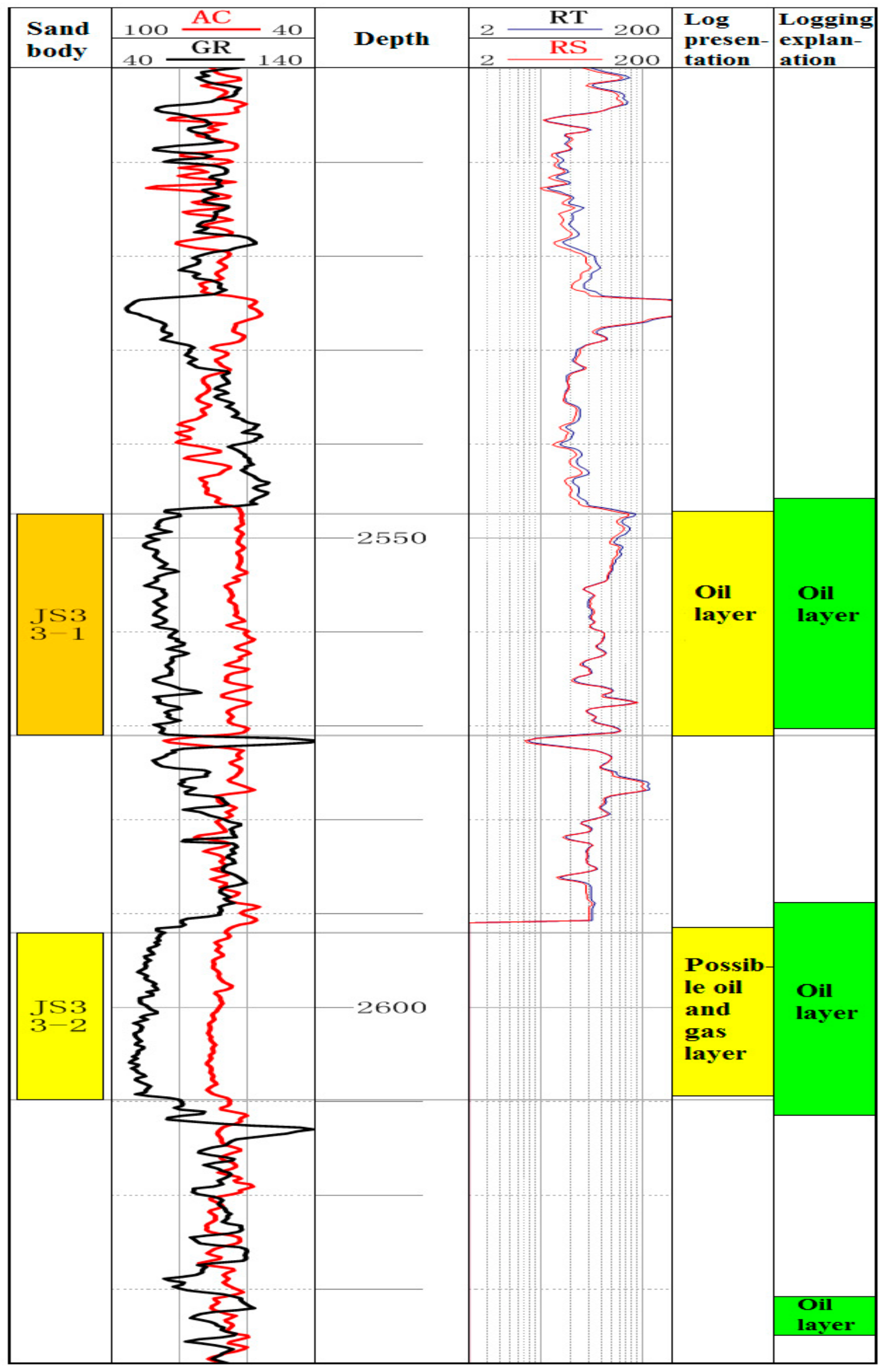
The seismic section consists of 304 traces with 1126 sampling points and a sampling interval of 2 ms, which is shown in Figure 7. The green curve in the horizontal direction at around 1.35 ms is a seismic horizon and the green vertical line represents a gas well. The area within the blue ellipse is a gas-bearing reservoir, which is our study area. Figure 8 is a histogram based on comprehensive analysis of log data. There are two sets of hydrocarbon reservoirs in the study area: the first set of reservoirs (JS33-1) is located in near a depth of 2560 m and thickness of about 22 m, and the second set of reservoirs (JS33-2) is located in near a depth of 2600 m and thickness of about 18 m.

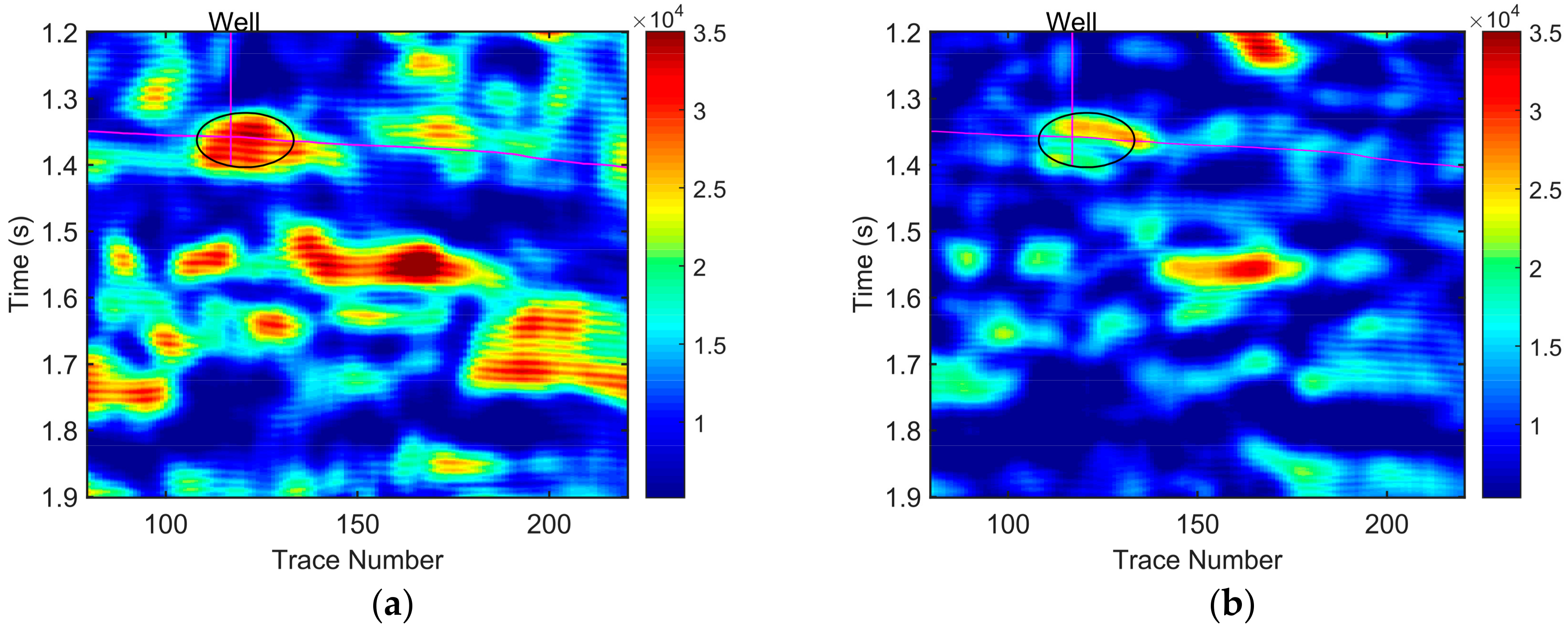
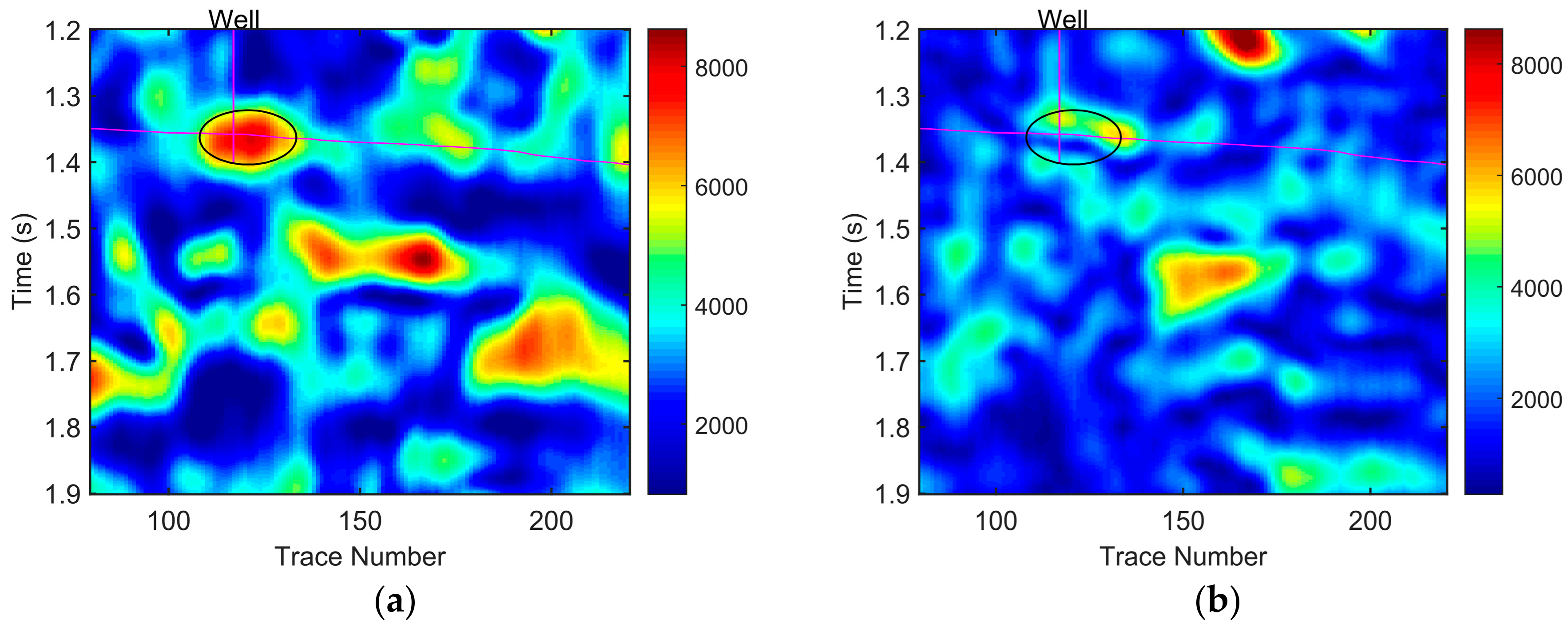
We used the CWT, GST, SSCWT, and SSGST methods respectively to processes the seismic data and extract the constant frequency sections at 40 Hz and 50 Hz, as shown in Figure 9, Figure 10, Figure 11 and Figure 12. The results are enlarged, and only the areas with time ranging from 1.2 s to 1.9 s are displayed in these constant frequency sections. In the constant frequency sections at 40 Hz (Figure 9a, Figure 10a, Figure 11a and Figure 12a), we can see a strong energy in the study area. However, obvious energy attenuation can be seen in each of the 50 Hz sections (Figure 9b, Figure 10b, Figure 11b and Figure 12b). This phenomenon is consistent with objective reality. Therefore, the four methods are all effective for hydrocarbon detection.

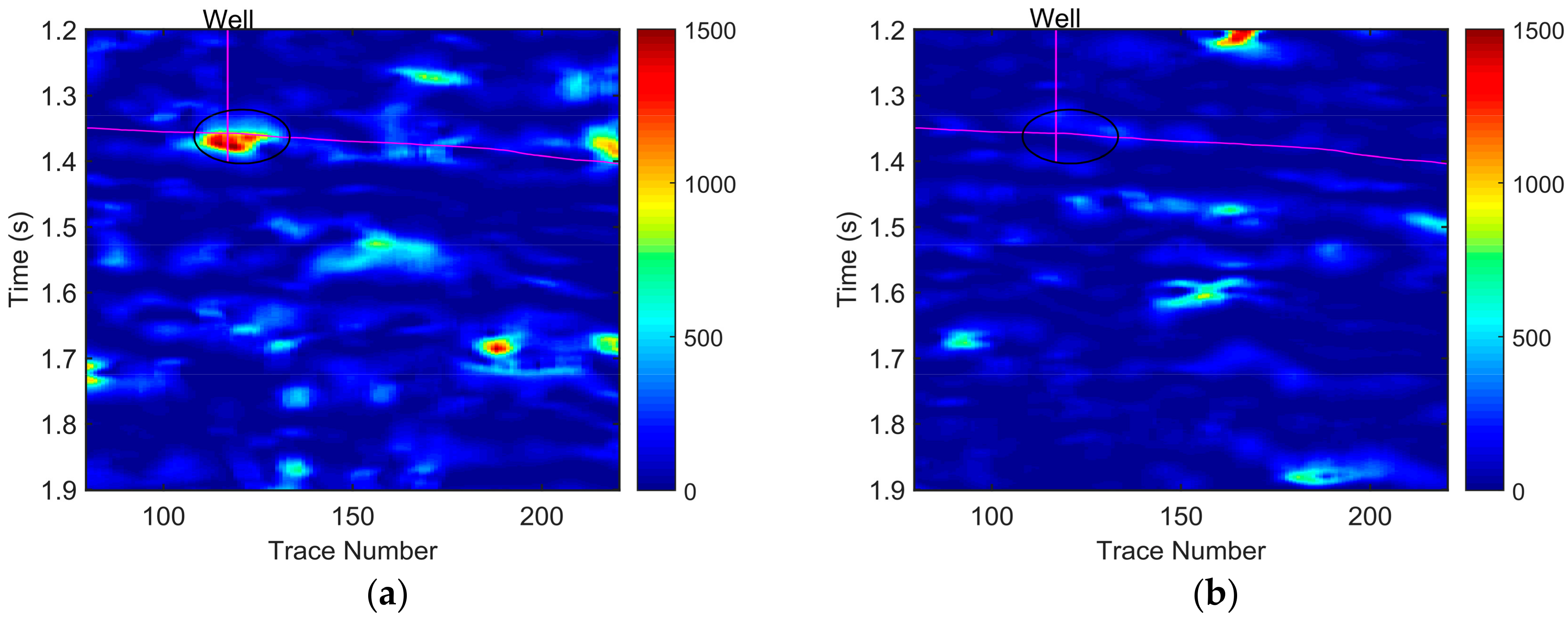
Although the analysis results of the CWT and GST can observe the abnormal attenuation in the hydrocarbon reservoir, they offer rough reservoir information due to the poor time-frequency resolution of CWT and GST (Figure 9 and Figure 10). Compared with the CWT and GST methods, the SSCWT method can improve the time-frequency resolution and obtain the accurate reservoir information but cannot identify the boundaries of the two sets of hydrocarbon reservoirs, as shown in Figure 11.

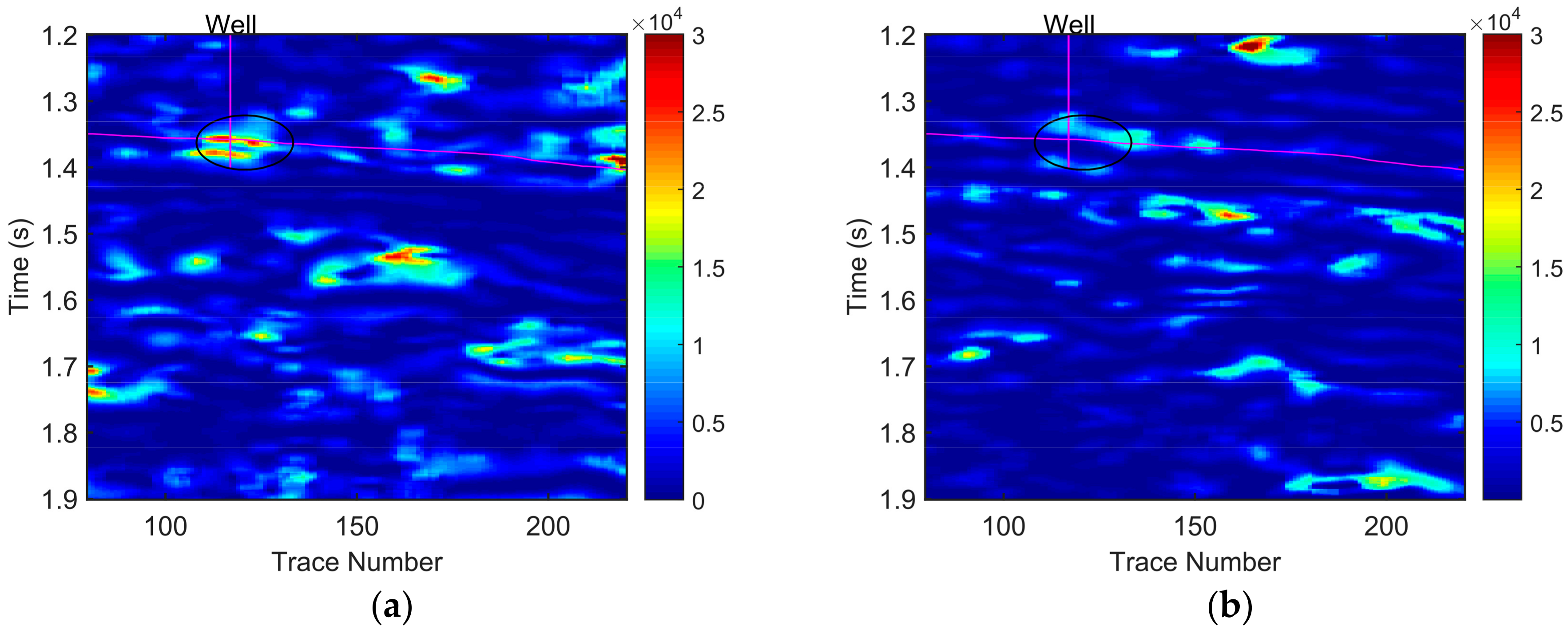
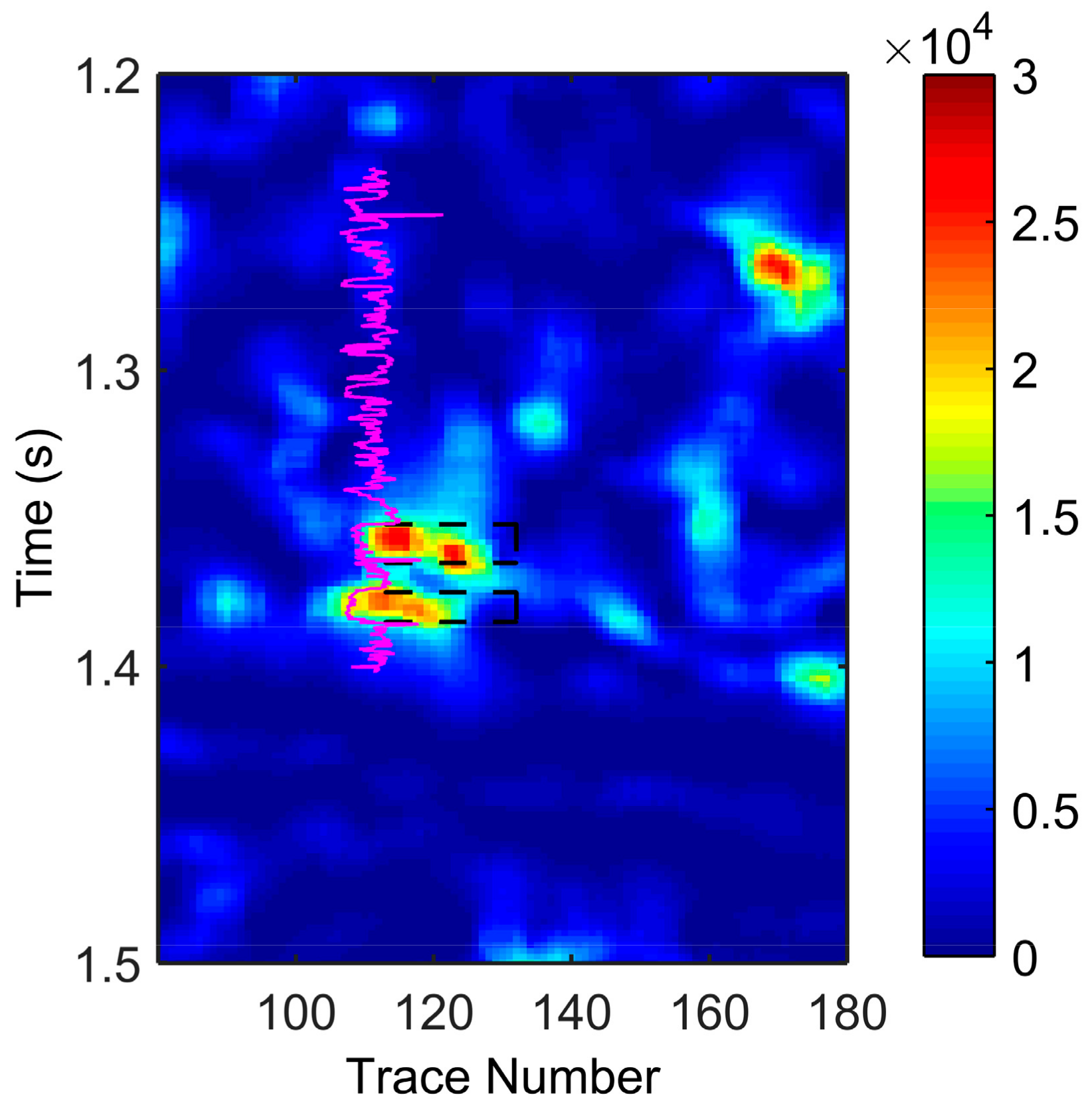
The constant frequency sections at 40 Hz and 50 Hz obtained by SSGST are shown in Figure 12. By comparing these two constant frequency sections, we can conclude that the hydrocarbon reservoir is in the elliptical area. To highlight more details about the elliptical area in Figure 12, we have locally enlarged the 40 Hz constant frequency section and combined it with the red acoustic velocity logging curve to analysis. The strong energy group in the two black-dashed, rectangular areas in Figure 13 represent the two hydrocarbon reservoirs, namely JS33-1 and JS33-2, respectively. According to the comparison with CWT, GST, and SSCWT, we can find that SSGST can provide higher time-frequency resolution and can more accurately extract the abnormal response characteristics of seismic signals. Therefore, the SSGST method can locate hydrocarbon reservoirs effectively and depicts the reservoir boundary accurately with higher precision.

5. Conclusions

A more energy-concentrated time-frequency result denotes better time-frequency location and better characterization of the time-varying feature. In this paper, the new synchrosqueezing algorithm based on the generalized S-transform (GST), namely the SSGST method, squeezes and reconstructs the complex coefficient spectra produced by the GST along the frequency direction so that the energy distributions on the time-frequency spectra are concentrated around the real instantaneous frequency of the target signal, thus showing satisfying time-frequency resolution. SSGST is a promising technique for the extraction of time-varying features of seismic signals. Results of the three synthetic examples demonstrate that the SSGST method can correctly obtain time-frequency representations of the signals and depict instantaneous frequency information better compared with CWT, GST, and SSCWT. Moreover, SSGST can reconstruct the original signal with small errors. The feasibility and validity of the SSGST method in seismic time-frequency analysis for hydrocarbon detection is confirmed via an applied example. Therefore, the SSGST method can be used as a new high-precision time-frequency analysis method in seismic signal processing and analysis.