Enhancement of Sea Wave Potential Energy with Under-Sea Periodic Structures: A Simulation and Laboratory Study
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Numerical Simulation Set-Up
3.1.1. Model A: Triangular Lattice
3.1.2. Model B: Square Lattice
3.1.3. Model C: Hexagonal Lattice
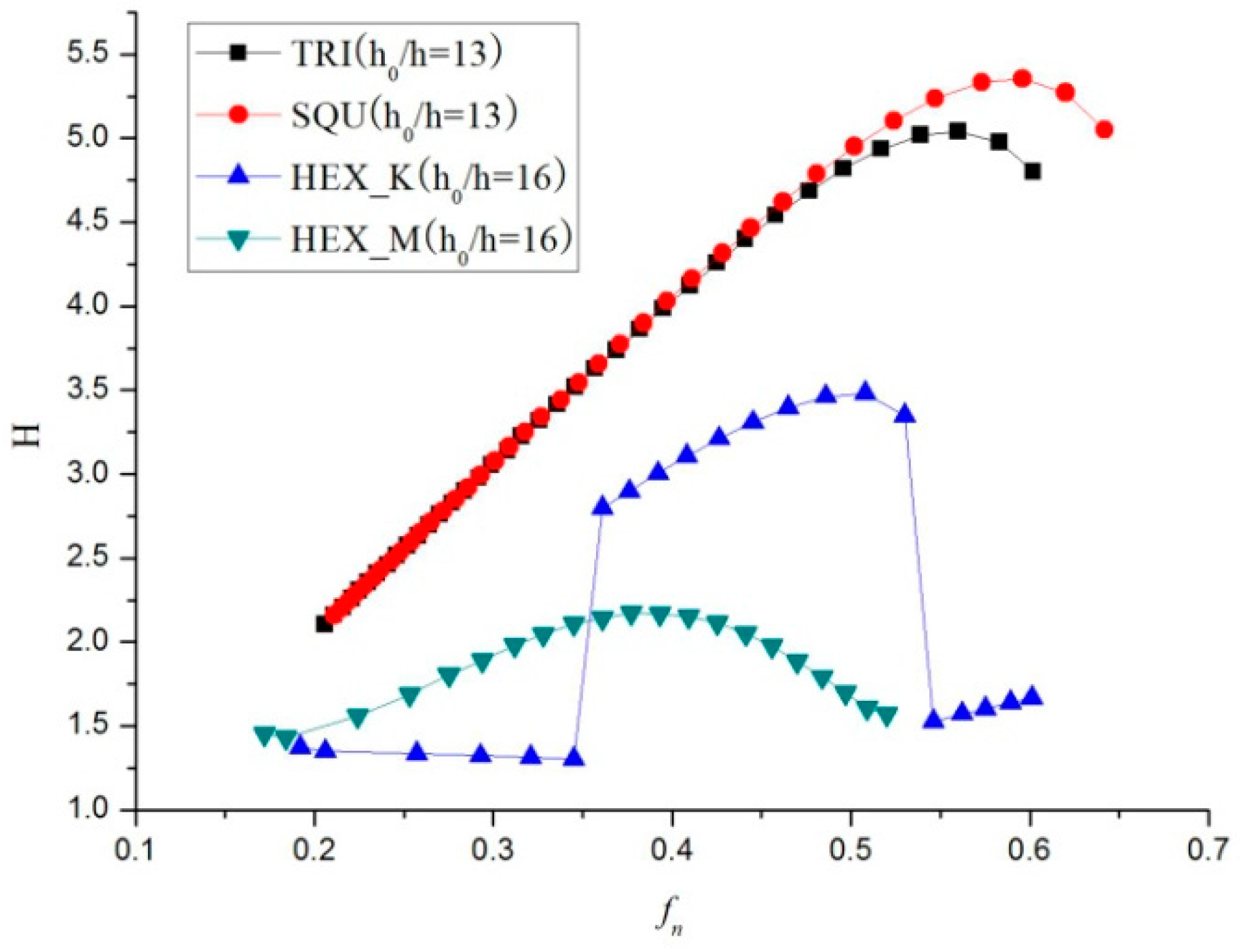
3.1.4. Optimization
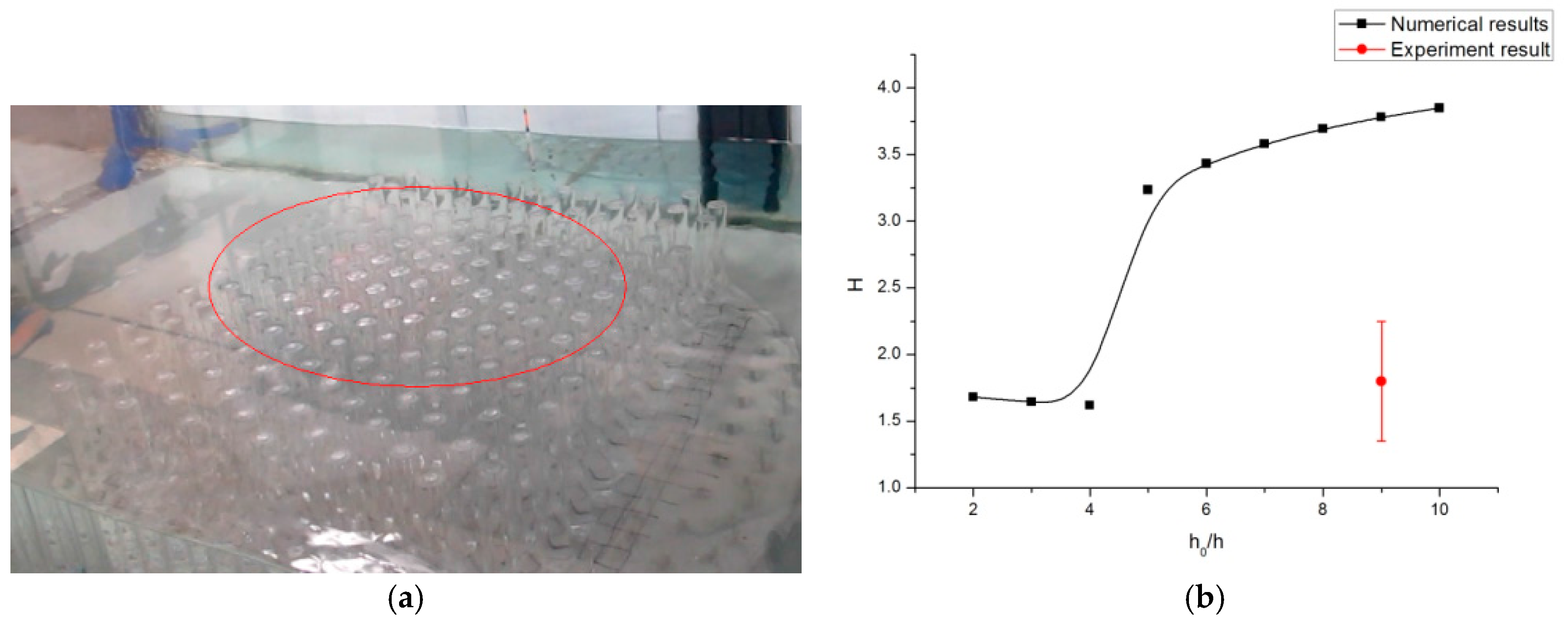
3.2. Laboratory Demonstration
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ghosh, T.K.; Prelas, M.A. Energy Resources and System; Springer: New York, NY, USA, 2011; Volume 2, pp. 267–320. [Google Scholar]
- Esteban, M.; Leary, D. Current developments and future prospects of offshore wind and ocean energy. Appl. Energy 2012, 90, 128–136. [Google Scholar] [CrossRef]
- Antonio, F.D.O. Wave energy utilization: A review of the technologies. Renew. Sust. Energy Rev. 2010, 14, 899–918. [Google Scholar]
- Chen, F.L.; Lu, S.M.; Tseng, K.T.; Lee, S.C.; Wang, E. Assessment of renewable energy reserves in Taiwan. Renew. Sust. Energy Rev. 2010, 14, 2511–2528. [Google Scholar] [CrossRef]
- Tsai, C.P.; Hwang, C.H.; Hwa, C.; Chang, H.Y. Study on the wave climate variation to the renewable wave energy assessment. Renew. Energy 2012, 38, 50–61. [Google Scholar]
- Silva, D.; Rusu, E.; Guedes-Soares, C. High-resolution wave energy assessment in shallow water accounting for tides. Energies 2016, 9, 761. [Google Scholar] [CrossRef]
- Tollefson, J. Blue energy. Nature 2014, 508, 302–304. [Google Scholar] [CrossRef] [PubMed]
- Yemm, R.; Pizer, D.; Retzler, C.; Henderson, R. Pelamis: Experience from concept to connection. Philos. Trans. R. Soc. A-Math. Phys. Eng. Sci. 2012, 370, 365–380. [Google Scholar] [CrossRef] [PubMed]
- Iuppa, C.; Contestabile, P.; Cavallaro, L.; Foti, E.; Vicinanza, D. Hydraulic Performance of an Innovative Breakwater for Overtopping Wave Energy Conversion. Sustainability 2016, 8, 1226. [Google Scholar] [CrossRef]
- Naty, S.; Viviano, A.; Foti, E. Wave Energy Exploitation System Integrated in the Coastal Structure of a Mediterranean Port. Sustainability 2016, 8, 1342. [Google Scholar] [CrossRef]
- Vicinanza, D.; Margheritini, L.; Kofoed, J.P.; Buccino, M. The SSG Wave Energy Converter: Performance, Status and Recent Developments. Energies 2012, 5, 193–226. [Google Scholar] [CrossRef]
- Belibassakis, K.A.; Gerostathis, T.P.; Athanassoulis, G.A. A coupled-mode model for water wave scattering by horizontal, non-homogeneous current in general bottom topography. Appl. Ocean Res. 2011, 33, 384–397. [Google Scholar] [CrossRef]
- Ardhuin, F.; Magne, R. Scattering of surface gravity waves by bottom topography with a current. J. Fluid Mech. 2007, 576, 235–264. [Google Scholar] [CrossRef]
- Reikard, G.; Robertson, B.; Buckham, B.; Bidlot, J.R.; Hiles, C. Simulating and forecasting ocean wave energy in western Canada. Ocean Eng. 2015, 103, 223–236. [Google Scholar] [CrossRef]
- Molin, B.; Remy, F.; Arnaud, G.; Rey, V.; Touboul, J.; Sous, D. On the dispersion equation for linear waves traveling through or over dense arrays of vertical cylinders. Appl. Ocean Res. 2016, 61, 148–155. [Google Scholar] [CrossRef]
- Mei, C.C.; Chan, I.C.; Liu, P.L.F. Waves of intermediate length through an array of vertical cylinders. Environ. Fluid Mech. 2014, 14, 235–261. [Google Scholar] [CrossRef]
- Carter, B.G.; Mclver, P. Water-wave propagation through an infinite array of floating structures. J. Eng. Math. 2013, 81, 9–45. [Google Scholar] [CrossRef]
- Brule, S.; Javelaud, E.H.; Enoch, S.; Guenneau, S. Experiments on Seismic Metamaterials: Molding Surface Waves. Phys. Rev. Lett. 2014, 112, 133901. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Yang, J.; Zi, J.; Chan, C.T.; Ho, K.M. Experimental Observation of Negative Effective Gravity in Water Waves. Sci. Rep. 2013, 3, 1916. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Li, Y.; Shao, H.; Zhong, Y.Z.; Zhang, S.; Zhao, Z.X. Band gaps and localization of surface water waves over large-scale sand waves with random fluctuations. Phys. Rev. E 2012, 85, 066319. [Google Scholar] [CrossRef] [PubMed]
- Reyes-Ayona, E.; Torrent, D.; Sanchez-Dehesa, J. Homogenization theory for periodic distributions of elastic cylinders embedded in a viscous fluid. J. Acoust. Soc. Am. 2012, 132, 2896–2908. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Wei, Y.; Li, S.; Xu, Y.; Lu, D.; Yu, B. Propagation of liquid surface waves over finite graphene structured arrays of cylinders. Theor. Appl. Mech. Lett. 2011, 1, 052007. [Google Scholar] [CrossRef]
- Flocard, F.; Finnigan, T.D. Laboratory experiments on the power capture of pitching vertical cylinders in waves. Ocean. Eng. 2010, 37, 989–997. [Google Scholar] [CrossRef]
- Yang, J.; Tang, Y.F.; Ouyang, C.F.; Liu, X.H.; Hu, X.H.; Zi, J. Observation of the focusing of liquid surface waves. App. Phys. Lett. 2009, 95, 094106. [Google Scholar] [CrossRef]
- Erselcan, İ.Ö.; Kükner, A. A numerical analysis of several wave energy converter arrays deployed in the Black Sea. Ocean Eng. 2017, 131, 68–79. [Google Scholar] [CrossRef]
- Chao, S.D.; Chiu, S.F.; Huang, Y.H.; Wang, C.C.; Wang, S.C.; Chu, C.C. Wave Energy Gathering and Enhancing Device. U.S. Patent 20140300110 A1, 9 October 2014. [Google Scholar]
- Yu, D.J.; Kim, K. Influence of bottom topography on the propagation of linear shallow water waves: An exact approach based on the invariant imbedding method. Waves Random Complex Media 2008, 18, 325–341. [Google Scholar] [CrossRef]
- Henderson, R. Design, simulation, and testing of a novel hydraulic power take-off system for the Pelamis wave energy converter. Renew. Energy 2006, 31, 271–283. [Google Scholar] [CrossRef]
- Johnson, S.G.; Joannopoulos, J.D. Block-iterative frequency-domain methods for Maxwell’s equations in a planewave basis. Opt. Express 2001, 8, 173–190. [Google Scholar] [CrossRef] [PubMed]
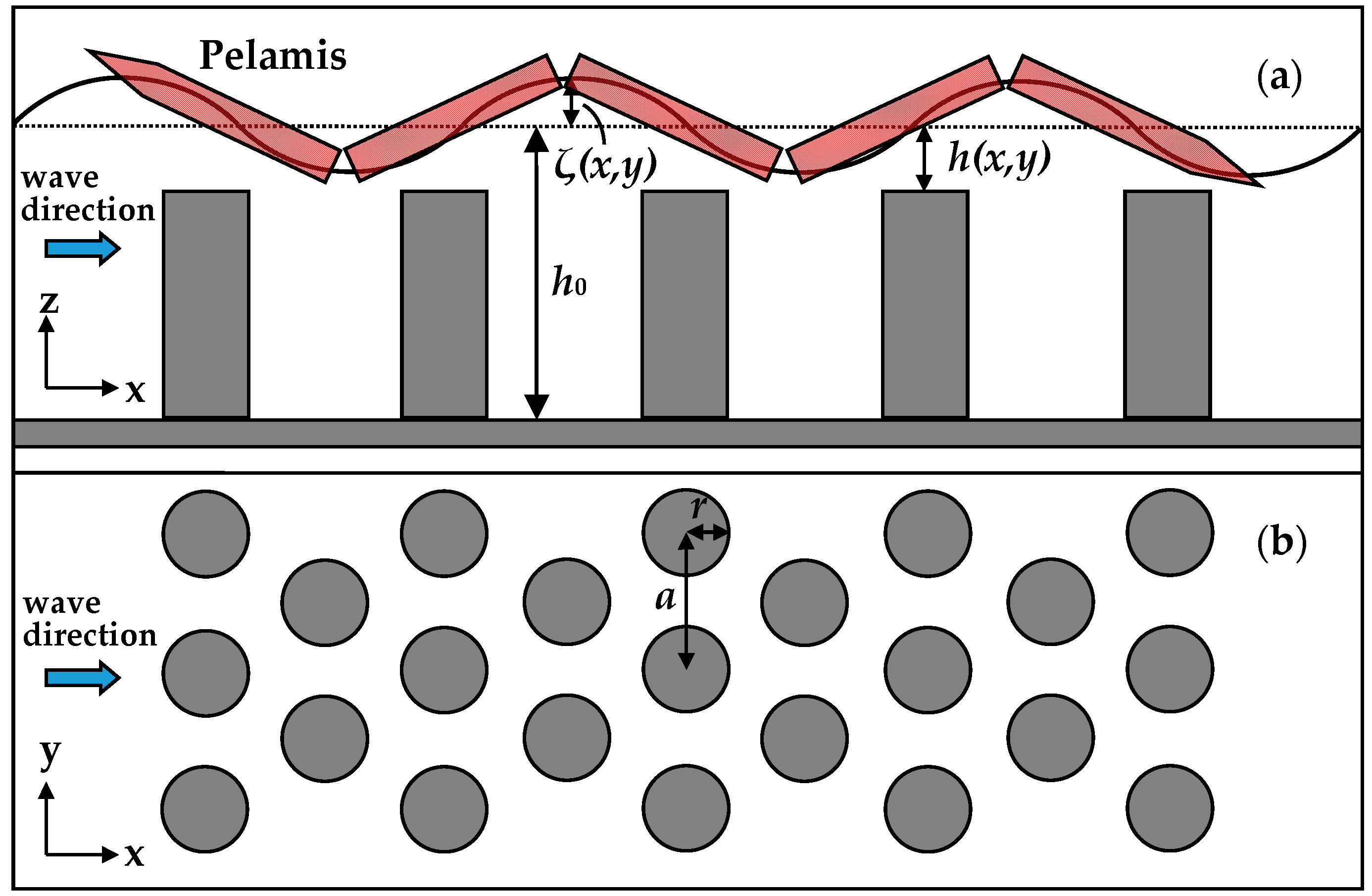

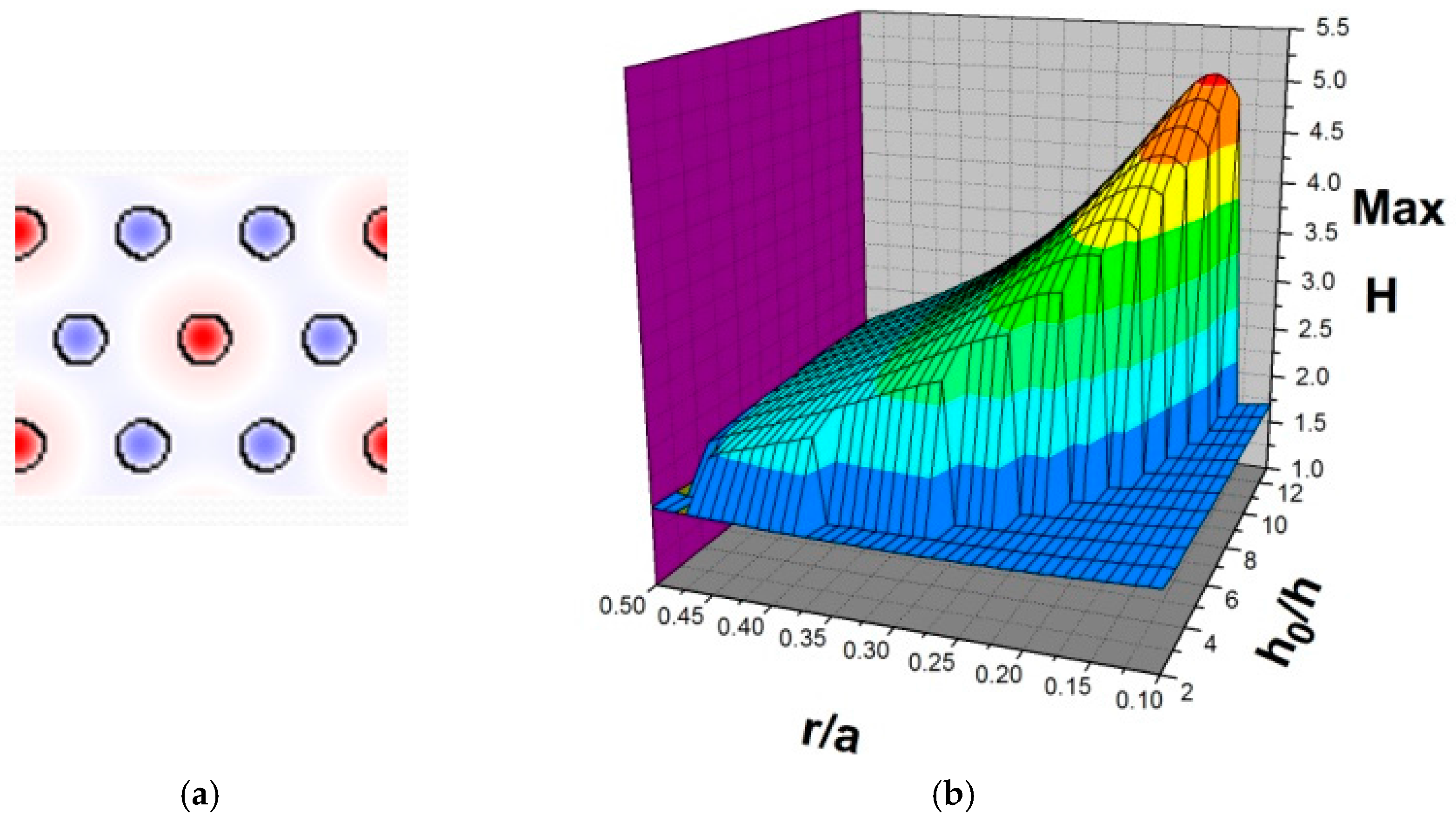
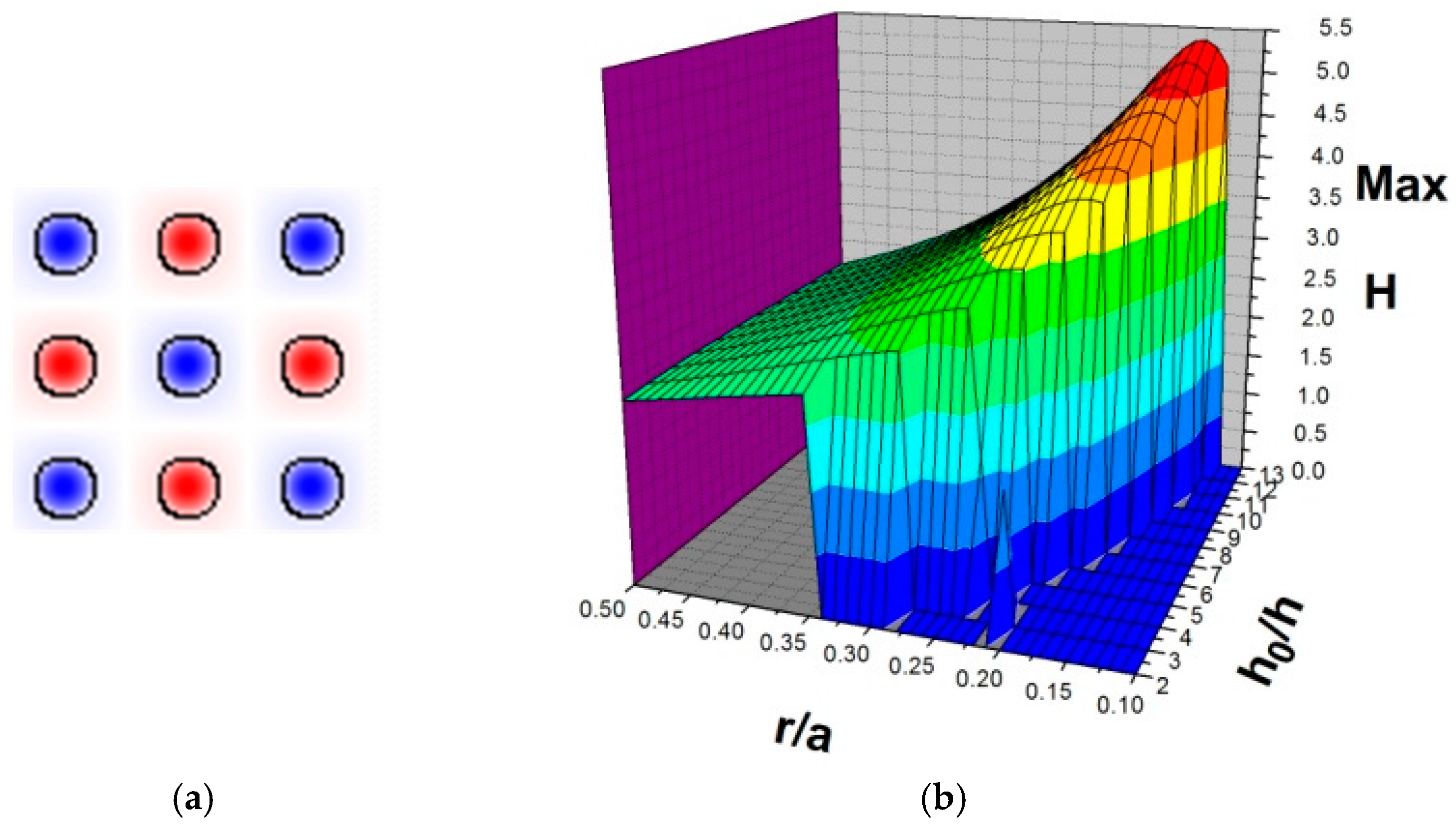
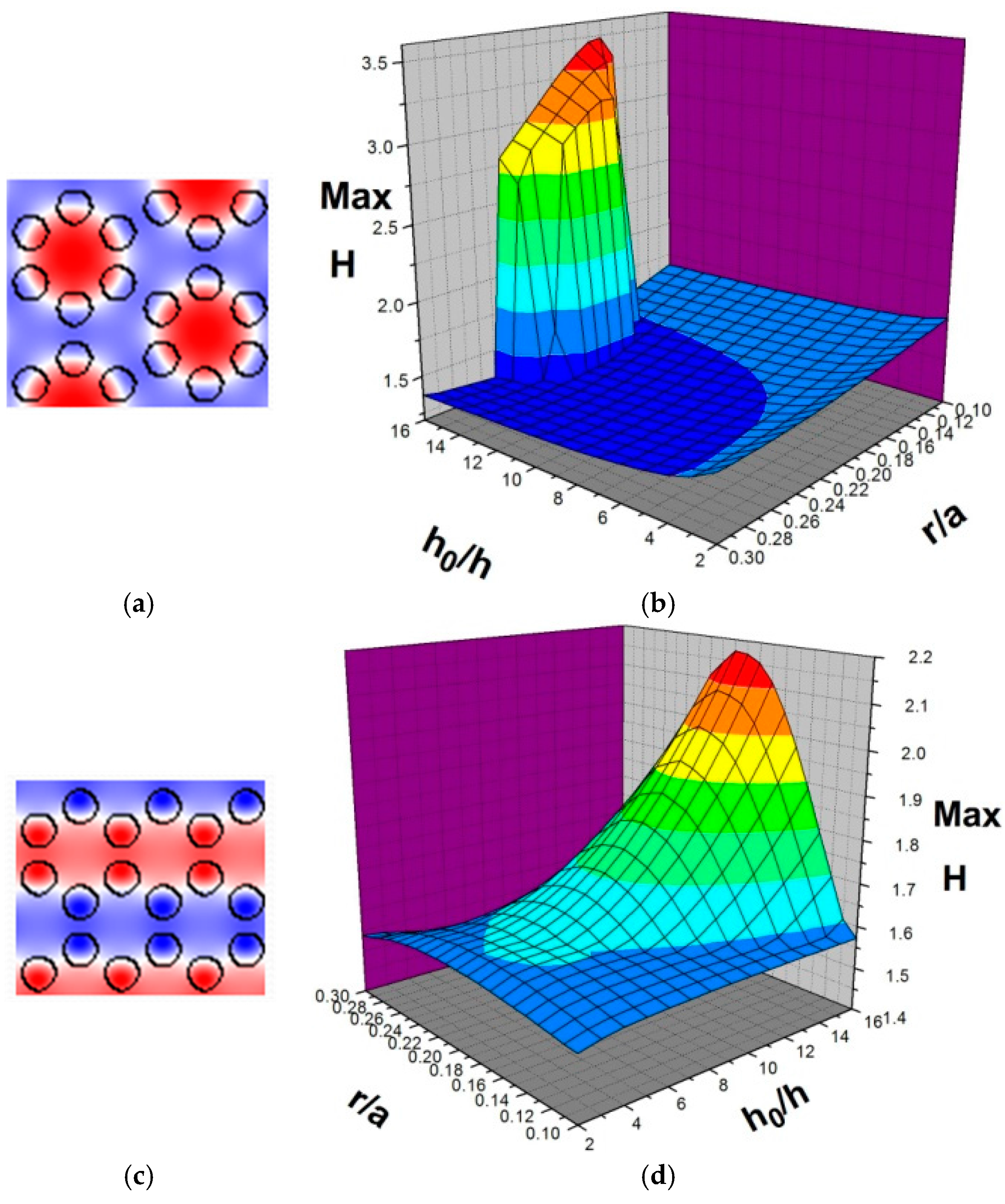

| Notation | Definition | Units |
|---|---|---|
| r | Radius of cylinder | m |
| L | Length of cylinder | m |
| h0 | Mean water level | m |
| h | Water depth | m |
| v | Velocity vector | m·s−1 |
| p | Fluid pressure | kg·m−1·s−2 |
| ρ | Fluid density | kg·m3 |
| g | Gravitational acceleration | m·s−2 |
| ζ | Vertical displacement from the mean water level | m |
| pa | Atmospheric pressure | kg·m−1·s−2 |
| A | Cross-sectional area | m2 |
| H | Enhancement factor | none |
| a | Lattice constant | m |
| λ | Wavelength | m |
| c | Wave velocity | m·s−1 |
| fn | Normalized frequency | none |
| N | Number of grid | none |
| r/a | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| h0/h | 0.14 | 0.15 | 0.16 | 0.17 | 0.18 | 0.19 | 0.20 | 0.21 | 0.22 | 0.23 | 0.24 |
| 8 | 1.658 | 0.167 | 1.637 | 1.625 | 3.906 | 4.003 | 4.004 | 3.974 | 3.923 | 3.855 | 3.78 |
| 9 | 1.654 | 1.643 | 1.631 | 4.16 | 4.221 | 4.229 | 4.199 | 4.139 | 4.063 | 3.975 | 3.882 |
| 10 | 1.65 | 1.638 | 4.331 | 4.419 | 4.445 | 4.419 | 4.358 | 4.272 | 4.175 | 4.069 | 3.963 |
| 11 | 1.647 | 4.45 | 4.594 | 4.648 | 4.637 | 4.578 | 4.489 | 4.38 | 4.265 | 4.145 | 4.028 |
| 12 | 1.635 | 4.723 | 4.831 | 4.847 | 4.799 | 4.709 | 4.596 | 4.468 | 4.338 | 4.207 | 4.08 |
| 13 | 4.799 | 4.974 | 5.041 | 5.017 | 4.935 | 4.818 | 4.684 | 4.54 | 4.399 | 4.257 | 4.123 |
| r/a | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| h0/h | 0.14 | 0.15 | 0.16 | 0.17 | 0.18 | 0.19 | 0.20 | 0.21 | 0.22 | 0.23 | 0.24 |
| 8 | 0 | 0 | 0 | 4.219 | 4.257 | 4.252 | 4.211 | 4.144 | 4.065 | 3.976 | 3.876 |
| 9 | 0 | 0 | 4.42 | 4.488 | 4.492 | 4.452 | 4.379 | 4.284 | 4.183 | 4.077 | 3.962 |
| 10 | 0 | 4.597 | 4.694 | 4.722 | 4.689 | 4.615 | 4.514 | 4.396 | 4.277 | 4.157 | 4.029 |
| 11 | 4.712 | 4.876 | 4.937 | 4.923 | 4.853 | 4.75 | 4.624 | 4.487 | 4.353 | 4.221 | 4.084 |
| 12 | 5.001 | 5.129 | 5.149 | 5.092 | 4.99 | 4.86 | 4.713 | 4.56 | 4.414 | 4.273 | 4.128 |
| 13 | 5.271 | 5.354 | 5.332 | 5.235 | 5.104 | 4.951 | 4.787 | 4.621 | 4.465 | 4.316 | 4.164 |
| r/a | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| h0/h | 0.14 | 0.15 | 0.16 | 0.17 | 0.18 | 0.19 | 0.20 | 0.21 | 0.22 | 0.23 | 0.24 | 0.25 |
| 13 | 1.552 | 1.525 | 1.495 | 1.469 | 1.44 | 1.411 | 1.376 | 1.369 | 1.363 | 1.354 | 1.347 | 1.343 |
| 14 | 1.547 | 1.519 | 1.485 | 1.417 | 3.128 | 3.131 | 3.07 | 2.984 | 2.894 | 1.652 | 1.335 | 1.332 |
| 15 | 1.541 | 1.511 | 2.72 | 3.346 | 3.301 | 3.232 | 3.148 | 3.053 | 2.958 | 2.853 | 2.649 | 1.322 |
| 16 | 1.529 | 3.349 | 3.482 | 3.462 | 3.394 | 3.308 | 3.211 | 3.107 | 3.004 | 2.897 | 2.798 | 1.304 |
| r/a | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| h0/h | 0.14 | 0.15 | 0.16 | 0.17 | 0.18 | 0.19 | 0.20 | 0.21 | 0.22 | 0.23 | 0.24 | 0.25 |
| 13 | 1.718 | 1.776 | 1.829 | 1.873 | 1.905 | 1.923 | 1.935 | 1.922 | 1.906 | 1.868 | 1.828 | 1.769 |
| 14 | 1.767 | 1.834 | 1.894 | 1.944 | 1.98 | 1.998 | 2.008 | 1.991 | 1.969 | 1.923 | 1.877 | 1.807 |
| 15 | 1.823 | 1.901 | 1.968 | 2.026 | 2.064 | 2.08 | 2.087 | 2.065 | 2.036 | 1.982 | 1.928 | 1.847 |
| 16 | 1.885 | 1.975 | 2.05 | 2.114 | 2.153 | 2.169 | 2.174 | 2.142 | 2.109 | 2.043 | 1.981 | 1.89 |
| Lattice | r/a | h0/h | fn |
|---|---|---|---|
| Triangular | 0.2~0.32 | 5~13 | 0.32~0.60 |
| Square | 0.14~0.34 | 4~13 | 0.33~0.64 |
| Hexagonal (K point) | 0.15~0.24 | 14~16 | 0.36~0.53 |
| Hexagonal (M point) | 0.16~0.23 | 14~16 | 0.33~0.44 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiu, S.-F.; Wang, J.-J.; Wang, S.-C.; Chao, S.D. Enhancement of Sea Wave Potential Energy with Under-Sea Periodic Structures: A Simulation and Laboratory Study. Appl. Sci. 2017, 7, 782. https://doi.org/10.3390/app7080782
Chiu S-F, Wang J-J, Wang S-C, Chao SD. Enhancement of Sea Wave Potential Energy with Under-Sea Periodic Structures: A Simulation and Laboratory Study. Applied Sciences. 2017; 7(8):782. https://doi.org/10.3390/app7080782
Chicago/Turabian StyleChiu, Shuo-Feng, Jyun-Jie Wang, Ssu-Che Wang, and Sheng D. Chao. 2017. "Enhancement of Sea Wave Potential Energy with Under-Sea Periodic Structures: A Simulation and Laboratory Study" Applied Sciences 7, no. 8: 782. https://doi.org/10.3390/app7080782






