Inverse Optimal Design for Position Control of a Quadrotor

Abstract

In this paper, we propose an inverse optimal design method for the position control of a quadrotor. First, we derive the dynamics of a quadrotor using the Newton-Euler formulation. Second, we present the state transformation technique to derive the position dynamics from the kinematic and dynamic models of a quadrotor. Then, we present the nonlinear inverse optimal position control of a quadrotor. The stability analysis based on Lyapunov theorem shows that the proposed control method can realize a quadrotor system that is exponentially stabilized. In addition, we show the inverse optimality of the proposed inverse optimal controller for the position control of a quadrotor. The inverse optimality can simply and clearly be shown using the state transformation technique. Finally, we present some simulation results to verify the effectiveness of the proposed control method.

1. Introduction

Over the past few years, the field of unmanned aerial vehicles (UAVs) has rapidly expanded. In addition, because of the advantage of UAVs, there has been an increase in their applications, such as aerial reconnaissance, where life-saving operations are risky for pilots, and disaster surveillance and monitoring. In particular the quadrotor, one type of UAV, has many advantages. It has the advantage of easy implementation compared to other aerial vehicles. In addition, it has vertical take-off and landing (VTOL) ability, high agility and maneuverability.

Recently, there has been significant interest in the application of quadrotors, so there has been much attention on the studies that focus on the control of a quadrotor. In the field of a quadrotors, the problem of control design has focused primarily on typical quadrotor missions including attitude stabilization and movement from one position to another position. Linear control methods such as proportional-integral-differential (PID) control and the linear quadratic regulation (LQR) control methods are proposed in [1,2]. However, linear control methods simplify the model and focus only on the local behavior of the system.

In practice, quadrotors have complicated dynamics with coupled states that cause nonlinearities. Furthermore, the dynamics of a quadrotor are not only nonlinear, but they are also difficult to characterize because of the complexity of the aerodynamic properties.

For these reasons, various nonlinear control methods have been proposed including nested saturations [3], dynamic inversion control approach [4], sliding mode control methods [5,6], feedback linearization method [7], backstepping control approaches [8,9,10], integral predictive nonlinear $H_{\infty }$ control [11], and neural network based output feedback control method [12]. Meanwhile, using optimal control techniques, research for battery operation and missions to consider the optimality have been performed [13,14]. In other words, researchers are interested in realizing the optimality of controllers other than the stability.

The optimal control problem for nonlinear systems is usually attributed to the solvability of the Hamilton-Jacobi-Bellman (HJB) equation. Because the HJB equation involves partial differential equations, optimal control design is generally too difficult to be solved analytically, with the exception of a few special cases. An alternative method is the so-called inverse optimal control method, which does not require a solution to the HJB equation [15]. In this case, the minimization of the performance index is determined a posteriori according to the given controller, so the aforementioned difficulty can be alleviated.

In [16], the author proposed an inverse optimal control of a quadrotor by employing the backstepping technique. However, it involves controlling only the attitude of a quadrotor. Moreover, to the best of the authors’ knowledge, there have been no reports on the application of inverse optimal based position control for quadrotor systems.

Most of the research into the position control of quadrotors use the small-angle assumption to simplify the position of the dynamic equation of a quadrotor [1,3,17], and they derive the reference roll and pitch angles that are outputs from the position controller. Unlike the aforementioned methods, in this paper, we derive the reference roll and pitch angle caused by the modified dynamics of the position of a quadrotor using the state transformation technique without any assumption. Furthermore, we employed the state transformation technique to simplify the design process of the inverse optimal controller. In addition, it can make the proof of inverse optimality simple.

In this paper, we propose an inverse optimal position control of a quadrotor. First, we derive the dynamics of the quadrotor using the Newton-Euler formulation. Then, we present the state transformation technique to derive the position dynamics from the kinematic and dynamic models of a quadrotor. Our proposed design of the nonlinear inverse optimal position control of a quadrotor is based on the work in [18], where Movric and Lewis suggest the algebraic Riccati equation (ARE)-based inverse optimal controller design for general time-invariant systems. The stability analysis based on Lyapunov theorem shows that the proposed control method result in a quadrotor system that is exponentially stabilized. Further, we show the inverse optimality of the proposed inverse optimal controller for the position control of a quadrotor. The inverse optimality can simply and clearly be shown using the state transformation technique. Finally, we perform simulations to verify the effectiveness of the proposed method.

The remainder of the paper is as follows: In Section 2, we describe the dynamics of the quadrotor, which is derived using the Newton-Euler formulation. In Section 3, we propose an altitude controller based on inverse optimal position control method. We show the stability and inverse optimality of the proposed inverse optimal controller for the position control of a quadrotor. In Section 4, we present the simulation results, and conclude the paper in Section 5.

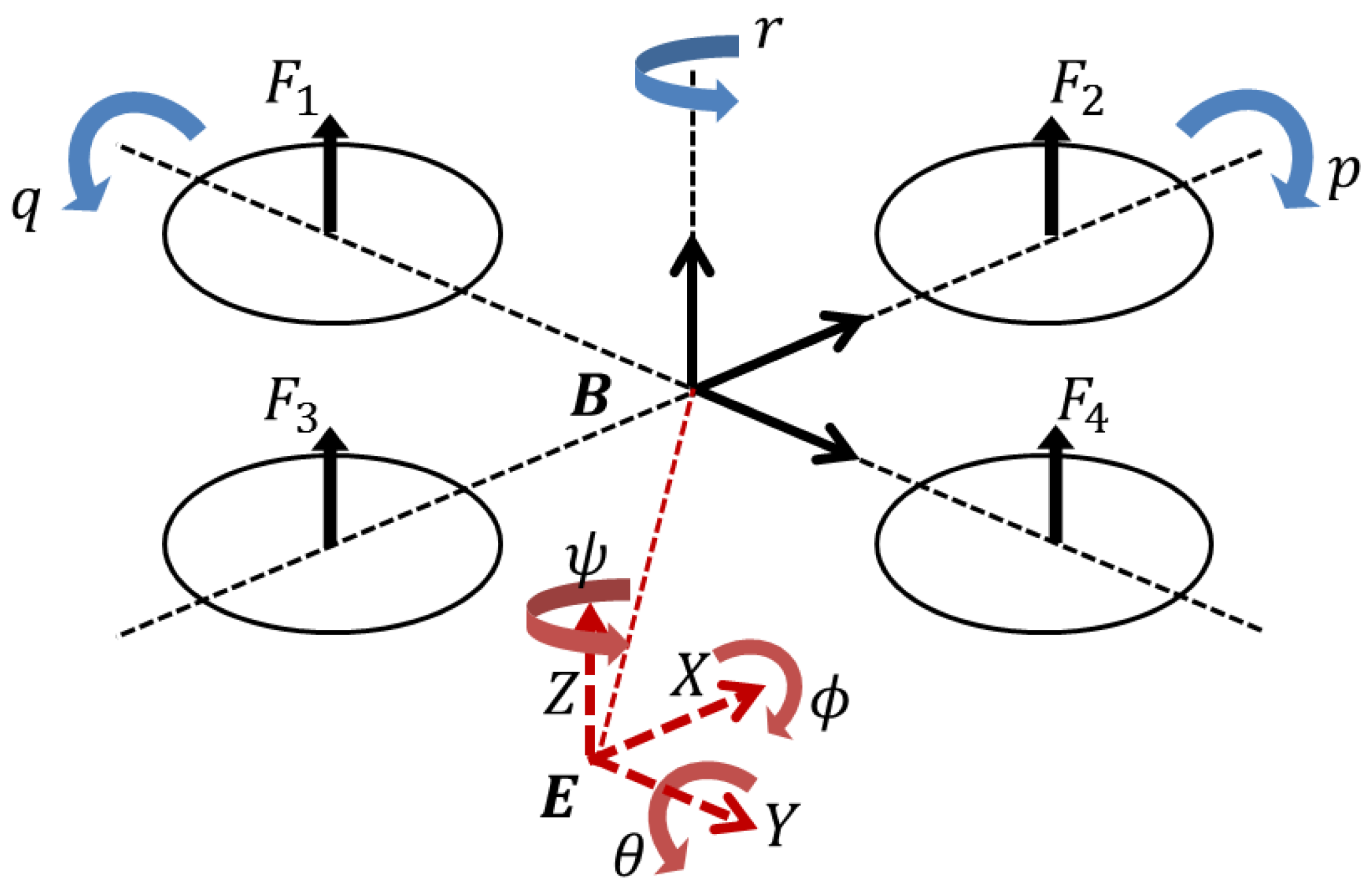
2. Dynamic Model of a Quadrotor

A quadrotor has a cross configuration with four motors, each of which is attached to each end of a cross-shaped body. The four motors are equipped with propellers whose axes of rotation are all parallel to each other. The behavior of a quadrotor can be controlled by adjusting the rotational velocities of these four propellers. The equations describing the position and attitude motions of a quadrotor are those of a rotating rigid body with six degrees-of-freedom (DoFs).

To derive the equation for the movement of a quadrotor, we should to consider the coordinates of a quadrotor system. The generalized coordinates of a quadrotor system is shown in Figure 1, where B and E denote the body-fixed and earth inertial frames, respectively.

Let us assume that the generalized velocity vectors with respect to the earth inertial and body-fixed frames are in the form of $\dot{\xi }={\left[\begin{array}{cc}\dot{{\Gamma }^E}& \dot{{\Theta }^E}\end{array}\right]}^T$ and $\nu ={\left[\begin{array}{cc}{V}^B& {\omega }^B\end{array}\right]}^T$, respectively. Here, ${\Gamma }^E=(X,Y,Z)$ represents the position of the center of mass of a quadrotor and ${\Theta }^E=(\varphi ,\theta ,\psi )$ are the Euler angles representing the orientation of a quadrotor, namely roll-pitch-yaw, with respect to the earth inertial frame. Similarly, $V^B=(u,v,w)$ and ${\omega }^B=(p,q,r)$ represents the linear and angular velocity of the quadrotor with respect to the body-fixed frame, respectively.

Now, we describe the kinematics of a generic six-DoF rigid-body as follows:

$$\begin{array}{c}\hfill \dot{\xi }=\left[\begin{array}{cc}R& 0_{3\times 3}\\ 0_{3\times 3}& T\end{array}\right]\nu ,\end{array}$$

(1)

where, $0_{3\times 3}$ is a 3 by 3 submatrix filled with all zeros, R is the coordinate transformation matrix from the body-fixed frame to the earth inertial frame, and T is the angle-rates transformation matrix from the body-fixed frame to the earth-inertial frame. Here, matrices R and T are defined, respectively, as follows:

$$\begin{array}{c}\hfill R=\left[\begin{array}{ccc}{c}_{\psi }{c}_{\theta }& -s_{\psi }{c}_{\varphi }+c_{\psi }{s}_{\theta }{s}_{\varphi }& s_{\psi }{s}_{\varphi }+c_{\psi }{s}_{\theta }{c}_{\varphi }\\ s_{\psi }{c}_{\theta }& c_{\psi }{c}_{\varphi }+s_{\psi }{s}_{\theta }{s}_{\varphi }& -c_{\psi }{s}_{\varphi }+s_{\psi }{s}_{\theta }{c}_{\varphi }\\ -s_{\theta }& s_{\varphi }{c}_{\theta }& c_{\varphi }{c}_{\theta }\end{array}\right],\end{array}$$

(2)

$$\begin{array}{c}\hfill T=\left[\begin{array}{ccc}1& s_{\varphi }{t}_{\theta }& c_{\varphi }{t}_{\theta }\\ 0& c_{\varphi }& -s_{\varphi }\\ 0& s_{\varphi }/c_{\theta }& c_{\varphi }/c_{\theta }\end{array}\right],\end{array}$$

(3)

where $c_k=cos(k)$, $s_k=sin(k)$, and $t_k=tan(k)$.

To describe the dynamic model of the position of a quadrotor, we use the Newton-Euler formalism. The dynamics of a generic six-DoF rigid-body takes into account the mass of the body. The dynamics of the position is described by

$$\begin{array}{c}\hfill m·{\dot{V}}^B+{\omega }^B\times \left(m{V}^B\right)=F^B,\end{array}$$

(4)

where m is the mass of a quadrotor, $I_{3\times 3}$ refers to a 3 by 3 identity matrix, $V^B$ is the linear velocity vector, ${\dot{V}}^B$ is the linear acceleration vector of the body-fixed frame, ${\omega }^B$ is the angular velocity vector of the body-fixed frame, and $F^B$ is the force vector of the body-fixed frame. However, it may be useful to express the dynamics of the position using the earth-inertial frame.

The nonlinear dynamics of a quadrotor can be described by

$$\begin{array}{cc}\hfill \ddot{X}& =\left(cos(\varphi )sin(\theta )cos(\psi )+sin(\varphi )sin(\psi )\right)\frac{u_1}{m},\hfill \\ \hfill \ddot{Y}& =\left(cos(\varphi )sin(\theta )sin(\psi )-sin(\varphi )cos(\psi )\right)\frac{u_1}{m},\hfill \\ \hfill \ddot{Z}& =\left(cos(\theta )cos(\varphi )\right)\frac{u_1}{m}-g.\hfill \end{array}$$

(5)

where g is the gravitational acceleration, and $u_1$ is the attitude control input represented by

$$\begin{array}{cc}\hfill u_1& =b({{\Omega }_1}^2+{{\Omega }_2}^2+{{\Omega }_3}^2+{{\Omega }_4}^2).\hfill \end{array}$$

(6)

Here, ${\Omega }_i(i=1,2,3,4)$ is the propeller speed of the i-th rotor and b is the thrust factor of a quadrotor.

3. Design of Inverse Optimal Position Controller

In this section, we design an inverse optimal position controller to converge the position states of a quadrotor to the reference values.

For the position control, inverse optimal based altitude controller is designed. Next, the reference roll and pitch angles are calculated through altitude control based position control. Finally, the position control of the quadrotor is performed through attitude tracking control. The overall control scheme is expressed by the block diagram as Figure 2.

In (5), the ($x,y$) positions dynamics of a quadrotor can be represented, using the states $P={[XY]}^T$ and $V=\dot{P}$, as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\dot{P}=V\hfill \\ \dot{V}=u_1\left[\begin{array}{c}{u}_x\\ u_y\end{array}\right]/m\hfill \end{array}\right.\end{array}$$

(7)

where $u_x=cos\varphi sin\theta cos\psi +sin\varphi sin\psi$, and $u_y=cos\varphi sin\theta sin\psi -sin\varphi cos\psi$.

Using the redefined control input U and the input-coupling transformation matrix $T^{*}$, which is invertible, (7) can be rewritten as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\dot{P}=V\hfill \\ \dot{V}=T^{*}U\hfill \end{array}\right.\end{array}$$

(8)

We analyze the position control problems of a quadrotor from two perspectives. The first one is the exponential stability, while the other one is the inverse optimality.

The position of a quadrotor converges to the reference position. In other words, the position state P of a quadrotor satisfies the following equation related to the position control of a quadrotor:

$$\begin{array}{c}\hfill \parallel P(t)-P_d\parallel \le \alpha e^{-\beta t}\parallel P_0-P_d\parallel ,\end{array}$$

(9)

where $P_0$ and $P_d$ are the initial and reference positions, respectively.

In this paper, we also show the inverse optimality of the proposed control input. The control input U, which makes the position error zero, minimizes the following objective functional:

$$\begin{array}{c}\hfill J(\delta (0),U):={\int }_0^{\infty }({\delta }^T\Theta \delta +U^T\Gamma U)dt,\end{array}$$

(10)

for a positive definite matrix $\Theta$ and $\Gamma$. Here, the position error is defined as $\delta :=P-P_d$.

Using the position dynamics of a quadrotor, as expressed in (5), we can find the altitude control input $u_1$ of a quadrotor, which is presented as the dynamics of its ($x,y$) position. In this paper, using the characteristics of the position dynamics, as explained above, we design the ($x,y$) position control input using the altitude control input $u_1$.

In this paper, to design an inverse optimal position controller, we use the following assumption:

Assumption 1.

In the control system, the position and attitude values of the quadrotor can be perfectly estimated.

3.1. Altitude Control of a Quadrotor

In this paper, we propose an altitude control input based on the inverse optimal position control method. To do this, the altitude dynamics in (5) can be rewritten in state-space form using the following states:

$$\begin{array}{c}\hfill x_5=Z,x_6=\dot{Z}.\end{array}$$

We have the altitude state-space equation of a quadrotor as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\dot{x_5}=x_6\hfill \\ \dot{x_6}=\frac{cos\varphi cos\theta }{m}\left(u_1-g\frac{m}{cos\varphi cos\theta }\right)=T_1(\varphi (t),\theta (t))·v_1\hfill \end{array}\right.\end{array}$$

(11)

where $v_1$ is the pseudo altitude control input defined by

$$\begin{array}{c}\hfill v_1:=\left(u_1-g\frac{m}{cos\varphi cos\theta }\right),\end{array}$$

(12)

and $T_1(\varphi (t),\theta (t))$ is the first transformation variable given by

$$\begin{array}{c}\hfill T_1(\varphi (t),\theta (t))=\frac{cos\varphi cos\theta }{m}.\end{array}$$

(13)

The states $x_5$ and $x_6$ related to the altitude of a quadrotor can be rewritten by the state ${\chi }_z$, as follows:

$$\begin{array}{c}\hfill {\chi }_z=\left[\begin{array}{c}{x}_5-z_d\\ x_6-{\dot{z}}_d\end{array}\right],\end{array}$$

(14)

where $z_d$ is the reference value of the altitude.

Differentiating ${\chi }_z$ with respect to time, we obtain

$$\begin{array}{c}\hfill \dot{{\chi }_z}=A_z{\chi }_z+B_z(\varphi (t),\theta (t))v_1,\end{array}$$

(15)

where $A_z$ and $B_z(\varphi (t),\theta (t))$ are defined as $A_z:=\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]$ and $B_z(\varphi (t),\theta (t)):=\left[\begin{array}{c}0\\ T_1(\varphi (t),\theta (t))\end{array}\right]$, respectively.

For the invertibility of $T_1(\varphi (t),\theta (t))$, throughout the paper, we use the following assumption.

Assumption 2.

The attitude angles $\varphi$, θ, and ψ satisfy the following conditions:

$$\begin{array}{c}\hfill \parallel \varphi ,\theta ,\psi \parallel <\frac{\pi }{2}(\forall \varphi ,\theta \in \mathbb{R})\end{array}$$

The parameters, $\varphi (t)$ and $\theta (t)$ are function of time, so we can express (15) as (16):

$$\begin{array}{c}\hfill \dot{{\chi }_z}=A_z{\chi }_z+B_z(t)v_1.\end{array}$$

(16)

where we denote $B_z(t):=B_z(\varphi (t),\theta (t))$ with a slight abuse of notation.

For the system (16), we propose the following inverse optimal pseudo altitude control input $v_1$ of a quadrotor:

$$\begin{array}{c}\hfill v_1=-k_z(\varphi ,\theta )·{\chi }_z,\end{array}$$

(17)

where $k_z(\varphi ,\theta )$ is given by

$$\begin{array}{c}\hfill k_z(\varphi ,\theta )={\gamma }_{alt}^{-1}(\varphi ,\theta )·B_z^T(t)·P_z.\end{array}$$

(18)

where we denote ${\gamma }_{alt}(t):={\gamma }_{alt}(\varphi (t),\theta (t))$ with a slight abuse of notation.

Here, the ${\gamma }_{alt}(t)$ is given by

$$\begin{array}{c}\hfill {\gamma }_{alt}(t)=T_1^2(\varphi (t),\theta (t))·{\gamma }_z,\end{array}$$

(19)

and $P_z=\left[\begin{array}{cc}{P}_{11z}& P_{12z}\\ P_{12z}& P_{22z}\end{array}\right]$ is the solution of the ARE

$$\begin{array}{c}\hfill A_z^T{P}_z+P_z{A}_z-\frac{1}{{\gamma }_z}{P}_z{B}_{z,0}{B}_{z,0}^T{P}_z+Q_z=0_{2\times 2},\end{array}$$

(20)

where $A_z:=\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]$ , $B_{z,0}:=\left[\begin{array}{c}0\\ 1\end{array}\right]$, and a positive definite matrix $Q_z:=\left[\begin{array}{cc}{q}_{z,1}& 0\\ 0& q_{z,2}\end{array}\right]$, $q_{z,1},q_{z,2}>0$, respectively.

Therefore, based on the definition of $v_1$ in (17) and (11), we can derive the actual altitude control input as follows:

$$\begin{array}{c}\hfill u_1=v_1+g\frac{m}{cos\varphi cos\theta }.\end{array}$$

(21)

Theorem 1.

Consider the transformation variable $T_1(\varphi (t),\theta (t))$, as shown in (13), and the altitude system (16) of a quadrotor using the pseudo altitude control input (17). Then,

(i) Stability: The pseudo altitude control input (17) asymptotically stabilizes the altitude system (16) of a quadrotor. In addition, the state ${\chi }_z$ in (14) decreases exponentially with regard to the initial value, i.e.,

$$\begin{array}{c}\hfill {\chi }_z(t)\le \alpha {\chi }_z^{-\kappa t},\underset{t\to \infty }{lim}{\chi }_z(t)=0,\end{array}$$

with positive constants α and κ.

(ii) Inverse Optimality: The pseudo altitude control input (17) of a quadrotor minimizes the objective functional

$$\begin{array}{c}\hfill J\left({\chi }_z(0),v_1(.)\right)={\int }_0^{\infty }\left({\chi }_z^T(t)Q_z{\chi }_z(t)+{\gamma }_{alt}(t){\parallel v_1(t)\parallel }^2\right)dt,\end{array}$$

for a positive definite matrix $Q_z$ and the ${\gamma }_{alt}(t)>0$.

Proof of Theorem 1.

 

(i) Stability: Substituting (17) into (16), we obtain the altitude system (16) of a quadrotor as follows:

$$\begin{array}{cc}{\dot{\chi }}_z\hfill & =A_z{\chi }_z-{\gamma }_{alt}^{-1}(t)B_z(t)\left(B_z^T(t)P_z{\chi }_z\right)\hfill \\ & =\left(A_z-{\gamma }_{alt}^{-1}(t)B_z(t)B_z^T(t)P_z\right){\chi }_z\hfill \\ & =\left(A_z-{\gamma }_{alt}^{-1}(t)B_{z,0}{T}_1^2(\varphi ,\theta )B_{z,0}^T{P}_z\right){\chi }_z.\hfill \end{array}$$

(22)

By using (19), (22) can be rewritten as follows:

$$\begin{array}{cc}\hfill {\dot{\chi }}_z=& \left(A_z-\frac{1}{{\gamma }_z}{B}_{z,0}{B}_{z,0}^T{P}_z\right){\chi }_z.\hfill \end{array}$$

(23)

Consider the positive definite function $V({\chi }_z)$ = ${\chi }_z^T{P}_z{\chi }_z$ as a Lyapunov function candidate. Differentiating $V({\chi }_z)$ with respect to the time and substituting (23), we obtain

$$\begin{array}{cc}\dot{V}({\chi }_z)\hfill & ={\dot{\chi }}_z^T{P}_z{\chi }_z+{\chi }_z^T{P}_z{\dot{\chi }}_z\hfill \\ & ={\left\{\left(A_z-\frac{1}{{\gamma }_z}{B}_{z,0}{B}_{z,0}^T{P}_z\right){\chi }_z\right\}}^T{P}_z{\chi }_z+{\chi }_z^T{P}_z\left(A_z-\frac{1}{{\gamma }_z}{B}_{z,0}{B}_{z,0}^T{P}_z\right){\chi }_z\hfill \\ & ={\chi }_z^T\left(A_z^T{P}_z-\frac{1}{{\gamma }_z}{P}_z^T{B}_{z,0}{B}_{z,0}^T{P}_z\right){\chi }_z+{\chi }_z^T\left(P_z{A}_z-\frac{1}{{\gamma }_z}{P}_z{B}_{z,0}{B}_{z,0}^T{P}_z\right){\chi }_z.\hfill \end{array}$$

Since $P_z$ is a symmetric matrix satisfying $P_z=P_z^T$, we obtain

$$\begin{array}{cc}\dot{V}({\chi }_z)\hfill & ={\chi }_z^T\left(A_z^T{P}_z+P_z{A}_z-2\frac{1}{{\gamma }_z}{P}_z^T{B}_{z,0}{B}_{z,0}^T{P}_z\right){\chi }_z\hfill \\ & ={\chi }_z^T\left(-Q_z-\frac{1}{{\gamma }_z}{P}_z^T{B}_{z,0}{B}_{z,0}^T{P}_z\right){\chi }_z\hfill \\ & =-{\chi }_z^T\left(Q_z+\frac{1}{{\gamma }_z}{P}_z^T{B}_{z,0}{B}_{z,0}^T{P}_z\right){\chi }_z\hfill \\ & \le -{\chi }_z^T{Q}_z{\chi }_z\hfill \\ & \le -\alpha V({\chi }_z).\hfill \end{array}$$

Therefore, we have $V\left({\chi }_z(t)\right)\le V\left({\chi }_z(0)\right)e^{-\alpha t}$, which implies the exponential stability of the system. When the time becomes infinity, the state ${\chi }_z(t)$ related to the altitude of a quadrotor becomes zero.

(ii) Inverse Optimality: In order to prove the inverse optimality, we use the comparison Lemma [19]. Then, we have

$$\begin{array}{c}\hfill 0<V\left({\chi }_z(t)\right)\le V\left({\chi }_z(0)\right)e^{-\alpha t}<\infty .\end{array}$$

Therefore, we can check that $V({\chi }_z(t))$ has a finite value. In addition, using (17)–(19), $\dot{V}({\chi }_z)$ can be rewritten as follows:

$$\begin{array}{c}\hfill -\dot{V}({\chi }_z)={\chi }_z^T{Q}_z{\chi }_z+{\gamma }_{alt}(t)v_1^T{v}_1.\end{array}$$

(24)

From the definition of $V({\chi }_z)={\chi }_z^T{P}_z{\chi }_z$, we can show that ${lim}_{t\to \infty }V\left({\chi }_z(t)\right)=0$ is satisfied. Therefore, integrating (24) with respect to time from zero to infinity, we have

$$\begin{array}{cc}V\left({\chi }_z(0)\right)\hfill & =-\left[\underset{t\to \infty }{lim}V\left({\chi }_z(t)\right)-V\left({\chi }_z(0)\right)\right]\hfill \\ & ={\int }_0^{\infty }\left({\chi }_z^T(t)Q_z{\chi }_z(t)+{\gamma }_{alt}(t){\parallel v_1(t)\parallel }^2\right)dt.\hfill \end{array}$$

(25)

Because $Q_z$ and $P_z$ are positive definite matrices, the matrices $Q_z$, $P_z$, ${\gamma }_{alt}(t)$, $A_z$, and $B_z(t)$ satisfy the matrix-type HJB equation

$$\begin{array}{c}\hfill A_z^T{P}_z+P_z{A}_z-{\gamma }_{alt}^{-1}(t)P_z{B}_z(t)B_z^T(t)P_z+Q_z=0_{2\times 2}.\end{array}$$

(26)

Then, $v_1=-k_z(\varphi ,\theta )·{\chi }_z$ is the optimal solution for the objective functional (25).

By using (19), (26) can be changed as follows:

$$\begin{array}{c}\hfill A_z^T{P}_z+P_z{A}_z-\frac{1}{{\gamma }_z}{P}_z{B}_{z,0}{B}_{z,0}^T{P}_z+Q_z=0_{2\times 2}.\end{array}$$

(27)

Therefore, the inverse optimal pseudo altitude control input (17) is the optimal solution for the objective functional (25), because (27) has the same form as that of the HJB equation.

Therefore, the pseudo altitude control input $v_1$ is the optimal solution for the objective functional (25) and the altitude system (16) of a quadrotor. This result thus solves the problem of inverse optimality. ☐

Remark 1.

In the system expressed by (16), for input coupling matrix $B_z(t)$ given in (15) and the ${\gamma }_{alt}(t)$ given in (19), are satisfied the following equation:

$$\begin{array}{c}\hfill \frac{1}{{\gamma }_{alt}(t)}{B}_z(t)B_z{(t)}^T=\frac{1}{{\gamma }_z}{B}_{z,0}{B}_{z,0}^T\end{array}$$

(28)

Specially, if ${\gamma }_{alt}(t)$ is set appropriately like (19), the time varying matrix term, such as the left side of (28), is replaced by a constant matrix term like the right side of (28). Meanwhile, (28) is used to demonstrate stability and inverse optimality.

Remark 2.

For the following objective functional J subject to system (16), and the given attitude trajectory $\varphi (t)$ and $\theta (t)$, the input $v_1(t)$ is the optimal solution to minimize the following objective functional J.

$$\begin{array}{cc}\hfill J\left({\chi }_z(0),v_1(.)\right)=& \underset{t_f\to \infty }{lim\; sup}\left\{{\chi }^T(t_f)\overline{Q_z}\chi (t_f)+{\int }_0^{t_f}\left({\chi }_z^T(t)Q_z{\chi }_z(t)+{\gamma }_{alt}(t){\parallel v_1(t)\parallel }^2\right)dt\right\},\hfill \\ \hfill =& {\int }_0^{\infty }\left({\chi }_z^T(t)Q_z{\chi }_z(t)+{\gamma }_{alt}(t){\parallel v_1(t)\parallel }^2\right)dt,\hfill \end{array}$$

$$\begin{array}{c}\hfill v_1(t)=-{\gamma }_{alt}^{-1}(t)B_z^T(t)P_z{\chi }_z(t).\end{array}$$

(29)

The $P_z$ is the solution of the ARE (20), and it is the convergence value of the solution $P_z(t)$ of the following differential Riccati equation when $t_f$ goes to infinity.

$$\begin{array}{c}\hfill \dot{P_z}(t)=-P_z(t)A_z-A_z^T{P}_z(t)-Q_z+{\gamma }_{alt}^{-1}(t)P_z(t)B_z(t)B_z^T(t)P_z(t).\end{array}$$

This is equivalent to the optimal solution of matrix-type HJB (26) mentioned in the proof of this paper.

This Remark applies in a similar way to the ($x,y$) position control in the next Section 3.2. Therefore, the Remark is omitted in the position control in Section 3.2.

3.2. Position Control of a Quadrotor Based on Altitude Control

In this section, to realize the position control of a quadrotor, we define the variable $\widetilde{u_1}$, using the actual altitude control input $u_1$, as follows:

$$\begin{array}{c}\hfill {\tilde{u}}_1=T_1(\varphi (t),\theta (t))u_1=\frac{cos\varphi cos\theta }{m}{v}_1+g.\end{array}$$

(30)

To design the position control of a quadrotor, the dynamics of a quadrotor (5) can be rewritten in state-space form using the following states:

$$\begin{array}{c}\hfill x_1=X,x_2=\dot{X},x_3=Y,x_4=\dot{Y}\end{array}$$

We obtain the ($x,y$) position state-space equations of a quadrotor as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\dot{x_1}=x_2\hfill \\ \dot{x_2}=u_1\left(cos\varphi sin\theta cos\psi +sin\varphi sin\psi \right)/m\hfill \\ \dot{x_3}=x_4\hfill \\ \dot{x_4}=u_1\left(cos\varphi sin\theta sin\psi -sin\varphi cos\psi \right)/m\hfill \end{array}\right.\end{array}$$

(31)

Rearranging these equations, we finally obtain the following position dynamics (7) of a quadrotor as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\dot{P}=V\hfill \\ \dot{V}=u_1/m\left[\begin{array}{c}{u}_x\\ u_y\end{array}\right]\hfill \end{array}\right.\end{array}$$

(32)

where P and V are defined as $P:={[XY]}^T$ and $V:=\dot{P}$, respectively, $u_x$ and $u_y$ are the effective control inputs are defined by

$$\begin{array}{c}\hfill \left[\begin{array}{c}{u}_x\\ u_y\end{array}\right]=\left[\begin{array}{c}cos\varphi sin\theta cos\psi +sin\varphi sin\psi \\ cos\varphi sin\theta sin\psi -sin\varphi cos\psi \end{array}\right].\end{array}$$

(33)

To express (32) in a form like that of (8), substituting the altitude input (30) of a quadrotor into the position dynamics (32) of a quadrotor and using the transformation matrix $T_2({\chi }_z(t),\varphi (t),\theta (t),\psi (t))$ given by

$$\begin{array}{c}\hfill T_2({\chi }_z(t),\varphi (t),\theta (t),\psi (t))={\tilde{u}}_1\left[\begin{array}{cc}cos\psi & sin\psi \\ sin\psi & -cos\psi \end{array}\right],\end{array}$$

(34)

we obtain the matrix-type position dynamics of a quadrotor as follows:

$$\begin{array}{cc}\dot{P}\hfill & =V\hfill \\ \hfill \dot{V}& ={\tilde{u}}_1\left[\begin{array}{cc}cos\psi & sin\psi \\ sin\psi & -cos\psi \end{array}\right]\left[\begin{array}{c}tan\theta \\ sec\theta ·tan\varphi \end{array}\right]\hfill \\ & =T_2({\chi }_z(t),\varphi (t),\theta (t),\psi (t))\left[\begin{array}{c}{u}_{11}\\ u_{22}\end{array}\right],\hfill \end{array}$$

(35)

where $u_{11}=tan\theta$ and $u_{22}=sec\theta ·tan\varphi$.

The states P and V, which are related to the position of a quadrotor, can be rewritten as the state ${\chi }_p$, as follows:

$$\begin{array}{c}\hfill {\chi }_p=\left[\begin{array}{c}P-P_d\\ V-V_d\end{array}\right],\end{array}$$

(36)

where $P_d$ is the reference value of the position, $V_d={\dot{P}}_d$ is the reference velocity value along the X and Y axes.

Differentiating ${\chi }_p$ with respect to time, we have

$$\begin{array}{c}\hfill \dot{{\chi }_p}=A_p{\chi }_p+B_p({\chi }_z(t),\varphi (t),\theta (t),\psi (t))u_p,\end{array}$$

(37)

where $A_p$ and $B_p({\chi }_z(t),\varphi (t),\theta (t),\psi (t))$ are defined as $A_p:=\left[\begin{array}{cc}{0}_{2\times 2}& I_{2\times 2}\\ 0_{2\times 2}& 0_{2\times 2}\end{array}\right]$ and $B_p({\chi }_z(t),\varphi (t),\theta (t),\psi (t)):=\left[\begin{array}{c}{0}_{2\times 2}\\ T_2({\chi }_z(t),\varphi (t),\theta (t),\psi (t))\end{array}\right]$, respectively, and $u_p:=\left[\begin{array}{c}{u}_{11}\\ u_{22}\end{array}\right]$.

The parameters, ${\chi }_z(t)$, $\varphi (t)$, $\theta (t)$, and $\psi (t)$ are function of time, so we can express (37) as follows:

$$\begin{array}{c}\hfill \dot{{\chi }_p}=A_p{\chi }_p+B_p(t)u_p.\end{array}$$

(38)

where we denote $B_p(t):=B_p({\chi }_z(t),\varphi (t),\theta (t),\psi (t))$ with a slight abuse of notation.

For the system (38), we also propose the following inverse optimal ($x,y$) position control input $u_p$ of a quadrotor:

$$\begin{array}{c}\hfill u_p=-k_p({\chi }_z,\varphi ,\theta ,\psi )·{\chi }_p,\end{array}$$

(39)

where $k_p$ is given by

$$\begin{array}{c}\hfill k_p({\chi }_z,\varphi ,\theta ,\psi )={\Gamma }_p^{-1}(t)·B_p^T(t)·P_p.\end{array}$$

(40)

where we denote ${\Gamma }_p(t):={\Gamma }_p({\chi }_z(t),\varphi (t),\theta (t),\psi (t))$ with a slight abuse of notation.

Here, a positive definite matrix ${\Gamma }_p(t)$ is given by

$$\begin{array}{c}\hfill {\Gamma }_p(t)={\gamma }_p·I_{2\times 2}·{\tilde{u}}_1^2,\end{array}$$

(41)

and $P_p=\left[\begin{array}{cc}{P}_{11p}& P_{12p}\\ P_{12p}^T& P_{22p}\end{array}\right]$ is the solution of the ARE

$$\begin{array}{c}\hfill A_p^T{P}_p+P_p{A}_p-\frac{1}{{\gamma }_p}{P}_p{B}_{p,0}{B}_{p,0}^T{P}_p+Q_p=0_{4\times 4},\end{array}$$

where $A_p:=\left[\begin{array}{cc}{0}_{2\times 2}& I_{2\times 2}\\ 0_{2\times 2}& 0_{2\times 2}\end{array}\right]$ and $B_{p,0}:=\left[\begin{array}{c}{0}_{2\times 2}\\ I_{2\times 2}\end{array}\right]$, respectively, and a positive definite matrix $Q_p:=\left[\begin{array}{cc}{q}_{p,1}& 0_{2\times 2}\\ 0_{2\times 2}& q_{p,2}\end{array}\right]$, $q_{p,1},q_{p,2}$ are the positive matrices.

Through the ($x,y$) position dynamics (35) of a quadrotor, which is expressed in terms of P, V, and $T_2({\chi }_z(t),\varphi (t),\theta (t),\psi (t))$ given by (34), we can consider the position control input defined by

$$\begin{array}{c}\hfill u_p=\left[\begin{array}{c}{u}_{11}\\ u_{22}\end{array}\right]=\left[\begin{array}{c}tan\theta \\ sec\theta tan\varphi \end{array}\right].\end{array}$$

(42)

Assumption 3.

To derive a reference attitude value for position control, the attitude of the quadrotor is assumed to be perfect tracking.

The motion along the x and y axes is related to the pitch and roll angles, respectively. The reference roll(${\theta }_d$) and pitch(${\varphi }_d$) angles of a quadrotor that enable the quadrotor to converge in the desired position are obtained from the inverse optimal position control input $u_p$ designed in Section 3.2. Therefore, the reference roll(${\theta }_d$) and pitch(${\varphi }_d$) angles are obtained by using the position control input (42) as follows:

$$\begin{array}{ll}\hfill {\theta }_d& =arctan\left(u_{11}\right)\hfill \end{array}$$

(43)

$$\begin{array}{ll}\hfill {\varphi }_d& =arctan\left(\frac{u_{22}}{sec{\theta }_d}\right).\hfill \end{array}$$

(44)

For notational convenience, we will use the state vector ${\chi }_p$ throughout the following lemma and theorem that gives the stability and inverse optimality of the position control input (39).

Lemma 1.

$T_2({\chi }_z(t),\varphi (t),\theta (t),\psi (t)){\Gamma }_p^{-1}(t)T_2^T({\chi }_z(t),\varphi (t),\theta (t),\psi (t))={\gamma }_p^{-1}{I}_{2\times 2}.$

Proof of Lemma 1.

Using (34) and (41), we obtain

$$\begin{array}{cc}\hfill T_2({\chi }_z(t),\varphi (t),\theta (t),\psi (t)){\Gamma }_p^{-1}(t)& T_2^T({\chi }_z(t),\varphi (t),\theta (t),\psi (t))\hfill \\ \hfill =& \left\{{\tilde{u}}_1·\left[\begin{array}{cc}cos\psi & sin\psi \\ sin\psi & -cos\psi \end{array}\right]·{({\gamma }_p·I_{2\times 2}·{\tilde{u}}_1^2)}^{-1}·{\left({\tilde{u}}_1·\left[\begin{array}{cc}cos\psi & sin\psi \\ sin\psi & -cos\psi \end{array}\right]\right)}^T\right\}\hfill \\ \hfill =& \left\{\left[\begin{array}{cc}cos\psi & sin\psi \\ sin\psi & -cos\psi \end{array}\right]·{{\gamma }_p}^{-1}·I_{2\times 2}·{\left[\begin{array}{cc}cos\psi & sin\psi \\ sin\psi & -cos\psi \end{array}\right]}^T\right\}\hfill \\ \hfill =& {\gamma }_p^{-1}{I}_{2\times 2}.\hfill \end{array}$$

☐

Theorem 2.

Consider the transformation matrix $T_2({\chi }_z(t),\varphi (t),\theta (t),\psi (t))$, as shown in (34) satisfying Lemma 1, and the ($x,y$) position system (38) of a quadrotor with the position control input (39). Then,

(i) Stability: The position control input (39) asymptotically stabilize the ($x,y$) position system (38) of a quadrotor. Further, the state ${\chi }_p$ in (36) decreases exponentially with regard to the initial value, i.e.,

$$\begin{array}{c}\hfill {\chi }_p(t)\le \alpha {\chi }_p^{-\kappa t},\underset{t\to \infty }{lim}{\chi }_p(t)=0,\end{array}$$

with positive constants α and κ.

(ii) Inverse Optimality: The ($x,y$) position control input (39) of a quadrotor minimizes the objective functional

$$\begin{array}{c}\hfill J\left({\chi }_p(0),u_p(.)\right)={\int }_0^{\infty }\left({\chi }_p^T{Q}_p{\chi }_p+u_p^T{\Gamma }_p(t)u_p\right)dt,\end{array}$$

for some positive definite matrix $Q_p$ and a time varying positive definite matrix ${\Gamma }_p(t)$.

Proof of Theorem 2.

 

(i) Stability: Substituting (39) into the ($x,y$) position system (38) of a quadrotor, we obtain

$$\begin{array}{cc}{\dot{\chi }}_p\hfill & =A_p{\chi }_p+B_p(t)\left(-{\Gamma }_p^{-1}(t)B_p^T(t)P_p{\chi }_p\right)\hfill \\ & =\left(A_p-B_p(t){\Gamma }_p^{-1}(t)B_p^T(t)P_p\right){\chi }_p\hfill \\ & =\left(A_p-B_{p,0}{T}_2({\chi }_z(t),\varphi (t),\theta (t),\psi (t)){\Gamma }_p^{-1}(t)T_2^T({\chi }_z(t),\varphi (t),\theta (t),\psi (t))B_{p,0}^T{P}_p\right){\chi }_p.\hfill \end{array}$$

(45)

From Lemma 1, (45) can be rewritten as

$$\begin{array}{cc}{\dot{\chi }}_p\hfill & =\left\{A_p-B_{p,0}{\gamma }_p^{-1}{I}_{2\times 2}{B}_{p,0}^T{P}_p\right\}{\chi }_p\hfill \\ & =\left\{A_p-{\gamma }_p^{-1}{B}_{p,0}{B}_{p,0}^T{P}_p\right\}{\chi }_p\hfill \end{array}$$

(46)

Consider the positive definite function $V({\chi }_p)$ = ${\chi }_p^T{P}_p{\chi }_p$ as a Lyapunov function candidate. Differentiating $V({\chi }_p)$ with respect to the time and substituting (45), we obtain

$$\begin{array}{cc}\dot{V}({\chi }_p)\hfill & ={\dot{\chi }}_p^T{P}_p{\chi }_p+{\chi }_p^T{P}_p{\dot{\chi }}_p\hfill \\ & ={\left\{\left(A_p-\frac{1}{{\gamma }_p}{B}_{p,0}{B}_{p,0}^T{P}_p\right){\chi }_p\right\}}^T{P}_p{\chi }_p+{\chi }_p^T{P}_p\left(A_p-\frac{1}{{\gamma }_p}{B}_{p,0}{B}_{p,0}^T{P}_p\right){\chi }_p\hfill \\ & ={\chi }_p^T\left(A_p^T{P}_p-\frac{1}{{\gamma }_p}{P}_p^T{B}_{p,0}{B}_{p,0}^T{P}_p\right){\chi }_p+{\chi }_p^T\left(P_p{A}_p-\frac{1}{{\gamma }_p}{P}_p{B}_{p,0}{B}_{p,0}^T{P}_p\right){\chi }_p.\hfill \end{array}$$

Since $P_p$ is a symmetric matrix satisfying the equation $P_p=P_p^T$, we obtain

$$\begin{array}{cc}\dot{V}({\chi }_p)\hfill & ={\chi }_p^T\left(A_p^T{P}_p+P_p{A}_p-2\frac{1}{{\gamma }_p}{P}_p^T{B}_{p,0}{B}_{p,0}^T{P}_p\right){\chi }_p\hfill \\ & ={\chi }_p^T\left(-Q_p-\frac{1}{{\gamma }_p}{P}_p^T{B}_{p,0}{B}_{p,0}^T{P}_p\right){\chi }_p\hfill \\ & =-{\chi }_p^T\left(Q_p+\frac{1}{{\gamma }_p}{P}_p^T{B}_{p,0}{B}_{p,0}^T{P}_p\right){\chi }_p\hfill \\ & \le -{\chi }_p^T{Q}_p{\chi }_p\hfill \\ & \le -\alpha V({\chi }_p).\hfill \end{array}$$

Therefore, we have $V\left({\chi }_p(t)\right)\le V\left({\chi }_p(0)\right)e^{-\alpha t}$, which implies the exponential stability of the system. When the time goes to infinity, the state ${\chi }_p$ related to the ($x,y$) position of a quadrotor goes to zero. Therefore this result solves the position control problem (9).

(ii) Inverse Optimality: In order to prove the inverse optimality, we use the comparison Lemma [19]. Then, we have

$$\begin{array}{c}\hfill 0<V\left({\chi }_p(t)\right)\le V\left({\chi }_p(0)\right)e^{-\alpha t}<\infty .\end{array}$$

Therefore, we can check that $V\left({\chi }_p(t)\right)$ has a finite value. In addition, using (39) and (40), $\dot{V}({\chi }_p)$ can be rewritten as

$$\begin{array}{c}\hfill -\dot{V}({\chi }_p)={\chi }_p^T{Q}_p{\chi }_p+u_p^T{\Gamma }_p(t)u_p.\end{array}$$

(47)

From the definition of $V({\chi }_p)={\chi }_p^T{P}_p{\chi }_p$, we know that ${lim}_{t\to \infty }V\left({\chi }_p(t)\right)=0$ is satisfied. Therefore, integrating (47) with respect to time from zero to infinity, we obtain

$$\begin{array}{cc}V\left({\chi }_p(0)\right)\hfill & =-\left[\underset{t\to \infty }{lim}V\left({\chi }_p(t)\right)-V\left({\chi }_p(0)\right)\right]\hfill \\ & ={\int }_0^{\infty }\left({\chi }_p^T{Q}_p{\chi }_p+u_p^T{\Gamma }_p(t)u_p\right)dt.\hfill \end{array}$$

(48)

Because $Q_P$ and $P_p$ are positive definite matrices, matrices $Q_p$, $P_p$, ${\Gamma }_p(t)$, $A_p$, and $B_p(t)$ satisfy the matrix-type HJB equation

$$\begin{array}{c}\hfill A_p^T{P}_p+P_p{A}_p-P_p{B}_p(t){\Gamma }_p^{-1}(t)B_p^T(t)P_p+Q_p=0_{4\times 4}.\end{array}$$

(49)

Then, $u_p=-k_p({\chi }_z,\varphi ,\theta ,\psi )·{\chi }_p$ is the optimal solution for the objective functional (48).

From Lemma 1, $B_p(t){\Gamma }_p^{-1}(t)B_p^T(t)$ in (49) becomes

$$\begin{array}{cc}{B}_p(t){\Gamma }_p^{-1}(t)B_p^T(t)\hfill & =\left(B_{p,0}{T}_2({\chi }_z(t),\varphi (t),\theta (t),\psi (t))\right){\Gamma }_p^{-1}(t){\left(B_{p,0}{T}_2({\chi }_z(t),\varphi (t),\theta (t),\psi (t))\right)}^T\hfill \\ & =B_{p,0}\left(T_2({\chi }_z(t),\varphi (t),\theta (t),\psi (t)){\Gamma }_p^{-1}{T}_2^T({\chi }_z(t),\varphi (t),\theta (t),\psi (t))\right)B_{p,0}^T\hfill \\ & =\frac{1}{{\gamma }_p}{B}_{p,0}{B}_{p,0}^T.\hfill \end{array}$$

(50)

Using (50), (49) can be rewritten as follows:

$$\begin{array}{c}\hfill A_p^T{P}_p+P_p{A}_p-\frac{1}{{\gamma }_p}{P}_p{B}_{p,0}{B}_{p,0}^T{P}_p+Q_p=0_{4\times 4}.\end{array}$$

(51)

Therefore, the inverse optimal position control input (39) is the optimal solution for the objective functional (48), because (51) has the same form as that of the HJB equation.

Further, the position control input $u_p$ is the optimal solution for the objective functional (48) and the ($x,y$) position (38) of a quadrotor. Therefore this result solves the inverse optimality problem (10) of the position control of a quadrotor.  ☐

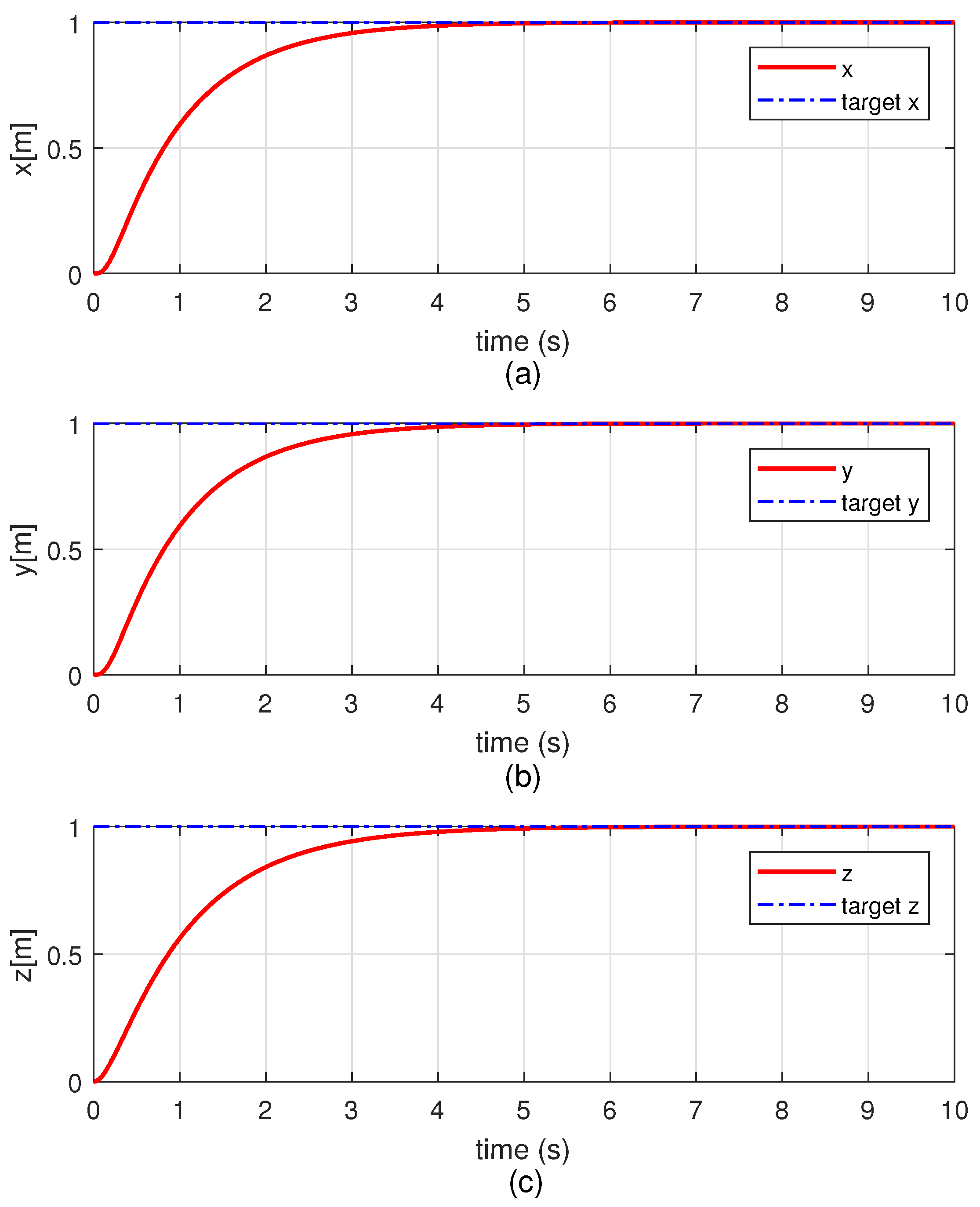
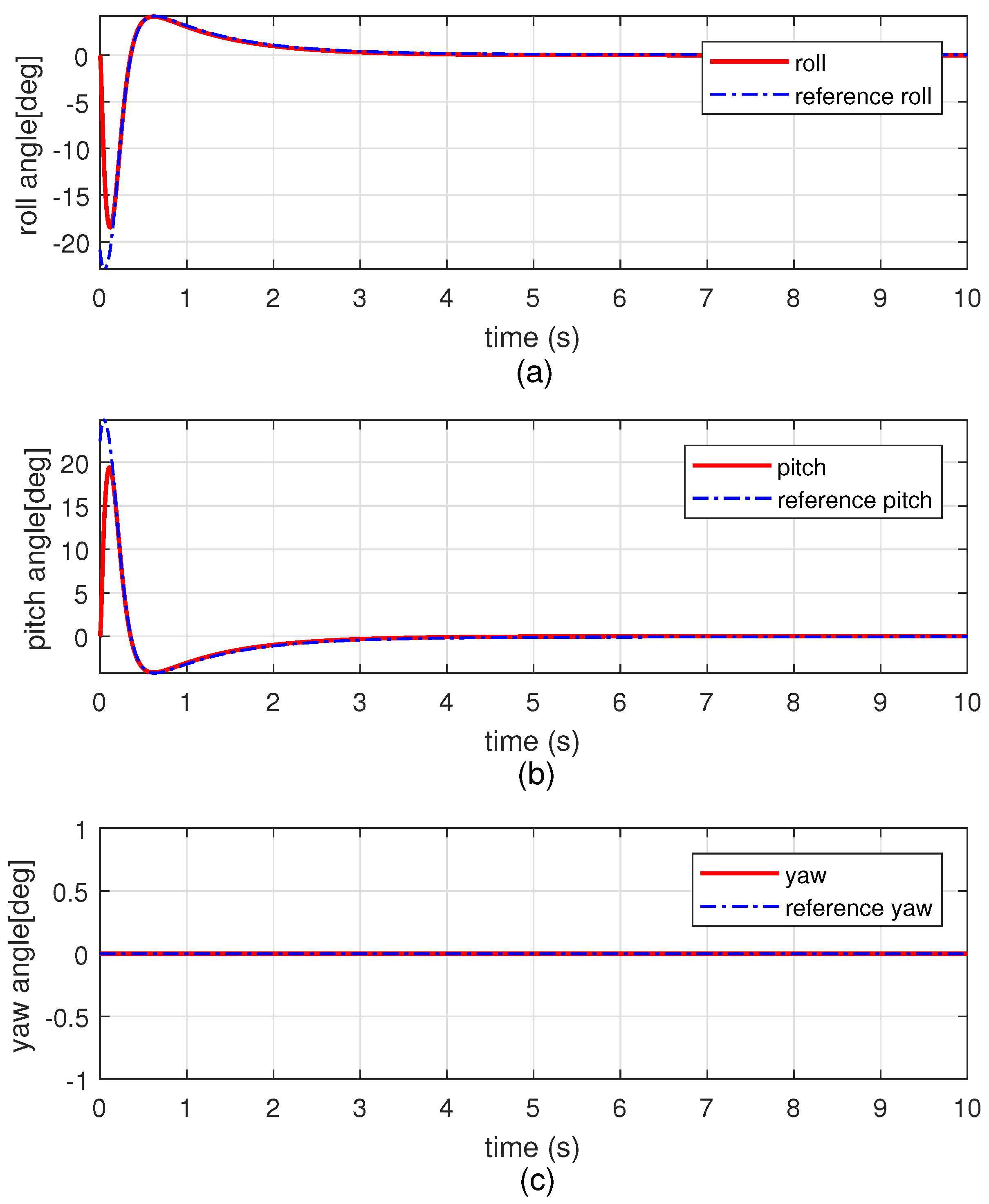
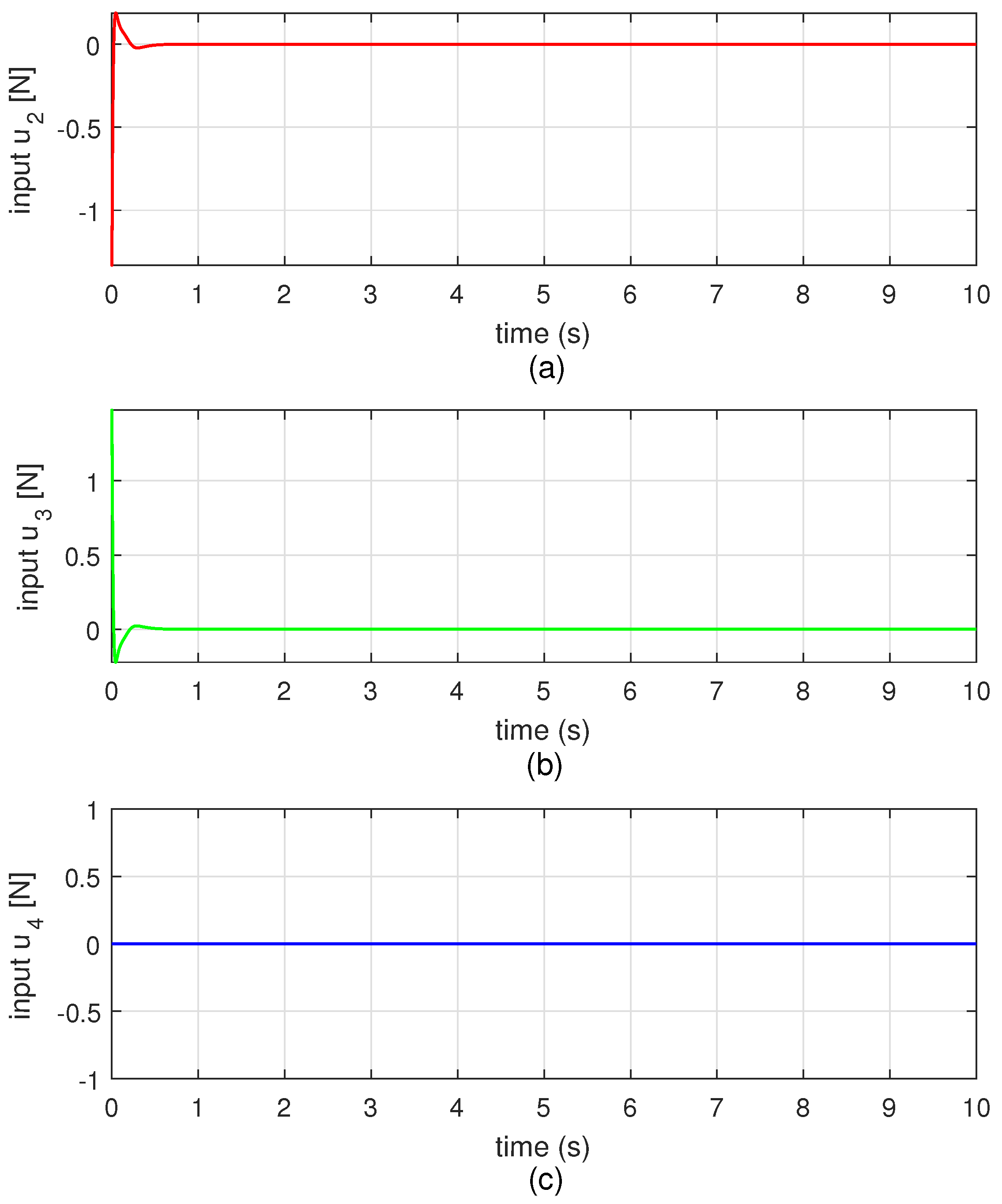
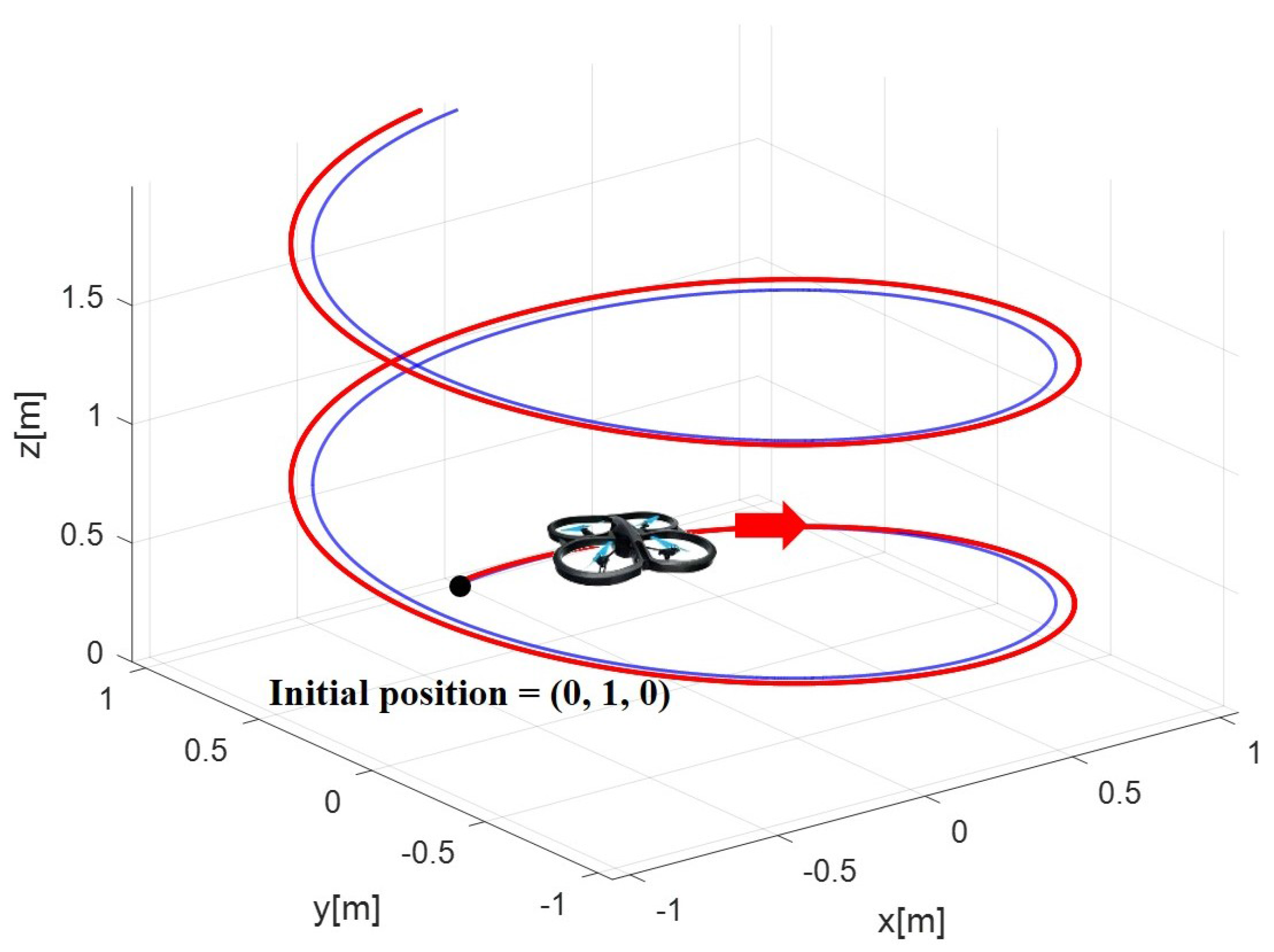
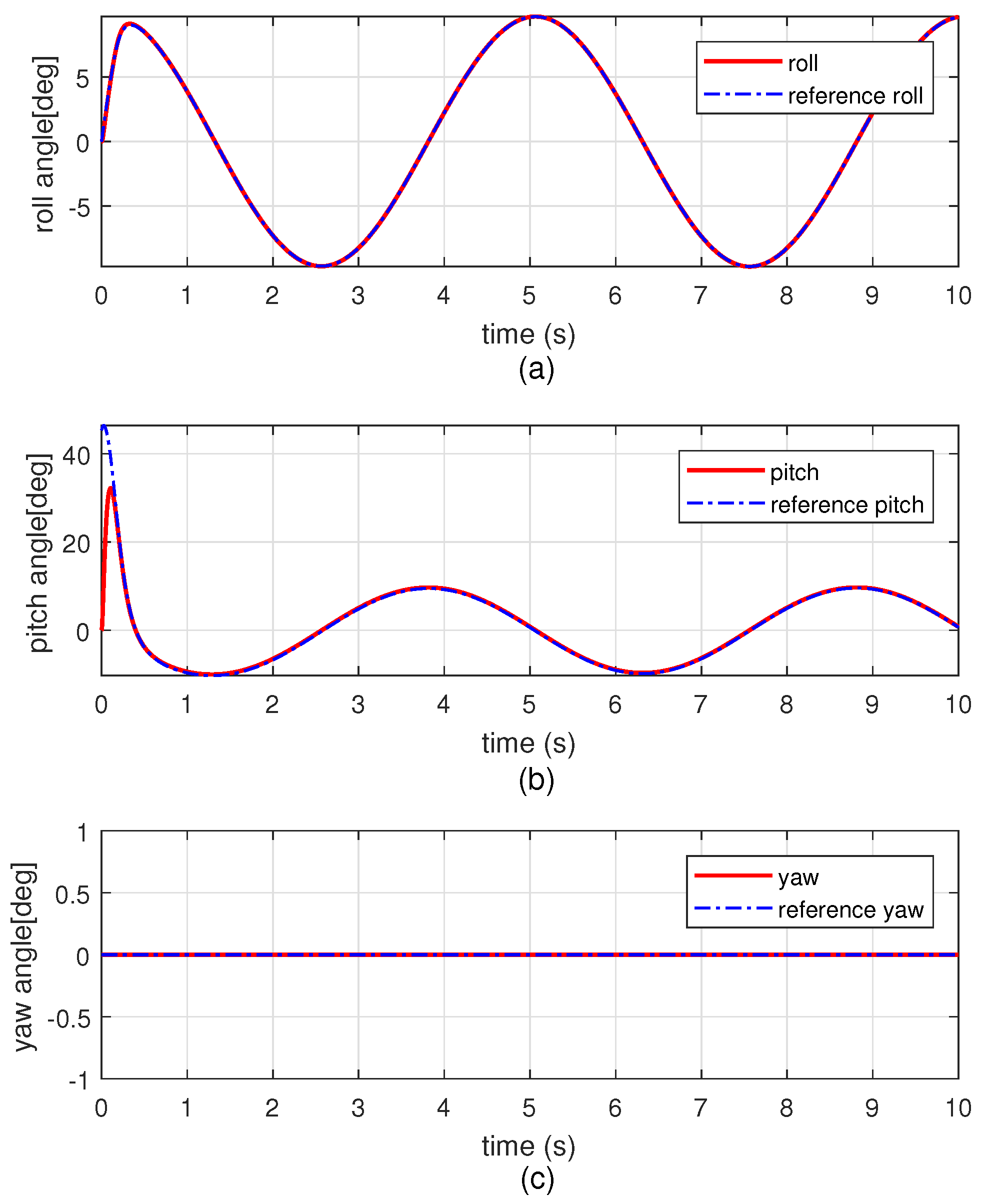
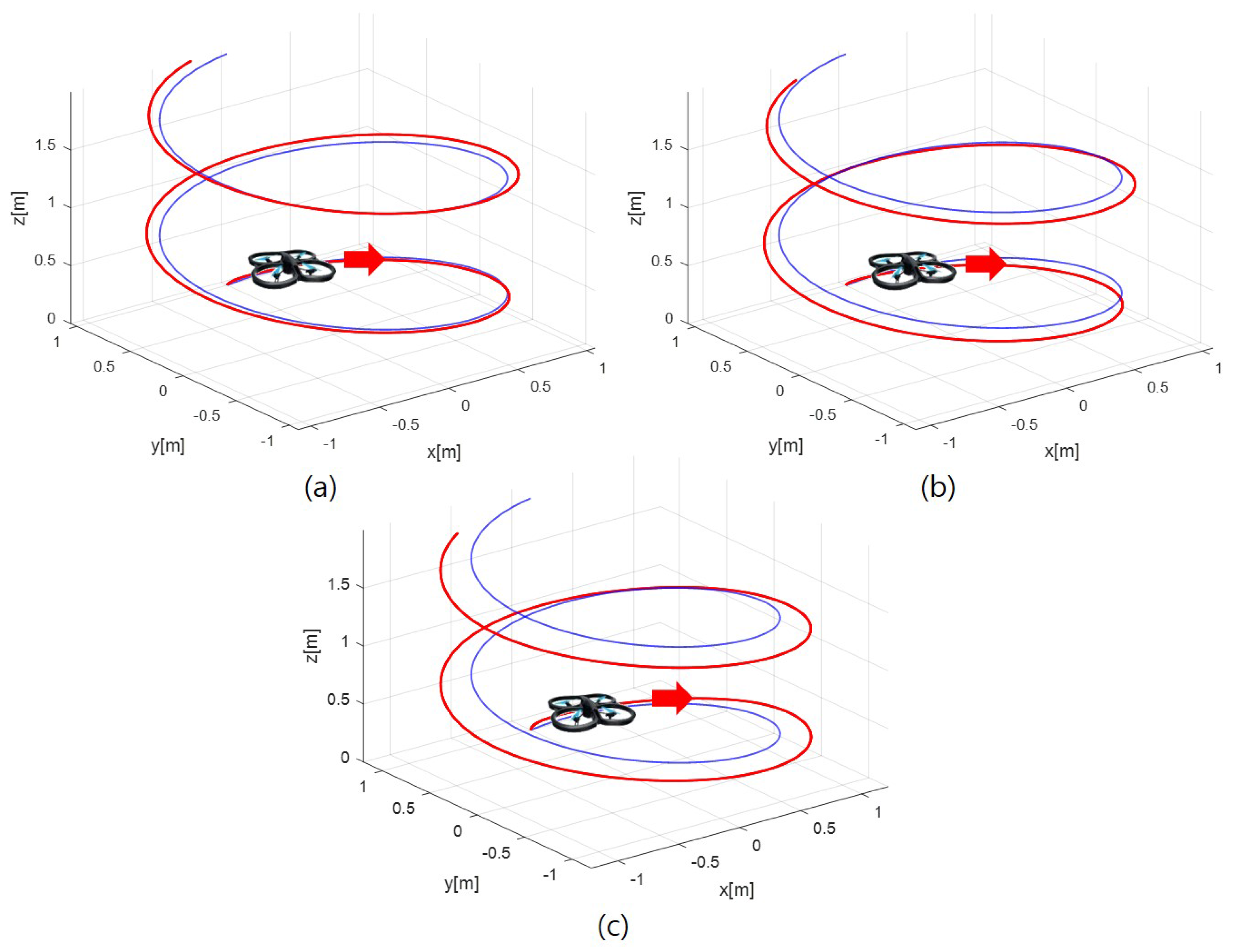
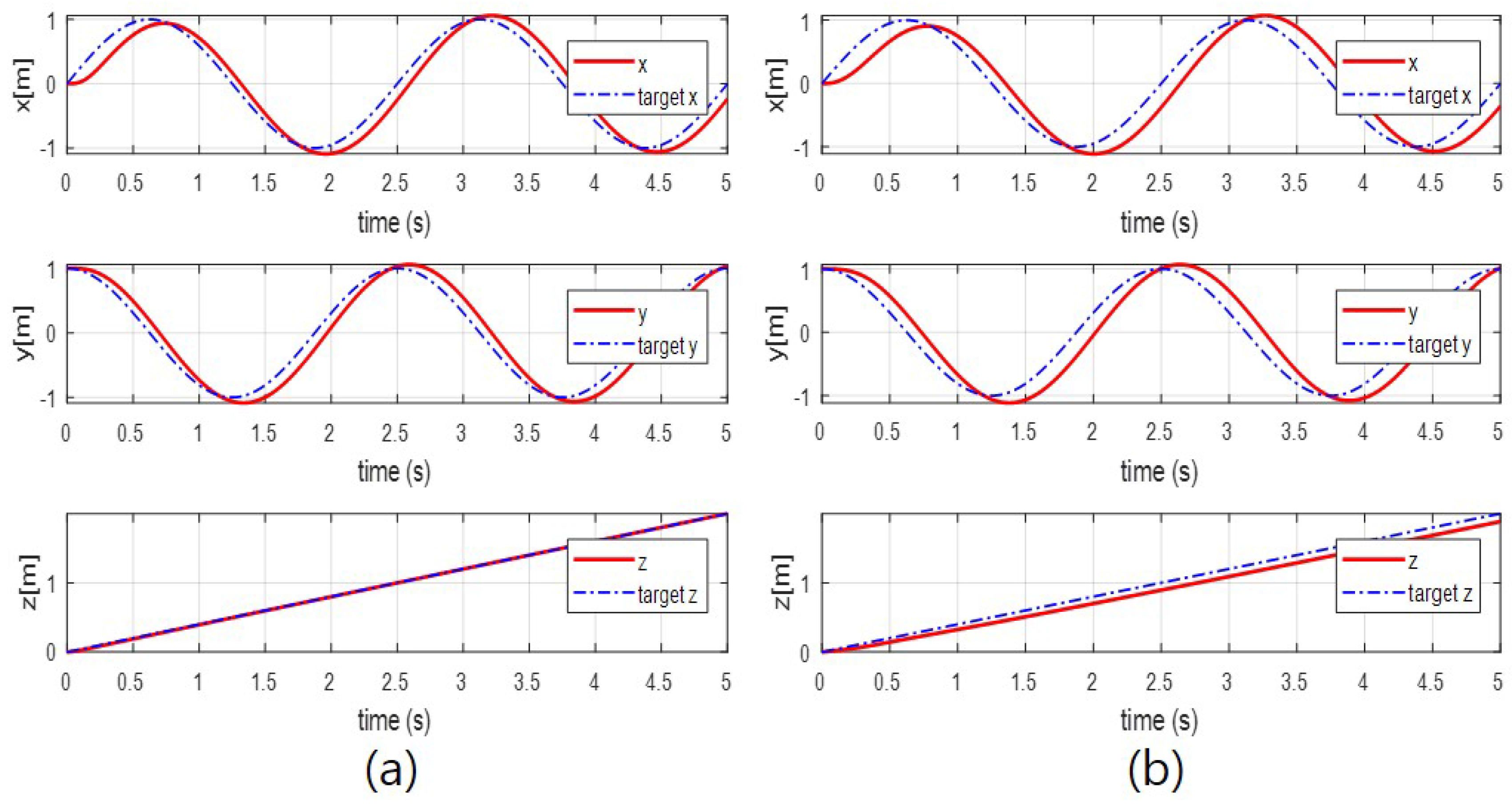
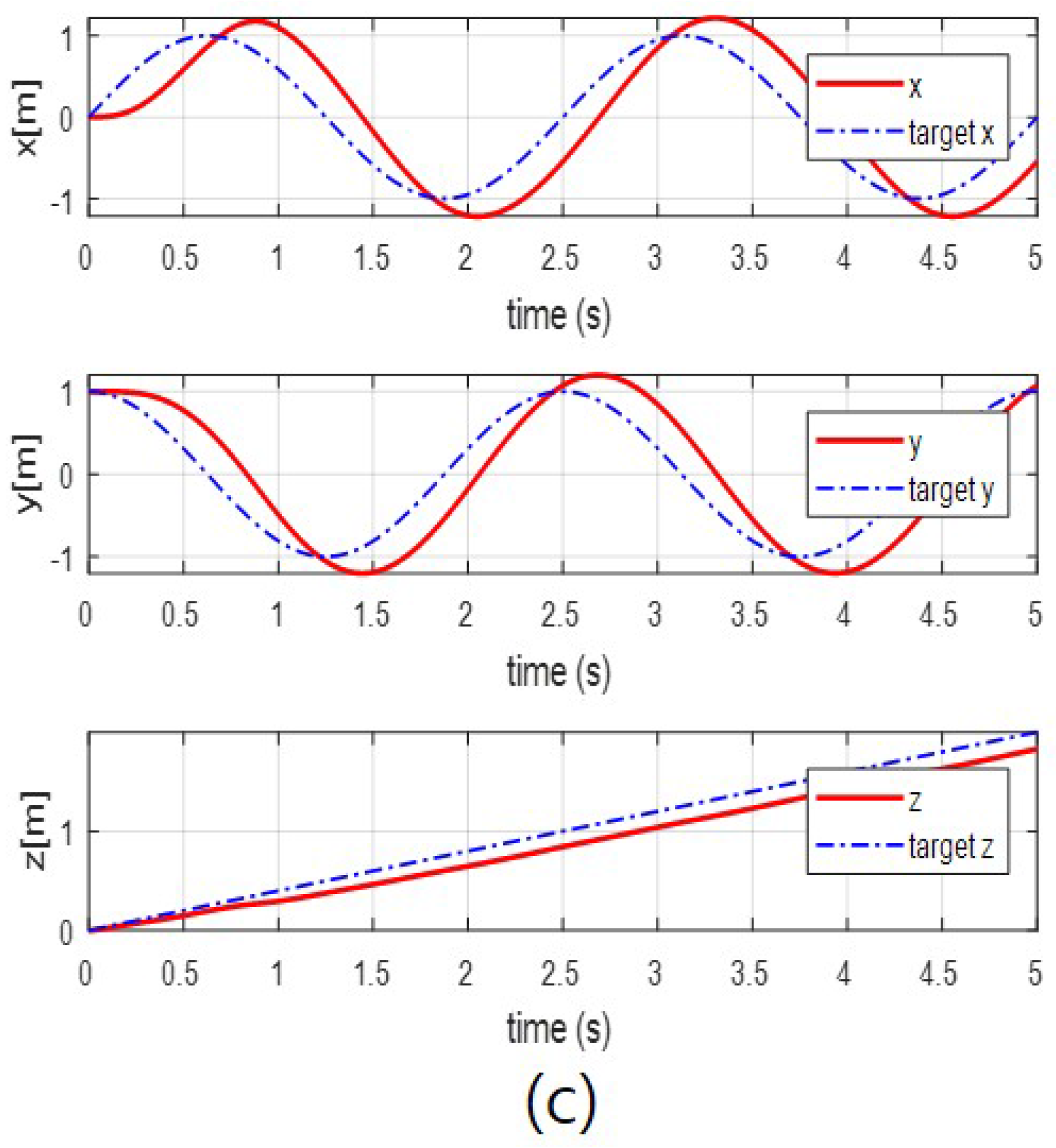
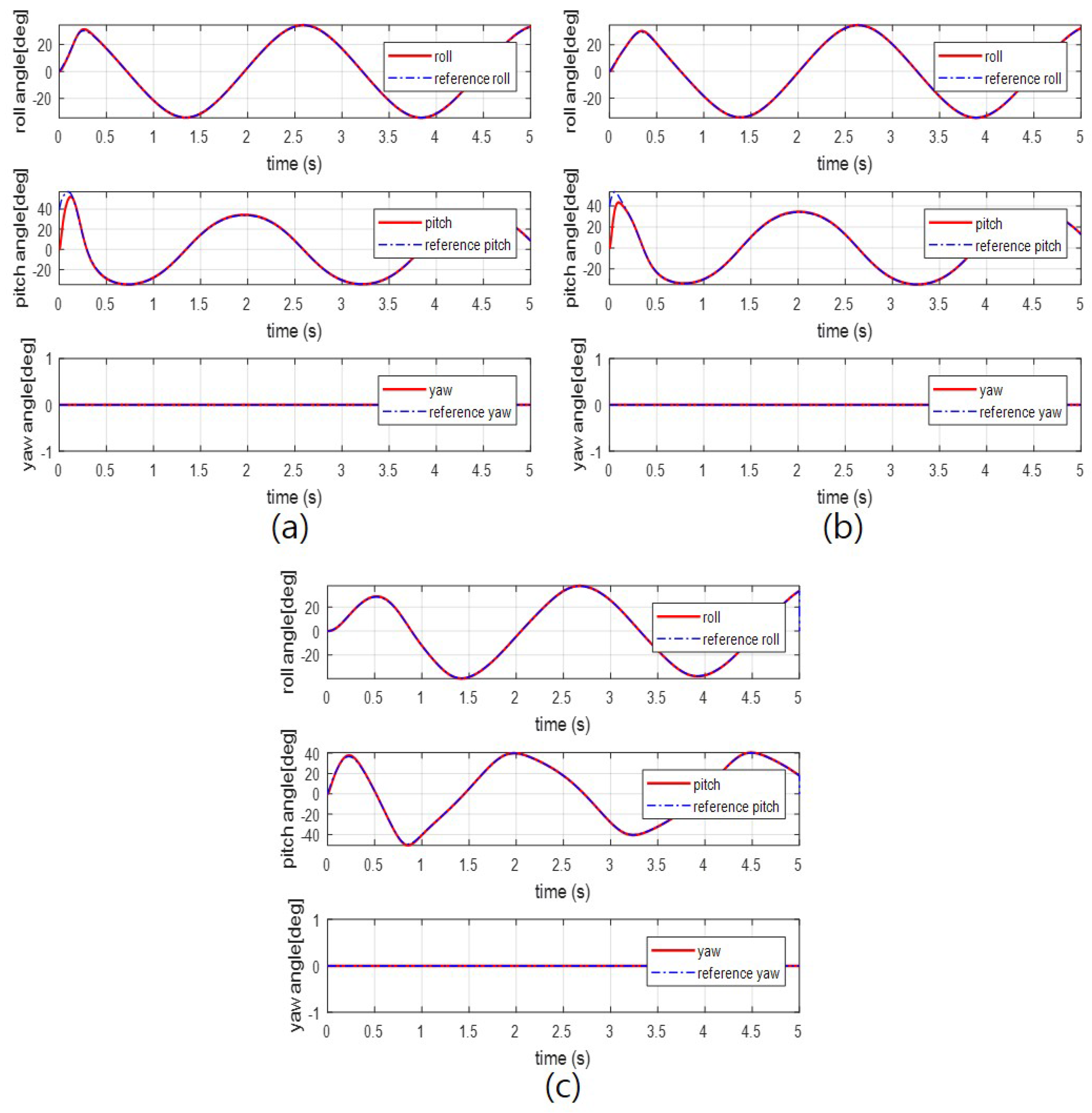
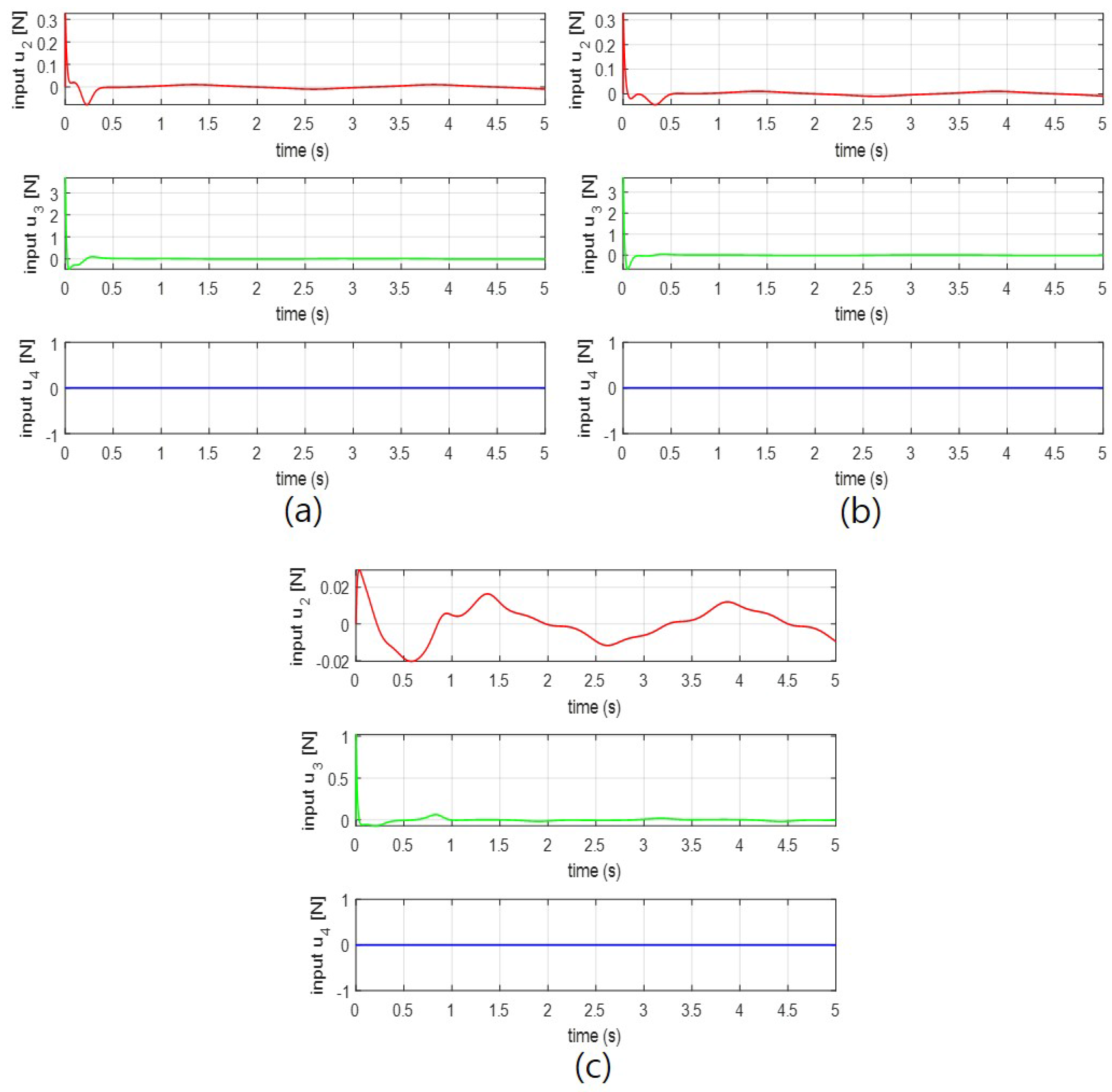
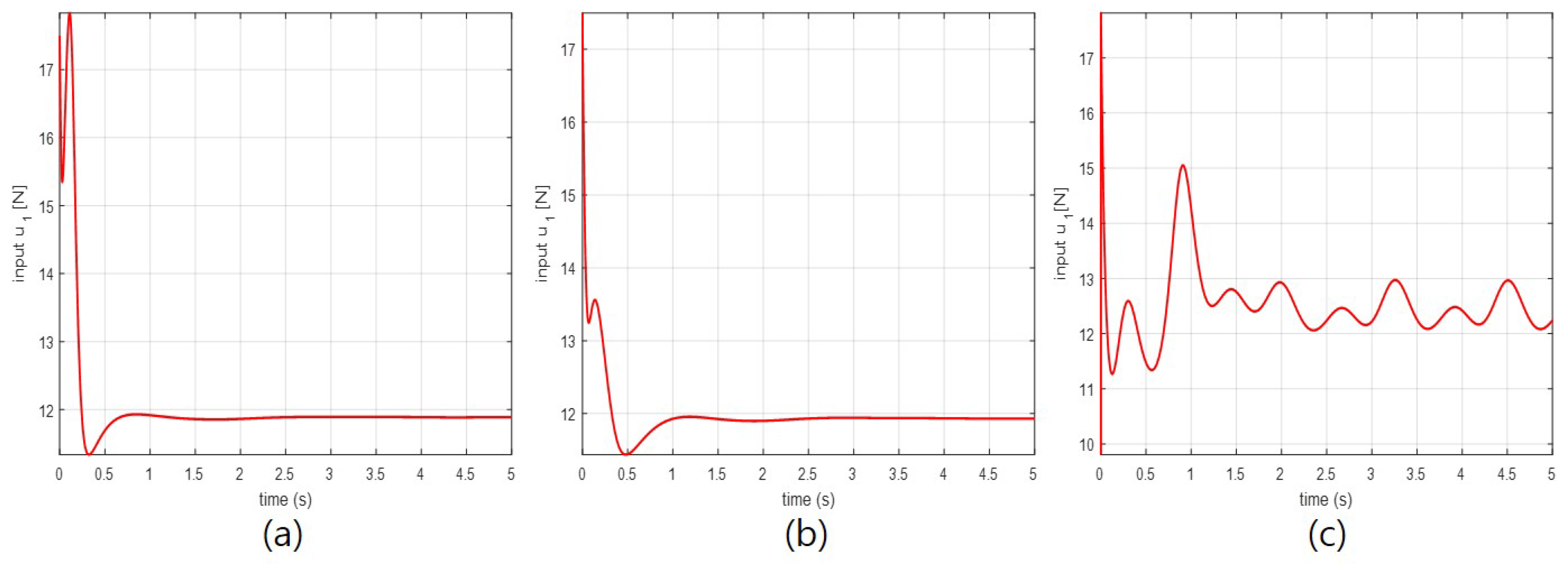
4. Simulation Results and Analysis

4.1. Testing/Evaluation Methodology

In order to verify the effectiveness of the proposed inverse optimal position controller of a quadrotor, we perform some computer simulations. The position dynamics (5) of a quadrotor is employed in the simulations. This paper focuses on position control using inverse optimal control. Therefore, for attitude control, we considered simplified attitude dynamic of the quadrotor ignoring gyroscopic and centrifugal term as follows [20]:

$$\begin{array}{c}\hfill \ddot{\varphi }=\frac{u_2}{I_{xx}},\ddot{\theta }=\frac{u_3}{I_{yy}},\ddot{\psi }=\frac{u_4}{I_{zz}}.\end{array}$$

In addition, we did not consider the rotor dynamics of the quadrotor. Therefore, the input of the system is not the thrust of each motor, but the newly defined inputs $u_{1-4}$ made by the calculation of each motor thrust.

The simulations parameters are chosen as follows: m = 1.0 [kg], g = 9.806 [m/s${}^2$], $I_{xx}$ = 2.3×10${}^{-3}$ [kg · m${}^2$], $I_{yy}$ = 2.3×10${}^{-3}$ [kg · m${}^2$], $I_{zz}$ = 5.09×10${}^{-3}$ [kg · m${}^2$] and J = 6.5×10${}^{-5}$ [kg · m${}^2$]. In addition, the sampling time was fixed at 0.001 [s] for simulation.

The attitude control inputs of a quadrotor are given as follows:

$$\begin{array}{cc}\hfill u_2& =l·b({{\Omega }_1}^2-{{\Omega }_3}^2),\hfill \\ \hfill u_3& =l·b({{\Omega }_2}^2-{{\Omega }_4}^2),\hfill \\ \hfill u_4& =d({{\Omega }_1}^2+{{\Omega }_3}^2-{{\Omega }_2}^2-{{\Omega }_4}^2),\hfill \\ \hfill {\Omega }_r& ={\Omega }_1+{\Omega }_3-{\Omega }_2-{\Omega }_4,\hfill \end{array}$$

(52)

where l is the distance between the center of a quadrotor and the center of a propeller, b and d are the thrust and drag factors of the quadrotor, respectively, $u_2$, $u_3$, and $u_4$ are the inputs for the roll (x-axis), the pitch (y-axis), and the yaw (z-axis), respectively, and ${\Omega }_i(i=1,2,3,4)$ is the propeller speed of the i-th rotor.

In the simulation, we employ the PID control which is a typical linear-control techniques for the attitude control of a quadrotor. Also we use the attitude control input to realize the convergence of the attitude of a quadrotor to the reference attitude of a quadrotor, which is the output of the position control.

To design the attitude control inputs of a quadrotor, we define the errors $e_{\varphi }$, $e_{\theta }$, and $e_{\psi }$, which are related to the attitude of a quadrotor respectively, as follows:

$$\begin{array}{c}\hfill e_{\varphi }={\varphi }_d-\varphi ,e_{\theta }={\theta }_d-\theta ,e_{\psi }={\psi }_d-\psi .\end{array}$$

We designed the attitude control inputs $u_2$, $u_3$, and $u_4$ using the following expressions [20]:

$$\begin{array}{cc}\hfill u_2& =K_{p,\varphi }{e}_{\varphi }+K_{d,\varphi }\dot{e_{\varphi }}+K_{i,\varphi }\int e_{\varphi }dt\hfill \\ \hfill u_3& =K_{p,\theta }{e}_{\theta }+K_{d,\theta }\dot{e_{\theta }}+K_{i,\theta }\int e_{\theta }dt\hfill \\ \hfill u_4& =K_{p,\psi }{e}_{\psi }+K_{d,\psi }\dot{e_{\psi }}+K_{i,\psi }\int e_{\psi }dt.\hfill \end{array}$$

In these controllers, $K_{p,q}>0$, $K_{d,q}>0$, and $K_{i,q}>0$ for $q=\varphi ,\theta ,\psi$ are the proportional, derivative, and integral control gains, respectively. The simulation is performed with the PID parameters presented in

Table 1. Feedback gains of the position and the rotational controllers.

Feedback gains of the position controller
${\gamma }_z$		0.03
${\gamma }_p$		0.001
PID parameters of rotational controller
	$q=\varphi$	$q=\theta$	$q=\psi$
$K_{p,q}$	3	3	3
$K_{i,q}$	0.3	0.3	0.3
$K_{d,q}$	0.2	0.2	0.2

.

In this paper, the feedback gain of PID controllers used in attitude control is selected by changing slightly based on gain of PID controller used in [21]: These gains were tuned to ensure acceptable tracking performance while minimizing the overshoot and the undershoot of error signals.

4.2. Simulation Results

Figure 3 shows the simulation result obtained by applying the inverse optimal position control of a quadrotor, when the initial and target positions are (0, 0, 0), (1, 1, 1), respectively. More details, the time histories of the $x,y,z$ for each motion of a quadrotor are shown in Figure 4. From the simulation results, we verify that the proposed control method successfully makes a quadrotor move to the target position.

Figure 5 shows simulation results of the attitude control. We can be found that when the initial state of a quadrotor is $(roll,pitch,yaw)=(0,0,0)$ [rad], the current attitude angles follow the reference attitude angles that enable a quadrotor to converge in the desired position. After a quadrotor reach to the target position, the roll, pitch, and yaw converge to 0, respectively, and then, it maintains a stable posture.

Figure 6 and Figure 7 show the altitude and attitude control inputs of a quadrotor. As shown in the simulation result, the altitude control input $u_1$ is positive value and from 5 s when the quadrotor reaches the target position, $u_1$ is maintained at about 9.8 [N], which is magnitude of gravity. Also we can check that the size changes of input $u_2$, $u_3$ and $u_4$ are within a reasonable range.

From the simulation results, we verify that the proposed control method successfully makes the position of a quadrotor converge to the references.

We conducted additional simulations to verify that the proposed controller has good performance even though the input coupling matrix $B_z(t)$ changes over time. In the additional simulation, the ascending circular trajectory is set as the reference trajectory, we tested whether the quadrotor track the trajectory well in nonlinear motion.

Figure 8 and Figure 9 show that the quadrotor successfully tracking the given trajectory. Figure 10 shows the reference attitude angle for trajectory tracking control. It can be found that the proposed controller maintains good trajectory tracking performance even when the input matrix is changes with time by nonlinear motion such as Figure 10.

In order to verify the performance of the proposed controller in this paper, we have conducted simulation to compared the performance with other control techniques. In this simulation, the ascending circular trajectory is set as the reference trajectory, we tested whether the quadrotor track the trajectory well in nonlinear motion.

We compared the proposed inverse optimal control, LQR control that is a typical optimal control, and PD control. Since, this paper focuses on position control, so all of the quadrotor attitude control uses the same PID control and same PID gains of attitude. The PID gains of attitude is equal to the gains of the previous simulation. For the PD position control, the control performance depends on the PD gain. Therefore, proper PD gain setting is important for proper performance comparison. To select the proper PD gain, the range of the reference attitude angle and the magnitude of the altitude input were selected in comparison with the other two control methods. Since, the range of the reference attitude angle for position control changes according to the position control gain.

Figure 11 and Figure 12 show trajectory tracking control simulation results for three control methods, when the initial position is (0, 1, 0) with the ascending circular reference trajectory. More details, the time histories of the $x,y,z$ for each motion of a quadrotor are shown in Figure 12. From the simulation results, we verify that the proposed inverse optimal control has better trajectory tracking performance than other control methods. Figure 13 shows the reference attitude angle for trajectory tracking. In Figure 13, we can see that the attitude of the quadrotor changes continuously around 40 degrees, and if the attitude angle changes greatly, the linear control method like LQR control, PD control does not perform well. The proposed inverse optimal control is an optimal control method for nonlinear system, unlike LQR control method, it can be expected good performance even in the circular trajectory like Figure 11. Looking at the range of attitude angles of Figure 13 and the magnitudes of the inputs of Figure 14 and Figure 15, we can see that the three control methods are simulated in very similar conditions.

Along with the simulation results, we can say the advantage of inverse optimal is in terms of nonlinearity and optimality. The proposed inverse optimal control is of great significance that we dealt with the optimal concept in a nonlinear system and we can find an optimal solution. Simulation results show that the inverse optimal control is better performance because it overcomes the limitation of LQR that are designed based on linear systems. It is an advantage of inverse optimal control from a nonlinear point of view.

In addition, unlike controllers that are not based on optimal control such as PD controllers, it is possible to control the convergence performance and energy consumption of the controller by adjusting ($Q_z$, ${\gamma }_z$) and ($Q_p$, ${\Gamma }_p$). It is an advantage of inverse optimal control from a optimality point of view.

5. Conclusions

In this paper, we focused on the inverse optimal position control of a quadrotor. First, we derived the dynamics of a quadrotor using the Newton-Euler formulation. Then, we presented the state transformation technique to derive the position dynamics from the kinematic and dynamic models of a quadrotor. Based on the obtained results, we proposed an inverse optimal position control technique using the altitude control input of a quadrotor. The stability analysis based on the Lyapunov theorem showed that the proposed control method resulted in the exponential stability of a quadrotor system. In addition, we reinterpreted the optimal control problem for a system with a time varying input matrix as an optimal control problem with a constant matrix by appropriately setting the weighting parameters of the performance index. Using this technique, we proved that the proposed control input is the optimal solution of the objective functional and satisfies inverse optimality. Finally, from the simulation results, we verified that the proposed control method is more effective in terms of nonlinearity and optimality than other controllers.