Optimal Steady-State Range Prediction Filter for Tracking with LFM Waveforms
Abstract
:Featured Application
Abstract
1. Introduction
2. Problem Definition and Conventional Filter Design
2.1. - Filter for LFM Waveforms
2.2. Conventional Filter Design Methods
- Tracking-index-based method [8]: a well-known and useful design parameter is the tracking index, which is defined as [8,14]:where is the standard deviation of the process noise of the measurement model used in Kalman filter tracking [14]. Equation (9) is obtained by steady-state assumption for the Kalman filter using a random acceleration process noise [8]. In steady-state conditions, both the prediction and estimation error covariance matrices converge and the optimal gain relations are obtained using these fixed matrices in the Kalman filter equations. The value of determines and by Equations (7) and (9). In filter design, a suitable is selected empirically based on the assumed degree of maneuvering of targets.
- Maximum RMS error (RMSE)-based method [10]: the tracking index-based approach requires an empirical setting of . To resolve this problem, Jain and Blair [10] proposed the deterministic evaluation function and a design parameter to optimize the range estimation. Their proposed evaluation function corresponds to a maximum RMSE determined by a maximum target acceleration, which is defined as:where denotes the mean, the true range of the target undergoing constant acceleration, the steady-state variance of the range estimation error assuming only measurement noise, corresponds to the steady-state lag (bias error) for constant-acceleration target, and is called the deterministic tracking index defined using the maximum acceleration and ; these are expressed as:where is the maximum acceleration of the target. The optimal is determined by minimizing RMSE using Equation (7) and the known (i.e., and are known).
3. Proposed Optimal Range Prediction Filter Design
3.1. RMS-Index for LFM - Filter
3.2. Filter Design Method
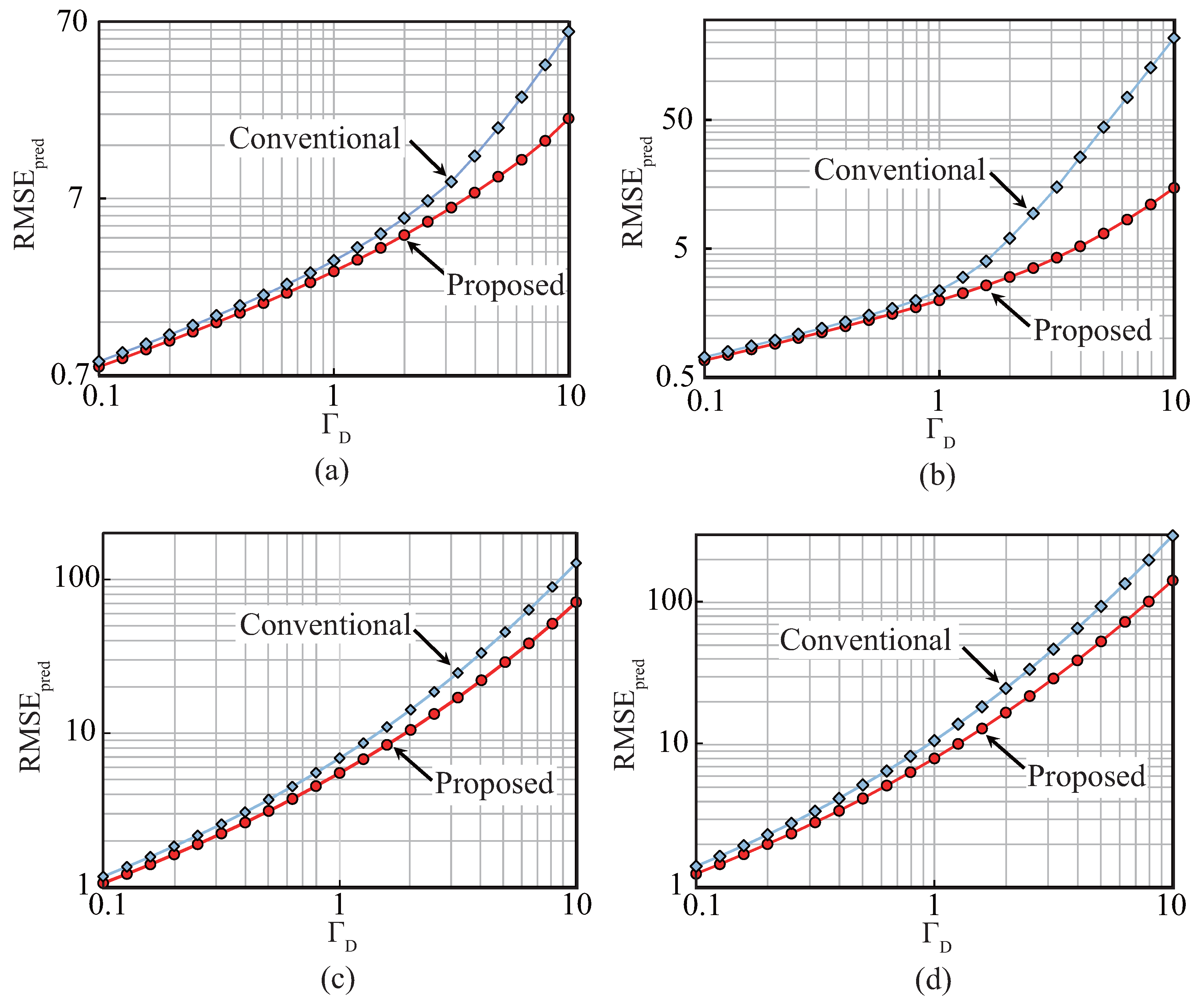
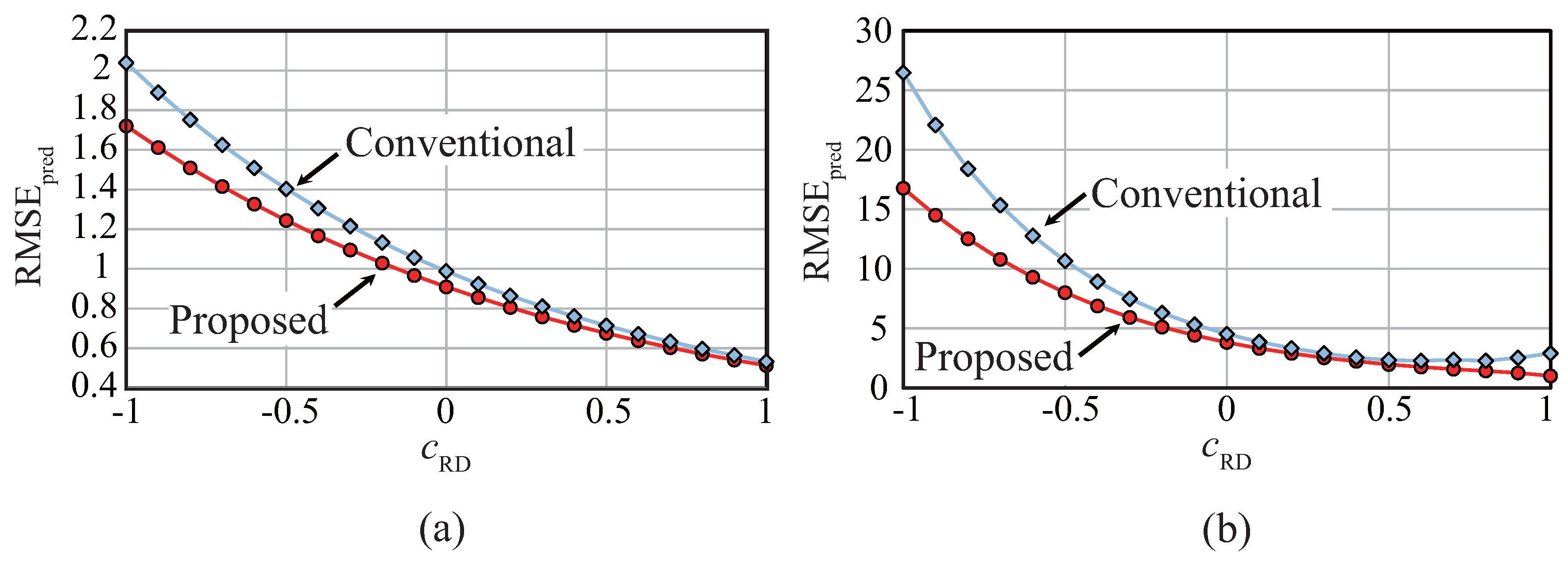
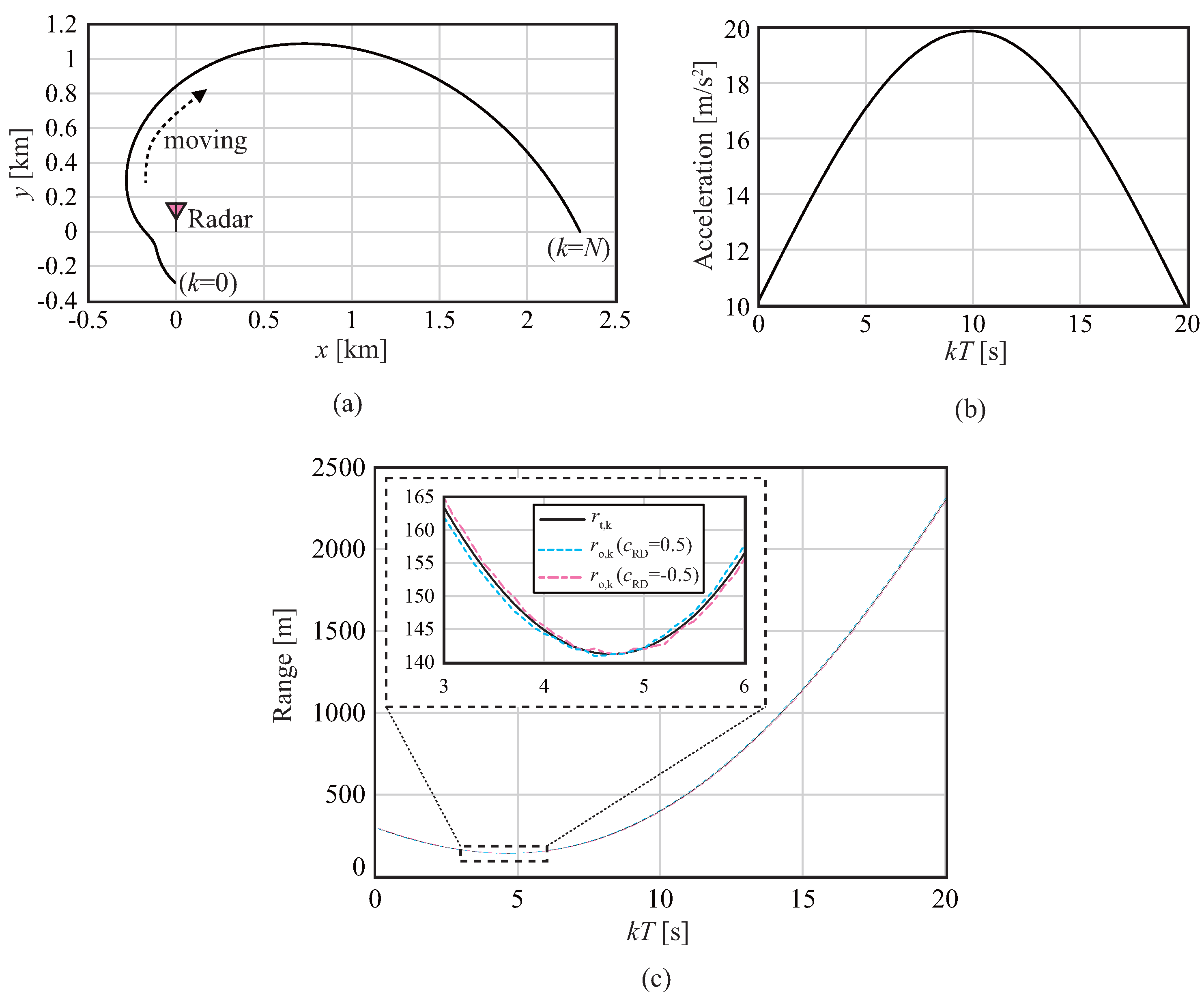
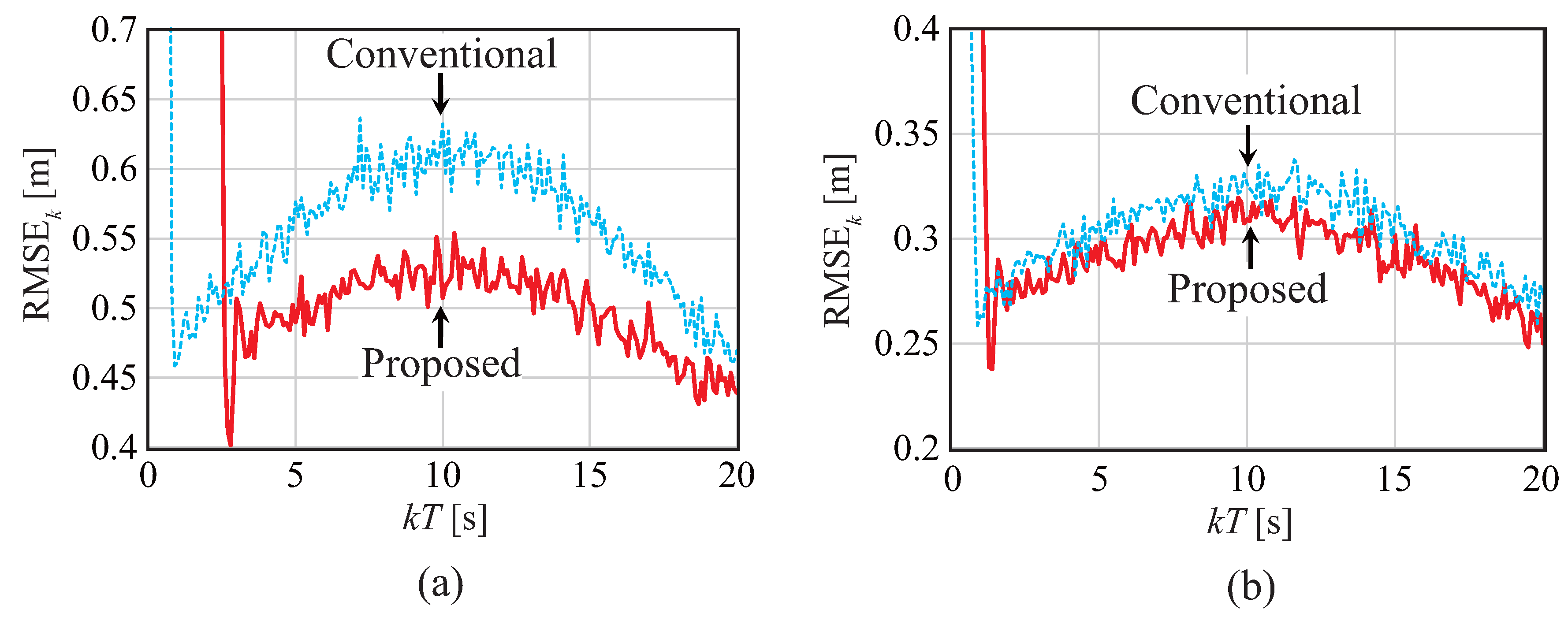
4. Performance Evaluation
4.1. Theoretical Analysis
4.2. LFM Radar Simulation
5. Conclusions
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of Equation (15)
Appendix B. Derivation of (16)
References
- Guo, N.; Gao, C.; Xue, M.; Niu, L.; Zhu, S.; Feng, L.; He, H.; Cao, Z. Ranging method based on linear frequency modulated laser. Laser Phys. 2017, 27, 065108. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Hong, R.J.; Yang, C.F.; Zhang, Y.J.; Deng, Z.M.; Jin, S. A Fast Motion Parameters Estimation Method Based on Cross-Correlation of Adjacent Echoes for Wideband LFM Radars. Appl. Sci. 2017, 7, 500. [Google Scholar] [CrossRef]
- Chua, M.Y.; Koo, V.C.; Lim, H.S.; Sumantyo, J.T.S. Phase-Coded Stepped Frequency Linear Frequency Modulated Waveform Synthesis Technique for Low Altitude Ultra-Wideband Synthetic Aperture Radar. IEEE Access 2017, 5, 11391–11403. [Google Scholar] [CrossRef]
- Othman, M.A.B.; Belz, J.; Farhang-Boroujeny, B. Performance Analysis of Matched Filter Bank for Detection of Linear Frequency Modulated Chirp Signals. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 41–54. [Google Scholar] [CrossRef]
- Bruno, L.; Braca, P.; Horstmann, J.; Vespe, M. Experimental Evaluation of the Range-Doppler Coupling on HF Surface Wave Radars. IEEE Geosci. Remote Sens. Lett. 2013, 10, 850–854. [Google Scholar] [CrossRef]
- Maresca, S.; Braca, P.; Horstmann, J.; Grasso, R. Maritime Surveillance Using Multiple High-Frequency Surface-Wave Radars. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5056–5071. [Google Scholar] [CrossRef]
- Zhou, G.; Yu, C.; Cui, N.; Quan, T. A Tracking Filter in Spherical Coordinates Enhanced by De-noising of Converted Doppler Measurements. Chin. J. Aeronaut. 2012, 25, 757–765. [Google Scholar] [CrossRef]
- Wong, W.; Blair, W.D. Steady-state tracking with LFM waveforms. IIEEE Trans. Aerosp. Electron. Syst. 2000, 36, 701–709. [Google Scholar] [CrossRef]
- Amishima, T.; Ito, M.; Kosuge, Y. Stability condition and steady-state solution of various alpha-beta filters for linear FM pulse compression radars. Electron. Commun. Jpn. 2004, 87, 13–22. [Google Scholar] [CrossRef]
- Vineet, J.; Blair, W.D. Filter design for steady-state tracking of maneuvering targets with LFM waveforms. IIEEE Trans. Aerosp. Electron. Syst. 2009, 45, 296–300. [Google Scholar]
- Fitzgerald, R.J. Effects of Range-Doppler Coupling on Chirp Radar Tracking Accuracy. IEEE Trans. Aerosp. Electron. Syst. 1974, AES-10, 528–532. [Google Scholar] [CrossRef]
- Saho, K.; Masugi, M. Automatic Parameter Setting Method for an Accurate Kalman Filter Tracker Using an Analytical Steady-State Performance Index. IEEE Access 2015, 3, 1919–1930. [Google Scholar] [CrossRef]
- Saho, K.; Masugi, M. Performance Analysis and Design Strategy for a Second-Order, Fixed-Gain, Position-Velocity-Measured (alpha-beta-eta-theta) Tracking Filter. Appl. Sci. 2017, 7, 758. [Google Scholar] [CrossRef]
- Kalata, P.R. The Tracking Index: A Generalized Parameter for α-β and α-β-γ Target Trackers. IEEE Trans. Aerosp. Electron. Syst. 1984, AES-20, 174–182. [Google Scholar] [CrossRef]
| Design Methods | Preset Parameter | Evaluating Function | Process Noise |
|---|---|---|---|
| Tracking index-based method of [8] | Not used | Random acceleration | |
| Tracking index-based method of [9] | Not used | Arbitrary random parameter | |
| Maximum root mean square error (RMSE) [10] | Equations (10)–(12) | Random acceleration | |
| Proposed method | Equation (17) | Not assumed |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saho, K. Optimal Steady-State Range Prediction Filter for Tracking with LFM Waveforms. Appl. Sci. 2018, 8, 17. https://doi.org/10.3390/app8010017
Saho K. Optimal Steady-State Range Prediction Filter for Tracking with LFM Waveforms. Applied Sciences. 2018; 8(1):17. https://doi.org/10.3390/app8010017
Chicago/Turabian StyleSaho, Kenshi. 2018. "Optimal Steady-State Range Prediction Filter for Tracking with LFM Waveforms" Applied Sciences 8, no. 1: 17. https://doi.org/10.3390/app8010017





