Modelling Nitrogen Losses from Sheep Grazing Systems with Different Spatial Distributions of Excreta
Abstract
:1. Introduction
2 Material and Methods
2.1. Pasture Model and Site Simulated

2.2. Nitrogen Predictions
2.3. Data Analysis
3. Results
3.1. Pasture Intake

| Pasture intake (t DM/ha) | N intake (kg N/ha) | N fixation (kg N/ha) | N excreta + N fixation | ||||||||
| U | R | U | R | U | R | U | R | ||||
| Sheep/ha | Mean (s.d.) | P value | Mean (s.d.) | P value | Mean (s.d.) | P value | Mean (s.d.) | ||||
| 200 | 0.8 (0.1) | 0.9 (0.1) | 40 (3) | 40 (3) | 86 (12) | 87 (12) | 121 (12) | 121 (12) | |||
| 400 | 1.7 (0.1) | 1.7 (0.1) | 78 (5) | 77 (5) | 87 (12) | 88 (12) | 153 (13) | 153 (13) | |||
| 600 | 2.5 (0.2) | 2.5 (0.2) | 114 (8) | 112 (7) | 83 (11) | 91 (14) | <0.05 | 180 (12) | 186 (16) | ||
| 800 | 3.3 (0.3) | 3.3 (0.3) | 149 (10) | 145 (10) | 87 (18) | 97 (31) | <0.05 | 214 (20) | 221 (34) | ||
| 1000 | 4.1 (0.3) | 4.0 (0.3) | 181 (13) | 176 (15) | 90 (21) | 99 (19) | <0.01 | 244 (25) | 249 (26) | ||
| 1200 | 4.8 (0.4) | 4.7 (0.5) | 210 (18) | 202 (19) | <0.05 | 87 (11) | 105 (17) | <0.001 | 265 (22) | 277 (28) | |
| 1400 | 5.4 (0.6) | 5.2 (0.6) | 235 (24) | 224 (24) | <0.05 | 89 (11) | 114 (25) | <0.001 | 289 (27) | 304 (40) | |
| 1600 | 5.8 (0.7) | 5.4 (0.7) | <0.01 | 252 (29) | 233 (28) | <0.01 | 90 (10) | 116 (19) | <0.001 | 305 (32) | 314 (39) |
| 1800 | 6.1 (0.7) | 5.6 (0.7) | <0.01 | 264 (31) | 242 (31) | <0.001 | 94 (12) | 118 (21) | <0.001 | 319 (35) | 324 (43) |
| 2000 | 6.4 (0.8) | 5.8 (0.7) | <0.001 | 274 (33) | 248 (31) | <0.001 | 96 (12) | 120 (22) | <0.001 | 329 (38) | 330 (44) |
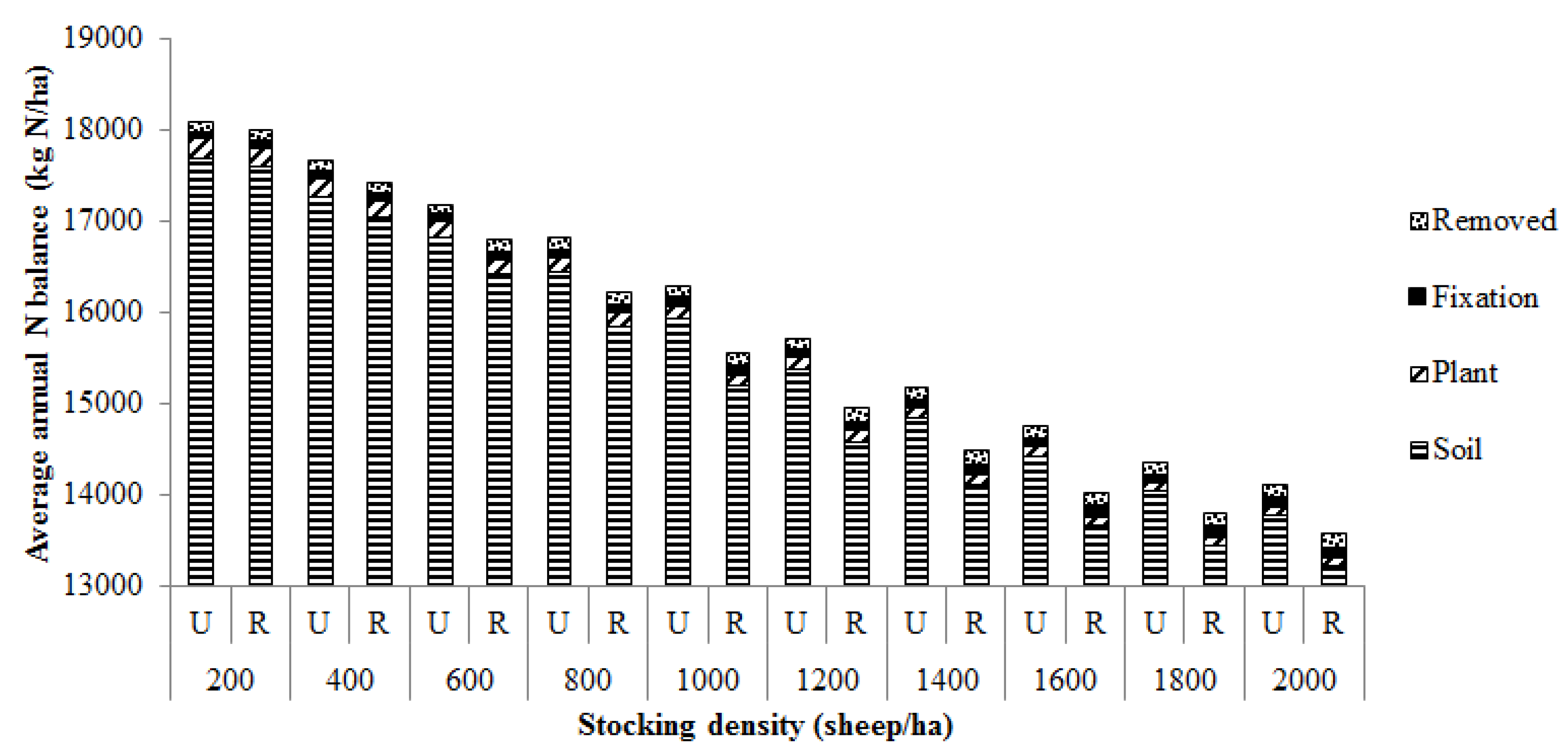
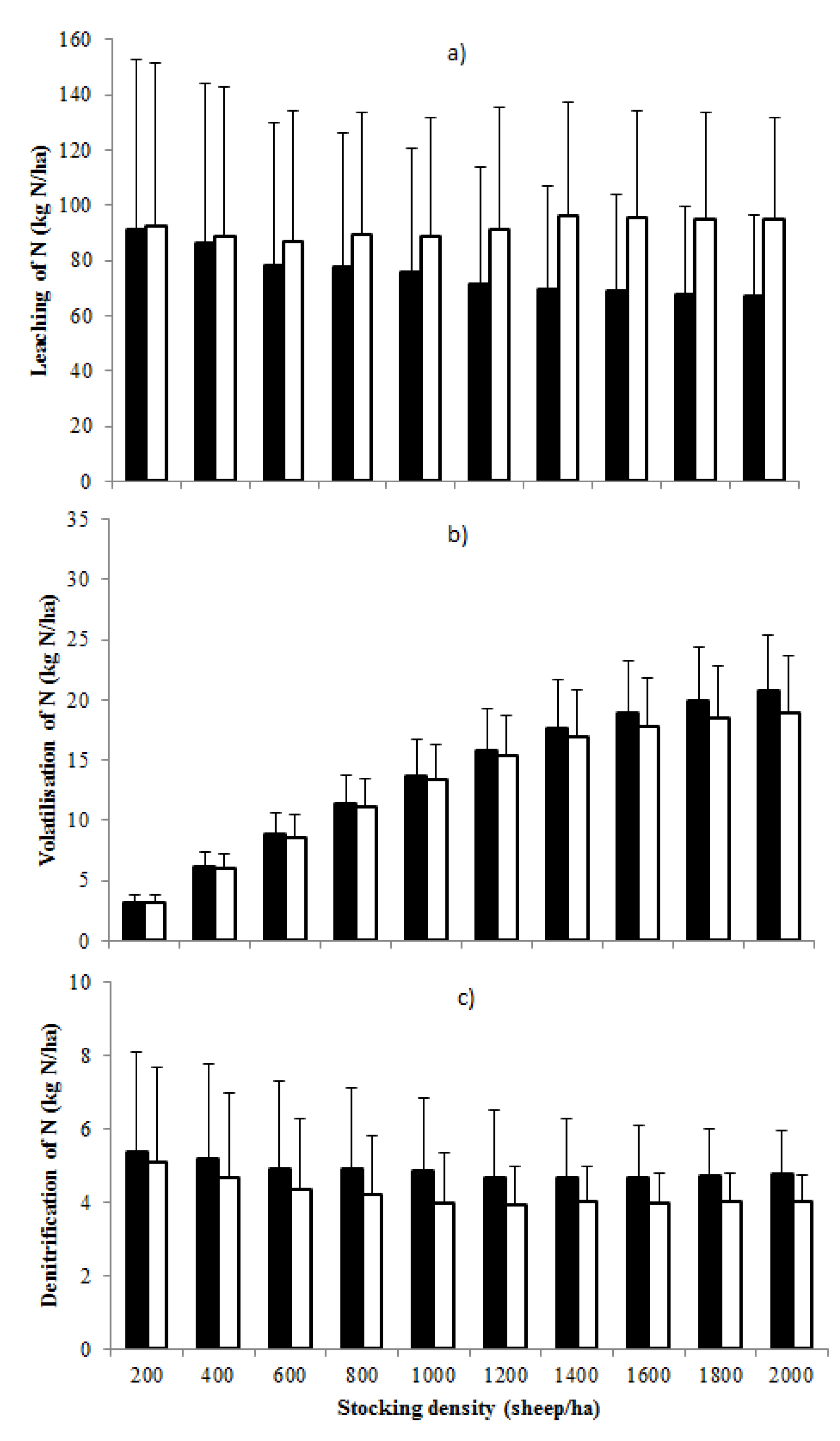
3.2. Nitrogen Inputs and Losses from the Grazing System
3.3. Proportion of Total Nitrogen Inputs Lost from the Grazing System
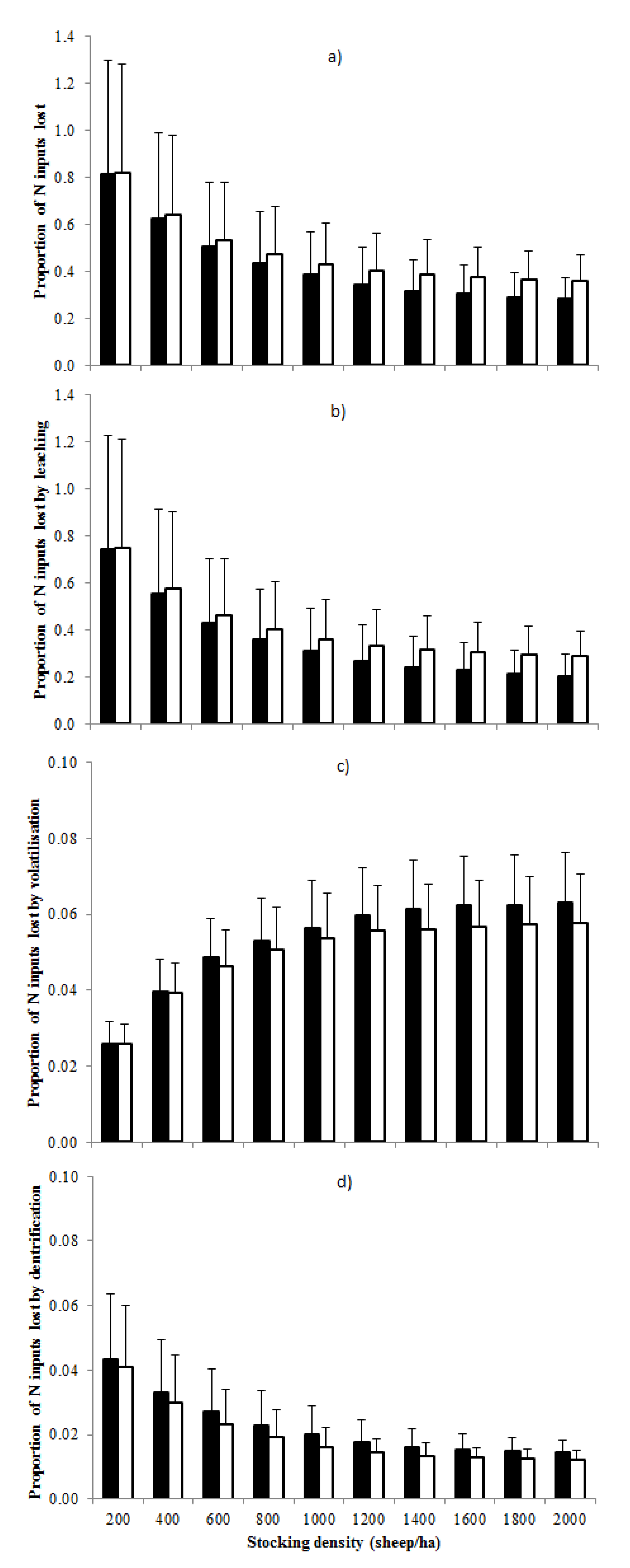
4. Discussion
5. Conclusions
Acknowledgments
References and Note
- De Klein, C.A.M.; Eckard, R.J. Targeted technologies for nitrous oxide abatement from animal agriculture. Aust. J. Agr. Res. 2008, 48, 14–20. [Google Scholar]
- Eckard, R.J.; Chapman, D.F.; White, R.E. Nitrogen balances in temperate perennial grass and clover dairypastures in south-eastern Australia. Aust. J. Agr. Res. 2007, 58, 1167–1173. [Google Scholar] [CrossRef]
- Morton, J.D.; Baird, D.B. Spatial distribution of dung patches under sheep grazing. New Zeal. J. Agr. Res. 1990, 33, 285–294. [Google Scholar]
- Pleasants, A.B.; Shorten, P.R.; Wake, G.C. The distribution of urine deposited on a pasture from grazing animals. J. Agr. Sci. 2007, 145, 81–86. [Google Scholar] [CrossRef]
- Hanegraaf, M.C.; den Boer, D.J. Perspectives and limitations of the Dutch minerals accounting system (MINAS). Eur. J. Agron. 2003, 20, 25–31. [Google Scholar] [CrossRef]
- Haynes, R.J.; Williams, P.H. Nutrient cycling and soil fertility in the grazed pasture ecosystem. Adv. Agron. 1993, 49, 119–199. [Google Scholar] [CrossRef]
- Johnson, I.R. Biophysical Pasture Model Documentation: Model Documentation for Dairymod, Ecomod and the Sgs Pasture Model; IMJ Consultants: Fitzroy, Australia, 2008. Available online: http://www.imj.com.au (accessed on 1 July 2012).
- Cullen, B.R.; Eckard, R.J.; Callow, M.N.; Johnson, I.R.; Chapman, D.F.; Rawnsley, R.P.; Garcia, S.C.; White, T.; Snow, V.O. Simulating pasture growth rates in Australian and New Zealand grazing systems. Aust. J. Agr. Res. 2008, 59, 761–768. [Google Scholar] [CrossRef]
- Chapman, D.F.; Cullen, B.R.; Johnson, I.R.; Beca, D. Interannual variation in pasture growth rate in Australian and New Zealand dairy regions and its consequences for system management. Anim. Prod. Sci. 2009, 49, 1071–1079. [Google Scholar] [CrossRef]
- Lodge, G.M.; Johnson, I.R. Agricultural drought analyses for temperate Australia using a biophysical pasture model. 1. Identifying and characterising drought periods. Aust. J. Agr. Res. 2008, 59, 1049–1060. [Google Scholar] [CrossRef]
- Chapman, D.F.; Kenny, S.N.; Beca, D.; Johnson, I.R. Pasture and crop options for non-irrigated dairy farms in southern Australia. 2. Inter-annual variation in forage supply, and business risk. Agr. Syst. 2008, 97, 126–138. [Google Scholar] [CrossRef]
- Cullen, B.R.; Johnson, I.R.; Eckard, R.J.; Lodge, G.M.; Walker, R.G.; Rawnsley, R.P.; McCaskill, M.R. Climate change effects on pasture systems in south-eastern Australia. Crop Pasture Sci. 2009, 60, 933–942. [Google Scholar] [CrossRef]
- Cullen, B.R.; Eckard, R.J.; Rawnsley, R.P. Resistance of pasture production to projected climate changes in south-eastern Australia. Crop Pasture Sci. 2012, 63, 77–86. [Google Scholar] [CrossRef]
- Snow, V.O.; Johnson, I.R.; Parsons, A.J. The single heterogeneous paddock approach to modelling the effects of urine patches on production and leaching in grazed pastures. Crop Pasture Sci. 2009, 60, 691–696. [Google Scholar] [CrossRef]
- Eckard, R.J.; Cullen, B.R. Impacts of future climate scenarios on N2O emissions from pasture-based dairy systems in SE Australia. Anim. Feed Sci. Technol. 2011, 166, 736–748. [Google Scholar] [CrossRef]
- Boeckx, P.; van Cleemput, O. Estimates of N2O and CH4 fluxes from agricultural lands in various regions in Europe. Nutr. Cycl. Agroecosyst. 2001, 60, 35–47. [Google Scholar] [CrossRef]
- Bell, M.; Cullen, B.; Eckard, R. Effect on nitrogen losses from a sheep grazing system by the randomised distribution of excreta. In Proceedings of 2011 International Congress on Modelling and Simulation (MODSIM 2011), Perth, Australia, 12–16 December 2011.
- Johnson, I.R.; Chapman, D.F.; Snow, V.O.; Eckard, R.J.; Parsons, A.J.; Lambert, M.G.; Cullen, B.R. DairyMod and EcoMod: Biophysical pastoral simulation models for Australia and New Zealand. Aust. J. Exp. Agric. 2008, 48, 621–631. [Google Scholar] [CrossRef]
- Jeffrey, S.J.; Carter, J.O.; Moodie, K.M.; Beswick, A.R. Using spatial interpolation to construct a comprehensive archive of Australian climate data. Environ. Modell. Softw. 2001, 16, 309–330. [Google Scholar] [CrossRef]
- Isbell, R.F. Australian Soil and Land Survey Handbook: The Australian Soil Classification; CSIRO Publishing: Collingwood, Australia, 1996. [Google Scholar]
- McLaren, C. Dry Sheep Equivalents for Comparing Different Classes of Livestock; Information Notes; Department of Primary Industries: Victoria, Australia, 1997. Available online: http://www.agronomy.com.au/download/DSEratings.pdf (accessed on 1 July 2012).
- The model is programmed using the software package Embaracadero® Delphi® (www.embarcadero.com) and random numbers were generated using the inbuilt random number generator.
- Dalal, R.; Wang, W.; Robertson, G.; Parton, W. Nitrous oxide emission from Australian agricultural lands and mitigation options: A review. Aust. J. Soil Res. 2003, 41, 165–195. [Google Scholar] [CrossRef]
- Granli, T.; Bøckman, O.C. Nitrous oxide from agriculture. Norw. J. Agr. Sci. Suppl. 1994, 12, 7–128. [Google Scholar]
- Lawes Agricultural Trust; Genstat 12, Version 12.1 Reference Manual; Clarendon Press: London, UK, 2011.
- Petersen, R.G.; Lucas, H.L.; Woodhouse, W.W. The distribution of excreta by freely grazing cattle and its effects on pasture fertility. I. Excretal distribution. Agron. J. 1956, 48, 440–444. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Bell, M.J.; Cullen, B.R.; Johnson, I.R.; Eckard, R.J. Modelling Nitrogen Losses from Sheep Grazing Systems with Different Spatial Distributions of Excreta. Agriculture 2012, 2, 282-294. https://doi.org/10.3390/agriculture2040282
Bell MJ, Cullen BR, Johnson IR, Eckard RJ. Modelling Nitrogen Losses from Sheep Grazing Systems with Different Spatial Distributions of Excreta. Agriculture. 2012; 2(4):282-294. https://doi.org/10.3390/agriculture2040282
Chicago/Turabian StyleBell, Matthew J., Brendan R. Cullen, Ian R. Johnson, and Richard J. Eckard. 2012. "Modelling Nitrogen Losses from Sheep Grazing Systems with Different Spatial Distributions of Excreta" Agriculture 2, no. 4: 282-294. https://doi.org/10.3390/agriculture2040282





