On the Optimization of Point Absorber Buoys
Abstract
:1. Introduction
2. The WEC Concept of the Lysekil Project

3. Method
3.1. Simulation Model
3.2. Optimizing Buoy Geometry
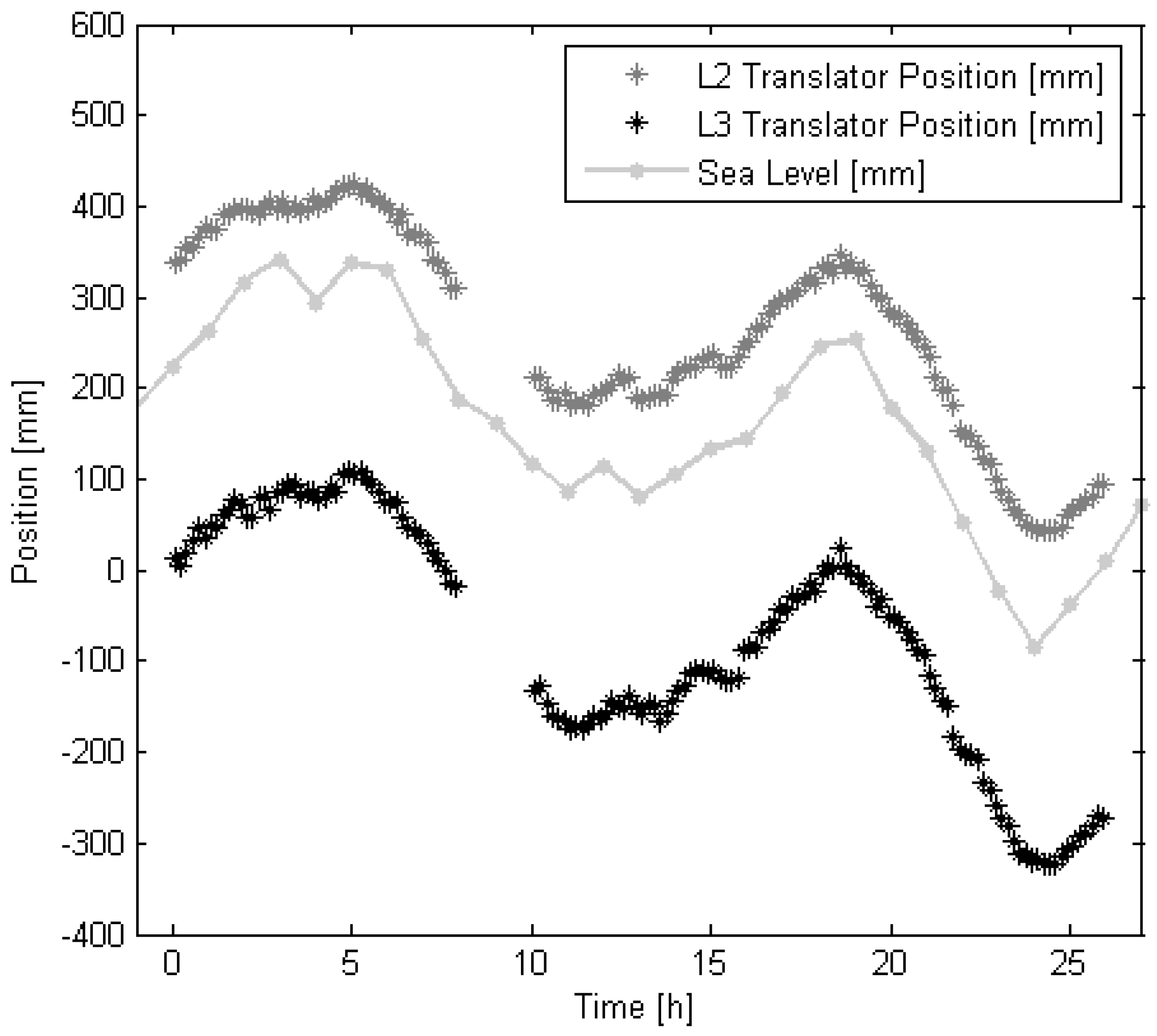
3.3. Experimental Verification
| WEC | L2 | L3 |
|---|---|---|
| Nominal power | 10 kW | 10 kW |
| Rated voltage (line-to-line) | 200 V | 200 V |
| Rated speed | 0.67 m/s | 0.67 m/s |
| Free strokelength | 1.797 m | 1.797 m |
| Total strokelength | 2.21 m | 2.21 m |
| Stator length | 1.26 m | 1.26 m |
| Translator length | 1.87 m | 1.87 m |
| Translator mass | 1200 kg | 1200 kg |
| Buoy radius | 1.5 m | 2.0 m |
| Bouy height | 1.2 m | 0.7 m |
| Buoy draft | 0.65 m | 0.4 m |
| Buoy mass | 2000 kg | 2500 kg |
| Mass of lines and chains | 340 kg | 360 kg |
| Retraction spring constant | 6200 N/m | 6200 N/m |
| Pretension | 10,620 N | 8760 N |
| Translator position offset | +0.1 m | −0.2 m |
4. Results
4.1. Analysis in Frequency Domain
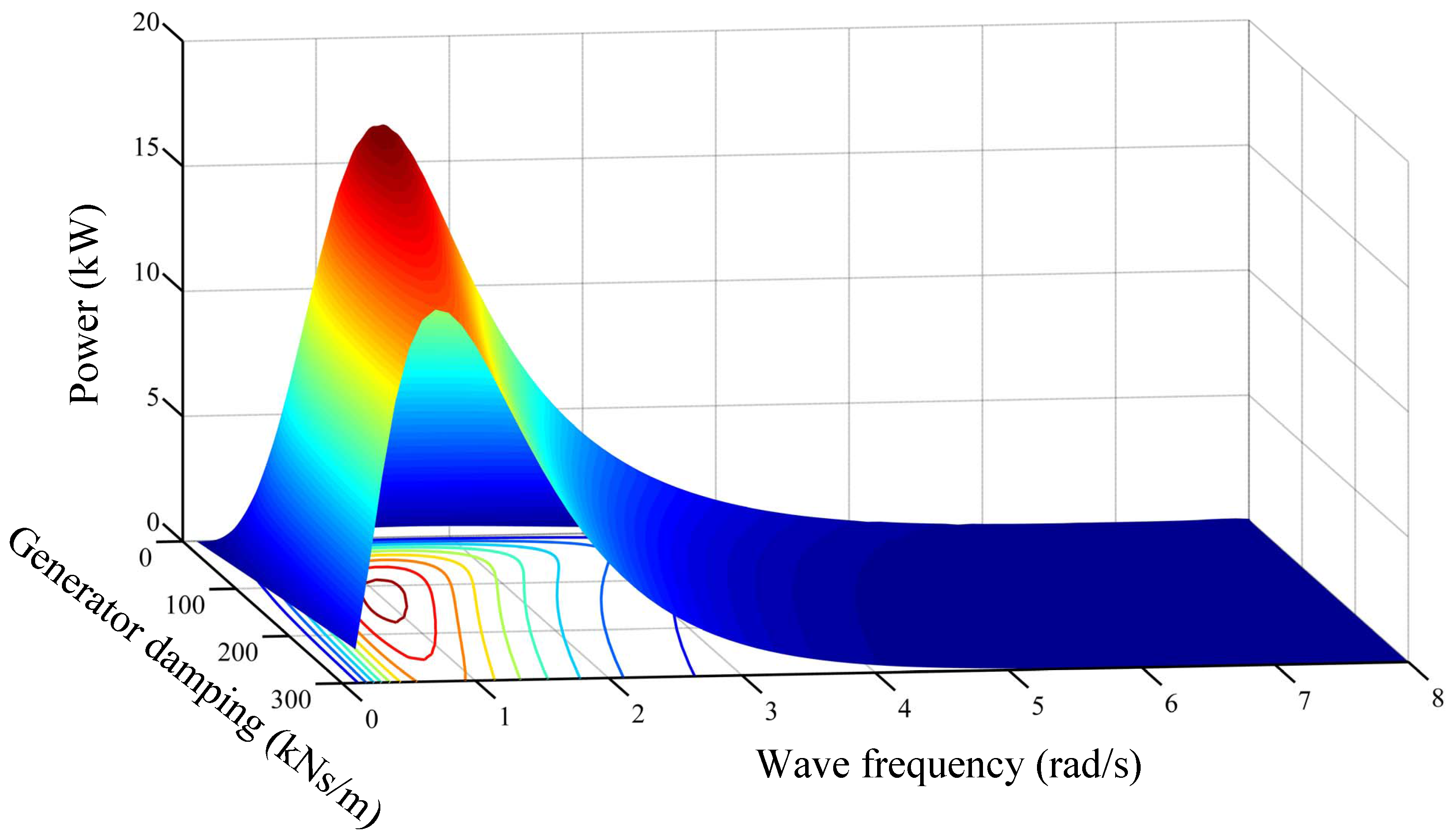
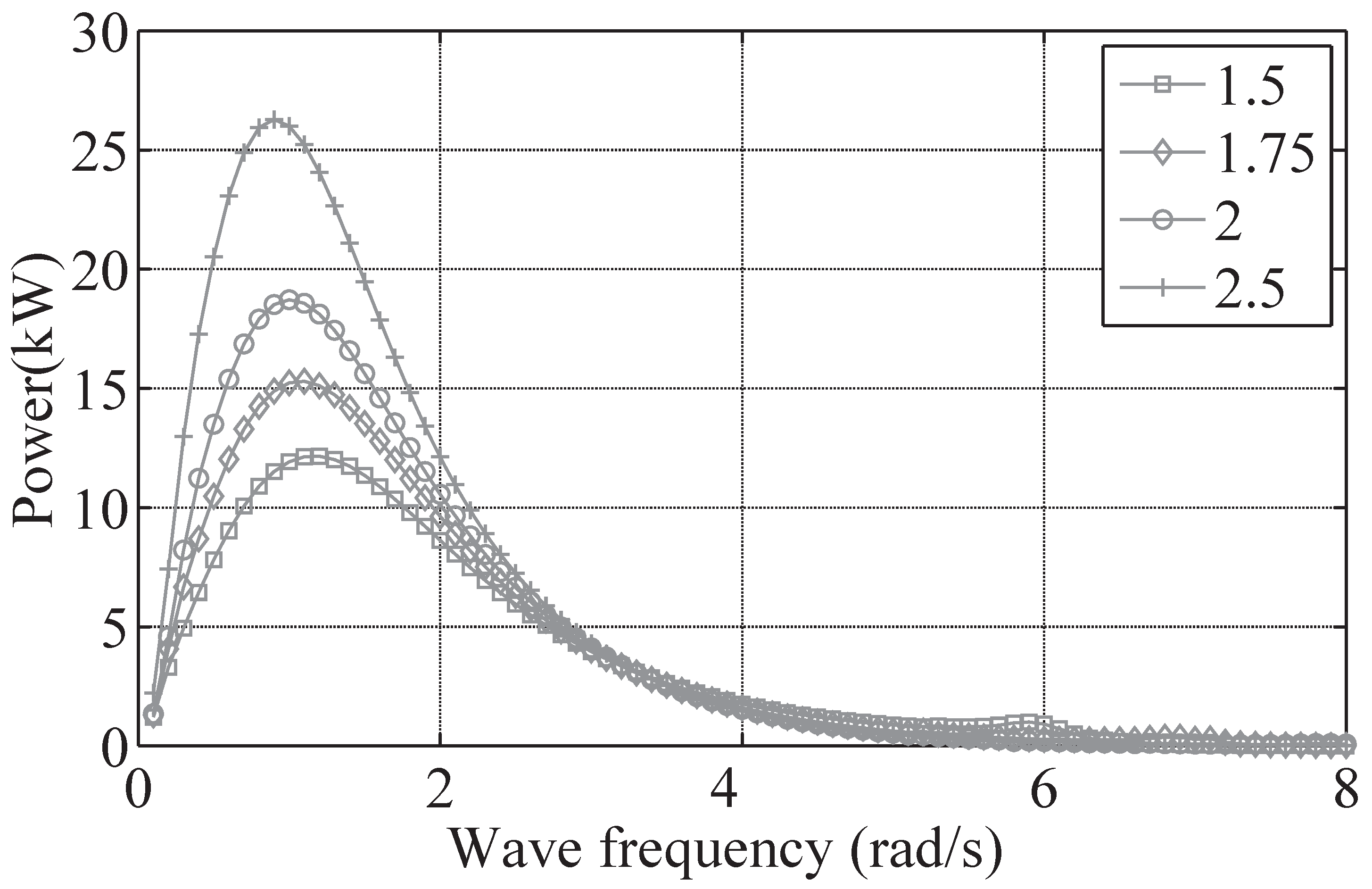
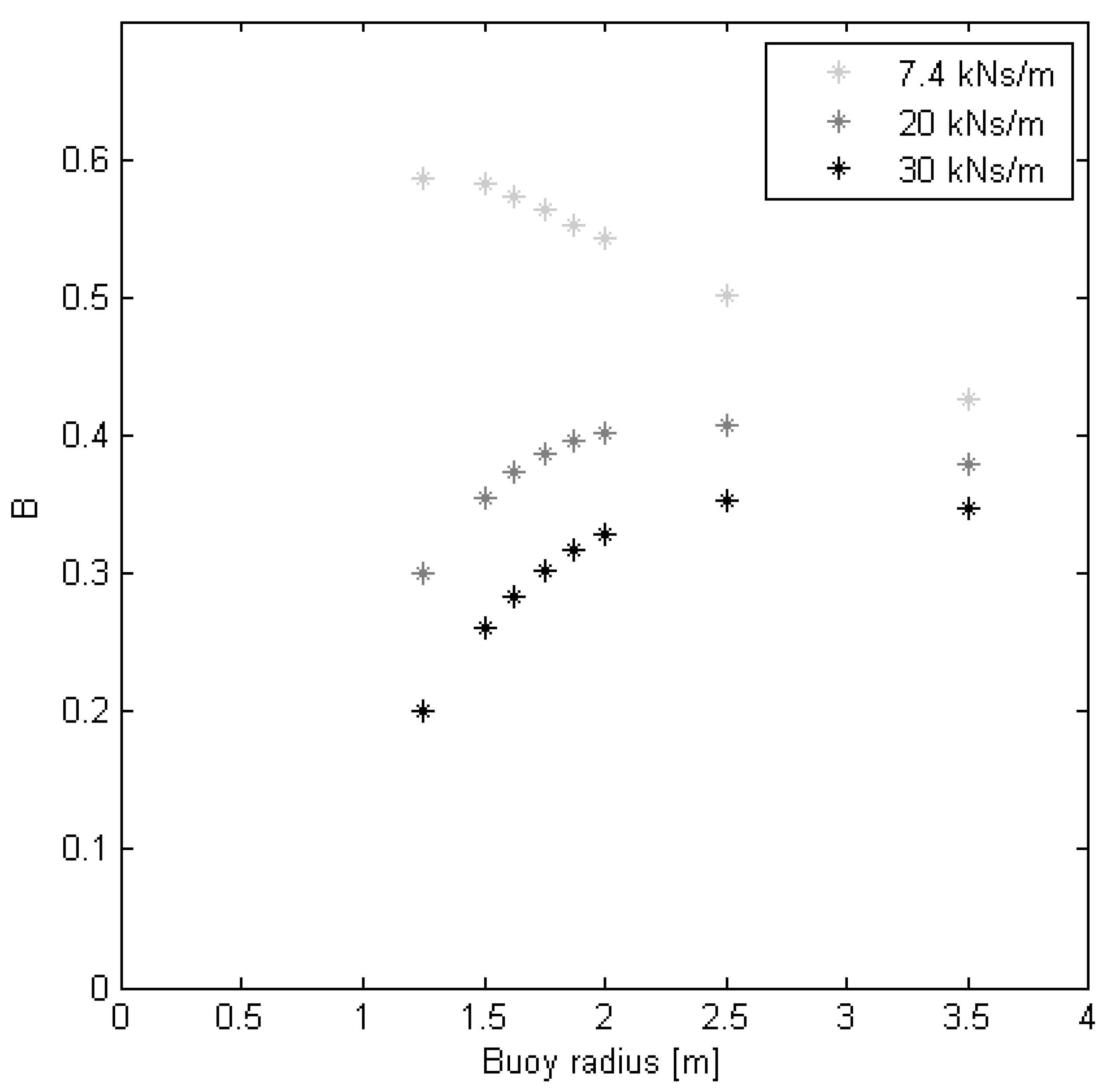
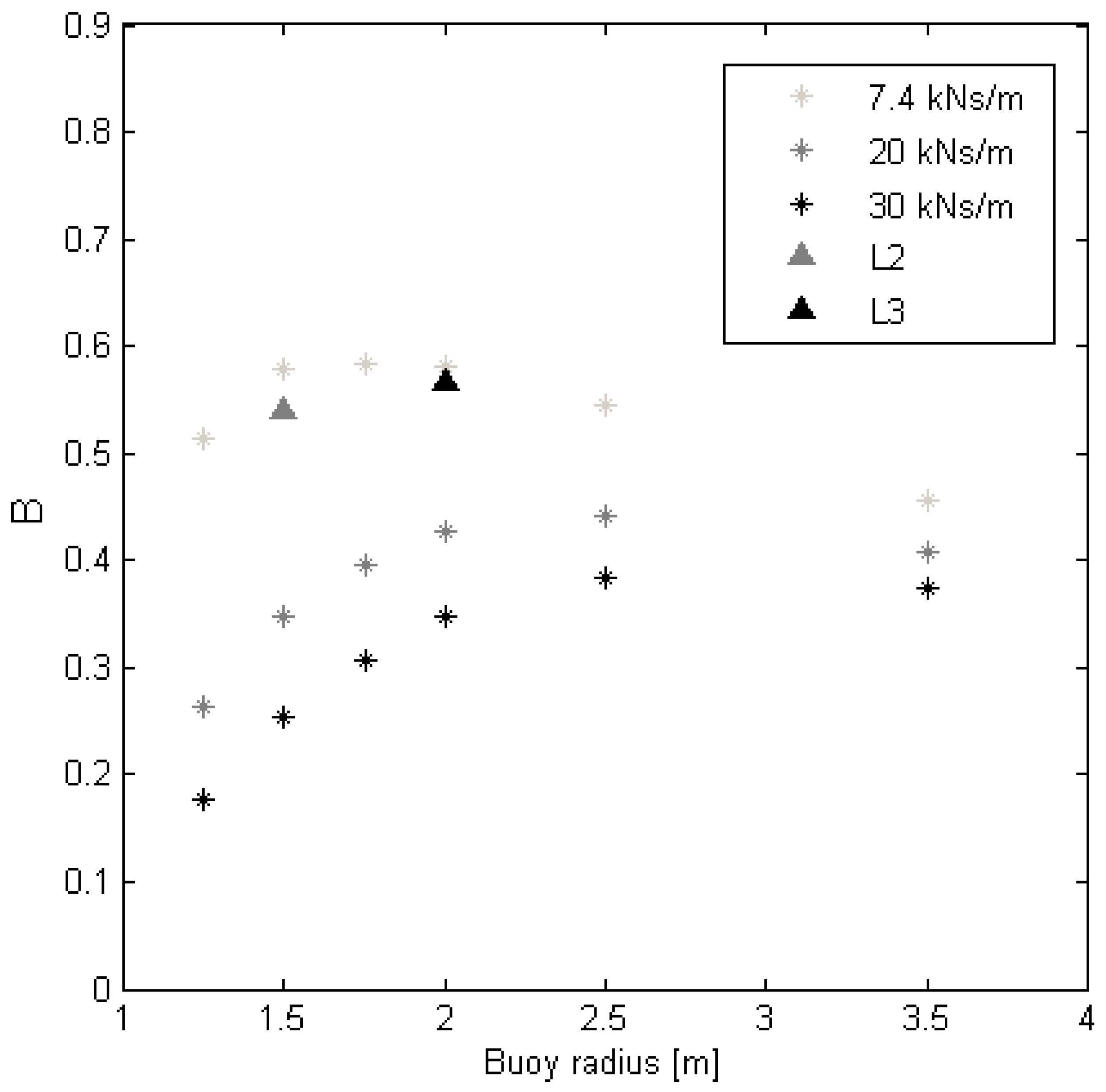
4.2. Optimization of Buoy Geometry

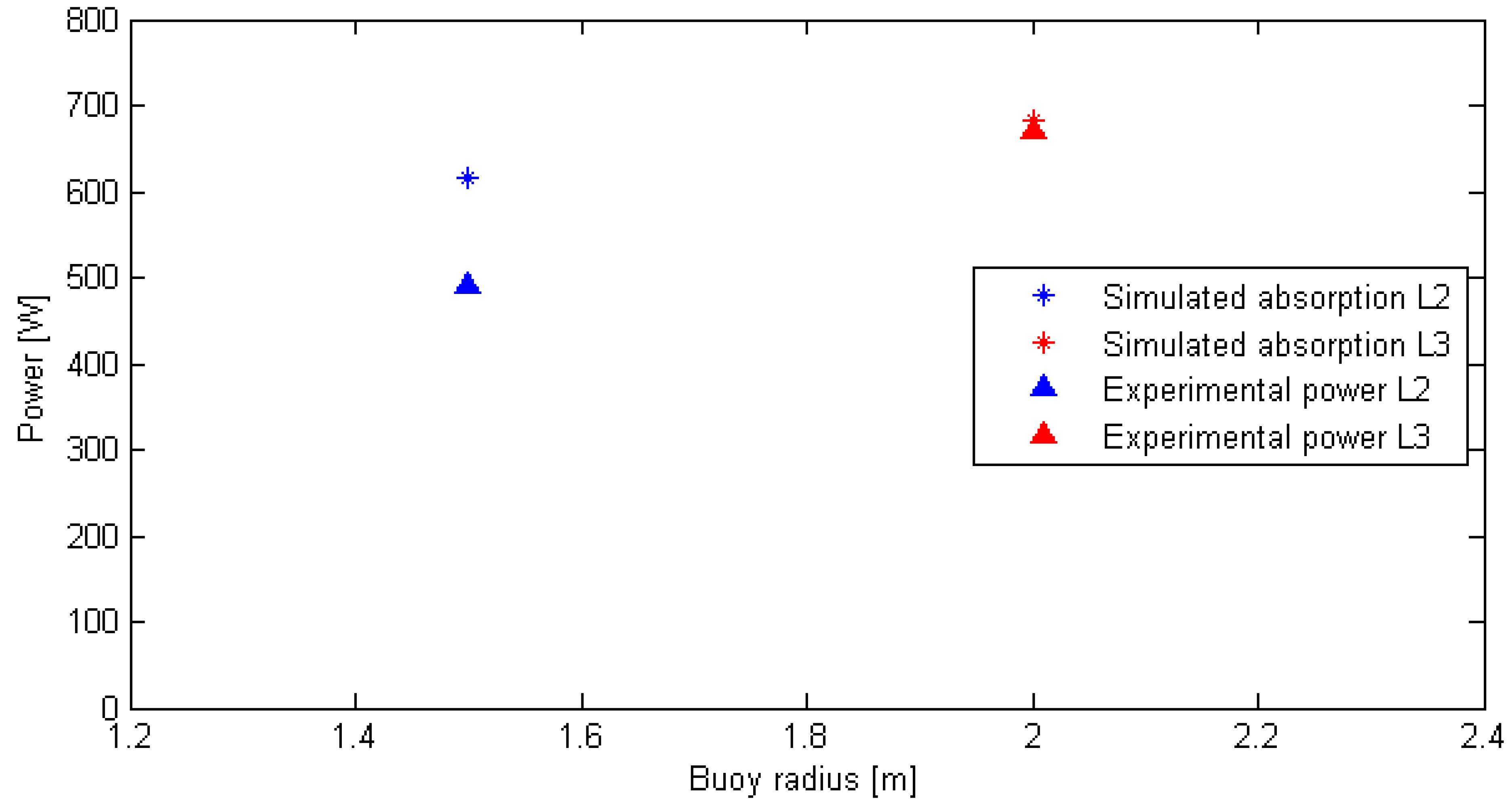
4.3. Comparing with Experiment
| WEC | L2 | L3 | |
|---|---|---|---|
| Translator offset during experiment | +0.3 m | 0 m | |
| Pretension in retraction spring | 11,860 N | 10,000 N | |
| Damping coefficient, experiment | γ | 7400 | 7300 |
| Simulated average velocity | 0.23 m/s | 0.24 m/s | |
| Simulated velocity | 0.083 | 0.093 | |
| Velocity ratio | B | 0.48 | 0.54 |
| Simulated power | 617 W | 682 W | |
| Simulated power · Q | 537 W | 634 W | |
| Experimental average power | 490 W | 670 W | |
| Deviation, simulation to experiment | +9% | −5% |
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Palm, J.; Eskilsson, C.; Paredesy, G.M.; Bergdahl, L. CFD simulation of a moored floating wave energy converter. In Proceedings of the 10th European Wave and Tidal Energy Conference, Aalborg, Denmark, 2–5 September 2013.
- Cummins, W. The impulse response function and ship motions. Schiffstechnik 1962, 9, 101–109. [Google Scholar]
- McIver, M.; McIver, P. Water waves in the time domain. J. Eng. Math. 2011, 70, 111–128. [Google Scholar] [CrossRef]
- Eriksson, M.; Isberg, J.; Leijon, M. Hydrodynamic modeling of a direct drive wave energy converter. Int. J. Eng. Sci. 2005, 43, 1377–1387. [Google Scholar] [CrossRef]
- Engström, J.; Kurupath, V.; Isberg, J.; Leijon, M. A resonant two body system for a point absorbing wave energy converter with direct-driven linear generator. J. Appl. Phys. 2011, 110, 124904:1–124904:8. [Google Scholar] [CrossRef]
- Evans, D.V. A theory for wave-power absorption by oscillating bodies. J. Fluid Mech. 1975, 77(Part 1), 1–25. [Google Scholar] [CrossRef]
- Evans, D.V.; Jeffrey, D.C.; Salter, H.; Taylor, J.R.M. Submerged cylinder wave energy device: Theory and experiment. Appl. Ocean Res. 1979, 1, 3–12. [Google Scholar] [CrossRef]
- Falnes, J. Radiation impedance matrix and optimum power absorption for interacting oscillators in surface waves. Appl. Ocean Res. 1980, 2, 75–80. [Google Scholar] [CrossRef]
- Evans, D.V. Maximum wave-power absorption under motion constraints. Appl. Ocean Res. 1981, 3, 200–204. [Google Scholar] [CrossRef]
- Pizer, D.J. Maximum wave-power absorption of point absorbers under motion constraints. Appl. Ocean Res. 1993, 15, 227–234. [Google Scholar] [CrossRef]
- Falnes, J. A review of wave-energy extraction. Mar. Struct. 2007, 20, 185–201. [Google Scholar] [CrossRef]
- Falcao, A. Wave energy utilization: A review of the technologies. Renew. Sustain. Energy Rev. 2010, 14, 899–918. [Google Scholar] [CrossRef]
- Boström, C.; Leijerskog, E.; Tyrberg, S.; Svensson, O.; Waters, R.; Savin, A.; Bolund, B.; Eriksson, M.; Leijon, M. Experimental results from an offshore wave energy converter. J. Offshore Mech. Arct. Eng. 2010, 132. [Google Scholar] [CrossRef]
- Waters, R.; Rahm, M.; Eriksson, M.; Svensson, O.; Strömstedt, E.; Boström, C.; Sundberg, J.; Leijon, M. Ocean wave energy absorption in response to wave period and amplitude—Offshore experiments on a wave energy converter. IET Renew. Power Gener. 2011, 5, 465–469. [Google Scholar] [CrossRef]
- Waters, R.; Engström, J.; Isberg, J.; Leijon, M. Wave climate off the Swedish west coast. Renew. Energy 2009, 34, 1600–1606. [Google Scholar] [CrossRef]
- Eriksson, M.; Waters, R.; Svensson, O.; Isberg, J.; Leijon, M. Wave power absoption: Experiments in open sea and simulation. J. Appl. Phys. 2007, 102, 084910:1–084910:5. [Google Scholar] [CrossRef]
- Stålberg, M.; Waters, R.; Danielsson, O.; Leijon, M. Influence of generator damping on peak power and variance of power for a direct drive wave energy converter. J. Offshore Mech. Arct. Eng. 2008, 130, 031003:1–031003:4. [Google Scholar] [CrossRef]
- Hagerman, G.; Bedard, R. Guidlines for Preliminary Estimation of Power Production, by Offshore Wave Energy Conversion Devices; EPRI Report. 297213; Electric Power Research Institute: Palo Alto, California, CA, USA, 2003. [Google Scholar]
- Strömstedt, E.; Svensson, O.; Leijon, M. A set-up of 7 laser triangulation sensors and a draw-wire sensor for measuring relative displacementof a piston rod mechanical lead-through transmission in an offshore wave energy converter on the ocean floor. ISRN Renew. Energy 2011, 2012, 746865:1–746865:32. [Google Scholar]
- Mei, C.; Stiassnie, M.; Yue, D. Floating body dynamics. In Theory and Applications of Ocean Surface Waves—Part 1: Linear Aspects; Liu, P.L.-F., Ed.; World Scientific Publishing Co. Pte. Ltd.: Singapore, Singapore, 2005; pp. 337–450. [Google Scholar]
- Tyrberg, S.; Waters, R.; Leijon, M. Wave power absorption as a function of water level and wave height: Theory and experiment. IEEE J. Ocean. Eng. 2010, 35, 558–564. [Google Scholar] [CrossRef]
- Rahm, M.; Svensson, O.; Boström, C.; Waters, R.; Leiojon, M. Experimental results from the operation of aggregated wave energy converters. IET Renew. Power Gener. 2012, 6, 149–160. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sjökvist, L.; Krishna, R.; Rahm, M.; Castellucci, V.; Anders, H.; Leijon, M. On the Optimization of Point Absorber Buoys. J. Mar. Sci. Eng. 2014, 2, 477-492. https://doi.org/10.3390/jmse2020477
Sjökvist L, Krishna R, Rahm M, Castellucci V, Anders H, Leijon M. On the Optimization of Point Absorber Buoys. Journal of Marine Science and Engineering. 2014; 2(2):477-492. https://doi.org/10.3390/jmse2020477
Chicago/Turabian StyleSjökvist, Linnea, Remya Krishna, Magnus Rahm, Valeria Castellucci, Hagnestål Anders, and Mats Leijon. 2014. "On the Optimization of Point Absorber Buoys" Journal of Marine Science and Engineering 2, no. 2: 477-492. https://doi.org/10.3390/jmse2020477




