Sub-Ensemble Coastal Flood Forecasting: A Case Study of Hurricane Sandy
Abstract
:1. Introduction
2. Data
3. Mathematical Background
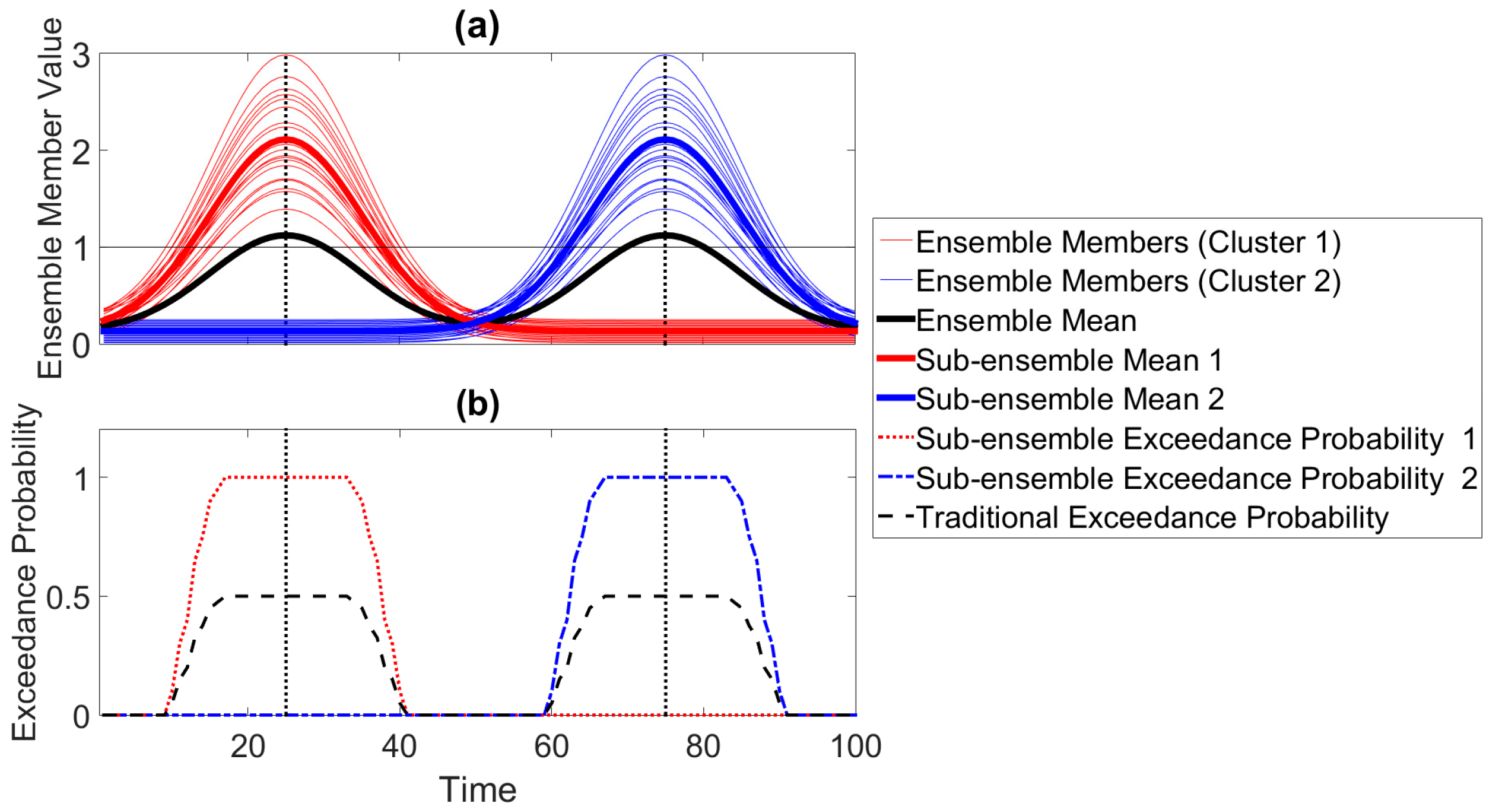
3.1. Sub-Ensemble Forecasting Theory
3.2. Sub-Ensemble Mean
3.3. Probability of Exceedance
4. Cluster Analysis Metrics
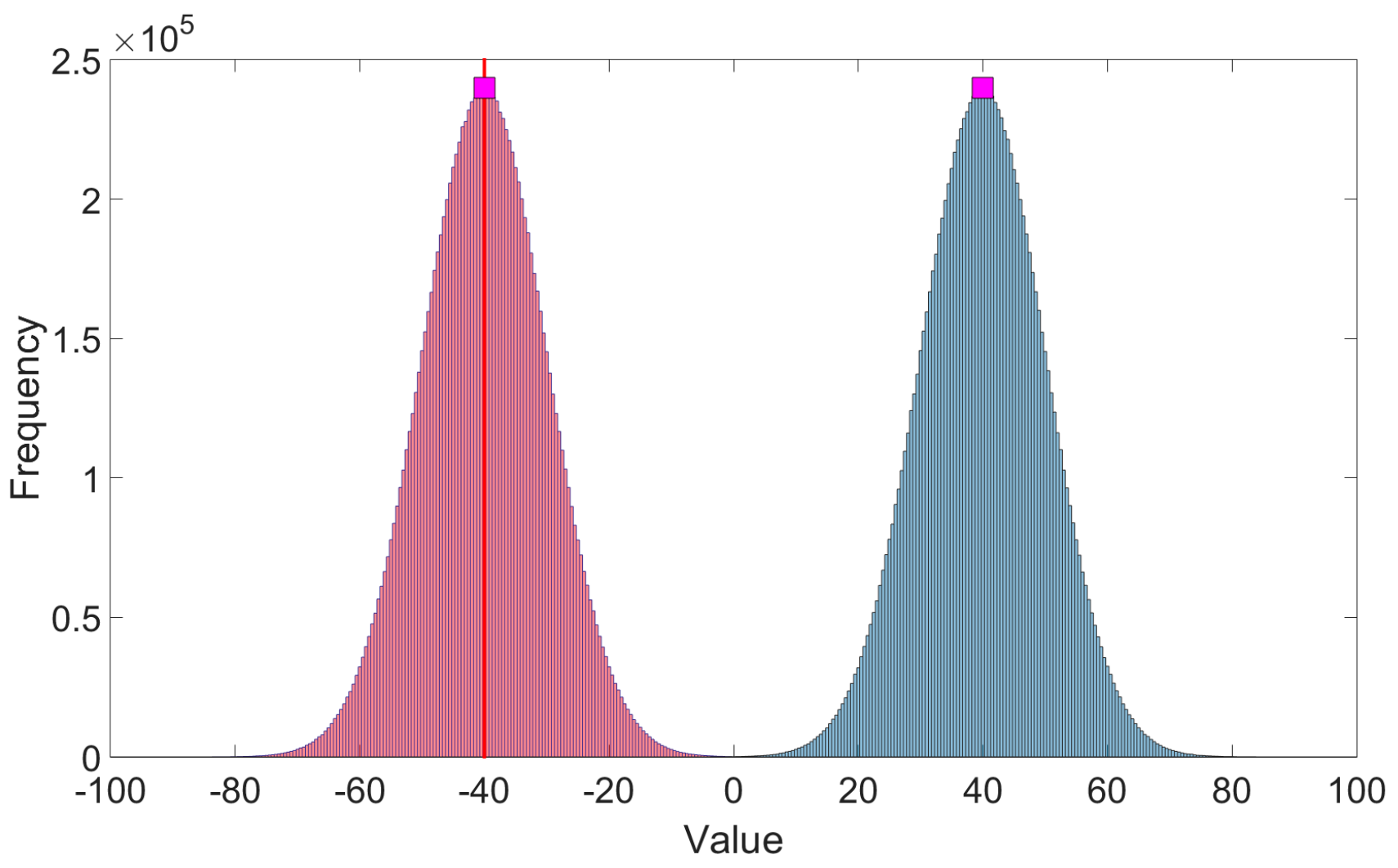
4.1. The Cluster Uncertainty Index
4.2. Cluster Forecast Skill
4.3. Sub-Ensemble Forecast Skill
4.4. Cluster and Sub-Ensemble Probability Estimates
5. Sub-Ensemble Forecasting for Periodic Flows
5.1. Theoretical Background
5.2. Cluster Analysis for Periodic Flows
6. Practical Applications
6.1. Sub-Ensemble Forecast Example
6.2. Probability of Exceedance
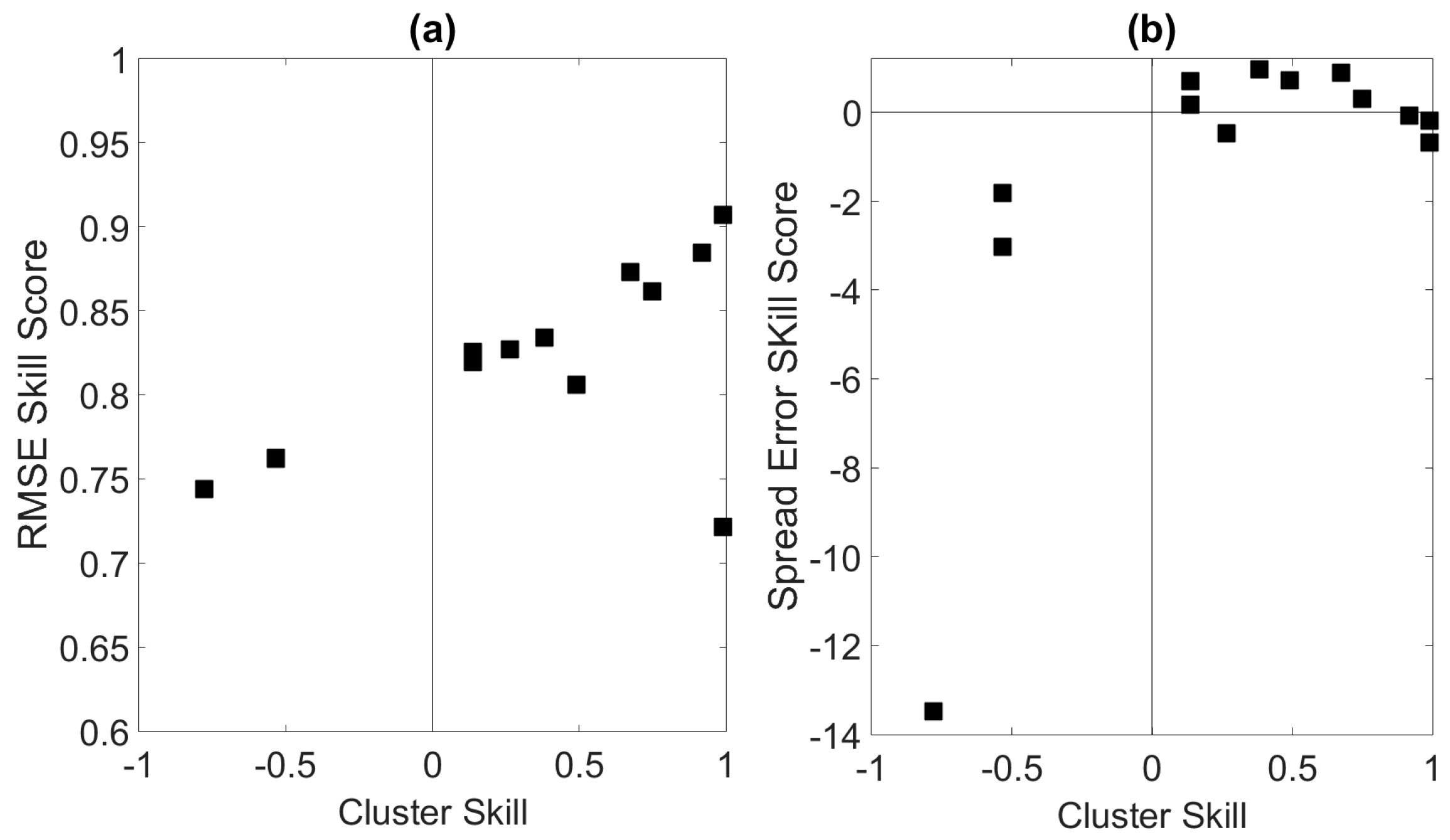
6.3. Cluster Forecast Skill
7. Conclusions and Discussion
Acknowledgments
Conflicts of Interest
References
- Choke, H.L.; Pappenberger, F. Ensemble flood forecasting: A review. J. Hydrol. 2009, 375, 613–626. [Google Scholar]
- Leith, C.E. Theoretical skill of Monte Carlo forecasts. Mon. Weather Rev. 1974, 102, 409–418. [Google Scholar] [CrossRef]
- Molteni, F.; Buizza, R.; Palmer, T.N.; Petroliagis, T. The ECMWF ensemble prediction system: Methodology and validation. Q. J. R. Meteorol. Soc. 1996, 122, 73–119. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences: An Introduction, 1st ed.; Academic Press: Cambridge, MA, USA, 1995; p. 467. [Google Scholar]
- Warner, T.T. Numerical Weather and Climate Prediction; Cambridge University Press: Cambridge, UK, 2011; p. 526. [Google Scholar]
- Buizza, R. Potential forecast skill of ensemble prediction and spread and skill distributions of the ECMWF ensemble prediction system. Mon. Weather Rev. 1997, 125, 99–119. [Google Scholar] [CrossRef]
- Eckel, F.A.; Walters, M.K. Calibrated probabilistic quantitative precipitation forecasts based on the MRF ensemble. Weather Forecast. 1998, 13, 1132–1147. [Google Scholar] [CrossRef]
- Richardson, D.S. Measures of skill and value of ensemble prediction systems, their interrelationship and the effect of ensemble size. Q. J. R. Meteorol. Soc. 2001, 127, 2473–2489. [Google Scholar] [CrossRef]
- Mullen, S.L.; Baumhefner, D.P. The impact of initial condition uncertainty on numerical simulations of larger-scale explosive cyclogenesis. Mon. Weather Rev. 1989, 117, 2800–2821. [Google Scholar] [CrossRef]
- Palmer, T.N. Extended-Range atmospheric prediction and the Lorenz model. Bull. Am. Meteorol. Soc. 1993, 74, 49–65. [Google Scholar] [CrossRef]
- Smith, L.A.; Suckling, E.B.; Thompson, E.L.; Maynard, T.; Du, H. Towards improving the framework for probabilistic forecast evaluation. Clim. Chang. 2015, 132, 31–45. [Google Scholar] [CrossRef] [Green Version]
- Epstein, E.S. A scoring system for probability forecasts of ranked categories. J. Appl. Meteorol. 1969, 8, 985–987. [Google Scholar] [CrossRef]
- Roulston, M.S.; Smith, L.A. Evaluating probabilistic forecasts using information theory. Mon. Weather Rev. 2002, 130, 1653–1660. [Google Scholar] [CrossRef]
- Christensen, H.M.; Moroz, I.M.; Palmer, T.N. Evaluation of ensemble forecast uncertainty using a new proper score: Application to medium-range and seasonal forecasts. Q. J. R. Meteorol. Soc. 2015, 141, 538–549. [Google Scholar] [CrossRef]
- Gilleland, E.; Ahijevych, D.; Brown, B.G.; Casati, B.; Ebert, E.E. Intercomparison of spatial forecast verification methods. Weather Forecast. 2009, 24, 1416–1430. [Google Scholar] [CrossRef]
- Marzban, C.; Sandgathe, S. Cluster analysis for verification of precipitation fields. Weather Forecast. 2006, 21, 824–838. [Google Scholar] [CrossRef]
- Marzban, C.; Sandgathe, S.; Lyons, H. An object-oriented verification of three NWP model formulations via cluster analysis: An objective and a subjective analysis. Mon. Weather Rev. 2008, 136, 3392–3407. [Google Scholar] [CrossRef]
- Marzban, C.; Sandgathe, S.; Lyons, H.; Lederer, N. Three spatial verification techniques: Cluster analysis, variogram, and optical flow. Weather Forecast. 2009, 24, 1457–1471. [Google Scholar] [CrossRef]
- Johnson, A.; Wang, X.; Xue, M.; Kong, F. Hierarchical cluster analysis of a convection-allowing ensemble during the Hazardous Weather Testbed 2009 Spring Experiment. Part II: Season-long ensemble clustering and implication for optimal ensemble design. Mon. Weather Rev. 2011, 139, 3694–3710. [Google Scholar] [CrossRef]
- Yussouf, N.; Stensrud, D.; Lakshmivarahan, S. Cluster analysis of multimodel ensemble data over New England. Mon. Weather Rev. 2004, 132, 2452–2462. [Google Scholar] [CrossRef]
- Flowerdew, J.; Horsburgh, K.; Wilson, C.; Mylne, K. Development and evaluation of an ensemble forecasting system for coastal storm surges. Q. J. R. Meteorol. Soc. 2010, 136, 1444–1456. [Google Scholar] [CrossRef]
- Flowerdew, J.; Mylne, K.; Jones, C.; Titley, H. Extending the forecast range of the UK storm surge ensemble. Q. J. R. Meteorol. Soc. 2012, 139, 184–197. [Google Scholar] [CrossRef]
- Georgas, N.; Blumberg, A.; Herrrington, T.; Wakeman, T.; Saleh, F.; Runnels, D.; Jordi, A.; Ying, K.; Yin, L.; Ramaswamy, V.; et al. The Stevens Flood Advisory System: Operational H3e Flood Forecasts for the Greater New York/New Jersey Metropolitan Region. Int. J. Saf. Secur. Eng. 2016, 6, 648–662. [Google Scholar] [CrossRef]
- Georgas, N.; Yin, L.; Jiang, Y.; Wang, Y.; Howell, P.; Saba, V.; Schulte, J.; Orton, P.; Wen, B. An open-access, multi-decadal, three-dimensional, hydrodynamic hindcast dataset for the Long Island Sound and New York/New Jersey Harbor Estuaries. J. Mar. Sci. Eng. 2016, 4, 48. [Google Scholar] [CrossRef]
- Hamill, T.M.; Scheuerer, M.; Bates, G.T. Analog Probabilistic Precipitation Forecasts Using GEFS Reforecasts and Climatology-Calibrated Precipitation Analyses. Mon. Weather Rev. 2015, 143, 3300–3309. [Google Scholar] [CrossRef]
- Schulte, J.A.; Georgas, N. Theory and Practice of Phase-aware Ensemble Forecasting. Q. J. R. Meteorol. Soc. 2017. in review. [Google Scholar]
- Kalajdzievski, S. An Illustrated Introduction to Topology and Homotopy; Chapman and Hall/CRC: Boca Raton, FL, USA, 2015; p. 485. [Google Scholar]
- Brier, G.W. Verification of forecasts expressed in terms of probability. Mon. Weather Rev. 1950, 78, 1–3. [Google Scholar] [CrossRef]
- Kumar, P.; Foufoula-Georgiou, E. Wavelet analysis for geophysical applications. Rev. Geophys. 1997, 35, 385–412. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Mulligan, G.W.; Cooper, M.C. An Examination of Procedures for Determining the Number of Clusters in a Data Set. Psychometrika 1985, 50, 159–179. [Google Scholar] [CrossRef]
- Calinski, R.B.; Harabasz, J. A Dendrite Method for Cluster Analysis. Commun. Stat. 1985, 3, 1–27. [Google Scholar]
- Tibshirani, R.; Walther, G.; Hastie, T. Estimating the number of clusters in a data set via the gap statistic. J. R. Soc. B 2001, 61, 411–423. [Google Scholar] [CrossRef]
- Kaufman, L.; Rousseeuw, P.J. Finding Groups in Data: An Introduction to Cluster Analysis; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1990; p. 368. [Google Scholar]
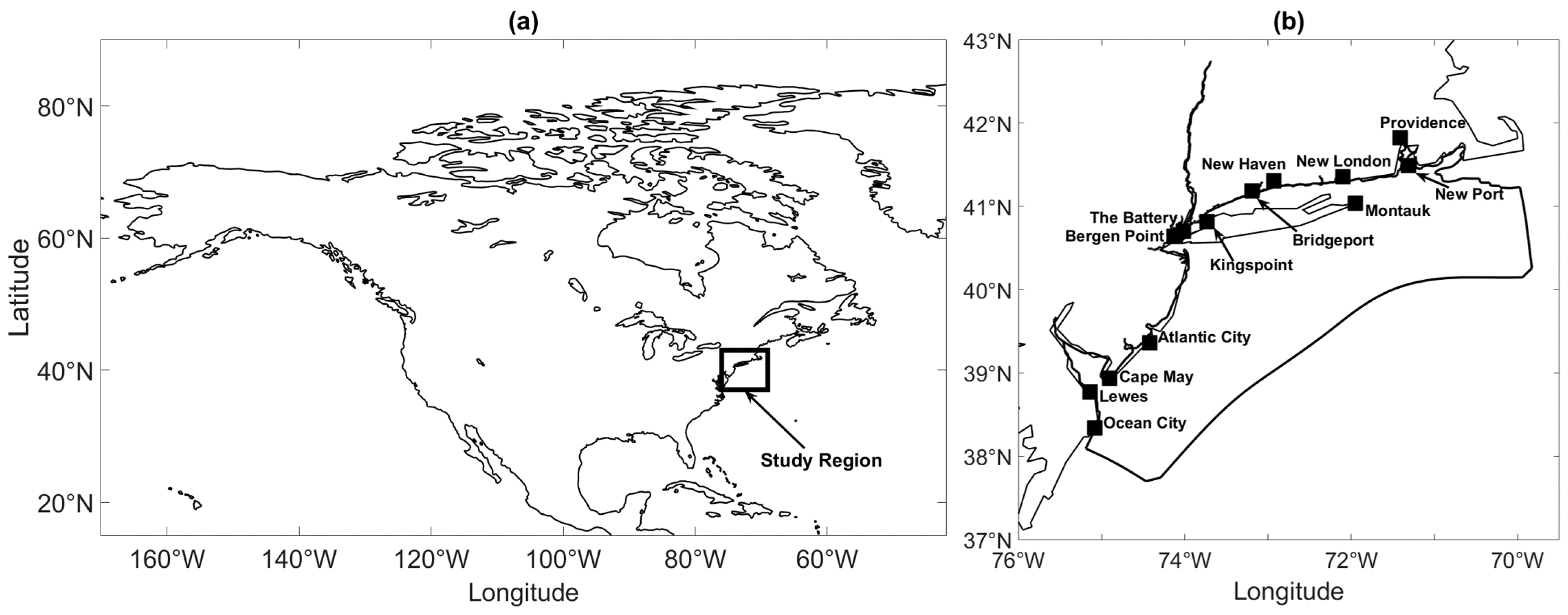
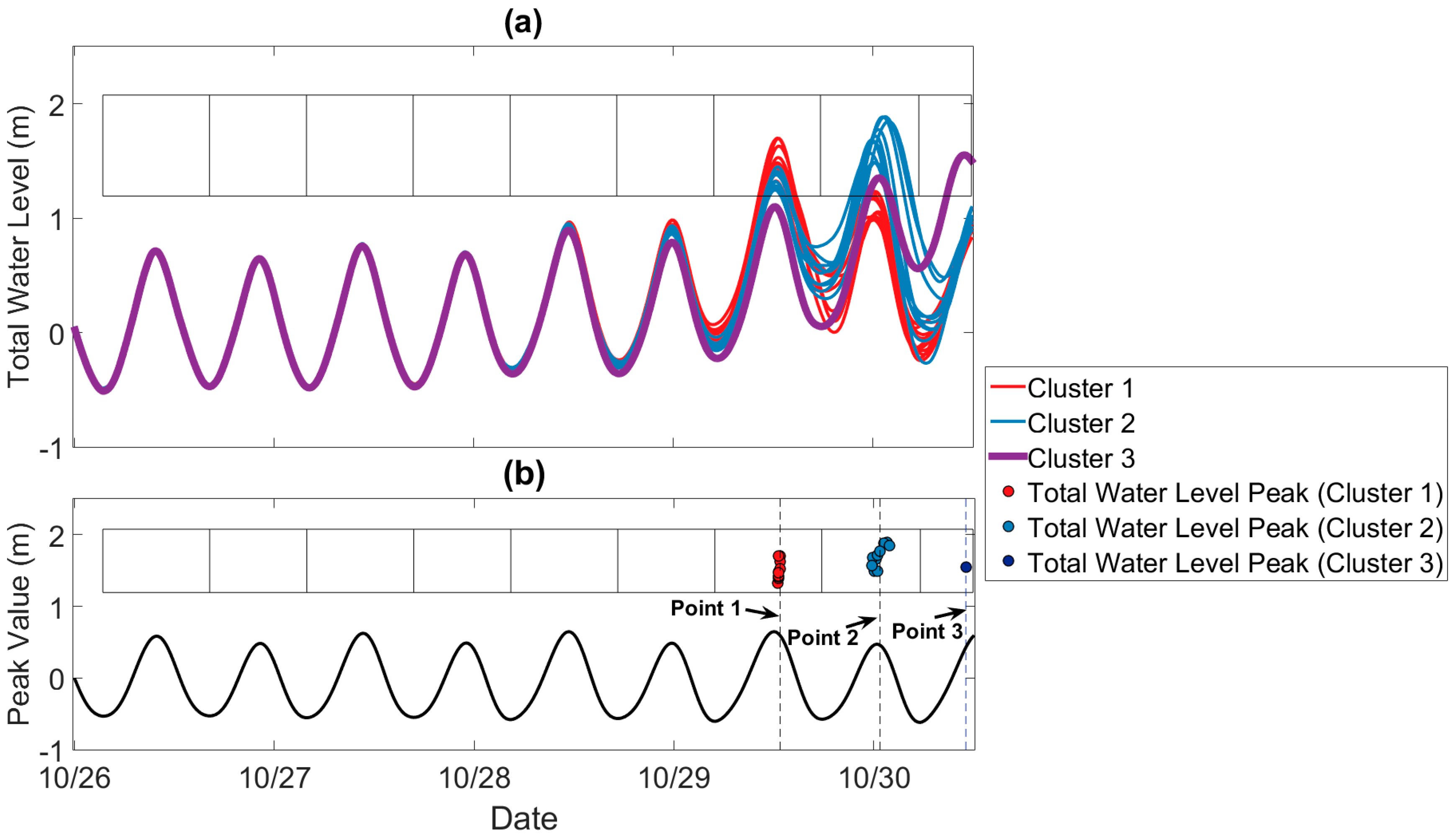
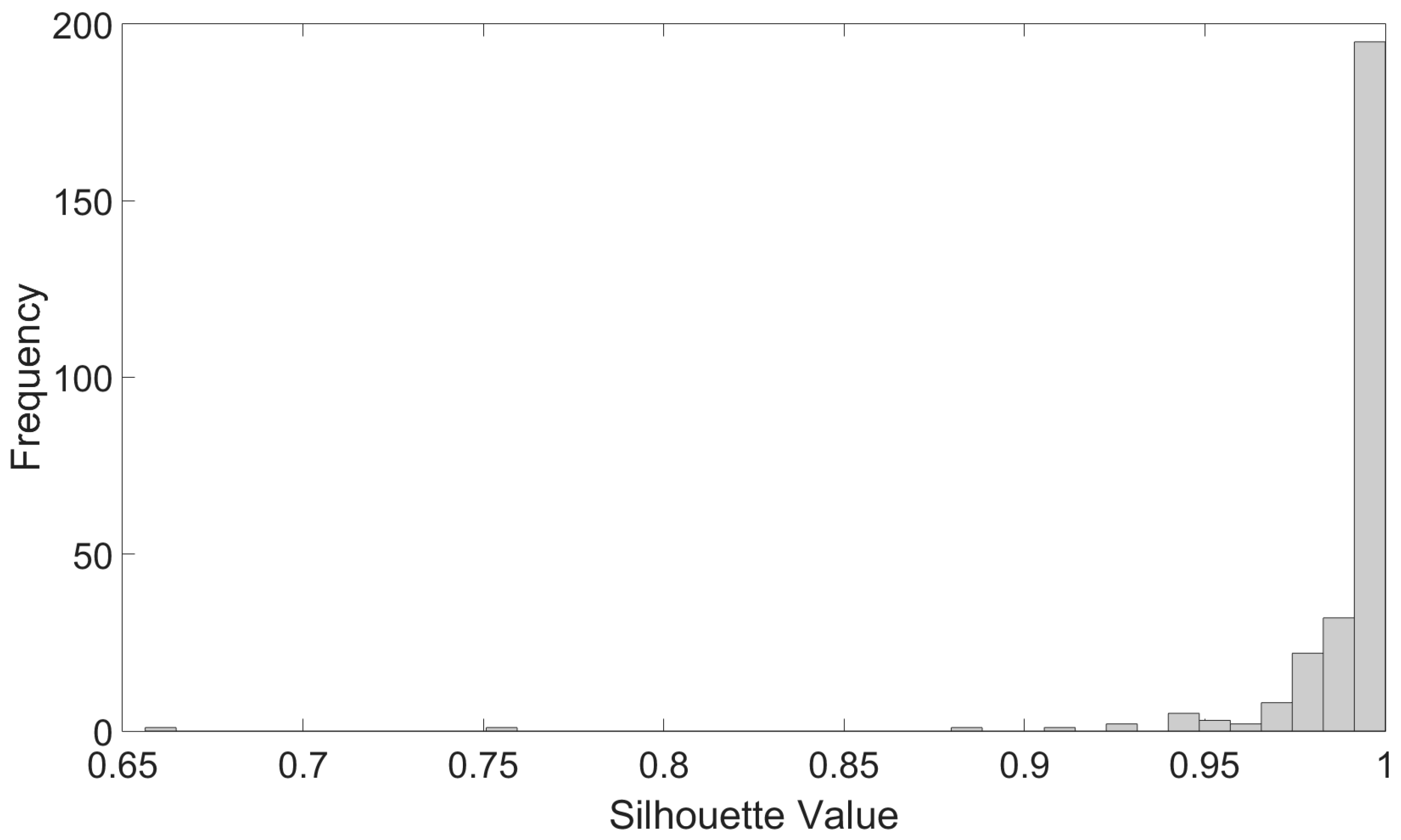
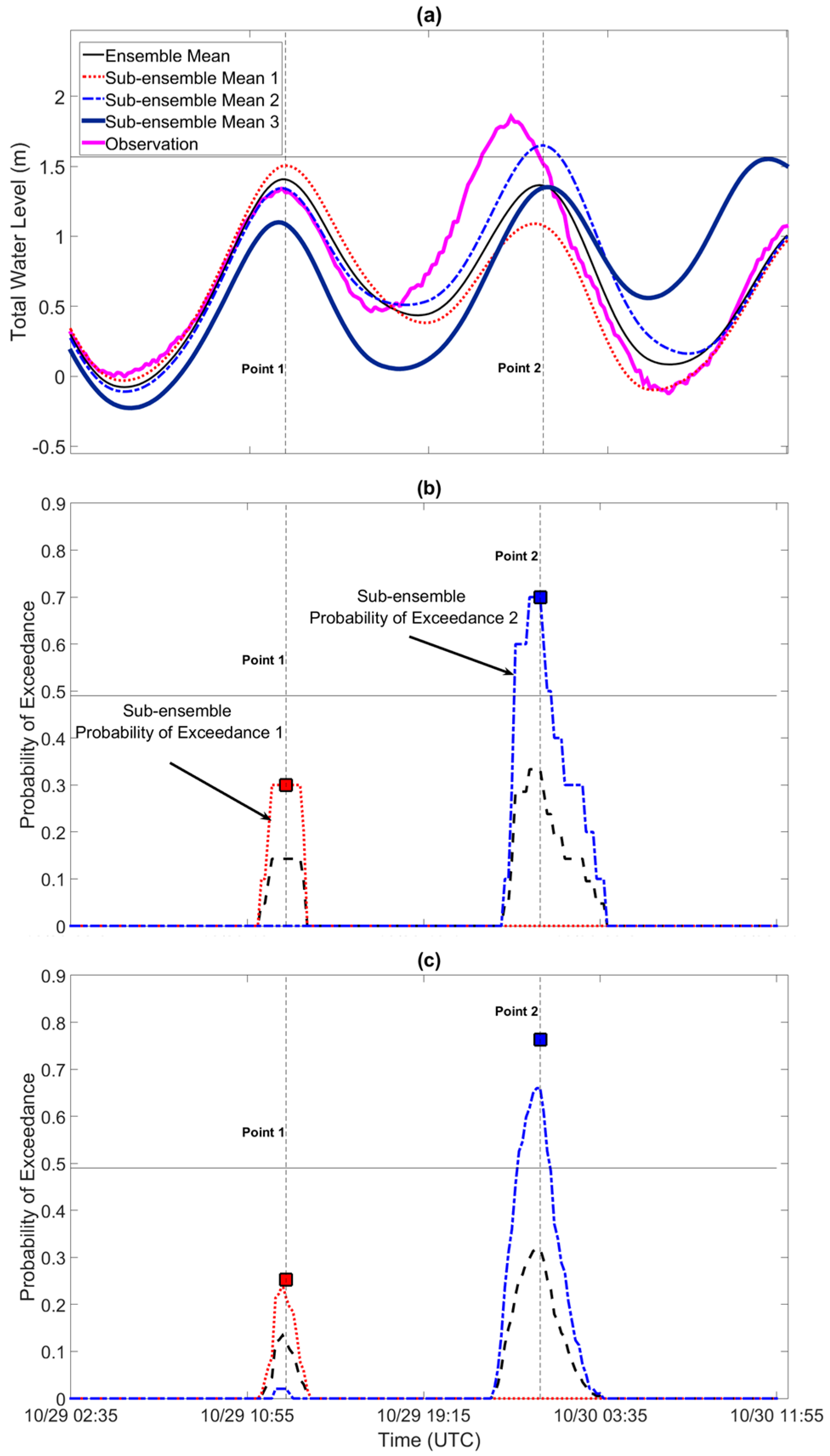
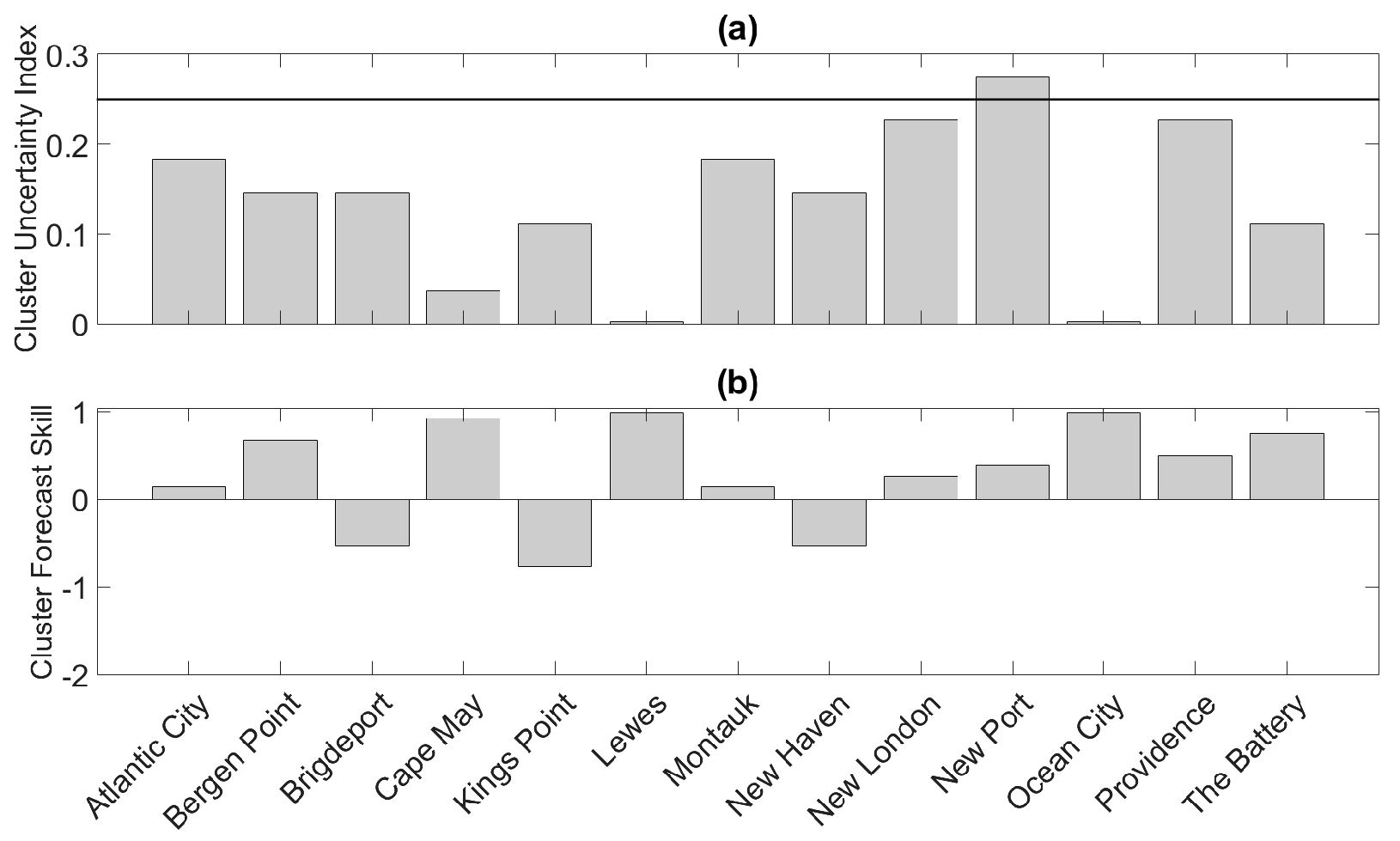
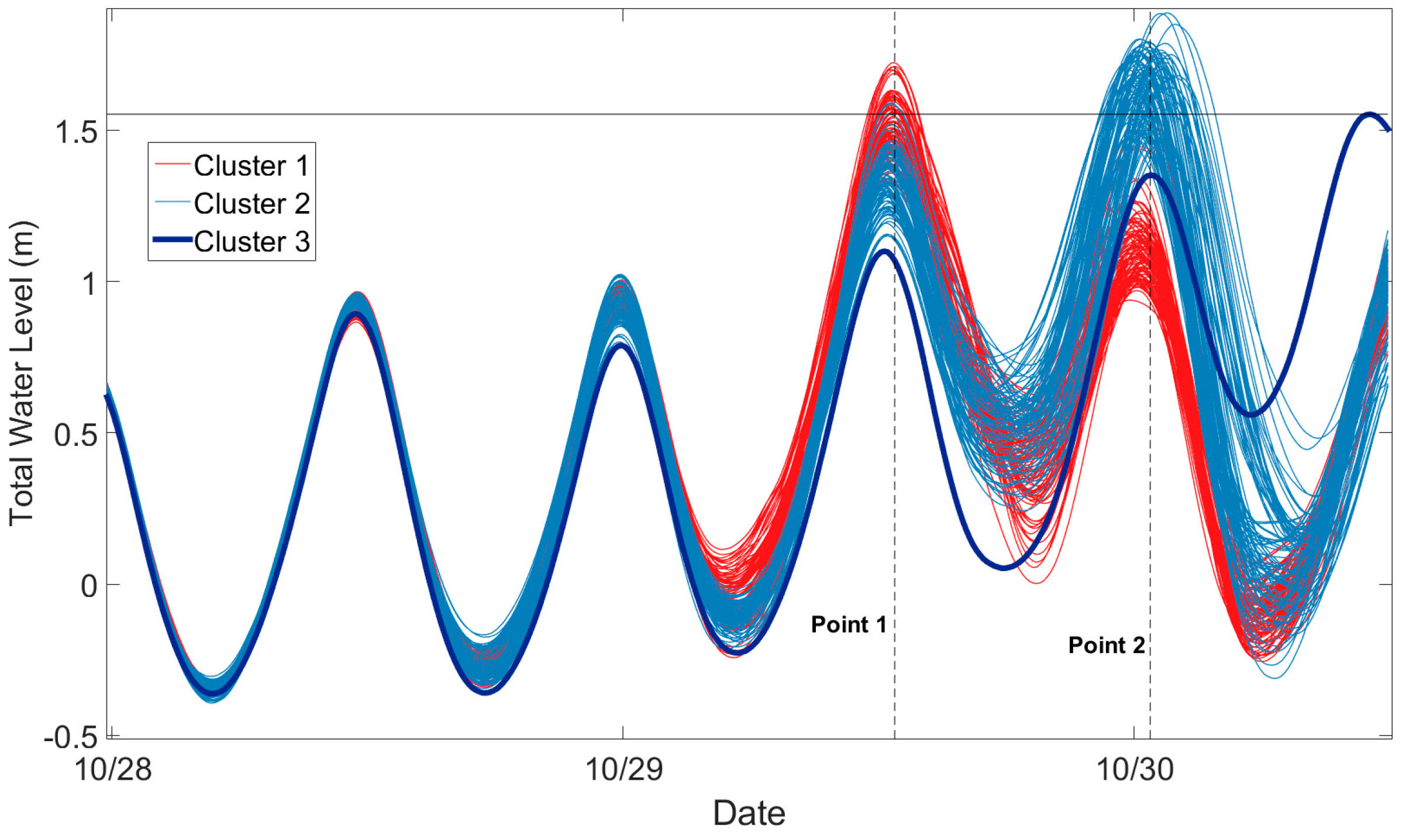
| Station | Point 1 (UTC) | Point 2 (UTC) |
|---|---|---|
| Atlantic City | 10/29/2012 12:25 | 10/29/2012 23:45 |
| Bergen Point | 10/29/2012 13:55 | 10/30/2012 0:35 |
| Bridgeport | 10/29/2012 16:05 | 10/30/2012 3:35 |
| Cape May | 10/29/2012 13:15 | 10/30/2012 1:05 |
| Kings Point | 10/29/2012 16:25 | 10/30/2012 3:55 |
| Lewes | 10/29/2012 1:05 | 10/29/2012 13:25 |
| Montauk | 10/29/2012 13:45 | 10/30/2012 0:45 |
| New Haven | 10/29/2012 16:05 | 10/30/2012 3:35 |
| New London | 10/29/2012 14:25 | 10/30/2012 0:45 |
| New Port | 10/29/2012 12:35 | 10/30/2012 0:25 |
| Ocean City | 10/29/2012 12:55 | 10/29/2012 0:45 |
| Providence | 10/30/2012 0:35 | 10/29/2012 12:55 |
| The Battery | 10/29/2012 13:45 | 10/30/2012 0:35 |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schulte, J.A. Sub-Ensemble Coastal Flood Forecasting: A Case Study of Hurricane Sandy. J. Mar. Sci. Eng. 2017, 5, 59. https://doi.org/10.3390/jmse5040059
Schulte JA. Sub-Ensemble Coastal Flood Forecasting: A Case Study of Hurricane Sandy. Journal of Marine Science and Engineering. 2017; 5(4):59. https://doi.org/10.3390/jmse5040059
Chicago/Turabian StyleSchulte, Justin A. 2017. "Sub-Ensemble Coastal Flood Forecasting: A Case Study of Hurricane Sandy" Journal of Marine Science and Engineering 5, no. 4: 59. https://doi.org/10.3390/jmse5040059




