A Linear Bayesian Updating Model for Probabilistic Spatial Classification
Abstract
:1. Introduction
2. Linear Bayesian Updating
3. Theoretical Foundations of Linear Bayesian Updating
3.1. Parameter Ranges for Linear Bayesian Updating
3.2. Interpreting Parameters as Regression Coefficients for Linear Bayesian Updating
3.3. Invertible Conditions of Linear Bayesian Updating
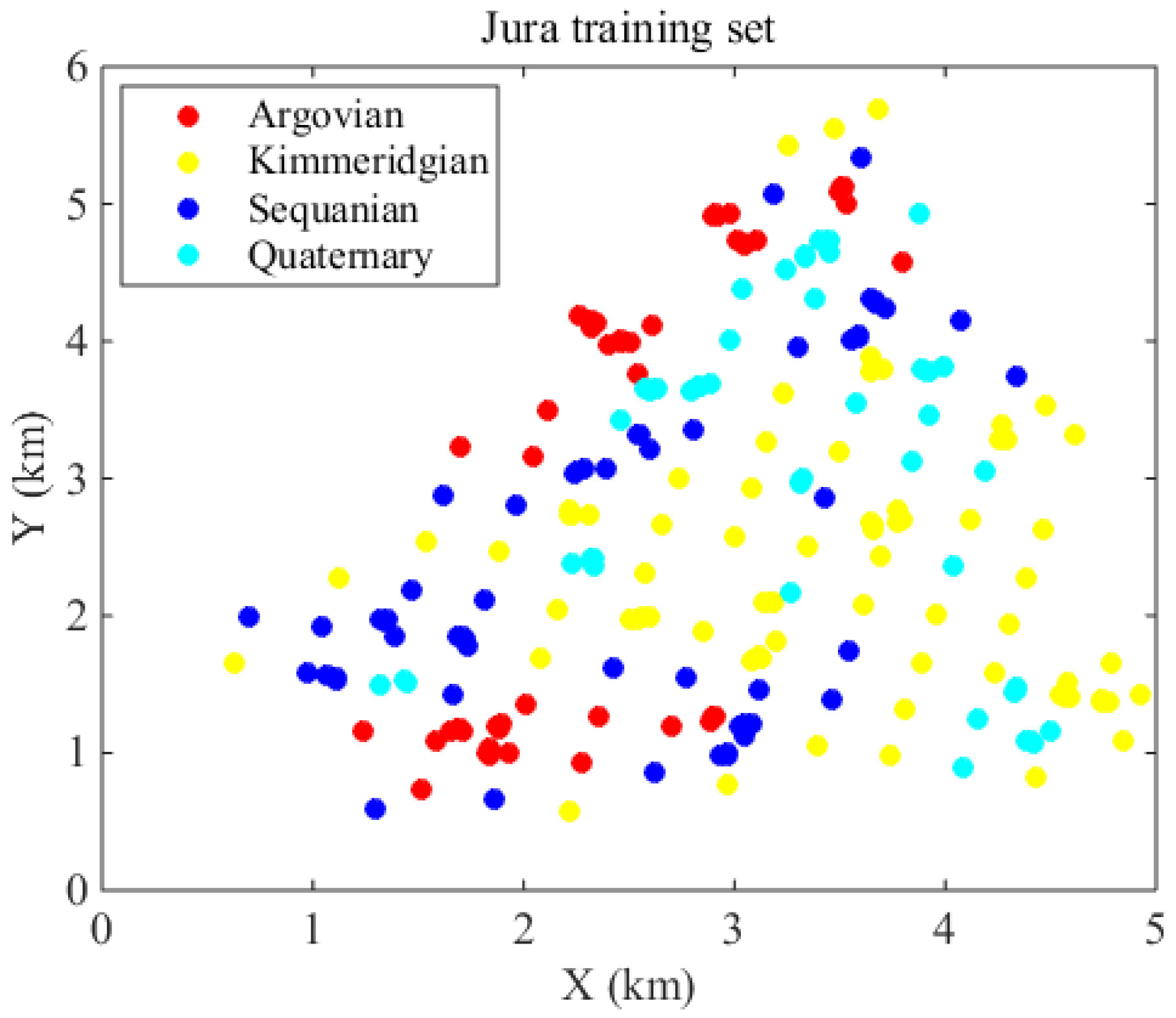
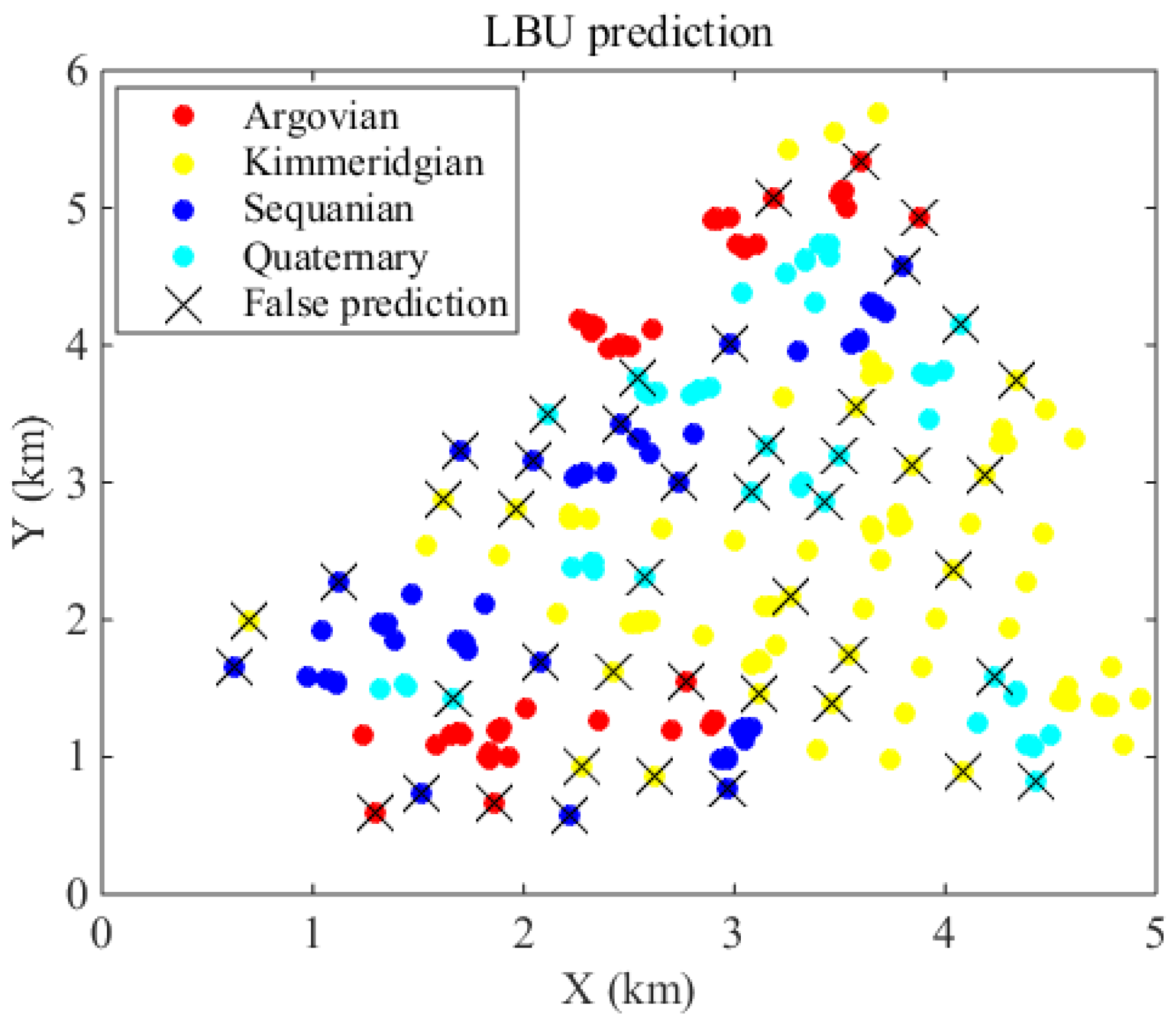
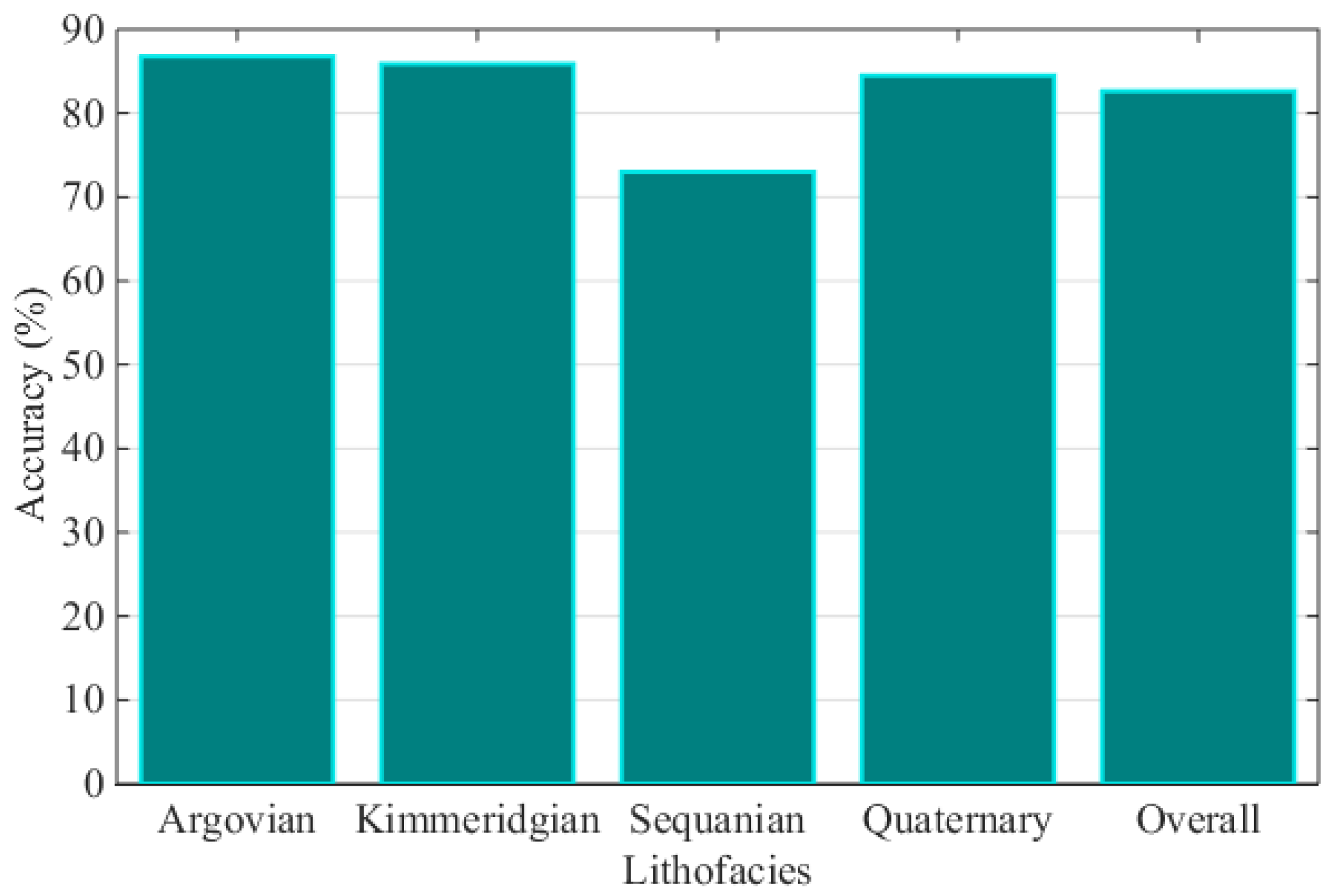
4. Case Study
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cao, G.; Kyriakidis, P.C.; Goodchild, M.F. Combining spatial transition probabilities for stochastic simulation of categorical fields. Int. J. Geogr. Inf. Sci. 2011, 25, 1773–1791. [Google Scholar] [CrossRef]
- Ricotta, C.; Carranza, M.L. Measuring scale-dependent landscape structure with Rao’s quadratic diversity. ISPRS Int. J. Geo-Inf. 2013, 2, 405–412. [Google Scholar] [CrossRef]
- Huang, X.; Li, J.; Liang, Y.; Wang, Z.; Guo, J.; Jiao, P. Spatial hidden Markov chain models for estimation of petroleum reservoir categorical variables. J. Petrol. Explor. Prod. Technol. 2016. [Google Scholar] [CrossRef]
- Li, W. Markov chain random fields for estimation of categorical variables. Math. Geol. 2007, 39, 321–335. [Google Scholar] [CrossRef]
- Li, W. A fixed-path Markov chain algorithm for conditional simulation of discrete spatial variables. Math. Geol. 2007, 39, 159–176. [Google Scholar] [CrossRef]
- Cao, G.; Kyriakidis, P.C.; Goodchild, M.F. A multinomial logistic mixed model for the prediction of categorical spatial data. Int. J. Geogr. Inf. Sci. 2011, 25, 2071–2086. [Google Scholar] [CrossRef]
- Krishnan, S. The tau model for data redundancy and information combination in earth sciences: Theory and application. Math. Geosci. 2008, 40, 705–727. [Google Scholar] [CrossRef]
- Polyakova, E.I.; Journel, A.G. The Nu expression for probabilistic data integration. Math. Geol. 2007, 39, 715–733. [Google Scholar] [CrossRef]
- Allard, D.; Comunian, A.; Renard, P. Probability aggregation methods in geoscience. Math. Geosci. 2012, 44, 545–581. [Google Scholar] [CrossRef]
- Genest, C.; Schervish, M.J. Modeling expert judgments for Bayesian updating. Ann. Stat. 1985, 13, 1198–1212. [Google Scholar] [CrossRef]
- Huang, X.; Wang, Z.; Guo, J. Prediction of categorical spatial data via Bayesian updating. Int. J. Geogr. Inf. Sci. 2016, 30, 1426–1449. [Google Scholar] [CrossRef]
- Li, W. Transiogram: A spatial relationship measure for categorical data. Int. J. Geogr. Inf. Sci. 2006, 20, 693–699. [Google Scholar]
- Stone, M. The opinion pool. Ann. Math. Stat. 1961, 32, 1339–1342. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
| Transition Probability | Mean | Median | Maximum | Minimum | Standard Deviation |
|---|---|---|---|---|---|
| 0.270 | 0.201 | 1.000 | 0.000 | 0.250 | |
| 0.290 | 0.292 | 0.632 | 0.000 | 0.173 | |
| 0.254 | 0.239 | 0.769 | 0.000 | 0.140 | |
| 0.186 | 0.193 | 0.436 | 0.000 | 0.123 | |
| 0.227 | 0.239 | 0.563 | 0.000 | 0.134 | |
| 0.332 | 0.282 | 1.000 | 0.091 | 0.198 | |
| 0.254 | 0.256 | 0.436 | 0.000 | 0.090 | |
| 0.187 | 0.192 | 0.387 | 0.000 | 0.088 | |
| 0.220 | 0.200 | 0.636 | 0.000 | 0.141 | |
| 0.313 | 0.309 | 1.000 | 0.000 | 0.155 | |
| 0.294 | 0.262 | 1.000 | 0.000 | 0.203 | |
| 0.173 | 0.185 | 0.469 | 0.000 | 0.119 | |
| 0.219 | 0.182 | 0.720 | 0.000 | 0.154 | |
| 0.312 | 0.318 | 0.562 | 0.000 | 0.142 | |
| 0.256 | 0.238 | 0.586 | 0.000 | 0.123 | |
| 0.213 | 0.184 | 1.000 | 0.000 | 0.208 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Wang, Z. A Linear Bayesian Updating Model for Probabilistic Spatial Classification. Challenges 2016, 7, 21. https://doi.org/10.3390/challe7020021
Huang X, Wang Z. A Linear Bayesian Updating Model for Probabilistic Spatial Classification. Challenges. 2016; 7(2):21. https://doi.org/10.3390/challe7020021
Chicago/Turabian StyleHuang, Xiang, and Zhizhong Wang. 2016. "A Linear Bayesian Updating Model for Probabilistic Spatial Classification" Challenges 7, no. 2: 21. https://doi.org/10.3390/challe7020021





